九年级数学下册5.3用待定系数法确定二次函数表达式课件新版苏科版
九年级数学下册2.3.2确定二次函数的表达式课件1新版北师大版

【例题】
【例2】已知一个二次函数的图象过(-1,10),(1,4),(2,7)三 点,求这个函数的表达式.
解析: 设所求的二次函数为y=ax2+bx+c,
由条件得:
a-b+c=10, a+b+c=4, 解方程组得: 4a+2b+c=7,
a=2, b=-3, c=5
因此,所求二次函数的表达式是
y=2x2-3x+5.
∴所求抛物线的表达式为
C
O
B
x
y
1 2 2 x x 1. 3 3
【议一议】
一个二次函数的图像经过A(0,-1),B(1, 2),C(2,1)三点,你能确定这个二次函 数的表达式吗?你有几种方法?与同伴进行 交流.
【议一议】
解析(一)设该抛物线的表达式为y=ax2+bx+c, 根据题意,得
3.(潼南·中考)如图,在平面直角坐标系中,四边形OABC是菱形, 点C的坐标为(4,0),∠AOC= 60°,垂直于x轴的直线l从y轴出发, 沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC 的两边分别交于点M,N(点M在点N的上方),若△OMN 的面积为S,直线l的运动时间为t 秒(0≤t≤4),则 能大致反映S与t的函数关系的图象是(
ห้องสมุดไป่ตู้
1.(衢州·中考)下列四个函数图象中,当x>0时,
y随x的增大而增大的是(
)
C
2.(莆田·中考)某同学用描点法画y=ax2+bx+c(a≠0)的图象时,列出
如下表格:
x y 0 3 1 0 2 2 3 0 4 3
经检查,发现只有一处数据计算错误,请你写出这个二次函数的表达 式 . y=x24x+3
5.3 用待定系数法确定二次函数表达式 课件

解:由二次函数y=ax²
+bx+c的图像经过点(-3,6)、(-2,-1)和(0,-3),
得
= (-)² − + ,
൞− = (-)² − + ,
− = ,
= .
解得 ቐ = .
= −.
所求这个二次函数的表达式为y=2x2+3x-3.
抛物线的顶点式
y=a(x+h)2+k(a≠0)
归纳总结
你能总结出用顶点式确定二次函数表达式的一般步骤吗?
步骤:
1.设:
(表达式)
2.代:
(坐标代入)
3.解:
方程(组)
4.还原:
(写表达式)
①设函数表达式为y=a(x+h)2+k(a≠0);
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
5.如图,平面直角坐标系中,函数图像的表达式应是_______.
y
5
4
3
2
1
O
-4 -3 -2 -13-1
1 2 x
当堂检测
6.已知二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x
…
0
1
2
3
4
5
…
y
…
3
0
-1
0
m
8
…
(1)可求得m的值为_____;
3
y=x2-4x+3
(2)这个二次函数的表达式为______________.
解:把x=2,y=8代入y=ax²,得
8=2²×a
解得a=2.
所求这个二次函数的表达式为y=2x2.
2020最新苏科版九年级数学下册(全套)精品课件

第5章 二次函数
2020最新苏科版九年级数学下册( 全套)精品课件
5.2 二次函数的图象和性质
2020最新苏科版九年级数学下册( 全套)精品课件
5.3 用待定系数法确定二次函数 的表达式
2020最新苏科版九年级数学下册( 全套)精品课件
5.4 二次函数与一元二次方程
2020最新苏科版九年级数学下册( 全套)精品课件
2020最新苏科版九年级数学下册( 全套)精品课件目录
0002页 0064页 0095页 0149页 0181页 0203页 0235页 0273页 0311页 0328页 0355页 0368页 0370页 0385页
第5章 二次函数 5.3 用待定系数法确定二次函数的表达式 5.5 用二次函数解决问题 6.1 图上距离与实际距离 6.3 相似图形 6.5 相似三角形的性质 6.7用相似三角形解决问题 7.1 正切 7.3 特殊角的三角函数 7.5 解直角三角形 第8章 统计和概率的简单应用 8.2 货比三家 8.4 抽签方法合理吗 8.6 收取多少保险费合理
初三年级奥数知识点:用待定系数法确定二次函数表达式

初三年级奥数知识点:用待定系数法确定二次函数表达式待定系数法仅仅一种方法,是一套固定程序,并不是什么公式。
就比如说二次函数,有一种一般表达式y=ax2+bx+c(a≠0),那么a、b、c叫做系数,它们未知,有待确定所以叫“待定系数法”。
待定系数法就是要想办法找出这个二次函数过的三个已知点(x1,y1)(x2,y2)(x3,y3)(x1、x2、x3、y1、y2、y3都是已知数),把它们代入表达式ax12+by1+c=0ax22+by2+c=0ax32+by3+c=0解这三个方程能够求出a、b、c就算出了二次函数表达式。
有时候也不一定非要把这三个数都求出来,仅仅要它们之间的某些关系。
比如x=1代入可得y=a+b+c,也就是说如果图上画了横坐标为1的点就能够估算a+b+c的范围,如果图上这个点纵坐标大于0就能够知道a+b+c>0,如果小于零则能够知道a+b+c<0,等于零则能够知道a+b+c=0。
同样,画了一个横坐标是-1的点则代入y=a-b+c,横坐标为-1的点纵坐标就是a-b+c,也能够判断。
还比如与x轴交点有两个不同的则b2-4ac>0,只有一个则b2-4ac=0,没有则b2-4ac<0。
还有比如与y轴交点纵坐标就是c,等等。
另外二次函数还有两种形式,是两根式y=a(x-x1)(x-x2),x1、x2分别是一元二次方程y=0的两个根,这时候a是系数未知,只要再找到一个在图像上的点代入坐标就能够求出a。
还有顶点式y=a(x-h)2+k,(h,k)是顶点坐标(或者最低点),a是待定的系数,这时候还要知道图象上的一个点带入坐标算出a。
总结一下就是三种形式,必须知道三个普通点的坐标或者一个顶点、一个普通点的坐标就能够通过待定系数法确定二次函数表达式。
课后练习当运动中的汽车撞到物体时,汽车所受到的损坏水准能够用“撞击影响”来衡量.某型汽车的撞击影响能够用公式I=2v 2来表示,其中v(千米/分)表示汽车的速度.① 列表表示I与v的关系;② 当汽车的速度扩大为原来的2倍时,撞击影响扩大为原来的多少倍 ?答案:①略②4倍。
下册第二章第8课用待定系数法求二次函数表达式-北师大版九年级数学全一册课件

13. 如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3,
那么c=( C )
A. 8
B. 14
C. 8或14
D. -8或-14
二级能力提升练
14. 抛物线的顶点为(1,-4),与y轴交于点(0,
-3),求该抛物线的函数表达式.
解:设抛物线的表达式为y=a(x-1)2-4. 将(0,-3)代入y=a(x-1)2-4, 得-3=a(0-1)2-4. 解得a=1. 所以抛物线的表达式为y=(x-1)2-4=x2-2x-3.
D.
-4
D.
与y=2(x-1)2+3形状相同的抛物线的函数表达式为( )
(例3)已知二次函数图象与x轴的两个交点坐标(-3,0),(2,0),且与y轴的交点坐标为(0,-6),求这个二次函数的解析式.
知识点2 顶点式法求二次函数的表达式
5. (例2)求顶点为M(-2,1),且图象经过原点的
二次函数函数表达式. ∴该二次函数表达式为y=(x-1)2-4=x2-2x-3.
设解析式为y=a(x+3)·(x-1),由图可得(0,3)是抛物线上的一点,把(0,3)代入解析式得3=-3a. 把x=-2代入,得y=5.
(1)求抛物线的函数表达式;
知识点2 顶点式法求二次函数的表达式
∴设函数表达式为y=a(x-1)2-4.
解得b=-4,c=-1.
-4
D.
二次函数的图象经过点(4,-3),且当x=3时,有最大值-1,求该二次函数的表达式.
所以抛物线的顶点坐标为(-2,4).
设解析式为y=a(x+3)·(x-1),由图可得(0,3)是抛物线上的一点,把(0,3)代入解析式得3=-3a.
用待定系数法确定二次函数解析式

二、求二次函数的解析式 (1)关键是求出待定系数的值. (2)设解析式的形式:解(1)∵图象顶点为(1,-6),
∴设其解析式为 y=a(x-1)2-6.
∵图象经过点(2,-8),
∴-8=a(2-1)2-6.∴a=-2.
∴函数解析式为 y=-2(x-1)2-6.
例3拓展应用:抛物线 y=ax2+bx+c经过A(-2,-4),
O(0,0),B(2,0)三点 (1)求抛物线 y=ax2+bx+c的解析式。 (2)若点M是该抛物线对称轴上的一点,求AM+OM的 最小值。 y
-2
O。 B 。 x
。 M 。
A。
-4
x=1
。 A1 (4,-4)
【变式训练】
1.二次函数y x 2 bx c的图象的最低点为( - 1,3),
此函数解析式 _____________ 2.抛物线 y=-x2+bx+c 的图象如图 所示, 求此抛物线的解析式。 3.已知二次函数 y=ax2+bx+c 中的 x,y 满足下表:
当已知抛物线上三个点时,设一般式
例1 二次函数的图象经过点A(1,3) ,B(0,3) ,C(-1,1)三点 求此函数的解析式;
解:设所求函数关系式为 y=ax2+bx+c,
∵图象经过点 A(1,3), B(0,3), C(-1,1),
c=3, ∴a+b+c=3, a-b+c=1. a=-1, 解得b=1, c=3.
北师大版九年级数学下册确定二次函数的表达式课件(第1、2课时20张)

顶点式 = ( − ) 能使问题简化。
教学过程
新
知
新
授
做一做
类型三 已知抛物线与轴交点的坐标,求二次函数的表达式
例3.已知二次函数的图象与 轴交于点M(-2,0)、N(3,
-0),且抛物线经过P(2,4),求这个二次函数的表达式.
解:设函数的表达式为 = ( + )( − )
知
新
答一答
1.二次函数的达式有几种情势?
一般式: = + + (a≠0)
顶点式: = ( − ) + (a≠0)
交点式: = ( − )( − )(a≠0)
2.已知函数 = − − ,函数的开口方向 向上 ,
对称轴是直线 =1 ,顶点坐标是 (1,-7)
除了以上四种类型外,还有一些特殊方法。
对二次函数 = + + .
抛物线与轴交点(0,c).
当 = , = 时,抛物线顶点在原点,以轴为对称轴.
当 = 时,抛物线顶点(0,c),以轴为对称轴.
当 = 时,抛物线必过原点.
当 − = 时,抛物线顶点在轴上.
= −
所以,所求二次函数表达式为 = −
教学过程
方
法
总
结
记一记
方法总结:所求二次函数表达式有两个
待定系数时,需要两个独立条件或两个
点的坐标。
教学过程
新
知
新
授
做一做
类型二
已知抛物线顶点的坐标,求二次函数的表达式
例2.已知二次函数的图象以M(-2,3)为顶点,且经过点
N(-1,-3),求这个二次函数的表达式.
苏科版九年级数学下册5-3 用待定系数法确定二次函数表达式 同步课时提优训练【含答案】
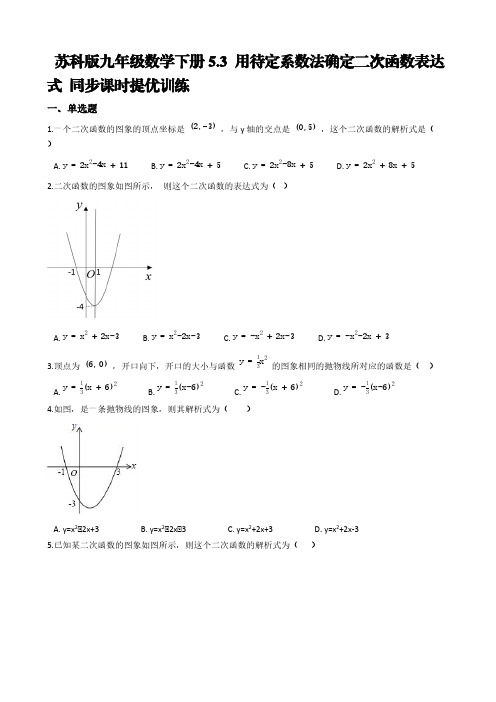
苏科版九年级数学下册5.3 用待定系数法确定二次函数表达式 同步课时提优训练一、单选题1.一个二次函数的图象的顶点坐标是 ,与y 轴的交点是 ,这个二次函数的解析式是( (2,−3)(0,5))A. B. C. D. y =2x 2−4x +11y =2x 2−4x +5y =2x 2−8x +5y =2x 2+8x +52.二次函数的图象如图所示, 则这个二次函数的表达式为( )A. B. C. D. y =x 2+2x −3y =x 2−2x −3y =−x 2+2x −3y =−x 2−2x +33.顶点为 ,开口向下,开口的大小与函数 的图象相同的抛物线所对应的函数是( ) (6, 0)y =13x 2A.B. C. D.y =13(x +6)2y =13(x −6)2y =−13(x +6)2y =−13(x −6)24.如图,是一条抛物线的图象,则其解析式为( )A. y=x 2﹣2x+3B. y=x 2﹣2x﹣3C. y=x 2+2x+3D. y=x 2+2x-35.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )A. B. C. D. y =2(x +1)2+8y =18(x +1)2−8y =29(x −1)2+8y =2(x −1)2−86.若抛物线经过 三点,则此抛物线的表达式为( )(0,1),(−1,0),(1,0)A. B. C. D. y =−x 2+1y =−x 2−1y =x 2+1y =x 2−17.2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作.若将垫球后排球的运动路线近似的看作抛物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点A )离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点B )越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点C )距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )A. y =﹣B. y =﹣ 1475x 2−815x+521475x2+815x +52C. y =D. y = 1475x 2−815x +521475x 2+815x +52二、填空题8.写出一个图象开口向上,顶点在x 轴上的二次函数的解析式________.9.抛物线 与 轴的两个交点坐标分别为 , ,其形状及开口方向与抛y =ax 2+bx +c x (−1,0)(3,0)物线 相同,则 的函数解析式为________.y =−2x 2y =ax 2+bx +c 10.如果一个二次函数图象开口向下,对称轴为 ,则该二次函数表达式可以为________.(任意写x =1出一个符合条件的即可)11.二次函数y =ax²+bx +c 图象上部分点的横坐标x ,纵坐标y 的对应值如下表: x ...﹣2﹣1012...m ...y 04664…﹣6…则这个二次函数的对称轴为直线x =________,m =________(m >0).12.如图,经过原点的抛物线是二次函数 的图象,那么a 的值是________.y =ax 2−3x +a +1AB=4D(0,8)C x 13.如图,平行四边形ABCD中,,点的坐标是,以点为顶点的抛物线经过轴上的点A,B,则此抛物线的解析式为________.三、解答题14.一个二次函数的图象经过A(0,0),B(1,9),C(-1,-1),求这个二次函数的解析式.(1,−3)P(2,0)15.已知二次函数的图象的顶点为,且过点,求这个二次函数的解析式.16.已知二次函数y=﹣2x2+bx+c的图象经过点A(0,4)和B(1,﹣2).求此二次函数的解析式.y=ax2+bx+c(a≠0)17.抛物线上部分点的横坐标x,纵坐标y的对应值如下表:x…-2-1012…y…04664…求这个二次函数的表达式,并利用配方法求出此抛物线的对称轴、顶点坐标四、综合题y=2x2+mx18.如图,已知经过原点的抛物线与x轴交于另一点A(2,0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-4
A
-2
B
2
4
课堂小结
通过本堂课的学习, 说说你的收获和体会!
二次函数常用的几种解析式
已知三个点坐标三对对应值,选择一般式
一般式
y=ax2+bx+c
(a≠0)
已知顶点坐标或对称轴或最值,选择顶点式
顶点式
y=a(x-h)2+k
(a≠0)
已知抛物线的顶点为(1,-4), 且过点(0,-3),求抛物线的解析式?
解: 设所求的二次函数为 y=a(x-1)2-4 ∵点( 0,-3)在抛物线上 ∴ a-4=-3, ∴ a=1
∴所求的抛物线解析式为 y=(x-1)2-4
已知一个二次函数的图象过点(0,-3) (4,5) 对称轴为直线x=1,求这个函数的解析式? 思考:怎样设二次函数关系式
变式一:
已知二次函数的图像经过点(4,-3), 且当x=3时有最大值4,求出对应的函数的关 系式。
变式二: 二次函数的图象过点A(0,5),B(5,0) 两点,它的对称轴为直线x=3,求这个二次 函数的解析式。 ∵ 二次函数的对称轴为直线x=3 ∴设二次函数表达式 为 y=a(x-3)2+k
二次函数的表达式:
0
2、已知抛物线y=a(x-h)2+k 顶点坐标是(-3,4), 则 -3 4 h=_____,k=______ ,
2+4 a ( x+3 ) 代入得y=______________
对称轴为直线x=1,则___________
2+k a ( x -1 ) 代入得y=______________
h=1
二次函数常用的几种解析式
2+bx+c 一般式 y=ax ( a ≠0) 用待定系数法确定二次函数的解析式时,应 该根据条件的特点,恰当地选用一种函数表 已知三个点坐标三对对应值,选择一般式 达式。 顶点式 y=a(x-h)2+k (a≠0)
已知顶点坐标或对称轴或最值,选择顶点式
已知二次函数y=ax2的图像经过点(2,8),求a的值。
y= (x-3)2-4
变式三:
已知当x=-1时,抛物线最高点的纵 坐标为4,抛物线与x轴两交点的距离为6, 求这
个函数的表达式。
根据条件求出下列二次函数解析式: (1)过点(2,4),且当x=1时,y有最值 为6;
(2)如图所示,
O
-1 -1
2
二次函数图象如图所示, (1)直接写出点的坐标; (2)求这个二次函数的解析式
1、已知抛物线y=ax2+bx+c
ห้องสมุดไป่ตู้
当x=1时,y=0,则a+b+c=_____ a-b+c=0 经过点(-1,0),则___________ 经过点(0,-3),则___________ c=-3 16a+4b+c=5 经过点(4,5),则___________
- b =1 2 a 对称轴为直线x=1,则___________
已知一个二次函数的图象过点(0, -3) (-1,0) (3,0) 三点,求这个函数的解析式?
解: 设所求的二次函数为 y=ax2+bx+c c=-3 a= 1 依题意得 a-b+c=0 解得 b= -2 9a+3b+c=0 c= -3 ∴所求二次函数为 y=x2-2x-3
最低点为( x=1,y最值 1, =-4 -4)
问题2:
已知二次函数y=ax2+c的图像经过点 (-2,8)和(-1,5),求a、c。
16a+4b=8 a-b=3
4a+b=2 a-b=3
已知一个二次函数的图象过点(0,-3) (4,5) (-1, 0)三点,求这个函数的解析式?
解:设所求的二次函数为 y=ax2+bx+c
∵二次函数的图象过点(0,-3)(4,5)(-1, 0) c=-3 a= x=0时,y=-3; 解得 b= ∴ 16a+4b+c=5 a-b+c=0 c= -3 x=4时,y=5;
x=-1时,y=0;
已知一个二次函数的图象过点(0,-3) (4,5) (-1, 0)三点,求这个函数的解析式?
解:设所求的二次函数为 y=ax2+bx+c
∵二次函数的图象过点(0,-3)(4,5)(-1, 0) c=-3 a= 1 x=0时,y=-3; 解得 b=-2 一、设 ∴ 16a+4b+c=5 x=4时,y=5; a-b+c=0 c= -3 二、代 三、解 x =-1 时 , y =0; 2 四、还原 ∴所求二次函数为 y=x -2x-3
你还有其他揭发吗
解: 设所求的二次函数为 y=a(x-1)2+k
已知一个二次函数的图象过点(0,-3) (4,5) 对称轴为直线 x=1,求这个函数的解析式? 对称轴为直线 x=1
解:设所求的二次函数为 y=ax2+bx+c c=-3 依题意得 16a+4b+c=0 - b =1 2a
已知抛物线的顶点坐标为(-2,3), 且经过点(-1,7),求函数的表达式。
