【天津市】2017-2018年度南开翔宇初三第一次月考数学答案
天津市南开区九年级上学期数学第一次月考试卷附解析版答案

综合上所述 a≥5. 应选B.
【分析】由于二次函数的顶点坐标不能确定,故应分对称轴不在[1,3]和对称轴在[1,3]内两种情况进行解
答.此题考查了二次函数的最值确定与自变量 x 的取值范围的关系,难度较大. 10.【解析】【解答】解:∵对称轴是 x= ,0<x1<
.
y=ax2﹣12ax+36a﹣5 的图象在 4<x<5 这一段位于 x 轴下方,在 8<x<9 这一段位于 x 轴上方,那么 a 的 值为
18.如图,将
放在每个小正方形的边长为 1 的网格中,点 ,点 ,点 均落在格点上.
〔1〕
.
〔2〕请在如以下列图的网格中,用无刻度的直尺,画出一个以
为底边的等腰
D. y=〔x﹣3〕2+3
y=x2﹣2x+1 与 x 轴的交点个数是〔 〕
A. 0
B. 1
C. 2
D. 3
4.假设
,
,
为二次函数
的图象上的三点,那么 ,
, 的大小关系是〔 〕
5.在同一坐标系中一次函数y=ax+b 和二次函数 y=ax2+bx 的图象可能为〔 〕
A.
B.
C.
6.假设关于的方程
没有实数根,那么函数
案。 2.【解析】【解答】由题意得原抛物线的顶点为〔0,1〕,平移后抛物线的顶点为〔3,﹣1〕,所以新 抛 物线解析式为 y=〔x﹣3〕2﹣1, 故答案为:C. 【分析】抛物线向下移动,需在常数项上加下减,抛物线向左向右,需在 x 后左加右减。 3.【解析】【解答】由△=b2-4ac=〔-2〕2-4×1×1=0,可得二次函数 y=x2-2x+1 的图象与 x 轴有一个交点. 故答案为:B.
天津市南开区2018届九年级上期中抽考数学试题含答案

2017-2018学年天津市南开区九年级(上)期中数学试卷一、选择题(本题共12个小题,每小题3分,共36分)1.关于x的一元二次方程x2+3x+m=0有两个不相等的实数根,则m的可以取的数值为()A.B.C.9 D.72.下面四个手机应用图标中,属于中心对称图形的是()A.B.C.D.3.对于二次函数y=﹣(x﹣1)2+2的图象与性质,下列说法正确的是()A.对称轴是直线x=1,最小值是2B.对称轴是直线x=1,最大值是2C.对称轴是直线x=﹣1,最小值是2D.对称轴是直线x=﹣1,最大值是24.不论x为何值,函数y=ax2+bx+c(a≠0)的值恒大于0的条件是()A.a>0,△>0 B.a>0,△<0 C.a<0,△<0 D.a<0,△>05.如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是()A.45°B.60°C.75°D.85°6.下列命题中,正确的是()A.圆心角相等,所对的弦的弦心距相等B.三点确定一个圆C.平分弦的直径垂直于弦,并且平分弦所对的弧D.弦的垂直平分线必经过圆心7.如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2017时,顶点A的坐标为()A.(4,0)B.(﹣4,0) C.(2,2)D.(﹣2,2)8.如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON 的大小为()A.108°B.144°C.150°D.166°9.已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c的值为()A.1:2:3 B.3:2:1 C.1:: D.::110.如图,在边长为1的正方形ABCD中,将射线AC绕点A按顺时针方向旋转α度(0<α≤360)得到射线AE,点M是点D关于射线AE的对称点,则线段CM长度的最小值为()A.﹣1 B.0.5 C.1 D.11.在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是()A.B. C.D.12.如图,直线y=kx+c与抛物线y=ax2+bx+c的图象都经过y轴上的D点,抛物线与x 轴交于A、B两点,其对称轴为直线x=1,且OA=OD.直线y=kx+c与x轴交于点C(点C在点B的右侧).则下列命题中正确命题的个数是()①abc>0;②3a+b>0;③﹣1<k<0;④k>a+b;⑤ac+k>0.A.1 B.2 C.3 D.4二、填空题(本大题共6小题,每小题3分,共18分)13.点P(2,﹣1)关于原点的对称点坐标为(﹣2,m),则m=.14.二次函数y=x2+3x﹣2,当x满足时,y随x的增大而增大.15.将二次函数y=x2+1的图象向左平移2个单位,再向下平移3个单位,所得二次函数解析式为.16.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M是BC的中点,P是A′B′的中点,连接PM,若BC=2,∠BAC=30°,则线段PM的最大值是.17.受益于国家支持新能源汽车发展等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计,2014年利润为2亿元,2016年利润为2.88亿元.则该企业从2014年到2016年利润的平均增长率为;若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润(填“能”或“不能”)超过34亿元.18.已知,如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆于G、F两点,连接CF、BG.则下列结论:①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于BG.则其中正确的是(只需填序号)三、解答题(共66分)19.(8分)按要求解一元二次方程(Ⅰ)(3x﹣1)2=(x+1)2(适当方法)(Ⅱ)x2﹣x﹣=0(配方法)20.(8分)已知m、n是方程x2﹣4x﹣12的两个实数根,且m<n,抛物线y=﹣x2+bx+c 的图象经过点A(m,0),B(0,n)(1)求该抛物线的解析式(2)将抛物线图象向右平移几个单位,可使平移后所得图象经过坐标原点?21.(10分)已知△ABC内接于⊙O,过点A作直线EF.(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).(ī)(īī)(īīī)(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?22.(10分)如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC、AB分别相切于C、D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于点M (1)求证:点M是CF的中点;(2)若E是弧DF的中点,BC=2,求⊙O的半径.23.(10分)某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m.设饲养室长为x(m),占地面积为y(m2).(1)如图1,问饲养室长x为多少时,占地面积y最大?(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.24.(10分)如图,将边长为a的正方形OABC绕顶点O按顺时针方向旋转角α(0°<α<45°),得到正方形OA1B1C1.设边B1C1与OC的延长线交于点M,边B1A1与OB 交于点N,边B1A1与OA的延长线交于点E,连接MN.(1)求证:△OC1M≌△OA1E;(2)试说明:△OMN的边MN上的高为定值;(3)△MNB1的周长p是否发生变化?若发生变化,试说明理由;若不发生变化,请给予证明,并求出p的值.25.(10分)如图,已知在平面直角坐标系xoy中,抛物线y=ax2+2x+c与x轴交于点A (﹣1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.(Ⅰ)求这条抛物线的解析式,并写出其对称轴和顶点M的坐标;(Ⅱ)如果直线CM与x轴交于点D,点C关于直线l的对称点为N,试证明四边形CDAN 是平行四边形;(Ⅲ)点P在直线l上,且以点P为圆心的圆经过A、B两点,并且与直线CM相切,求点P的坐标.2017-2018学年天津市南开区九年级(上)期中数学试卷参考答案一、选择题(本题共12个小题,每小题3分,共36分)1.B;2.B;3.B;4.B;5.D;6.D;7.C;8.B;9.C;10.A;11.D;12.D;二、填空题(本大题共6小题,每小题3分,共18分)13.1;14.x>﹣;15.y=(x+2)2﹣2;16.3;17.20%;能;18.①②④;三、解答题(共66分)19.20.21.22.23.24.25.。
天津南开翔宇学校 2018-2019学年九年级第一次月考数学试卷

南开翔宇2018-2019年度初三第一次月考数学试卷一、选择题1. 下列函数中是二次函数的是()A. y=2(x-1)B. y=2(x-1)²-2x²C. y=a(x-1)² D y=2x²-12. 已知关于x的一元二次方程x²+2x+m-2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为()A. 6B. 5C. 4D. 33. 二次函数y=-2x²+4x+1的图象如何移动就得到y=-2x²的图象()A. 向左移动1个单位,向上移动3个单位B. 向右移动1个单位,向上移动3个单位C. 向左移动1个单位,向下移动3个单位D. 向右移动1个单位,向下移动3个单位4. 某同学将如图两水平线L1、L2的其中一条当成x轴,且向右为正向;两铅直线L3、L4的其中一条当成y轴,且向上为正向,并在此坐标平面上画出二次函数y=ax ²+2ax+1的图形、关于他选择x、y轴的叙述,下列哪个结论正确? ()A. L1为x轴,L3为y轴 B. L1为x轴,L4为y轴C. L2为x轴,L3为y轴D. L2为x轴,L4为y轴5. 如图,已知二次函数y=(x+1)²-4,当-2≤x≤2时,则函数y的最小值和最大值()A. -3和5B. -4和5C. -4和-3D. -1和56. 如果其二次函数的图像与已知二次函数y=x²-2x的图像关于y轴对称,那么这个二次函数的解析式是()A. y=-x²+2xB. y=x²+2xC. y=-x²-2xD. y=x²-2x7. 已知过点A(-1,m),B(1,m)和C(2,m-1)的抛物线的图象大致为()8. 如图,Rt△ABC中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图像为下列选项中的()9. 由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数y=ax²+bx+c 的图象过点(1,0)…,求证:这个二次函数的图象关于直线x=2对称,根据现有信息,题中的二次函数具有的性质:(1)过点(3,0);(2).顶点是(1,-2)(3)在x轴土截得的线段的长度是2;(4)c=3a;其中正确的个数()A. 3个B. 2个C. 1个D. 0个10. 一副三角板(△BCM和△AEG)如图放置,点E在BC上滑动,AE交BM于D,EG交MC于F,且在滑动过程中始终保持EF=ED,若MB=4,设BE=x,△EFC的面积为y,则y关于x的函数表达式是()A. y=x2B. y=x2+1C. y=x(x2-x)D. y=x(x2-x)+111. 已知函数y=x²-2m+2016(m为常教)的图像上有三点:A(x1,y1),B (x2,y2),C(x3,y3),其中x1=-+m,x2=,x3=m-1,则y1,y2,y3的大小关系是()A. y2<y3<y1B. y3<y1<y2C. y1<y2<y3D. y1<y3<y212. 当-2≤x≤1时,二次函数y=-(x-m)²+m²+1有最大值为4,则实数m的值为()A.3B. 3或-3C. 2或-3D. 2或3或-3二. 填空题13. 若关于x的方程(a-1)x1+a²=1是一元二次方程,则a的值是14. 已知二次函数y=ax²'+bx-1(a≠0)的图象经过点(1,1),则代数式3-a-b 的值为15. 已知二次函数y=ax²+bx+c(a≠0)中,函数值y与自变量x的部分对应值如下表:则关于x的一元二次方程ax²+bx+c=-2的根是16. 如图抛物线y=x²+2x-3与x轴交于A,B两点,与y轴交于点C,点P是抛物线对称轴上任意一点,若点D、E、F分别是BC、BP、PC的中点,连接DE,DF,则DE+DF的最小值为17. 如图,在平面直角坐标系中,抛物线y=-x²+4x+5与x辅交A,B两点,与y轴交于点C,垂直于y轴的直线l与抛物线交于点P(x1,y1),Q(x2,y2),(x2<x1),与直线BC交于点N(x3,y3),若x3<x2<x1,设S=x1+x2+x3,则S 的取值范围是18. 如图,已知二次函数y=ax²+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y 轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b²<-4a;④;⑤b<c. 其中正确结论有(填写所有正确结论的序号)。
2018年天津市南开区中考数学一模试卷和解析答案

2018年天津市南开区中考数学一模试卷一、选择题(本大题共12小题,每小题3分,共36分。
在每小题给出地四个选项中,只有一项是符合题目要求地)1.(3分)(﹣2)×(﹣6)地结果等于()A.12 B.﹣12 C.8 D.﹣82.(3分)计算tan60°地值等于()A.B.C.1 D.3.(3分)甲骨文是我国地一种古代文字,是汉字地早期形式,下列甲骨文中,不是轴对称地是()A.B.C. D.4.(3分)在网络上用“Google”搜索引擎搜索“中国梦”,能搜索到与之相关地结果个数约为45100000,这个数用科学记数法表示为()A.451×105B.45.1×106C.4.51×107D.0.451×1085.(3分)如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面图是由7个立方体叠成地几何体,从正前方观察,可画出地平面图形是()A. B. C. D.6.(3分)如果实数a=,且a在数轴上对应点地位置如图所示,其中正确地是()A.B.C.D.7.(3分)化简+,其结果为()A. B. C.D.8.(3分)半径为a地正六边形地面积等于()A.B.C.a2D.9.(3分)已知点A(x1,y1),B(x2,y2)是反比例函数y=地图象上地两点,若x1<0<x2,则有()A.y1<0<y2B.y2<0<y1C.y1<y2<0 D.y2<y1<010.(3分)如图,平行四边形ABCD中,E为AD地中点,已知△DEF地面积为S,则四边形ABCE地面积为()A.8S B.9S C.10S D.11S11.(3分)如图,将菱形纸片ABCD折叠,使点A恰好落在菱形地对称中心O 处,折痕为EF,若菱形ABCD地边长为2cm,∠A=120°,则EF地长为()A.2 B.2 C.D.412.(3分)如图,抛物线y=ax2+bx+3(a≠0)地对称轴为直线x=1,如果关于x 地方程ax2+bx﹣8=0(a≠0)地一个根为4,那么该方程地另一个根为()A.﹣4 B.﹣2 C.1 D.3二、填空题(本大题共6小题,每小题3分,共18分)13.(3分)计算(﹣2a)3地结果是.14.(3分)计算(﹣)2地结果等于.15.(3分)将正比例函数y=2x地图象向下平移,则平移后所得图象对应地函数解析式可以是.(写出一个即可)16.(3分)“赵爽弦图”是四个全等地直角三角形与中间一个小正方形拼成地大正方形.有一“赵爽弦图”飞镖板,其直角三角形地两条直角边地长分别是2和4.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷地飞镖均扎在飞镖板上),则投掷一次飞镖扎在中间小正形区域(含边)地概率是.17.(3分)如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC 地中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成地图形)分成两部分,则这两部分面积之差地绝对值是.18.(3分)如图,是大小相等地边长为1地正方形构成地网格,A,B,C,D均为格点.(Ⅰ)△ACD地面积为;(Ⅱ)现只有无刻度地直尺,请在线段AD上找一点P,并连结BP,使得直线BP 将四边形ABCD地面积分为1:2两部分,在图中画出线段BP,并在横线上简要说明你地作图方法..三、解答题(本大题共7小题,共计66分。
天津市南开区 翔宇中学 2017-2018学年 九年级数学上册 旋转 单元检测题(含答案)

2017-2018学年九年级数学上册旋转单元检测题一、选择题:1、剪纸是扬州的非物质文化遗产之一,下列剪纸作品中是中心对称图形的是( )A. B. C. D.2、下列四个图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D.3、在平面直角坐标系中,把点P(﹣3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )A.(3,2)B.(2,﹣3)C.(﹣3,﹣2)D.(3,﹣2)4、下列图形中,是中心对称图形又是轴对称图形的有( )①平行四边形;②菱形;③矩形;④正方形;⑤等腰梯形;⑥线段;⑦角.A.2个B.3个C.4个D.5个5、.如图,将正方形图案绕中心O旋转180°后,得到的图案是( )A. B. C. D.6、如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )A.(0,1)B.(1,﹣1)C.(0,﹣1)D.(1,0)7、如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )A.15°B.20°C.25°D.30°8、如图,将矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′的位置,旋转角为α(0<α<90°),若∠1=110°,则∠α=( )A.10°B.20°C.25°D.30°9、如图,在△ABO中,AB⊥OB,OB=,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )A.(﹣1,﹣)B.(﹣1,﹣)或(﹣2,0)C.(﹣,1)或(0,﹣2)D.(﹣,1)10、如图,在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心是A.点AB.点BC.点CD.点D11、如图,已知▱ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )A.130°B.150°C.160°D.170°12、如图,正方形ABCD绕D旋转90°到了正方形CDEF处,那么旋转方向是( )A.逆时针B.顺时针C.顺时针或逆时针D.无法确定二、填空题:13、点P(﹣3,4)关于原点对称的点的坐标是 .14、如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为.15、在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1是关于某一点中心对称,则对称中心的坐标为 .16、如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是.17、如图,Rt△ABC中,已知∠C=90°,∠B=55°,点D在边BC上,BD=2CD.把线段BD 绕着点D逆时针旋转α(0<α<180)度后,如果点B恰好落在Rt△ABC的边上,那么α= .18、如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为 .三、作图题:19、△ABC在方格中的位置如图所示.(1)请在方格纸上建立平面直角坐标系,使得A、B两点的坐标分别为A(2,﹣1)、B(1,﹣4).并求出C点的坐标;(2)作出△ABC关于横轴对称的△,再作出△ABC以坐标原点为旋转中心、旋转180°后的△A2B2C2,并写出C1,C2两点的坐标.四、解答题:20、如图,△ABO与△CDO关于点O中心对称,点E,F在线段AC上,且AF=CE.求证:FD=BE.21、如图,△ABC三个顶点的坐标分别为A(-2,3),B(-3,1),C(-1,2).(1)将△ABC向右平移4个单位,画出平移后的△A1B1C1;(2)画出△ABC关于x轴对称的△A2B2C2;(3)将△ABC绕原点O旋转180°,画出旋转后的△A3B3C3;(4)在△ABC,△A1B1C1,△A2B2C2,△A3B3C3中,________与________成轴对称,对称轴是______;______与______成中心对称,对称中心是_________________.22、如图,△ABC三个顶点的坐标分别为A(﹣1,1),B(﹣4,2),C(﹣3,4).(1)请画出△ABC向右平移5个单位长度后得到△A1B1C1;(2)请画出△ABC关于原点对称的△A2B2C2;(3)在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标.23、如图,点C为线段AB上一点,△ACM、△CBN是等边三角形,直线AN、MC交于点E,直线BM、CN交于点F.(1)求证:AN=MB;(2)求证:△CEF为等边三角形;(3)将△ACM绕点C按逆时针方向旋转900,其它条件不变,在图②中补出符合要求的图形,并判断(1)题中的结论是否依然成立,说明理由.24、推理证明:如图1,在正方形ABCD和正方形CGFE中,连结DE、BG,设△DCE的面积为S1,△BCG的面积为S2,求证:S1=S2.猜想论证:如图2,将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG,连结DE、BG,设△DCE 的面积为S1,△BCG的面积为S2,猜想S1、S2的数量关系,并加以证明.拓展探究:如图3,在△ABC中,AB=AC=10cm,∠B=30°,把△ABC沿AC翻折到△ACE,过点A作AD ∥CE交BC于点D,在线段CE上存在点P,使△ABP的面积等于△ACD的面积,请你直接写出CP的长.参考答案1、C.2、B.3、D.4、C5、C6、B.7、C8、B9、B10、B11、C12、A13、答案为:(3,﹣4).14、答案为:50°15、答案为:(2,1)16、答案为:(-4,3);17、答案为:70°或120°.18、答案为:(36,0).19、解:(1)坐标系如图所示,C(3,﹣3);(2)△A1B1C1,△A2B2C2如图所示,C1(3,3),C2(﹣3,3).20、证明:∵△ABO与△CDO关于O点中心对称,∴△ABO≌△CDO.∴AO=CO,BO=DO. 又∵AF=CE,∴AO-AF=CO-CE,即OF=OE.∵∠FOD=∠EOB,∴△FOD≌△EOB(SAS).∴FD=BE.21、解:(1)~(3)作图略;(4)△A2B2C2△A3B3C3y轴△A1B1C1△A3B3C3(2,0)22、解:(1)如图所示:△A1B1C1,即为所求;(2)如图所示:△A2B2C2,即为所求;(3)如图所示,此时△PAB的周长最小,P点坐标为:(﹣2,0).23、证明:(1)因为△ACM,△CBN是等边三角形,所以AC=MC,BC=NC,∠ACM=600,∠NCB=600.在△CAN和△MCB中,AC=MC,∠ACN=∠MCB,NC=BC.所以△CAN≌△MCB(SAS),所以AN=BM.(2)因为△CAN≌△MCB,所以∠CAN=∠CMB.又因为∠MCF=1800-∠ACM-∠NCB=600.所以∠MCF=∠ACE.在△CAE和△CMF中,∠CAE=∠CMF,CA=CM,∠ACE=∠MCF,所以△CAE≌△CMF(ASA)所以CE=CF,所以△CEF为等腰三角形,又因为∠ECF=600,所以△CEF为等边三角形.(3)解:连接AN,BM. 因为△ACM、△CBN是等边三角形所以AC=MC,BC=CN,∠ACM=∠BCN=600,因为∠ACB=900,所以∠ACN=∠BCM.在△ACN与△MCB中,AC=CM,∠ACN=∠BCM,NC=BC,所以△ACN≌△MCB(SAS).所以AN=BM.当把MC逆时针旋转900后,AC也旋转了900,因此∠ACB=900,很显然∠FCE>900,因此三角形FCE不可能是等边三角形,即结论1成立,结论2不成立。
2020年天津市南开翔宇学校初三第一次月考数学试卷(含答案)

时,它是二次函数。
14. 已知二次函数 y=ax²+bx+c 中,函数 y 与自变量 x 的部分对应值如下表:
x
…
-4
-3
-2
-1
0
…
Y
…
3
-2
-5
-6
-5
则 y<-2 时,x 的取值范围是
15. 已知抛物线 y=ax²-2ax+c 与 x 轴一个交点的坐标为(-1,0),则一元二次方程 ax²-2ax+c=0 的根为
16. 如图,把抛物线 y= x²平移得到抛物线 m,抛物线 m 经过点 A(-6,0)和原点(0,0),它的顶点为 P,
它的对称轴与抛物线 y= x²交于点 Q,则图中阴影部分的面积为
17. 二次函数 y=ax²-12ax+36a-5 的图象在 4<x<5 这一段位于 x 轴下方,在 8<x<9 这一段位于 x 轴上方,则 a 的值为 18. 如图,将△ABC 放在每个小正方形的边长为 1 的网格中,点 A、点 B、点 C 均落在格点上. (1)S△ABC= (2)请在如图所示的网格中;用无刻度的直尺,画出一个以 AB 为底边的等腰△ABD,使△ABD 的面积等于△ABC 的面积,并简要说明点的位置是如何找到的(不要求证明)
A.
B.
C.
D.
9. 已知 y=x²+(1-a)x+1 是关于 x 的二次函数,当 x 的取值范围是 1≤x<3 时,y 在 x=1 时取得最大值,则
实数 a 的取值范图是
A. a=5
B. a≥5
C. a=3
D. a≥3
10. 二次函数 y=x²-x+m 的图象如图所示,当 x=a 时 y<0;那么当 x=a-1 时,函数值
天津市南开区九年级上学期数学第一次月考试卷含答案解析
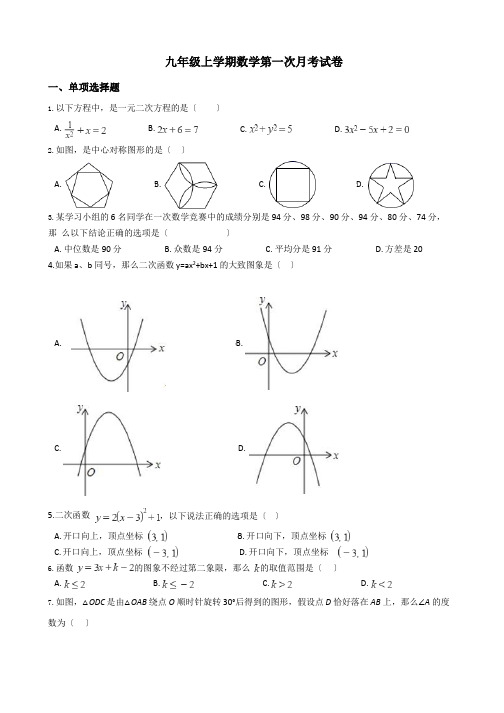
〔1〕求点 C 的坐标; 〔2〕假设平行于 y 轴的直线 x=a 交于直线 1 于点 E 2DM , 求 a 的值;
, 交直线 l2 于点 D
, 交 x 轴于点 M
, 且 ED=
〔3〕如图 2,点 P 是第四象限内一点,且∠BPO=135°,连接 AP , 探究 AP 与 BP 之间的位置关系,并
证明你的结论.
B. y3<y2<y1
C. y1<y2<y3
D. y3<y1<y2
10.如图,四边形ABCD 是菱形,AC=8,DB=6,DH⊥AB 于 H,那么 DH 等于〔 〕
A.
B.
C. 5
D. 4
y= x+4 与 x 轴、y 轴分别交于点 A 和点 B , 点 C , D 分别为线段 AB , OB 的中点,点 P 为 OA 上一动点,PC+PD 值最小时点 P 的坐标为〔 〕.
断重复,共摸球 40 次,其中 10 次摸到黑球,那么估计盒子中大约有
个白球.
x=0 是关于 x 的一元二次方程〔m+2〕x2﹣3x+m2﹣4=0 的一个根,那么 m 的值为
.
16.〕如图,Rt△ABC 中,C= 90o , 以斜边 AB 为边向外作正方形 ABDE,且正方形对角线交于点 D,连接
OC,AC=5,OC=6 ,那么另一直角边 BC 的长为
∵由 D′和点 D 关于 x 轴对称,
∴点 D′的坐标为〔0,﹣2〕. 设直线 CD′的解析式为 y=kx+b,
∵直线 CD′过点 C〔﹣3,2〕,D′〔0,﹣2〕,
∴
,
解得:
,
∴直线 CD′的解析式为 y=﹣ x﹣2. 令 y=0, ∴0=﹣ x﹣2,
解得:x=﹣ ,
天津市南开区翔宇中学 2017年九年级数学中考综合练习题及答案4.4

2017年九年级数学中考综合练习题一、单选题:1.如图数轴上有O ,A ,B ,C ,D 五点,根据图中各点所表示的数,判断18在数轴上的位置会落在下列哪一线段上( )A .OAB .ABC .BCD .CD 2.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是轴对称的是( )A. B. C. D.3.在实数范围内,下列正确的是( )A.若|a|=|b|,则a=bB.若|a|=(b )2,则a=bC.若a >b ,则a 2>b 2D.若33b a =,则a=b4.下列说法:①要了解一批灯泡的使用寿命,应采用普查的方式;②若一个游戏的中奖率是1%,则做100次这样的游戏一定会中奖;③甲、乙两组数据的样本容量与平均数分别相同,若方差=0.1,=0.2,则甲组数据比乙组数据稳定;④“掷一枚硬币,正面朝上”是必然事件. 正确说法的序号是( )A.①B.②C.③D.④ 5.如图:∠DAE=∠ADE=15°,DE ∥AB ,DF ⊥AB ,若AE=8,则DF 等于( )A.5B.4C.3D.2 6.计算:aa a a a 112122-÷++-,其结果正确的是( )A.0.5B.1+a a C.a a 1+ D.21++a a 7.已知关于x 、y 的二元一次方程组⎩⎨⎧=-+=-m y x m y x 32823的解适合x-y=4,则m 的值( )A.14B.-14C.6 B.-68.根据下列表格的对应值,判断方程ax 2+bx+c=0一个解的范围是( )A.3<x <3.23B.3.23<x <3.24C.3.24<x <3.25D.3.25<x <3.26 10.一次函数y=ax-a(a ≠0)的大致图像是( )A.B. C. D.10.如图,在平面直角坐标系中,点A 在第一象限,AB ⊥y 轴于点B,函数y=xk(k>0,x>0)的图象与线段AB 交于点C,且AB=3BC ,若△AOB 的面积为12,则k 的值( )A.4B.6C.8D.1211.如图,在扇形AOB 中∠AOB=90°,正方形CDEF 的顶点C 是弧AB 的中点,点D 在OB 上,点E 在OB 的延长线上,当正方形CDEF 的边长为22时,则阴影部分的面积为( )A.2π-4B.4π-8C.2π-8D.4π-412.抛物线y=ax 2+bx+c 的顶点为D(-1,2),与x 轴的一个交点A 在点(-3,0和-2,0)之间,其部分图象如图所示,则以下结论:①b 2-4ac<0;②a+b+c<0;③c-a=2;④方程ax 2+bx+c-2=0有两个相等的实数根,其中正确结论的个数为( )A.1个B.2个C.3个D.4个二、填空题:13.计算:|1-3|-12=_____________________.14.从-1、0、1、2这四个数中,任取一个数记为b,再从余下的三个数中任取一个为c,则二次函数y=x2-bx+c的图像与x轴有两个交点的概率为.15.若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根,则实数k的取值范围是.16.有一个进、出水管的容器,某时刻起4分钟只开进水管,此后进水管,出水管同时开放,经过8分钟注满容器,随后只打开出水管,得到时间x(分钟)与水量Y(升)之间的函数关系如图,那么容器的容积为升。
