密码学要点总结
密码学——第1章密码学概述

第 1 章密码学概述1.1 信息安全Alvin Toffler 在《第三次浪潮》中预言:计算机网络的建立和普及将彻底改变人类生存和生活模式。
信息化以它有别于传统方式的信息获取、存储、处理、传输和使用,给现代社会的正常发展带来了一系列的前所未有的风险和威胁。
传统的一切准则在电子信息环境中如何体现与维护,到现在并没有根本解决,一切都在完善中。
今天,人们一方面享受着信息技术带来的巨大变革,同时也承受着信息被篡改、泄露、伪造的威胁,以及计算机病毒及黑客入侵等安全问题。
信息安全的风险制约着信息的有效使用,并对经济、国防乃至国家的安全构成威胁。
一方面:没有信息安全,就没有完全意义上的国家安全。
另一方面:信息安全还涉及个人权益、企业生存和金融风险防范等。
密码技术和管理是信息安全技术的核心,是实现保密性、完整性、不可否认性的关键。
“ 9.11 事件”后,各国政府纷纷站在国家安全的角度把信息安全列入国家战略。
重视对网络信息和内容传播的监控,更加严格的加固网络安全防线,把信息安全威胁降到最低限度。
2000 年我国开始着力建立自主的公钥基础设施,并陆续启动了信息系统安全等级保护和网络身份认证管理服务体系。
因此,密码学的基本概念和技术已经成为信息科学工作者知识结构中不可或缺的组成部分。
1.2 密码学引论1. 密码学的发展概况密码学是一门既古老又年轻的学科。
自有了战争,就有了加密通信。
交战双方都为了保护自己的通信安全,窃取对方的情报而研究各种信息加密技术和密码分析技术。
古代行帮暗语和一些文字游戏等,实际上就是对信息的加密。
这种加密方法通过原始的约定,把需要表达的信息限定在一定的范围内流通。
古典密码主要应用于政治、军事及外交等领域。
电报发明以后,商业方面对密码学的兴趣主要集中在密码本的编制上。
20 世纪初,集中在与机械和电动机械加密的设计和制造上。
进入信息时代,大量敏感信息要通过公共通信设施或计算机网络进行交换,密码学的应用已经不仅仅局限在政治、军事、外交等领域,其商业和社会价值日益显著,并与人们的日常生活紧密相关。
密码学复习1
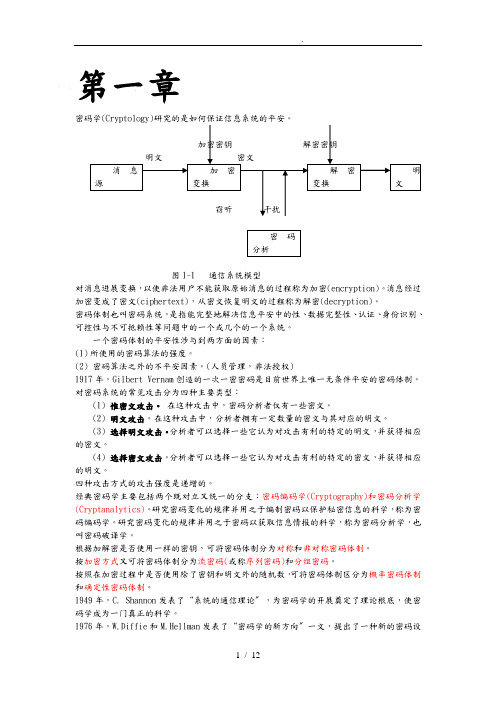
第一章密码学(Cryptology)研究的是如何保证信息系统的平安。
图1-1 通信系统模型对消息进展变换,以使非法用户不能获取原始消息的过程称为加密(encryption)。
消息经过加密变成了密文(ciphertext),从密文恢复明文的过程称为解密(decryption)。
密码体制也叫密码系统,是指能完整地解决信息平安中的性、数据完整性、认证、身份识别、可控性与不可抵赖性等问题中的一个或几个的一个系统。
一个密码体制的平安性涉与到两方面的因素:(1)所使用的密码算法的强度。
(2) 密码算法之外的不平安因素。
(人员管理,非法授权)1917年,Gilbert Vernam创造的一次一密密码是目前世界上唯一无条件平安的密码体制。
对密码系统的常见攻击分为四种主要类型:(1) 惟密文攻击。
在这种攻击中,密码分析者仅有一些密文。
(2) 明文攻击。
在这种攻击中,分析者拥有一定数量的密文与其对应的明文。
(3) 选择明文攻击。
分析者可以选择一些它认为对攻击有利的特定的明文,并获得相应的密文。
(4) 选择密文攻击。
分析者可以选择一些它认为对攻击有利的特定的密文,并获得相应的明文。
四种攻击方式的攻击强度是递增的。
经典密码学主要包括两个既对立又统一的分支:密码编码学(Cryptography)和密码分析学(Cryptanalytics)。
研究密码变化的规律并用之于编制密码以保护秘密信息的科学,称为密码编码学。
研究密码变化的规律并用之于密码以获取信息情报的科学,称为密码分析学,也叫密码破译学。
根据加解密是否使用一样的密钥,可将密码体制分为对称和非对称密码体制。
按加密方式又可将密码体制分为流密码(或称序列密码)和分组密码。
按照在加密过程中是否使用除了密钥和明文外的随机数,可将密码体制区分为概率密码体制和确定性密码体制。
1949年,C. Shannon发表了“系统的通信理论〞,为密码学的开展奠定了理论根底,使密码学成为一门真正的科学。
现代密码学总结汇总

现代密码学总结第一讲绪论•密码学是保障信息安全的核心•安全服务包括:机密性、完整性、认证性、不可否认性、可用性•一个密码体制或密码系统是指由明文(m或p)、密文(c)、密钥(k)、加密算法(E)和解密算法(D)组成的五元组。
•现代密码学分类:•对称密码体制:(又称为秘密密钥密码体制,单钥密码体制或传统密码体制)密钥完全保密;加解密密钥相同;典型算法:DES、3DES、AES、IDEA、RC4、A5 •非对称密码体制:(又称为双钥密码体制或公开密钥密码体制)典型算法:RSA、ECC第二讲古典密码学•代换密码:古典密码中用到的最基本的处理技巧。
将明文中的一个字母由其它字母、数字或符号替代的一种方法。
(1)凯撒密码:c = E(p) = (p + k) mod (26) p = D(c) = (c –k) mod (26)(2)仿射密码:明文p ∈Z26,密文c ∈Z26 ,密钥k=(a,b) ap+b = c mod (26)(3)单表代换、多表代换Hill密码:(多表代换的一种)——明文p ∈(Z26)m,密文c ∈(Z26)m,密钥K ∈{定义在Z26上m*m的可逆矩阵}——加密c = p * K mod 26 解密p = c * K-1 mod 26Vigenere密码:查表解答(4)转轮密码机:•置换密码•••:将明文字符按照某种规律重新排列而形成密文的过程列置换,周期置换•密码分析:•统计分析法:移位密码、仿射密码和单表代换密码都没有破坏明文的频率统计规律,可以直接用统计分析法•重合指数法• 完全随机的文本CI=0.0385,一个有意义的英文文本CI=0.065• 实际使用CI 的估计值CI ’:L :密文长。
fi :密文符号i 发生的数目。
第三讲 密码学基础第一部分 密码学的信息论基础• Shannon 的保密通信系统模型发送者接收者信源分析者加密解密安全信道无噪信道安全信道MM MCK K密钥源发送者接收者信源分析者加密解密无噪信道安全信道MM MC KK ’密钥源无噪信道•一个密码体制是一个六元组:(P, C, K 1, K 2, E, D )P--明文空间 C--密文空间 K 1 --加密密钥空间K2 --解密密钥空间E --加密变换D --解密变换对任一k∈K1,都能找到k’∈K2,使得D k’ (E k (m))=m,m M. •熵和无条件保密•)(1log)()(≥=∑i iaixpxpXH设随机变量X={xi | i=1,2,…,n}, xi出现的概率为Pr(xi) ≧0, 且, 则X的不确定性或熵定义为熵H(X)表示集X中出现一个事件平均所需的信息量(观察前);或集X中每出现一个事件平均所给出的信息量(观测后).•设X={x i|i=1,2,…,n}, x i出现的概率为p(x i)≥0,且∑i=1,…,n p(x i)=1;Y={y i|i=1,2,…,m}, y i出现的概率为p(y i)≥0,且∑i=1,…,m p(y i)=1;则集X 相对于集Y的条件熵定义为•X视为一个系统的输入空间,Y视为系统的输出空间,通常将条件熵H(X|Y)称作含糊度,X和Y之间的平均互信息定义为:I(X,Y)=H(X)-H(X|Y)表示X熵减少量。
密码学重点题归纳

重点知识点归纳:3、IDEA 分组密码算法的明文分组长度为 比特,密钥长度为 比特,经过 圈迭代后,再经过一个输出变换,得到 比特的密文。
整个运算过程全部以 位字为运算单位,便于软件实现。
算法通过交替使用 、 、和 三种不同的群运算来实现混乱和扩散。
(64;128;8;64;16;按位模2加;模216加法;模216+1乘法)14、设一个线性移位寄存器的反馈多项式为41)(x x x f ⊕⊕=,则其线性递推式为 。
给定初始状态0001,则输出序列为 ,t =3时的自相关系数为 。
15、已知 a 是 6 次本原多项式生成的 m 序列,则 a 的周期为 ,在 a 的一个周期内(首尾相接),游程总数有 个,其中长度为 5 的 0 游程有 个,长度为 3 的 1 游程有 个。
19、设RSA 公钥密码体制的模数N=221,则 (N )= ,从理论上讲,加密指数e 共有 种可能取法。
20、公钥密码RSA 的安全性基础是 ,签名算法DSA 的安全性基础是 。
3、简述密钥分层管理的基本思想及其必要性。
答:密钥分层保护也称为逐级保护,一般将密钥分为三层,一级密钥保护二级密钥,二级密钥保护三级密钥等。
对密钥实行分层管理是十分必要的,分层管理采用了密码算法,一级对下一级进行保护,底层密钥的泄露不会危及上层密钥的安全,当某个密钥泄露时,最大限度的减少损失。
4、 简述密钥分散管理的基本思想及其必要性。
答:密钥分散保护通常指将密钥分成几个部分,存放在不同的地方或由不同的人掌管,使用时再将几部分结合起来,结合方式一般为模2加。
当一部分泄露时,不会危及整个主密钥的安全。
在一个密码系统中,无论密钥如何分层保护,最高一级的密钥(一般是主密钥)总是明的,无法采用密码算法保护,而直接将主密钥明放在计算机中是不允许的,因此必须对主密钥采取相应的保护措施,即对主密钥实行分散管理,将主密钥拆分成几部分,由不同的人来管理或人机共同管理,最大限度的保证主密钥的安全。
密码学知识要点

1. 安全服务有哪些?认证、访问控制、数据加密性、数据完整性、不可否认性和可用性。
2. 密码学研究的主要问题?pl密码学研究确保信息的秘密性和真实性技术。
密码学(密码技术)分类:密码编码学:对信息进行编码实现信息隐蔽:密码分析学:研究分析破译密码4. 何谓Kerckhoff假设?假定密码分析中或敌手知道除密钥外所有的密码系统,这个假设称作Kerckhoff 假设。
一个系统的基本设计目标就是在Kerckhoff假设下是安全的,即一个密码系统的安全性不依赖于算法,而仅与密钥有关。
5. 无条件的安全性?如果无论破译员有多少密文,仍无足够信息能恢复明文,这样的算法是无条件安全的。
事实上只有一次一用的密码本是不可攻破的。
其它所有密码系统在惟密文攻击下都是可以攻破的。
6. 攻击密码体制的一般方法?惟密文攻击、已知明文攻击、选择明文攻击,选择文本,选择密文攻击,选择密钥攻击,软磨硬泡式破译。
7. 传统密码学使用的技术?对称密码加密、代换技术、置换技术转轮机、隐写术8. 密码体制的构成要素?明文空间、密文空间、密钥空间和密码算法。
9. 密码体制的分类?根据密钥的特点:分为传统和公钥密码体制;按照对明文发消息的加密方式的不同:分为分组密码和流密码。
10•计算上安全的准则?。
破译该密码的成本超过被加密信息的价值。
破译该密码的时间超过该信息有用的生命周期。
11. 分组密码的工作模式?电码体(ECB、密文组链接(CBQ、密文反馈(CFB、输出反馈(OFB和计时器(CTR)12. Feistle密码的理论基础?基于1945年Shannon理论引进的混淆和扩散p46,使用乘积密码的概念来逼近简单代换密码,交替的使用代换和置换。
13. 雪崩效应?明文或密钥的一点小的变动都引起密文的较大的变化。
14. DES的强度?使用64比特的分组和56比特的密钥(56位的密钥共有2的56次方种可能,这个数字大约是7.2X10的16次方)穷举攻击:2人56次尝试、强力攻击:2人55次尝试、差分密码分析法:47,线性密码分析法:43次尝试。
现代密码学知识点整理:

第一章 基本概念1. 密钥体制组成部分:明文空间,密文空间,密钥空间,加密算法,解密算法 2、一个好密钥体制至少应满足的两个条件:(1)已知明文和加密密钥计算密文容易;在已知密文和解密密钥计算明文容易; (2)在不知解密密钥的情况下,不可能由密文c 推知明文 3、密码分析者攻击密码体制的主要方法: (1)穷举攻击 (解决方法:增大密钥量)(2)统计分析攻击(解决方法:使明文的统计特性与密文的统计特性不一样) (3)解密变换攻击(解决方法:选用足够复杂的加密算法) 4、四种常见攻击(1)唯密文攻击:仅知道一些密文(2)已知明文攻击:知道一些密文和相应的明文(3)选择明文攻击:密码分析者可以选择一些明文并得到相应的密文 (4)选择密文攻击:密码分析者可以选择一些密文,并得到相应的明文【注:①以上攻击都建立在已知算法的基础之上;②以上攻击器攻击强度依次增加;③密码体制的安全性取决于选用的密钥的安全性】第二章 古典密码(一)单表古典密码1、定义:明文字母对应的密文字母在密文中保持不变2、基本加密运算设q 是一个正整数,}1),gcd(|{};1,...,2,1,0{*=∈=-=q k Z k Z q Z q q q(1)加法密码 ①加密算法:κκ∈∈===k X m Z Z Y X q q ;,;对任意,密文为:q k m m E c k m od )()(+== ②密钥量:q (2)乘法密码 ①加密算法:κκ∈∈===k X m Z Z Y X q q ;,;*对任意,密文为:q km m E c k m od )(== ②解密算法:q c k c D m k mod )(1-==③密钥量:)(q ϕ (3)仿射密码 ①加密算法:κκ∈=∈∈∈===),(;},,|),{(;21*2121k k k X m Z k Z k k k Z Y X q q q 对任意;密文q m k k m E c k m od )()(21+==②解密算法:q k c k c D m k mod )()(112-==-③密钥量:)(q q ϕ (4)置换密码 ①加密算法:κσκ∈=∈==k X m Z Z Y X q q ;,;对任意上的全体置换的集合为,密文)()(m m E c k σ==②密钥量:!q③仿射密码是置换密码的特例 3.几种典型的单表古典密码体制 (1)Caeser 体制:密钥k=3 (2)标准字头密码体制: 4.单表古典密码的统计分析(二)多表古典密码1.定义:明文中不同位置的同一明文字母在密文中对应的密文字母不同2.基本加密运算 (1)简单加法密码 ①加密算法:κκ∈=∈====),...,(,),...,(,,11n n n nq n q n n k k k X m m m Z Z Y X 对任意设,密文:),...,()(11n n k k m k m m E c ++==②密钥量:nq (2)简单乘法密码 ①密钥量:n q )(ϕ 1.简单仿射密码①密钥量:n n q q )(ϕ2.简单置换密码 ①密钥量:nq )!( (3)换位密码 ①密钥量:!n(4)广义置换密码①密钥量:)!(nq(5)广义仿射密码 ①密钥量:n n r q3.几种典型的多表古典密码体制 (1)Playfair 体制: ①密钥为一个5X5的矩阵②加密步骤:a.在适当位置闯入一些特定字母,譬如q,使得明文字母串的长度为偶数,并且将明文字母串按两个字母一组进行分组,每组中的两个字母不同。
密码学复习

•只要选择合适的反馈函数便可使序列的周期达到 最大值2n -1,周期达到最大值的序列称为m序列。
反馈函数:b1+b3
4.4 线性移位寄存器的一元多项式表示
设n级线性移位寄存器的输出序列{ ai } 满足递推关系 ak+n=c1 ak+n-1 c2 ak+n-2 ... cn ak,
对任何k≥1成立。将这种递推关系用一个一 元高次多项式
表4.1 三级反馈移位 寄存器的输出状态表
图4.4 一个3级反馈移位寄存器
•三级反馈移位寄存器,其初始状态为(a1,a2,a3)=(1,0,1),
•输出可由表4.1求出,其输出序列为10111011101…,周期为4。
线性反馈移位寄存器(LFSR)
如果移位寄存器的反馈函数f(a1, a2, …, an)是a1, a2, …, an的线性函数,则称之为线性 反馈移位寄存器(LFSR)。
现代密码学理论与实践05 50/28
2013-8-15
扩展欧几里德算法求逆
元素{01}是乘法单位元。对任意次数小于8 的非零二元多项式b(x),其 乘法逆元记为b-1(x),可通过下述方法找到:使用扩展欧几里德算法计 算多项式a(x)和c(x)使得 b(x)a(x)+m(x)c(x)=1 m(x) = x8 + x4 + x3 + x +1
习题
1、对于线性替代密码,设已知明码字母J(9) 对应于密文字母P(15),即9k mod 26 = 15, 试 计算密钥k以破译此密码。
答: k=9-1*15 mod 26 9-1 mod 26=3 k=3*15 mod 26=19
第四章 序列密码
4.1 序列密码的基本概念
密码学知识点总结csdn

密码学知识点总结csdn1. 密码学基础密码学基础包括对称加密、非对称加密、哈希函数、消息认证码等概念的介绍。
对称加密即加密和解密使用相同的密钥,常用算法有DES、AES、RC4等;非对称加密则分为公钥加密和私钥解密,常用算法有RSA、ECC等;哈希函数则是将任意长度的消息压缩为固定长度的摘要信息,常用算法有MD5、SHA-1、SHA-256等;消息认证码是在消息传输中保障数据完整性的重要手段,主要分为基于对称加密的MAC和基于非对称加密的数字签名。
2. 随机数生成密码学安全性的基础在于随机数的生成,常用的随机数生成算法有伪随机数生成器(PRNG)和真随机数生成器(TRNG)。
PRNG是通过确定性算法生成随机数,安全性依靠其内部逻辑结构;TRNG则是依靠物理过程生成随机数,如放射性衰变、指纹图像等,安全性更高。
密码学攻击主要分为三类:密码分析攻击、椭圆曲线攻击和量子攻击。
密码分析攻击是通过推测、猜测等方法攻破密码;椭圆曲线攻击是因为非对称加密算法中的基于椭圆曲线离散对数问题存在可解性,从而破解密码;量子攻击则是通过量子计算机的强大计算能力破解传统密码学算法。
4. 密码学综合应用密码学在实际应用中广泛应用于电子邮件加密、数字证书、数字签名、数字支付、VPN安全通信等领域。
其中,AES算法被广泛应用于SSL/TLS等加密通信协议中;RSA算法则是数字证书和电子邮件加密中最常用的算法;数字签名则应用于身份认证、电子合同、电子票据等领域;数字支付则依赖于密码学原理来保证支付的安全性。
5. 密码学的未来发展当前,密码学面临着来自量子计算机的挑战,需要进一步开发抗量子攻击的加密算法。
同时,在移动互联网、物联网等领域中,新的安全需求也对密码学技术提出了挑战。
未来发展的重点可能包括量子密码学研究、密码学与人工智能技术的结合等方面。
总之,密码学是信息安全的重要组成部分,掌握相关知识点将有助于提高信息安全意识和防范风险能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)秘钥分配方案假定TA与每个网络用户共享一个秘密秘钥
①Needham-Schroeder会话秘钥方案
Needham-Schroeder方案的已知会话秘钥攻击:
②Kerberos密钥分发方案
NS方案存在Denning-Sacco攻击,但Kerberos方案通过检查时间和有效期来限定了实施Denning-Sacco攻击的时间周期
第二章香农理论
5.密码体制安全性准则
计算安全性(Computational security)
可证明安全(Provable Security)
无条件安全(unconditional security)
第三章分组密码
6.SPN网络概念文字描述加密过程计算:
SPN网络是指在迭代加密过程中使用了代换和置换的加密网络。
注意gcd(b, (n))=1 ,否则b的逆不存在
21.(1)RSA正确性的证明
① ,由于 ,所以有
② n/ ,
综上,可证RSA是正确的
(2)对RSA的攻击
(1)分解n
一般推荐p,q取512比特的素数,n就是1024比特的模数,分解超过了现有因子算法的能力
(2)计算 (n),但不比因式分解n容易
n = pq , (n)= (p-1)(q-1)
27.RSA签名认证方案
K={(n,p,q,a,b): n = pq, p,q为素数ab (mod )}
(n,b)为公钥,(p,q,a)为私钥
定义
以及 ,其中x,y
验证算法使用RSA的加密规则
伪造签名:
(1)选择y← ,并计算 ,则y是x的有效签名(唯秘钥攻击的存在性造)
(2)已知合法消息签名对(x1,y1),(x2,y2),可以构造x1x2的签名为y1y2(已知消息攻击的存在性伪造)
17.HMAC(找到伪造)很有可能出课后练习题?
第五章RSA密码体制Rabin
18.PPT上的照片
19.数论知识如计算28-1 mod 75
(1)扩展欧几里Extended Euclidean Algorithm(a, b)
,
例:计算28-1 mod 75
i
075 10
1 28 2 0 1
2 19 1 1-2
SPN网络的主要过程要求掌握其中一步的计算,给出S盒和P盒。见教材P59例3.1
SPN有Nr轮,在每一轮(最后一轮有所不同),先用异或操作混入该轮的轮秘钥,再用 进行m次代换,然后用 进行一次置换
7.SPN的线性密码分析思想
(1)通过分析S-盒,找到一个明文比特子集与最后一轮即将进行代换的输入状态比特子集之间的一个概率线性关系,即存在一个比特子集使得其中元素的异或表示出非随机的分布。
Pad(x)是由函数填充对x作用后得到的,如:填充|x|的值,并填充一些额外的比特(比如0)
(2)Merkle-Damgard(课本P102)
15.SHA-1参数:消息摘要大小160,消息大小x小于2^64,分组大小512,步数80。
16.Hash函数的安全性
对于长度为n的理想HASH算法,找到原像、弱碰撞和强碰撞需要穷举的消息数分别为:
(3)已知x,计算x x1x2modn ,分别请求计算x1和x2的签名y1和y2,则x的签名为y1y2
(选择消息攻击的选择性伪造)
28.签名和Hash函数
对消息x签名,首先生成消息摘要z=h(x),然后计算z的签名y= 。将有序对(x,y)在信道上传输。验证者首先通过公开Hash函数重构消息摘要z=h(x),然后检查 。
解密密钥不能从加密密钥推算出来,反过来不一定成立。
2.加密算法的安全性
加密算法的安全性由能抵抗的攻击和达到的安全目标来衡量
(1)加密算法的安全目标:
攻击者不能获得解密密钥
攻击者不能获得明文
攻击者不能获得明文的任何部分信息
攻击者不能获得明文的任何函数
(2)假设攻击者已知加密算法的实现细节,在未知密钥的情况下,攻击密码系统的强度由弱到强的四种基本攻击:
(2)假定希望破解的密钥,然后在该密钥下验证概率线性关系,最后确定密钥的部分比特。
线性密码分析是已知明文攻击。
8.Feistel密码结构,只要求掌握计算其中一步:
9.(1)DES加密算法标准
基本参数:DES是一个16轮的Feistel型密码,分组长度为64,用一个56比特的密钥来加密一个64比特的明文串,并获得一个64比特的密文串。
DES加密过程不要求掌握。
S盒的查询(课本例3.4)
(2)AES加密标准概要
算法基本参数:
AES分组长度为128,迭代型密码,轮数依赖于秘钥长度,有三种可选秘钥长度
密钥长度128,加密轮数10;
密钥长度192,加密轮数12;
密钥长度256,加密轮数14;
AES的4个步骤查表(步骤MixColumns不考)
(1)实数上的椭圆曲线
点的运算如给出曲线与x算出y, 等要求掌握椭圆曲线上的加法运算。
方程
情形1
情形2 , 时,第三点就是O,(x,y)+(x,-y) = O
情形3 ,
(2)模素数的椭圆曲线(课本P205例6.8)
25.Diffie-Hellman问题(难度关系)
CDHDDH问题
第七章签名方案
26.数字签名介绍攻击目标
选择密文攻击(Chosen-ciphertext attack):分析者可以根据破解需要,选择系列密文并获得对应的明文,恢复出其他密文的明文或者密钥。
3.密码学提供的安全服务
机密性(Confidentiality),又称私密性
机密性是指保证信息与信息系统不被非授权者所获取与使用。
完整性(integrity)
唯密文攻击(Ciphertext-only attack):分析者通过同一密钥加密的密文,恢复出明文或者密钥。
已知明文攻击(Known-plaintext attack):分析者通过同一密钥加密的明文/密文对,恢复出其他密文的明文或者密钥。
选择明文攻击(Chosen-plaintext attack):分析者可以根据破解需要,选择系列明文并获得对应的密文,恢复出其他密文的明文或者密钥。
(1)数字签名介绍
(2)签名方案的攻击模型
1)唯密钥攻击(key-only attack)
2)已知消息攻击(Know Message Attack)
2)选择消息攻击(Chosen Message Attack)
(3)攻击者的目标
1)选择性伪造(Selective Forgery)
2)存在性伪造(Existential Forgery)
过程:
1.给定一个明文x,将State初始化为x,并进行AddRoundKey操作。
2.对于前Nr-1轮中的每一轮,即从第一轮到倒数第二轮,用S盒对State进行一次代换操作SubBytes(查S盒);对State做一次置换ShiftRows,再对State做一次操作MixColumns,然后进行AddRoundKey操作。
密钥协商是指网络用户通过一个交互协议来建立会话密钥的情形。这样的协议称为密钥协商方案,并且记为KAS。密钥协商可以基于对称密码体制,也可以基于公钥密码体制,通常不需要一个在线的TA。
(2)Diffie-Hellman秘钥协商方案
(3)STS端-端秘钥协商方案
(4)MTI/A0密钥协商方案
29.椭圆曲线数字签名
第八章身份识别和实体认证
30.实体认证
(1)不安全的挑战-响应方案
(2)安全问题(并行会话攻击)
Oscar正在向Bob模仿Alice,Oscar发起第二个会话,主动让Bob来识别自己
(3)安全的挑战-响应方案(身份标识ID抵抗并行会话攻击)
由于K只有Alice和Bob知道,Oscar不可能构造出MACk(ID(Alice||r))
安全性证明(课本P279)
(4)无法抵抗的攻击
31.双向认证(很大可能出习题)
(1)内容
(2)不安全的交互挑战-响应方案
攻击:把一个会话中的消息重用到另一个会话的不同消息流中
(3)安全的交互挑战-响应方案:保证每个消息流以不同的方式计算
32.公钥身份识别方案
(1)证书
Bob想确认Alice公钥( )的真实性,Alice把证书发给Bob,Bob通过验证TA的签名: (ID(Alice)|| ,s)= true
(2)安全的公钥身份识别方案
(3)不安全的公钥身份识别方案
并行会话攻击:第三个消息流签名的构造方式与第二个消息流构造方式相同3
第九章秘钥分配秘钥协商方案
33.(1)会话秘钥分发
在会话密钥分发中,当网络用户请求会话密钥时,一个在线的TA选择会话密钥并通过一个交互协议分发给他们。这样的协议称为会话密钥分发方案并记为S。会话秘钥用于在指定的、相当短的时间内加密信息。会话秘钥由TA利用事先分发的秘密秘钥进行加密(假定每个网络用户拥有一个秘密秘钥,其值为TA所知)
3 9 2-1 3
4 1 9 3-8
3×75– 8×28=1 , mod 75 = -8 mod 75 = 67
(2)中国剩余定理
(3)乘法群的相关定理,本原元的证明
的阶为 (n), 为模n的余数与n互素的全体
20.RSA的过程见教材P136例5.5
和
其中n=p×q, ab mod (n))
公钥:n,b私钥:a,p,q
③Bellare-Rogaway方案
方案没有实现密钥确认。也就是说,Alice/Bob在收到会话密钥后无法确认Bob/Alice也获得了会话密钥
该方案可以保证任何其他人都不能计算出新的会话密钥。否则,就存在一个多项式时间算法要么可以攻陷加密算法,要么可以攻陷MAC算法。(证明见PPT18)
