勾股定理全章复习
勾股定理全章
勾股定理及其逆定理1.勾股定理（从形到数）：在△ABC中，∠C=90°(通常∠C=90°)，∠A、∠B、∠C的对边为a、b、c。
则a2＋b2=c2。
变式如下：⑴c= 。
（已知a、b，求c）⑵a= 。
（已知b、c，求a）⑶b= 。
（已知a、c，求b）2.记住一些勾股数。
3.如图，直角△ABC的主要性质是：∠C=90°，（用几何语言表示）⑴两锐角之间的关系：；⑵若D为斜边中点，则斜边中线；⑶若∠B=30°，则∠B的对边和斜边：；∠B=45°，则两直角边⑷三边之间的关系：（结合以上知识可在直角三角形中（1）知两边求另一边（2）知一边及两边关系，求边（3）知一边及一特殊角度求边。
）例1：在Rt△ABC，∠C=90°⑴已知a=b=5,求c。
⑵已知a=1,c=2, 求b。
⑶已知c=17,b=8, 求a。
⑷已知a：b=1：2,c=5, 求a。
⑸已知b=15，∠A=30°，求a，c。
（注意;（1）数形结合思想，方程思想运用）练习：⑴在Rt△ABC，∠C=90°，a=8，b=15，则c= 。
⑵在Rt△ABC，∠B=90°，a=3，b=4，则c= 。
⑶在Rt△ABC，∠C=90°，c=10，a：b=3：4，则a= ，b= 。
（5）求出下列直角三角形中未知的边．（6）已知直角△ABC 中，∠C=90°.S 3=25,S 2=144则S 1为多少？例2：已知直角三角形的两边长分别为5和12，求第三边。
（注意;分类讨论思想）练习：1（1）已知直角三角形的两边长分别为3cm 和5cm ，，则第三边长为。
（2）已知等边三角形的边长为2cm ，则它的高为 ，面积为 。
2．已知：如图，在△ABC 中，∠C=60°，AB=34，AC=4，AD 是BC 边上的高，求BC 的长。
610ACB 245°A230°S 2S 1S 33．已知等腰三角形腰长是10，底边长是16，求这个等腰三角形的面积。
勾股定理全章综合复习
勾股定理全章综合复习A. 1个B . 2个C . 3个D . 4个(2)已知a, b, c为厶ABC三边，且满足(a2—b2)(a2+b2—c2)= 0,则它的形状为( )A.直角三角形B.等腰三角形C.等腰直角三角形 D.等腰三角形或直角三角形(3)三角形的三边为a、b、c,由下列条件不能判断它是直角三角形的是( )2 2 2A. a: b: c=8 : 16 :仃B. a - b =cC. a2=(b+c)(b-c)D. a: b: c=13 : 5 : 12(4)三角形的三边长为(a+b ) 2=c2+2ab,则这个三角形是( )A.等边三角形；B.钝角三角形；C.直角三角形；D.锐角三角形(5)直角三角形中一直角边的长为9,另两边为连续自然数，则直角三角形的周长为________(6)若厶ABC的三边长a,b,c满足a2 b2+c2 +200 = 12a + 16b + 20c,试判断△ ABC的形状。
例3:求最大、最小角的问题(1)若三角形三条边的长分别是7,24,25,则这个三角形的最大内角是度。
(2)已知三角形三边的比为1 : 3 : 2,则其最小角为。
考点三：勾股定理的应用例1:面积问题（1）下图是一株美丽的勾股树，其中所有的四边形都 是正方形，所有的三角形都是直角三角形，若正方形A 、 B 、C 、D 的边长分别是3、 3）（2）如图，△ ABC 为直角三角形，分别以 为直径向外作半圆，用勾股定理说明三个半圆的面积 关系，可得（ ） A. S 1+ S 2> S 3B. S 1+ S 2= S 3C. S 2+S 3< S ID.以上都不是 （3 ）如图所示，分别以直角三角形的三边向外作三个 正三角形，其面积分别是 S 、S 、S,贝陀们之间的关 系是（ ）A. S 1- S 2= S 3B. S 1+ S 2= S 3C. S 2+Sv S 1D. S 2- S 3=S 5、2、3,则最大正方形ED.（图AB, BC47 2)例2:求长度问题（1）小明想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开5米后, 发现下端刚好接触地面，求旗杆的高度。
北师大版八年级上册数学第一章勾股定理全章知识点及习题
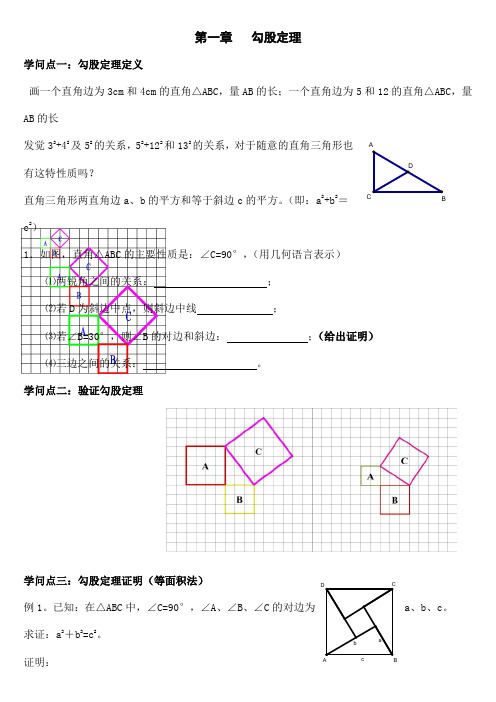
cbaD CA B第一章 勾股定理学问点一：勾股定理定义画一个直角边为3cm 和4cm 的直角△ABC ，量AB 的长；一个直角边为5和12的直角△ABC ，量AB 的长发觉32+42及52的关系，52+122和132的关系，对于随意的直角三角形也有这特性质吗？直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
（即：a 2+b 2＝c 2）1．如图，直角△ABC 的主要性质是：∠C=90°，（用几何语言表示）⑴两锐角之间的关系： ； ⑵若D 为斜边中点，则斜边中线 ；⑶若∠B=30°，则∠B 的对边和斜边： ；（给出证明） ⑷三边之间的关系： 。
学问点二：验证勾股定理学问点三：勾股定理证明（等面积法）例1。
已知：在△ABC 中，∠C=90°，∠A 、∠B 、∠C 的对边为a 、b 、c 。
求证：a 2＋b 2=c 2。
证明：ACBD例2。
已知：在△ABC 中，∠C=90°，∠A 、∠B 、∠C 的对边为a 、b 、c 。
求证：a 2＋b 2=c 2。
证明：学问点四：勾股定理简洁应用 在Rt △ABC 中，∠C=90°(1) 已知：a=6, b=8，求c (2) 已知：b=5，c=13，求a学问点五：勾股定理逆定理假设三角形的三边长为c b a ,,，满意222c b a =+，那么，这个三角形是直角三角形． 利用勾股定理的逆定理判别直角三角形的一般步骤： ①先找出最大边（如c ）②计算2c 及22a b +，并验证是否相等。
若2c =22a b +，则△ABC 是直角三角形。
若2c ≠22a b +，则△ABC 不是直角三角形。
1.下列各组数中，以a ，b ，c 为边的三角形不是Rt △的是（ ） A.a=7,b=24,c=25 B.a=7,b=24,c=24C.a=6,b=8,c=10D.a=3,b=4,c=52.三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A. 等边三角形B. 钝角三角形C. 直角三角形D. 锐角三角形 3.已知0)10(862=-+-+-z y x ,则由此z y x ,,为三边的三角形是 三角形. 学问点六：勾股数bbba（1）满意222c b a =+的三个正整数，称为勾股数．（2）勾股数中各数的一样的整数倍，仍是勾股数，如3、4、5是勾股数，6、8、10也是勾股数．（3）常见的勾股数有：①3、4、5②5、12、13；③8、15、17；④7、24、25； ⑤11、60、61；⑥9、40、41．1.设a 、b 、c 是直角三角形的三边,则a 、b 、c 不行能的是（ ）.A.3,5,4B. 5,12,13C.2,3,4D.8,17,151.若线段a ，b ，c 组成Rt △，则它们的比可以是（ ）A.2∶3∶4B.3∶4∶6C.5∶12∶13D.4∶6∶7学问点七：确定最短路途1.一只长方体木箱如图所示，长、宽、高分别为5cm 、4cm 、3cm,有一只甲虫从A 动身，沿外表爬到C '，最近间隔 是多少？2.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A 爬到点B 处吃食,要爬行的最短路程（π 取3）是 .学问点八：逆定理推断垂直1．在△ABC 中，已知AB 2－BC 2＝CA 2，则△ABC 的形态是( )A ．锐角三角形；B ．直角三角形；C ．钝角三角形；D ．无法确定．2．如图，正方形网格中的△ABC ，若小方格边长为1，则△ABC 是( )A ．直角三角形B ．锐角三角形C ．钝角三角形D ．以上答案都不对学问点九：勾股定理应用题1.在我国古代数学著作《九章算术》中记载了一道好玩的问题，这个问题的意思是：有一个水ABCD A 'B 'C 'D 'ABC5米3米池，水面是一个边长为10尺的正方形，在水池正中央有一根新生的芦苇，它高出水面1尺，假设把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，请问这个水池的深度和这根芦苇的长度各是多少？2.如图为某楼梯,测得楼梯的长为5米,高3米,安排在楼梯外表铺地毯,地毯的长度至少须要________米.3.一根直立的桅杆原长25m，折断后，桅杆的顶部落在离底部的5m处，则桅杆断后两局部各是多长？4.某中学八年级学生想知道学校操场上旗杆的高度，他们发觉旗杆上的绳子垂到地面还多1米，当他们把绳子的下端拉开5米后，发觉下端刚好触地面，你能帮他们把旗杆的高度和绳子的长度计算出来吗？综合练习一一、选择题1、下面几组数:①7,8,9;②12,9,15;③m 2 + n 2, m 2 – n 2, 2mn(m,n 均为正整数,m >n);④2a ,12+a ,22+a .其中能组成直角三角形的三边长的是( )A.①②;B.①③;C.②③;D.③④2已知一个Rt △的两边长分别为3和4，则第三边长的平方是（ ）A.25B.14C.7D.7或253.三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A. 等边三角形;B. 钝角三角形;C. 直角三角形;D. 锐角三角形. 4.△ABC 的三边为a 、b 、c 且(a+b)(a-b)=c 2，则( )A.a 边的对角是直角B.b 边的对角是直角C.c 边的对角是直角D.是斜三角形5.以下列各组中的三个数为边长的三角形是直角三角形的个数有（ ）①6、7、8，②8、15、17，③7、24、25，④12、35、37，⑤9、40、41 A 、1个 B 、2个 C 、3个 D 、4个6.将直角三角形的三边扩大一样的倍数后，得到的三角形是 ( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.不是直角三角形7.若△ABC 的三边a 、b 、c 满意(a-b)(a 2+b 2-c 2)=0，则△ABC 是 ( ) A.等腰三角形 B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形8.如图，∠C =∠B =90°，AB =5，BC =8，CD =11，则AD 的长为 （ ）A 、10B 、11C 、12D 、139.如图、山坡AB 的高BC =5m ，程度间隔 AC =12m ，若在山坡上每隔0.65m 栽一棵茶树,则从上到下共 ( )A 、19棵B 、20棵C 、21棵D 、22棵10.Rt △ABC 中，∠C =90°，∠A 、∠B 、∠C 所对的边分别是a 、b 、c ，若c =2，则2a +2b +2c 的值是 （ ）A 、6B 、8C 、10D 、4 11.下列各组数据中，不能构成直角三角形的一组数是（ ）Ａ、9，12，15 B 、45，1，43 C 、0.2，0.3，0.4 D 、40，41，9 12.已知，一轮船以16海里/时的速度从港口A 动身向东北方向航行，另一轮船以12海里/时的速度同时从港口A 动身向东南方向航行，分开港口2小时后，则两船相距（ ）A.25海里B.30海里C.35海里D.40海里二、填空题1.在Rt △ABC 中，∠C=90°，①若a=5，b=12，则c=___________；②若a=15，c=25，则b=___________；③若c=61，b=60，则a=__________；④若a ∶b=3∶4，c=10则S Rt △ABC =________2.现有长度分别为2cm 、3cm 、4cm 、5cm 的木棒，从中任取三根，能组成直角三角形，则其周长为 cm ．3.勾股定理的作用是在直角三角形中，已知两边求 ；勾股定理的逆定理的作用是用来证明 ．4.如图中字母所代表的正方形的面积：A = B = ．400225AB812255.在△ABC中，∠C＝90°，若a＝5，b＝12，则c＝．6.△ABC中，AB=AC=17cm，BC=16cm，则高AD= ，S△ABC = 。
勾股定理中考章节复习(知识点+经典题型分析总结)
勾股定理中考章节复习(知识点+经典题型分析总结)【知识要点】1. 勾股定理的概念：如果直角三角形的两直角边长分别为a ，b ，斜边长为c ，那么 a 2＋b 2＝c 2. 即直角三角形两直角边的平方和等于斜边的平方。
2. 勾股定理的逆定理：如果三角形的三边长a ，b ，c 有下面关系：a 2＋b 2＝c 2，那么这个三角形是直角三角形，其中c 为斜边。
3. 勾股数：①满足a 2＋b 2＝c 2的三个正整数叫做勾股数（注意：若a ，b ，c 、为勾股数，那么ka ，kb ，kc 同样也是勾股数组。
）②记住常见的勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25；8,15,17等 ③用含字母的代数式表示n 组勾股数：221,2,1n n n -+（2,n ≥n 为正整数）；2221,22,221n n n n n ++++（n 为正整数）2222,2,m n mn m n -+（,m n >m ，n 为正整数）4.命题、定理、证明⑴ 命题的概念：判断一件事情的语句，叫做命题。
理解：命题的定义包括两层含义：（1）命题必须是个完整的句子；（2）这个句子必须对某件事情做出判断。
⑵ 命题的分类（按正确、错误与否分）真命题（正确的命题）命题假命题（错误的命题）所谓正确的命题就是：如果题设成立，那么结论一定成立的命题。
所谓错误的命题就是：如果题设成立，不能证明结论总是成立的命题。
⑶ 公理：人们在长期实践中总结出来的得到人们公认的真命题，叫做公理。
⑷ 定理：用推理的方法判断为正确的命题叫做定理。
⑸ 证明：判断一个命题的正确性的推理过程叫做证明。
⑹ 证明的一般步骤① 根据题意，画出图形。
② 根据题设、结论、结合图形，写出已知、求证。
③ 经过分析，找出由已知推出求证的途径，写出证明过程。
AB C a b c 弦股勾A BD 5.判断直角三角形：（1）有一个角为90°的三角形是直角三角形。
勾股定理全章复习教学设计
勾股定理全章复习一、复习要求：1．体验勾股定理的探索过程；已知直角三角形的两边长，会求第三边长。
2．会用勾股定理知识解决简单问题；会用勾股定理逆定理判定直角三角形。
3．会用勾股定理解决有关的实际问题。
二、知识网络：二、知识梳理：1、勾股定理(1)重视勾股定理的三种叙述形式：①在直角三角形斜边上的正方形等于直角边上的两个正方形(《几何原本》)．②直角三角形直角边上的两个正方形的面积之和等于斜边上的正方形的面积．③直角三角形斜边长度的平方，等于两个直角边长度平方之和．从这三种提法的意义来看，勾股定理有“形的勾股定理”和“数的勾股定理”之分。
(2)定理的作用：①已知直角三角形的两边，求第三边。
②证明三角形中的某些线段的平方关系。
③作长为的线段。
勾股定理揭示的是平面几何图形本身所蕴含的代数关系。
利用勾股定理探究长度为，，……的无理数线段的几何作图方法，并在数轴上将这些点表示出来，进一步反映了数与形的互相表示、相互交融，加深对无理数概念的直观认识。
(3)勾股定理的证明：经典证法有：①欧几里得证法②赵爽《勾股圆方图注》证法③刘徽《青朱出入图》证法④美国总统加菲的证明⑤印度婆什迦罗的证明⑥面积法证明；除此之外，还有文字证明、拼图证明和动态证明。
(4)勾股定理的应用：勾股定理只适用于直角三角形，首先分清直角及其所对的斜边。
当已知中没有直角时，可作辅助线，构造直角三角形后，再运用勾股定理解决问题。
求线段的长度，常常综合运用勾股定理和直角三角形的其它性质，等腰三角形的性质，轴对称的性质来解决。
2、勾股定理的逆定理(1)勾股定理的逆定理的证明方法，也是学生不熟悉的，引导学生用所学过的全等三角形的知识，通过构造一个三角形与直角三角形全等，达到证明的目的。
(2)逆定理的作用：判定一个三角形是否为直角三角形。
(3)勾股定理的逆定理是把数转化为形，是利用代数计算来证明几何问题。
要注意叙述及书写格式。
运用勾股定理的逆定理的步骤：①首先确定最大的边(如c)②验证：与是否具有相等关系：若，则△ABC是以∠C为90°的直角三角形。
第18章 勾股定理的逆定理及全章复习
18.2 勾股定理的逆定理（一）教学目标1．体会勾股定理的逆定理得出过程，掌握勾股定理的逆定理。
2．探究勾股定理的逆定理的证明方法。
3．理解原命题、逆命题、逆定理的概念及关系。
重点：掌握勾股定理的逆定理及简单应用。
难点：勾股定理的逆定理的证明。
教学过程：一.预习新知（阅读教材P73 — 75 , 完成课前预习）1.三边长度分别为3 cm 、4 cm 、5 cm 的三角形与以3 cm 、4 cm 为直角边的直角三角形之间有什么关系？你是怎样得到的？2.你能证明以6cm 、8cm 、10cm 为三边长的三角形是直角三角形吗？3.如图18.2-2，若△ABC 的三边长a 、b 、c 满足222c b a =+，试证明△ABC 是直角三角形，请简要地写出证明过程．4.此定理与勾股定理之间有怎样的关系？ （1）什么叫互为逆命题（2）什么叫互为逆定理（3）任何一个命题都有 _____，但任何一个定理未必都有 __ 5.说出下列命题的逆命题。
这些命题的逆命题成立吗？ （1） 两直线平行，内错角相等；（2） 如果两个实数相等，那么它们的绝对值相等； （3） 全等三角形的对应角相等；（4） 角的内部到角的两边距离相等的点在角的平分线上。
二．课堂展示例1：判断由线段a 、b 、c 组成的三角形是不是直角三角形： （1）17,8,15===c b a ； （2）15,14,13===c b a ． （3）25,24,7===c b a ； （4）5.2,2,5.1===c b a ；三.随堂练习1.完成书上P75练习1、2图18.2-22.如果三条线段长a,b,c 满足222b c a -=，这三条线段组成的三角形是不是直角三角形？为什么？3.A,B,C 三地的两两距离如图所示，A 地在B 地的正东方向，C 地在B 地的什么方向？4.思考：我们知道3、4、5是一组勾股数，那么3k 、4k 、5k （k 是正整数）也是一组勾股数吗？一般地，如果a 、b 、c 是一组勾股数，那么ak 、bk 、ck （k 是正整数）也是一组勾股数吗？四.课堂检测1.若△ABC 的三边a ，b ，c 满足条件a 2+b 2+c 2+338=10a+24b+26c ，试判定△ABC 的形状．2.一根24米绳子，折成三边为三个连续偶数的三角形，则三边长分别为多少米？此三角形的形状为？3.已知：如图，在△ABC 中，CD 是AB 边上的高，且CD 2=AD ·BD 。
《勾股定理》专题复习(含答案)
第一章《勾股定理》专项练习专题一：勾股定理考点分析：勾股定理单独命题的题目较少，常与方程、函数，四边形等知识综合在一起考查，在中考试卷中的常见题型为填空题、选择题和较简单的解答题典例剖析例1．（1）如图1是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸（单位：mm ），计算两圆 孔中心A 和B 的距离为______mm ．（2）如图2，直线l 上有三个正方形a b c ，，， 若a c ，的面积分别为5和11，则b 的面积为（ ）Ａ．4 Ｂ．6Ｃ．16Ｄ．55分析：本题结合图中的尺寸直接运用勾股定理计算即可．解：（1）由已知得：AC=150-60=90，BC=180—60=120，由勾股定理得: AB 2=902+1202=22500,所以AB=150（mm ）（2)由勾股定理得：b=a+c=5+11=16，故选C ．点评：以上两例都是勾股定理的直接运用，当已知直角三角形的两边,求第三边时，往往要借助于勾股定理来解决．例2．如图3，正方形网格的每一个小正方形的边长都是1，试求122424454A E A A E C A E C ++∠∠∠的度数．解：连结32A E ．32122222A A A A A E A E ==，，32212290A A E A A E ∠=∠=，322122Rt Rt A A E A A E ∴△≌△（SAS ）．322122A E A A E A ∴∠=∠．由勾股定理,得:4532C E C E ===，4532A E A E ===,44332A C A C ==,445332A C E A C E ∴△≌△（SSS ）．323454A E C A E C ∴∠=∠图1 图21A2A3A 4A 5A 5E 2E 1E 1D 1C 1B 4C1A 2A 3A4A 5A 5E2E 1E1D 1C 1B 4C 3C 2C图3122424454324424323224A E A A E C A E C A E C A E C A E C A E C ∴∠+∠+∠=∠+∠+∠=∠．由图可知224E C C △为等腰直角三角形．22445A E C ∴∠=． 即12242445445A E A A E C A E C ∠+∠+∠=．点评：由于在正方形网格中，它有两个主要特征：（1）任何格点之间的线段都是某正方形或长方形的边或对角线，所以格点间的任何线段长度都能求得．（2）利用正方形的性质，我们很容易知道一些特殊的角，如450、900、1350，便一目了然．以上两例就是根据网格的直观性，再结合图形特点，运用勾股定理进行计算，易求得线段和角的特殊值，重点考查学生的直觉观察能力和数形结合的能力． 专练一：1、△ABC 中，∠A ：∠B ：∠C=2:1：1,a ，b ，c 分别是∠A 、∠B 、∠C 的对边，则下列各等式中成立的是（ ）（A ）222a b c +=；（B ）222a b =; （C)222c a =； (D ）222b a = 2、若直角三角形的三边长分别为2，4,x,则x 的可能值有（ ） （A ）1个； （B ）2个； (C ）3个； (D ）4个3、一根旗杆在离底面4.5米的地方折断，旗杆顶端落在离旗杆底部6米处，则旗杆折断前高为（ ）（A ）10.5米； （B ）7。
北师大八年级数学上册总复习(知识点+例题)
北师大版八年级数学上册知识点及典型习题讲解目录《勾股定理》全章复习与巩固 (2)《实数和二次根式》全章复习与巩固 (8)《平面直角坐标系》全章复习与巩固 (16)《平面直角坐标系》全章复习与巩固 (24)《二元一次方程组》 (32)《平行线的证明》全章复习与巩固 (41)《勾股定理》全章复习与巩固要点一、勾股定理 1.勾股定理：直角三角形两直角边的平方和等于斜边的平方.（即：） 2.勾股定理的应用勾股定理反映了直角三角形三边之间的关系，是直角三角形的重要性质之一，其主要应用是： （1）已知直角三角形的两边，求第三边；（2）利用勾股定理可以证明有关线段平方关系的问题； （3）解决与勾股定理有关的面积计算； （4）勾股定理在实际生活中的应用． 要点二、勾股定理的逆定理 1.勾股定理的逆定理如果三角形的三边长，满足，那么这个三角形是直角三角形. 要点诠释：应用勾股定理的逆定理判定一个三角形是不是直角三角形的基本步骤： （1）首先确定最大边，不妨设最大边长为； （2）验证：与是否具有相等关系：若，则△ABC 是以∠C 为90°的直角三角形； 若时，△ABC 是锐角三角形； 若时，△ABC 是钝角三角形． 2.勾股数满足不定方程的三个正整数，称为勾股数（又称为高数或毕达哥拉斯数），显然，以为三边长的三角形一定是直角三角形. 要点诠释：a b 、c 222a b c +=a b c 、、222a b c +=c 22a b +2c 222a b c +=222a b c +＞222a b c +＜222x y z +=x y z 、、知识点常见的勾股数：①3、4、5；②5、12、13；③8、15、17；④7、24、25；⑤9、40、41.如果()是勾股数，当t为正整数时，以为三角形的三边长，此三角形必为直角三角形. 观察上面的①、②、④、⑤四组勾股数，它们具有以下特征：1.较小的直角边为连续奇数；2.较长的直角边与对应斜边相差1.3.假设三个数分别为，且，那么存在成立.（例如④中存在＝24＋25、＝40＋41等）要点三、勾股定理与勾股定理逆定理的区别与联系区别：勾股定理是直角三角形的性质定理，而其逆定理是判定定理；联系：勾股定理与其逆定理的题设和结论正好相反，两者互为逆定理，都与直角三角形有关.类型一、勾股定理及逆定理的应用例1、如图所示，等腰直角△ABC中，∠ACB＝90°，E、F为AB上两点(E左F右)，且∠ECF＝45°，求证：.举一反三：a b c、、at bt ct、、a b c、、a b c<<2a b c=+27 29222AE BF EF+=典型例题【变式】已知凸四边形ABCD 中，∠ABC ＝30°，∠ADC ＝60°，AD ＝DC ，求证：.例2、如图，在△ABC 中，∠ACB=90°，AC=BC ，P 是△ABC 内的一点，且PB=1，PC=2，PA=3，求∠BPC 的度数．类型二、勾股定理及逆定理的综合应用222BD AB BC =+例3、如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积．例4、如图：正方形ABCD中，E是DC中点，F是EC中点.求证：∠BAF=2∠EAD.举一反三：【变式】如图所示，在△ABC中，AB：BC：CA=3：4：5，且周长为36cm，点P从点A开始沿边向B点以每秒1cm的速度移动；点Q从点B沿BC边向点C以每秒2cm的速度移动，如果同时出发，问过3秒时，△BPQ 的面积为多少？类型三、勾股定理的实际应用例5、如图所示，牧童在A处放牛，其家在B处，A、B到河岸的距离分别为AC＝400米，BD＝200米，CD ＝800米，牧童从A处把牛牵到河边饮水后再回家．试问在何处饮水，所走路程最短？最短路程是多少？举一反三：【变式】如图所示，正方形ABCD的AB边上有一点E，AE＝3，EB＝1，在AC上有一点P，使EP＋BP最短．求EP＋BP的最小值．例6、台风是一种自然灾害，它以台风中心为圆心，在周围数十千米范围内形成气旋风暴，有极强的破坏力．如图台风中心在我国台湾海峡的B处，在沿海城市福州A的正南方向240千米，其中心风力为12级，每远离台风中心25千米，台风就会减弱一级，如图所示，该台风中心正以20千米/时的速度沿北偏东30°方向向C移动，且台风中心的风力不变，若城市所受风力达到或超过4级，则称受台风影响．试问：（1）该城市是否会受到台风影响？请说明理由．（2）若会受到台风影响，那么台风影响该城市的持续时间有多长？（3）该城市受到台风影响的最大风力为几级？《实数和二次根式》全章复习与巩固要点一、平方根和立方根 类型 项目平方根立方根 被开方数 非负数任意实数符号表示性质一个正数有两个平方根，且互为相反数； 零的平方根为零； 负数没有平方根；一个正数有一个正的立方根；一个负数有一个负的立方根； 零的立方根是零；重要结论要点二、无理数与实数 有理数和无理数统称为实数. 1.实数的分类实数 要点诠释：（1）所有的实数分成三类：有限小数，无限循环小数，无限不循环小数．其中有限小数和无限循环小数统称有理数，无限不循环小数叫做无理数． （2等；②有特殊意义的数，如π； ③有特定结构的数，如0.1010010001…（3）凡能写成无限不循环小数的数都是无理数，并且无理数不能写成分数形式.a ±3a ⎩⎨⎧<-≥==≥=)0()0()0()(22a a a a a a a a a 333333)(aa a a aa -=-==⎧⎧⎫⎪⎪⎪⎨⎬⎪⎪⎪⎪⎨⎩⎭⎪⎧⎫⎪⎨⎬⎪⎩⎭⎩正有理数有理数零有限小数或无限循环小数负有理数正无理数无理数无限不循环小数负无理数532知识点2.实数与数轴上的点一 一对应数轴上的任何一个点都对应一个实数，反之任何一个实数都能在数轴上找到一个点与之对应. 3.实数的三个非负性及性质在实数范围内，正数和零统称为非负数。
八年级上册第一章《勾股定理》复习要点
八年级上册第一章《勾股定理》复习要点知识点一：勾股定理要点：⑴•勾股定理：直角三角形两直角边的平方和等于斜边的平方如果直角三角形的两条直角边分别为a、b,斜边为c,那么，a2 +b2 =c2，(2).历史文化:勾股定理在西方文献中又称毕达哥拉斯定理。
我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边为弦。
⑶格式：a=8 b=15 解：由勾股定理得c2 =a2 +b2=82+152=64+225=289•/ C>0 ••• C=17【典例精析】1•一架2.5m长的梯子斜靠在一竖直的墙上，这时梯足距墙脚0.7m •那么梯子的顶端距墙脚的距离是( )•(A)0.7m (B)0.9m (C)1.5m (D)2.4m2•如图，为了求出湖两岸A、B两点之间的距离，一个观测者在点C设桩，使三角形ABC恰好为直角三角形.通过测量，得到AC长160m, BC长128m ,则AB长________________ m.3•利用四个全等的直角三角形可以拼成如图所示的图形, 这个图形被称为弦图•从图中可以看到：大正方形面积=小正方形面积+四个直角三角形面积. 因而c2= +•化简后即为c2= __________ •知识点二：直角三角形的判别要点;*如果三角形三边长为a、b、c, c为最长边，只要符合a2 +b2 =c2，这个三角形是直角三角形。
(勾股定理逆定理，是直角三角形的判别条件)【典例精析】1、在下列长度的各组线段中，能组成直角三角形的是( )A.5、6、7B.1 、4、9C.5 、12、13D.5、11、122、满足下列条件的厶ABC不是直角三角形的是（A.b2=c2- a2B.a : b : c=3 : 4 : 5C. / C=Z A-Z BD. / A：/ B：/C=12： 13 : 1553、三角形的三边长分别是15, 36, 39,这个三角形是______ 三角形。
4、将直角三角形的三条边同时扩大4倍后，得到的三角形为（）A.直角三角形B. 锐角三角形C. 钝角三角形D. 不能确定5•有两棵树，一棵高6米，另一棵高2米, 两树相距5米•一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了多少米？知识点三：勾股定理的综合应用【典例精析】1、如图1- 1，在钝角VABC 中，CB = 9, AB = 17, AC = 10, AD BC 于D，求AD 的长。
勾股定理知识点总结
第18章 勾股定理复习一．知识归纳１．勾股定理内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：如果直角三角形的两直角边分别为a ，b ，斜边为c ，那么222a b c +=勾股定理的由来：勾股定理也叫商高定理，在西方称为毕达哥拉斯定理．我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦．早在三千多年前，周朝数学家商高就提出了“勾三，股四，弦五”形式的勾股定理，后来人们进一步发现并证明了直角三角形的三边关系为：两直角边的平方和等于斜边的平方 ２.勾股定理的证明勾股定理的证明方法很多，常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后，只要没有重叠，没有空隙，面积不会改变 ②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理 常见方法如下：方法一：4EFGH S S S ∆+=正方形正方形ABCD ，2214()2ab b a c ⨯+-=，化简可证．cbaHG F EDCB A方法二：bacbac cabcab四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=方法三：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证a bcc baE D CBA３.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征，因而在应用勾股定理时，必须明了所考察的对象是直角三角形 ４.勾股定理的应用①已知直角三角形的任意两边长，求第三边在ABC ∆中，90C ∠=︒，则22c a b =+，22b c a =-，22a c b =- ②知道直角三角形一边，可得另外两边之间的数量关系 ③可运用勾股定理解决一些实际问题5、利用勾股定理作长为的线段作长为、、的线段。
勾股定理知识点总结
第18章 勾股定理复习一．知识归纳１．勾股定理内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：如果直角三角形的两直角边分别为a ，b ，斜边为c ，那么222a b c +=勾股定理的由来：勾股定理也叫商高定理，在西方称为毕达哥拉斯定理．我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦．早在三千多年前，周朝数学家商高就提出了“勾三，股四，弦五”形式的勾股定理，后来人们进一步发现并证明了直角三角形的三边关系为：两直角边的平方和等于斜边的平方 ２.勾股定理的证明勾股定理的证明方法很多，常见的是拼图的方法 用拼图的方法验证勾股定理的思路是①图形进过割补拼接后，只要没有重叠，没有空隙，面积不会改变 ②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理 常见方法如下： 方法一：4EFGHS S S ∆+=正方形正方形ABCD ，2214()2ab b a c ⨯+-=，化简可证．方法二：四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=方法三：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证３.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征，因而在应用勾股定理时，必须明了所考察的对象是直角三角形 ４.勾股定理的应用①已知直角三角形的任意两边长，求第三边在ABC ∆中，90C ∠=︒，则c =b，a = ②知道直角三角形一边，可得另外两边之间的数量关系 ③可运用勾股定理解决一些实际问题c b aH G F ED CB Abacbac cabcab a bcc baE D CBA5、利用勾股定理作长为的线段作长为、、的线段。
勾股定理-全章
第一章勾股定理勾股定理：直角三角形的两直角边的平方和等于斜边的平方。
说明：若直角三角形的两条直角边为a、b，斜边为c，则a²+b²=c²。
勾股定理的逆定理：如果三角形的三边长a，b，c有下面关系：a²+b²=c²，那么这个三角形是直角三角形。
说明：根据勾股定理的逆定理，可以判定一个三角形是否是直角三角形：若已知三角形的三条边，只需验证最大边的平方是否等于另两边的平方和，若相等，则是直角三角形；若不等，则不是。
勾股数：满足a²+b²=c²的三个正整数，称为勾股数。
若a，b，c是一组勾股数，则ak，bk，ck（k为正整数），也必然是一组勾股数。
常用的几组勾股数有3,4,5；6,8,10；5,12,13；8,15,17等勾股定理的应用求两点之间的距离和线段的长度常构造直角三角形，利用勾股定理求解，求立体图形上两点之间的最短距离大致可分为：(1)圆柱形物体表面上的两点间的最短距离；(2)长方体或正方体表面上两点间的最短距离问题，直角三角形三边之间的关系不等量关系是：斜边的长大于每条直角边的长，其依据是“垂线段最短”；等量关系是：勾股定理，勾股定理是我们求直角三角形边长的依据，在直角三角形中，已知任意两边的长，可求第三边的长．直角三角形的判别直角三角形的判别有两种方法：(1)利用定义，判断一个三角形中有一个角是直角；(2)根据三角形一边的平方等于另外两边的平方和，来判定该三角形是直角三角形，勾股定理中的方程思想勾股定理三角形有一个直角的“形”的特征，转化为三边“数”的关系，因此它是数形结合的一个典范．对于一些几何问题，往往借助于勾股定理，利用代数方法来解决．把一条边的长设为未知数，根据勾股定理列出方程，解方程求出未知数的值，即使有时出现了二次方程，大多可通过抵消而去掉二次项．勾股定理中的转化思想在利用勾股定理计算时，常先利用转化的数学思想构造出直角三角形，比如立体图形上两点之间的最短距离的求解，解答时先把立体图形转化为平面图形，在平面图形中构造直角三角形求解，【例题1-勾股定理及其逆定理的基本用法】若直角三角形两直角边的比是3：4，斜边长是20，求此直角三角形的面积。
人教版初中数学八年级下册第十七章《勾股定理》复习教案
第17章勾股定理全章复习教学目标：1.会用勾股定理解决简单问题。
2.会用勾股定理的逆定理判定直角三角形。
3.会用勾股定理解决综合问题和实际问题。
教学重点：回顾并思考勾股定理及逆定理教学难点：勾股定理及逆定理在生活中的广泛应用。
教学过程：(一)知识结构图：见PPT(二)基础知识：1.勾股定理如果直角三角形两直角边分别为a ，b ，斜边为c ，那么a2 + b2 = c2几何语言：在Rt △ABC 中, ∠C=90°∴a2+b2=c2练习：1.求出下列直角三角形中未知的边．2.已知:直角三角形的三边长分别是 3,4,X,则X=3. 三角形ABC 中,AB=10,AC=17,BC 边上的高线AD=8,求BC8A 15B 30° 2C B A 2 45° A CB2 .勾股定理的逆定理如果三角形的三边长a ，b ，c 满足a2 +b2=c2 ，那么这个三角形是直角三角形 几何语言： 在△ABC 中,∵a2+b2=c2∴ △ABC 是直角三角形，∠C=90°互逆定理 如果一个定理的逆命题经过证明是真命题, 那么它也是一个定理, 这两个定理叫做互逆定理, 其中一个叫做另一个的逆定理.基础练习二：1．在已知下列三组长度的线段中，不能构成直角三角形的是 ( )A 5，12，13B 2，3，3C 4，7，5D 1， 2 ， 52.若△ABC 中 ,AB=5 ,BC=12 ,AC=13 ,求AC 边上的高.三、典例分析：例1、如图，四边形ABCD 中，AB ＝3，BC=4,CD=12,AD=13, ∠B=90°，求四边形ABCD 的面积变式 有一块田地的形状和尺寸如图所示，试求它的面积。
121334归纳： 转化思想例2、下图是学校的旗杆,小明发现旗杆上的绳子垂到地面还多1米，如图（1），当他把绳子的下端拉开5米后，发现下端刚好接触地面，如图（2），你能帮他D BA C归纳： 方程思想 例3、如图，矩形纸片ABCD 的边AB=10cm,BC=6cm,E 为BC 上一点，将矩形纸片沿AE 折叠，点B 恰好落在DC 边上的点G 处，求BE 的长。
八年级数学勾股定理全章复习与巩固
《勾股定理》全章复习与巩固 要点一、勾股定理1.勾股定理：直角三角形两直角边的平方和等于斜边的平方.（即：）2.勾股定理的应用勾股定理反映了直角三角形三边之间的关系，是直角三角形的重要性质之一，其主要应用是：（1）已知直角三角形的两边，求第三边；（2）利用勾股定理可以证明有关线段平方关系的问题；（3）解决与勾股定理有关的面积计算；（4）勾股定理在实际生活中的应用．要点二、勾股定理的逆定理1.勾股定理的逆定理如果三角形的三边长，满足，那么这个三角形是直角三角形.要点诠释：应用勾股定理的逆定理判定一个三角形是不是直角三角形的基本步骤：（1）首先确定最大边，不妨设最大边长为；（2）验证：与是否具有相等关系：若，则△ABC 是以∠C 为90°的直角三角形；若时，△ABC 是锐角三角形；若时，△ABC 是钝角三角形．2.勾股数满足不定方程的三个正整数，称为勾股数（又称为高数或毕达哥拉斯数），显然，以为三边长的三角形一定是直角三角形.要点诠释：常见的勾股数：①3、4、5； ②5、12、13；③8、15、17；④7、24、25；⑤9、40、41. a b 、c 222a b c +=a b c 、、222a b c +=c 22a b +2c 222a b c +=222a b c +＞222a b c +＜222x y z +=x y z 、、知识点如果()是勾股数，当t为正整数时，以为三角形的三边长，此三角形必为直角三角形. 观察上面的①、②、④、⑤四组勾股数，它们具有以下特征：1.较小的直角边为连续奇数；2.较长的直角边与对应斜边相差1.3.假设三个数分别为，且，那么存在成立.（例如④中存在＝24＋25、＝40＋41等）要点三、勾股定理与勾股定理逆定理的区别与联系区别：勾股定理是直角三角形的性质定理，而其逆定理是判定定理；联系：勾股定理与其逆定理的题设和结论正好相反，两者互为逆定理，都与直角三角形有关.类型一、勾股定理及逆定理的应用例1、如图所示，等腰直角△ABC中，∠ACB＝90°，E、F为AB上两点(E左F右)，且∠ECF＝45°，求证：.a b c、、at bt ct、、a b c、、a b c<<2a b c=+27 29222AE BF EF+=典型例题举一反三：【变式】已知凸四边形ABCD 中，∠ABC ＝30°，∠ADC ＝60°，AD ＝DC ，求证：.例2、如图，在△ABC 中，∠ACB=90°，AC=BC ，P 是△ABC 内的一点，且PB=1，PC=2，PA=3，求∠BPC 的度数．222BD AB BC =+类型二、勾股定理及逆定理的综合应用例3、如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积．例4、如图：正方形ABCD中，E是DC中点，F是EC中点.求证：∠BAF=2∠EAD.【变式】如图所示，在△ABC中，AB：BC：CA=3：4：5，且周长为36cm，点P从点A开始沿边向B点以每秒1cm的速度移动；点Q从点B沿BC边向点C以每秒2cm的速度移动，如果同时出发，问过3秒时，△BPQ 的面积为多少？类型三、勾股定理的实际应用例5、如图所示，牧童在A处放牛，其家在B处，A、B到河岸的距离分别为AC＝400米，BD＝200米，CD ＝800米，牧童从A处把牛牵到河边饮水后再回家．试问在何处饮水，所走路程最短？最短路程是多少？【变式】如图所示，正方形ABCD的AB边上有一点E，AE＝3，EB＝1，在AC上有一点P，使EP＋BP最短．求EP＋BP的最小值．例6、台风是一种自然灾害，它以台风中心为圆心，在周围数十千米范围内形成气旋风暴，有极强的破坏力．如图台风中心在我国台湾海峡的B处，在沿海城市福州A的正南方向240千米，其中心风力为12级，每远离台风中心25千米，台风就会减弱一级，如图所示，该台风中心正以20千米/时的速度沿北偏东30°方向向C移动，且台风中心的风力不变，若城市所受风力达到或超过4级，则称受台风影响．试问：（1）该城市是否会受到台风影响？请说明理由．（2）若会受到台风影响，那么台风影响该城市的持续时间有多长？（3）该城市受到台风影响的最大风力为几级？。
八年级数学勾股定理知识点
八年级数学勾股定理知识点(总5页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第18章 勾股定理复习一．知识归纳１．勾股定理内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：如果直角三角形的两直角边分别为a ，b ，斜边为c ，那么222a b c +=勾股定理的由来：勾股定理也叫商高定理，在西方称为毕达哥拉斯定理．我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦．早在三千多年前，周朝数学家商高就提出了“勾三，股四，弦五”形式的勾股定理，后来人们进一步发现并证明了直角三角形的三边关系为：两直角边的平方和等于斜边的平方２.勾股定理的证明勾股定理的证明方法很多，常见的是拼图的方法用拼图的方法验证勾股定理的思路是①图形进过割补拼接后，只要没有重叠，没有空隙，面积不会改变②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理常见方法如下：方法一：4EFGH S S S ∆+=正方形正方形ABCD ，2214()2ab b a c ⨯+-=，化简可证．c ba HG FEDCB A方法二：b ac b a cca b c a b四个直角三角形的面积与小正方形面积的和等于大正方形的面积． 四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++所以222a b c +=方法三：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证a b ccb a E DCB A３.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征，因而在应用勾股定理时，必须明了所考察的对象是直角三角形４.勾股定理的应用①已知直角三角形的任意两边长，求第三边在ABC ∆中，90C ∠=︒，则c，b，a =②知道直角三角形一边，可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题５.勾股定理的逆定理如果三角形三边长a ，b ，c 满足222a b c +=，那么这个三角形是直角三角形，其中c 为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和22a b +与较长边的平方2c 作比较，若它们相等时，以a ，b ，c 为三边的三角形是直角三角形；若222a b c +<，时，以a ，b ，c 为三边的三角形是钝角三角形；若222a b c +>，时，以a ，b ，c 为三边的三角形是锐角三角形；②定理中a ，b ，c 及222a b c +=只是一种表现形式，不可认为是唯一的，如若三角形三边长a ，b ，c 满足222a c b +=，那么以a ，b ，c 为三边的三角形是直角三角形，但是b 为斜边 ③勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形是直角三角形６.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数，即222a b c +=中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数②记住常见的勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25等③用含字母的代数式表示n 组勾股数：221,2,1n n n -+（2,n ≥n 为正整数）；2221,22,221n n n n n ++++（n 为正整数）2222,2,m n mn m n -+（,m n >m ，n 为正整数）７．勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题．在使用勾股定理时，必须把握直角三角形的前提条件，了解直角三角形中，斜边和直角边各是什么，以便运用勾股定理进行计算，应设法添加辅助线（通常作垂线），构造直角三角形，以便正确使用勾股定理进行求解．８.．勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形，在具体推算过程中，应用两短边的平方和与最长边的平方进行比较，切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论．９.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中，是密不可分的一个整体．通常既要通过逆定理判定一个三角形是直角三角形，又要用勾股定理求出边的长度，二者相辅相成，完成对问题的解决．常见图形：A B C 30°D CB A AD B CCB D A题型一：直接考查勾股定理例１.在ABC ∆中，90C ∠=︒．⑴已知6AC =，8BC =．求AB 的长⑵已知17AB =，15AC =，求BC 的长分析：直接应用勾股定理222a b c +=解：⑴10AB =⑵8BC =题型二：应用勾股定理建立方程例２.⑴在ABC ∆中，90ACB ∠=︒，5AB =cm ，3BC =cm ，CD AB ⊥于D ，CD ＝ ⑵已知直角三角形的两直角边长之比为3:4，斜边长为15，则这个三角形的面积为 ⑶已知直角三角形的周长为30cm ，斜边长为13cm ，则这个三角形的面积为 分析：在解直角三角形时，要想到勾股定理，及两直角边的乘积等于斜边与斜边上高的乘积．有时可根据勾股定理列方程求解解：⑴4AC ， 2.4AC BC CD AB⋅==DB AC⑵设两直角边的长分别为3k ，4k ∴222(3)(4)15k k +=，3k ∴=，54S = ⑶设两直角边分别为a ，b ，则17a b +=，22289a b +=，可得60ab =1302S ab ∴==2cm例３.如图ABC ∆中，90C ∠=︒，12∠=∠， 1.5CD =， 2.5BD =，求AC 的长21E DCBA分析：此题将勾股定理与全等三角形的知识结合起来解：作DE AB ⊥于E ，12∠=∠，90C ∠=︒∴ 1.5DE CD ==在BDE ∆中90,2BED BE ∠=︒=Rt ACD Rt AED ∆≅∆AC AE ∴=在Rt ABC ∆中，90C ∠=︒222AB AC BC ∴=+，222()4AE EB AC +=+3AC ∴=例4.如图Rt ABC ∆，90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆，求阴影部分面积答案：6题型三：实际问题中应用勾股定理例5.如图有两棵树，一棵高8cm ，另一棵高2cm ，两树相距8cm ，一只小鸟从一棵树的树梢飞到另一棵数的树梢，至少飞了 mAB C D E分析：根据题意建立数学模型，如图8AB =m ，2CD =m ，8BC =m ，过点D 作DE AB ⊥，垂足为E ，则6AE =m ，8DE =m在Rt ADE ∆中，由勾股定理得10AD =答案：10m题型四：应用勾股定理逆定理，判定一个三角形是否是直角三角形例6.已知三角形的三边长为a ，b ，c ，判定ABC ∆是否为Rt ∆ ① 1.5a =，2b =， 2.5c = ②54a =，1b =，23c =解：①22221.52 6.25a b +=+=，222.5 6.25c ==∴ABC ∆是直角三角形且90C ∠=︒ ②22139b c +=，22516a =，222b c a +≠ABC ∴∆不是直角三角形 例7.三边长为a ，b ，c 满足10a b +=，18ab =，8c =的三角形是什么形状？解：此三角形是直角三角形理由：222()264a b a b ab +=+-=，且264c =222a b c ∴+= 所以此三角形是直角三角形题型五：勾股定理与勾股定理的逆定理综合应用例8.已知ABC ∆中，13AB =cm ，10BC =cm ，BC 边上的中线12AD =cm ，求证：AB AC =证明：D CB AAD 为中线，5BD DC ∴==cm在ABD ∆中，22169AD BD +=，2169AB =222AD BD AB ∴+=， 90ADB ∴∠=︒，222169AC AD DC ∴=+=，13AC =cm ，AB AC ∴=。
勾股定理题型分类(经典)
勾股定理全章复习类型一：已知两边求第三边例1：⑴已知6AC =，8BC =．求AB 的长⑵已知17AB =，15AC =，求BC 的长变式练习：已知两条线段的长分别为15和8，当第三条线段取整数_____时，这三条线段能围成一个直角三角形．类型二：判断三角形形状例1：下列线段不能组成直角三角形的是( )．A. B. C. D. 2、若三角形的三边长为a ，b ，c ，且满足等式(a ＋b)2－c 2＝2ab ，则此三角形是______三角形．变式练习1：判断由线段组成的三角形是不是直角三角形．（1）＝7，＝24，＝25；（2）＝，＝1，＝；（3），，()；2、若边长为a 的正方形的面积等于长为b ＋c ，宽为b －c 的长方形的面积，则以a ，b ，c 为三边长的三角形是______三角形．3、已知△ABC 的三边为a ，b ，c ，且a ＋b ＝7，ab ＝12，c ＝5，试判定△ABC 的形状．类型三：勾股树及变形例1：如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm,则正方形A ，B ，C ，D 的面积之和为___________cm 2。
6,8,10a b c ===3,2,1===c b a 43,1,45===c b a 6,3,2===c b a a b c ，，a b c a 43b c 3422a m n =-22b m n =+2c mn =0m n >> A B C D7cm15题 变式练习：如图，正方形ABCD 的边长为2，其面积标记为S 1，以CD 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S 2……按照此规律继续下去，则S 2018的值为( )A ．(22)2015 B ．(22)2016 C ．(12)2015 D ．(12)2016 类型四：勾股定理证明的应用例1：如图1，分别以直角△ABC 的三边AB ，BC ，CA 为直径向外作半圆.设直线AB 左边阴影部分的面积为S 1，右边阴影部分的面积和为S 2，则（ ）A S 1＝S 2B S 1＜S 2C S 1＞S 2D 无法确定变式练习：如图，Rt△ABC 中，AC =5，BC =12，分别以它的三边为直径向上作三个半圆，则阴影部分面积为 ．类型五：数轴表示数例题1：在数轴上表示√17变式练习：如图，数轴上有两个直角三角形Rt △ABO 、Rt △CDO ，OA 、OC 是斜边，且OB=1，AB=1，CD=1，OD=2，分别以O 为圆心，OA 、OC 为半径画弧交x 轴于E 、F ，则E 、F 分别对应的数是 。
八年级数学下册勾股定理全章复习与巩固(基础)巩固练习及答案解析
勾股定理全章复习与巩固（基础）巩固练习一.选择题1．如图，一棵大树被台风刮断，若树在离地面3m处折断，树顶端落在离树底部4m处，则树折断之前高( )A.5mB.7mC.8mD.10m2．如图，从台阶的下端点B到上端点A的直线距离为( )A.21012 B.3C.586 D.53.下列命题中是假命题的是（）A.三个内角的度数之比为1：3：4的三角形是直角三角形；B.三个内角的度数之比为1：3：2的三角形是直角三角形；C.三边长度之比1：3：2的三角形是直角三角形；D.三边长度之比2：2：2的三角形是直角三角形；4. 如图所示，在△ABC中，AB＝AC＝5，BC＝6，点E、F是中线AD上的两点，则图中阴影部分的面积是（）．A．6 B．12 C．24 D．305．下列三角形中，是直角三角形的是( )A.三角形的三边满足关系a b c+= B.三角形的三边比为1∶2∶3C.三角形的一边等于另一边的一半D.三角形的三边为9，40，416．某市在旧城改造中，计划在市内一块如图所示的三角形空地上种植草皮以美化环境，已知这种草皮每平方米售价a元，则购买这种草皮至少需要( )A.450a元B.225a元C.150a元D.300a元7.（2018•江阴市模拟）如图，Rt△ABC中，∠C=90°，AC=12，BC=5．分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH，四块阴影部分的面积分别为S1、S2、S3、S4．则S1+S2+S3+S4等于（）A.90B.60C.169D.1448. 已知，如图长方形ABCD中，AB＝3cm，AD＝9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）A.32cmcm D.122cm B.42cm C.62二.填空题9．若一个三角形的三边长分别为6，8，10，则这个三角形中最短边上的高为______．10．若等边三角形的边长为2，则它的面积为______．11．如图，B，C是河岸边两点，A是对岸岸边一点，测得∠ABC＝45°，∠ACB＝45°，BC＝60米，则点A到岸边BC 的距离是______米．12.下列命题中，其逆．命题成立的是______________．（只填写序号）①同旁内角互补，两直线平行；②如果两个角是直角，那么它们相等；③如果两个实数相等，那么它们的平方相等；④如果三角形的三边长a b c、、满足222+=，那么这个三a b c角形是直角三角形．13.（2018•杭州模拟）如图，圆柱形容器中，高为120cm，底面周长为100cm，在容器内壁离容器底部40cm的点B 处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿40cm与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为cm．（容器厚度忽略不计）14．在直角三角形中，一条直角边为11cm，另两边是两个连续自然数，则此直角三角形的周长为______．15.如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，若涂黑的四个小正方形的面积的和是102cm，则其中最大的正方形的边长为______cm．16．如图，△ABC中，∠ACB＝90°，AC＝BC＝1，取斜边的中点，向斜边做垂线，画出一个新的等腰直角三角形，如此继续下去，直到所画直角三角形的斜边与△ABC的BC边重叠为止，此时这个三角形的斜边长为__________．三.解答题17.若直角三角形两直角边的比是3：4，斜边长是20，求此三角形的面积.18．（2018春•安次区校级月考）甲乙两船从位于南北走向的海岸线上的港口A同时出发，甲以每小时30海里的速度向北偏东35°方向航行，乙船以每小时40海里的速度向另一方向航行，2小时后，甲船到C岛，乙船到达B岛，B、C两岛相距100海里，判断乙船所走方向，说明理由．19．如图，△ABC中，∠A＝90°，AC＝20，AB＝10，延长AB到D，使CD＋DB＝AC＋AB，求BD的长．20.如图，四边形ABCD是边长为9的正方形纸片，B'为CD边上的点，CB'＝3．将纸片沿某条直线折叠，使点B落在点B '处，点A 的对应点为A '，折痕分别与AD ，BC 边交于点M ，N ．求BN 的长.【答案与解析】 一.选择题 1.【答案】C ；【解析】树高为3358=+=.2.【答案】A ；=3.【答案】B ； 4.【答案】A ；【解析】由题意BEF CEF S S =△△，∴ 13462ABD S S ==⨯⨯=△阴影．5.【答案】D ；6.【答案】C ；【解析】作高，求得高为15 m ，所以面积为120151502⨯⨯=2m .7.【答案】A ；【解析】解：过D 作BM 的垂线交BM 于N ，∵图中S 2=S Rt △DOI ，S △BOC =S △MND ，∴S2+S4=S Rt△ABC．可证明Rt△AGE≌Rt△ABC，Rt△DNB≌Rt△BHD，∴S1+S2+S3+S4=S1+S3+（S2+S4），=Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积=Rt△ABC的面积×3=12×5÷2×3=90．故选：A．8.【答案】C；【解析】设AE＝x，则DE＝BE＝9－x，在Rt△ABE中，. 二.填空题9．【答案】8；10．；⨯=2211.【答案】30；12.【答案】①④；【解析】①的逆命题“两直线平行，同旁内角互补”显然正确；②的逆命题“如果两个角相等，那么它们是直角”很明显是错误的；③的逆命题“如果两个实数的平方相等，那么这两个实数相等”，两个实数可以互为相反数，所以该命题不正确；④的逆命题“如果三角形是直角三角形，那么三角形的三边长a b c、、满足222+=”也是a b c正确的，这是勾股定理的内容.13.【答案】130；【解析】解：如图，将容器侧面展开，作A关于EC的对称点A′，连接A′B交EC于F，则A′B即为最短距离．∵高为120cm，底面周长为100cm，在容器内壁离容器底部40cm的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿40cm与蚊子相对的点A处，∴A′D=50cm，BD=120cm，∴在直角△A′DB中，A′B===130（cm）．故答案是：130．14．【答案】132cm ；【解析】由题意()222111n n +=+，解得60n =，所以周长为11＋60＋61＝132. 15.【答案】【解析】根据勾股定理，四个小正方形的面积和等于最大正方形的面积. 16.【答案】81；三.解答题 17.【解析】解：设此直角三角形两直角边分别是3x ，4x ，由勾股定理得： ()()2223420x x +=化简得：216x =∴直角三角形的面积为： 21346962x x x ⨯⨯==.18．【解析】解：由题意得：甲2小时的路程=30×2=60海里，乙2小时的路程=40×2=80海里，∵602+802=1002， ∴∠BAC=90°，∵C 岛在A 北偏东35°方向， ∴B 岛在A 北偏西55°方向． ∴乙船所走方向是北偏西55°方向．19．【解析】解：设BD ＝x ，则CD ＝30－x ．在Rt △ACD 中根据勾股定理列出()222(30)1020x x -=++， 解得x ＝5． 所以BD ＝5. 20. 【解析】解：点A 与点A '，点B 与点B '分别关于直线MN 对称， ∴AM A M '=，BN B N '=． 设BN B N x '==，则9CN x =-． ∵ 正方形ABCD ， ∴ o 90C ∠=． ∴ 222CN B C B N ''+=．∵ C B '＝3， ∴ 222(9)3x x -+=．解得5x =．∴5BN .。
八下数学17.3勾股定理全章复习
知识回顾
10
1313或 5
10
(1)（2）（3）
到线段两短点距离相等的点在线段的平分线上
知识回顾
B
D
（1）a= 7
（2） a=6，b=8
（1）a= 7 （2） a=6，b=8
你会做么
1、小红折叠长方形纸片ABCD的一 边AD,点D落在BC边上的点F处,已知 AB=8CM,BC=10CM,求EC的长.
第18章 勾股定理
全章复习
学习目标
1.掌握勾股定理及勾股定理的逆定理。 2.勾股数常用的请记住的记住。 3.勾股定理的应用。
自学指导
• 1.复习勾股定理的定理与逆定理。长为无理 数线段的画法，互逆定理及勾股数的概念。
• 2.会运用勾股定理求直角三角形的边长，和 运用勾股定理的逆定理判定一个三角形是 不是指教三角形。
10
Dபைடு நூலகம்
A
8-X
8 10
E
8-X X
B
6
F4 C
牛刀小试
比一比谁做得好
当堂达标
B
B D
当堂达标
C 504 CD=6
本章你学到了些什么? c
a
• 拼图验证法
勾股定理
勾
• 勾股定理的应用 b
股
定 理
• 互逆命题、互逆定理
勾股定理的 • 勾股数 逆定理 • 勾股定理的逆定理的应用
作业
• 基础训练总复习.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
勾股定理全章复习
学习目标
1.理解并掌握勾股定理和勾股定理的逆定理.
2.能够利用勾股定理及其逆定理解决问题.
教学过程
活动一：知识梳理
活动二：考点例题选讲
考点1.有关勾股定理的计算
勾股定理是直角三角形特有的性质，因此应用的前提是在直角三角形中，有时需要添加辅助线，自己构造直角三角形.在应用勾股定理时，注意分清斜边和直角边.
例题1.如图将两个大小、形状完全相同的△ABC和△A'B'C'拼在一
起，其中点 A'与点A重合，点 C'落在边AB上，连接 B'C.若∠ACB=
∠AC'B'=90°，AC=BC=3，则B’C的长为（）
A.3
3 B.6
C.2
3 D.21。