2017离散数学问题详解1--5)(2)
《离散数学》试题及答案详解

一、填空题1设集合A,B,其中A={1,2,3}, B= {1,2}, 则A — B=________{3}____________;ρ(A) - ρ(B)=_____{{3},{1,3},{2,3},{1,2,3}}_______ 。
2. 2. 设有限集合A, |A|= n,则|ρ(A×A)|= __3.设集合A = {a, b}, B = {1, 2},则从A到B的所有映射是__α1= {(a,1), (b,1)}, α2= {(a,2),(b,2)},α3= {(a,1),(b,2)},α4= {(a,2), (b,1)};_,其中双射的是____α3,α4。
_4。
已知命题公式G=⌝(P→Q)∧R,则G的主析取范式是______(P∧⌝Q∧R)__________________.5.设G是完全二叉树,G有7个点,其中4个叶点,则G的总度数为___12_______,分枝点数为_______3_________.6设A、B为两个集合, A= {1,2,4}, B = {3,4},则从A⋂B=_______{4}__________________; A⋃B=_____{1, 2, 3, 4}____________;A-B=____{1, 2}_________________ .3.7。
设R是集合A上的等价关系,则R所具有的关系的三个特性是__自反性;对称性;传递性_______________________________.8. 设命题公式G=⌝(P→(Q∧R)),则使公式G为真的解释有____(1, 0, 0)________,___ _(1,0, 1)_________,____(1, 1,0)______________________。
9. 设集合A={1,2,3,4}, A上的关系R1 = {(1,4),(2,3),(3,2)},R1 = {(2,1),(3,2),(4,3)},则R1•R2 = _{(1,3),(2,2),(3,1)}__________,R2•R1=___{(2,4),(3,3),(4,2)}_____ __, R12 =_____{(2,2),(3,3)}__________________。
《离散数学》题库及问题详解

《离散数学》题库与答案一、选择或填空(数理逻辑部分)1、下列哪些公式为永真蕴含式?( A )(1)⌝Q=>Q→P (2)⌝Q=>P→Q (3)P=>P→Q (4)⌝P∧(P∨Q)=>⌝P答:在第三章里面有公式(1)是附加律,(4)可以由第二章的蕴含等值式求出(注意与吸收律区别)2、下列公式中哪些是永真式?( )(1)(┐P∧Q)→(Q→⌝R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q)答:(2),(3),(4)可用蕴含等值式证明3、设有下列公式,请问哪几个是永真蕴涵式?( )(1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ⌝(P→Q)=>P (6) ⌝P∧(P∨Q)=>⌝P答:(2)是第三章的化简律,(3)类似附加律,(4)是假言推理,(3),(5),(6)都可以用蕴含等值式来证明出是永真蕴含式4、公式∀x((A(x)→B(y,x))∧∃z C(y,z))→D(x)中,自由变元是( ),约束变元是( )。
答:x,y, x,z(考察定义在公式∀x A和∃x A中,称x为指导变元,A为量词的辖域。
在∀x A和∃x A的辖域中,x的所有出现都称为约束出现,即称x为约束变元,A中不是约束出现的其他变项则称为自由变元。
于是A(x)、B(y,x)和∃z C(y,z)中y为自由变元,x和z为约束变元,在D(x)中x为自由变元)5、判断下列语句是不是命题。
若是,给出命题的真值。
( )(1)是中华人民国的首都。
(2) 师大是一座工厂。
(3) 你喜欢唱歌吗? (4) 若7+8>18,则三角形有4条边。
(5) 前进! (6) 给我一杯水吧!答:(1)是,T (2)是,F (3)不是(4)是,T (5)不是(6)不是(命题必须满足是述句,不能是疑问句或者祈使句。
)6、命题“存在一些人是大学生”的否定是( ),而命题“所有的人都是要死的”的否定是( )。
《离散数学》试题带答案(二)

《离散数学》试题带答案试卷九试题与答案一、 填空 30% (每空 3分)1、 选择合适的论域和谓词表达集合A=“直角坐标系中,单位元(不包括单位圆周)的点集”则A= 。
2、 集合A={Φ,{Φ}}的幂集P (A) = 。
3、 设A={1,2,3,4},A 上二元关系R={<1,2>,<2,1>,<2,3>,<3,4>}画出R的关系图。
4、 设A={<1,2>,<2 , 4 >,<3 , 3 >} , B={<1,3>,<2,4>,<4,2>},则B A ⋃= 。
B A = 。
5、 设|A|=3,则A 上有 个二元关系。
6、 A={1,2,3}上关系R= 时,R 既是对称的又是反对称的。
7、 偏序集><≤R A ,的哈斯图为,则≤R = 。
8、 设|X|=n ,|Y|=m 则(1)从X 到Y 有 个不同的函数。
(2)当n , m 满足 时,存在双射有 个不同的双射。
9、 2是有理数的真值为 。
10、Q :我将去上海,R :我有时间,公式)()(Q R R Q →∧→的自然语言为 。
11、公式)()(Q P P Q ∧⌝∧→的 主合取范式是 。
12、 若} ,, , {21m S S S S =是集合A 的一个分划,则它应满足 。
二、 选择 20% (每小题 2分)1、 设全集为I ,下列相等的集合是( )。
A 、} |{是偶数或奇数x x A =;B 、)}2( |{y x I y y x B =∧∈∃=;C 、)}12( |{+=∧∈∃=y x I y y x C ;D 、},4,4,3,3,2,2,1,1,0|{ ----=x D 。
2、 设S={N ,Q ,R},下列命题正确的是( )。
A 、S S N N ∈∈∈2 ,2则; B 、S N S Q Q N ⊂∈⊂则 ,; C 、R N R Q Q N ⊂⊂⊂则 ,; D 、S N S N ⋂⊂Φ⊂Φ⊂Φ则 ,。
离散数学答案第二章习题解答

习题与解答1. 将下列命题符号化:(1) 所有的火车都比某些汽车快。
(2) 任何金属都可以溶解在某种液体中。
(3) 至少有一种金属可以溶解在所有液体中。
(4) 每个人都有自己喜欢的职业。
(5) 有些职业是所有的人都喜欢的。
解 (1) 取论域为所有交通工具的集合。
令x x T :)(是火车, x x C :)(是汽车, x y x F :),(比y 跑得快。
“所有的火车都比某些汽车快”可以符号化为))),()(()((y x F y C y x T x ∧∃→∀。
(2) 取论域为所有物质的集合。
令x x M :)(是金属, x x L :)(是液体, x y x D :),(可以溶解在y 中。
“任何金属都可以溶解在某种液体中” 可以符号化为))),()(()((y x D y L y x M x ∧∃→∀。
(3) 论域和谓词与(2)同。
“至少有一种金属可以溶解在所有液体中” 可以符号化为))),()(()((y x D y L y x M x →∀∧∃。
(4) 取论域为所有事物的集合。
令x x M :)(是人, x x J :)(是职业, x y x L :),(喜欢y 。
“每个人都有自己喜欢的职业” 可以符号化为))),()(()((y x L y J y x M x ∧∃→∀(5)论域和谓词与(4)同。
“有些职业是所有的人都喜欢的”可以符号化为))),()(()((x y L y M y x J x →∀∧∃。
2. 取论域为正整数集,用函数+(加法),•(乘法)和谓词<,=将下列命题符号化:(1) 没有既是奇数,又是偶数的正整数。
(2) 任何两个正整数都有最小公倍数。
(3) 没有最大的素数。
(4) 并非所有的素数都不是偶数。
解 先引进一些谓词如下:x y x D :),(能被y 整除,),(y x D 可表示为)(x y v v =•∃。
x x J :)(是奇数,)(x J 可表示为)2(x v v =•⌝∃。
2017离散数学答案1--5)(2)

06任务_0001试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 命题公式的析取范式是( ).A.B.C.D.2. 设个体域为整数集,则公式"x$y(x+y=0)的解释可为( ).A. 存在一整数x有整数y满足x+y=0B. 任一整数x对任意整数y满足x+y=0C. 对任一整数x存在整数y满足x+y=0D.存在一整数x对任意整数y满足x+y=03. 下列公式成立的为( ).A. ⌝P∧⌝Q ⇔P∨QB. P→⌝Q⇔⌝P→QC. Q→P⇒ PD. ⌝P∧(P∨Q)⇒Q4. 下列公式中( )为永真式.A. ⌝A∧⌝B ↔⌝A∨⌝BB. ⌝A∧⌝B ↔⌝(A∨B)C. ⌝A∧⌝B ↔A∨BD. ⌝A∧⌝B ↔⌝(A∧B)5. 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).A.B.C.D.6. 命题公式(P∨Q)→R的析取范式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R7. 命题公式(P∨Q)的合取范式是( ).A. (P∧Q)B. (P∧Q)∨(P∨Q)C. (P∨Q)D. ⌝(⌝P∧⌝Q)8. 设命题公式G:,则使公式G取真值为1的P,Q,R赋值分别是( ).A. 0, 0, 0B. 0, 0, 1C. 0, 1, 0D. 1, 0, 09. 命题公式P→Q的主合取范式是( ).A. (P∨Q)∧(∏∨⌝Θ)∧(⌝∏∨⌝Θ)B. ⌝P∧QC. ⌝P∨QD. P∨⌝Q10. 下列等价公式成立的为( ).A. ⌝P∧P⇔⌝Q∧QB. ⌝Q→P⇔P→QC. P∧Q⇔P∨QD. ⌝P∨P⇔Q06任务_0002试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 命题公式(P∨Q)→Q为( )A. 矛盾式B. 可满足式C. 重言式D. 合取范式2. 设个体域为整数集,则公式"x$y(x+y=0)的解释可为( ).A. 存在一整数x有整数y满足x+y=0B. 任一整数x对任意整数y满足x+y=0C. 对任一整数x存在整数y满足x+y=0D.存在一整数x对任意整数y满足x+y=03. 命题公式的析取范式是( ).A.B.C.D.4. 下列等价公式成立的为( ).A. ⌝P∧P⇔⌝Q∧QB. ⌝Q→P⇔P→QC. P∧Q⇔P∨QD. ⌝P∨P⇔Q5. 设命题公式G:,则使公式G取真值为1的P,Q,R赋值分别是( ).A. 0, 0, 0B. 0, 0, 1C. 0, 1, 0D. 1, 0, 06. 在谓词公式(∀x)(A(x)→B(x)∨C(x,y))中,().A. x,y都是约束变元B. x,y都是自由变元C. x是约束变元,y都是自由变元D. x是自由变元,y都是约束变元7. 命题公式P→Q的主合取范式是( ).A. (P∨Q)∧(∏∨⌝Θ)∧(⌝∏∨⌝Θ)B. ⌝P∧QC. ⌝P∨QD. P∨⌝Q8. 设A(x):x是人,B(x):x是教师,则命题“有人是教师”可符号化为().A. ⌝(x)(A(x)∧⌝B(x))B. (∀x)(A(x)∧B(x))C. ⌝(∀x)(A(x)→B(x))D. (x)(A(x)∧B(x))9. 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).A.B.C.D.10. 命题公式(P∨Q)→R的析取范式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R06任务_0003试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
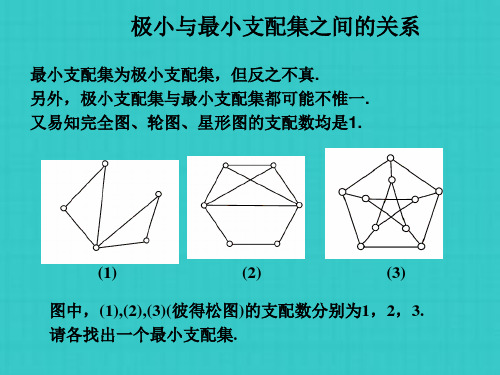
离散数学17
独立集(匹配)、点着色、边着色、面着色、色数等概念 会求阶数 n 较小或特殊图的 0, 0, 0, 1, 1 会用二部图中匹配的理论解简单问题 理解并记住地图面着色与它的对偶图点着色之间的关系 会用点色数及边色数解决一些实际问题.
路径 (7) M的交错圈——由M与EM中的边交替出现构成的G中圈
上图中,只有第一个图存在完美匹配
可增广路径及交错圈
(1)
(2)
(3)
设红色边在匹配M中,绿色边不在M中,则图(1)中的两条路 径均为可增广的交错路径;(2)中的全不是可增广的交错路 径;(3)中是一个交错圈. 不难看出,可增广交错路径中,不在M中的边比在M中的边 多一条. 交错圈一定为偶圈.
立集 (3) 最大点独立集——元素最多的点独立集 (4) 点独立数——最大点独立集中的元素个数,记为0
(1)
(2)
(3)
在图中,点独立数依次为2, 2, 3.
极大独立集与极小支配集
定理18.1 设G=<V,E>中无孤立点,则G的极大点独立集都是 极小支配集.
证明线索: (1) 设V*为G的极大点独立集,证明它也是支配集.
上图中各图的匹配数依次为3, 3, 4.
关于匹配中的其他概念
定义18.6 设M为G中一个匹配. (1) vi 与vj 被M匹配——(vi,vj)M (2) v为M饱和点——有M中边与v关联 (3) v为M非饱和点——无M中边与v关联 (4) M为完美匹配——G中无M非饱和点 (5) M的交错路径——从M与EM中交替取边构成的G中路径 (6) M的可增广交错路径——起、终点都是M非饱和点的交错
解 用二部图中的匹配理论解本题方便. 令G=<V1,V2,E>,其中V1={s, g, x},s, g, x分别表示上海、广 州和香港. V2={a, b, c, d, e}, E={(u,v) | uV1, vV2, v想去u}. G如图所示.
吉林大学离散数学课后习题问题详解

第一章集合论基础§ 1.1基本要求1.掌握集合、子集、超集、空集、幕集、集合族的概念。
懂得两个集合间相等和包含关系的泄义和性质,能够利用泄义证明两个集合相等。
熟悉常用的集合表示方法。
2.掌握集合的基本运算:并、交、余、差、直乘积、对称差的左义以及集合运算满足的基本算律,能够利用它们来证明更复杂的集合等式。
3.掌握关系、二元关系、空关系、全域关系、相等关系、逆关系的概念以及关系的性质:自反性、对称性、反对称性、传递性。
会做关系的乘积。
了解关系的闭包运算:自反闭包、对称闭包、传递闭包。
4.掌握等价关系、等价类、商集的概念,了解等价关系和划分的在联系。
5.掌握部分序关系、部分序集、全序关系、全序集的概念以及部分序集中的特殊元素:最大元、最小元、极大元、极小元、上确界、小确界的左义。
能画岀有限部分序集的Hasse 图,并根据图讨论部分序集的某些性质。
6.掌握映射、映像、1-1映射等概念,会做映射的乘枳。
了解可数集合的槪念,掌握可数集合的判定方法。
7.了解关系在数据库中的应用(数据的增、删、改)以及划分在计算机中的应用。
§ 1.2主要解题方法1.2.1证明集合的包含关系方法一.用泄义来证明集合的包含关系是最常用也是最基本的一种方法。
要证明ACB,首先任取xeA,再演绎地证出xeB成立。
由于我们选择的元素x是属于A的任何一个,而非特指的一个,故知给出的演绎证明对A中含有的每一个元素都成立。
当A是无限集时,因为我们不能对xwA,逐一地证明xeB成立,所以证明时的假设“x是任取的” 就特别重要。
例121设A, B, C, D是任意四个非空集合,若ACC, BCD,则AxBcCxDo证明:任取(x, y) e AxBt 往证(x, y) e CxD°由(x, y) e AxB 知,xe A, K ye Bo 又由AcC, BcD 知,xeC,且ye D,因此,(Xt y) e CxDo 故,AxBcCxDo方法二.还有一种证明集合包含关系的方法,基于集合的交和并运算的两个基本性质ACB<=> AnB=A <=> AuB=B以及一些已经证岀的集合等式。
考研数学离散数学常见题型解题技巧分享

考研数学离散数学常见题型解题技巧分享离散数学是考研数学中的一个重要知识点,常见的离散数学题型包括集合论、关系和函数、图论等。
解题技巧的掌握对于考生来说至关重要,下面将分享一些常见离散数学题型的解题技巧。
一、集合论题型1. 幂集的计算技巧在计算幂集的过程中,可以利用二进制数的特点,将集合中的元素与二进制数的位置对应起来。
例如一个集合A={a, b, c},则它的幂集的个数为2^n,其中n为集合A的元素个数。
可以将幂集的个数展示为二进制数的个数形式,从而便于计算。
2. 集合间关系的判断在判断两个集合的关系时,可以分别列出这两个集合的元素,然后进行对比。
如果两个集合的所有元素都相同,则它们是相等集;如果一个集合A的元素都是集合B的元素,则A是B的子集;反之,如果B的元素都是A的元素,则B是A的子集。
二、关系和函数题型1. 关系的性质判断在判断一个关系的性质时,可以利用以下几个常见的关系性质:- 自反性:如果对于集合A中的每一个元素a,都满足条件R(a, a),则称关系R是自反的。
- 对称性:如果对于集合A中的任意两个元素a和b,则当满足条件R(a, b)时,R(b, a)也成立,则称关系R是对称的。
- 传递性:如果对于集合A中的任意三个元素a、b和c,并且当满足条件R(a, b)和R(b, c)时,R(a, c)也成立,则称关系R是传递的。
2. 函数的性质判断在判断一个函数的性质时,可以利用以下几个常见的函数性质:- 单射性:如果函数f的每一个元素在定义域中唯一对应一个值,则称函数f是单射的。
- 满射性:如果函数f的值域等于定义域,则称函数f是满射的。
- 双射性:如果函数f既是单射又是满射,即每一个元素在定义域中唯一对应一个值,并且值域等于定义域,则称函数f是双射的。
三、图论题型1. 图的遍历技巧在遍历图的过程中,可以利用深度优先搜索(DFS)和广度优先搜索(BFS)两种常用的算法。
DFS以深度为优先原则进行搜索,而BFS 以广度为优先原则进行搜索。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
06任务_0001试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 命题公式的析取式是( ).A.B.C.D.2. 设个体域为整数集,则公式"x$y(x+y=0)的解释可为( ).A. 存在一整数x有整数y满足x+y=0B. 任一整数x对任意整数y满足x+y=0C. 对任一整数x存在整数y满足x+y=0D.存在一整数x对任意整数y满足x+y=03. 下列公式成立的为( ).A. ⌝P∧⌝Q ⇔P∨QB. P→⌝Q⇔⌝P→QD. ⌝P∧(P∨Q)⇒Q4. 下列公式中( )为永真式.A. ⌝A∧⌝B ↔⌝A∨⌝BB. ⌝A∧⌝B ↔⌝(A∨B)C. ⌝A∧⌝B ↔A∨BD. ⌝A∧⌝B ↔⌝(A∧B)5. 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).A.B.C.D.6. 命题公式(P∨Q)→R的析取式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R7. 命题公式(P∨Q)的合取式是( ).B. (P∧Q)∨(P∨Q)C. (P∨Q)D. ⌝(⌝P∧⌝Q)8. 设命题公式G:,则使公式G取真值为1的P,Q,R赋值分别是( ).A. 0, 0, 0B. 0, 0, 1C. 0, 1, 0D. 1, 0, 09. 命题公式P→Q的主合取式是( ).A. (P∨Q)∧(∏∨⌝Θ)∧(⌝∏∨⌝Θ)B. ⌝P∧QC. ⌝P∨QD. P∨⌝Q10. 下列等价公式成立的为( ).A. ⌝P∧P⇔⌝Q∧QB. ⌝Q→P⇔P→QC. P∧Q⇔P∨QD. ⌝P∨P⇔Q06任务_0002试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 命题公式(P∨Q)→Q为( )A. 矛盾式B. 可满足式C. 重言式D. 合取式2. 设个体域为整数集,则公式"x$y(x+y=0)的解释可为( ).A. 存在一整数x有整数y满足x+y=0B. 任一整数x对任意整数y满足x+y=0C. 对任一整数x存在整数y满足x+y=0D.存在一整数x对任意整数y满足x+y=03. 命题公式的析取式是( ).A.B.C.D.4. 下列等价公式成立的为( ).A. ⌝P∧P⇔⌝Q∧QB. ⌝Q→P⇔P→QC. P∧Q⇔P∨QD. ⌝P∨P⇔Q5. 设命题公式G:,则使公式G取真值为1的P,Q,R赋值分别是( ).A. 0, 0, 0B. 0, 0, 1C. 0, 1, 0D. 1, 0, 06. 在谓词公式(∀x)(A(x)→B(x)∨C(x,y))中,().A. x,y都是约束变元B. x,y都是自由变元C. x是约束变元,y都是自由变元D. x是自由变元,y都是约束变元7. 命题公式P→Q的主合取式是( ).A. (P∨Q)∧(∏∨⌝Θ)∧(⌝∏∨⌝Θ)B. ⌝P∧QC. ⌝P∨QD. P∨⌝Q8. 设A(x):x是人,B(x):x是教师,则命题“有人是教师”可符号化为().A. ⌝(x)(A(x)∧⌝B(x))B. (∀x)(A(x)∧B(x))C. ⌝(∀x)(A(x)→B(x))D. (x)(A(x)∧B(x))9. 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).A.B.C.D.10. 命题公式(P∨Q)→R的析取式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R06任务_0003试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).A.B.C.D.2. 下列公式成立的为( ).A. ⌝P∧⌝Q ⇔P∨QB. P→⌝Q⇔⌝P→QC. Q→P⇒ PD. ⌝P∧(P∨Q)⇒Q3. 下列公式( )为重言式.A. ⌝P∧⌝Q↔P∨QB. (Q→(P∨Q)) ↔(⌝Q∧(P∨Q))C. (P→(⌝Q→P))↔(⌝P→(P→Q))D. (⌝P∨(P∧Q)) ↔Q4. 命题公式(P∨Q)→R的析取式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R5. 命题公式P→Q的主合取式是( ).A. (P∨Q)∧(∏∨⌝Θ)∧(⌝∏∨⌝Θ)B. ⌝P∧QC. ⌝P∨QD. P∨⌝Q6. 在谓词公式(∀x)(A(x)→B(x)∨C(x,y))中,().A. x,y都是约束变元B. x,y都是自由变元C. x是约束变元,y都是自由变元D. x是自由变元,y都是约束变元7. 下列公式中( )为永真式.A. ⌝A∧⌝B ↔⌝A∨⌝BB. ⌝A∧⌝B ↔⌝(A∨B)C. ⌝A∧⌝B ↔A∨BD. ⌝A∧⌝B ↔⌝(A∧B)8. 设A(x):x是书,B(x):x是数学书,则命题“不是所有书都是数学书”可符号化为().A. ┐(∀x)(A(x)→B(x))B. ⌝(x)(A(x)∧B(x))C. (∀x)(A(x)∍B(x))D. ⌝(x)(A(x)∧⌝B(x))9. 设个体域D={a, b, c},那么谓词公式消去量词后的等值式为.A. (A(a)∨A(b)∨A(c))∨(B(a)∧B(b)∧B(b))B. (A(a)∧A(b)∧A(c))∨(B(a)∨B(b)∨B(b))C. (A(a)∨A(b)∨A(c))∨(B(a)∨B(b)∨B(b))D. (A(a)∧A(b)∧A(c))∨(B(a)∧B(b)∧B(b))10. 前提条件的有效结论是( ).A. PB. ⌝PC. QD. ⌝Q06任务_0004试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 下列公式成立的为( ).A. ⌝P∧⌝Q ⇔P∨QB. P→⌝Q⇔⌝P→QC. Q→P⇒ PD. ⌝P∧(P∨Q)⇒Q2. 命题公式(P∨Q)→R的析取式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R3. 设A(x):x是人,B(x):x是教师,则命题“有人是教师”可符号化为().A. ⌝(x)(A(x)∧⌝B(x))B. (∀x)(A(x)∧B(x))C. ⌝(∀x)(A(x)→B(x))D. (x)(A(x)∧B(x))4. 下列公式( )为重言式.A. ⌝P∧⌝Q↔P∨QB. (Q→(P∨Q)) ↔(⌝Q∧(P∨Q))C. (P→(⌝Q→P))↔(⌝P→(P→Q))D. (⌝P∨(P∧Q)) ↔Q5. 表达式中的辖域是( ).A. P(x, y)B. P(x, y)∨Q(z)C. R(x, y)D. P(x, y)∧R(x, y)6. 命题公式(P∨Q)的合取式是( ).A. (P∧Q)B. (P∧Q)∨(P∨Q)C. (P∨Q)D. ⌝(⌝P∧⌝Q)7. 下列等价公式成立的为( ).A. ⌝P∧P⇔⌝Q∧QB. ⌝Q→P⇔P→QC. P∧Q⇔P∨QD. ⌝P∨P⇔Q8. 在谓词公式(∀x)(A(x)→B(x)∨C(x,y))中,().A. x,y都是约束变元B. x,y都是自由变元C. x是约束变元,y都是自由变元D. x是自由变元,y都是约束变元9. 命题公式(P∨Q)→Q为( )A. 矛盾式B. 可满足式C. 重言式D. 合取式10. 设个体域D={a, b, c},那么谓词公式消去量词后的等值式为.A. (A(a)∨A(b)∨A(c))∨(B(a)∧B(b)∧B(b))B. (A(a)∧A(b)∧A(c))∨(B(a)∨B(b)∨B(b))C. (A(a)∨A(b)∨A(c))∨(B(a)∨B(b)∨B(b))D. (A(a)∧A(b)∧A(c))∨(B(a)∧B(b)∧B(b))06任务_0005试卷总分:100 测试时间:0单项选择题一、单项选择题(共10 道试题,共100 分。
)1. 命题公式P→Q的主合取式是( ).A. (P∨Q)∧(∏∨⌝Θ)∧(⌝∏∨⌝Θ)B. ⌝P∧QC. ⌝P∨QD. P∨⌝Q2. 设个体域D是整数集合,则命题"x$y (x×y = y)的真值是().A. TB. FC. 不确定D. 以上说法都不是3. 命题公式的析取式是( ).A.B.C.D.4. 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).A.B.C.D.5. 设个体域为整数集,则公式"x$y(x+y=0)的解释可为( ).A. 存在一整数x有整数y满足x+y=0B. 任一整数x对任意整数y满足x+y=0C. 对任一整数x存在整数y满足x+y=0D.存在一整数x对任意整数y满足x+y=06. 命题公式(P∨Q)→R的析取式是( )A. ⌝(P∨Q)∨RB. (P∧Q)∨RC. (P∨Q)∨RD. (⌝P∧⌝Q)∨R7. 下列公式成立的为( ).A. ⌝P∧⌝Q ⇔P∨QB. P→⌝Q⇔⌝P→QC. Q→P⇒ PD. ⌝P∧(P∨Q)⇒Q8. 设个体域D={a, b, c},那么谓词公式消去量词后的等值式为.A. (A(a)∨A(b)∨A(c))∨(B(a)∧B(b)∧B(b))B. (A(a)∧A(b)∧A(c))∨(B(a)∨B(b)∨B(b))C. (A(a)∨A(b)∨A(c))∨(B(a)∨B(b)∨B(b))D. (A(a)∧A(b)∧A(c))∨(B(a)∧B(b)∧B(b))9. 下列公式中( )为永真式.A. ⌝A∧⌝B ↔⌝A∨⌝BB. ⌝A∧⌝B ↔⌝(A∨B)C. ⌝A∧⌝B ↔A∨BD. ⌝A∧⌝B ↔⌝(A∧B)10. 下列等价公式成立的为( ).A. ⌝P∧P⇔⌝Q∧QB. ⌝Q→P⇔P→QC. P∧Q⇔P∨QD. ⌝P∨P⇔Q。
