统计学重要计算及公式
统计学常用公式

统计学常用公式统计学是一门研究数据收集、分析、解释和表达的科学。
在统计学中,有许多常用的公式被广泛应用于数据处理和推断分析。
本文将介绍一些统计学常用公式,并对其进行说明和用途解释。
一、描述统计学公式1. 平均值(Mean)平均值是一组数据的总和除以数据的个数,即:$\bar{X} = \frac{X_1 + X_2 + \cdots + X_n}{n}$其中,$\bar{X}$表示平均值,$X_i$表示第i个数据,n表示数据的个数。
2. 中位数(Median)中位数是将一组数据按照大小排列后,处于中间位置的数值。
当数据个数为奇数时,中位数即为排列后正中间的数;当数据个数为偶数时,中位数为排列后中间两个数的平均值。
3. 众数(Mode)众数是一组数据中出现频率最高的数值。
4. 标准差(Standard Deviation)标准差衡量数据的离散程度,其计算公式为:$SD = \sqrt{\frac{(X_1 -\bar{X})^2 + (X_2 -\bar{X})^2 + \cdots + (X_n -\bar{X})^2}{n-1}}$5. 方差(Variance)方差是标准差的平方,即:$Var = SD^2$6. 百分位数(Percentile)百分位数是指一组数据中某个特定百分比处的数值。
比如,第25百分位数是将一组数据从小到大排列后,处于前25%位置的数值。
二、概率与统计公式1. 随机变量期望(Expectation)随机变量期望是描述随机变量平均值的指标,也称为均值。
对于离散型随机变量X,其期望计算公式为:$E(X) = \sum_{i=1}^{n} X_i \cdot P(X_i)$对于连续型随机变量X,其期望计算公式为:$E(X) = \int_{-\infty}^{\infty} x \cdot f(x)dx$其中,$X_i$表示随机变量X的取值,$P(X_i)$表示对应取值的概率,$f(x)$表示X的概率密度函数。
统计学重要计算及公式
s2 s2 P x-t 2 (n 1) x+t 2 (n 1) 1 = n n
根据t分布性质,在置信水平1- 下总体均值的置信区间为:
x x
或:
x t 2 (n 1) x
s x t (n 1) 2 n
假设检验的类型:双侧检验和单侧检验
2
n 1
2
2
a a
1
a
2
f
1 1
an an
1
f fn-
2
1
fn-
1
环比发展速度和定基发展速度的关系
1.各个时期环比发展速度连乘积等于相应的定基发展
速度;
a1 a 2 a 3 an a 0 a1 a 2 an 1
展速度。
an a0
2.相邻时期的定基发展速度之比等于相应的环比发
x n
x
xf
f
σ (X X ) (X X ) F N F
2 2
( x x )2 ( x x )2 f n f
xp n1 n
总体平 Xp 标 均 数 志 总 总体标 体 准 差 性 质
N1 N
P
பைடு நூலகம்总体成数
标 志 总 体 性 质
p
σp PQ P(1 P)
在置信水平1- 下参数的置信区间为: 或:
x x
x z 2 x
x z
2
s n
2 3、总体服从正态分布、 未知、小样本时 ,均值的区间估计
总体方差未知且是在小样本情况下,则需用样本方差代替总体方差,这时 样本均值经过标准化以后的随机变量则服从自由度为(n-1)的t分布, 可 得到
统计学公式汇总

统计学公式汇总统计学是研究数据收集、分析、解释和预测的一门学科。
在统计学中,有许多重要的公式被广泛应用于数据的处理和分析过程中。
本文将汇总一些常见的统计学公式,并简要介绍其应用场景和使用方法。
1. 均值(Mean)均值是统计学中最常用的概念之一,用于衡量一组数据的集中趋势。
对于一个样本集合,均值可以通过将所有观测值相加,然后除以样本容量来计算。
其数学公式如下:均值= ∑(观测值) / 样本容量2. 方差(Variance)方差是用于衡量一组数据的离散程度的指标。
方差越大,表示数据的离散程度越高;方差越小,表示数据的离散程度越低。
方差的计算公式如下:方差= ∑((观测值-均值)^2) / 样本容量3. 标准差(Standard Deviation)标准差是方差的平方根,用于衡量数据的离散程度,并且具有和原始数据相同的单位。
标准差的计算公式如下:标准差 = 方差的平方根4. 相关系数(Correlation Coefficient)相关系数用于衡量两组变量之间的线性关系强度和方向。
相关系数的取值范围在-1到1之间,其中-1表示完全的负相关,1表示完全的正相关,0表示无相关。
相关系数的计算公式如下:r = Cov(X,Y) / (σX * σY)5. 回归方程(Regression Equation)回归方程用于建立一个或多个自变量与因变量之间的线性关系。
回归方程的一般形式为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中,Y表示因变量,X1、X2、...、Xn表示自变量,β0、β1、β2、...、βn表示回归系数,ε表示模型的误差项。
6. 样本容量和置信水平(Sample Size and Confidence Level)在统计学中,样本容量和置信水平是决定实验或调查结果可靠性的重要因素。
样本容量是指从总体中抽取的样本大小,而置信水平是指对总体参数的估计值的信任程度。
统计学主要计算公式

统计学主要计算公式统计学是研究数据收集、整理、分析、解释和呈现的科学。
在统计学中,有许多重要的计算公式被广泛应用于统计分析和推断,以下是一些常见的计算公式:1.平均值:平均值是一组数据的总和除以数据的数量。
公式:平均值=总和/数据数量2.中位数:中位数是一组有序数据中的中间值,将数据从小到大排列,若数据的数量为奇数,则中位数为中间的数值;若数据的数量为偶数,则中位数为中间两个数值的平均值。
3.众数:众数是一组数据中出现最频繁的值。
4.方差:方差是一组数据与其平均值的差的平方的平均值。
公式: 方差= (∑(xi-平均值)^2) / 数据数量5.标准差:标准差是方差的平方根,用于衡量一组数据的离散程度。
公式:标准差=√方差6.相关系数:用于衡量两个变量之间线性相关程度的统计量。
公式: r = Cov(X,Y) / (SD(X) * SD(Y))其中,Cov(X,Y)表示X和Y的协方差,SD(X)和SD(Y)分别表示X和Y的标准差。
7.正态分布概率密度函数:正态分布是统计学中最重要的分布之一,其概率密度函数可以描述随机变量的分布。
公式:f(x)=(1/(σ*√(2π)))*e^(-(x-μ)^2/(2σ^2))其中,μ表示均值,σ表示标准差,e表示自然常数。
8.合并概率公式:用于计算多个事件同时发生的概率。
公式:P(A∩B)=P(A)*P(B,A)其中,P(A)表示A事件发生的概率,P(B,A)表示在A事件发生的条件下B事件发生的概率。
9.条件概率公式:用于计算在已知其中一事件发生的条件下另一事件发生的概率。
公式:P(A,B)=P(A∩B)/P(B)其中,P(A,B)表示在B事件发生的条件下A事件发生的概率。
10.抽样误差公式:用于计算样本估计值与总体参数之间的误差。
公式:误差=Z*(标准误差)其中,Z表示置信水平对应的标准正态分布的分位数,标准误差表示样本估计的标准差。
这些计算公式是统计学中非常重要的工具,用于帮助我们理解和解释数据的特征和关系。
统计学原理重要公式

一.加权算术平均数和加权调和平均数的计算加权算术平均数: ∑∑=fxf x 或 ∑∑=ffxx加权调和平均数: ∑∑∑∑==fxf x m m x频数也称次数。
在一组依大小顺序排列的测量值中,当按一定的组距将其分组时出现在各组内的测量值的数目,即落在各类别(分组)中的数据个数。
再如在3.14159265358979324中,…9‟出现的频数是3,出现的频率是3/18=16.7% 一般我们称落在不同小组中的数据个数为该组的频数,频数与总数的比为频率。
频数也称“次数”,对总数据按某种标准进行分组,统计出各个组内含个体的个数。
而频率则每个小组的频数与数据总数的比值。
在变量分配数列中,频数(频率)表明对应组标志值的作用程度。
频数(频率)数值越大表明该组标志值对于总体水平所起的作用也越大,反之,频数(频率)数值越小,表明该组标志值对于总体水平所起的作用越小。
掷硬币实验:在10次掷硬币中,有4次正面朝上,我们说这10次试验中…正面朝上‟的频数是4例题:我们经常掷硬币,在掷了一百次后,硬币有40次正面朝上,那么,硬币反面朝上的频数为____.解答,掷了硬币100次,40次朝上,则有100-40=60(次)反面朝上,所以硬币反面朝上的频数为60.一.加权算术平均数和加权调和平均数的计算加权算术平均数: ∑∑=fxf x 或 ∑∑=ffxxx 代表算术平均数;∑是总和符合;f 为标志值出现的次数。
加权算术平均数是具有不同比重的数据(或平均数)的算术平均数。
比重也称为权重,数据的权重反映了该变量在总体中的相对重要性,每种变量的权重的确定与一定的理论经验或变量在总体中的比重有关。
依据各个数据的重要性系数(即权重)进行相乘后再相加求和,就是加权和。
加权和与所有权重之和的比等于加权算术平均数。
加权平均数 = 各组(变量值 × 次数)之和 / 各组次数之和 = ∑xf / ∑f加权调和平均数: ∑∑∑∑==fxf xm m x加权算术平均数以各组单位数f 为权数,加权调和平均数以各组标志总量m 为权数但计算内容和结果都是相同的。
统计学重要计算及公式公开课获奖课件百校联赛一等奖课件
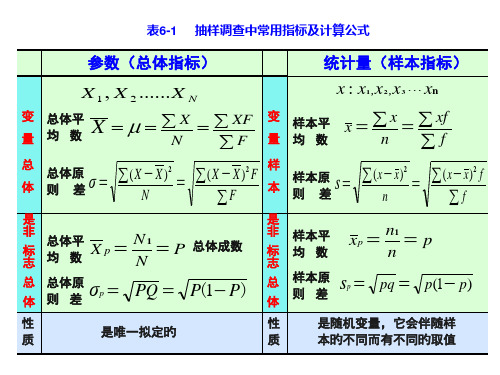
(1)反复抽样: x
2
nn
: 总体标准差
n : 样本容量
(2)不反复抽样:x
2 N n
n
N
1
n
1 n
N
N : 总体单位数
注意:在实际计算抽样平均误差时,当总体原则差σ未知
时,能够用样本原则差s来替代。即:
x
n
s n
s (x x)2
n
(大样本)
s
(x x)2 n 1
(小样本)
n
(x x)2 f
f
是
非
标 志
总体平 均数
Xp
N1 N
P
总体成数
总 体
总体原 则差
σp
PQ
P(1 P)
是
非 样本平
标 均数
xp
志
n1 n
p
总 体
s 样本原
则差 p
pq
p(1 p)
性 质
是唯一拟定旳
性
是随机变量,它会伴随样
质
本旳不同而有不同旳取值
简朴随机抽样下抽样平均误差计算公式
1.样本平均数旳抽样平均误差
环比发展速度和定基发展速度旳关系
1.各个时期环比发展速度连乘积等于相应旳定基发展 速度;
a1 a2 a3 an
an
a0 a1 a2
an 1
a0
2.相邻时期旳定基发展速度之比等于相应旳环比发 展速度。
an an 1
an
a0
a0
an 1
(1)时期数列 旳平均发 展水平
(2)时点数列 旳平均发 展水平
注意:首先要明 确时间序列旳种 类,然后选择相 应旳公式计算。
统计学贾俊平重要公式

方差未知 :Z = X − μ S/ n
38.小 样 本 总 体 均 值 的 检 验 统 计 量 : t = X − μ , df = n − 1
S/ n
39.总 体 比 率 检 验 统 计 量 : Z =
p) − p0
p0 (1 − p0 )
n
40.总 体 均 值 的 单 侧 检 验 中 所 需 样 本 容 量 :
32.估计μ时的抽样误差: X − μ
E(X ) = μ,
33.总体均值的区间估计
有限总体时σ = X
N −n⎛ σ ⎞ N −1 ⎜⎝ n ⎟⎠
无限总体时σ = σ 31.比例P)的数学X 期望n和标准差 : E( p)) = p,
(1)大样本且方差已知: X ± Zα 2
σ, n
(2)大样本且方差未知: X ± Zα 2
X
)2
=
n
∑ i=1
X
2 i
−
∑ ⎛ n
⎜⎝ i = 1 X n
⎞2 i ⎟⎠
,
L XY
=
( n
∑ Xi− i=1
X
) (Y i − Y ) =
n
∑ i=1
X iY i −
∑ ⎛ n
⎜⎝ i = 1
∑ ⎞ ⎛ n
⎞
X i ⎟⎠ ⎜⎝ i = 1 Y i ⎟⎠ ,
n
L YY=Βιβλιοθήκη ( ) n∑2
Yi − Y
=
i=1
n
∑ Y i2 − i=1
∑ ⎛ n
⎞2
⎜⎝ i = 1 Y i ⎟⎠
,
n
n
n
∑ Xi
∑ Yi
X = i=1
统计学重要公式考试必备

1.样本平均数:X2.总体平均数:3. 四分位差:Q D4. 方差:nXN IQR(1总体方差:(2) 样本方差:S27.标准分数分数8.样本协方差Cov9.皮尔逊相关系数XXXYYY Y i10. 加权平均数11. 分组数据样本平均数12. 分组数据样本方差13. 排列组合公式n !C mn m !2 Pm厂n m !C mn C n m n统计学重要公式5.标准差:(1总体标准差:X i~N2X i n 1X ,丫r XYY iY i(2)样本标准差:6•变异系数总体:CV样本:CVX i X"S-S XYS XYXY i22S S2100%100%标准差一100%平均数L XYL XX L YY2X iX i Y iI I1n 2Y i1nnY ii 114.事件补的概率 P(A) 1 P(A)15.加法公式 P(A B) P(A) P(B)-P(AB) 16.条件概率 P(A|B)P(A (B)B),P(A B)P(B)P(A) 17.乘法公式 P(A B) P(B) P(A|B) P(A) P(B|A)18.独立事件 P(A B)P(A)P(B)19.全概率公式P(B)nP(A i ) P(B|A i )i 120•贝叶斯公式P(A i |B)P(A)P(B|A i ).啥小叫)P(B)P(A j ) P(B|A j )j i33总体均值的区间估计21. 离散型随机变量的数学期望 E(X)22. 离散型随机变量的方差 Var(X) 223. 二项分布的概率函数 p(x) C ;p xq24.二项分布的数学期望和方差 E (X )xxe e x!x!x n xC C 25.泊松分布p(x) 27.超几何分布p(x),x xp(x) 2x p(x)0,1,2,..., n,q 1 p np,Var(X) 2n p(1 p)28.正态概率密度函数 29.标准正态分布变换 X 2f (x) ^2— e2 2Zx30. X 的数学期望和标准差32估计 时的抽样误差:X E(X)有限总体时(1大样本且方差已知:X 无限总体时Xn31比例P 的数学期望和标准差 E(p)⑵大样本且方差未知:XZ2 —,' nZ 2 S, ■■ np,有限总体时无限总体时 Pp(1 p) n(3)总体正态,小样本,方差已知X Z 2n S(4)总体正态,小样本,方差未知X t 2 SZ 2234估计 时所需的样本容量:n 一岂一XN n N 11(3)小样本,正态X 1X 2t2SX 1 X 235.总体比率 P 的区间估计 36. p 的区间估计时所需的样本容量 nnZ22 P 21P)37.大样本总体均值的检验统计量方差已知:Z X ,/ jn方差未知:Z X - s/ vn38.小样本总体均值的检验统计量 39.总体比率检验统计量:ZX :t , df n 1S M/nP 0P o (1 P o )40. 总体均值的单侧检验中所需样本容量2Z Zn ------------------------------------- 20 141. 独立样本时 ,两个总体均值之差的点估计量X 1X 2的期望值与标准差:2-,用Z 2代替Z 即为双侧检验的公式:X 1 X 2E(X 1 X 2)12,2212n ?42.两个总体均值之差的区间估计: (1)大样本(n 1, n , 30), 1, 2已知X1X2厶 2Z2 X 1 X 2X X 的点估计量为:S XX i X 2X i(2)大样本,XT X 21, 2未知 X 143. 两个总体均值之差的假设检验统计量Sd /J n44. 两个比率之差的点估计量P 2的期望值与标准差 P i45. 两个总体比率之差的区间估计 :大样本 n i P i , n i (i P i ),门2卩2, ^(i P 2)P2 Z S P i P 22(2)小样本t (1)大样本 Z S pin ii n 246. 两个总体比率之差的检验统计量 P 2 P iP 2总体比率合并估计 :Pn i P i n 2 n〔 n 2P iP 2时P i P 2的点估计量:S P i P 2P(i P)丄丄n 〔 n 2(3)相关样本2p ip2P i (i P i ) P 2(i P 2)n iP 2(i P 2)n ?(1i)p P 的点估计量 :Sp i p 22(i P 2)门 2n 1 S 247. 一个总体方差的区间估计 n 1 S 2------- 2(1 / 2)48. 一个总体方差的检验统计量49. 两个总体方差的检验统计量 50. 拟合优度检验统计量 s ; s ;2ei——,dfe i51. 独立假设条件下列联表的期望频数 第i 行之和 RT i CT j n 独立性检验统计量 eij第j 列之和 样本容量 ij e ij2ej ,df52.检验 K 个均值的相等性 第j 个处理的样本均值 n jX •• iji 1n jn j第j 个处理的样本方差 X iji 1X ij总样本均值 处理均方 :MSTRn t 1 SSTR_1处理平方和 :SSTR误差均方 :MSEjSSE误差平方和 :SSEX t )2k 个均值相等检 总平方和 :SST验统计量MSTR MSEij平方和分解 多重比较方法 :SSTi 1SSTRSSEFisher LSD 的检验统计量 :tMSE54.随机化区组设计求平方和的另一种方法55.析因试验:a b r总平方和 :SSTi 1 j 1 k 1a因子A 平方和:SSA bri 1 b 因子B 平方和:SSB arj 1交互作用平方和:SSAB误差平方和 :SSE SST57.简单线性回归模型:y °1X简单线性回归方程:Ey °1 x估计的简单线性回归方程:2 b °b 1 x最小二乘法:min y i2i 2总平方和 :SS t2 ijX ij ak,df t ak1,处理平方和 :SS b2X ij 区组平方和 :SS r 误差平方和:SS ea2 XijkSS t SS b SS r , df eX ijak2Xijakk 1,df b ,df rk 1,a 1,总平方和 :SS t____ 2X ; ,df tn t 1,处理平方和区组平方和 误差平方和SS b aj 1 X .j X t ,df b k1,SS r ak i 1X i.X t2,df ra 1, SS e SS tSS b SS r , df ek1 a 1X jkX t,df tn t1——2X i. X t,df Aa 1,2X .jX t,df Bb 1,ab2rX ij X i.X . jX t,df ABa 1b 1 i 1j 1SSA SSBSSAB, df e abr abab(r 1)b 1j 1 i 21k___ 2估计的回归方程的斜率和截距:x i y iX i y i -------------------------------------------n22X iX -------------------------------------nb°y b1 x平方和分解:SST SSR SSE 误差平方和:SSE总平方和:SST y i回归平方和:SSRy iX i Y iY iX i2判定系数(决定系数):R2样本相关系数:r xy均方误差(2的估计量估计量的标准误差X2^的估计的标准差:S b i2y ib2SSRSST2y iX i2t统计量:t 2回归均方:MSR F检验统计量:F 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
< 0
> 0
说明:1、单侧检验包括左侧检验和右侧检验
2、原假设在假设时包含等号 (=、≤、≥),备择假设在假设时不包 含等号=
3、备择假设在双侧检验时没有特定的方向,而单侧检验时有特定的方 向
由绝对数时间序列资料计算平均发展水平公式如下:
绝对数 时间数 列的平 均发展 水平
(1)时期数列 的平均发 展水平
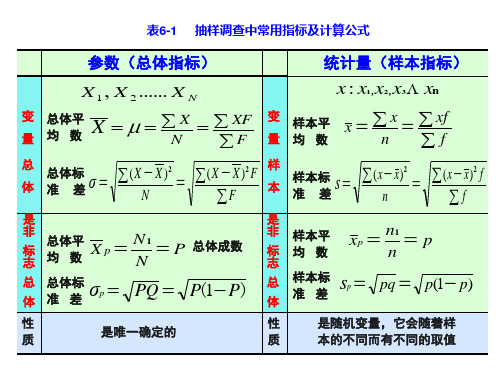
表6-1 抽样调查中常用指标及计算公式
参数(总体指标)
统计量(样本指标)
X 1 , X 2 ...... X N
变 量
总体平 均数
X
X
N
XF F
x: x1,x2 ,x3 xn
变 样本平 x x xf
量 均数
n f
总 体
总体标 准差
σ
(X X)2
N
(X X)2F
F
样 本
样本标 准差
s
(xx)2
=1
在置信水平1- 下参 数的置信区间为:
或: x z 2x
x z 2
n
x x
2、总体分布未知、 2 未知、大样本时,均值的
区间估计
2未知,大样本情况下,无论原有总体服从何种分布,样本均值的抽样
分布服从正态分布,可用样本方差替代总体方差。这时:
Hale Waihona Puke Px-z 2 s2 n
x+z 2
s2 n
(1)重复抽样: x
2
nn
:总体标准差
n:样本容量
(2)不重复抽样:x
2 N n
n
N
1
n
1 n
N
N :总体单位数
注意:在实际计算抽样平均误差时,当总体标准差σ未知
时,可以用样本标准差s来代替。即:
x
n
s n
s (x x)2
n
(大样本)
s
(x x)2 n 1
(小样本)
2.样本成数的抽样平均误差
由于总体成数可以表现为是非标志(0,1)分布的 平均数,而且它的标准差也可以从总体成数推算出来,
X p P P P(1 P)
因此,可以从样本平均数的抽样平均误差和总体标准
差的关系推出样本成数的抽样平均误差的计算公式。
(1)重复抽样:
p
P
n
P(1 P)
n
(2)不重复抽样: p
P(1 P) 1 n
(2)时点数列 的平均发 展水平
注意:首先要明 确时间序列的种 类,然后选择相 应的公式计算。
连续时 点数列
间断时 点数列
a
a n
a
a n
a
af f
a1 a2 a3 an
a 2
2
n 1
a1 a2 f 1 an 1 an fn-1
a 2
2
f 1 fn-1
环比发展速度和定基发展速度的关系
n
(x x)2 f
f
是
非
标 志
总体平 均数
Xp
N1 N
P
总体成数
σ 总 总体标
体准差 p
PQ
P(1 P)
是
非 样本平 标 均数
xp n1 p
n
志
总 体
s 样本标
准差 p
pq
p(1 p)
性 质
是唯一确定的
性
是随机变量,它会随着样
质
本的不同而有不同的取值
简单随机抽样下抽样平均误差计算公式
1.样本平均数的抽样平均误差
n N
注意:在实际计算抽样平均误差时,当总体成数P
未知时,可用样本成数 p 来代替。即:
三、一个总体参数的区间估计
(一)总体均值的区间估计 1 、总体为正态分布、 2已知时,均值的区间估计
当总体服从正态分布且方差已知,样本均值的抽样分布服从正态分布 , 这时
Px-z 2
2
n
x+z 2
2
n
2
(n
1)
s2 n
x+t 2 (n 1)
s2 n
=1
根据t分布性质,在置信水平1- 下总体均值的置信区间为:
x x
或:
x
t
2
(n
1) x
x t (n 1) 2
s n
假设检验的类型:双侧检验和单侧检验
假设
研究的问题 双侧检验 左侧检验
右侧检验
原假设H0 = 0 0 0
备择假设H1 ≠0
1.各个时期环比发展速度连乘积等于相应的定基发展 速度;
a1 a2 a3 an
an
a0 a1 a2
an 1
a0
2.相邻时期的定基发展速度之比等于相应的环比发 展速度。
an an 1
an
a0
a0
an 1
=1
在置信水平1- 下参数的置信区间为:
或: x z 2x
x z 2
s n
x x
3、总体服从正态分布、 未知、小2样本时,均值的区间估计
总体方差未知且是在小样本情况下,则需用样本方差代替总体方差,这时 样本均值经过标准化以后的随机变量则服从自由度为(n-1)的t分布, 可 得到
P
x-t
