混凝土T形截面受弯构件正截面承载力计算
合集下载
4-6受弯构件正截面承载力计算---T形截面
)
As1 =
M −M′ f yγ s h0
As = As1 + As 2
OK
混凝土结构设计原理 / 第4章 受弯构件正截面承载力计算
11
混凝土结构设计原理 / 第4章 受弯构件正截面承载力计算
12
例题1：
已知：T形截面b×h×b’f×h’f=250×600×500×80 采用：C30混凝土，纵向钢筋级别：HRB400 受拉钢筋面积：As＝1571mm2(5Ø (5Ø20) ， 构件安全等级为二级，环境类别为一类。 承受设计弯矩：M＝290kN290kN-m 待求：Mu=?
14
例题2：
已知：T形截面b×h×b’f×h’f=250 250×800× 600×100 采用：C20混凝土，纵向钢筋级别：HRB335 受拉钢筋面积：As＝2513mm2(8Ø (8Ø20) ， 构件安全等级为二级，环境类别为一类。 承受设计弯矩：M＝170kN170kN-m 待求：Mu=?
例题2解：
OK
f y As − α 1 f c (b ′f − b )h ′f
第一类T形： M u = α1 fcb′f x(h0 − 0.5x) + α1 fc (b′f − b)h′f (h0 − 0.5h′f )
ξ=
f y As
α1 f cb
≤ ξ b h0
α1 f cb′f h0
M u = α1 f c b′f h02ξ (1 − 0.5ξ )
6
4.6.3 第一类T形截面计算 基本公式：
4.6.4 第二类T形截面计算
∑ N = 0: ∑M = 0:
α1 f c b′f x = f y As
M ≤ M u = α1 f c b′f x(h0 − 0.5 x)
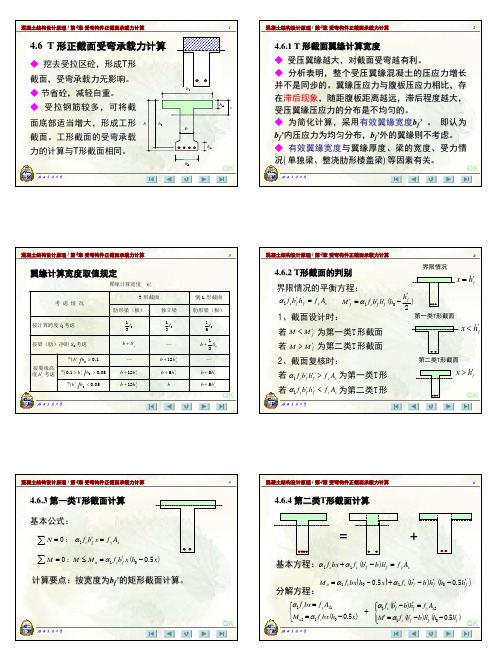
T形截面正截面承载力计算公式及适用条件
6.T形截面受弯构件正截面 承载力计算
(4) 例题
B.例4.9
截面类型判断：
1.0 9.6 600120 590 0.5 120 454106 M 515106 第2类截面
M f 1 f cb 'f h 'f h0 0.5h 'f
配筋计算：
s M 1 f c b 'f b h 'f h0 0.5h 'f 1 f cbh02
' ' N 0 : f b 1 c f h f f y As ' ' ' M 0 : M f b h h 0 . 5 h 1 c f f 0 f
因此若
1 f cb'f h'f f y As 1 f cb'f h'f f y As
或
M 1 fcb'f h'f h0 0.5h'f M 1 fcb'f h'f h0 0.5h'f
6.T形截面受弯构件正截面 承载力计算
(4) 例题
A.例4.8
确定翼缘宽度： 按梁跨度考虑：bf’=l0/3=6000/3=2000 按梁净距考虑：bf’=b+sn=200+2200=2400 按翼缘高考虑：bf’=b+12hf’=200+12 × 70=1040 最后取以上最小值：bf’=1040 截面类型判断：
1.0 9.6 1040 70 415 0.5 70 303.51106 120106
第1类截面
M f 1 f cb 'f h 'f h0 0.5h 'f
(整理)钢筋混凝土受弯构件正截面承载力的计算
第3章钢筋混凝土受弯构件正截面承载力的计算§1概述1、受弯构件（梁、板）的设计内容：图3-1①正截面受弯承载力计算：破坏截面垂直于梁的轴线，承受弯矩作用而破坏，叫做正截面受弯破坏。
②斜截面受剪承载力计算：破坏截面与梁截面斜交，承受弯剪作用而破坏，叫做斜截面受剪破坏。
③满足规范规定的构造要求：对受弯构件进行设计与校核时，应满足规范规定的要求。
比如最小配筋率、纵向2①板⑴板的形状与厚度：a.形状：有空心板、凹形板、扁矩形板等形式；它与梁的直观区别是高宽比不同，有时也将板叫成扁梁。
其计算与梁计算原理一样。
b.厚度：板的混凝土用量大，因此应注意其经济性；板的厚度通常不小于板跨度的1/35（简支）～1/40（弹性约束）或1/12（悬臂）左右；一般民用现浇板最小厚度60mm，并以10mm为模数（讲一下模数制）；工业建筑现浇板最小厚度70mm。
⑵板的受力钢筋：单向板中一般仅有受力钢筋和分布钢筋，双向板中两个方向均为受力钢筋。
一般情况下互相垂直的两个方向钢筋应绑扎或焊接形成钢筋网。
当采用绑扎钢筋配筋时，其受力钢筋的间距：当板厚度h≤150mm时，不应大于200mm，当板厚度h﹥150mm时，不应大于1.5h，且不应大于250mm。
板中受力筋间距一般不小于70mm，由板中伸入支座的下部钢筋，其间距不应大于400mm，其截面面积不应小于跨中受力钢筋截面面积的1/3，其锚固长度l as不应小于5d。
板中弯起钢筋的弯起角不宜小于30°。
板的受力钢筋直径一般用6、8、10mm。
对于嵌固在砖墙内的现浇板，在板的上部应配置构造钢筋，并应符合下列规定：a. 钢筋间距不应大于200mm，直径不宜小于８mm（包括弯起钢筋在内），其伸出墙边的长度不应小于l1/7(l1为单向板的跨度或双向板的短边跨度)。
b. 对两边均嵌固在墙内的板角部分，应双向配置上部构造钢筋，其伸出墙边的长度不应小于l1/4。
c. 沿受力方向配置的上部构造钢筋，直径不宜小于6mm，且单位长度内的总截面面积不应小于跨中受力钢筋截面面积的1/3。
T形截面受弯构件正截面承载力计算
1
fcb'f
h' f
M
1
fcb'f
h' f
h0
h' f
2
•说明仅仅翼缘高度内的混凝土受压尚 不足以与钢筋负担的拉力或弯矩设计值 M相平衡，中和轴将下移。
•即 x h'f
•属第二类T形截面
T形截面的基本计算公式及适用条件
• 第一类T形截面的基本计算公式及适用条件 • 1、计算公式
2、适用条件
x=h’f
由平衡条件得
如
f y As
1
fcb'f
h' f
或
M
1
f c b Leabharlann fh'fh0
h
' f
2
说明钢筋所承受的拉力小于或等于全部翼缘高度混凝土受压时所 承受的压力，不需要全部翼缘混凝土受压，足以与弯矩设计值 M相平衡 , 此时
x
h
' f
属于第一类T形截面
图 两类T形截面的界限
如果
f y As
主讲：
知识点:
• 1、T形截面的分类和判别 • 2、基本公式及适用条件
• 3、基本公式的应用
T形截面的分类和判别
• T形梁的判别
按照构件破坏时，中和轴位置的不同，T形截面可分为两类：
第一类T形截面：中和轴在
翼缘内，即 x h'f
第二类T形截面：中和轴在
梁肋内，即 x h'f
• 当中和轴恰好位于翼缘下边缘时，为两类T形梁的界限情况,此时
（方法一）直接计算法： 未知数个数 可直接解方程求解
若 x bh0 时，则满足条件；
如 x bh0 时，则为超筋梁，
混凝土受弯构件正截面承载力计算
h0—有效高度。 1.最大配筋率及界限相对受压区高度
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度，即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定（本构关系）
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段：裂缝开裂前 • 第二阶段：从开裂到钢筋屈服 • 第三阶段：从钢筋屈服到梁破坏
（1）第I阶段
当荷载比较小时，混凝土基本处 于弹性阶段，截面上应力分布为三 角形，荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大，挠度和截面曲率很小，钢筋 的应力也很小，且都于弯矩近似成 正比。
My
Mu
Failure”，破坏前
可吸收较大的应变
能。
0
f
2．超筋梁(Over reinforced)破坏
钢筋配置过多，将发生这种破坏。 破坏特征：破坏时钢筋没有达到屈服强度，破坏是由 于压区混凝土被压碎引起，没有明显预兆，为脆性破 坏。
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度，即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定（本构关系）
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段：裂缝开裂前 • 第二阶段：从开裂到钢筋屈服 • 第三阶段：从钢筋屈服到梁破坏
（1）第I阶段
当荷载比较小时，混凝土基本处 于弹性阶段，截面上应力分布为三 角形，荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大，挠度和截面曲率很小，钢筋 的应力也很小，且都于弯矩近似成 正比。
My
Mu
Failure”，破坏前
可吸收较大的应变
能。
0
f
2．超筋梁(Over reinforced)破坏
钢筋配置过多，将发生这种破坏。 破坏特征：破坏时钢筋没有达到屈服强度，破坏是由 于压区混凝土被压碎引起，没有明显预兆，为脆性破 坏。
钢筋混凝土受弯构件正截面承载力计算
为保证钢筋混凝土结构的耐久性、防火性以及钢
筋与混凝土的粘结性能，钢筋的混凝土保护层厚
５度、一配般筋不率小于2A 5msm% ； ....4...2()
bh0
用下述公式表示
As bh0
%
公式中各符号含义：
As为受拉钢筋截面面积； b为梁宽；h0为梁的有效 高度，h0=h-as；as为所有受拉钢筋重心到梁底面 的距离，单排钢筋as= 35mm ，双排钢筋as= 55~60mm 。
M/ M u
Mu
1.0
0.8 My
0.6
II
0.4
III III a II a
M cr I a
I
0
f cr
fy
fu f
加载过程中弯矩－曲率关系
说明：
对于配筋合适的梁，在III
阶段，其承载力基本保持不 变而变形可以很大，在完全
M/ M u
Mu
1.0
破坏以前具有很好的变形能 力，破坏预兆明显，我们把
0.8 My
通常采用两点对称集中加荷，加载点位于梁跨度 的1/3处，如下图所示。这样，在两个对称集中荷载间 的区段(称“纯弯段”)上，不仅可以基本上排除剪力的 影响(忽略自重)，同时也有利于在这一较长的区段上(L ／3)布置仪表，以观察粱受荷后变形和裂缝出现与开 展的情况。在“纯弯段”内，沿梁高两侧布置多排测 点，用仪表量测梁的纵向变形。
梁破坏时的极限弯矩Mu小于在正常情况下的开
裂弯矩Mcr。梁配筋率越小， Mcr -Mu的差值越大； 越大(但仍在少筋梁范围内)， Mcr -Mu的差值越小。
当Mcr -Mu =0时，它就是少筋梁与适筋梁的界限。这
时的配筋率就是适筋梁最小配筋率的理论值min。
钢筋混凝土受弯构件—T形截面梁正承载力计算
现浇肋梁楼盖（梁跨中截面） (a)
槽型板 (b)
(a)
(b)
空(c心) 板
(c)
单元4 T形截面梁正截面承载力计算
T形梁有效（计算）翼缘宽度：
离梁肋越远，T形梁翼缘受压的 压应力越小，因此对受压翼缘的宽 度有一定限制，在这个限制的宽度 范围内，认为翼缘的压应力均匀分 布。
单元4 T形截面梁正截面承载力计算
2.T形梁截面复核例题
上一例题中，若已配置受拉钢筋为8Φ25，即As=4418mm2，弯矩设计值 M=650KN.m，其余已知条件不变，试验算截面是否安全。
解题分析：T形梁首先需要确定计算翼缘宽度，之后判定T形截面类别，再进 行相应计算。 [解] （1）确定翼缘计算宽度
as
同上一题，取bf'=600mm
（2）判别T形截面类别
fc=9.6N/mm2，ft=1.1N/mm2； fy=300N/mm2， ξb=0.55
1
fcbf
hf
h0
hf 2
1.0 9.6
600
100
730
100 2
391 .7 10 6
N .mm
391 .7KN.m 450 KN.mm 第二类T形截面
（3）求M1
139.8mm b h0
0.55 740mm
（5）求As As
1 fcbx 1 fc b f
fy
bh f
1.0 9.6 250139.8 1.0 9.6 600 250100 2238mm2
300
（6）选钢筋 选用6Φ22，As=2281mm2
6Φ22
250
单元4 T形截面梁正截面承载力计算
求：验算截面是否安全
T形截面受弯构件正截面承载力计算
T形截面受弯构件正截面承载力计算对于T形截面受弯构件正截面承载力的计算，我们需要考虑以下几个因素：1.材料的力学性能：首先我们需要知道构件所使用的材料的弹性模量和屈服强度。
这些参数通常可以从材料的规格书或实验数据中获得。
2.受力分析：我们要确定在构件上产生最大弯矩的位置。
通常情况下，T形截面受弯构件在底部和侧面承受的弯矩是最大的。
根据受力分析，我们可以得出最大弯矩值。
3.截面形状：T形截面由顶横梁和底翼板组成。
我们需要确定这些截面的几何参数，例如顶横梁的宽度、厚度和底翼板的高度、厚度。
4.应力分布：根据受力分析，我们可以绘制出T形截面受弯构件的应力分布图。
根据构件上的应力分布，我们可以确定任意截面上的应力值。
5.截面承载力计算：正截面承载力的计算通常包括弯曲抗力和剪切抗力两个方面。
-弯曲抗力：根据截面形状和应力分布，我们可以计算出截面所能承受的最大弯矩。
根据材料的弹性模量和屈服强度，我们可以计算出构件所能承受的最大应力。
然后，我们可以通过应力与强度的比较来确定截面的弯曲抗力。
-剪切抗力：T形截面的底横梁和侧面翼板之间存在剪力作用。
根据剪力的大小，我们可以计算出截面上的剪应力。
同样，我们通过应力与强度的比较来确定截面的剪切抗力。
6.结构稳定性考虑：在计算截面承载力时，还需要考虑到结构的稳定性。
这包括了截面的屈曲和扭曲稳定性等。
需要注意的是，以上步骤只是一个大致的计算方法，具体的计算过程还需要根据具体的情况进行调整和修改。
在实际工程中，通常会根据设计规范和标准进行计算，确保构件的安全可靠。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
宽度bf 用下列三者中最小值： （1）简支梁计算跨径的1/3。
（2）相邻两梁的平均间距。
（3）b2bh 12h'f
。当 hh
bh
1
3时，取（
b6hh
12h' f
）
此处，b、b
h
、h
h
和
h
' f
分别如图示，h
h
为承托根部厚度。
翼板
边梁梁肋
承托 内梁梁肋
边梁受压翼板的有效宽度取相邻内梁翼缘有效宽度 之半加上边梁梁肋宽度之半，再加6倍的外侧悬臂板平均厚 度或外侧悬臂板实际宽度两者中的较小者。
（3）求得正截面抗弯承载力Mu
①当为第一类T形截面时
x
f sd As
f
c
d
b
' f
Mu
fcdb'f
x(h0
x) 2
或
Mu
fsdAs(h0
x) 2
②当为第二类T形截面时
x fsdAs fcdh'f b'f b fcdb
M ufcdb x(h 02 x)fcdb 'f bh 'f(h 0h 2 'f)
但 实 际 压 区 应 力 分 布 如 图 所 示 ， 纵 向 压 应 力
沿 宽 度 分 布 不 均 匀 。
办 法 ： 限 制 b 'f的 宽 度 ， 使 压 应 力 分 布 均 匀 , 并 取 f c d ? 。
实际应力图块
有效翼缘宽度 bf 等效应力图块
实际中和轴
《公路桥规》规定，T形截面梁（内梁）的受压翼板有效
（3）①当为第一类T形截面，即
0Md
fcdbfhf
h0
h2f
按bf ×h的矩形截面计算，求受压区高度x：
1
1
20Md
fcdbf h02
x h0
再由式（4-40）求As ： fcdb'f xfsdAs 得到
As
f cd b f x f sd
②当为第二类T形截面时
由基本公式（4-44）求受压区高度x
0Md Mu fcdbf xh02x
0Md Mu fsdAsh02 x
计算图式
（4-40） （4-41） （4-42）
适用条件
（1） x bh0
第 由 于 一 一 类 般 T形 T形 截 截 面 面 的 的 xh f较 h 0 小 ， h因 f， 而 即 值 也 h h 小 0 'f ， 。
截面设计：
（2）判定T形截面类型：
故属于第一类T形截面。 （3）求受压区高度x
x h 0 h 0 2 2 fc 0 d M b fd 1 1 7 9 1 1 7 9 2 2 1 1 1 .5 2 2 0 1 0 6 0 0 1 0 6 1 0 6 m m h f 1 2 0 m m
h0 所 以 一 般 均 能 满 足 这 个 条 件 。
（2） min
A s ， b为 T形 截 面 的 梁 肋 宽 度
bh0 在验算T形截面的值时，近似地取梁肋宽b来计算，为什么？
2.第二类T形截面 (x hf ) 计算图式
基本计算公：
C1C2 T fcb d x fch d 'fb 'f b fsA d s
注意：判断一个截面在计算时是否属于T形截面，不是看 截面本身形状，而是要看其翼缘板是否能参加抗压作用。
工字形截面、箱形截面、∏截面均可按T形截面处理。
倒T梁（图b）只能按矩形截面处理。
T形梁截面
❖ 截面换算 空心板截面换算成等效的工字形截面的换算原则是 抗弯等效的原则，即
❖ 保持截面面积不变； ❖ 保持惯性矩大小不变； ❖ 保持形心位置不变。
xh 0h 0 22 [0M dfcd(bffc db b)hf(h 00.5 hf)
并满足 hf xbh0 ，将各已知值及x值代入基本公式
fcb d x fch d 'fb 'f b fsA d s
求得所需受拉钢筋面积As。 不满足 x bh0 ，则修改设计。 （4）选择钢筋直径和数量，按构造要求布置，校核as。
当进行截面复核时，如果
fcdbfhf fsdAs
则为第一类T形截面 ，否则为第二类。
4.6.2截面承载力计算的两类问题
1.截面设计
已知截面尺寸，材料强度级别，弯矩计算值M=γ0Md ，求受
拉钢筋截面面积As。
（1）假设as，得到有效高度h0=h–as。
可假设as=30mm+（0.07~0.1）h
（2）判定T形截面类型
2.截面复核 已知受拉钢筋截面面积及钢筋布置、截面尺寸和材料强度级
别，要求复核截面的抗弯承载力Mu 。
解：（1）检查钢筋布置、最小配筋率是否符合构造要求 （2）判定T形截面类型,
若满足 fcdbfhf fsdAs
属于第一类T形截面，否则属于第二类T形截面。
（3）求得正截面抗弯承载力Mu
受 压 翼 缘 有 效 宽 度 b 'f的 确 定
(1) 翼缘有效宽度 翼缘上应力分布非均匀。为便于计算，设计中，根据
等效受力原则，把与梁肋共同工作的翼板宽度限制在一定 的范围内，称为受压翼板的有效宽度。
(2 )T 形 截 面 翼 缘 计 算 宽 度 b 'f的 取 值 T形 截 面bf 越 宽 ， h0越 大 ， 抗 弯 内 力 臂 越 大 。
（4-43）
M0
0 M d M u fcb d(h 0 x 2 x ) fcd b 'f b h 'f(h 0 h 2 'f)（4-44）
适用条件：（1）x bh0
（ 2 ） m （ in一 般 均 能 满 足 ）
3.判定截面类型 当进行截面设计时，如果
0Md
fcdbfhf
h0
h2f
T形截面受弯构件
概述
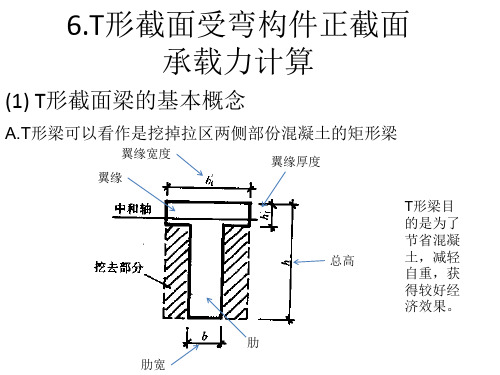
T：矩形截面梁在破坏时，开裂截面处受拉区混凝土对截 面的抗弯承载力已退出工作，因此可将受拉区混凝 土挖去一部分，将受拉钢筋集中布置在剩余拉区混 凝土内，形成T形截面。
优点：不降低截面承载能力，节省混凝土用量和减轻自重， 增大跨越能力。
翼缘板（简称翼板）：截面伸出部分
梁肋或梁腹：其宽度为b的部分
As
f
cd
b
' f
x
f sd
11.5 1600 106 280
6966mm 2
（5）选择布置钢筋
截面复核：
（3）正截面抗弯承载力
此外，《公路桥规》还规定，计算超静定梁内力时， T形梁受压翼缘的计算宽度取实际全宽度。
4.6.1 基本计算公式及适用条件
按受压区高度的不同分为两类：
第一类T形截面 (x hf )
第二类T形截面 (x hf )
T形截面的分类
1.第一类T形截面 (x hf )
视同bf ×h的矩形截面，基本计算公式 ： fcdbf x fsdAs