五年级数学思维训练作业10(答案)
【精品奥数】五年级上册数学思维训练讲义-第十讲 作图法解题 人教版(含答案)

第十讲作图法解题第一部分:趣味数学谁是作业本的主人在学完乘法分配律后,老师发现一作业本的姓名一栏写着:木(1+2+3)。
老师问:“这是谁的作业本?”一个学生站起来:“是我的。
”老师:“你叫什么名字?”学生:“木林森!”老师:“那你怎么把名字写成这样呢?”学生:“我用的是乘法分配律!”老师很开心的说:“那木(0.1+0.2+0.3)就是我们班的小木林森喽?”第二部分:奥数小练【例题1】五(1)班的男生人数和女生人数同样多。
抽去18名男生和26名女生参加合唱队后,剩下的男生人数是女生的3倍。
五(1)班原有男、女生各多少人?【思路导航】根据题意作出示意图:从图中可以看出,由于女生比男生多抽去26-18=8名去合唱队,所以,剩下的男生人数是女生人数的3倍,而这8名同学正好相当于剩下女生人数的2倍,剩下的女生人数有8÷2=4名,原来女生人数是26+4=30名。
练习一:1.两根电线一样长,第一根剪去50厘米,第二根剪去180厘米后,剩下部分,第一根是第二根长度的3倍。
这两根电线原来共长多少厘米?2.甲、乙两筐水果个数一样多,从第一筐中取出31个,第二筐中取出19个后,第二筐剩下的个数是第一筐的4倍。
原来两筐水果各有多少个?3.哥哥现存的钱是弟弟的5倍,如果哥哥再存20元,弟弟再存100元,二人的存款正好相等。
哥哥原来存有多少钱?【例题2】同学们做纸花,做了36朵黄花,做的红花比黄花和紫花的总数还多12朵。
红花比紫花多几朵?【思路导航】通过线段图来观察:从图中可以看出:红花比紫花多的朵数由两部分组成,一部分是36朵,另一部分是12朵,所以,红花比紫花多36+12=48朵。
练习二:1.奶奶家养了25只鸭子,养的鸡比鸭和鹅的总数还多10只。
奶奶家养的鸡比鹅多几只?2.批发部运来一批水果,其中梨65筐,苹果比梨和香蕉的总数还多24筐。
运来的香蕉比苹果少多少筐?3.期末测试中,明明的语文得了90分。
数学比语文和作文的总分少70分。
小学五年级数学思维训练100题(附答案)

小学五年级数学思维训练100题(附解析及答案)1. 765×213÷27+765×327÷272.(9999+9997+...+9001)-(1+3+ (999)3.19981999×19991998-19981998×199919993.(873×477-198)÷(476×874+199)5.2000×1999-1999×1998+1998×1997-1997×1996+…+2×16.297+293+289+…+2097.计算:8.9.有7个数,它们的平均数是18。
去掉一个数后,剩下6个数的平均数是19;再去掉一个数后,剩下的5个数的平均数是20。
求去掉的两个数的乘积。
10. 有七个排成一列的数,它们的平均数是 30,前三个数的平均数是28,后五个数的平均数是33。
求第三个数。
11. 有两组数,第一组9个数的和是63,第二组的平均数是11,两个组中所有数的平均数是8。
问:第二组有多少个数?12.小明参加了六次测验,第三、第四次的平均分比前两次的平均分多2分,比后两次的平均分少2分。
如果后三次平均分比前三次平均分多3分,那么第四次比第三次多得几分?13. 妈妈每4天要去一次副食商店,每 5天要去一次百货商店。
妈妈平均每星期去这两个商店几次?(用小数表示)14.乙、丙两数的平均数与甲数之比是13∶7,求甲、乙、丙三数的平均数与甲数之比。
15.五年级同学参加校办工厂糊纸盒劳动,平均每人糊了76个。
已知每人至少糊了70个,并且其中有一个同学糊了88个,如果不把这个同学计算在内,那么平均每人糊74个。
糊得最快的同学最多糊了多少个?51. 一副扑克牌共54张,最上面的一张是红桃K。
如果每次把最上面的12张牌移到最下面而不改变它们的顺序及朝向,那么,至少经过多少次移动,红桃K才会又出现在最上面?52. 爷爷对小明说:“我现在的年龄是你的7倍,过几年是你的6倍,再过若干年就分别是你的5倍、4倍、3倍、2倍。
小学五年级数学思维专题训练—等积变形(含答案解析)
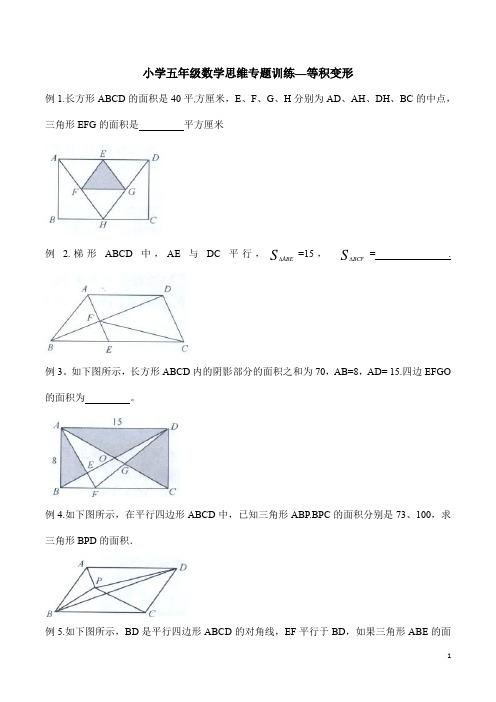
小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。
小学数学五年级上册思维训练题(附解析和答案)

五年级数学上册思维训练题1班级考号姓名总分1.已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元?2. 3箱苹果重45千克。
一箱梨比一箱苹果多5千克,3箱梨重多少千克?3. 甲乙二人从两地同时相对而行,经过4小时,在距离中点4千米处相遇。
甲比乙速度快,甲每小时比乙快多少千米?4. 李军和张强付同样多的钱买了同一种铅笔,李军要了13支,张强要了7支,李军又给张强0.6元钱。
每支铅笔多少钱?5. 甲乙两辆客车上午8时同时从两个车站出发,相向而行,经过一段时间,两车同时到达一条河的两岸。
由于河上的桥正在维修,车辆禁止通行,两车需交换乘客,然后按原路返回各自出发的车站,到站时已是下午2点。
甲车每小时行40千米,乙车每小时行 45千米,两地相距多少千米?(交换乘客的时间略去不计)6. 学校组织两个课外兴趣小组去郊外活动。
第一小组每小时走4.5千米,第二小组每小时行3.5千米。
两组同时出发1小时后,第一小组停下来参观一个果园,用了1小时,再去追第二小组。
多长时间能追上第二小组?7. 有甲乙两个仓库,每个仓库平均储存粮食32.5吨。
甲仓的存粮吨数比乙仓的4倍少5吨,甲、乙两仓各储存粮食多少吨?8. 甲、乙两队共同修一条长400米的公路,甲队从东往西修4天,乙队从西往东修5天,正好修完,甲队比乙队每天多修10米。
甲、乙两队每天共修多少米?9. 学校买来6张桌子和5把椅子共付455元,已知每张桌子比每把椅子贵30元,桌子和椅子的单价各是多少元?10. 一列火车和一列慢车,同时分别从甲乙两地相对开出。
快车每小时行75千米,慢车每小时行65千米,相遇时快车比慢车多行了40千米,甲乙两地相距多少千米?11. 某玻璃厂托运玻璃250箱,合同规定每箱运费20元,如果损坏一箱,不但不付运费还要赔偿100元。
运后结算时,共付运费4400元。
托运中损坏了多少箱玻璃?12. 五年级一中队和二中队要到距学校20千米的地方去春游。
五年级下册数学思维训练题及答案

五年级下册小学数学思维训练题1.新民小学133个少先队员担任卫生宣传,把他们分成几个人数相等的小组,有()种分法。
2.三根钢筋的长分别是18米、24米、36米。
现在要把它们截成同样长的小段而没有剩余,每段最长可截成()米。
3.把110个桔子分装在10全篮子里,每个篮子里所装的桔子数正好是10个连续偶数,是怎样分装的?4、99个连续的自然数相加,它们的和是奇数还是偶数?()99个连续的奇数相加,它们的和是奇数还是偶数?()99个连续的偶数相加的和是奇数还是偶数?()5.四个连续自然数的乘积是3024,这四个数分别是()。
6.一个长方体沿着高的方向截去2cm,表面积就减少48cm2,剩下的部分成为一个正方体,求原长方体的体积是()。
7.已知60 = 2X2X3X5,,知道60除了有因数1以外,还有因数()。
8.从2、3、5、7、11这五个数中,任取两个不同的数分别当作一个分数的分子和分母, 这样的分数有()个。
9.把一些橙和柑分装入袋,如果每袋6个橙、5个柑,橙分完了还剩3个柑;如果每袋8个柑、6个橙,柑分完了还剩18个橙。
橙和柑一共有()个。
10.有一筐苹果每次按2个、3个、4个、5个地数,数到最后都是多一个,如果按每次数6个,最后篮子里还剩1个。
这个篮子里至少有()个苹果。
11. 一个两位数十位上的数字是个位上数字的3倍,这个两位数减9,则个位上的数字与十位上的数字相等。
这个两位数是()。
12.计算22+42+62+……+402=()13.五年级数学竞赛,小明获得的名次与他的年龄和竞赛的成绩相乘之积是2134,小明获得的名次()名,成绩是()分。
14、把三个长5dm、宽4dm、高3dm的长方体礼品盒包装在一起,怎样包装用的包装纸最少?(请画出图)要用()平方分米的包装纸。
15、把210个零件分装在几个盒子里,要使每个盒子的零件数相等,有()种装法。
16、迎宾仪仗队由男生48人、女生32人组成,要分成若干小组,每组男、女生人数分别相等,有()种分法。
小学五年级数学思维训练(奥数)《分数的加法和减法》讲解及练习题(含答案)

分数的加法和减法专题简析:在分数加减法运算中,同分母分数相加减,分母不变,只把分子相加减。
异分母分数相加减,要先通分,然后按照同分母分数加减法的法则进行计算。
在分数加减法中,整数的一些加减运算定律同样适用。
例1 计算:16-272-375分析与解答:可根据题目的特点把后面减去的两个分数相加,再用16减去这两个分数的和,这样计算比较简便。
16-272-375=16-(272+375)=16-6=10随堂练习:计算下面各题 12-85-833 851-213-514例2 计算42235+(83-235)-21 分析与解答:观察算式发现,如果利用去括号的性质,去掉括号后计算比较简便。
42235+(83-235)-21 =42235-235+83-21 =42+83-21 =4283-84 =8741有些分数加减法试题,利用运算性质和定律去掉括号,添加括号,变换加数、减数的位置,改变运算顺序,可以达到简算的目的。
随堂练习:用简算方法计算下面各题。
45333+(452-274)-275 125612-( 125106-6011)-601例3 计算 207+1.35+52+8.65 207+1.35+52+8.65=(1.35+8.65)+(207+52) =10+43 =4310随堂练习: 254+2.75+207+2.25 1135-(2.375-1181)-853例4 计算1-101-1001-10001-100001 分析与解答:可先给后面四个分数加上括号,求出括号中四个分数之和,然后用1减去所得的和即可。
1-101-1001-10001-100001 =1-(101+1001+10001+100001) =1-100001111 =100008889 随堂练习:计算下面各题。
1-21-41-81-161 1-21-201-2001-20001例题5 计算分析与解答:先利用算式中分子的特点计算出分子,再约分。
五年级数学思维训练10 排列与组合(原卷 解析版)

五年级数学思维训练10 排列与组合1、奥运吉祥物中的5个“福娃”—贝贝、京京、欢欢、迎迎、妮妮取“北京欢迎您”的谐音。
如果在盒子中从左向右放5个不同的“福娃”,有多少种不同的放法。
2、5家企业中的每两家都签订了一份合同,那么他们共签订了多少份合同?3、如果一个自然数中任一数位上的数字都大于其左边的每个数字,则称这个数是“上升数”。
由1,2,3,4,5这5个数字组成的4位数中“上升数”共有多少个。
4、某次宴会共有n个人参加,每个人都与其他的人互相恰好握手一次,若在此宴会中总共握手231次,请问n的值为多少?5、一种号码有4位,其中前两位上取26个字母中的字母,后两位取0~9这10个数字中的数字,没有相同的数字的四位号码的个数有多少个?6、从6双不同的鞋中取出2只,其中没有成双的鞋,共有多少种不同取法?7、将A、B、C、D、E、F、G七位学生在操场排成一列,其中学生B与C必须相邻,请问共有多少种不同的排列方法?8、6位小朋友玩游戏,他们打算分成3组,每组2人,请问共有多少种不同的分法?9、4个男孩和4个女孩参加歌唱比赛,他们一下接着一个地唱。
如果假定两个女孩不能连着唱,必须隔开,那么能排成多少种不同的顺序?10、新年晚会共有8个节目,其中有3个非歌唱类节目,排列节目单时规定,非歌唱类节目相邻,而且第一个和最后一个节目都是歌唱类节目,则节目单可有多少种不同的排法?11、有4名同学约定去上网,现只有3台电脑,只好有两个同学上同一台电脑,则共有种不同的上网方式。
A.64B.81C.36D.7212、把同一排6张座位编号为1、2、3、4、5、6的电影票全部分给4个人,每人至少分一张最多分2张,且这2张具有连续的编号,那么不同的分法为多少种?13、A、B和C被安排坐入排成一列的6个座位中,若任意二个人都不可以相邻而坐,共有多少种不同的入座方式?14、请问由1,2,3,4,5五个数字所构成的所有不同的五位数之总和(不允许数字重复)等于多少?15、从0、1、2、3、4、5这6个数字中,任取3个组成三位数,共可组成多少个不同的三位数。
小学五年级数学思维练习题100道及答案

小学五年级数学思维练习题100道及答案1.765×213÷27+765×327÷27解:原式=765÷27×(213+327)= 765÷27×540=765×20=153002.(9999+9997+...+9001)-(1+3+ (999)解:原式=(9999-999)+(9997-997)+(9995-995)+……+(9001-1)=9000+9000+…….+9000 (500个9000)=45000003.19981999×19991998-19981998×19991999解:(19981998+1)×19991998-19981998×19991999=19981998×19991998-19981998×19991999+19991998=19991998-19981998=100004.(873×477-198)÷(476×874+199)解:873×477-198=476×874+199因此原式=15.2000×1999-1999×1998+1998×1997-1997×1996+…+2×1解:原式=1999×(2000-1998)+1997×(1998-1996)+…+3×(4-2)+2×1=(1999+1997+…+3+1)×2=2000000。
6.297+293+289+…+209解:(209+297)*23/2=58197.计算:解:原式=(3/2)*(4/3)*(5/4)*…*(100/99)*(1/2)*(2/3)*(3/4)*…*(98/99) =50*(1/99)=50/998.解:原式=(1*2*3)/(2*3*4)=1/49. 有7个数,它们的平均数是18。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级数学思维训练作业(十)
班级:姓名:家长签名:
1.小明和小刚两家相距3.6千米,他们分别从自己家同时出发,相向而行,小明骑车,每分钟行400米,小刚步行,每分钟走80米,2
分钟后,小明发现有东西忘记带,又返回家去取,然后又立即出发(不考虑取东西的时间),一共经过多长时间两人相遇?
思路点拨:小明从出发到回家一共行了4分钟,这4分钟小刚一直在走,因此可以看成是小刚先出发4分钟,走了:
80×4=320(米)
然后再看成同时出发,此时的路程为:3600-320=3280(米)
所以相遇时间为:3280÷(400+80)≈6.8(分钟)
一共用时:6.8+4=10.8(分钟)
2. 一辆公共汽车和一辆小轿车同时从相距299千米的两地相向而行,公共汽车每小时行40千米,小轿车每小时行52千米。
问:几小时后两车第一次相距69千米?再过多少时间两车再次相距69千米?思路点拨:第一次相距69千米,是相遇前相距,此时两车所行的总路程为:299-69=230(千米)
时间为:230÷(40+52)=2.5(小时)
第二次相距69千米,是相遇后相距,此时两车所行的总
路程为:299+69=368(千米)
时间为:368÷(40+52)=4(小时)
从2.5小时到4小时,经过了:4-2.5=1.5(小时)
3.某县举行长跑比赛,运动员跑到离起点5千米处要返回到起跑点。
领先的运动员每分跑320米,最后的运动员每分跑305米。
起跑后多少分这两个运动员相遇?相遇时离返回点有多少米?
思路点拨:此题的运动方向是“同向”的(如下示意图)。
如果将领先的运动员的“起跑点”放到“返回点”的另一侧(如下图中的另一起跑点),
这时就成了最基本的从两地相向而行的相遇问题,根据相遇问题的解法,就可以很快地求出相遇时间:
1000×5×2÷(320+305)=16(分)。
继而求出相遇点与返回点之间的距离:
320×16-1000×5=120(米)。
或者1000×5-305×16=120(米)。
这里,巧妙地将“同向”变为“相向”,使本来较为复杂的行程问题变成最基本的相遇问题,从而使问题迎刃而解。
4.两人分别骑摩托车和自行车从相距208千米的甲、乙两地相向开
出,摩托车的速度为每小时48千米,自行车的速度为每小时16千米,途中摩托车发生故障,停车修理1小时后继续前进。
两车相遇时自行车行了多少小时?
思路点拨:这是一道“假同时”出发的相遇问题。
由于“途中摩托车发生故障,停车修理1小时”,因此事实上,从出发到相遇摩托车比自行车少
行1小时。
要使两车行驶的时间相同,可以有两种处理方法:
(1)让摩托车再多行1小时。
这样,两车同时行的路程就比208千米多出48×1=48(千米),即208+48=256(千米)。
再根据相遇问题的
解法,求出相遇时间,即:256÷(48+16)= 4(小时),这个时间就是
自行车行驶的时间。
列成综合算式是:
(208+48×1)÷(48+16=4(小时)。
(2)让自行车少行1小时。
那么,两车同时行的路程就比 208千米少去16 ×1= 16(千米),即 208-16=192(千米)。
再根据相遇问题的
解法,求出相遇时间,即:192÷(48+16)=3(小时),这个时间是摩托
车实际行驶的时间,自行车行的时间应该是3+1=4(小时)。
列成综合算
式是:
(208-16×1)÷9(48+16)+1=4(小时)。
上述两题的解法都是将“不同时”变为“同时”,从而使问题得以解决。
