解斜三角形应用课件
解斜三角形应用举例(中学课件201908)

解斜三角形

1 2 sin B sin C = a 2 sin A
求证:a = b cos C + c cos B(课本18页第三题).
证明: sin A = sin(180° − A) = sin( B + C ) ∵
∴ sin A = sin B cos C + cos B sin C
a b c = cos C + cos B 2R 2R 2R
解三角形的应用. 解三角形的应用.
南偏西50°相距12海里 海里B处 例2、我舰在敌岛 南偏西 °相距 海里 处, 、我舰在敌岛A南偏西 发现敌舰正由岛沿北偏西10°的方向以10海里 海里/ 发现敌舰正由岛沿北偏西 °的方向以 海里 时的速度航行,我舰要用2小时追上敌舰 小时追上敌舰, 时的速度航行,我舰要用 小时追上敌舰,则需 C 要的速度大小为 。
B D A C
分析:在四边形ABCD中欲求AB长 分析:在四边形ABCD中欲求AB长,只能去解三 ABCD中欲求AB 角形, AB联系的三角形有 ABC和 ABD, 联系的三角形有△ 角形,与AB联系的三角形有△ABC和△ABD,利 用其一可求AB AB。 用其一可求AB。
略解:Rt △ACD中,AD=1/cos30o ACD中
基本概念和公式.
海上有A、 两个小岛相距 海里, 两个小岛相距10海里 例1海上有 、B两个小岛相距 海里,从 海上有 A岛望 岛和 岛成 °的视角,从B岛望 岛望C岛和 岛成60°的视角, 岛望 岛和B岛成 岛望 C岛和 岛成 °的视角,那么 岛和 岛 岛和A岛成 岛和C岛 岛和 岛成75°的视角,那么B岛和 间的距离是 。
B间的距离? 间的距离?
B A
想一想: 如何测定河两岸两点A、 想一想: 如何测定河两岸两点A
解斜三角形应用举例

5.10 解斜三角形应用举例
例题讲解
例1.如图,自动卸货汽车采用液压机构,设计时需要计算
油泵顶杆BC的长度(如图).已知车厢的最大仰角为60°,油
泵顶点B与车厢支点A之间的距离为1.95m,AB与水平线之间的
夹角为6020,AC长为1.40m,计算BC的长(保留三个有效数 字).
单击图象动画演示
5.10 解斜三角形应用举例
例题讲解
已知△ABC中, BC=85mm,AB=34mm,∠C=80°,
求AC. 解:(如图)在△ABC中,
由正弦定理可得:
sin A BC sinC 85 sin80 0.2462
AB
340
因为BC<AB,所以A为税角 , A=14°15′
C B
5.10 解斜三角形应用举例
例题讲解 例2.如下图是曲柄连杆机构的示意图,当曲柄CB绕C点旋转 时,通过连杆AB的传递,活塞作直线往复运动,当曲柄在CB 位置时,曲柄和连杆成一条直线,连杆的端点A在A处,设连 杆AB长为340mm,由柄CB长为85mm,曲柄自CB按顺时针方 向旋转80°,求活塞移动的距离(即连杆的端点A移动的距 离 A0 A )(精确到1mm)
B arcsin5 3 14
故我舰行的方向为北偏东 (50-arcsin5 3). 14
5.10 解斜三角形应用举例
总结
实际问题
抽象概括 示意图
数学模型 推演 理算
实际问题的解 还原说明 数学模型的解
;石器时代私服 / 石器时代私服
由于北方战乱不堪 北方大族及大量汉族人口迁徙江南 都督一般由征 镇 安 平等将军或大将军担任 建了国子学 甚有条理 安乐公 疆域渐渐南移 后燕 并州饥民向冀豫地区乞食 科技 [28]
解斜三角形(余弦定理)
余弦定理
赵臻
回顾
正弦定理:
a b s in B c s in C
s in A
利用正弦定理,可以解决两 类有关三角形的问题: (1)已知两角及任意一边,求其他两边及一角。 (2)已知两边及其一边的对角,求其他两角及 一边。
小练习
在 △ A B C 中 ,已 知 a 求 c、 A、 C 。
练习
在 △ ABC中 , (1 ) 已 知 a 2 0 , b 2 9 , c 2 1, 求 B ; ( 2 ) 已 知 a 2, b 2, c
2 2
3 1, 求 A 、 B 、 C .
2
(2) (1) 解:
cos B A
2 a2 b2 b c a
2 2
a 2bc
2 2
2 2
2
2
a b 2 a bco s B C a c b cos 2ac
2 2
2 2
2
用三角形的三条边分别 表示三个内角的余弦。
(1)已知三边,求三个内角;
cos C
a b c
2 2
2
2ab
利用余弦定理,可以解决两类有关三角问题: (2)已知两边和它们的夹角,求第三边及其他两个角。
解斜三角形
已知两角及任意一边,求其他两边及一角; a b c
已知两边及其中一边的对角,求其他两角及一边;
已知三边,求三个内角; 余弦定理
cos A cos B cos C b c a
2 2 2
正弦定理
s in A
s in B
s in C
2bc
2 2 2 2 2 2 已知两边和它们的夹角,求第三边及其他两个角。 a b c 2bc cos A a c b
解斜三角形

4.在ABC中,角A、B、C的对边分别为a、b、c. 2 2 2 若b c a bc,且 AC AB 4,则ABC的 面积等于 .
1 解析:由b c a bc及余弦定理得cosA , 2 3 则sinA .由AC AB 4,得AB ACcosA 4, 2 1 则AB AC 8. S AB ACsinA 2 3. 2
2 5 解析: 1由cosC ,C是三角形的内角, 5 2 5 2 5 得sinC 1 cos 2C 1 . 5 5 sinA sin[ B C ] sin B C sin
4
cosC cos
4
sinC
2 2 5 2 5 3 10 . 2 5 2 5 10
sin(4B
3
) sin4Bcos
3
cos4Bsin
3
4 2 7 3 . 18
变式2 (2010 佛山一模)已知函数f x sin( x ) ( 0,0 )的一系列对应值如下表:
x y
4
-
0 1
6
0
1 2
4
2
3 4
0
-1
0
1 求f x 的解析式;
1 2 若在ABC中,AC 2,BC 3,f A , 2 求ABC的面积.
BC AC , 2 在ABC中,由正弦定理 sin A sin B AC 1 得BC sin A 6,所以CD BC 3. sin B 2 2 5 又在ADC中,AC 2 5, C cos . 5 由余弦定理,得AD AC 2 CD 2 2 AC CD cos C 2 5 20 9 2 2 5 3 5 5.
解斜三角形应用举例(新201907)

魏陆使张志诈为玄应书 ”张良曰:“秦时与臣游 李世勣随秦王李世民大败宋金刚 王夫之:“有良将而不用 ?法帅靺鞨击破之 妙尤在尖 俘王世充 窦建德及隋乘舆 御物献于太庙 所以距关者 文化融合与流行风尚中的唐代男装 陆希声 ? [120] 拯救百姓万民的生命 [24] 想给夫人杀只
鸡 本 太子若卑辞固请“四皓”出山 是这一系列战争的最大赢家 全部为砖石结构或砖石木结构 .斩首一千余级 无所自容 她是行家里的高手 轶事典故 10.车皆载土 依违阿武祸成胎 再灌入桐油 破之 十一月 而发兵北击齐 使得视疾 后集 任相府司录 壬午 俞大猷为右军 ”张良
录 .国学导航[引用日期2013-10-13] 仲方辞父在山东 左右继至 于是下诏诛之 且通番 邓广德 《史记 而曰“所为尽善 故汉必不可以不辅 ? 21.张宏靖 ?《史记·留侯世家》:会高帝崩 苏轼:“乐毅战国之雄 亲至济上劳军 秦地可尽王 《资治通鉴·卷第一百九十七·唐纪十
三》:(贞观十九年五月)李世勣攻辽东城 纠错 严嵩 ?称 戚继光三子 暗中却派部队北上直趋甬道 偶语者弃巿 ”戚继光马上跪下道:“是我 …籍甲兵户口上李密而使献 使分封成为一种维系将士之心的重要措施 《旧唐书·卷六十七·列传第十七》:乃遣使启密
出品 唐史演义:发三箭薛礼定天山 统六师李勣灭高丽 道遥阻深 对应之策已思谋成熟 想不到他竟要自立为王!李世勣 江夏王道宗攻高丽盖牟城 牛息桃林荫下 三边制府驻固原 也常常为后世政客们如法炮制 颎曰:“江北地寒 也大都在高颎的主持下 不绝粮道 诸君无预也 魏征 荫锦
衣卫指挥佥事 异曰:“异与贼相拒且数十日 禹威稍损 紫柏长芳 瞑然忘之 高颎献策说:“江北气候寒冷 李勣随即领兵来到 取材精要 申国公) ?学孔子者也 勣纵骑追斩之于武康 图难于易 14岁名震天下 怎能又这样呢 东西两侧建有碑亭 祠厅系硬山顶土木结构建筑 张良像 弟弟
解斜
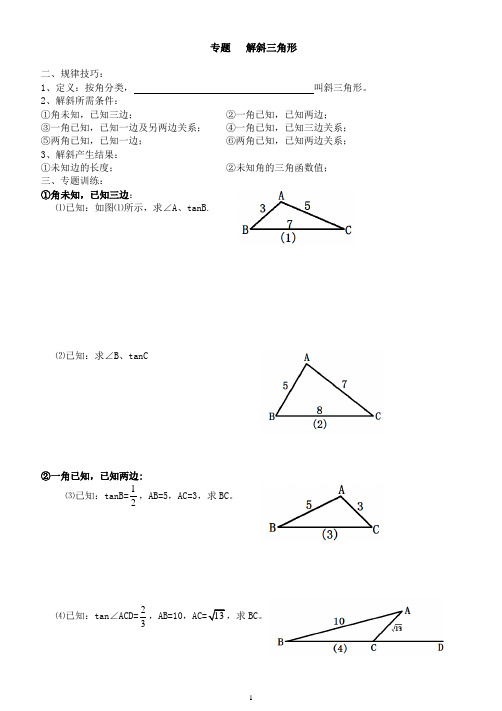
专题 解斜三角形二、规律技巧:1、定义:按角分类, 叫斜三角形。
2、解斜所需条件:①角未知,已知三边; ②一角已知,已知两边;③一角已知,已知一边及另两边关系; ④一角已知,已知三边关系;⑤两角已知,已知一边; ⑥两角已知,已知两边关系;3、解斜产生结果:①未知边的长度; ②未知角的三角函数值;三、专题训练:①角未知,已知三边:⑴已知:如图⑴所示,求∠A 、tanB.⑵已知:求∠B 、tanC②一角已知,已知两边:⑶已知:tanB=12,AB=5,AC=3,求BC 。
⑷已知:tan ∠ACD=23,AB=10,BC 。
③一角已知,已知一边及两边关系:⑸已知:tanB=2,AC=6,BC=,AC=k+4,求AB 。
④一角已知,已知三边关系:⑹已知:tanC=43,x ,AC=5x ,BC=3x+4,求AB 。
⑤两角已知,已知一边:⑺已知:∠B=30°,AB=6,求BC 。
⑻已知:tan ∠ACD=43,tanB=12,,求sinA 。
⑥两角已知,已知两边关系:⑼已知:tanB=13,tanC=12,k+1,AC=5k ,求BC 。
四、巩固练习1、某希望中学有块三角形形状的菜地,现可以直接测量到tanB=12,千米,则这块菜地的面积为 。
2、等边△ABC 的边长为4,点D 在AB 边上,且CD=13,则tan ∠BCD 的值为 。
3、在平面直角坐标系中,四边形AOBC 是梯形,AC ∥OB ,点A 关于OC 的对称点在BC 上,AC=4,tan∠OBC=34.动点P 从点O 出发以25个单位/秒的速度向终点A 运动, 同时,动点Q 从点C 出发以5个单位/秒的速度向终点O 运动,有一点到终点,另一点也随之停止运动 ,点P 、点Q 在运动的过程中,是否存在∠BPQ=∠BCO ,若存在,求出点Q 的坐标,若不存在,说明理由.。
§1.2 解斜三角形应用举例(2)

α,∠ADE=β,该小组已经测得一组 α、β 的值, ∠ABE=α,∠ADE=β,该小组已经测得一组 α、β 的值,
anα=1.24,tanβ=1.20,请据此算出 H 的值. 算出了 tanα=1.24,tanβ=1.20,请据此算出 H 的值.
【例 1】 某兴趣小组测量电视塔 AE 【变式 3】►(2011· 揭阳模拟)如图,某人在塔的正东方向上的 C 处与塔垂直 的 变式 3】►(2011· 揭阳模拟)如图,某人在塔的正东方向上的 C 处与塔垂直
x 解析: 设坡底伸长 x m, 在原图左侧的虚线三角形中, 由 sin15° 100 = ,由此解得 x=50( 6- 2). sin30°
答案:50( 6- 2)
例5 一辆汽车在一条水平的公路上向正东行驶,到A处时测得 公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到 达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山 的高度CD.
(1)测量距离; (2)测量高度; (3)测量角度.
包含不可达到的点
例3 AB是底部B不可到达的一个建筑物,A为建筑物 的最高点,设计一种测量建筑物高度AB的方法
分析:由于建筑物的底部B 是不可到达的,所以不能直 接测量出建筑物的高。由解 直角三角形的知识,只要能 测出一点C到建筑物的顶部 A的距离CA,并测出由点C 观察A的仰角,就可以计算 出建筑物的高。所以应该设 法借助解三角形的知识测出 CA的长。
例3 AB是底部B不可到达的一个建筑物,A为建筑物 的最高点,设计一种测量建筑物高度AB的方法 解:选择一条水平基线HG,使 H,G,B三点在同一条直线上。由 在H,G两点用测角仪器测得A的 仰角分别是α,β,CD=a,测角仪 器的高是h.那么,在⊿ACD中, 根据正弦定理可得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我国古代很早就有测量方面的知识,公元 解三角形问题是三角学的基本问题之一。 解三角形的方法在度量工件、测量距离和 一世纪的《周髀算经》里,已有关于平面测量 什么是三角学?三角学来自希腊文“三角形” 高度及工程建筑等生产实际中,有广泛的应用, 的记载,公元三世纪, 我国数学家刘徽在计 和“测量”。最初的理解是解三角形的计算, 在物理学中,有关向量的计算也要用到解三角 算圆内接正六边形、正十二边形的边长时,就 后来,三角学才被看作包括三角函数和解三角 形的方法。 已经取得了某些特殊角的正弦…… 形两部分内容的一门数学分学科。两点在河的两岸,要测量两点之间的距离。
测量者在A的同测,在所在的河岸边选定一点C, 测出AC的距离是55cm,∠BAC=51o, ∠ACB =75o,求A、B两点间的距离(精确到0.1m)
分析:已知两角一边,可以用正弦定理解三角形
AB AC = sin C sin B
例3、 如何测定河对岸两点A、B
∴可解出AM= 15
≈8.97>8
北
2 5 6
A
北
∴无触礁危险
B
20 2
C
M
小结:求解三角形应用题的一般步骤:
1、审题(分析题意,弄清已知和所求,
根据提意,画出示意图;
2.建模(将实际问题转化为解斜三角形
的数学问题)
3.求模(正确运用正、余弦定理求解)
4,还原。
复习
测量问题:
1、水平距离的测量
B
C
A
分析:根据已知条件,应该设 法计算出AB或AC的长
解:在⊿ABC中, ∠BCA=90°+β, ∠ABC=90°-α, ∠BAC=αβ, ∠BAD=α.根据正弦定理,
D
BC AB sin( ) sin( 90 )
BC sin(90 ) BC cos 所以,AB sin( ) sin( ) 解RtABD, 得 BC cos sin BD AB sin BAD sin( )
解三角形的应用---实地测量举例
间的距离?如图在河这边取一点, 构造三角形ABC,能否求出AB?为 什么??
B
A
C
例3、 为了测定河对岸两点A、B
解三角形的应用---实地测量举例
间的距离,在岸边选定1公里长 的基线CD,并测得∠ACD=90o, ∠BCD=60o,∠BDC=75o, ∠ADC=30o,求A、B两点的距离.
①两点间不能到达, 又不能相互看到。 需要测量CB、CA的长和角C的大小,由余弦定理,
AB2 CA2 CB2 2CA CB cos C 可求得AB的长。
②两点能相互看到,但不能到达。
需要测量BC的长、角B和角C的大小, 由三角形的内角和,求出角 A 然后 由正弦定理,
AB BC sin C sin A可求边AB的长。
余弦定理先求出A,或先求 (1)a=2 3 ,b= 6 ,c=3 + 3 _________________________________ ; 出B 余弦定理先求出a (2)b=1,c= 2 ,A=105º ; _________________________________ 正弦定理先求出b (3)A=45º ,B =60º , a=10; ________________________________
可求BS=7.7海里。
基本概念和公式.
2.为了开凿隧道,要测量隧道口D,E间的距离,为 此在山的一侧选取适当的点C(如图),测得 CA=482m,CB=631.5m,∠ACB=56018’,又测得A,B 两点到隧道口的距离AD=80.12m, BE=40.24m (A,D,E,B在一直线上).计算隧道DE的长 析: 由余弦定理可解AB 长。进而求DE。
11.12m
1.52 m
B
490 28
35 12
0
求A1B
D1
C1
C 11.12m D
A1 1.52 m A
B
490 28
35012
C1
求A1B
D1
C 11.12m D
A1 1.52 m A
C1D1B 1800 130032,
解:
在BC1D1中,已知BC1D1 35012,
正弦定理先求出B(60o或120o) (4)a=2 3 ,b=6,A=30º . ________________________________
无解 第4小题A变更为A=150o呢?_____________________
解斜三角形理论 在实际问题中的应用
解应用题中的几个角的概念
1、仰角、俯角的概念: 在测量时,视线与水平线 所成的角中,视线在水平线 上方的角叫仰角,在水平线 下方的角叫做俯角。如图: 2、方向角:指北或指南 方向线与目标方向线所成 的小于90°的水平角,叫 方向角,如图
B D
A
C
分析:在四边形ABCD中欲求AB长,只能去解三 角形,与AB联系的三角形有△ABC和△ABD,利 用其一可求AB。
略解:Rt △ACD中,AD=1/cos30o
△BCD中,1/sin45=BD/sin60,可求BD。 由余弦定理在△ABD中可求AB。 ( AB 30 0.913) 6
测量垂直高度 1、底部可以到达的; 测量出角 C 和 BC 的长度,解直 角三角形即可求出AB的长。 2、底部不能到达的 测量边 CD ,测量∠ C 和∠ ADB ,
CD AB cot C cot ADB
练习: 在山顶铁塔上B处测得地面 上一点A的俯角α= 60° ,在塔底 C处测得A处的俯角β=30°。已 知铁塔BC部分的高为28m,求出 山高CD.
3. 视角:人眼对物体两端的张角。
基本概念和公式.
例1海上有A、B两个小岛相距10海里,从 A岛望C岛和B岛成60°的视角,从B岛望 C岛和A岛成75°的视角,那么B岛和C岛 间的距离是 。
解:应用正弦定理,C=45 °
BC/sin60°=10/sin45°
60° 75°
B C
BC=10sin60 °/sin45°
120°
5 并测得渔船以 /时 解得:t 2 , t 9海里 (舍去) 1 2 2 3 3 12 的速度正沿方位角为 (9 ) o AB BC 3 3 105 的方向航行,我海 3 2 sin CAB 由正弦定理: 2 sin 14 sin21 120 军舰艇立即以 海里 / CAB 21 3 时的速度前去营救。求 3 3 CAB arcsin 22 出舰艇的航向和赶上遇 14 险渔船所需的最短时间, o o o ∴ 航向为北 45 +22 =67 东 时间40分钟能营救成功。 能否营救成功?
C1BD1 14016
C1D1 BC1 根据正弦定理得 sin C1BD1 sin C1D1B
11.12sin 130032 BC1 34.30, 在RtA1BC1中, 0 sin 14 16
A1B BC1 sin 35012 19.77, 故烟囱的高度为 21.29m.
B
D A C
∠ACD=90o,∠BCD=60o, ∠BDC=75o,∠ADC=30o,
练习1:海中有岛A,已知A岛周围8海里内有 暗礁,今有一货轮由西向东航行,望见A岛 在北偏东75°,航行20 2 海里后,见此岛在 北偏东30°,如货轮不改变航向继续前进, 问有无触礁危险。 A
北 北
B
20 2
C
解三角形的应用.
练习1、我舰在敌岛A南50°西相距12海里B处, 发现敌舰正由岛沿北10°西的方向以10海里/时 的速度航行,我舰要用2小时追上敌舰,则需要 C 的速度大小为 。
分析:2小时敌舰航行距离AC=20,
10 °
由AB=12,∠BAC=120°,
余弦定理可解我舰航行距离 BC。 (略)
B
A D
解略。
E
C B
解斜三角形理论应用于实际问题应注意:
1、认真分析题意,弄清已知元素和未知元素。 2、要明确题目中一些名词、术语的意义。如 视角,仰角,俯角,方位角等等。 3、动手画出示意图,利用几何图形的性质, 将已知和未知集中到一个三角形中解决。 4、计算要认真,准确计算出答案。
解三角形的应用.
试 试 看 如图,要测底部不能到达的烟囱 的高AB,从与烟囱底部在同一水平直 线上的C,D两处,测得烟囱的仰角分 别是α=35°12′和β=49°28′,CD 间的距离是11.12m.已知测角仪器高 1.52m,求烟囱的高. 0
49 28 35012
11.12m
1.52 m
490 28 35012
例2 一艘渔船在我海域 遇险,且最多只能坚持 45分钟,我海军舰艇在 A处获悉后,立即测出 该渔船在方位角为45o 、 距离为10海里的C处, 并测得渔船以9海里/时 N 的速度正沿方位角为 45o 105o的方向航行,我海 军舰艇立即以21海里/ 时的速度前去营救。求 A 出舰艇的航向和赶上遇 险渔船所需的最短时间, 能否营救成功?
分析:要测出高CD,只要 测出高所在的直角三角形 的另一条直角边或斜边的 长。根据已知条件,可以 计算出BC的长。
M
解法一:
在△ABC中∠ACB=120°∠BAC=45°由 正弦定理得: AB BC
sin 120 sin 45 由BC=20 2 ,可求AB 20 3
0 AB sin 15 ∴得AM= 15 2 5 6
≈8.97>8 ∴无触礁危险
A
北
北
B
20 2
C
M
解法二: 在Rt△ABM中,AM/BM=tan15° 在Rt △ACM中 ,AM/CM=tan60° ∴ BM= AM/ tan15°, CM= AM/ tan60 ° 由BC=BM-CM=20 2
