机械动力学
机械动力学课程教学大纲

机械动力学课程教学大纲一、课程简介机械动力学是机械工程中的重要基础课程之一,主要研究物体的运动规律和动力学原理。
本课程旨在培养学生对物体运动的分析和动力学理论的理解能力,为学生提供运动学和动力学的基础知识,为他们今后的学习和研究奠定牢固基础。
二、教学目标1. 培养学生对物体运动的观察和分析能力;2. 熟悉运动学和动力学的基本概念和原理;3. 掌握常见的力学定律和公式;4. 培养学生的问题解决能力和实践能力;5. 培养学生的团队合作能力和沟通能力。
三、教学内容1. 运动学基础1.1 位置、位移和速度1.2 加速度和曲线运动 1.3 圆周运动和角速度1.4 相对运动2. 动力学基础2.1 牛顿运动定律2.2 动量和动量守恒2.3 力和加速度2.4 动能和功2.5 能量守恒和机械能3. 静力学3.1 弹簧力和弹性势能 3.2 引力和万有引力定律3.3 惯性力和离心力4. 动力学4.1 圆周运动的力学分析4.2 非惯性系和转动惯量4.3 力矩和角动量4.4 角动量守恒和刚体转动4.5 飞行器的运动学和动力学四、教学方法1. 讲授理论知识:通过课堂讲解、示范等方式,向学生介绍理论知识和基本概念。
2. 实验教学:设计相关实验,让学生进行实验操作和数据分析,提高他们的实践能力。
3. 小组讨论:设置小组活动,让学生在团队中合作解决问题,培养团队合作和沟通能力。
4. 课堂练习:布置课后作业和练习题,加强对知识的巩固和运用能力。
五、考核方式1. 平时表现(20%):包括课堂参与、作业完成情况等。
2. 实验报告(30%):根据实验要求撰写实验报告并提交。
3. 期中考试(20%):考察对课程内容的理解和掌握程度。
4. 期末考试(30%):综合考察整个课程的学习成果。
六、参考教材1. 赵凤岐,机械动力学,高等教育出版社,2015年。
2. 谢振波,机械力学基础,清华大学出版社,2013年。
七、参考网址无。
八、备注本课程的教学大纲可根据实际教学需求进行调整和补充,以确保教学内容的连贯性和可操作性。
机械动力学分析

机械动力学分析机械动力学是研究物体受到外力作用时的运动规律和力学性质的学科。
它对于机械设计和工程分析非常重要。
本文将对机械动力学的基本概念、分析方法和实际应用进行详细探讨。
第一部分:机械动力学基础1.运动和力学运动是物体的位置随时间变化的过程。
力学是研究物体运动和力之间关系的学科。
在机械动力学中,重要的概念包括位移、速度、加速度和质量等。
2.牛顿定律牛顿定律是机械动力学的基石。
根据牛顿定律,物体受到的合力等于物体质量乘以加速度。
这个定律适用于解决物体在恒力作用下的运动问题。
3.动力学原理动力学原理描述了物体在受到外力作用时的运动规律。
其中,动量守恒原理和能量守恒原理是常用的分析工具。
动量守恒原理指出,在没有外力作用的情况下,物体的动量保持不变。
能量守恒原理指出,在封闭系统中,能量的总量保持不变。
第二部分:机械动力学分析方法1.静力学分析静力学是机械动力学的基础。
它研究物体在平衡状态下的受力和受力转矩。
静力学分析常使用受力图和受力平衡方程来求解。
2.运动学分析运动学研究物体的运动状态,包括位置、速度和加速度等。
运动学分析常使用位移、速度和加速度的关系式进行计算。
3.动力学分析动力学分析研究物体在受力作用下的运动规律。
它涉及物体的质量、力、加速度和位移等参数的计算。
常见的动力学分析方法包括牛顿第二定律、动量守恒和能量守恒的应用。
第三部分:机械动力学的实际应用1.机械设计机械动力学分析在机械设计中起着重要的作用。
通过对机械系统的动力学分析,可以评估机械的工作性能和可靠性,优化设计方案,减少能量消耗和材料使用等。
2.工程分析机械动力学分析在工程领域中广泛应用。
例如,在桥梁设计中,需要对桥梁受力和振动进行动力学分析,以保证结构的安全性和可靠性。
在汽车工程中,需要对汽车的运动性能和悬挂系统进行动力学分析,以提高驾驶舒适性和行驶稳定性。
3.故障诊断与维修机械动力学分析可以用于故障诊断和设备维修。
通过对受损机械的动力学分析,可以确定故障原因,并采取相应的维修措施。
第7章机械动力学
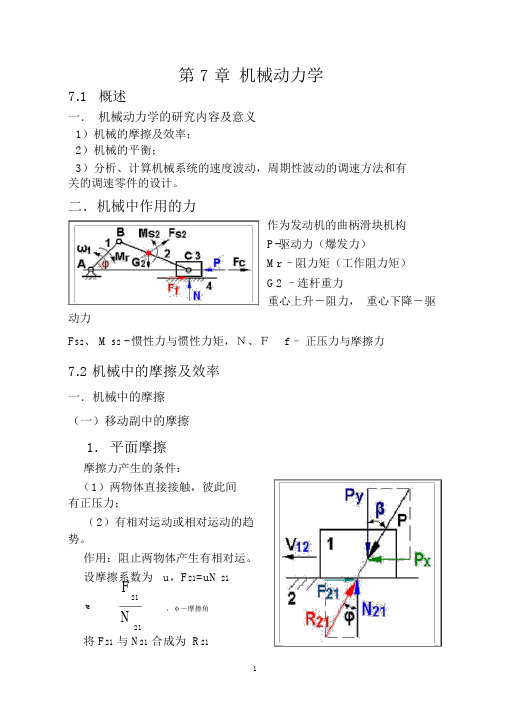
第 7 章机械动力学7.1概述一.机械动力学的研究内容及意义1)机械的摩擦及效率;2)机械的平衡;3)分析、计算机械系统的速度波动,周期性波动的调速方法和有关的调速零件的设计。
二.机械中作用的力作为发动机的曲柄滑块机构P-驱动力(爆发力)Mr –阻力矩(工作阻力矩)G2 –连杆重力重心上升-阻力,重心下降-驱动力F S2、 M S2 - 惯性力与惯性力矩,N、F f –正压力与摩擦力7.2 机械中的摩擦及效率一.机械中的摩擦(一)移动副中的摩擦1.平面摩擦摩擦力产生的条件:(1)两物体直接接触,彼此间有正压力;(2)有相对运动或相对运动的趋势。
作用:阻止两物体产生有相对运。
设摩擦系数为u,F21=uN 21F21tg,φ-摩擦角N21将 F21与 N21合成为 R21R21-总反力(全反力)P X P分解为 P和 P ,tgX Y P Y( P X P sin、 P Y P cos )F21P X,有F21tgY 方向平衡: Py=N 21,即:tg tg P Xtg讨论:①总反力 R21恒与相对速度V 12成 90° +φ②当β >φ, P X > F21,滑块作加速运动;当β =φ, P X = F21,动则恒动,静则恒静;当β <φ, P X < F21,原来运动,作减速运动,原来静止,永远静止,称自锁。
③ 自锁条件:β≤φβ=φ,条件自锁(静止);β<φ,无条件自锁。
2.斜面摩擦斜面机构如图,滑块置于升角α的斜面上,摩擦角为φ,作用于滑块上的铅垂力为Q,求滑块等速上升和下降时所需水平平衡力P 和 P’。
(1)求等速上升水平平衡力 PP-驱动力, Q-阻力PQ R 21 0 ,tg ()P,P Qtg () (1)Q( 2)求等速下降水平平衡力 P ’Q -驱动力, P ’-阻力P'Q R 21 0 ,tg () P ',P 'Qtg () (2)Q讨论:① 欲求下滑 (反行程) P ’,只需将式 ( 1)中 P →P ’,φ→ (-φ )② 下滑时,当α >φ, P ’为平衡力α <φ, P ’为负,成为驱动力的一部分,该条件下,若无 P ’,则无论 Q 多大,滑块不下滑,称自锁,自锁条件:α≤φ。
机械动力学

机械动力学
机械动力学是一种力学分支,用来研究物体的运动规律。
机械力学的基本原理是,物体受力时要考虑它的动量、势能和力学运动状态。
机械力学研究物体受力后,如何协调运动以实现力学系统的最终目标。
机械动力学的基本方程是力学平衡方程,它描述了物体在力学运动中,受力的情况下,动能、势能和运动状态变化的情况。
力学平衡方程主要由三个部分组成:力学定制、力学规律和力学流形。
力学定制是机械动力学的基本原理,它涉及物体的力学变化,包括物体的运动状态、势能和动能。
力学定制可以用来计算物体受力时,各变量的变化速率。
力学规律是机械动力学的第二个基本原理,它涉及物体在力学运动中受力所产生的力学变化。
力学规律具体表示为:物体受力时,质量、动量、势能和动能会发生变化。
力学流形是机械动力学的第三个基本原理,它涉及物体在力学运动中受力的情况下,力学参数的变化。
力学流形是由力学规律的积累,它可以提供物体在各种力学变化状态下的精确的运动状态。
机械动力学是一种比较复杂的力学,研究不仅仅限于物体受力时的运动状态,还可以涉及力学设计与分析、力学模拟、力学断裂以及力学仿真等方面。
它可以帮助科学家们深入了解物体运动规律,为人们在有限工作环境中分析残缺机械参数提供技术支持,实现更加省力、精确且有效的力学分析。
在当今社会,机械动力学已成为一门重要的科学,广泛应用于工
程设计、航天技术、发动机技术、精密仪器等领域。
未来,机械动力学将继续发挥重要作用,在复杂的工程设计及技术开发过程中,与其他科学形成有机结合,以实现精确、有效的力学应用。
机械工程中的机械动力学分析

机械工程中的机械动力学分析机械动力学是机械工程中的一门重要课程,它主要研究机械系统的运动规律、力学特性和动力学特性等问题。
从广义上讲,机械动力学可以分为静力学和动力学两部分,其中静力学研究机械系统在静止状态下的受力情况和平衡条件,而动力学则研究机械系统在运动状态下的运动规律和动力学特性。
本文将针对机械动力学中的动力学部分进行分析和讨论。
一、机械系统的运动规律机械系统的运动规律可以通过牛顿第二定律和角动量定理来描述。
牛顿第二定律表明,机械系统受到的合外力等于其质量乘以加速度,即F=ma。
对于刚性物体,牛顿第二定律可以表示为:ΣF=ma其中ΣF表示作用在物体上的合力,m表示物体的质量,a表示物体的加速度。
在运用牛顿第二定律求解机械系统运动规律时,需要根据实际情况选择适当的坐标系,并建立相应的运动方程。
角动量定理则是描述旋转运动的重要定律。
对于刚性物体的旋转运动,它的角动量可以通过以下公式来计算:L=Iω其中,L表示角动量,I表示物体的转动惯量,ω表示角速度。
根据角动量定理,系统中的合外力矩等于角动量的导数,即M=dL/dt通过角动量定理可以求解物体在旋转运动中的角加速度和角速度等参数。
二、力学特性的分析在机械动力学中,机械系统的力学特性包括弹性变形、破坏和能耗等方面。
弹性变形是机械系统在受到外力作用时,发生一定程度的形变而能够恢复原状的特性。
破坏是机械系统在受到过大的外力作用时,无法再恢复原状的特性。
能耗则是机械系统在运动或变形过程中所消耗的能量。
机械系统的弹性变形特性可以采用胡克定律来描述。
根据胡克定律,弹性形变发生时的应变与应力成线性关系。
对于一维弹性形变的情况,胡克定律可表示为:σ=Eε其中,σ表示应力,E表示弹性模量,ε表示应变。
胡克定律可以用来计算机械系统的弹性变形量。
机械系统的破坏特性可以采用强度学说来描述。
强度学说认为,在机械系统被外力破坏之前,其受到的最大应力应小于其材料的屈服强度。
机械动力学

机械动力学机械动力学是机械工程的一个重要分支,它是一门研究物体的大小、形状、机构及运动的科学。
内容涵盖物理、力学、化学、材料科学、计算机科学和生物学等学科领域,并研究机械系统、工程机械以及各种物质运动问题,为机械工程领域提供理论支持。
机械动力学主要攻克三大难题:第一是关于物质在力械系统中传递、转换及被能量影响的机制。
第二个难题是关于机械系统的动力学性能,包括阻尼、刚度、转动惯量等,它们在物理学中被称作系统参数,它们能反映出物质运动的宏观特性。
第三个难题是关于物体的结构、机构、形状等,这反映出物质运动的宏观特性,例如物体的柔性或者刚性。
机械动力学的研究方法和应用广泛,有数学分析法,特别是拉格朗日多元微分方程,以描述物质在运动中变换的过程;还有实验测量法,如力计、振动计和粒子传感器,它们可以快速准确测量物质运动中的参数变化;有数值模拟法,如有限元法、离散元法、库伦法等,它们可以模拟物质在各种复杂条件下的运动;还有控制理论和正反控制等,这些也是机械动力学领域的重要研究内容。
机械动力学的应用领域非常广泛,如机械工程中的机械设计、机械制造、机械运动分析、机械传动系统、阻尼控制、模型分析、机械修理等;航空航天工程中的空气动力学、宇宙物理学、力学、气动学等;军事工程中的弹道学、飞行动力学、航空发动机等;还有汽车工程、核工程等,机械动力学的理论及技术应用极为广泛。
未来,机械动力学将会给对机械工程设计、制造及保养带来积极变化,有助于各种设备的优化设计和更高效的运行,改善机械系统的可靠性和可用性,缩短交付时间,降低成本。
未来,机械动力学将会发展为一门非常重要的工程学科,以实现更高质量、更低成本的技术进步。
从机械动力学的发展及应用来看,它为机械工程领域提供了重要理论支持。
它极大地促进了现代机械设计、制造和修理,使机械系统具有更高的可靠性和可用性,对现代工程技术的发展有着重要的意义。
机械动力学

机械动力学机械动力学是研究机械构件运动的科学,它强调机械构件的物理性质、物理规律和运动规律的分析以及所产生的结果。
它是工程学和物理学的一门重要学科。
机械动力学的研究对象也包括机械系统和机械结构,它涵盖了机械中所有的构件和元件,其中包括弹簧、螺栓、联接杆以及多节折杆、活动构件等等。
机械动力学的研究包括动力分析、结构动力分析、运动学模型以及弹性动力学研究等多方面的研究。
动力分析是研究机械构件的运动规律、受力规律以及受力的来源。
结构动力分析是分析机械构件的结构特性,包括构件的静态特性、动态特性和动态反应特性。
运动学模型是利用运动学分析来求解机械系统或机械构件的运动规律,找出其位置、速度和加速度的关系。
弹性动力学研究是分析机械构件或机械系统在受力时位移和变形的变化规律,研究机械构件弹性变形特性和稳定性等方面的内容。
机械动力学在工程设计和研究中占据重要地位。
在工程中,机械动力学的研究主要集中在机械设备的动力设计和动力分析方面。
例如,在设计某种机械设备时,需要对机械构件的运动规律进行动力分析,以便确定机械设备的动态特性,使机械设备能够满足其安全、可靠和持续可用的要求。
在工程研究中,机械动力学要求研究者清楚地了解机械构件的运动规律,以及构件可能出现的不确定性和冲击力对机械构件的影响,使其能有效的研究机械系统的运动特性。
在实际工程应用中,机械动力学的研究是应用最广泛的,它不仅能够发掘机械系统的运动规律,而且能够发现机械构件或机械系统在运行过程中可能出现的缺陷和质量问题,从而帮助设计和实现更高效、更安全的机械设备。
机械动力学是实际工程应用中重要的科学,它不仅能够提供基础理论,而且能够有效地帮助设计和实现高效、安全的机械设备,使机械设备的效率有所提高。
本文就机械动力学的基本概念、研究内容以及在工程设计和研究中的应用进行了阐述,以期提供一定的理论参考,促进对机械动力学的研究。
第七章机械动力学

二、机械中作用的力 按力对机械的影响分类 驱动力(driving force)—驱使机械运动,力作用线与构 件运动速度方向夹角为锐角。与构件角速度方向一致的力矩 称为驱动力矩(driving moment)。 考虑构件惯性力的重要性 驱动力类型举例 常数 重力FdC 位移的函数 弹簧力FdFd(s)、内燃机驱动力矩MdMd(s) 速度的函数 电动机驱动力矩Md Md()
当螺母顺着力Q的方向等速向下运动时,即放松螺母, 则应在螺旋中径处施加的维持螺母等速下滑的圆周力为 PQtan()。松开螺母时的维持力矩为 考虑构件惯性力的重要性)d/2 MdPd/2Qtan( Q/2 1 R12 n Q/2
2 v21
2
P
1
Q n d
l
d1 d d2
N
N
(三)转动副中的摩擦 速度波动的有害影响 (1)径向轴颈中的摩擦
(三)转动副中的摩擦 速度波动的有害影响 (2)止推轴颈中的摩擦
(四)高副中的摩擦 速度波动的有害影响
速度波动的有害影响 (五)考虑摩擦的机构静力分析 对机构进行静力分析考虑摩擦时,转动副中的反力不是 通过回转中心,而是切于摩擦圆;移动副中的反力不是与移 动方向垂直,而是与接触面的法向偏斜一个摩擦角。对于受 力比较简单的平面连杆机构,掌握了转动副、移动副中总反 力的确定方法,就不难对平面连杆机构作计及摩擦时的静力 分析。
14
4
R32
14
R43
R23
(4)列力平衡矢量方程
d
R41 R21 R41 Fb0 Fb 大小 √ ? ? 考虑运动副摩擦的静力学分析例题2 c R21 方向 √ √ √ R43 R23 Fb= F da a b Fr Fb Fb R12 R21 21 v34 B B R41 23 2 C C 1 1 Fr Fr A A 3 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
…………………② …………………③ 阻力(矩)不变。
M r0 r M d d
0 Md Md
=
不计摩擦驱动力(矩)
计摩擦驱动力(矩) 计摩擦阻力(矩)
Mr = 0 Mr
不计摩擦阻力(矩)
驱动力(矩)不变。
第四节 刚性转子的平衡设计
1.静平衡设计(D/b5)
o表征几何形状对摩擦力的影响。
θ
Q
θ
N 21 2
②
N 21 2
①
3)o 总汇 (1) 简单平面移动副
o =
N21
v12 P
f21 1 2 Q
3)o 总汇
(2) V形槽移动副
Q
o=/sin
θ
θ
N 21 2
②
N 21 2
①
3)o 总汇
比较槽面摩擦:o=/sin
(3) 三角螺旋副 Q
34
FR R32
1 4
2
R41
R43
R12
21 23
Md R41
2
R43
FR
1
4
3 V34
R32
【教师例7-2】图示平底摆动从动件盘状凸轮机构的 凸轮为圆盘,摩擦圆、摩擦角、驱动力矩Md、阻力FR 如图所示。试画出图示机构的静力分析图。
【解】 R12 2 R32 FR
1、Md
二、单自由度系统等效力学模型的建立 1.建立系统运动方程 建立依据: dE dW Ndt
1 1 1 1 2 2 2 2 J J m m E S1 1 S2 2 2 S2 3 S3 2 2 2 2 N M d 1 m2 g S 2 cos Fr S 3
Md
1 4
2
3
FR
【解】 1.从二力杆(连杆)入手,注意拉压杆。
21 Md 23
1 4
2
3
FR
21
Md
23 1 4 2
3
FR
21 23
Md
1 4
2
3
FR
【解】 1.从二力杆(连杆)入手,注意拉压杆。 2.分析滑块,注意三力汇交。
3.分析曲柄,注意力偶平衡力拒。 R12 Md 90o+ 3
2 3 4 J e J1 J 2 3J 3 J4 1 1 1
2 2 2
2 3 4 J e J1 J 2 3J 3 J4 1 1 1
二、作用在机械上的力 1. 工作阻力 2. 驱动力
第二节 机械中的摩擦与效率 一、机构中的摩擦 (一)滑动摩擦力的大小和总反力 1.滑动摩擦力的大小 f21= N21 Q一定时,决定 f21 的两个因素: ● ●运动副元素的几何形状 1)简单平面移动副 N21=Q f21= N21= Q 1 2 Q f21
1 1 1 1 2 2 2 2 d J S 11 J S 2 2 m2 v S 2 m3 v S 3 2 2 2 2
M d 1 m2 g S 2 cos Fr S 3 dt
Md 2 s2 1 1
1
B
3
C
s2
Fr
b C B CB
0 M r r M d d
…………………②
同一减速器,总效率为1(不计摩擦);输入轴 角速度还是d 、扭矩还是Μd ;输出轴角速度还 是r 、扭矩为Μr0 。问:输出轴功率与输入轴功 率是什么关系?
M r0 r M d d
…………………③
M r r M d d …………………①
' 2
m
'' l1
'' 3
' m3
l
' 1
l
'' 2
' l2
l
'' 3
l
' 3
l
结论
(1)动平衡的条件:各偏心质量的离心惯性力的合力为 零、合力矩为零。 (2)对动不平衡的转子:只需在任选的2个平面内各增 加1个平衡质量即可获得动平衡。 (3)静平衡转子不一定动平衡;动平衡转子一定静平衡。
第五节 机械的运转及动力学模型 一、机械的运转过 程 T T
p
A( S1 )
c
m2g
M d 1 m2 g S 2 cos Fr S 3 dt
1 1 1 1 2 2 2 2 d J S 1 1 J S 2 2 m2 v S 2 m3 v S 3 2 2 2 2
2 2 2 S2 S3 1 2 2 1 重写: d J S 1 J S 2 m2 m3 2 1 1 1 S2 S3 M d m2 g cos Fr 1dt 1 1
2 S2 S3 J e J S1 J S 2 m2 m3 1 1 1
2
2
2
S2 S3 1 M e M d m2 g cos Fr d ( J e12 ) M e1dt 1 1 2
z2' z1 z2' z1 z1 J e J1 J 2 z 3J 3 zz zz J4 2 4 2 3 2
2 2
2
2
2
20 20 20 20 20 J e J 1 J 2 3J 3 J4 40 40 40 100 40
Q'
Md
Q
Q'Q'
Q'
12
1
R
N21
' 21
Mf
R21
方向:与12相反。
●总反力 2 R21恒切于摩擦圆。 对轴心矩的方向与12相反。 ●自锁
f21
总外力割于摩擦圆则自锁。
(三)平面连杆机构的静力学分析 【教师例7-1】已知机构简图、各摩擦角、摩擦园 半径、阻力FR。试画出各运动副静力图。
1
3
C
s2
Fr
b C B CB
p
A( S1 )
c
1 d ( J e12 ) M e1dt 2
等效动力学模型
1 1
Me
1为等效构件
Je为等效转动惯量 Me为等效力矩
Md B 2 s2 1 1
1
3
C
A( S1 )
Fr
关于等效构件: 是系统中的一个构件;
1
1
Me
2
J 2 3J 3 J 4 J1 4 16 100
R21
N21
v12
(o ,v )─当量摩擦角。
摩擦锥----以R21为母线所作圆锥。
2
Q
●总反力 R21与v12夹钝角(90+) R21 恒切于摩擦锥。 ●自锁 1 P f21
R21
φ
N21
v12 90+
2
总外力落在摩擦椎以内则自锁。 Q
(二)转动副
f21 = oQ 摩擦力矩的大小 Mf= f21 r = Q or = Q
3 R31
1
二、 机械的效率
一减速器,总效率为 (计摩擦) ;输出轴角 速度是r 、扭矩是Μr ;输入轴角速度是d 、扭 矩为Μd 。问:输出轴功率与输入轴功率是什么关 系? M r r =M d d …………………①
同一减速器,总效率为1(不计摩擦);输出轴 角速度还是r 、扭矩还是Μr ;输入轴角速度还 是d 、扭矩为Μd 0。问:输出轴功率与输入轴功 率是什么关系?
等效构件的动能=系统动能
【教师例7-2】 图示轮系各构件 的质心均在其转轴上,3轮有3个, 轮1上作用有驱动力矩M1,轮4上 作用有阻力矩M4,又知各构件 2 的齿数和转动惯量,以构件1为 等效构件,求Je 及Me 。 1 【解】 1.求Je
3 2' 4
1 1 1 3 1 2 2 2 2 J e1 J 11 J 2 2 J 3 3 J 4 42 2 2 2 2 2
(mbr1)x= -m1r1sin1- m2r2 sin2
(mbrb ) x - mi ri cosi (mbrb ) y - mi ri sini
b arctan[( mbrb ) y /(mbrb ) x ]
2 mb rb ( mb rb )2 ( m r ) x b b y
具有真实角速度(速度);
具有假想的Je( me ); 作用有假想的Me(Fe);
Fe
s1
Байду номын сангаас
1
具有与真实系统相同的动能和外力功。
只求单自由度系统的一个构件的真实规律。
2. 等效量的计算 Me(Fe)计算原则:功率相等; 等效力(矩)的功率=系统中所有外力(矩)的功率 Je(me)计算原则:动能相等。
F=F1+ F2 +Fb=0 =m12r1+ m2 2r2 +mb2rb =0 e=0 me=m1r1+ m2r2 +mbrb=0 mr─质径积 Fb m2e
y
F2
m2 r2
2
O
m1
F1
b
mb rb
r1
1
x
me=m1r1+ m2r2 +mbr1=0
mbrb= -m1r1- m2r2 (mbrb)x= -m1r1cos1- m2r2 cos2
