经典题解
基本不等式题解[1]
![基本不等式题解[1]](https://img.taocdn.com/s3/m/ca81ef503b3567ec102d8ad2.png)
3.4基本不等式经典例题:若a,b,c都是小于1的正数,求证:,,不可能同时大于.思路分析:本题是一个含否定词的命题,考虑用反证法进行证明.证明:假设(1-a)b>,(1-b)c>,(1-c)a>同时成立,则>,>,>.三式相加得++>.①又≤, ≤, ≤,三式相加得++≤ ++=.②②与①矛盾.∴(1-a)b,(1-b)c,(1-c)a不能同时大于.当堂练习:1. 若,下列不等式恒成立的是( A )A.B.C.D.2. 若且,则下列四个数中最大的是( B )A.B.C.2abD.a3. 设x>0,则的最大值为( C )A.3B.C.D.-14. 设的最小值是( D )A. 10B.C.D.5. 若x, y是正数,且,则xy有(C)A.最大值16B.最小值C.最小值16D.最大值6. 若a, b, c∈R,且ab+bc+ca=1, 则下列不等式成立的是( D )A. B.C. D.7. 若x>0, y>0,且x+y4,则下列不等式中恒成立的是(B )A. B. C. D.8. a,b是正数,则三个数的大小顺序是(D)A.B.C.D.9. 某产品的产量第一年的增长率为p,第二年的增长率为q,设这两年平均增长率为x,则有(C)A.B.C.D.10.下列函数中,最小值为4的是(C)A.B.C.D.11. 函数的最大值为 1/212. 建造一个容积为18m3, 深为2m的长方形无盖水池,如果池底和池壁每m2的造价为200元和150元,那么池的最低造价为 5400 元.13. 若直角三角形斜边长是1,则其内切圆半径的最大值是(根号2-1)/2。
14. 若x, y为非零实数,代数式的值恒为正,对吗?答对.15. 已知:, 求mx+ny的最大值. 根号ab16. 已知.若、, 试比较与的大小,并加以证明.17. 已知正数a, b满足a+b=1(1)求ab的取值范围;(2)求的最小值.18. 设.证明不等式对所有的正整数n 都成立.参考答案:经典例题:【 解析】 证法一 假设,,同时大于,∵ 1-a>0,b>0,∴≥,同理,.三个不等式相加得,不可能,∴ (1-a)b ,(1-b)c ,(1-c)a 不可能同时大于.证法二 假设,,同时成立,∵ 1-a>0,1-b>0,1-c>0,a>0,b>0,c>0,∴,即. (*) 又∵≤,同理≤,≤,∴≤与(*)式矛盾,故不可能同时大于.当堂练习:1.A;2.B;3.C;4.D;5.C;6.D;7.B;8.D;9.C; 10.C;11. ; 12. 5400 ;13. ; 14. 对; 15.答案:当堂练习1. 解:A :原式化为:a 2-a+)21(2+43 >0 即:(a - 21)2+43>0 成立B :因为a 2+1≥1 则112 a ≤1 有等于1的时候,则不成立C : a 2+9≤2a 29 =6a 即a 2+9≤6a,则不成立D :lg 上面的a 2+1≤21·2a即a 2+1≤2a 有相等,则不成立2. 解:A :B :≥2ba 22=2ab 而(a+b)2=a 2+b 2+2ab=1 则a 2+b 2=1-2ab ,又a+b ≥2ab ,即2ab ≤1 ,两边平方得4ab ≤1 则2ab ≤,即a 2+b 2=1-2ab ≥1-, a 2+b 2≥C :2abD :0<a<b ,则a<2ab 则B>C>D ,又B ≥,即B>A 选B3.解:化为y=3-(3x+x1) 根据基本不等式a+b ≥2ab 设a=3x ,b=x 1,就有3x+x 1≥2xx 1·3 即3x+x 1≥23则≤3-(3x+x1)=3-23 即≤3-23 选C这题中:a 可以是3x ,b 是x1 4. 解:3X +3Y ≥233yx (此题中设a=3x ,b=3y ) ,3X +3Y ≥23yx +=235=2·93=1835. 解:x 1+y 4≥2y x 4·1=2xy 4,即2xy 4≤1, x, y 是正数,两边平方xy16≤1,xy ≥16(最小值是16)6. 解:基本不等式a+b+c ≥33abc ,ab+bc+ca ≥33abbcca =33222c b a ,即1≥33222c b a ,此式开平方为1≥33cb aA :a 2+b 2+c 2≥33222cb a (1≥33222cb a ) 即a 2+b 2+c 2≥2不成立B :(a+b+c)2≥33222cb a ·33222cb a (1≥33222cb a ) 即a+b+c)2≥3不成立(小于1的数乘小于1的数应小于1)C :cb a 111++≥331abc =331abc =3333abc≥33,(1≥33c b a 代入)D :基本不等式a+b+c ≥33abc (1≥33cb a 代入,注意不等号反向)则a+b+c ≤3·1=3 成立选D7. 解:A :已知x+y ≤4,则yx +1 ≥41B :x+y ≥2xy ,x1+y1≥2xy 1 =xy 24≥yx +4=4/4=1,即x 1+y 1≥1成立C :x+y ≥2xy ,即4≥2xy ,2≥xy (这里要注意:x+y 最大值是4)D :x+y ≥2xy 两边平方得(x+y)2≥4xy 即16≥4xy ,xy 1≥41(两边同除xy 的前提是x>0, y>0)8. 解:根据基本不等式a+b ≥2ab ,2b a +≥abb a ab +2≥ab ab 22=ab ,而b a ab +2=ba ab +)2(221≤ba b a ++)(221=21(a+b )则选D9. 解:设原年产量为y ,则第1年总产量为y(1+p),第2年为y(1+p)(1+q)=y(1+x)2, 即(1+p)(1+q)=(1+x)2 ,x=)1)(1(q p ++-1而(1+p)+(1+q)≥2)1)(1(q p ++即p+q+2≥2)1)(1(q p ++ ,2q p +≥()1)(1(q p ++ -1)=x 选C这道题要清楚年产量与增长率的关系,p 、q 是增长的部分的百分比率。
材料力学典型例题与详解(经典题目)
= 3.64
2、按挤压强度条件确定铆钉数:挤压面面积 A = δ d ,铆钉挤压强度条件为
σ bs
=
Fb Abs
=
F nδ d
≤ [σ
bs]
得
n
≥
δ
d
F [σ
bs
]
=
10
× 10 −3
m
×
160 ×103 20 ×10−3 m
N × 320
× 10 6
N/m 2
= 2.5
两者取大值,最后确定铆钉数 n = 4。
衡条件得 F 作用截面上侧轴力为
FNB +
=
L a2ρ 2
=
4 m × (0.2 m)2 2
× 20 × 103
N/m 3
= 1.6 × 103 N = 1.6 kN
然后将杆沿 F 作用截面(B-B)下侧截开,设截面上轴力为压力 FNB− ,研究上半部分
杆段。这时杆段受本身重量作用和集中力 F 作用,所以由静力平衡条件得 F 作用截面下侧 轴力为
FNB−
=
L a2ρ 2
+
F
=
4 m × (0.2 m)2 2
× 20 ×103
N/m 3
+ 10 ×103
N = 11.6 ×103 N = 11.6 kN
4、计算 A-A 截面轴力:从 A-A 截面将杆截开,设截面上轴力为压力 FNA ,则 FNA 应与该杆
上所有外力平衡。杆所受外力为杆的自重和集中力 F ,杆段自重为 La 2 ρ ,方向向下。于是
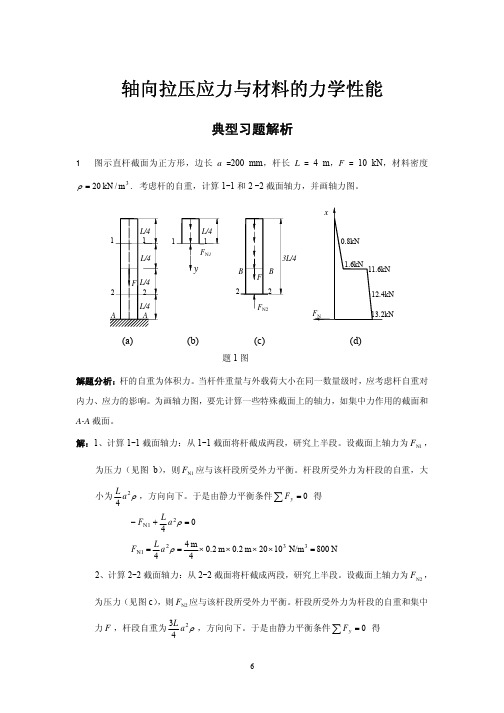
2 图示石柱桥墩,压力 F = 1000 kN,石料密度 ρ = 25 kN / m3 ,许用应力 [σ ] =1 MPa。试 比较下列三种情况下所需石料体积。(1)等截面石柱;(2)三段等长度的阶梯石柱;(3)等 强度石柱(柱的每个截面的应力都等于许用应力 [σ ] )。 解题分析:设计这样的桥墩时,要考虑桥墩自重对强度的影响。可以想象,在桥墩顶截面只 有压力 F 作用,轴力最小;在桥墩底截面,除压力 F 外,还承受桥墩本身重量,该处轴力 最大。当桥墩采用等截面石柱时,只要考虑底部截面的强度即可。如果采用阶梯型石柱,需 考虑每段的强度。如果要求各个截面强度相等,则需要对石柱的各截面进行特别设计。 解:1、采用等截面石柱
小学数学50道经典应用题解题思路+模板

小学数学50道经典应用题解题思路+模板1、一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元?解题思路:由条件可知,一张桌子比一把椅子多的288元,正好是一把椅子价钱的〔10-1〕倍,由此可求得一把椅子的价钱。
再根据椅子的价钱,就可求得一张桌子的价钱。
答题:解:一把椅子的价钱:288÷〔10-1〕=32〔元〕一张桌子的价钱:32×10=320〔元〕答:一张桌子320元,一把椅子32元。
2、3箱苹果重45千克。
一箱梨比一箱苹果多5千克,3箱梨重多少千克?解题思路:可先求出3箱梨比3箱苹果多的重量,再加上3箱苹果的重量,就是3箱梨的重量。
答题:解:45+5×3=45+15=60〔千克〕答:3箱梨重60千克。
3、甲乙二人从两地同时相对而行,经过4小时,在距离中点4千米处相遇。
甲比乙速度快,甲每小时比乙快多少千米?解题思路:根据在距离中点4千米处相遇和甲比乙速度快,可知甲比乙多走4×2千米,又知经过4小时相遇。
即可求甲比乙每小时快多少千米。
答题:解:4×2÷4=8÷4=2〔千米〕答:甲每小时比乙快2千米。
4、李军和张强付同样多的钱买了同一种铅笔,李军要了13支,张强要了7支,李军又给张强0.6元钱。
每支铅笔多少钱?解题思路:根据两人付同样多的钱买同一种铅笔和李军要了13支,张强要了7支,可知每人应该得〔13+7〕÷2支,而李军要了13支比应得的多了3支,因此又给张强0.6元钱,即可求每支铅笔的价钱。
答题:÷[13-〔13+7〕÷÷[13—20÷÷3=0.2〔元〕答:每支铅笔0.2元。
5、甲乙两辆客车上午8时同时从两个车站出发,相向而行,经过一段时间,两车同时到达一条河的两岸。
由于河上的桥正在维修,车辆制止通行,两车需交换乘客,然后按原路返回各自出发的车站,到站时已是下午2点。
初一数学经典题型解析

初一数学经典题型解析1、如图,将一个含30°角的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2的度数是()A。
95°B。
85° C. 75°D。
65°考点:平行线的性质;三角形的外角性质.专题:计算题.分析:根据题画出图形,由直尺的两对边AB与CD平行,利用两直线平行,同位角相等可得∠1=∠3,由∠1的度数得出∠3的度数,又∠3为三角形EFG的外角,根据外角性质:三角形的外角等于与它不相邻的两内角之和得到∠3=∠E+∠2,把∠3和∠E的度数代入即可求出∠2的度数.解答:已知:AB∥CD,∠1=115°,∠E=30°,求:∠2的度数?解:∵AB∥CD(已知),且∠1=115°,∴∠3=∠1=115°(两直线平行,同位角相等),又∠3为△EFG的外角,且∠E=30°,∴∠3=∠2+∠E,则∠2=∠3﹣∠E=115°﹣30°=85°.故选B.点评:此题考查了平行线的性质,以及三角形的外角性质,利用了转化的数学思想,其中平行线的性质有:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,熟练掌握性质是解本题的关键.2、如图,AB∥CD,DE交AB于点F,且CF⊥DE于点F,若∠EFB=125°,则∠C=35°.考点:平行线的性质.专题:计算题分析:根据对顶角相等,得出∠AFD=∠EFB,由∠EFB的度数求出∠AFD的度数,再根据垂直的定义得到∠CFD=90°,利用∠AFD﹣∠CFD得出∠AFC的度数,最后由两直线平行内错角相等,即可得到所求的角的度数.解答:解:∵∠EFB=125°(已知),∴∠AFD=∠EFB=125°(对顶角相等),又∵CF⊥DE(已知),∴∠CFD=90°(垂直定义),∴∠AFC=∠AFD﹣∠CFD=125°﹣90°=35°,∵AB∥CD(已知),∴∠C=∠AFC=35°(两直线平行内错角相等).故答案为:35点评:此题考查了平行线的性质,垂直定义,以及对顶角的性质,利用了转化的数学思想,其中平行线的性质有:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,熟练掌握平行线的性质是解本题的关键.3、如果关于x不等式组的整数解仅为1,2,3,则a的取值范围是0<a≤9,b的取值范围是24<b≤32.考点:一元一次不等式组的整数解;不等式的性质;解一元一次不等式.专题:计算题.分析:求出不等式的解集,找出不等式组的解集,根据已知和不等式组的解集得出0<≤1,3<≤4,求出即可.解答:解:,由①得:x≥,由②得:x<,∴不等式组的解集是≤x<,∵不等式组的整数解是1,2,3.∴0<≤1,3<≤4,解得:0<a≤9,24<b≤32,故答案为:0<a≤9,24<b≤32.点评:本题考查了对不等式的性质,解一元一次不等式(组),一元一次不等式组的整数解等知识点的理解和掌握,关键是根据不等式组的解集和已知得出0<a≤9,24<b≤32.4、已知:a2﹣4b﹣4=0,a2+2b2=3,则的值为()A。
条件概率经典习题(含解析)

一.选择题(共11小题)1.从5名女生2名男生中任选3人参加学校组织的演讲比赛,则在女生甲被选中的条件下,男生至少一人被选中的概率是()A.B.C.D.2.已知P(B)=0.3,P(B|A)=0.9,P(B|)=0.2,则P()=()A.B.C.D.3.从某班包含甲、乙的5名班干部中选出3人参加学校的社会实践活动,在甲被选中的情况下,乙也被选中的概率为()A.B.C.D.4.将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率P(B|A),P(A|B)分别等于()A.,B.,C.,D.,5.已知P(A)>0,P(B)>0,P(C)>0,下列说法错误的是()A.若事件A,B独立,则P(A)=P(A|B)B.若事件A,B互斥,则P(B|A)=P(A|B)C.若事件A,B独立,则P(C|AB)=P(C|A)P(C|B)D.若事件A,B互斥,事件A,C独立,事件B,C独立,则P(C|(A+B))=P(C|A).6.6道题目中有5道理科题目和1道文科题目,如果不放回地依次抽取2道题目,则在第1次抽到理科题目的条件下,第2次抽到理科题目的概率为()A.B.C.D.7.盒子里有1个红球与n个白球,随机取球,每次取1个球,取后放回,共取2次.若至少有一次取到红球的条件下,两次取到的都是红球的概率为,则n=()A.3B.4C.6D.88.甲袋中有4个红球,4个白球和2个黑球;乙袋中有3个红球,3个白球和4个黑球.先从甲袋中随机取出一球放入乙袋,分别以A,B,C表示事件“取出的是红球”、“取出的是白球”、“取出的是黑球”;再从乙袋中随机取出一球,以D表示事件“取出的是红球”,则P(D)=()A.B.C.D.9.已知桌上放有3本语文书和3本数学书.小明现从这6本书中任意抽取3本书,A表示事件“至少抽到1本数学书”,B表示事件“抽到语文书和数学书”,则P(B|A)=()A.B.C.D.10.设A,B为两个事件,已知P(B)=0.4,P(A)=0.5,P(B|A)=0.3,则P(A|B)=()A.0.24B.0.375C.0.4D.0.511.袋中有除颜色外完全相同的5个球,其中3个红球和2个白球.现从袋中不放回地连取两个.已知第一次取得红球,则第二次取得白球的概率为()A.0.4B.0.5C.0.6D.0.7二.填空题(共4小题)12.从﹣2,﹣1,1,2,3这5个数中任取2个不同的数,记“两数之积为正数”为事件A,“两数均为负数为事件B.则P(B|A)=.13.一个数学兴趣小组共有2名男生3名女生,从中随机选出2名参加交流会,在已知选出的2名中有1名是男生的条件下,另1名是女生的概率为.14.已知随机事件A,B,P(A)=,P(B)=,P(A|B)=,则=.15.已知,,则P(B)=.参考答案与试题解析一.选择题(共11小题)1.从5名女生2名男生中任选3人参加学校组织的演讲比赛,则在女生甲被选中的条件下,男生至少一人被选中的概率是()A.B.C.D.解答:解:设女生甲被选中为事件A,事件A表示女生甲被选中后再从剩下的6人中选2人,故,设男生至少一人被选中为事件B,事件AB表示女生甲被选中后再选2男生或1男生和1女生(从剩余4女生中选),故,则在女生甲被选中的条件下,男生至少一人被选中的概率是.故选:C.2.已知P(B)=0.3,P(B|A)=0.9,P(B|)=0.2,则P()=()A.B.C.D.解答:解:P(B)=P(A)P(B|A)+,∵P(B)=0.3,P(B|A)=0.9,P(B|)=0.2,∴0.3=P(A)×0.9+[(1﹣P(A)]×0.2,解得P(A)=,∴.故选:A.3.从某班包含甲、乙的5名班干部中选出3人参加学校的社会实践活动,在甲被选中的情况下,乙也被选中的概率为()A.B.C.D.解答:解:令事件A为甲被选中的情况,事件B为乙被选中的情况,故P(A)=,P(AB)=,故P(B|A)=.故选:A.4.将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率P(B|A),P(A|B)分别等于()A.,B.,C.,D.,解答:解:由题意知:事件AB=“三个点数都不同且至少出现一个6点”,∵,,,∴,.故选:B.5.已知P(A)>0,P(B)>0,P(C)>0,下列说法错误的是()A.若事件A,B独立,则P(A)=P(A|B)B.若事件A,B互斥,则P(B|A)=P(A|B)C.若事件A,B独立,则P(C|AB)=P(C|A)P(C|B)D.若事件A,B互斥,事件A,C独立,事件B,C独立,则P(C|(A+B))=P(C|A).解答:解:A,若事件A,B独立,则P(A|B)===P(A),故A正确,B,若事件A,B互斥,则P(AB)=0,则P(B|A)==0,P(A|B)==0,∴P(B|A)=P(A|B),∴B正确,C,若事件A,B独立,则P(AB)=P(A)P(B),∴P(C|(AB))===+≠P(C|A)P(C|B),故C错误,D,∵事件A,B互斥,∴P(A+B)=P(A)+P(B),∵事件A,C独立,事件B,C独立,∴P(AC)=P(A)P(C),P(BC)=P(B)P(C),∴P(C|(A+B))=====P(C)==P(C|A),故D正确.故选:C.6.6道题目中有5道理科题目和1道文科题目,如果不放回地依次抽取2道题目,则在第1次抽到理科题目的条件下,第2次抽到理科题目的概率为()A.B.C.D.解答:解:由题意,6道题目中有5道理科题目和1道文科题目,不放回地抽取两次,设第一次抽到理科题目为事件A,第二次抽到理科题目为事件B,则,P(AB)=,则P(B|A)=.故选:B.7.盒子里有1个红球与n个白球,随机取球,每次取1个球,取后放回,共取2次.若至少有一次取到红球的条件下,两次取到的都是红球的概率为,则n=()A.3B.4C.6D.8解答:解:设事件A为至少有一次取到红球,事件B为两次都取到红球,由每次取后放回知,两次都取到白球的概率为,故,,故n=4.故选:B.8.甲袋中有4个红球,4个白球和2个黑球;乙袋中有3个红球,3个白球和4个黑球.先从甲袋中随机取出一球放入乙袋,分别以A,B,C表示事件“取出的是红球”、“取出的是白球”、“取出的是黑球”;再从乙袋中随机取出一球,以D表示事件“取出的是红球”,则P(D)=()A.B.C.D.解答:解:由题意可得,P(A)=,P(B)=,P(C)=,故P(D)=P(AD)+P(BD)+P(CD)=.故选:C.9.已知桌上放有3本语文书和3本数学书.小明现从这6本书中任意抽取3本书,A表示事件“至少抽到1本数学书”,B表示事件“抽到语文书和数学书”,则P(B|A)=()A.B.C.D.解答:解:根据题意可得,,由条件概率的公式得.故选:D.10.设A,B为两个事件,已知P(B)=0.4,P(A)=0.5,P(B|A)=0.3,则P(A|B)=()A.0.24B.0.375C.0.4D.0.5解答:解:设A,B为两个事件,由已知P(A)=0.5,P(B|A)=0.3,得P(AB)=P (B|A)⋅P(A)=0.15,所以,故选:B.11.袋中有除颜色外完全相同的5个球,其中3个红球和2个白球.现从袋中不放回地连取两个.已知第一次取得红球,则第二次取得白球的概率为()A.0.4B.0.5C.0.6D.0.7解答:解:袋中有除颜色外完全相同的5个球,其中3个红球和2个白球.现从袋中不放回地连取两个.设事件A表示“第一次取到红球”,事件B表示“第二次取到白球”,P(A)=,P(AB)==,∴第一次取得红球的条件下第二次取得白球的概率为:P(B|A)===0.5.故选:B.二.填空题(共4小题)12.从﹣2,﹣1,1,2,3这5个数中任取2个不同的数,记“两数之积为正数”为事件A,“两数均为负数为事件B.则P(B|A)=.解答:解:从﹣2,﹣1,1,2,3这5个数中任取2个不同的数有种取法,其中满足两数之积为正数的有种取法,满足两数之积为正数且两数均为负数的有种取法,所以,,所以.故答案为:13.一个数学兴趣小组共有2名男生3名女生,从中随机选出2名参加交流会,在已知选出的2名中有1名是男生的条件下,另1名是女生的概率为.解答:解:若A表示“2名中至少有1名男生”,B表示“2名中有1名女生”,所以2名中有1名是男生的条件下,另1名是女生的概率为,而,,故.故答案为:.14.已知随机事件A,B,P(A)=,P(B)=,P(A|B)=,则=.解答:解:依题意得,所以,故,所以.故答案为:.15.已知,,则P(B)=.解答:解:由题意得,而,得,而,解得,故答案为:.。
一元二次函数经典题目带答案附解析

一元二次函数经典题目带答案附解析一元二次函数经典题目及解析一、单选题(共7题;共14分)1.如图,已知二次函数 $y=ax^2+bx+c$ 的图象与 $x$ 轴分别交于 $A$、$B$ 两点,与 $y$ 轴交于 $C$ 点,$OA=OC$。
则由抛物线的特征写出如下结论()。
A。
$abc>0$。
B。
$4ac-b^2>0$。
C。
$a-b+c>0$。
D。
$ac+b+1=0$2.已知二次函数 $y=ax^2+bx+c$ ($a≠0$)的图象如图所示,则下列结论正确的是()。
A。
$abc0$。
D。
$2a+b=0$3.“学雷锋”活动月中,“XXX”班将组织学生开展志愿者活动,XXX和XXX从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是()。
A。
$\frac{1}{3}$。
B。
$\frac{1}{9}$。
C。
$\frac{1}{6}$。
D。
$\frac{1}{2}$4.在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球。
已知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数为()。
A。
27.B。
23.C。
22.D。
185.如图,平面直角坐标系中,点 $B$ 在第一象限,点$A$ 在 $x$ 轴的正半轴上,$\angle AOB=\angle B=30°$,$OA=2$,将 $\triangle AOB$ 绕点 $O$ 逆时针旋转90°,点$B$ 的对应点的坐标是()。
A。
$(\sqrt{3},-2)$。
B。
$(\sqrt{3},2)$。
C。
$(-\sqrt{3},2)$。
D。
$(-\sqrt{3},-2)$6.如图,一条公路的转弯处是一段圆弧 $(AB)$,点$O$ 是这段弧所在圆的圆心,$AB=40m$,点 $C$ 是 $AB$ 的中点,且 $CD=10m$,则这段弯路所在圆的半径为()。
相似三角形经典大题解析答案

1.【答案】解:(1)MN BC ∥AMN ABC ∴△∽△ 68h x ∴= 34xh ∴= (2)1AMN A MN △≌△1A MN ∴△的边MN 上的高为h ,①当点1A 落在四边形BCNM 内或BC 边上时,1A MN y S =△=211332248MN h x x x ==··(04x <≤) ②当1A 落在四边形BCNM 外时,如下图(48)x <<,设1A EF △的边EF 上的高为1h , 则132662h h x =-=- 11EF MNA EF A MN ∴ ∥△∽△11AMN ABC A EF ABC ∴ △∽△△∽△ 1216A EF S h S ⎛⎫= ⎪⎝⎭△△ABC168242ABC S =⨯⨯= △22363224122462EFx S x x ⎛⎫- ⎪∴==⨯=-+ ⎪⎪⎝⎭1△A 1122233912241224828A MN A EF y S S x x x x x ⎛⎫=-=--+=-+- ⎪⎝⎭△△所以 291224(48)8y x x x =-+-<<综上所述:当04x <≤时,238y x =,取4x =,6y =最大 当48x <<时,2912248y x x =-+-, 取163x =,8y =最大 86> ∴当163x =时,y 最大,8y =最大 2.【答案】解:(1) 该抛物线过点(02)C -,,∴可设该抛物线的解析式为22y ax bx =+-.将(40)A ,,(10)B ,代入,得1642020a b a b .+-=⎧⎨+-=⎩,解得1252a b .⎧=-⎪⎪⎨⎪=⎪⎩,∴此抛物线的解析式为215222y x x =-+-.(2)存在.如图,设P 点的横坐标为m ,则P 点的纵坐标为215222m m -+-, 当14m <<时,4AM m =-,215222PM m m =-+-. 又90COA PMA ∠=∠= °,∴①当21AM AO PM OC ==时, APM ACO △∽△,即21542222m m m ⎛⎫-=-+- ⎪⎝⎭.解得1224m m ==,(舍去),(21)P ∴,. ②当12AM OC PM OA ==时,APM CAO △∽△,即2152(4)222m m m -=-+-. 解得14m =,25m =(均不合题意,舍去)∴当14m <<时,(21)P ,. 类似地可求出当4m >时,(52)P -,. 当1m <时,(314)P --,.综上所述,符合条件的点P 为(21),或(52)-,或(314)--,. 3.【答案】(1)解:由28033x +=,得4x A =-∴.点坐标为()40-,.由2160x -+=,得8x B =∴.点坐标为()80,.∴()8412AB =--=.由2833216y x y x ⎧=+⎪⎨⎪=-+⎩,.解得56x y =⎧⎨=⎩,.∴C 点的坐标为()56,. ∴111263622ABC C S AB y ==⨯⨯=△·. (2)解:∵点D 在1l 上且2888833D B D x x y ==∴=⨯+=,.∴D 点坐标为()88,. 又∵点E 在2l 上且821684E D E E y y x x ==∴-+=∴=,.. ∴E 点坐标为()48,.∴8448OE EF =-==,. (3)解法一:①当03t <≤时,如图1,矩形DEFG 与ABC △重叠部分为五边形CHFGR (0t =时,为四边形CHFG ).过C 作CM AB ⊥于M ,则R t R t R G B C M B△∽△.∴BG RG BM CM =,即36t RG=,∴2RG t =. Rt Rt AFH AMC △∽△,∴()()11236288223ABC BRG AFH S S S S t t t t =--=-⨯⨯--⨯-△△△.即241644333S t t =-++.当83<≤t 时,如图2,为梯形面积,∵G (8-t,0)∴GR=32838)8(32t t -=+-,∴38038]32838)4(32[421+-=-++-⨯=t t t s 当128<≤t 时,如图3,为三角形面积,4883)12)(328(212+-=--=t t t t s 4【答案】解: (1)34PM =, (2)2t =,使PNB PAD △∽△,相似比为3:2 (3)PM AB CB AB AMP ABC ∠=∠ ⊥,⊥,,AMP ABC △∽△,PM AM BN AB ∴=即()PM a t t a t PM t a a--== ,,A DB EORF xy1l 2lM(图3)G CA DB EO CF xy1l 2lG (图1)RM A D B EO C F xy1l 2lG (图2)RM(1)3t a QM a-∴=-当梯形PMBN 与梯形PQDA 的面积相等,即()()22QP AD DQ MP BN BM++=()33(1)()22t a t t a a t t ta a -⎛⎫⎛⎫-+--+ ⎪ ⎪⎝⎭⎝⎭==化简得66a t a =+,3t ≤,636aa∴+≤,则636a a ∴<≤,≤, (4)36a < ≤时梯形PMBN 与梯形PQDA 的面积相等∴梯形PQCN 的面积与梯形PMBN 的面积相等即可,则CN PM =()3t a t t a∴-=-,把66a t a =+代入,解之得23a =±,所以23a =.所以,存在a ,当23a =时梯形PMBN 与梯形PQDA 的面积、梯形PQCN 的面积相等. 5.【答案】 解:(1)△BPQ 是等边三角形,当t=2时,AP=2×1=2,BQ=2×2=4,所以BP=AB-AP=6-2=4,所以BQ=BP.又因为∠B=600,所以△BPQ 是等边三角形.(2)过Q 作QE ⊥AB,垂足为E,由QB=2y,得QE=2t ·sin600=3t,由AP=t,得PB=6-t,所以S △BPQ=21×BP ×QE=21(6-t)×3t=-23t 2+33t ; (3)因为Q R ∥BA,所以∠QRC=∠A=600,∠RQC=∠B=600,又因为∠C=600, 所以△QRC 是等边三角形,所以QR=RC=QC=6-2t.因为BE=BQ ·cos600=21×2t=t, 所以EP=AB-AP-BE=6-t-t=6-2t,所以EP ∥QR,EP=QR,所以四边形EPRQ 是平行四边形, 所以PR=EQ=3t,又因为∠PEQ=900,所以∠APR=∠PRQ=900.因为△APR ~△PRQ,所以∠QPR=∠A=600,所以tan600=PR QR ,即3326=-tt,所以t=56, 所以当t=56时, △APR ~△PRQ 6. (1)证明:在ADC △和EGC △中, Rt ADC EGC ∠=∠=∠ ,C C ∠=∠ ADC EGC ∴△∽△ EG CG AD CD∴= 3分 (2)FD 与DG 垂直4分 证明如下:在四边形AFEG 中,FAGCED B90FAG AFE AGE ∠=∠=∠=∴四边形AFEG 为矩形 AF EG ∴=由(1)知EG CG AD CD= AF CGAD CD ∴=6分ABC △为直角三角形,AD BC ⊥FAD C ∴∠=∠ AFD CGD ∴△∽△ ADF CDG ∴∠=∠8分又90CDG ADG ∠+∠=90ADF ADG ∴+∠=即90FDG ∠=FD DG ∴⊥10分(3)当AB AC =时,FDG △为等腰直角三角形, 理由如下:AB AC = ,90BAC ∠= AD DC ∴=由(2)知:AFD CGD △∽△1FD ADGD DC∴== FD DG ∴= 又90FDG ∠=FDG ∴△为等腰直角三角形12分7. (1)34PM =, (2)2t =,使PNB PAD △∽△,相似比为3:2 (3)PM AB CB AB AMP ABC ∠=∠ ⊥,⊥,,AMP ABC △∽△,PM AM BN AB ∴=即()PM a t t a t PM t a a--== ,,(1)3t a QM a-∴=-当梯形PMBN 与梯形PQDA 的面积相等,即()()22QP AD DQ MP BN BM++=()33(1)()22t a t t a a t t ta a -⎛⎫⎛⎫-+--+ ⎪ ⎪⎝⎭⎝⎭==化简得66a t a =+,3t ≤,636aa∴+≤,则636a a ∴<≤,≤, (4)36a < ≤时梯形PMBN 与梯形PQDA 的面积相等∴梯形PQCN 的面积与梯形PMBN 的面积相等即可,则CN PM =()3t a t t a∴-=-,把66a t a =+代入,解之得23a =±,所以23a =.所以,存在a ,当23a =时梯形PMBN 与梯形PQDA 的面积、梯形PQCN 的面积相等.例1. 解 ABCD 是平行四边形,∴CD AB CD AB =,//,∴AEF ∆∽CDF ∆,又2:1:=EB AE ,∴3:1:=CD AE ,∴AEF ∆与CDF ∆的周长的比是1:3. 又)cm (6,)31(22==∆∆∆AEF CDF AEF S S S ,∴)cm (542=∆CD F S . 例3 由于ABD ∆∽ACE ∆,则CAE BAD ∠=∠,因此DAE BAC ∠=∠,如果再进一步证明AECAAD BA =,则问题得证. 证明 ∵ABD ∆∽ACE ∆,∴CAE BAD ∠=∠.又DAC BAD BAC ∠+∠=∠ ,∴CAE DAC DAE ∠+∠=∠, ∴DAE BAC ∠=∠.∵ABD ∆∽ACE ∆,∴AEACAD AB =. 在ABC ∆和ADE ∆中,∵AEACAD AB ADE BAC =∠=∠,,∴ABC ∆∽ADE ∆例5.解:例11.分析 有一个角是65°的等腰三角形,它的底角是72°,而BD 是底角的平分线,∴︒=∠36CBD ,则可推出ABC ∆∽BCD ∆,进而由相似三角形对应边成比例推出线段之间的比例关系.证明 AC AB A =︒=∠,36 ,∴︒=∠=∠72C ABC . 又BD 平分ABC ∠,∴︒=∠=∠36CBD ABD .∴BC BD AD ==,且AB C ∆∽BCD ∆,∴BC CD AB BC ::=,∴CD AB BC ⋅=2,∴CD AC AD ⋅=2.说明 (1)有两个角对应相等,那么这两个三角形相似,这是判断两个三角形相似最常用的方法,并且根据相等的角的位置,可以确定哪些边是对应边.(2)要说明线段的乘积式cd ab =,或平方式bc a =2,一般都是证明比例式,b dc a =,或caa b =,再根据比例的基本性质推出乘积式或平方式. 例16. 分析:要求BC 的长,需画图来解,因AB 、AC 都大于高AD ,那么有两种情况存在,即点D 在BC 上或点D 在BC 的延长线上,所以求BC 的长时要分两种情况讨论.求正方形的面积,关键是求正方形的边长. 解:(1)如上图,由AD ⊥BC ,由勾股定理得BD =3,DC =1,所以BC =BD +DC =3+1=4.如下图,同理可求BD =3,DC =1,所以BC =BD -CD =3-1=2.(2)如下图,由题目中的图知BC =4,且162)32(2222=+=+AC AB ,162=BC ,∴222BC AC AB =+.所以△ABC 是直角三角形.由AE G F 是正方形,设G F =x ,则FC =2-x , ∵G F ∥AB ,∴AC FC AB GF =,即2232xx -=. ∴33-=x ,∴3612)33(2-=-=AEG F S 正方形.如下图,当BC =2,AC =2,△ABC 是等腰三角形,作CP ⊥AB 于P ,∴AP =321=AB ,在Rt △APC 中,由勾股定理得CP =1,∵GH ∥AB ,∴△C GH ∽△CBA ,∵x x x -=132,32132+=x ∴121348156)32132(2-=+=GFEH S 正方形 因此,正方形的面积为3612-或121348156-.。
勾股定理经典例题(全解版)

类型一:勾股定理的直接用法1、在Rt△ABC中,∠C=90°(1)已知a=6, c=10,求b, (2)已知a=40,b=9,求c; (3)已知c=25,b=15,求a.思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。
解析:(1) 在△ABC中,∠C=90°,a=6,c=10,b=(2) 在△ABC中,∠C=90°,a=40,b=9,c=(3) 在△ABC中,∠C=90°,c=25,b=15,a=举一反三【变式】:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?【答案】∵∠ACD=90°AD=13, CD=12∴AC2 =AD2-CD2=132-122=25∴AC=5又∵∠ABC=90°且BC=3∴由勾股定理可得AB2=AC2-BC2=52-32=16∴AB= 4∴AB的长是4.类型二:勾股定理的构造应用2、如图,已知:在中,,,. 求:BC的长.思路点拨:由条件,想到构造含角的直角三角形,为此作于D,则有,,再由勾股定理计算出AD、DC的长,进而求出BC的长.解析:作于D,则因,∴(的两个锐角互余)∴(在中,如果一个锐角等于,那么它所对的直角边等于斜边的一半).根据勾股定理,在中,.根据勾股定理,在中,.∴.举一反三【变式1】如图,已知:,,于P. 求证:.解析:连结BM,根据勾股定理,在中,.而在中,则根据勾股定理有.∴又∵(已知),∴.在中,根据勾股定理有,∴.【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。
求:四边形ABCD的面积。
分析:如何构造直角三角形是解本题的关键,可以连结AC,或延长AB、DC交于F,或延长AD、BC交于点E,根据本题给定的角应选后两种,进一步根据本题给定的边选第三种较为简单。
解析:延长AD、BC交于E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经典题解
一、单选题
1.以下属于信息的是()。
A.晚会实况录像带B.记录成绩的纸张
C.一段天气预报D.一张软磁盘
答:C
【解析】信息不是物质,录像带、纸张、磁盘这些物质本身并不是信息,而一段天气预报,则是综合分析各种天气相关数据得出的分析预测,属于信息。
解题要点:比较各题的异同,抓住命题者的本意。
这里要强调说明的一点:有的信息技术老师语言功底比较差,会命出一些含混不清的题目。
例如“红绿灯”算不是信息就会引起理解上的歧义,单从字面上看“红绿灯”是物质本身,不是信息;但口语“红绿灯”通常就是指红绿灯信号,它发出的是指挥走与停的信息。
遇到这类麻烦,要细心领会命题人的本意。
考查信息技术变成了考查语文,固然从老师的角度来看是笑话,但作为学生,有时候也只能学聪明一点。
2.1946年世界是第一台名为ENIAC的电子计算机在()诞生
A.中国B.德国C.英国D.美国
答:D
【解析】这部分属于“拓展”知识的内容,时而考查到。
计算机发展史的几个重大事件,必须有所了解,它们是:世界上第一台电子计算机ENIAC是1946年2月在美国诞生的,主要元件是电子管(电子管的概念出现在人教版,广东版未涉及)。
1981年美国IBM第一台PC(个人电脑),为计算机发展带来突破性发展。
1984年第一台多媒体计算机出现。
1969年美国建立世界上第一个计算机网络——ARPANET(阿帕网),以后发展成为因特网。
3.下列不是信息载体的是()。
A.文具B.符号C.图形D.语音
答:A
【解析】广东省教版没有涉及这部分内容。
实际上这已经是大学课程了,什么是“载体”呢?“数据”是信息的载体,那么什么是数据呢?显然是指各种符号、图形、语言、电磁波、光信号等等。
硬件本身不是数据,不算信息载体。
4.提出计算机的结构和设计思想是()
A.布尔B.摩尔C.冯·诺依曼D.申农
答:C
【解析】广东省教版上基本没有涉及这部分内容,而且广东版对计算机组成原理示意讲解也极为浅显。
同学们只要记住这位大名鼎鼎的美藉匈牙利人科学家约翰·冯·诺依曼(John Von
Neumann,1903~1957),就可以了。
(他被人称为“计算机之父”。
此外称为计算机之父的还有图灵、巴贝奇)。
冯·诺依曼的名字,出现在第二册上17页的拓展知识中。
5.早期的计算机主要是用来进行()
A.科学计算B.系统仿真C.自动控制D.动画设计
答:A
【解析】电子计算机早期,以前更早的机械式计算机,都是用来进行科学计算的。
6.能够快捷、准确地处理大容量信息的工具是()。
A.计算器B.算盘C.电子计算机D.运算器
答:C
【解析】它们都属于信息技术工具。
计算器对应英文的Calculator,即平时数学课上用的那种小工具;运算器是CPU的组成部分;“电子计算机”在港台会引起误解(误解为计算器),但大陆地区电子计算机即电脑,是现代信息技术的重要工具,有代表意义。
7.下列不属于信息传递方式的是()
A.上网B.发信C.思考D.电影
答:C
【解析】前面我们说过,信息过程有“获取、识别、处理、表达、传递”几种。
“思考”显然属于信息的处理过程,而不是传递方式。
8.信息技术简称()。
A.CEO B.IT C.NT D.Internet
答:B
【解析】这里想强调一下,每一册都有《部分中英文术语对照》,请同学们务必对一些常见信息技术的英语拼写有一些了解。
不求你全部记住,但最起码做到“有印象”,当看到他们的时候,能正确分辨哪一个是正确的。
这里不妨罗列几个:
IT:Information Technology信息技术PC:Personal Computer个人计算机
Blog:博客BBS:电子公告版
LAN:局域网WAN:广域网
URL:统一资源定位器FTP:文件传输协议
HTML:超文本标识语言HTTP:超文本传输协议
IIS:因特网信息服务E-mail:电子邮件
二、判断题
1.信息技术的进步极大推动了社会发展,对社会只有益处没有危害。
()
答:错
【解析】任何新技术的产生,都会有两面性。
信息技术不利的因素:一是设备的电磁辐射等等会危害人的健康;二是便利的获取与复制技术可能助长知识产权的侵权;三是人为利用信息技术的破坏力会更强。
2.古代没有信息技术,信息技术的产生只是近几十年的事。
()
答:错
【解析】信息技术古已有之,例如结绳记事、烽火传令等等。
以光电磁技术为基础的所谓“现代信息技术”才是近几十年飞速发展起来的。
