浙教版八年级数学下册 《一元二次方程的应用与几何图形(第2课时)》ppt课件
合集下载
2021年浙教版八年级数学下册第二章《一元二次方程》公开课课件 (2).ppt
No
并且未知数的最高次数是1次,这样的方程叫做 一元一次方程.
像这样,两边都是整式,只含有Im一个a未g知e数,
并且两未边都知是数整的式,只最含高有次一个数未是知数2次, ,这样的方程叫做 一元并二且未次知方数程的最. 高次数是1次,这样的方程叫做 一元一次方程.
2.1一元二次方程(1)
x2 12x 20 0 x23x4 6700(1x)29200
能使一元二次方程两边相等的未知数的值叫一元 二次方程的解(或根).
已知关于x的一元二次方程 x2+ax+a=0 的一个根是3,求a的值。
畅谈收获
1、一元二次方程的定义 2、一元二次方程的一般形式
ax2+bx+c=0(a, b,c为常数, a≠0)
3、会用一元二次方程表示实际生活中的数 量关系
布置作业: 1、作业本(2)
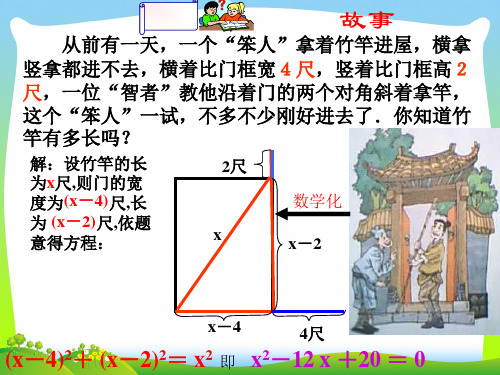
故事
从前有一天,一个“笨人”拿着竹竿进屋,横拿
竖拿都进不去,横着比门框宽4尺,竖着比门框高2
尺,一位“智者”教他沿着门的两个对角斜着拿竿,
这个“笨人”一试,不多不少刚好进去了.你知道竹 竿有多长吗?
解:设竹竿的长
为x尺,则门的宽 度为(x-4)尺,长 为 (x-2)尺,依题 意得方程:
2尺 x
数学化 x-2
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/142020/12/14Monday, December 14, 2020
• 10、人的志向通常和他们的能力成正比例。2020/12/142020/12/142020/12/1412/14/2020 5:02:38 PM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/12/142020/12/142020/12/14Dec-2014-Dec-20 • 12、越是无能的人,越喜欢挑剔别人的错儿。2020/12/142020/12/142020/12/14Monday, December 14, 2020 • 13、志不立,天下无可成之事。2020/12/142020/12/142020/12/142020/12/1412/14/2020
浙教初中数学八下《2.1 一元二次方程》PPT课件 (2)

2.若一个数的平方等于这个数本身,你能求 出这个数吗(要求列出一元二次方程求解)?
能说出你这节课的收获和体验让大 家与你分享吗?
注意:当方程的一边为0时,另一边容易分解成两个
一次因式的积时,则用因式分解法解方程比较方便.
因式分解法解一元二次方程的基本步骤 (1)将方程变形,使方程的右边为零; (2)将方程的左边因式分解;
学科网
复习回顾
1、一元二次方程的定义
2、一元二次方程的一般式:
ax2 bx c 0(a≠0)
3、一元二次方程的根的含义
复习回顾
因式分解: 把一个多项式化成几个整式的积的形式
主要方法:
学科网
(1)提取公因式法
(2)公式法:
a2-b2=(a+b) (a-b)
a2±2ab+b2=(a±b)2
在学习因式分解时,我们已经知道, 可以利用因式分解求出某些一元二次方 程的解
请利用因式分解解下列方程:
(1)y2-3y=0;
解:(1)y(y-3)=0 ∴ y=0或y-3=0 ∴ x1=0, x2=3
(2) 4x2=9
(2)移项,得 4x2-9=0 (2x+3)(2x-3)=0 ∴x1=-1.5, x2=1.5
例2 、解下列一元二次方程:
(1)(x-5) (3x-2)=10; (2) (3x-4)2=(4x-3)2.
解:(1) 化简方程,得 3x2-17x=0.
将方程的左边分解因式,得 x(3x-17)=0, ∴x=0 ,或3x-17=0 解得 x1=0, x2=17/3
(2)移项,得(3x-4)2-(4x-3)2=0. 将方程的左边分解因式,得 〔能(用3x因-式4)分+(解4x法-解3)一〕元〔二(次3x方-程4)遇-到(类4x似-例3)2〕这=样0,的, 移即项后(能7x直-接7)因(式-x分-解1)就=0直.接因式分解,否则移项后 先∴化7x成-一7=般0,式或再因-x式-分1=解0.. ∴x1=1, x2=-1
能说出你这节课的收获和体验让大 家与你分享吗?
注意:当方程的一边为0时,另一边容易分解成两个
一次因式的积时,则用因式分解法解方程比较方便.
因式分解法解一元二次方程的基本步骤 (1)将方程变形,使方程的右边为零; (2)将方程的左边因式分解;
学科网
复习回顾
1、一元二次方程的定义
2、一元二次方程的一般式:
ax2 bx c 0(a≠0)
3、一元二次方程的根的含义
复习回顾
因式分解: 把一个多项式化成几个整式的积的形式
主要方法:
学科网
(1)提取公因式法
(2)公式法:
a2-b2=(a+b) (a-b)
a2±2ab+b2=(a±b)2
在学习因式分解时,我们已经知道, 可以利用因式分解求出某些一元二次方 程的解
请利用因式分解解下列方程:
(1)y2-3y=0;
解:(1)y(y-3)=0 ∴ y=0或y-3=0 ∴ x1=0, x2=3
(2) 4x2=9
(2)移项,得 4x2-9=0 (2x+3)(2x-3)=0 ∴x1=-1.5, x2=1.5
例2 、解下列一元二次方程:
(1)(x-5) (3x-2)=10; (2) (3x-4)2=(4x-3)2.
解:(1) 化简方程,得 3x2-17x=0.
将方程的左边分解因式,得 x(3x-17)=0, ∴x=0 ,或3x-17=0 解得 x1=0, x2=17/3
(2)移项,得(3x-4)2-(4x-3)2=0. 将方程的左边分解因式,得 〔能(用3x因-式4)分+(解4x法-解3)一〕元〔二(次3x方-程4)遇-到(类4x似-例3)2〕这=样0,的, 移即项后(能7x直-接7)因(式-x分-解1)就=0直.接因式分解,否则移项后 先∴化7x成-一7=般0,式或再因-x式-分1=解0.. ∴x1=1, x2=-1
浙教版数学八年级下册2.3《一元二次方程的应用》教学课件(共18张PPT)

“1”,或设为a等.常用的是设为“1”.
课堂小结
谈谈你这节课的收获
列方程解应用题的一般步骤是怎样的? 审 即审题,找出题中所涉及的数量和基本数量关系;
设元,设出未知数,用含未知数的代数式表示其 设 他相关量;
列 根据等量关系列出方程;
解 解方程; 检 检验根的准确性及是否符合实际意义并作答。
布置作业:
例题精讲
如果设每盆花苗增加的株数为x株呢?
解:设每盆花苗增加的株数为x株,则每盆花苗 平均每株盈利×每盆株数(x+3)=每盆盈利; (x +3) 株,平均单株盈利为 (3-0.5 x) 元. 有 ______ ________ 平均每株盈利=3-0.5×每盆增加的株数x. 由题意,得 (x+3)(30.5x)=10. 化简、整理,得 x23x+2=0. 解这个方程,得 x1=1, x2=2. 经检验,x1=1,x2=2都是方程的解,且符合题 意. 答:要使每盆的盈利达到10元,每盆应植入4株 或5株.
设元,包括设直接未知数或间接未知数,以及用未知 数字母的代数式表示其他相关量。 根据等量关系列出方程。 解方程。 检验根的准确性及是否符合实际意义。 作答。
设 列
解
检
答
例3:如图甲,有一张长40cm,宽25cm的
长方形硬纸片,裁去角上四个小正方形之后,折
成如图乙所示的无盖纸盒。若纸盒的底面积是
随堂练习
1.已知两个连续正奇数的积是143, 利用一元二次方程求这两个数.
随堂练习 2.某校坚持对学生进行近视眼的防治,近视
学生人数逐年减少.据统计,今年的近视学生人数
是前年人数的75℅,那么这两年平均每年近视学生 人数降低的百分率是多少(精确到1℅)?
课堂小结
谈谈你这节课的收获
列方程解应用题的一般步骤是怎样的? 审 即审题,找出题中所涉及的数量和基本数量关系;
设元,设出未知数,用含未知数的代数式表示其 设 他相关量;
列 根据等量关系列出方程;
解 解方程; 检 检验根的准确性及是否符合实际意义并作答。
布置作业:
例题精讲
如果设每盆花苗增加的株数为x株呢?
解:设每盆花苗增加的株数为x株,则每盆花苗 平均每株盈利×每盆株数(x+3)=每盆盈利; (x +3) 株,平均单株盈利为 (3-0.5 x) 元. 有 ______ ________ 平均每株盈利=3-0.5×每盆增加的株数x. 由题意,得 (x+3)(30.5x)=10. 化简、整理,得 x23x+2=0. 解这个方程,得 x1=1, x2=2. 经检验,x1=1,x2=2都是方程的解,且符合题 意. 答:要使每盆的盈利达到10元,每盆应植入4株 或5株.
设元,包括设直接未知数或间接未知数,以及用未知 数字母的代数式表示其他相关量。 根据等量关系列出方程。 解方程。 检验根的准确性及是否符合实际意义。 作答。
设 列
解
检
答
例3:如图甲,有一张长40cm,宽25cm的
长方形硬纸片,裁去角上四个小正方形之后,折
成如图乙所示的无盖纸盒。若纸盒的底面积是
随堂练习
1.已知两个连续正奇数的积是143, 利用一元二次方程求这两个数.
随堂练习 2.某校坚持对学生进行近视眼的防治,近视
学生人数逐年减少.据统计,今年的近视学生人数
是前年人数的75℅,那么这两年平均每年近视学生 人数降低的百分率是多少(精确到1℅)?
2021年浙教版八年级数学下册第二章《一元二次方程的应用》精品课件.ppt

由题意得:(10-X)(40+8X)= 432
整理得: X2-5X+4=0 解得: X1=1 X2=4 检验:X1=1 ,X2=4 都是方程的解 答: 小新家每天要盈利432元,
那么每束玫瑰应降价1元或4元。
因式分 解法
情急之下,小新家准备零售这批玫 瑰.如果每束玫瑰盈利10元,平均 每天可售出40束.为扩大销售,经 调查发现,若每束降价1元,则平 均每天可多售出8束. 如果小新家 每天要盈利432元, 同时也让顾客 获得最大的实惠.那么每束玫瑰应 降价多少元?
3+1间接设未知数
3+2
…
…
3﹣0.5x
3+x
10
回顾与思索
如果每束玫瑰盈利10元, 小新家的花圃用花盆培育 平均每天可售出40束.为扩 玫瑰花苗,经过试验发现, 大销售,经调查发现,若 每盆植入3株时,平均每株 每束降价1元,则平均每天 盈利3元;以同样的栽培条 可多售出8束.如果小新家每 件,每盆每增加1株,平均 天要盈利432元,那么每束 每株盈利就减少0.5元。要 玫 瑰 应 降 价 多 少 元 ? 使每盆的盈利达到10元,
(万棵)
3200 2400
2083 3089
1600
892 1254
800 350
0 2000年 2000年 2001年 2002年 2003年 年份
1月1日 12月31日 12月31日 12月31日12月31日
⑴你能从图中获得哪些信息,说说看!
⑵求2000年12月31日至2002年12月31日 花苗株数的年平均增长率。
小新家的花圃用花盆培育玫瑰花苗.经 过试验发现,每盆植入3株时,平均每 株盈利3元;以同样的栽培条件,每盆 每增加1株,平均每株盈利就减少0.5 元.要使每盆的盈利达到10元,并尽量 降低成本,则每盆应该植多少株?
2021年浙教版八年级数学下册第二章《一元二次方程的应用(第二课时)》公开课课件.ppt

,与此同时,点Q从点B开始沿边BC向点C以
2cm/s的速度移动。如果P、Q分别
从A,B同时出发,经过
C
几秒, △ PBQ的面积 等于8cm2 ?
2秒或4秒
Q 8cm P A 6cm B
练习1:
如图,矩形ABCD中,AB=6cm,BC=3cm,
动点P、Q分别从点A、D出发,点P以2cm/s
的速度沿AB方向向点B移动,一直到达B为止;
小结
•列一元二次方程解应用题的步骤与 列一元一次方程解应用题的步骤类似,
即审、设、列、解、检、答.
• 这里要特别注意:在列一元二次方 程解应用题时,由于所得的根一 般有两个,所以要检验这两个根 是否符合实际问题的要求.
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2021/1/92021/1/9Saturday, January 09, 2021
•
THE END 17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2021/1/92021/1/92021/1/92021/1/9
t1 8.35 t2 19.34
问:(1) 这方程解得的t1,t2的实际意义是什么?
(2) 从t1,t2的值中,还可得到什么结论?
(3) 如何才能避免轮船不进入台风影响区? 提高题:(4) 这艘轮船受台风影响的时间有多长?
问题2:1、如图,在△ABC中,∠B=90o。点
P从点A开始沿边AB向点B以1cm/s的速度移动
如果要使整个挂图的面积是5400cm2,设金色纸
边的宽为xcm,那么x满足的方程是【B】
A.x2+130x-1400=0 B.x2+65x-350=0
2021年浙教版八年级数学下册第二章《一元二次方程的应用》公开课课件.ppt

问题: (2)上网计算机总数2001年12月31日至2003年
12月31日的年平均增长率与2000年12月31日至2002年12
月31日的年平均增长率相比,哪段时间年平均增长率较
大?
想一想:
(1)已知哪段时
间的年平均增
倍 长率?
速 课
(2)需要求哪个
时 时间段的年平
学 练
均增长率?
上网计算 机总台数
列 根据等量关系列出方程
倍
速 课 时
解 解方程并检验根的准确性及是否符合实际意义并作答。
学
练
练一练:
某单位为节省经费,在两个月内将开支从 每月1600元降到900元,求这个单位平均每 月降低的百分率是多少?
倍 速 课 时 学 练
练一练:
某校坚持对学生进行近视眼的防治,近视学生 人数逐年减少.据统计,今年的近视学生人数是 前年人数的75℅,那么这两年平均每年近视学 生人数降低的百分率是多少(精确到1℅)?
2.3一元二次方程的应用(1)
(1)某公司今年的销售收入是a万元,如果每年的增长率都是x,
那么一年后的销售收入将达到__a__•(_1x_)万元(用代数式表示
(2)某公司今年的销售收入是a万元,如果每年的增长率都是x,
那么两年后的销售收入将达到__a•( 1_x__)2_万元(用代数式表
示) 倍 速 课 时 学 练
如果直接设每盆植x株,怎样表示问题中相关的量?
如果设每盆花苗增加的株数为x株呢?
解:设每盆花苗增加的株数为x株,则每盆花苗有(__x_+_3_)_株,平均单
倍 速
株盈利为_(_3_-_0_.__5_x_)_元. 由题意,得
课 (x+3)(3-0.5x)=10 化简,整理,得 x2-3x+2=0
一元二次方程的应用PPT课件

2、教学目标
知识目标: 能用一元二次方程解决简单的几何 型应用问题。
能力目标: 进一步提高数学建模的能力,培养学 生动手操作、观察归纳能力,培养学 生问题意识能力。
情感目标: 帮助学生体验数学学习活动中的成功 与快乐,使他们认识到数学来源于生 活,在生活中学习数学,学好数学更 好地为生活服务。
3、重难点分析:
)
又AC=AC (
)
所以△ABC≌△CDA (
)
所以: AB=CD,AD=B 平(行四边形的)性质定理:平行四边形 的两组对边分别相等。
❖(1)定义、命题、公理、定理的概 念。
❖(2)命题的真假。
❖(3)命题的形式与命题的题设和结 论。
(4) 说明一个命题是假命题,只需举 一反例
❖
(假)
3、圆的切线垂直于圆的半径。 (假)
4、等腰三角形的底角必是锐角。 (真)
5、正数与负数的和仍是负数。
(假)
6、一个数的平方必是正数。
(假)
7、一个三角形的两个角、一边和另一三角形的两个
角、一边分别相等的三角形全等。
(假)
阅读理解
阅读教材P93第二段及以后的内 容并回答下列内容: ❖ 1、公理与定理有什么区别? ❖ 2、公理与定理有什么相同的? 有什么作用? 3、你能说出一个学过的定理吗?
小考卷2
一、把下面的命题改写成“如果……那 么……”的形式。 1、两直线平行,同旁内角互补。 2、同圆的半径相等。 3、有两个角相等的两个三角形相似。 4、等角的补角相等。 5、圆是轴对称图形,又是中心对称图形。
小考卷3
判断下列命题的真假:
细心!
1、相等的两角是对顶角。 (假)
2、若XY=0,则X=0。
2021年浙教版八年级数学下册第二章《一元二次方程的应用2》公开课课件.ppt

一元二次方程的应用(2)
包装盒是同学们非常熟悉的,手工课上, 老师给同学发下一张长40厘米,宽25厘米 的长方形硬纸片,要求做一个无盖纸盒,请问 你该如何做?(可以有余料)
问题: 1、为什么同学做的纸盒大小不同?与什么 有关?
2、若确定小正方形边长为5厘米,你还能 计算哪些量?
X
3、若折成的无盖纸盒的底面积是450平方 厘米,那么纸盒的高是多少?
解:设当轮船接到台风警报后,经过t小时, 则:令 (400-30t)2+(300-20t)2=2002
t1 8.35 t2 19.34
问:(1) 这方程解得的t1,t2的实际意义是什么?
(2) 从t1,t2的值中,还可得到什么结论?
(3) 如何才能避免轮船不进入台风影响区?
如果船速为10 km/h, 结果将怎样?
学生参与设计。现选取了几位同学设计的方案(图纸
如下):
(1)甲同学方案如图,设计草坪的总面积为 540平方米。
20
问:道路的宽为多少?
32
(2)若选取乙同学方案(如图),已知设计草坪 的总面积为540平方米。丙同学方案(如图),已知设计草坪 的总面积为570平方米。则道路宽又为多少?
THE END 17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2020/12/142020/12/142020/12/142020/12/14
谢谢观看
(1)图中C表示什么?B表
示什么?圆又表示什么?
(2) ABC是什么三角形?
能求出AC吗?
A C
(3)显然当轮船接到台风警报时,
没有受到台风影响,为什么?
B
一轮船以30km/h的速度由西向东航行在途中接到台风警报, 台风中心正以20km/h的速度由南向北移动,已知距台风中心 200km的区域(包括边界)都属于受台风影响区,当轮船接到台风 警报时,测得BC=500km,BA=300km.
包装盒是同学们非常熟悉的,手工课上, 老师给同学发下一张长40厘米,宽25厘米 的长方形硬纸片,要求做一个无盖纸盒,请问 你该如何做?(可以有余料)
问题: 1、为什么同学做的纸盒大小不同?与什么 有关?
2、若确定小正方形边长为5厘米,你还能 计算哪些量?
X
3、若折成的无盖纸盒的底面积是450平方 厘米,那么纸盒的高是多少?
解:设当轮船接到台风警报后,经过t小时, 则:令 (400-30t)2+(300-20t)2=2002
t1 8.35 t2 19.34
问:(1) 这方程解得的t1,t2的实际意义是什么?
(2) 从t1,t2的值中,还可得到什么结论?
(3) 如何才能避免轮船不进入台风影响区?
如果船速为10 km/h, 结果将怎样?
学生参与设计。现选取了几位同学设计的方案(图纸
如下):
(1)甲同学方案如图,设计草坪的总面积为 540平方米。
20
问:道路的宽为多少?
32
(2)若选取乙同学方案(如图),已知设计草坪 的总面积为540平方米。丙同学方案(如图),已知设计草坪 的总面积为570平方米。则道路宽又为多少?
THE END 17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2020/12/142020/12/142020/12/142020/12/14
谢谢观看
(1)图中C表示什么?B表
示什么?圆又表示什么?
(2) ABC是什么三角形?
能求出AC吗?
A C
(3)显然当轮船接到台风警报时,
没有受到台风影响,为什么?
B
一轮船以30km/h的速度由西向东航行在途中接到台风警报, 台风中心正以20km/h的速度由南向北移动,已知距台风中心 200km的区域(包括边界)都属于受台风影响区,当轮船接到台风 警报时,测得BC=500km,BA=300km.
