2014年春学期八年级数学期中试卷
2014年春八年级下期中数学试卷

2014年春季八年级期中检测数学试题一、精心挑选一个正确答案〔每题2分,共12分〕 1. 计算 25a a÷的结果是 〔 〕A. 4a ;B. 3a ; C. 2a ; D. a . 2.函数2-=x y 中自变量x 的取值围是 〔 〕A.2≥x ;B.2>x ;C.2≤x ;D.2<x . 3.以下约分正确的选项是〔 〕A 、326x x x =; B 、0=++y x y x ; C 、x xy x y x 12=++; D 、214222=y x xy . 4.如果把分式xx y+中的x 和y 都扩大3倍,那么分式的值是( ) A.扩大3倍; B.不变; C.缩小3倍; D.缩小6倍. 5.反比例函数xy 2=的图像上有三点(-3,a ),(-1,b ),(2,c ),那么( ) A.a >b >c ; B.b >c >a ; C.c >b >; D.c >a >b . 6.如右图是教师早晨出门散步时,离家的距离..y 〔米〕 与时间x 〔分钟〕之间的函数图象.假设用黑点表示老 师家的位置,那么教师散步行走的路线可能是〔 〕二、请你耐心细算〔每空格2分,共24分〕1.计算:aa 21+= ;b a b b a a +++=.2.如果分式22+x x的值为0,那么x =__________.A.B.C.D.3.点P 〔2,3〕关于原点对称的点的坐标是.4.科学家发现一种病毒的直径为0.000043米,用科学记数法表示为_____________米. 5.反比例函数xy 2=,当x =4时,y 的值为. 6.写出一个含有字母x 的分式__________ .(要求:无论x 取任何数,该分式的值为正数) 7.直线6+=x y 与x 轴,y 轴围成一个三角形,那么这个三角形面积为. 8.把命题“全等三角形的对应边相等〞改写成“如果……,那么……〞的形式. _________________________________________________ . 9.如图,点∠C=∠D=90°,补充条件:___________ (写出一个即可) ,使△ABC ≌△ABD.10.如图甲,四边形纸片ABCD 中∠B=120︒,∠D=50︒. 假设将其右下角向折出△PCR ,恰使CP//AB ,RC//AD ,如图乙所示,那么∠C 等于________ .95︒ 11.将图①所示的正六边形进展分割得到图②,再将图②中最小的某一个正六边形按同样的方式进展分割得到图③,再将图③中最小的某一个正六边形按同样的方式 进展分割,…,那么第5个图形中共有个正六边形.13三、你来细心算一算〔每题5分,共20分〕 1.03220092)31(++- 2.422-a a +a -21 .第9题A B CD PR 图乙AB C D 图甲 第10题图第11题图① •••② ③3.先化简后求值:22)11(b a abb a b a -÷-++, 其中2=a ,3=b .4.解方程:223-x +x-11 =3.四、〔每题6分,共18分〕1.在同一直角坐标系上画出函数xy x y 1,12=+-=的图像.2.如图,AC =BD , BC =AD ,求证: △ABC ≌△BAD .3. 如图,∠C =∠D , CE =DE .求证: ∠BAD =∠ABC .五、〔每题6分,共18分〕1.某工厂需要加工1200个零件,实际工作效率比原计划提高了50%,结果 提前10小时完成任务.求原计划每小时加工多少个零件.2.在生活中我们知道大气压随着高度的增加而减小.设在离海平面2km ,山高y (km )与x cm〔1〕求出x 与y 之间的关系式.〔2〕估计当大气压为64cm 时,山的高度.3.:反比例函数kyx=和一次函数y mx n=+图象的一个交点为A(-3,4)且一次函数的图象与x轴的交点到原点的距离为5.分别求出反比例函数和一次函数的解析式.六〔8分〕.如图,ABCD是边长为4的正方形,M是AD的中点,动点P从A点出发,沿A→B→C→D匀速运动,设点P运动的路程为x,直线MP扫过正方形所形成的面积为y.x=时,求y的值;〔1〕当1〔2〕求y与x之间的函数关系式.。
2014年春八年级期中考试数学试卷(附答案)

A B CD2014年春八年级期中考试数学试卷考试时间:120分钟,卷面满分:120分一、选择题(1-7小题每小题3分,8-10小题每小题4分,共33分)1.已知实数a 、b 满足22(24)(62)0a b -+-=,则ab 的算术平方根为( ) A . ±6 B. 6 C. ±2.已知|1|)1)(8(-+-x x x 的值为0,则x 的值为( )A.±1B.-1C. 8D. -1或83.已知22()8,()12a b a b +=-=,则22a b +的值为( )A. 10B. 8C. 6D. 44.三角形的三边长分别为整数a 、b 、c ,a ≤b ≤c ,当b=3时,这样的不全等的三角形共有( )个。
A. 4B. 5C. 6D. 7 5.当=x1时,代数式2()()111x x x x x x-÷-+-的值为( ) A.136.在同一直角坐标系中,一次函数k kx y -=与反比例函数y=2kx的图像的大致位置是( )7. 如图,A 在DE 上,F 在AB 上,且AC=CE ,∠1=∠2=∠3, 则DE 的长等于( )A. DCB. BCC. ABD. AE+AC8. 设直线2)1(=++y n nx (n 为自然数)与两坐标轴围成的三角形面积为nS A B C EDF 1 2 3(n=1,2,……,2010),则122010S S S +++ 的值为( ) A. 1 B.20102009 C. 20112010 D. 201020119. 如图,梯子AB 斜靠在墙面上,AC ⊥BC ,AC=BC ,当梯子的顶点A 沿AC 方向向下滑动xm 时,梯足B 沿CB 方向滑动ym ,则x 与y 的大小关系是( ) A. x=y B. x >y C. x <y D. 不确定10. 甲、乙两人同时从A 地沿一条路线去B 地,若甲一半的时间以akm/h 的速度行走,另一半时间以bkm/h 速度行走;而乙一半的路程以akm/h 的速度行走,另一半的路程以bkm/h 的速度行走(a 、b 均大于0,且a ≠b )则( ) A. 甲、乙同时到达B 地 B. 甲先到达B 地 C. 乙先到达B 地 D. 不确定二、填空题(每小题4分,共32分) 11. 若a b b c a ck c a b+++===,则直线y kx k =+的图象经过 象限。
2014年春八年数学期中考试
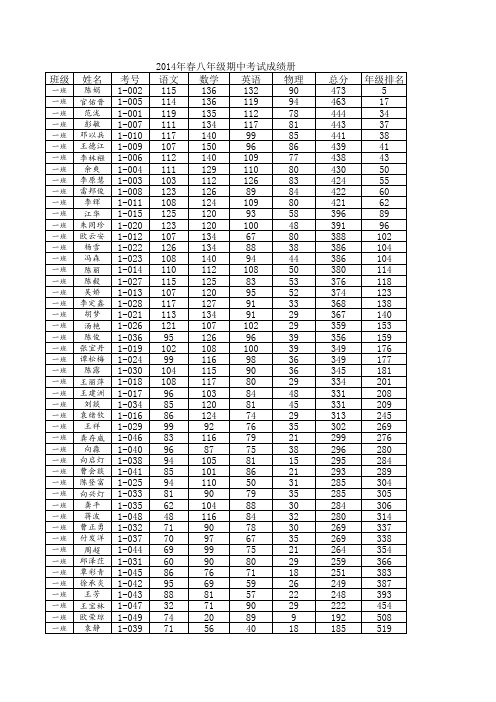
2014年春八年级期中考试成绩册 语文 数学 英语 物理 120 142 122 73 124 138 127 66 125 125 116 79 124 128 106 65 119 130 61 62 121 104 86 57 115 115 64 62 128 106 66 45 126 90 80 45 94 125 55 64 120 87 86 44 129 120 44 38 106 92 67 43 118 66 55 56 83 124 60 26 101 68 66 54 96 80 84 27 106 93 46 35 100 64 78 33 92 70 60 49 89 72 63 42 101 84 47 32 95 82 45 39 83 82 38 41 111 46 47 40 75 72 40 54 95 64 33 45 93 86 37 21 106 36 50 44 75 67 72 13 85 72 24 35 41 100 40 21 88 36 52 25 86 42 44 26 79 60 37 18 91 40 22 25 69 48 33 24 69 34 36 32 68 4 26 40 29 16 9 26
班级
二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班 二班
姓名
谭乔珍 卢帮辉 向晓霞 李德坤 许世勇 谭乔梅 何时清 王彬彬 向光礼 潘定钊 黄霞 黄世艳 邓啟芳 李云焱 曾其林 牛馨瑶 代地辉 杨功辉 许燕 刘和淡 向敏 伍成萍 乔玉鑫 陈良 向存 向焱 陈世林 黄群 李徐帆 谭乔勇 张圣敏 方莉 向洺 蒋祖艳 聂玉清 张苗 谭桥香 向铭 向绍明 赖扬名 陈怡 向超 赵园园 王辉 向东 邹传德 邹贤慧 侯庆
西峡县2014年春期期中考试八年级数学试题答案及评分建议

西峡县2014年春期期中考试八年级数学试题答案及评分建仪 一、选择题(每小题3分,共24分.)下列各小题均有四个答案,其中二、填空题(每小题3分共21分)9、11;10、2-y x ;11、-1;12、-1;13、四;14、y =2x -2;15、l =123+x 或[l =123+x (x ≥-23), l =1-23-x (x <-23)]三、解答题(本大题共8个小题,满分75分)16、解(1))-2(2)2-(22x xy x y •÷ =)x xy x y -2(24222××…………………………2分=21-x …………………………………………4分(2)1-1-2+x x x =1-x 1--1-22)(x x x ………………………………1分=1-x 1-2-22x x x +………………………………3分=1-1-2x x …………………………………………4分17、解:方程两边同乘以(x -3),约去分母,得 x +1=x 2-6,解这个整式方程,得x =7……………………………………………………6分 检验:把x =7代入(x -3)得7-3≠0,………………………………………………7分 所以,x =7是原方程的解.………………………………8分18、解:19-)17-9(2+÷++x x x x x =9-1)11x 7-9(22x x x x x x +×++++ =9-1196-22x x x x x +×++=)3-)(3(113-2x x x x x ++×+)( =33-+x x …………………………………………7分 要使原分式有意义,x 的值不能等于-1、±3. 当x =0时,原式=33-+x x =303-0+=-1.………………………………………9分19、AE//CF ,AE=CF …………2分 证明:∵四边形ABCD 是平行四边形∴AB=CD ,∠ABE=∠CDF …………4分 ∵BF=DE即:BE+EF=DF+EF ∴BE=DF在△ABE 和△CDF 中∵7分 ∴AE=CF ,∠AEB=∠CFD∵∠AEB+∠AEF=∠CFD+∠CFE ∴∠AEF=∠CFE∴AE//CF …………………………………9分20、解:画图(如图所示)…………4分(1)-1≤x <0和x ≥2…………6分(2)设直线与x 、y 轴的交点为C 、D 当x=0时,y=-1,当y=0时x=1 A O B s ∆=AOD s ∆+BOD s ∆=21-211-1-21××+××=23……………………………10分Dy xC -12BAO21、解:(1)乙……………………1分 (2)甲y =x 4.0(x >0)………2分 乙y =200+x 15.0(x >0)……3分 (3)依题意,得;xy x y 0.15200;0.4+==乙甲即x 4.0=200+x 15.0 解得:x =800甲y =x 4.0=0.4×800=320∴点P 的坐标为(800,320)…………………………………8分(4)由图象知:当每月的复印量小于800页时选择甲文印门市省钱;当每月的复印量等于800页时两家门市花费一样;当每月的复印量多于800页时选择乙文印门市省钱。
2014年春新人教版八年级下册数学期中试卷及答案

数学(考试时间:120分钟满分120分)一、选择题(每小题2分,共24分)1.下列式子中,属于最简二次根式的是()A. 9B. 7C. 20D.312. 如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则MDAM等于()A.83B.32C.53D.543.方程x2-2x=0的根是(). A.x1=0,x2=2 B.x1=0,x2=-2 C.x=0 D.x=24.若x1,x2是一元二次方程3x2+x-1=0的两个根,则1211x x+的值是().A.-1 B.0 C.1 D.25.已知一直角三角形的三边长为a、b、c,∠B=90°,那么关于x的方程a(x2-1)•-2x+b(x2+1)=0的根的情况为().A.有两个相等的实数根 B.有两个不相等的实数根 C.没有实数根 D.无法确定6.若代数式1-xx有意义,则实数x的取值范围是()A. x≠ 1B. x≥0C. x>0D. x≥0且x≠17. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12B. 24C. 312 D. 3168. 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5 º,NM DB CA2题图4题图5题图EF ⊥AB ,垂足为F ,则EF 的长为( )A .1B . 2C .4-2 2D .32-4 9、关于x 的方程3x 2-2x+m=0的一个根是﹣1,则m 的值为( )A .5B .﹣5C .1D .﹣1 10、用公式法解﹣x 2+3x=1时,先求出a 、b 、c 的值,则a 、b 、c 依次为( ) A .﹣1 3 ﹣1 B .1 ﹣3 ﹣1 C .﹣1 ﹣3 ﹣1 D .1 ﹣3 1 11.解下面方程:(1)()225x -=(2)2320x x --=(3)260x x +-=,较适当的方法分别为( )A 、(1)直接开平法方(2)因式分解法(3)配方法B 、(1)因式分解法(2)公式法(3)直接开平方法C 、(1)公式法(2)直接开平方法(3)因式分解法D 、(1)直接开平方法(2)公式法(3)因式分解法12、某农户种植花生,原来种植的花生亩产量为200千克,出油率为50%(即每100千克花生可加工成花生油50千克).现在种植新品种花生后,每亩收获的花生可加工成花生油132千克,其中花生出油率的增长率是亩产量的增长率的21.则新品种花生亩产量的增长率为 ( ) A 、20% B 、30% C 、50% D 、120% 二、填空题:(每小题3分,共24分) 13.计算:()()3132-+-= .14.若实数a 、b 满足042=-++b a ,则ba= .15.已知21,x x 是方程04322=-+x x 的两个根,那么:=+2212x x ;16、已知关于x 的方程x 2+(k 2-4)x +k -1=0的两实数根互为相反数,则k = 17.如图,ABCD 是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件____________,使ABCD 成为菱形.(只需添加一个即可)18 .如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF.若菱形ABCD 的边长为2cm ,∠A=120°,则EF= .19.如图,矩形ABCD 中,AB =3,BC =4,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B ′处,当△CEB ′为直角三角形时,BE 的长为_________.20、关于x 的方程2x m2-1-3=0是一元二次方程,则m=三、解答题(每小题5分,共20分) (21.)计算:1021128-⎪⎭⎫ ⎝⎛+--+π (22)x x 4132=-(公式法)(23))12(3)12(2+=+x x (24)06)32(5)32(2=+---x x25.用配方法推导一元二次方程ax 2+bx+c=0(a ≠0)的求根公式(5分)26.(6分) 如图,在平行四边形ABCD 中,对角线AC,BD 交于点O,经过点O 的直线交AB 于E ,交CD 于F.求证:OE=OF.四、解答题(每小题4分,共46分)27.(9分)某农户2004年粮食产量为50吨,2006年粮食产量上升到60.5吨,这两年平均每年增长的百分率是多少?ECDBA B ′OFED CBABA 17题图28.(12分) 如图,在四边形ABCD 中,AB =BC ,对角线BD 平分 ∠ABC ,P 是BD 上一点,过点P 作PM ⊥AD ,PN ⊥CD ,垂 足分别为M 、N 。
2014-2015学年度第一学期期中八年级数学
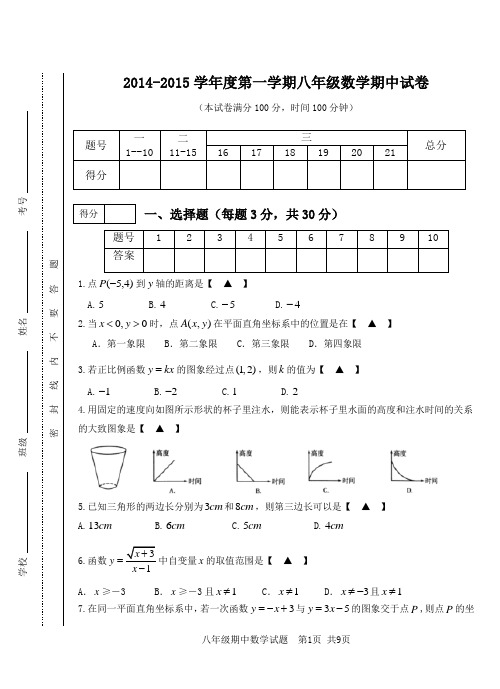
2014-2015学年度第一学期八年级数学期中试卷(本试卷满分100分,时间100分钟)题号 一 1--10 二11-15三总分 16 17 18 19 20 21 得分一、选择题(每题3分,共30分)题号 12345678910 答案1.点)4,5(-P 到y 轴的距离是【 ▲ 】A.5B.4C.5-D.4-2.当0,0><y x 时,点(,)A x y 在平面直角坐标系中的位置是在【 ▲ 】 A .第一象限 B .第二象限 C .第三象限 D .第四象限3.若正比例函数y kx =的图象经过点(1,2),则k 的值为【 ▲ 】 A.1- B.2- C.1 D.24.用固定的速度向如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是【 ▲ 】5.已知三角形的两边长分别为cm 3和cm 8,则第三边长可以是【 ▲ 】 A.cm 13 B.cm 6 C.cm 5D.cm 46.函数3x y +=中自变量x 的取值范围是【 ▲ 】 A .x ≥-3 B .x ≥-3且1x ≠ C .1x ≠ D .3x ≠-且1x ≠7.在同一平面直角坐标系中,若一次函数3y x =-+与35y x =-的图象交于点P ,则点P 的坐得分学校 班级 姓名 考号密封 线 内 不 要 答 题标为【 ▲ 】A.(1,4)-B.(1,2)-C.(2,1)-D.(2,1) 8.一次函数b kx y +=的图象如图所示,则不等式2>+b kx 的 解集为【 ▲ 】A.0>xB.0<xC.1-<xD.1->x9.一个三角形的两个内角分别是ο55和ο72,这个三角形的外角不可能是【 ▲ 】 A. 125° B.108° C.127° D.137°10.甲、乙两个同学从m 400环形跑道上的同一点出发,同时同向而行,甲的速度为s m /6,乙的速度为s m /4.设经过x (s )后,跑道上此两人间的较短部分的长度为y (m ),则y 与x (0≤x ≤300)之间函数关系可用图象表示为【 ▲ 】A. B. C. D.二、填空题(每题4分,共20分)11.如图,是某风景区几个主要景点示意图,根据图中信息可确定 九疑山的中心位置C 点的坐标为 .12.已知直线3-=x y 与22+=x y 的交点为)8,5(--,则方程组 的⎩⎨⎧=+-=--02203y x y x 解是 .13.直线a x y +-=2经过点),3(1y 和点),2(2y -,则1y 2y (填“>”、 “<”或“=”). 14.如果将函数x y 2=的图象向左平移m (0>m )个单位,正好等于将它向上平移n (0>n )个单位,则m 和n 之间的关系为 .15.某人用80元充值卡坐某种刷卡出租车,按行驶里程收费.km 3内收费8元,以后每超过km1得分第8题图第11题图加收5.1元.若此人第一次坐出租车(331)xkm x ≤≤,则充值卡中所余的费用y (元)与x ()km 之间的关系式是 . 三、解答题(共55分)16.(本小题7分)如图,A B C 、、三点的坐标分别为3,4()、1,2()、5,0(),将ABC ∆先向下平移四个单位得到'''A B C ∆,再将'''A B C ∆向左平移五个单位得到111A B C ∆.(1)请你在图上画出'''A B C ∆和111A B C ∆; (2)观察所画的图形写出'A 和1A 的坐标;(3)计算ABC ∆的面积.17.(本小题8分)综合与实践世界上大部分国家都使用摄氏温度()C o,但美国、英国等国家的天气预报仍然使用华氏温度()F o.两种计量之间有如下对应:(1(2)求出华氏0度时摄氏是多少度?(3)华氏温度的值与对应摄氏温度的值有相等的可能吗?如果有,请求出该值.xy –1–2–3–4–512345–1–2–3–4–512345O18.(本小题8分)如图,在ABC ∆中,AC AB =,AC 上的中线把三角形的周长分为cm 24和cm 30的两个部分,求三角形各边的长.19.(本小题10分) 已知2+y 与x 成正比例,且2-=x 时,0=y . (1)求y 与x 之间的函数关系式; (2)画出函数的图象;(3)设点P 在y 轴负半轴上,(2)中的图象与x 轴、y 轴分别交于B A 、两点,且4=∆ABP S ,求P 点的坐标.20.(本小题10分) 已知,如图,在ABC ∆中,角平分线BD 、CD 相交于点D , (1)若ο80=∠A ,求BDC ∠的度数; (2)若ο120=∠BDC ,求A ∠的度数;(3)若βα=∠=∠BDC A ,,试求α、β之间的数量关系.第20题图21. (本小题12分) 我市某企业利用机器生产一种科技产品,机器从早上八点开始工作,中午十二点停止.产品生产出来后,需要包装入库.通常的办法是,机器先工作一段时间,包装工人再开始包装.某次包装工人工作了一段时间后,因临近下班,又抽掉了一部分工人来帮忙,使包装入库的速度提高了一倍.如图是生产出来后待包装入库的产品数量y(件)与时间t(h)的函数关系的图象.根据图象解决以下问题:(1)机器每小时生产件产品;工人包装入库的速度是件/h;(2)求线段BC的解析式;(3)如果要保证生产的产品恰好在半天(4h)时全部包装入库,原有包装工人应该在机器开始工作后多长时间时开始包装?2014-2015学年度第一学期八年级数学期中测试参考答案一、选择题1---5:ABDCB 6----10:BDADC 二、填空题 11.(3,1) 12.⎩⎨⎧-=-=85y x 13.< 14.2m=n 15.5.765.1+-=x y三、解答题16.(1)图略………………2分(2)'A (3,0);1A (-2,0)………………4分 (3)42214221222144⨯⨯-⨯⨯-⨯⨯-⨯=∆ABC S ………………6分 6=………………7分 17.解:(1)是一次函数.………………1分设摄氏温度值为x ,华氏温度值为y ,令y=kx+b321050b k b =⎧⎨+=⎩解得9,325k b == 9325y x =+………………4分 (2)当y=0时,93205x +=,解得1609x =-,即华氏0度时,摄氏是1609-.…………6分 (3)依题意得9325y x y x⎧=+⎪⎨⎪=⎩ 解得40y x ==-即华氏温度的值与摄氏温度的值在-40时相等.………………8分 18.解:设AB=AC=2x ,则AD=CD=x ,(1)当AB +AD=30,BC +CD=24时,有2x +x=30, ∴x=10,………………2分 2x=20,BC=24-10=14,三边分别为:20cm ,20cm ,14cm .………………4分(2)当AB +AD=24,BC +CD=30,有2x +x=24∴x=8,………………6分BC=30-8=22,三边分别为:16cm ,16cm ,22cm .………………8分19.解:(1)∵y+2与x 成正比例,∴设y+2=kx (k 是常数,且k ≠0)∵当x=-2时,y=0. ∴0+2=k ·(-2),∴k =-1. ∴函数关系式为x+2=-x , 即y=-x-2.………………3分 (2)列表;x 0 -2 y-2描点、连线,图象如图所示.………………6分 (3)函数y=-x-2分别交x 轴、y 轴于A ,B 两点, ∴A (-2,0),B (0,-2). ∵S △ABP =21·|BP|·|OA|=4, ∴|BP|=428||8==OA . ∴点P 与点B 的距离为4. 又∵B 点坐标为(0,-2),且P 在y 轴负半轴上, ∴P 点坐标为(0,-6).………………10分 20.(1)∵∠A=80°,∴∠ABC+∠ACD=180°-80°=100° ∵BD 、CD 是角平分线 ∴∠DBC+∠DCB=οο5010021)(21=⨯=∠+∠ACB ABC ∴∠BDC=180°-∠DBC-∠DCB=180°-50°=130°;………………3分 (2)当∠BDC=120°,∴∠DBC+∠DCB=180°-120°=60° ∵BD 、CD 是角平分线∴οο120602)(2=⨯=∠+∠=∠+∠DCB DBC ACB ABC∴∠A=180°-(∠ABC+∠ACB)=180°-120°=60°;………………6分 (3)∵∠A=α,∴∠ABC+∠ACB=180°-α ∵BD 、CD 是角平分线 ∴∠DBC+∠DCB=)180(21)(21α-⨯=∠+∠οACB ABC ∴∠BDC=180°-(∠DBC+∠DCB)=180°-αα2190)180(21+=-οο ∴︒+=9021αβ………………10分 21.(1)150,250………………4分(2)由包装速度提高一倍可知,最后阶段包装速度为500件/时,100÷500=0.2,所以点C 的坐标为(4.2,0),………………6分设y=kt+b ,则41004.20k b k b +=⎧⎨+=⎩,解得500,2100k b =-= 5002100y t =-+………………8分(3)设机器开始工作后t 小时,包装工人开始包装,则 150×4=250(4-t ) 解得t=1.6即原有工人应该在机器开始工作1.6小时后开始包装.………………12分。
2014学年第一学期八年级数学期中阶段性测试试卷
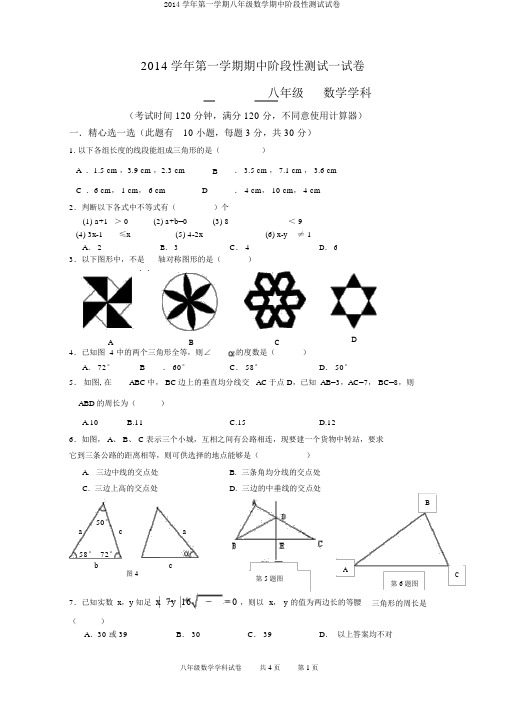
2014学年第一学期期中阶段性测试一试卷八年级数学学科(考试时间 120 分钟,满分 120 分,不同意使用计算器)一.精心选一选(此题有10 小题,每题 3 分,共 30 分)1. 以下各组长度的线段能组成三角形的是()A .1.5 cm ,3.9 cm ,2.3 cm B. 3.5 cm , 7.1 cm , 3.6 cmC .6 cm, 1 cm, 6 cm D. 4 cm, 10 cm, 4 cm2.判断以下各式中不等式有()个(1) a+1> 0(2) a+b=0(3) 8< 9(4) 3x-1≤x(5) 4-2x(6) x-y≠ 1A. 2B. 3C. 4D. 63.以下图形中,不是轴对称图形的是()..A B C D4.已知图 4 中的两个三角形全等,则∠的度数是()A. 72°B. 60°C. 58°D. 50°5.如图, 在ABC中, BC边上的垂直均分线交 AC于点 D,已知 AB=3,AC=7, BC=8,则ABD的周长为()A.10B.11C.15D.126.如图, A、 B、 C 表示三个小城,互相之间有公路相连,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地点能够是()A.三边中线的交点处B. 三条角均分线的交点处C. 三边上高的交点处D. 三边的中垂线的交点处Ba 50°c a58° 72°c b图 4A第 5题图C第 6题图7.已知实数 x,y 知足x 7y 160 ,则以x,y的值为两边长的等腰三角形的周长是()A.30 或 39B. 30C. 39D.以上答案均不对110 x8、不等式组2的整数解有()111x2A、5个B、6 个C、7 个D、8 个9.如图, A,B,C,D,E,F 是平面上的 6 个点,则∠ A+∠B+∠C+∠D+∠E+∠F的度数是()A. 180 °B.360°C.540°D.720°10.已知:如图在△ABC,△ ADE 中,∠ BAC=∠DAE =90°, AB=AC, AD=AE,点 C,D ,E 三点在同一条直线上,连接 BD,BE.以下四个结论:① BD=CE;② BD ⊥ CE;③∠ ACE +∠ DBC =45°;④∠ ACE=∠ DBC 此中结论正确的个数有()A. 4 B. 3 C. 2 D. 1第9题图第 10题图二.仔细填一填(此题有10 小题,每题 4 分,共 24 分)11.若1B1________三角形 . ABC的三个内角知足A C ,则这个三角形是2312.写出定理“直角三角形斜边上的中线是斜边一半”的抗命题:13.直角三角形的两条边长分别是4 和 9,则此三角形的面积为 ____________.14. 在ABC中, AB=13, AC=12, BC=5,则∠ C= ___________度15.如下图的一块地,∠ ADC = 90°, AD = 12m, CD = 9m, AB = 39m, BC = 36m,则这块地的面积为 ___________ m2.16.如图,在 Rt△ ABC中,∠ C=90°,∠ A=30 ° ,AB=8cm,按图中所示方法将△BCD沿 BD 折叠,使点 C 落在 AB 边的 C′点,那么 AD的长是cm.三.耐心做一做(此题有8 小题,此中 17 题 10 分,(1)题 4 分, (2) 题 6 分, 18、19、 20 题各 6 分, 21、22 题各 8 分, 23 题 10 分,24 题 12 分,共 66 分)17. 解不等式和不等式组B( 1)不等式x2( x1)121 1 xN2 x4M( 2)不等式组22并把解集表示在数轴上A C 3 x1x第18题图2218.如图,两个班的学生疏别在M、 N两处参加植树劳动,现要在道路AB、 AC的交错地区内设一个茶水供给点P,使 P 到两条道路的距离相等,且使PM=PN,请你经过尺规作图找出这一P 点,(不写作法,保存作图印迹) .19.假如一个长为 10m 的梯子 AB ,斜靠在墙上,梯子的顶端距地面的垂直距离AC 为 8m.如果梯子的顶端 A 下滑1m 到 A 1,请猜想梯子底端 B 滑动的距离能否也会是1m,若不是,请求出滑动的距离.AA1108B1C第 19题B 20.如图,在△ ABC 中,BD=DC ,∠ ADB= ∠ADC ,求证: AD ⊥BC.ADB第20题图C 21.某产品的商标如下图,O是线段 AC、DB的交点,且AC=BD,AB=DC,小林以为图中的两个三角形全等,他的思虑过程是:∵AC=DB,∠ AOB=∠DOC,AB=DC,∴ △ABO≌△ DCO.你以为小林的思虑过程对吗?假如正确,指出他用的是鉴别三角形全等的哪个方法;假如不正确,写出你的证明过程。
2014年春季学期八年级期中考试数学试卷及答案(实)

2014年春季学期八年级期中考试数学试卷(实)一、选择题(每小题3分,共30分) 01.函数y =21x +中,自变量x 的取值范围是( ). A .x ≥12-且x ≠1 B .x ≠1 C .x ≥12- D .x >12-且x ≠102.如图,平行四边形ABCD 的对角线交于点O ,且AB =5,△OCD 的周长为23,则平行四边形ABCD 的两条对角线的和是( ). A .18 B .28 C .36 D .46 03.对于函数y =-3x +1,下列结论正确的是( ). A .它的图象必经过点(-1,3) B .它的图象经过第一、二、三象限 C .当x >1时,y <0 D .y 的值随x 值的增大而增大 04.如图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在36≤x <38小组,而不在34≤x <36小组),根据图形提供的信息,下列说法中错误的是( ).A .该学校教职工总人数是50人B .年龄在40≤x <42小组的教职工人数占该学校全体教职工总人数的20%C .教职工年龄的中位数一定落在40≤x <42这一组D .教职工年龄的众数一定在38≤x <40这一组05.如果三角形的两边分别为3和5,那么连结这个三角形三边中点所得三角形的周长可能是( ).A .5.5B .5C .4.5D .406.如图,正方形ABCD 的边长为4,点E 在对角线BD 上,且∠BAE =22.5°,EF ⊥AB ,垂足为F ,则EF 的长为( ).A .1B .2C .4-22D .32-407.如图,直线y =kx +b 经过点A (-1,-2)和点B (-2,0),直线y =2x 过点A ,则不等式2x <kx+b <0的解集为( ). A .x <-2 B .-2<x <-1 C .-2<x <0 D .-1<x <008.已知a 、b 、c 是△ABC 的三边长,且满足a 3+ab 2+bc 2=b 3+a 2b +ac 2,则△ABC 的形状是( ).A .等腰三角形B .直角三角形C .等腰三角形或直角三角形D .等腰直角三角形09.如图,剪两张对边平行的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,有下列结论:①∠ABC =∠ADC ,∠BAD =∠BCD ;②AB =BC ;③AB =CD ,AD =BC ;④∠DAB +∠BCD =180°,其中一定成立的结论个数为( ). A .1 B .2 C .3 D .410.小文、小亮从学校出发到青少年宫参加书法比赛,小文步行一段时间后,小亮骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小文出发时间t (分)之间的函数关系如图所示.下列说法:①小亮先到达青少年宫;②小亮的速度是小文速度的2.5倍;③a =24;④b =480.其中正确的是( ).A .①②③B .①②④C .①③④D .①②③④二、填空题(每小题3分,共24分)11.已知m =20121-,则m 5-2m 4-2011m 3的值________.12.如图,圆柱形容器中,高为1.2m ,底面周长为1m ,在容器内壁离容器底部0.3m 的点B 处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m 与蚊子相对的点A 处,则壁虎捕捉蚊子的最短距离为__________m (容器厚度忽略不计).13.小明和小华做投掷飞镖游戏各5次,两人成绩(单位:环)如图所示,根据图中的信息可以确定成绩更稳定的是___________.(填“小明”或“小华”)14.如图,□ABCD 中,∠ABC =60°,E 、F 分别在CD 和BC 的延长线上,AE ∥BD ,EF ⊥BC ,EF =3,则AB 的长是__________. 15.若直角三角形的两边长为a 、b ,且满足 269a a -++|b −4|=0,则该直角三角形的斜边长为___________.16.已知直线y =(1)2n n -++x +12n +(n 为正整数)与坐标轴围成的三角形的面积为S n ,则S 1+S 2+S 3+…+S 2012=___________.17.如图,线段AC =n +1(其中n 为正整数),点B 在线段AC 上,在线段AC 同侧作正方形ABMN 及正方形BCEF ,连接AM 、ME 、EA 得到△AME .当AB =1时,△AME 的面积记为S 1;当AB =2时,△AME 的面积记为S 2;当AB =3时,△AME 的面积记为S 3;…;当AB =n 时,△AME 的面积记为S n .当n ≥2时,S n -S n -1=____________.18.如图,五边形ABCDE 中,AB ⊥BC ,AE ∥CD ,∠A =∠E =120°,AB =CD=1,AE =2,则五边形ABCDE 的面积等于_______.三、解答题(共8小题,共66分) 19.计算(每小题4分,共8分)(01)18-92-363++(3-2)0+2(12)-. (02)12×(3-1)2+21-+3-(2)-1.第17题图 第10题图第02题图第04题图第06题图 第14题图第18题图 第13题图 第12题图 第07题图 第09题图20.(8分)已知,关于x 的一次函数y =(1-3a )x +2a -4的图象不经过第三象限.(1)当-2≤x ≤5时,____________≤____________(用含a 的代数式表示); (2)确定a 的取值范围.21.(8分)在矩形ABCD 中,将点A 翻折到对角线BD 上的点M 处,折痕BE 交AD 于点E .将点C 翻折到对角线BD 上的点N 处,折痕DF 交BC 于点F . (1)求证:四边形BFDE 为平行四边形;(2)若四边形BFDE 为菱形,且AB =2,求BC 的长.22.(8分)(1)点(0,1)向下平移2个单位后的坐标是_____________,直线y =2x +1向下平移2个单位后的解析式是_____________;(2)直线y =2x +1向右平移2个单位后的解析式是_____________;(3)如图,已知点C 为直线y =x 上在第一象限内一点,直线y =2x +1交y轴于点A ,交x 轴于B ,将直线AB 沿射线OC 方向平移32个单位,求平移后的直线的解析式.23.(8分)某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6序号项目 1 2 3 4 5 6 笔试成绩/分 85 92 84 90 84 80 面试成绩/分908886908085(综合成绩的满分仍为100分)(1)这6名选手笔试成绩的中位数是________分,众数是________分;(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩个占的百分比; (3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.24.(6分)(1)如图,在直线l 的同侧有A 、B 两点,在直线l 上找点P ,P '使P A +PB 最小,P B P A ''-最大;(保留作图痕迹)(2)平面直角坐标系内有两点A (2,3),B (4,5),请分别在x 轴,y 轴上找两点P ,P ',使AP +BP 最小,BP AP ''-最大,则P ,P '的坐标分别为__________,__________;(3)代数式2841x x -++2413x x -+的最小值为_______,此时x =_______;代数式2841x x -+-2413x x -+的最大值为_______,此时x =_______;25.(10分)某社区活动中心为鼓励居民加强体育锻炼,准备购买10副某种品牌的羽毛球拍,每副球拍配x (x ≥2)个羽毛球,供社区居民免费借用.该社区附近A 、B 两家超市都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均为30元,每个羽毛球的标价为3元,目前两家超市同时在做促销活动:A 超市:所有商品均打九折(按标价的90%)销售;B 超市:买一副羽毛球拍送2个羽毛球.设在A 超市购买羽毛球拍和羽毛球的费用为y A (元),在B 超市购买羽毛球拍和羽毛球的费用为y B (元).请解答下列问题:(1)分别写出y A 、y B 与x 之间的关系式;(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?(3)若每副球拍配15个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.26.(10分)在平行四边形ABCD 中,∠BAD 的平分线交直线BC 于点E ,交直线DC 的延长线于点F ,以EC 、CF 为邻边作平行四边形ECFG . (1)如图1,证明平行四边形ECFG 为菱形;(2)如图2,若∠ABC =90°,M 是EF 的中点,求∠BDM 的度数; (3)如图3,若∠ABC =120°,请直接写出∠BDG 的度数.第22题图第21题图 第26题图 A第24题图B2014年春季学期八年级期中考试数学参考答案(实)一、选择题(每小题3分,共30分)01~10 ACC DAC BCC B二、填空题(每小题3分,共24分) 11.0 12.1.313.小明14.115.5或4 16.503201417.212n -18.1334三、解答题(共8小题,共66分) 19.计算(每小题4分,共8分)(01)322-1(02) 320.(8分)(1)∵当x =-2时,y =-2(1-3a )+2a -4=8a -6; ∴当x =5时,y =5(1-3a )+2a -4=-13a +1;∵关于x 的一次函数y =(1-3a )x +2a -4的图象不经过第三象限, ∴y 的值随x 的值增大而减小, ∴当-2≤x ≤5时,-13a +1≤y ≤8a -6;(2)关于x 的一次函数y =(1-3a )x +2a -4的图象不经过第三象限,即一次函数y =(1-3a )x +2a -4的图象经过一、二、四象限或二、四象限,∴130240<a a -⎧⎨-≥⎩, ∴a ≥2.21.(8分)(1)证明:∵四边形ABCD 是矩形, ∴∠A =∠C =90°,AB =CD ,AB ∥CD , ∴∠ABD =∠CDB ,∵在矩形ABCD 中,将点A 翻折到对角线BD 上的点M 处,折痕BE 交AD 于点E .将点C 翻折到对角线BD 上的点N 处,∴∠ABE =∠EBD =12∠ABD ,∠CDF =12∠CDB ,∴∠ABE =∠CDF , 在△ABE 和△CDF 中∠A =∠C , AB =CD ,∠ABE =∠CDF ,∴△ABE ≌△CDF (ASA ), ∴AE =CF ,∵四边形ABCD 是矩形, ∴AD =BC ,AD ∥BC , ∴DE =BF ,DE ∥BF ,∴四边形BFDE 为平行四边形; (2)解:∵四边形BFDE 为为菱形, ∴BE =ED ,∠EBD =∠FBD =∠ABE , ∵四边形ABCD 是矩形, ∴AD =BC ,∠ABC =90°, ∴∠ABE =30°, ∵∠A =90°,AB =2, ∴AE =3=23,BE =2AE =43, ∴BC =AD =AE +ED =AE +BE =23+43=23.22.(8分)(1)(0,-1),y =2x +1-2=2x -1; (2)y =2(x -2)+1=2x -3;(3)∵点C 为直线y =x 上在第一象限内一点,则直线上所有点的坐标横纵坐标相等,∴将直线AB 沿射线OC 方向平移32个单位,其实是先向右平移2个单位长度,再向上平移2个单位度. ∴y =2(x -2)+1+2,即y =2x -1.23.(8分)(1)把这组数据从小到大排列为,80,84,84,85,90,92, 最中间两个数的平均数是(84+85)÷2=84.5(分), 则这6名选手笔试成绩的中位数是84.5, 84出现了2次,出现的次数最多, 则这6名选手笔试成绩的众数是84; 故答案为:84.5,84;(2)设笔试成绩和面试成绩各占的百分比是x ,y ,根据题意得:1859088==x y x y +⎧⎨+⎩,解得:0.40.6==x y ⎧⎨⎩, 笔试成绩和面试成绩各占的百分比是40%,60%; (3)2号选手的综合成绩是92×0.4+88×0.6=89.6(分),第22题图第21题图A第24题图B3号选手的综合成绩是84×0.4+86×0.6=85.2(分),4号选手的综合成绩是90×0.4+90×0.6=90(分),5号选手的综合成绩是84×0.4+80×0.6=81.6(分),6号选手的综合成绩是80×0.4+85×0.6=83(分),则综合成绩排序前两名人选是4号和2号.24.(6分)(1)如图;(2)(114,0),(0,1)(3)217,x=114,22,x=-1.25.(10分)(1)由题意,得y A=(10×30+3×10x)×0.9=27x+270;y B=10×30+3(10x-20)=30x+240;(2)当y A=y B时,27x+270=30x+240,得x=10;当y A>y B时,27x+270>30x+240,得x<10;当y A<y B时,27x+270<30x+240,得x>10∴当2≤x<10时,到B超市购买划算,当x=10时,两家超市一样划算,当x>10时在A超市购买划算.(3)由题意知x=15,15>10,∴选择A超市,y A=27×15+270=675(元),先选择B超市购买10副羽毛球拍,送20个羽毛球,然后在A超市购买剩下的羽毛球:(10×15-20)×3×0.9=351(元),共需要费用10×30+351=651(元).∵651<675,∴最佳方案是先选择B超市购买10副羽毛球拍,然后在A超市购买130个羽毛球.26.(10分)(1)证明:∵AF平分∠BAD,∴∠BAF=∠DAF,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAF=∠CEF,∠BAF=∠CFE,∴∠CEF=∠CFE,∴CE=CF,又∵四边形ECFG是平行四边形,∴四边形ECFG为菱形.(2)如图,连接BM,MC,∵∠ABC=90°,四边形ABCD是平行四边形,∴四边形ABCD是矩形,又由(1)可知四边形ECFG为菱形,∠ECF=90°,∴四边形ECFG为正方形.∵∠BAF=∠DAF,∴BE=AB=DC,∵M为EF中点,∴∠CEM=∠ECM=45°,∴∠BEM=∠DCM=135°,在△BME和△DMC中,∵BE=CD,∠BEM=∠DCM,EM=CM,∴△BME≌△DMC(SAS),∴MB=MD,∠DMC=∠BME.∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,∴△BMD是等腰直角三角形,∴∠BDM=45°;(3)∠BDG=60°,延长AB、FG交于H,连接HD.∵AD∥GF,AB∥DF,∴四边形AHFD为平行四边形,∵∠ABC=120°,AF平分∠BAD,∴∠DAF=30°,∠ADC=120°,∠DF A=30°,∴△DAF为等腰三角形,∴AD=DF,∴平行四边形AHFD为菱形,∴△ADH,△DHF为全等的等边三角形,∴DH=DF,∠BHD=∠GFD=60°,∵FG=CE,CE=CF,CF=BH,∴BH=GF,在△BHD与△GFD中,∵DH=DF,∠BHD=∠GFD,BH=GF,∴△BHD≌△GFD(SAS),∴∠BDH=∠GDF∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°.第26题图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年春学期八年级数学期中试卷
一、选择题(每小题3分,共30分)
A B C D
2.已知x y >,则下列不等式不成立的是 ( ) A.66x y ->- B.33x y > C.22x y -<- D.3636x y -+>-+
3.下列四个从左到右的变形中,是因式分解的是 ( )
A.()()9332-=-+a a a
B.()5152-+=-+x x x x
C.⎪⎭
⎫ ⎝
⎛+=+x x
x x 112 D.()2
2244+=++x x x
4.在平面直角坐标系中将点A (﹣2,3)向右平移3个单位长度后那么平移后对应的点A ′的坐标
是 ( ) A .(﹣2,﹣3) B .(﹣2,6) C . (1,3) D .(﹣2,1) 5.不等式组
的解集在数轴上表示正确的是 ( )
A .
B .
C .
D .
6.下列多项式能分解因式的是 ( ) A .x 2+y 2 B .-x 2-y 2 C .-x 2+2xy-y 2 D .x 2-xy+y 2
7.直角三角形的两条直角边分别是6和8,则斜边上的高是 ( )
A .4.8
B .5
C .3
D .10 8. 在△ABC 中,AB=AC ,AB 的垂直平分线与AC 所在直线相交所得的锐角为50°,则∠B 的度数为
( )
A .20°
B .70°
C .70°或20°
D .无法确定
9.如图28-8所示,在方格纸上建立的平面直角坐标系中,将△ABC 绕点O 按顺时针方向旋转90度,得到△A /B /O ,则点A /
的坐标为( )
A .(3 , 1)
B .(3 , 2)
C .(2 , 3)
D .(1 , 3)
10. 某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有( ) A .29人 B .30人 C .31人 D . 32人 二、填空题:(每小题3分,共24分) 11.分解因式:x 2﹣9= .
12.不等式2x+9≥3(x+2)的正整数解是 .
13.如果等腰三角形的一个角是80°,那么顶角是 度. 14.等腰三角形的周长为16,其一边长为6,则另两边为 . 15.如果x 2+kxy+9y 2是一个完全平方式,那么k 的值是
16.已知32,5221+-=-=x y x y ,如果21y y <,则x 的取值范围是 ;
17.点A 的坐标为(2,0),把点A 绕着坐标原点顺时针旋转135º到点B ,那么点B 的坐标是 _________.
18.若关于x 的不等式组
有实数解,则a 的取值范围是 .
三、解答题(共计66分)
19.(5分)两个城镇A 、B 与两条公路l 1、l 2位置如图所示,电信部门需在C 处修建一座信号反射塔,要求发射塔到两个城镇A 、B 的距离必须相等,到两条公路l 1,l 2的距离也必须相等,那么点C 应选在何处?请在图中,用尺规作图找出所有符合条件的点C .(不写已知、求作、作法,只保留作图痕迹)
20.解下列不等式(组),并把它们的解集在数轴上表示出来(每小题4分,共12分).
(1)112x x -+≥ (2)⎩⎨⎧-<-<-2235x x (3)⎪⎩⎪
⎨⎧+<-≤+--)
1(315121
5312x x x x
21.分解因式(每小题4分,共16分)
(1)()()x y y y x x --- (2)3222y xy y x +-
(3) 4
416n m (4)(x+1)(x+3)+1
22.(6分)如图,在平面直角坐标系中, Rt △ABC 的三个顶点分别是A (-3,2),B (0,4),C
(0,2).
(1)将△ABC 以点C 为旋转中心旋转180°,画出旋转后对应的△11B A C ;平移△ABC ,若A 的对应点2A 的坐标为(0,4),画出平移后对应的△222C B A ;
(2)若将△11B A C 绕某一点旋转可以得到△222C B A ,请直接写出旋转中心的坐标;
23.(5分)已知:如图,在△ABC 中,AD 是它的角平分线,且BD=CD,DE ⊥AB,DF ⊥AC,垂足分别是E,F.求证:EB=FC. 24.(5分)学校为家远的学生安排住宿,现有房间若干间,若每间住5人,还剰14人安排不下,若每间住7人,则有一间还余一些床位,问学校可能有多少房间安排学生住宿?住宿的学生可能有多少人?
25.(8分). 如图,在△ABC 中,已知AC=BC,∠C=900,AD 是△ABC 的角平分线,DE ⊥AB,垂足为E. (1)如果CD=5cm,AC 的长; (2)求证:AB=AC+CD
26.(9分)为了抓住金张掖旅游文化艺术节的商机,某商店决定购进A 、B 两种艺术节纪念品.若购进A 种纪念品8件,B 种纪念品3件,需要950元;若购进A 种纪念品5件,B 种纪念品6件,需要800元.
(1)求购进A 、B 两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A 种纪念品可获利润20元,每件B 种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?。
