2010年长春市中考数学试题及答案
2024年长春市中考数学试卷

选择题在平面直角坐标系中,点A(3, -2)关于x轴对称的点的坐标是:A. (-3, 2)B. (-3, -2)C. (3, 2)(正确答案)D. (2, 3)已知等腰三角形的两边长分别为3和5,则这个等腰三角形的周长为:A. 8B. 11C. 13(正确答案)D. 11或13函数y = 2x + 1与y = 2x - 3的图象:A. 平行且关于x轴对称B. 平行且关于y轴对称C. 相交且交点在y轴上D. 平行且关于直线y = x对称(正确答案)若关于x的一元二次方程x2 - 4x + m = 0有两个相等的实数根,则m的值为:A. -4B. 4(正确答案)C. 2D. -2下列计算正确的是:A. 3a + 2b = 5abB. a2 · a3 = a6C. (a2)3 = a6(正确答案)D. a6 ÷ a3 = a1已知圆的半径为r,圆心到直线l的距离为d,若直线l与圆相切,则:A. d > rB. d < rC. d = r(正确答案)D. d与r的大小关系不确定在比例尺为1:1000的地图上,测得某矩形区域的图上面积为2cm2,则该矩形区域的实际面积为:A. 2m2B. 20m2C. 200m2(正确答案)D. 2000m2下列不等式组中,解集为x > 2的是:A. {x | x > 1, x > 3}B. {x | x > 1, x ≤ 2}C. {x | x ≥ 2, x < 3}D. {x | x > 1, x > 2}(正确答案)若a、b、c为三角形的三边长,且满足(a - 5)2 + |b - 12| + c2 - 26c + 169 = 0,则此三角形的形状为:A. 等腰三角形B. 等边三角形C. 直角三角形(正确答案)D. 等腰直角三角形。
2010年长春市中考数学试题及标准答案
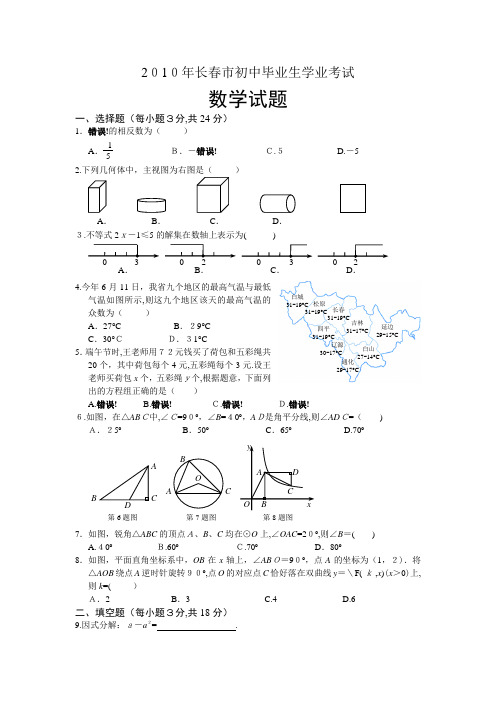
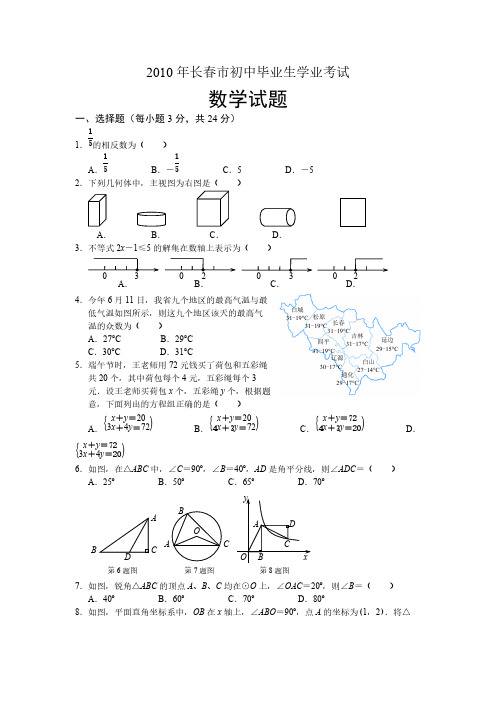
2010年长春市初中毕业生学业考试数学试题一、选择题(每小题3分,共24分)1.错误!的相反数为( ) A .15B.-错误! C.5 D.-5 2.下列几何体中,主视图为右图是( )3.不等式2x-1≤5的解集在数轴上表示为( )4.今年6月11日,我省九个地区的最高气温与最低气温如图所示,则这九个地区该天的最高气温的众数为( ) A .27°C B .29°C C .30°C D.31°C5.端午节时,王老师用72元钱买了荷包和五彩绳共20个,其中荷包每个4元,五彩绳每个3元.设王老师买荷包x 个,五彩绳y个,根据题意,下面列出的方程组正确的是( )A.错误!B.错误! C.错误! D.错误! 6.如图,在△AB C中,∠C=90º,∠B =40º,A D是角平分线,则∠AD C=( ) A.25º B .50º C .65º D.70º7.如图,锐角△ABC 的顶点A、B 、C 均在⊙O 上,∠OAC =20º,则∠B =( ) A.40º B.60º C.70º D .80º 8.如图,平面直角坐标系中,OB 在x 轴上,∠AB O=90º,点A 的坐标为(1,2).将△AOB 绕点A 逆时针旋转90º,点O 的对应点C 恰好落在双曲线y =\F( k ,x )(x >0)上,则k =( )A.2 B .3 C.4 D.6二、填空题(每小题3分,共18分)9.因式分解:a-a 2= .OBAD Cyx第8题图BACD第6题图A .B .C .D . A . B . C . D .0 0 0 3 3 2 2 BACO第7题图白城31-19°C松原 31-19°C 长春 31-19°C吉林31-17°C 延边 29-15°C 白山27-14°C四平 31-19°C 通化29-17°C 辽源30-17°C10.写一个比错误!小的正整数,这个整数是 (写出一个即可).11.为了帮助玉树地区重建家园,某班全体师生积极捐款,捐款金额共3200元,其中5名教师人均捐款a 元,则该班学生共捐款 元(用含有a的代数式表示).12.如图,双曲线y1=错误!(k1>0)与直线y 2=k 2x +b (k 2>0)的一个交点的横坐标为2,那么当x =3时,y 1 y 2(填“>”、“=”或“<”).13.如图,⊙P 与x轴切于点O,点P 的坐标为(0,1),点A 在⊙P上,并且在第一象限,∠APO =120º.⊙P 沿x 轴正方向滚动,当点A 第一次落在x轴上时,点A 的横坐标 为 (结果保留 ).14.如图,抛物线y =ax 2+c (a <0)交x 轴于点G 、F ,交y 轴于点D ,在x 轴上方的抛物线上有两点B 、E,它们关于y 轴对称,点G 、B在y轴左侧.BA ⊥OG 于点A,BC ⊥O D于点C .四边形O AB C与四边形OD EF 的面积分别为6和10,则△A BG 与△BCD 的面积之和为 .三、解答题(每小题5分,共20分)15.先化简,再求值:(x +1)2-2x +1,其中x =2.16.一个不透明的口袋中装有红、黄、白小球各1个,小球除颜色外其余均相同.从口袋中随机摸出一个小球,记下颜色放回,再随机摸出一个小球.请你用画树形图(或列表)的方法,求出两次摸出的小球颜色相同的概率.17.第16届亚运会将在广州举行.小李预定了两种价格的亚运会门票,其中甲种门票共花费280元,乙种门票共花费300元,甲种门票比乙种门票多2张,乙种门票价格是甲种门票价格的1.5倍,求甲种门票的价格.第14题图。
长春市中考数学试题含答案解析(word版)

一、选择题:本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 3的相反数是()A.﹣3 B.﹣13C.13D.3【答案】A【解析】试题分析: 3的相反数是﹣3故选A.考点:相反数.2.据统计,2016年长春市接待旅游人数约人次,这个数用科学记数法表示为()A.67×106B.×105C.×107D.×108【答案】C考点:科学记数法.3.下列图形中,可以是正方体表面展开图的是()A.B.C.D.【答案】D【解析】试题分析:下列图形中,可以是正方体表面展开图的是,故选D考点:几何体的展开图.4.不等式组10251xx-≤⎧⎨-<⎩的解集为()A.x<﹣2 B.x≤﹣1 C.x≤1 D.x<3【答案】C【解析】试题分析:10 251 xx-≤⎧⎨-<⎩①②解不等式①得:x≤1,解不等式②得:x<3,∴不等式组的解集为x≤1,故选C.考点:解一元一次不等式组.5.如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC.若∠A=62°,∠AED=54°,则∠B的大小为()A.54° B.62° C.64° D.74°【答案】C考点:1.平行线的性质;2.三角形的内角和.6.如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为()A.3a+2b B.3a+4b C.6a+2b D.6a+4b【答案】A【解析】试题分析:依题意有3a﹣2b+2b×2=3a﹣2b+4b=3a+2b.故这块矩形较长的边长为3a+2b.故选A.考点:列代数式.7.如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为()A.29° B.32° C.42° D.58°【答案】B考点:1.切线的性质;2.等腰三角形的性质;3.三角形的外角的性质;4.三角形的内角和定理.8.如图,在平面直角坐标系中,平行四边形OABC的顶点A的坐标为(﹣4,0),顶点B在第二象限,∠BAO=60°,BC交y轴于点D,DB:DC=3:1.若函数y=kx(k>0,x>0)的图象经过点C,则k的值为()A.33B.32C.233D.3【答案】D【解析】试题分析:∵四边形ABCD是平行四边形,点A的坐标为(﹣4,0),∴BC=4,∵DB:DC=3:1,∴B(﹣3,OD),C(1,OD),∵∠BAO=60°,∴∠COD=30°,∴OD=3,∴C(1,3),∴k=3,故选D.考点:1.平行四边形的性质;2.反比例函数图象上点的坐标特征.二、填空题(每题3分,满分18分,将答案填在答题纸上)9.计算:2×3= .【答案】6【解析】试题分析:2×3=6;考点:二次根式的乘法.10.若关于x的一元二次方程x2+4x+a=0有两个相等的实数根,则a的值是.【答案】4考点:根的判别式.11.如图,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB:BC=1:2,DE=3,则EF的长为.【答案】6【解析】试题分析:∵a∥b∥c,∴AB DEBC EF=,∴132EF=,∴EF=6.考点:平行线分线段成比例定理.12.如图,则△ABC中,∠BAC=100°,AB=AC=4,以点B为圆心,BA长为半径作圆弧,交BC于点D,则的长为.(结果保留π)【答案】8 9π考点:1.弧长公式;2.等腰三角形的性质;3.三角形内角和定理.13.如图①,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图②,其中四边形ABCD和四边形EFGH都是正方形,△ABF、△BCG、△CDH、△DAE是四个全等的直角三角形.若EF=2,DE=8,则AB的长为.【答案】10【解析】试题分析:依题意知,BG=AF=DE=8,EF=FG=2∴BF=BG ﹣BF=6,∴直角△ABF 中,利用勾股定理得:AB=22AF BF =10.考点:勾股定理的证明.14.如图,在平面直角坐标系中,△ABC 的顶点A 在第一象限,点B ,C 的坐标为(2,1),(6,1),∠BAC=90°,AB=AC ,直线AB 交x 轴于点P .若△ABC 与△A'B'C'关于点P 成中心对称,则点A'的坐标为 .【答案】(-1,-2)考点:等腰直角三角形.三、解答题(本大题共10小题,共78分.解答应写出文字说明、证明过程或演算步骤.)15.先化简,再求值:3a(a2+2a+1)﹣2(a+1)2,其中a=2.【答案】3a3+4a2﹣a﹣2,36.【解析】试题分析:原式利用单项式乘以多项式,以及完全平方公式化简,去括号合并得到最简结果,把a的值代入计算即可求出值.试题解析:原式=3a3+6a2+3a﹣2a2﹣4a﹣2=3a3+4a2﹣a﹣2,当a=2时,原式=24+16﹣2﹣2═36.考点:整式的混合运算﹣化简求值.16.一个不透明的口袋中有一个小球,上面分别标有字母a,b,c,每个小球除字母不同外其余均相同,小园同学从口袋中随机摸出一个小球,记下字母后放回且搅匀,再从可口袋中随机摸出一个小球记下字母.用画树状图(或列表)的方法,求小园同学两次摸出的小球上的字母相同的概率.【答案】1 3考点:列表法与树状图法.17.如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,求大厅两层之间的距离BC 的长.(结果精确到米)(参考数据:sin31°=,cos31°=,tan31°=)【答案】大厅两层之间的距离BC的长约为米.考点:解直角三角形的应用﹣坡度坡角问题.18.某校为了丰富学生的课外体育活动,购买了排球和跳绳.已知排球的单价是跳绳的单价的3倍,购买跳绳共花费750元,购买排球共花费900元,购买跳绳的数量比购买排球的数量多30个,求跳绳的单价.【答案】跳绳的单价是15元.【解析】试题分析:首先设跳绳的单价为x元,则排球的单价为3x元,根据题意可得等量关系:750元购进的跳绳个数﹣900元购进的排球个数=30,依此列出方程,再解方程可得答案.试题解析:设跳绳的单价为x元,则排球的单价为3x元,依题意得:7509003x x=30,解方程,得x=15.经检验:x=15是原方程的根,且符合题意.答:跳绳的单价是15元.考点:分式方程的应用.19.如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.【答案】86°考点:1.菱形的性质;2.旋转的性质;3.三角形的性质和判定.20.某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A,B,C,D,E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:(1)求n的值;(2)根据统计结果,估计该年级600名学生中睡眠时长不足7小时的人数.【答案】(1)n=60;(2)估计该年级600名学生中睡眠时长不足7小时的人数为90人.【解析】考点:条形统计图的综合运用.21.甲、乙两车间同时开始加工一批服装.从幵始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.(1)甲车间每小时加工服装件数为件;这批服装的总件数为件.(2)求乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;(3)求甲、乙两车间共同加工完1000件服装时甲车间所用的时间.【答案】(1)80;1140;(2)乙车间加工服装数量y与x之间的函数关系式为y=60x﹣120(4≤x≤9);(3)甲、乙两车间共同加工完1000件服装时甲车间所用的时间为8小时.【解析】试题分析:(1)根据工作效率=工作总量÷工作时间,即可求出甲车间每小时加工服装件数,再根据这批服装的总件数=甲车间加工的件数+乙车间加工的件数,即可求出这批服装的总件数;(2)根据工作效率=工作总量÷工作时间,即可求出乙车间每小时加工服装件数,根据工作时间=工作总量÷工作效率结合工作结束时间,即可求出乙车间修好设备时间,再根据加工的服装总件数=120+工作效率×工作时间,即可求出乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;(3)根据加工的服装总件数=工作效率×工作时间,求出甲车间加工服装数量y与x之间的函数关系式,将甲、乙两关系式相加令其等于1000,求出x值,此题得解.试题解析:(1)甲车间每小时加工服装件数为720÷9=80(件),这批服装的总件数为720+420=1140(件).故答案为:80;1140.(2)乙车间每小时加工服装件数为120÷2=60(件),乙车间修好设备的时间为9﹣(420﹣120)÷60=4(时).∴乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式为y=120+60(x﹣4)=60x﹣120(4≤x≤9).(3)甲车间加工服装数量y与x之间的函数关系式为y=80x,当80x+60x﹣120=1000时,x=8.答:甲、乙两车间共同加工完1000件服装时甲车间所用的时间为8小时.考点:1.一次函数的应用;2.解一元一次方程.22.【再现】如图①,在△ABC中,点D,E分别是AB,AC的中点,可以得到:DE∥BC,且DE=12 BC.(不需要证明)【探究】如图②,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,判断四边形EFGH 的形状,并加以证明.【应用】在(1)【探究】的条件下,四边形ABCD中,满足什么条件时,四边形EFGH是菱形你添加的条件是:.(只添加一个条件)(2)如图③,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,对角线AC,BD相交于点O.若AO=OC,四边形ABCD面积为5,则阴影部分图形的面积和为.【答案】【探究】平行四边形.理由见解析;【应用】(1)添加AC=BD,理由见解析;(2)54.(2)先判断出S△BCD=4S△CFG,同理:S△ABD=4S△AEH,进而得出S四边形EFGH=52,再判断出OM=ON,进而得出S阴影=12S四边形EFGH即可.试题解析:【探究】平行四边形.理由:如图1,连接AC,∵E是AB的中点,F是BC的中点,∴EF∥AC,EF=12 AC,同理HG∥AC,HG=12 AC,综上可得:EF∥HG,EF=HG,故四边形EFGH是平行四边形.【应用】(1)添加AC=BD,理由:连接AC,BD,同(1)知,EF=12 AC,同【探究】的方法得,FG=12 BD,∵AC=BD,∴EF=FG,∵四边形EFGH是平行四边形,∴▱EFGH是菱形;故答案为AC=BD;考点:1.三角形的中位线定理;2.平行四边形的判定;3.菱形的判定;4.相似三角形的判定和性质.23.如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒43个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.(1)求线段AQ的长;(用含t的代数式表示)(2)连结PQ,当PQ与△ABC的一边平行时,求t的值;(3)如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF,点D为AC的中点,连结DF.设矩形PEQF与△ABC重叠部分图形的面积为S.①当点Q在线段CD上运动时,求S与t之间的函数关系式;②直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.【答案】(1)AQ=8﹣43t(0≤t≤4);(2)t=32s或3s时, PQ与△ABC的一边平行;(3)①当0≤t≤32时,S=﹣16t2+24t.当32<t≤2时,S=﹣163t2+40t-48.当2<t≤3时,S=﹣203t2+30t﹣24.②当t=914s或3631s时,DF将矩形PEQF分成两部分的面积比为1:2.【解析】(3)①如图1中,a、当0≤t≤32时,重叠部分是四边形PEQF.S=PE•EQ=3t•(8﹣4t﹣43t)=﹣16t2+24t.b、如图2中,当32<t≤2时,重叠部分是四边形PNQE.S=S四边形PEQF﹣S△PFN=(16t2﹣24t)﹣12•45[5t﹣54(8﹣43t)]•35[5t﹣54(8﹣43t0]=﹣163t2+40t-48.C、如图3中,当2<t≤3时,重叠部分是五边形MNPBQ.S=S四边形PBQF S△FNM=43t•[6﹣3(t﹣2)]﹣12•[43t﹣4(t﹣2)]•34[43t﹣4(t﹣2)]=﹣203t2+30t﹣24.∴DE:DQ=NE:FQ=1:3,∴(3t﹣3):(3﹣43t)=1:3,解得t=36 31s,综上所述,当t=914s或3631s时,DF将矩形PEQF分成两部分的面积比为1:2.考点:1.矩形的性质;2.勾股定理;3.相似三角形的性质和判定;4.平行线分线段成比例定理.24.定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它们的相关函数为y=()()1010x xx x-+<⎧⎪⎨-≥⎪⎩.(1)已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;(2)已知二次函数y=﹣x2+4x﹣12.①当点B(m,32)在这个函数的相关函数的图象上时,求m的值;②当﹣3≤x≤3时,求函数y=﹣x2+4x﹣12的相关函数的最大值和最小值;(3)在平面直角坐标系中,点M,N的坐标分别为(﹣12,1),(92,1}),连结MN.直接写出线段MN与二次函数y=﹣x2+4x+n的相关函数的图象有两个公共点时n的取值范围.【答案】(1)a=1;(2)①m=2﹣5或m=2+2或m=2﹣2.②当﹣3≤x≤3时,函数y=﹣x2+4x﹣12的相关函数的最大值为432,最小值为﹣12;(3)n的取值范围是﹣3<n≤﹣1或1<n≤54.(2)二次函数y=﹣x2+4x﹣12的相关函数为y=()()2214021402x x xx x x⎧-+<⎪⎪⎨⎪-+-≥⎪⎩①当m<0时,将B(m,32)代入y=x2﹣4x+12得m2﹣4m+12=32,解得:5或m=25当m≥0时,将B(m,32)代入y=﹣x2+4x﹣12得:﹣m2+4m﹣12=32,解得:2或m=22.综上所述:m=252或m=22.②当﹣3≤x<0时,y=x2﹣4x+12,抛物线的对称轴为x=2,此时y随x的增大而减小,∴此时y的最大值为432.当0≤x≤3时,函数y=﹣x2+4x﹣12,抛物线的对称轴为x=2,当x=0有最小值,最小值为﹣12,当x=2时,有最大值,最大值y=72.综上所述,当﹣3≤x≤3时,函数y=﹣x2+4x﹣12的相关函数的最大值为432,最小值为﹣12;(3)如图1所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有1个公共点.所以当x=2时,y=1,即﹣4+8+n=1,解得n=﹣3.如图2所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有3个公共点考点:二次函数的综合应用.。
吉林省长春市初中中考数学真题试卷试题含解析.docx

吉林省长春市 2017 年中考数学真题试题一、选择题:本大题共8 个小题,每小题 3 分,共 24 分 . 在每小题给出的四个选项中,只有一项是符合题目要求的 .1. 3 的相反数是()A.﹣ 3B.﹣1C.3【答案】 A【解析】试题分析: 3 的相反数是﹣ 313D . 3故选 A.考点:相反数.2.据统计, 2016 年长春市接待旅游人数约67000000 人次, 67000000 这个数用科学记数法表示为()A. 67×106B.6.7 × 105C. 6.7 ×107D.6.7 × 108【答案】 C考点:科学记数法.3.下列图形中,可以是正方体表面展开图的是()A.B.C.D.【答案】 D【解析】试题分析:下列图形中,可以是正方体表面展开图的是,故选 D考点:几何体的展开图.x 1 0 )4.不等式组5的解集为(2x 1A . x <﹣ 2B .x ≤﹣ 1C . x ≤ 1D . x < 3【答案】 C【解析】x 1 0①试题分析:2x 5 1②解不等式①得: x ≤ 1,解不等式②得: x < 3,∴不等式组的解集为x ≤ 1,故选 C .考点:解一元一次不等式组.5.如图, 在△ ABC 中,点 D 在 AB 上,点 E 在 AC 上,DE ∥ BC .若∠ A=62°, ∠AED=54°, 则∠ B 的大小为()A .54°B .62°C .64°D .74°【答案】 C考点: 1. 平行线的性质; 2. 三角形的内角和.6.如图,将边长为 3a 的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长 2b 的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为()A . 3a+2bB .3a+4bC . 6a+2bD .6a+4b【答案】 A【解析】试题分析:依题意有3a﹣2b+2b× 2=3a﹣ 2b+4b=3a+2b.故这块矩形较长的边长为3a+2b.故选 A.考点:列代数式.7.如图,点 A,B,C在⊙ O上,∠ABC=29°,过点 C 作⊙ O的切线交OA的延长线于点D,则∠ D 的大小为()A.29° B .32° C .42° D .58°【答案】 B考点: 1. 切线的性质; 2. 等腰三角形的性质; 3. 三角形的外角的性质; 4. 三角形的内角和定理.8.如图,在平面直角坐标系中,平行四边形OABC的顶点 A 的坐标为(﹣ 4,0),顶点 B 在第二象限,∠BAO=60°,BC交 y 轴于点 D, DB: DC=3: 1.若函数y= k( k> 0,x> 0)的图象经过点C,则 k 的值为()xA.3B.3C .23D.3 323【答案】 D【解析】试题分析:∵四边形ABCD是平行四边形,点 A 的坐标为(﹣4,0),∴ BC=4,∵DB:DC=3: 1,∴ B(﹣ 3, OD), C( 1, OD),∵∠ BAO=60°,∴∠ COD=30°,∴OD= 3,∴ C(1, 3 ),∴k= 3 ,故选 D.考点: 1. 平行四边形的性质;2. 反比例函数图象上点的坐标特征.二、填空题(每题 3 分,满分18 分,将答案填在答题纸上)9.计算: 2 × 3 =.【答案】6【解析】试题分析: 2 × 3 = 6 ;考点:二次根式的乘法.10.若关于 x 的一元二次方程2有两个相等的实数根,则 a 的值是.x +4x+a=0【答案】 4考点:根的判别式.11.如图,直线a∥ b∥ c,直线l 1,l 2 与这三条平行线分别交于点 A, B, C 和点D, E, F.若AB:BC=1: 2,DE=3,则 EF 的长为.【答案】 6【解析】试题分析:∵ a∥b∥ c,∴ABDE,∴13,∴ EF=6. BC EF2EF考点:平行线分线段成比例定理.12.如图,则△ ABC中,∠ BAC=100°, AB=AC=4,以点 B 为圆心, BA长为半径作圆弧,交BC于点 D,则的长为.(结果保留π )【答案】8 9考点: 1. 弧长公式; 2. 等腰三角形的性质; 3. 三角形内角和定理.13.如图①,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图②,其中四边形ABCD和四边形EFGH都是正方形,△ABF、△ BCG、△ CDH、△ DAE是四个全等的直角三角形.若EF=2, DE=8,则 AB的长为.【答案】 10【解析】试题分析:依题意知,BG=AF=DE=8,EF=FG=2∴ BF=BG﹣ BF=6,∴直角△ ABF中,利用勾股定理得: AB= AF2BF 2=10.考点:勾股定理的证明.14.如图,在平面直角坐标系中,△ ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线 AB交 x 轴于点 P.若△ ABC与△ A'B'C'关于点P成中心对称,则点A' 的坐标为.【答案】( -1 , -2 )考点:等腰直角三角形.三、解答题(本大题共10 小题,共78 分 . 解答应写出文字说明、证明过程或演算步骤. )15.先化简,再求值:3a( a2+2a+1)﹣ 2( a+1 )2,其中 a=2.【答案】 3a3+4a2﹣ a﹣ 2, 36.【解析】试题分析:原式利用单项式乘以多项式,以及完全平方公式化简,去括号合并得到最简结果,把 a 的值代入计算即可求出值.试题解析:原式=3a3+6a2+3a﹣2a2﹣ 4a﹣ 2=3a3+4a2﹣ a﹣ 2,当 a=2 时,原式 =24+16﹣2﹣ 2═ 36.考点:整式的混合运算﹣化简求值.16.一个不透明的口袋中有一个小球,上面分别标有字母a,b,c,每个小球除字母不同外其余均相同,小园同学从口袋中随机摸出一个小球,记下字母后放回且搅匀,再从可口袋中随机摸出一个小球记下字母.用画树状图(或列表)的方法,求小园同学两次摸出的小球上的字母相同的概率.【答案】1 3考点:列表法与树状图法.17.如图,某商店营业大厅自动扶梯 AB的倾斜角为 31°,AB的长为 12 米,求大厅两层之间的距离 BC的长.(结果精确到 0.1 米)(参考数据: sin31 °=0.515 ,cos31°=0.857 ,tan31 °=0.60 )【答案】大厅两层之间的距离BC的长约为 6.18 米 .考点:解直角三角形的应用﹣坡度坡角问题.18.某校为了丰富学生的课外体育活动,购买了排球和跳绳.已知排球的单价是跳绳的单价的 3 倍,购买跳绳共花费750 元,购买排球共花费900 元,购买跳绳的数量比购买排球的数量多30 个,求跳绳的单价.【答案】跳绳的单价是 15 元.【解析】试题分析:首先设跳绳的单价为x 元,则排球的单价为3x 元,根据题意可得等量关系:750 元购进的跳绳个数﹣ 900 元购进的排球个数=30,依此列出方程,再解方程可得答案.试题解析:设跳绳的单价为x 元,则排球的单价为3x 元,依题意得:750900=30,x3x解方程,得x=15.经检验: x=15 是原方程的根,且符合题意.答:跳绳的单价是15 元.考点:分式方程的应用.19.如图,在菱形ABCD中,∠ A=110°,点E 是菱形 ABCD内一点,连结CE绕点 C 顺时针旋转110°,得到线段 CF,连结 BE, DF,若∠ E=86°,求∠F的度数.【答案】 86°考点: 1. 菱形的性质; 2. 旋转的性质; 3. 三角形的性质和判定.20.某校八年级学生会为了解本年级600 名学生的睡眠情况,将同学们某天的睡眠时长t (小时)分为 A,B,C, D, E( A: 9≤ t ≤ 24; B: 8≤ t < 9; C: 7≤ t <8; D: 6≤ t < 7; E:0≤ t < 6)五个选项,进行了一次问卷调查,随机抽取n 名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:( 1)求 n 的值;( 2)根据统计结果,估计该年级600 名学生中睡眠时长不足7 小时的人数.【答案】( 1) n=60;( 2)估计该年级600 名学生中睡眠时长不足7 小时的人数为90 人.【解析】考点:条形统计图的综合运用.21.甲、乙两车间同时开始加工一批服装.从幵始加工到加工完这批服装甲车间工作了9 小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时), y 与 x 之间的函数图象如图所示.( 1)甲车间每小时加工服装件数为件;这批服装的总件数为件.( 2)求乙车间维修设备后,乙车间加工服装数量y 与 x 之间的函数关系式;( 3)求甲、乙两车间共同加工完1000 件服装时甲车间所用的时间.【答案】( 1) 80; 1140;(2)乙车间加工服装数量y 与 x 之间的函数关系式为y=60x ﹣ 120( 4≤ x≤ 9);(3)甲、乙两车间共同加工完1000 件服装时甲车间所用的时间为8 小时.【解析】试题分析:(1)根据工作效率=工作总量÷工作时间,即可求出甲车间每小时加工服装件数,再根据这批服装的总件数 =甲车间加工的件数+乙车间加工的件数,即可求出这批服装的总件数;( 2)根据工作效率 =工作总量÷工作时间,即可求出乙车间每小时加工服装件数,根据工作时间=工作总量÷工作效率结合工作结束时间,即可求出乙车间修好设备时间,再根据加工的服装总件数=120+工作效率×工作时间,即可求出乙车间维修设备后,乙车间加工服装数量y 与 x 之间的函数关系式;( 3)根据加工的服装总件数=工作效率×工作时间,求出甲车间加工服装数量y 与 x 之间的函数关系式,将甲、乙两关系式相加令其等于1000,求出 x 值,此题得解.试题解析:( 1)甲车间每小时加工服装件数为720÷ 9=80(件),这批服装的总件数为720+420=1140(件).故答案为: 80;1140.(2)乙车间每小时加工服装件数为 120÷ 2=60(件),乙车间修好设备的时间为 9﹣( 420﹣ 120)÷ 60=4(时).∴乙车间维修设备后,乙车间加工服装数量y 与 x 之间的函数关系式为y=120+60( x﹣ 4) =60x﹣120( 4≤ x ≤ 9).( 3)甲车间加工服装数量y 与 x 之间的函数关系式为y=80x ,当80x+60x ﹣ 120=1000 时, x=8.答:甲、乙两车间共同加工完1000 件服装时甲车间所用的时间为8 小时.考点: 1. 一次函数的应用; 2. 解一元一次方程.22.【再现】如图①,在△ABC中,点 D, E 分别是 AB,AC的中点,可以得到:DE∥ BC,且 DE=1BC.(不需要2证明)【探究】如图②,在四边形ABCD中,点 E, F,G, H分别是 AB, BC,CD, DA的中点,判断四边形EFGH的形状,并加以证明.【应用】在(1)【探究】的条件下,四边形ABCD中,满足什么条件时,四边形EFGH是菱形?你添加的条件是:.(只添加一个条件)( 2)如图③,在四边形ABCD中,点 E,F,G,H分别是 AB,BC,CD,DA的中点,对角线 AC,BD相交于点 O.若AO=OC,四边形A BCD面积为 5,则阴影部分图形的面积和为.【答案】【探究】平行四边形.理由见解析;【应用】(1)添加 AC=BD,理由见解析;( 2)5.4( 2)先判断出 S△BCD=4S△CFG,同理: S△ABD=4S△AEH,进而得出 S 四边形EFGH=5,再判断出OM=ON,进而得出 S阴影 =1S 22四边形 EFGH即可.试题解析:【探究】平行四边形.理由:如图 1,连接 AC,∵ E 是 AB 的中点, F 是 BC的中点,∴ EF∥ AC,EF=1AC,21同理 HG∥ AC, HG=AC,综上可得: EF∥HG, EF=HG,故四边形EFGH是平行四边形.【应用】( 1)添加 AC=BD,理由:连接AC,BD,同( 1)知, EF=1AC,2同【探究】的方法得,FG=1BD,2∵AC=BD,∴ EF=FG,∵四边形EFGH是平行四边形,∴?EFGH是菱形;故答案为AC=BD;考点: 1. 三角形的中位线定理; 2. 平行四边形的判定; 3. 菱形的判定; 4. 相似三角形的判定和性质.23.如图①,在Rt △ABC中,∠ C=90°, AB=10, BC=6,点 P 从点 A 出发,沿折线AB﹣ BC向终点 C 运动,在AB上以每秒 5 个单位长度的速度运动,在BC上以每秒 3 个单位长度的速度运动,点Q从点 C 出发,沿CA方向以每秒4个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时3间为t 秒.( 1)求线段 AQ的长;(用含 t 的代数式表示)( 2)连结 PQ,当 PQ与△ ABC的一边平行时,求t 的值;( 3)如图②,过点P 作 PE⊥ AC于点 E,以 PE, EQ为邻边作矩形PEQF,点PEQF与△ ABC重叠部分图形的面积为S.①当点Q在线段 CD上运动时,求写出 DF将矩形 PEQF分成两部分的面积比为1: 2 时 t 的值.D 为S 与AC的中点,连结 DF.设矩形t 之间的函数关系式;②直接【答案】( 1) AQ=8﹣4t (0≤ t ≤ 4);( 2) t=3s 或 3s 时, PQ 与△ ABC的一边平行;( 3)①当0≤ t ≤3时,322S=﹣ 16t 2+24t .当3<t ≤ 2 时,S=﹣16t2+40t-48 .当 2< t ≤ 3 时,S=﹣20t 2+30t ﹣ 24.②当 t=9 s或 36 s 2331431时, DF将矩形 PEQF分成两部分的面积比为1: 2.【解析】( 3)①如图 1 中, a 、当 0≤ t ≤ 3时,重叠部分是四边形PEQF .22.S=PE?EQ=3t?( 8﹣ 4t ﹣ 4t )=﹣ 16t +24t3b 、如图 2 中,当3< t ≤ 2 时,重叠部分是四边形 PNQE .2S=S2)﹣14﹣5(8﹣43﹣5( 8﹣4﹣162.﹣ S =( 16t ﹣24t? [5t t ) ] ? [5t t0]=t+40t-48四边形 PEQF△PFN25435433C、如图 3 中,当2< t ≤ 3 时,重叠部分是五边形MNPBQ.S=S四边形PBQF S△FNM= 4t? [6﹣ 3(t ﹣ 2) ] ﹣1?[4t ﹣ 4( t ﹣ 2) ] ?3 [4t ﹣ 4( t ﹣ 2) ]= ﹣20t 2+30t ﹣ 24.323433∴ DE :DQ=NE : FQ=1: 3,∴( 3t ﹣ 3):( 3﹣ 4t ) =1:3,3解得 t=36s ,31综上所述,当t=9 s 或 36 s1431时, DF 将矩形PEQF 分成两部分的面积比为1:2.考点: 1. 矩形的性质 ;2. 勾股定理 ;3. 相似三角形的性质和判定24.定义:对于给定的两个函数,任取自变量 x 的一个值,当;4. 平行线分线段成比例定理.x < 0 时,它们对应的函数值互为相反数;当x≥ 0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x ﹣ 1,它们的相关函数为 y=x 1 x 0 x1 x.( 1)已知点 A (﹣ 5, 8)在一次函数 y=ax ﹣3 的相关函数的图象上,求a 的值;2﹣1.①当点 B ( m , 3)在这个函数的相关函数的图象上时,求m 的值;( 2)已知二次函数 y=﹣ x +4x22②当﹣ 3≤ x ≤ 3 时,求函数 y=﹣ x 2+4x ﹣ 1的相关函数的最大值和最小值;2( 3)在平面直角坐标系中,点M , N 的坐标分别为(﹣1, 1),( 9, 1} ),连结 MN .直接写出线段MN 与二2 2次函数 y=﹣ x 2 +4x+n 的相关函数的图象有两个公共点时 n 的取值范围.【答案】( 1) a=1;( 2)① m=2﹣5 或 m=2+ 2 或 m=2﹣ 2 .②当﹣21的相关3≤ x ≤3 时,函数 y= ﹣ x +4x ﹣2函数的最大值为43,最小值为﹣1;(3) n 的取值范围是﹣3< n ≤﹣ 1 或 1< n ≤ 5.2241x 24x 1 x2+4x ﹣2( 2)二次函数 y=﹣ x的相关函数为 y=12x2 4xx 02①当 m <0 时,将 B ( m ,322)代入 y=x ﹣4x+ 1得 m ﹣ 4m+1= 3,解得: m=2+ 5 (舍去)或 m=2﹣ 5 .2 2 2 23 21 2 1 3当 m ≥ 0 时,将 B ( m , )代入 y=﹣ x +4x ﹣得:﹣ m+4m ﹣=,解得: m=2+ 2 或 m=2﹣ 2 .222 2综上所述: m=2﹣ 5 或 m=2+ 2 或 m=2﹣ 2 .②当﹣ 3≤ x < 0 时, y=x 2﹣4x+ 1,抛物线的对称轴为 x=2,此时 y 随 x 的增大而减小, ∴此时 y 的最大值为43.22当 0≤ x ≤ 3 时 ,函数 y=﹣x 2+4x ﹣ 1,抛物线的对称轴为x=2,当 x=0 有最小值,最小值为﹣1,当 x=2 时,22有最大值,最大值 y= 7.2综上所述,当﹣ 3≤ x ≤ 3 时,函数 y=﹣ x 2+4x ﹣ 1的相关函数的最大值为43,最小值为﹣ 1 ;222( 3)如图 1 所示:线段 MN 与二次函数 y=﹣x 2+4x+n 的相关函数的图象恰有 1 个公共点.所以当 x=2 时, y=1,即﹣ 4+8+n=1,解得 n=﹣ 3.如图 2 所示:线段MN与二次函数y=﹣ x2+4x+n 的相关函数的图象恰有 3 个公共点考点:二次函数的综合应用.。
长春市近五年中考数学试卷及答案解析

长春市近五年中考数学试卷及答案解析2016年数学试卷及答案解析试卷内容:1. 选择题:包括单选题和多选题,涵盖整个数学知识点。
2. 解答题:包括计算题和证明题,要求学生掌握基本的计算方法和推理能力。
3. 应用题:涉及到实际生活中的问题,要求学生能够运用数学知识解决实际问题。
答案解析:1. 对于选择题,给出每个选项的解释和正确答案的理由。
2. 对于解答题,给出详细的解题步骤和答案。
3. 对于应用题,给出解题思路和关键步骤,帮助学生理解如何应用数学知识解决实际问题。
2017年数学试卷及答案解析试卷内容:1. 选择题:包括单选题和多选题,涵盖整个数学知识点。
2. 解答题:包括计算题和证明题,要求学生掌握基本的计算方法和推理能力。
3. 应用题:涉及到实际生活中的问题,要求学生能够运用数学知识解决实际问题。
答案解析:1. 对于选择题,给出每个选项的解释和正确答案的理由。
2. 对于解答题,给出详细的解题步骤和答案。
3. 对于应用题,给出解题思路和关键步骤,帮助学生理解如何应用数学知识解决实际问题。
2018年数学试卷及答案解析试卷内容:1. 选择题:包括单选题和多选题,涵盖整个数学知识点。
2. 解答题:包括计算题和证明题,要求学生掌握基本的计算方法和推理能力。
3. 应用题:涉及到实际生活中的问题,要求学生能够运用数学知识解决实际问题。
答案解析:1. 对于选择题,给出每个选项的解释和正确答案的理由。
2. 对于解答题,给出详细的解题步骤和答案。
3. 对于应用题,给出解题思路和关键步骤,帮助学生理解如何应用数学知识解决实际问题。
2019年数学试卷及答案解析试卷内容:1. 选择题:包括单选题和多选题,涵盖整个数学知识点。
2. 解答题:包括计算题和证明题,要求学生掌握基本的计算方法和推理能力。
3. 应用题:涉及到实际生活中的问题,要求学生能够运用数学知识解决实际问题。
答案解析:1. 对于选择题,给出每个选项的解释和正确答案的理由。
2010年吉林省长春市中考数学试题-推荐下载
k=( )
A.2
B.3
二、填空题(每小题 3 分,共 18 分)
9.因式分解:a-a2=
10.写一个比 5小的正整数,这个整数是
C.4
.
11.为了帮助玉树地区重建家园,某班全体师生积极捐款,捐款金额共 3200 元,其中 5 名
教师人均捐款 a 元,则该班学生共捐款
k1
12.如图,双曲线 y1= x (k1>0)与直线 y2=k2x+b(k2>0)的一个交点的横坐标为 2,那么
A,BC⊥OD 于点 C.四边形 OABC 与四边形 ODEF 的面积分别为 6 和 10,则△ABG
与△BCD 的面积之和为
三、解答题(每小题 5 分,共 20 分)
15.先化简,再求值:(x+1)2-2x+1,其中 x= 2.
.
16.一个不透明的口袋中装有红、黄、白小球各 1 个,小球除颜色外其余均相同.从口袋 中随机摸出一个小球,记下颜色放回,再随机摸出一个小球.请你用画树形图(或列表)的 方法,求出两次摸出的小球颜色相同的概率.
第 14 题图
F
x
17.第 16 届亚运会将在广州举行.小李预定了两种价格的亚运会门票,其中甲种门票共花 费 280 元,乙种门票共花费 300 元,甲种门票比乙种门票多 2 张,乙种门票价格是甲 种门票价格的 1.5 倍,求甲种门票的价格.
18.如图,将一个两边带有刻度的直尺放在半圆形纸片上,使其一边经过圆心 O,另一边 所在直线与半圆交于点 D、E,量出半径 OC=5cm,弦 DE=8cm,求直尺的宽.
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气,线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2007-2010长春数学中考试题及答案1

吉林省长春市2007年初中毕业生学业考试数学试题本试题卷包括七道大题,共26小题,共6页.全卷满分120分.考试时间为120分钟.考试结束后,将本试题卷和答题卡一并交回. 注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上,并将条形码准确粘贴在条形码区域内.2.答题时,考生务必按照考试要求在答题卡上的指定区域内作答,在草稿纸、试题卷上答题无效.一.选择题(每小题3分,共24分) 01.-6的相反数是( ).A 、-6B 、6C 、61-D 、6102.方程组⎩⎨⎧-=-=+1y 3x 24y 3x 的解是( ).A 、⎩⎨⎧-=-=1y 1xB 、⎩⎨⎧==1y 1xC 、⎩⎨⎧=-=2y 2xD 、⎩⎨⎧-=-=1y 2x03.某地区五月份连续6天的最高气温依次是:28、25、28、26、26、29(单位:°C),则这组数据的中位数是( ). A 、26°C B 、26.5°C C 、27°C D 、28°C04.如图,小手盖住的点的坐标可能为( ).A 、(5,2)B 、(-6,3)C 、(-4,-6)D 、(3,-4)05.如图,已知线段AB =8cm ,⊙P 与⊙Q 的半径均为1cm .点P 、Q 分别从A 、B 出发,在线段AB 上按箭头所示方向运动.当P 、Q 两点未相遇前,在下列选项中,⊙P 与⊙Q 不可能...出现的位置关系是( ). A 、外离 B 、外切 C 、相交 D 、内含06.一根单线从钮扣的4个孔中穿过(每个孔只穿过一次),其正面情形如图所示,下面4个图形中可能是其背面情形的是( ). 07.小华拿24元钱购买火腿肠和方便面,已知一盒方便面3元,一根火腿肠2元,他买了4盒方便面,x 根火腿肠,则关于x 的不等式表示正确的是( ). A 、3×4+2x <24 B 、3×4+2x ≤24 C 、3x +2×4≤24 D 、3x +2×4≥24 08.如图,△AOB 中,∠B =30°,将△AOB 绕点O 顺时针旋转52°得到△A ’OB ’,边A ’B ’与边OB 交于点C(A ’不在OB 上),则∠A ’CO 的度数为( ). A 、22° B 、52° C 、60° D 、82° 二.填空题(每小题3分,共18分) 09.计算:218+=_________.10.将下面四张背面都是空白的卡片混在一起,在看不到正面图案的情况下,从中随机选取一张,这张卡片上的图案恰好为2007年长春亚冬会吉祥物“鹿鹿”的概率是( ). 11.如图,下面的图案由三个叶片组成,绕点O 旋转120°后可以和自身重合.若每个..叶片Ox y(第04题图)P (第05题图) Q A B(第06题图)A B C D (第08题图)A B OA ’B ’的面积为4cm 2,∠AOB 为120°,则图中阴影部分的面积之和为_____________cm 2. 12.如图,过正方形ABCD 的顶点B 作直线l ,过A 、C 作l 的垂线,垂足分别为E 、F .若AE =1,CF =3,则AB 的长度为___________.13.在二次函数y =x 2+bx +c 中,函数y 与自变量x 的部分对应值如下表:x -2 -1 012 3 4 y72-1 -2m27则m 的值为__________.14.如图,∠1的正切值等于__________. 三.解答题(每小题5分,共20分)15.先化简,再求值:(x +2)(x -2)-x(x -1),其中x =-1.16.如图,在△ABC 中,AB =AC ,D 是BC 的中点,连接AD .DE ⊥AB ,DF ⊥AC ,E 、F是垂足.图中共有多少对全等三角形?请直接用“≌”符号把它们分别表示出来(不要求证明).17.张明与李强共同清点一批图书,已知张明清点完200本图书所用的时间与李强清点完300本图书所用的时间相同,且李强平均每分钟比张明多清点10本,求张明平均每分钟清点图书的数量.18.将5个完全相同的小球分装在甲、乙两个不透明的口袋中.甲袋中有3个球,分别标有数字2、3、4;乙袋中有2个球,分别标有数字2、4.从甲、乙两个口袋中各随机摸出一个球.(1)用列表法或画数形图法,求摸出的两个球上数字之和为5的概率; (2)摸出的两个球上数字之和为多少时的概率最(第11题图) A BO (第12题图) A l B CD E F (第10题图) 会 徽 鹿 鹿 会 徽 会徽 (第14题图)12 31 2 3 1O xy(第16题图) A B CD E F四.解答题(每小题6分,共12分)19.如图,Rt △ABC 中,∠C =90°,AC =4,BC =3,以△ABC 的一边为边画等腰三角形,使它的第三个顶点在△ABC 的其它边上.请在图①、图②、图③中分别画出一个符合条件的等腰三角形,且三个图形中的等腰三角形各不相同,并在图中表明所画等腰三角形的腰长(不要求尺规作图).20.小刚有一块含有30°角的直角三角板,他想测量其短直角边的长度,而手中另外只有一个量角器,于是他采用了如下的办法,并获得了相关数据:第一步,他先用三角板标有刻度的一边测出量角器的直径AB 的长度为9cm ;第二步,将三角板与量角器按如图所示的方式摆放,并量得∠BOC 为80°(O 为AB 的中点).请你根据小刚测得的数据,求出三角板的短直角边AC 的长.(参考数据:sin80°=0.98,cos80°=0.17,tan80°=5.67;sin40°=0.64,cos40°=0.77,tan40°=0.84,结果精确到0.1cm .)五.解答题(每小题6分,共12分)21.网瘾低龄化问题已引起社会各界的高度关注,有关部门在全国范围内对12~35岁的网瘾人群进行了抽样调查.下图是用来表示在调查的样本中不同年龄段的网瘾人数的,其中30~35岁的网瘾人数占样本总人数的20%. (1)被抽样调查的样本总人数为_________人; (2)请把统计图中缺失的数据、图形补充完整;(3)据报道,目前我国12~35岁网瘾人数约为200万人,那么其中12~17岁的网瘾人数约为多少人?A B C (第19题图)图① 图② 图③A B C ABC A (第20题图) BC O0 (第21题图)450 500 550 600650700750600 576 48012~17 18~23 24~2930~35年龄(岁)网瘾人数(人)22.在北方冬季,对某校一间坐满学生、门窗关闭的教室中CO 2的总量进行检测,部分数据如下:教室连续使用时间x (分)5 10 15 20 CO 2总量y(m 3)0.61.11.62.1经研究发现,该教室空气中CO 2总量y(m 3)是教室连续使用时间x (分)的一次函数. (1)求y 与x 的函数关系式(不要求写出自变量x 的取值范围);(2)根据有关资料推算,当该教室空气中CO 2总量达到6.7m 3时,学生将会稍感不适.请通过计算说明,该教室连续使用多长时间学生将会开始稍感不适?(3)如果该教室在连续使用45分钟时开门通风,在学生全部离开教室的情况下,5分钟可将教室空气中CO 2的总量减少到0.1m 3,求开门通风时教室空气中CO 2平均每分钟减少多少立方米?六.解答题(每小题7分,共14分)23.如图①,将一组对边平行的纸条沿EF 折叠,点A 、B 分别落在A ’、B ’处,线段FB ’与AD 交于点M .(1)试判断△MEF 的形状,并证明你的结论;(2)如图②,将纸条的另一部分CFMD 沿MN 折叠,点C 、D 分别落在C ’、D ’处,且使MD ’经过点F ,试判断四边形MNFE 的形状,并证明你的结论; (3)当∠BFE =_________度时,四边形MNFE 是菱形.24.如图,在平面直角坐标系中,A 为y 轴正半轴上一点,过A 作x 轴的平行线,交函数x 2y -=( x <0)的图象于B ,交函数x 6y =( x >0)的图象于C ,过C 作y 轴的平行线交BO 的延长线于D .(1)如果点A 的坐标为(0,2),求线段AB 与线段CA 的长度之比;(2)如果点A 的坐标为(0,a),求线段AB 与线段CA 的长度之比;(3)在(2)的条件下,四边形AODC 的面积为________.A (第23题图②)BC E FD A ’ B ’ AB C EF D A ’ B ’ D ’ C ’ M M N (第23题图①) A B yO x C D (第24题图)x 6y =x2y -=七.解答题(每小题10分,共20分)25.如图①,在Rt △ABC 中,∠C =90°,边BC 的长为20cm ,边AC 的长为hcm ,在此三角形内有一个矩形CFED ,点D 、E 、F 分别在AC 、AB 、BC 上,设AD 的长为xcm ,矩形CFED 的面积为y(单位:cm 2).(1)当h 等于30时,求y 与x 的函数关系式(不要求写出自变量x 的取值范围); (2)在(1)的条件下,矩形CFED 的面积能否为180cm 2?请说明理由; (3)若y 与x 的函数图象如图②所示,求此时h 的值.(参考公式:二次函数y =ax 2+bx +c ,当a2b x -=时,y 最大(小)值=a 4b ac 42-.)26.如图,在平面直角坐标系中,直线b x 21y +-=(b >0)分别交x 轴、y 轴于A 、B 两点,以OA 、OB 为边作矩形OACB ,D 为BC 的中点.以M(4,0),N(8,0)为斜边端点作等腰直角三角形PMN ,点P 在第一象限,设矩形OACB 与△PMN 重叠部分的面积为S . (1)求点P 的坐标;(2)当b 值由小到大变化时,求S 与b 的函数关系式;(3)若在直线b x 21y +-=(b >0)上存在点Q ,使∠OQM 等于90°,请直接写出....b 的取值范围;(4)在b 值的变化过程中,若△PCD 为等腰三角形,请直接写出....所有符合条件的b 值.A (第25题图②)B C EF D(第25题图①)O 10 150x(cm)y(cm 2)A BC M NDPOy x(第26题图)2008年吉林省长春市中考数学试题一、选择题(每小题3分,共分39,每小题给出4个答案,其中只有一个正确,把所选答案的编号写在题目后面的括号内)1、如图,是北京奥运会自行车比赛项目标志,则图中两轮所在圆的位置关系是【 】A .内含B .相交C .相切D .外离2、化简(-3)2的结果是【 】A.3B.-3C.±3 D .93、如果2是方程02=-c x 的一个根,那么c 的值是 【 】A .4B .-4C .2D .-24、下列成语所描述的事件是必然发生的是 【 】A. 水中捞月B. 拔苗助长C. 守株待免D. 瓮中捉鳖5、如图,AB 是⊙O 的直径,弦CD ⊥AB,垂足为E,如果AB=20,CD=16, 那么线段OE 的长为【 】 A 、10 B 、8 C 、6 D 、46、抛物线()223y x =++的顶点坐标是 【 】A.(-2,3)B.(2,3)C.(-2,-3)D.(2,-3) 7、观察下列银行标志,从图案看是中心对称图形的有( )个A 、1个B 、2个C 、3个D 、4个 8、二次函数362+-=x kx y 的图象与x 轴有交点,则k 的取值范围是【 】A .3<kB .03≠<k k 且C .3≤kD .03≠≤k k 且9、某校九年级(1)班50名学生中有20名团员,他们都积极报名参加学校开展的“文明劝导活动”。
DA吉林省中考真题

吉林省2010年初中毕业生学业考试数学试卷参考答案及评分标准阅卷说明:1.评卷采分最小单位为1分,每步标出的是累计分.2.考生若用本“参考答案”以外的解(证)法,可参照本“参考答案”的相应步骤给分. 一、填空题(每小题2分,共20分)1.2- 2.6.52410⨯ 3.5 4.5.2x > 6.17.492 8.大于或等于0并且小于或等于40的任意一个数皆可 9.25π310.42n +二、单项选择题(每小题3分,共18分)11.C 12.B 13.D 14.B 15.C 16.B 三、解答题(每小题5分,共20分)17.解:原式=2212111.(1)1x x x x x x x x x x --+-÷==--·(3分)当2x =时,原式=11.21=- (5分)评分说明:x 只要不取0和1,计算正确皆可得分.18.解:(1)② ①;(2分)(2)(5分)评分说明:(1)每填对一个得1分,填“V ”、“N ”不扣分. (2)作法1、作法2中不作虚线不扣分.19.解:设沙包落在A 区域得x 分,落在B 区域得y 分,(1分)根据题意,得3342232.x y x y +=⎧⎨+=⎩,(3分)解得97.x y =⎧⎨=⎩,(4分)第18题作法1 作法2 作法3393730.x y ∴+=+⨯=(5分)答:小敏的四次总分为30分. 20.解:(1)34; (3分)(2)1. (5分) 评分说明:(2)中填100%不扣分. 四、解答题(每小题6分,共12分)21.解:ADC ADF ADC CEB △≌△、△≌△、ADF CEB △≌(写出其中两对即可). (2分) 证法1:若选择ADC ADF △≌△,证明如下: AD 平分FAC CAD FAD ∠∴∠=∠,. (3分) 90AD CF ADC ADF ∴∠=∠= ⊥,°. (4分) 又AD AD = ,ADC ADF ∴≌. (6分) 证法2:若选择ADC CEB △≌△,证明如下: AD CE BE CE ⊥⊥ ,,90ADC CEB ∴∠=∠=°. (3分) 9090ACB ACD ECB ∠=∴∠+∠= ,°.又90ACD DAC DAC ECB ∠+∠=∴∠=∠ °,. (4分)又AC CB ADC CEB =∴ ,△≌△. (6分)评分说明:每正确写出一对全等三角形得1分. 22.解:(1)3 (2,1) 6; (3分) (2)如图,连接AC ,过点A 作AD BC ⊥于点D , 则2BC DC =. (4分) 由A (5,1)可得1AD =. 又2AC = ,∴在Rt ADC △中,DC =BC ∴=(6分)评分说明:(1)中每填对一个得1分.五、解答题(每小题7分,共14分) 23.解:(1)方案三;(2分)(2) (3分)(5分)第23题第22题(3)50030%150⨯=(名).(7分)答:七年级约有150名学生比较了解“低碳”知识. 评分说明:扇形图中每填对一个得1分.24.解:(1)在Rt DEF △中,90DEF DE BC ∠===°, 1.8,29F ∠=°.sin DE F DF =, 1.8 1.83.75 3.8sin sin 290.48DE DF F ∴===≈≈° (3分) (2)解法1:tan DE F EF = , 1.8 1.8 3.27.tan tan 290.55DE EF F ∴==≈≈° (5分)在Rt ABC △中,90ACB ∠=°.由45A ∠=°得 1.8.AC BC ==又0.5CE BD == ,1.80.5 3.27 5.6.AF AC CE EF ∴=++++≈≈(7分) 解法2:cos cos 29 3.750.87 3.26EF F EF DF DF=∴=⨯ ,·°≈≈. (5分)在Rt ABC △中,90ACB ∠=°.由45A ∠=°得 1.8.AC BC == 又0.5CE BD == ,1.80.5 3.26 5.6.AF AC CE EF ∴=++++≈≈ (7分)答:DF 长约为3.8m ,AF 约为5.6m.评分说明:(1)计算过程中不写“≈”不扣分. (2)求出 3.3EF ≈不扣分.(3)解法2中用 3.8DF =代入不扣分. 六、解答题(每小题8分,共16分) 25.(2)猜想:22BFD S b =△. (5分)证明:证法1:如图,BFD BCD BEF CEFD S S S S =+-△△△梯形 =2111()()222b a b a a b a ++-+ =212b . (8分) 证法2:如图,连接CF ,由正方形性质可知45DBC FCE ∠=∠=°,.BD CF ∴∥BFD ∴△与BCD △的BD 边上的高相等.212BFD BCD S S b ∴==△△.(8分)评分说明:(1)每填对一个得1分. (2)未写猜想但证明正确也可得满分. 26.解:(1)解法1:设火车行驶的速度为v 米/秒,根据题意,得 14120160.v =+解得20.v = (2分) 解法2:(120+160)÷14=20. (2分)答:火车行驶速度为20米/秒.FG DABC E第25题(2)①当06x <≤时,20y x =; (3分) ②当68x ≤≤时,120y =;(4分) ③解法1;当814x <≤时,120(20160)20280.y x x =--=-+ (6分) 解法2:当814x <≤时,1201602020280.y x x =+-=-+ (6分) 解法3:当84x <≤1时,20(14)20280.y x x =-=-+ (6分)(3) (8分)评分说明:(2)中自变量取值范围含或不含6、8均不扣分. 七、解答题(每小题10分,共20分)27.解:(1)设经过(10)(03)A B ,、,的直线AB 的解析式为3y kx =+。
