受迫振动与共振实验(精选)
实验报告 音叉的受迫振动与共振实验
1. 测量自由状态下的音叉幅频特性曲线：
频率
电压
频率
电压
频率
电压
频率
电压
(Hz)
(V)
(Hz)
(V)
(Hz)
(V)
(Hz)
(V)
267.58 0.070 270.49 1.619 270.576 1.834 270.761 1.217
268.58 0.117 270.5 1.655 270.591 1.823 270.871 0.900
m(g)
8
13
18
23
28
本图像的方程为：������2
=
4������2 ������
������0
+
4������2 ������
������������
由图可知：
4������2 ������
=
0.0318
×
10−5������2
∙
g−1
，
4������2 ������
������0
=
1.346110−5������2
令������02
=
������ ������
, ������
=
2������ ������
解方程可得������ = ������0������−������������ cos (√������02 − ������2������ + ������0) + ������������������������(������������ + ������)
270.366 1.342 270.516 1.841 270.703 1.282 274.733 0.098
受迫振动与共振现象的研究
受迫振动与共振现象的研究振动是自然界中一种常见的物理现象，无论是机械系统、电子电路还是分子结构，都可以发生振动。
受迫振动是其中一种特殊的振动形式，它在受到外界周期性激励后产生的振动。
共振现象则是在受迫振动中常见的一种现象，它描述了系统在外界激励频率与系统固有频率相匹配时的特殊状态。
本文将探讨受迫振动与共振现象的研究。
受迫振动是一种非平衡状态下的振动，不同于自由振动。
在受迫振动中，外界施加的周期性力或位移使系统产生周期性的响应。
例如，在机械系统中，一个悬挂在弹簧上的质点受到周期性的外力作用，就会引起该质点的受迫振动。
受迫振动通常可以通过线性微分方程来描述。
假设一个简谐振子受到一个周期性外力的作用，其运动方程可以表示为：\[m\frac{d^2x}{dt^2} + b\frac{dx}{dt} + kx = F_0\cos(\omega t)\]其中，m是振子的质量，x是振子的位移，b是阻尼系数，k是弹性系数，F0是外力振幅，ω是外力的角频率。
在进行受迫振动的研究时，共振现象是一个重要的现象。
共振是指当外界激励的频率与系统固有频率相等或接近时，系统会表现出极大的响应。
这是因为在共振状态下，外界激励与振动系统内部的自由振动频率相匹配，从而使得能量在系统内部得到最大的传递。
共振现象具有许多实际应用。
在建筑工程中，共振现象被广泛应用于减震器的设计，用于减少地震或风力对建筑物产生的振动影响。
在电子电路中，共振现象可以用于选择性放大或滤波，将特定频率信号从混杂的信号中提取出来。
此外，共振现象还存在于许多其他领域，如天文学、生物学和音乐等。
为了研究受迫振动和共振现象，科学家和工程师采用了许多不同的方法和技术。
在实验室中，他们可以使用震动台或其他类型的振动装置来模拟外界激励，并测量系统的响应。
通过改变激励频率、幅度或相位，研究者可以确定共振频率以及共振响应的特性。
此外，数值模拟也是研究受迫振动和共振现象的重要手段。
实验6受迫振动与共振实验
实验6受迫振动与共振实验实验六受迫振动与共振实验受迫振动与共振等现象在工程和科学研究中经常用到，如在建筑、机械等工程中，经常须避免共振现象，以保证工程的质量，而在一些石油化工企业中，用共振现象测量音叉式液体密度传感器和液体传感器在线检测液体密度和液位高度。
所以受迫振动与共振是重要的物理规律，受到物理和工程技术广泛重现。
实验目的1.研究音叉振动系统在周期外力作用下振幅与强迫力频率的关系，测量及绘制它们的关系曲线，并求出共振频率和振动系统振动的锐度（其值等于Q 值）。
2.音叉双臂振动与对称双臂质量关系的测量，求音叉振动频率f （即共振频率）与附在音叉双臂一定位置上相同物块质量m 的关系公式。
3.通过测量共振频率的方法，测量一对附在音叉上的物块m x 的未知质量。
4.在音叉增加阻尼力情况下，测量音叉共振频率及锐度，并与阻尼力小情况进行对比。
实验原理1.简谐振动与阻尼振动许多振动系统如弹簧振子的振动、单摆的振动、扭摆的振动等，在振幅较小而且在空气阻尼可以忽视的情况下，都可作简谐振动处理。
即此类振动满足简谐振动方程02022=+x dtx d ω （1）（1）式的解为)cos(0?ω+=t A x (2) 对弹簧振子振动圆频率00m m K +=ω，K 为弹簧劲度，m 为振子的质量，m 0为弹簧的等效质量。
弹簧振子的周期T 满足)(4022m m K T +=π （3）但实际的振动系统存在各种阻尼因素，因此（1）式左边须增加阻尼项。
在小阻尼情况下，阻尼与速度成正比，表示为dtdx β2，则相应的阻尼振动方程为 022022=++x dt dx dtx d ωβ (4) 式中β为阻尼系数。
2.受迫振动与共振阻尼振动的振幅随时间会衰减，最后回停止振动。
为了使振动持续下去，外界必须给系统一个周期变化的强迫力。
一般采用的是随时间作正弦函数或余弦函数变化的强迫力，在强迫力作用下，振动系统的运动满足下列方程t m F x dt dx dt x d ωωβcos '22022=++ （5）（5）式中，m ’=m+m 0为振动系统的质量，F 为强迫力的振幅，ω为强迫力的圆频率。
华中科技大学大学物理实验-受迫振动与共振实验(final)_zhb
2. 位移共振
A
2
F0
(m
k
)
2
m
2 0
F0
2 2
4 2 2
r 02 2 （位移共振条件）
Ar F0 2m 02 2
r 0
位移共振曲线
音叉的电磁激振与拾振
拾振/接收 线圈
激振/驱动 线圈
激振线圈在正弦交变电流作用下产生交变磁场激振音叉，使之 产生正弦振动。 拾振线圈靠近被磁化的音叉臂另一端放置，由于变化的磁场产生 感应电流输出到交流数字电压表中。
1.8 1.6 1.4 1.2 1 0.8 0.6 0.4 0.2 0 258
U(V)
258.5
259
259.5
260 260.5 f(Hz)
261
261.5
262
262.5
4、测量无阻尼状态下音叉的速度幅频特性以及相应 的共振频率f0和输出电压Umax。 测量范围从f0-2Hz至f0 +2Hz由小往大测，稀疏区Umax 隔约0.1V 取一个点，密集区改变驱动频率 f 的小数点 后倒数第二位(隔0.010Hz)取点。
v max
2
F0
(m ) 2
k
m k 0
( r 0 k ) m
F0 vr 2m
tg
F0 0
k m
速度共振曲线的锐度 (品质因素)：
f
速度共振曲线
f0 Q 2 1 f 2 f 1
阻尼： 估测f0: （有或无） Hz， 估测Umax: V, 0.707Umax: V
f (Hz)
Umax (V)
华科物理实验——音叉的受迫振动与共振
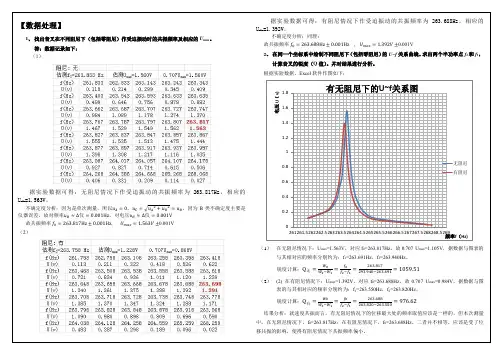
结果分析：就速度共振而言，有无阻尼情况下的位移最大处的频率取值应该是一样的，但本次测量中，在无阻尼情况下，f0=263.817Hz；在有阻尼情况下，f0=263.688Hz。二者并不相等，应该是受了位移共振的影响，使得有阻尼情况下共振频率偏小。
相对误差 ，故误差可忽略。
此外，从锐度的计算来看， ，所以阻尼使得速度在共振频率附近的变化幅度略微减小，这是正常的，因为设想阻尼无穷大的情况下，速度不再变化。
根据实验数据，Excel软件作图如下：
（1）在无阻尼情况下：Umax=1.563V，对应f0=263.817Hz，故0.707 Umax=1.105V，据数据与图表的与其相对应的频率分别约为：f1=263.691Hz，f2=263.940Hz。
锐度计算：
（2）(2)在有阻尼情况下：Umax=1.392V，对应f0=263.688Hz，故0.707 Umax=0.984V，据数据与图表的与其相对应的频率分别约为：f1=263.550Hz，f2=263.820Hz。
（2）人为操作时，测量前后可能调节了驱动信号输出幅度，即黑色旋钮，使实验结果不一致。
（3）测量环境中其它因素的影响，比如说温度，与其它音叉的共振等等。
3、绘制周期平方T2与质量m的关系图，分析其特点和意义。
答：数据如下：
注： s
根据实验数据，Excel软件作图如下：
据图的拟合曲线为：
结果分析：据图可知T2与m成正比，且实验测得的数据误差较小。由此可由测量音叉的振动周期来测量未知质量，并可制作测量质量和密度的传感器。
【拓展问】
1、平移阻尼块的位置，可能会发生什么现象？
故共振频率 , 0.001V
（2）
据实验数据可得：有阻尼情况下作受迫振动的共振频率为263.688Hz，相应的Umax=1.392V。
受迫振动和共振的研究
受迫振动和共振的研究振动科学是物理学的重要组成部分。
其中受迫振动．．．．和共振．．问题的研究，不但在理论上涉及经典和现代物理科学的发展；更在工程技术领域受到极大的重视并不断取得新的成果。
例如：在建筑、机械等工程问题中，经常须避免“共振”现象的出现以保证工程质量；但目前新研发的很多仪器和装置的工作原理又是基于各种“共振”现象的产生；在微观科学研究领域中“共振”也已成为重要的研究手段。
本实验以音叉振动系统为研究对象，用电磁激振线圈的电磁力作为驱动力使音叉起振；并以另一电磁线圈作为检测振幅传感器，观测受迫振动系统的振幅与驱动力频率之间的关系，以研究“受迫振动”与“共振”现象及其规律。
一、 实验目的（1） 研究音叉振动系统在周期性外力作用下振幅与外力频率的关系，测绘其关系曲线，并求出系统的共振频率和系统的振动锐度（和品质因素Q 值有关的参量）；（2） 通过改变音叉双臂同一位置处所加金属块的质量，研究系统的共振频率与系统质量的关系；（3） 通过测量音叉的共振频率，确定未知物体的质量，以了解音叉式传感器的工作原理；（4） 改变音叉阻尼状态，了解阻尼力对音叉系统的共振频率及其振动锐度的影响。
二、 实验原理1． 简谐振动与阻尼振动众所周知：弹簧振子、单摆、复摆、扭摆等振动系统在作小幅度振动，并且其所受各种阻尼力小到可以忽略的情况下，可视为简谐振动状态。
此类振动满足下述简谐振动．．．．方程： 02022=+x dtx d ω （1） 上式的解为：)cos(00ϕω+=t A x （2）以理想弹簧振子为例：其固有角频率mK =0ω，K 为弹簧的劲度系数，m 为振动系统的有效质量，振幅A 和初位相0ϕ与振动系统的初始状态有关，系统的振动周期T =Km πωπ220=。
即振动周期仅与系统的质量及弹簧的劲度系数有关；由此可知：理想弹簧振子的振动频率f=m K T π211=。
但是，实际的振动系统存在各种阻尼因素。
仍以弹簧振子为例：其振动幅度在摩擦力（空气阻力、内力等）的阻尼下会逐步减小直到零——即阻尼振动．．．．状态。
利用波尔共振仪研究受迫振动实验报告
利用波尔共振仪研究受迫振动实验报告一、实验目的1、观察摆轮在受迫振动时的振幅频率特性和相位频率特性。
2、研究不同阻尼力矩对受迫振动的影响，测定阻尼系数。
3、学习用频闪法测定动态物理量——相位差。
二、实验仪器波尔共振仪由振动仪与电器控制箱两部分组成。
振动仪部分由摆轮、摆盘、弹性钢丝、光电门、阻尼线圈等组成。
电器控制箱部分有电源开关、电机转速调节旋钮、闪光灯开关、振幅调节旋钮等。
三、实验原理1、受迫振动物体在周期性外力的持续作用下进行的振动称为受迫振动。
当外力的频率与物体的固有频率接近时，振幅会显著增大，这种现象称为共振。
2、运动方程设摆轮转动惯量为 J，扭转弹性系数为 k，阻尼系数为 b，强迫力矩为 M ＝ M₀cosωt，则摆轮的运动方程为：Jd²θ/dt² ＋bdθ/dt ＋kθ ＝ M₀cosωt其中，θ 为角位移，ω 为强迫力矩的角频率。
3、幅频特性和相频特性在小阻尼情况下，受迫振动的振幅和相位差与强迫力矩的频率之间存在特定的关系。
振幅 A 与强迫力矩频率ω 的关系为：A ＝ M₀/√（（k Jω²)² ＋（bω)²)相位差φ 与强迫力矩频率ω 的关系为：φ ＝arctan(bω/（k Jω²)）四、实验内容及步骤1、调整仪器将波尔共振仪调整至水平状态，打开电源，调节电机转速，使摆轮做自由摆动，观察其振幅和周期是否稳定。
2、测量固有频率在阻尼较小的情况下，让摆轮自由摆动，测量其振幅逐渐衰减到初始振幅的一半所经历的时间 t，根据公式计算固有频率ω₀＝2π/t。
3、测量幅频特性选择不同的阻尼档位，逐渐改变电机转速，即改变强迫力矩的频率ω，测量相应的振幅 A，绘制幅频特性曲线。
4、测量相频特性在测量幅频特性的同时，使用频闪法测量相位差φ，绘制相频特性曲线。
5、数据分析根据实验数据，分析阻尼系数对幅频特性和相频特性的影响，验证理论公式。
五、实验数据及处理以下是一组实验数据示例（实际数据应根据实验情况记录）：｜强迫力矩频率ω（Hz）｜振幅 A（mm）｜相位差φ（°）｜阻尼档位｜｜｜｜｜｜｜ 05 ｜ 50 ｜ 100 ｜小阻尼｜｜ 06 ｜ 65 ｜ 150 ｜小阻尼｜｜ 07 ｜ 80 ｜ 200 ｜小阻尼｜｜｜｜｜｜根据实验数据，以强迫力矩频率ω 为横坐标，振幅 A 和相位差φ 分别为纵坐标，绘制幅频特性曲线和相频特性曲线。
利用波尔共振仪研究受迫振动实验报告
利用波尔共振仪研究受迫振动实验报告一、实验目的1、观察摆轮的自由振动、阻尼振动和受迫振动现象。
2、研究不同阻尼力矩对受迫振动的影响，并测定阻尼系数。
3、研究受迫振动的幅频特性和相频特性，观察共振现象，测定受迫振动的共振频率和共振振幅。
二、实验仪器波尔共振仪，包括振动系统、电磁阻尼系统、电机驱动系统、光电计数系统和智能控制仪等部分。
三、实验原理1、自由振动无阻尼的自由振动方程为：＄m\frac{d^2\theta}｛dt^2}＝k\theta$，其中$m$为摆轮的转动惯量，＄k$为扭转弹性系数，＄＼theta$为角位移。
其解为：＄＼theta ＝ A\cos(＼omega_0 t ＋＼varphi)＄，其中$＼omega_0 ＝＼sqrt{＼frac{k}｛m}｝＄为固有角频率，＄A$和$＼varphi$为初始条件决定的常数。
2、阻尼振动考虑阻尼时，振动方程为：＄m\frac{d^2\theta}｛dt^2} ＋b\frac{d\theta}｛dt} ＋ k\theta ＝ 0$，其中$b$为阻尼系数。
根据阻尼的大小，可分为三种情况：小阻尼：＄＼omega ＝＼sqrt{＼omega_0^2 ＼frac{b^2}｛4m^2}｝＄，振动逐渐衰减。
临界阻尼：振动较快地回到平衡位置。
大阻尼：不产生振动。
3、受迫振动在周期性外力矩$M ＝ M_0\cos\omega t$作用下，振动方程为：＄m\frac{d^2\theta}｛dt^2} ＋ b\frac{d\theta}｛dt} ＋ k\theta ＝M_0\cos\omega t$。
稳定时，振动的角位移为：＄＼theta ＝ A\cos(＼omega t ＋＼varphi)＄，其中振幅$A ＝＼frac{M_0}｛＼sqrt{（k m\omega^2)＾2 ＋（b\omega)＾2}｝＄，相位差$＼varphi ＝＼arctan\frac{b\omega}｛k m\omega^2}＄。
音叉的受迫振动与共振实验
（4） 与无阻尼的周期相比，周期变大。 2、受迫振动 实际的振动都是阻尼振动，一切阻尼振动最后都要停止下来．要使 振动能持续下去，必需对振子施加持续的周期性外力，使其因阻尼而损 失的能量得到不断的补充．振子在周期性外力作用下发生的振动叫受迫 振动，而周期性的外力又称驱动力．实际发生的许多振动都属于受迫振 动．例如声波的周期性压力使耳膜产生的受迫振动，电磁波的周期性电 磁场力使天线上电荷产生的受迫振动等。 为简单起见，假设驱动力有如下的形式：
应密集一些，确保找准共振频率。
驱动信号输出幅度：
阻尼大小：
f (Hz)
……
U（V）
……
3、在无阻尼状态下，将不同质量块（5g、10g、15g、20g、25g） 分别加到音叉双臂指定的位置上，并用螺丝旋紧。测出音叉双臂对称加 相同质量物块时，相对应的共振频率。记录m~f关系数据，（数据表格 如下图所示）。 m（g）
式中为驱动力的幅值，为驱动力的角频率。
振子处在驱动力、阻力和线性回复力三者的作用下，其动力学方程
成为
（5）
仍令，得到：
（6）
微分方程理论证明，在阻尼较小时，上述方程的解是：
（7）
式中第一项为暂态项，在经过一定时间之后这一项将消失，第二项
是稳定项．在振子振动一段时间达到稳定后，其振动式即成为：
（8）
动力做正功，振子输人能量；反向时驱动力做功，振子输出能量。输
人功率的大小可由计算。设想在振子固有频率、阻尼大小、驱动力幅值
均固定的情况下，仅改变驱动力的频率，则不难得知，如果满足最大值
(整理)受迫振动的研究(共振实验).
引 言在机械制造和建筑工程等领域中，受迫振动所导致的共振现象引起工程技术人员的极大关注。
它既有破坏作用，也有实用价值，很多电声器件都是运用共振原理设计制作的。
另外，在微观科学研究中，“共振”也是一种重要的研究手段，例如：利用核磁共振和顺磁共振研究物质结构等。
表征受迫振动性质是受迫振动的振幅—频率特性和相位—频率特性（简称幅频和相频特性）。
本实验采用波尔共振仪定量测定机械受迫振动的幅频特性和相频特性，并利用频闪方法来测定动态的物理量——相位差。
数据处理与误差分析方面的内容也比较丰富。
【实验目的】1. 研究波尔共振仪中弹性摆轮受迫振动的幅频特性和相频特性。
2. 研究不同阻尼矩对受迫振动的影响，观察共振现象。
3. 学习用频闪法测定运动物体的某些量。
【实验原理】一、受迫振动物体在周期外力的持续作用下发生的振动称为受迫振动，这种周期性的外力称为强迫力。
如果外力是按简谐振动规律变化，那么稳定状态时的受迫振动也是简谐振动，此时，振幅保持恒定，振幅的大小与强迫力的频率和原振动系统无阻尼时的固有振动频率以及阻尼系数有关。
在受迫振动状态下，系统除了受到强迫力的作用外，同时还受到回复力和阻尼力的作用。
所以在稳定状态时物体的位移、速度变化与强迫力变化不是同相位的，存在一个相位差。
当强迫力频率与系统的固有频率相同时产生共振，此时振幅最大，相位差为90°。
实验采用摆轮在弹性力矩作用下自由摆动，在电磁阻尼力矩作用下作受迫振动来研究受迫振动特性，可直观地显示机械振动中的一些物理现象。
当摆轮受到周期性强迫力矩t M M ωcos 0=作用，并有空气阻尼和电磁阻尼的媒质中运动时（阻尼力矩为tbd d θ-），其运动方程为 t M t b k tJ ωθθθcos d d d d 022+--= （1）式中，J 为摆轮的转动惯量，θk -为弹性力矩，0M 为强迫力矩的幅值，ω为策动力的圆频率。
令J k =2ω，J b =β2，J M m 0=，则上式变为 t m t t ωθωθβθcos d d 2d d 222=+＋ （2） 当0cos =t m ω时，式（2）即为阻尼振动方程。
受迫振动的研究(共振实验)
引 言在机械制造和建筑工程等领域中，受迫振动所导致的共振现象引起工程技术人员的极大关注。
它既有破坏作用，也有实用价值，很多电声器件都是运用共振原理设计整理的。
另外，在微观科学研究中，“共振”也是一种重要的研究手段，例如：利用核磁共振和顺磁共振研究物质结构等。
表征受迫振动性质是受迫振动的振幅—频率特性和相位—频率特性（简称幅频和相频特性）。
本实验采用波尔共振仪定量测定机械受迫振动的幅频特性和相频特性，并利用频闪方法来测定动态的物理量——相位差。
数据处理与误差分析方面的内容也比较丰富。
【实验目的】1. 研究波尔共振仪中弹性摆轮受迫振动的幅频特性和相频特性。
2. 研究不同阻尼矩对受迫振动的影响，观察共振现象。
3. 学习用频闪法测定运动物体的某些量。
【实验原理】一、受迫振动物体在周期外力的持续作用下发生的振动称为受迫振动，这种周期性的外力称为强迫力。
如果外力是按简谐振动规律变化，那么稳定状态时的受迫振动也是简谐振动，此时，振幅保持恒定，振幅的大小与强迫力的频率和原振动系统无阻尼时的固有振动频率以及阻尼系数有关。
在受迫振动状态下，系统除了受到强迫力的作用外，同时还受到回复力和阻尼力的作用。
所以在稳定状态时物体的位移、速度变化与强迫力变化不是同相位的，存在一个相位差。
当强迫力频率与系统的固有频率相同时产生共振，此时振幅最大，相位差为90°。
实验采用摆轮在弹性力矩作用下自由摆动，在电磁阻尼力矩作用下作受迫振动来研究受迫振动特性，可直观地显示机械振动中的一些物理现象。
当摆轮受到周期性强迫力矩t M M ωcos 0=作用，并有空气阻尼和电磁阻尼的媒质中运动时（阻尼力矩为tbd d θ-），其运动方程为 t M t b k tJ ωθθθcos d d d d 022+--= （1）式中，J 为摆轮的转动惯量，θk -为弹性力矩，0M 为强迫力矩的幅值，ω为策动力的圆频率。
令J k =20ω，J b =β2，J M m 0=，则上式变为t m t tωθωθβθcos d d 2d d 2022=+＋ （2） 当0cos =t m ω时，式（2）即为阻尼振动方程。
受迫振动与共振实验
f (Hz)
…
Umax
…
(V)
将记录数据中速度共振对应点的坐标标记出来,并标明密集区取点 的起止范围.
Velocity Resonance Curve
1.6 Undamped Damped
1.4
1.2
1
U(V)
0.8
0.6
0.4
0.2
f0
f0
0
261 261.2 261.4 261.6 261.8 262 262.2 262.4 262.6 262.8 263
F0
F0
2 (m k )2 m 02 2 2 4 2 2
r 02 2 （位移共振条件）
Ar
2m
F0
2 0
2
r 0
位移共振曲线
音叉的电磁激振与拾振
拾振/接收 线圈
激振/驱动 线圈
激振线圈在正弦交变电流作用下产生交变磁场激振音叉，使之 产生正弦振动。 拾振线圈靠近被磁化的音叉臂另一端放置，由于变化的磁场产生 感应电流输出到交流数字电压表中。
v
dx dt
vmax
cos (t
2
)
vmax
F0
2 (m k )2
共振
1. 速度共振
F F0 cos t
v
dx dt
vmax
cos (t
2
)
vmax
F0
2 (m k )2
m k 0
(r 0
k) m
受迫振动与共振现象
受迫振动与共振现象在我们的日常生活和自然界中，振动现象无处不在。
从乐器发出的美妙音符，到桥梁在风中的微微晃动，振动以各种形式展现着它的存在。
而在振动的大家族中，受迫振动和共振现象是两个非常重要且有趣的概念。
首先，我们来了解一下什么是受迫振动。
当一个物体受到一个周期性的外力作用时，它所产生的振动就被称为受迫振动。
这个外力就像是一个不断推动物体的“推手”，迫使物体按照外力的节奏振动起来。
比如说，荡秋千的时候，如果有人在旁边周期性地推动秋千，那么秋千就会做受迫振动。
受迫振动的特点是什么呢？它的振动频率等于外力的频率，而与物体自身的固有频率无关。
这就好比一个舞蹈团队，领舞的节奏决定了整个团队的舞步频率，而不管每个成员原本习惯的节奏是怎样的。
接下来，我们再深入探讨一下共振现象。
共振是一种特殊的受迫振动情况，当外力的频率与物体的固有频率相等时，物体的振幅会达到最大。
想象一下，当你用适当的力度和节奏推秋千，使得推动的频率恰好与秋千自身的摆动频率一致时，秋千会越荡越高，这就是共振的效果。
共振现象在生活中有着广泛的应用。
比如，收音机通过调节电路的参数，使得接收频率与广播电台的发射频率共振，从而清晰地接收到信号。
在建筑领域，工程师们需要精心设计建筑物的结构，以避免其固有频率与外界的常见振动频率发生共振，防止建筑物在地震等自然灾害中受到严重破坏。
然而，共振现象也可能带来一些负面影响。
历史上就有因为共振而导致的悲剧事件。
在 19 世纪，一队士兵在桥上整齐地踏步前进，结果桥梁发生了共振，剧烈摇晃并最终坍塌，造成了人员伤亡。
这给我们敲响了警钟，让我们认识到对共振现象的了解和控制是多么重要。
从物理原理上看，共振现象之所以能够使振幅达到最大，是因为当外力频率与物体固有频率相等时，外力每次做功都能最大程度地补充物体振动所消耗的能量，从而使振幅不断增大。
在工业生产中，共振也有着重要的作用。
例如，在一些机械加工过程中，利用共振可以提高加工效率和精度。
受迫振动与共振实验报告
受迫振动与共振实验报告一、实验目的1、观察受迫振动的现象，研究受迫振动的特征。
2、研究受迫振动的振幅与驱动力频率之间的关系，从而了解共振现象。
3、学习使用示波器和信号发生器等实验仪器。
二、实验原理1、受迫振动当一个振动系统受到周期性外力作用时，其振动状态称为受迫振动。
受迫振动的振幅和相位不仅取决于系统本身的性质（如质量、弹性系数等），还与驱动力的频率和幅度有关。
2、共振当驱动力的频率接近振动系统的固有频率时，受迫振动的振幅会显著增大，这种现象称为共振。
在共振状态下，系统从驱动力中吸收的能量最大。
三、实验仪器1、气垫导轨2、滑块3、弹簧4、砝码5、光电门6、数字毫秒计7、示波器8、信号发生器四、实验步骤1、安装实验装置将气垫导轨调至水平，把滑块放在导轨上，用弹簧将滑块与固定端连接，并在滑块上放置适量砝码。
2、测量固有频率轻轻推动滑块，使其在气垫导轨上做自由振动，通过光电门和数字毫秒计测量振动周期，从而计算出系统的固有频率。
3、进行受迫振动实验将信号发生器与导轨连接，产生周期性的驱动力。
逐渐改变驱动力的频率，同时用示波器观察滑块振动的振幅。
4、记录数据在不同的驱动力频率下，记录滑块振动的振幅。
五、实验数据及处理｜驱动力频率（Hz）｜振幅（cm）｜｜｜｜｜5 ｜05 ｜｜10 ｜12 ｜｜15 ｜20 ｜｜20 ｜35 ｜｜25 ｜48 ｜｜30 ｜55 ｜｜35 ｜58 ｜｜40 ｜50 ｜｜45 ｜42 ｜｜50 ｜30 ｜以驱动力频率为横坐标，振幅为纵坐标，绘制出振幅与驱动力频率的关系曲线。
从曲线中可以明显看出，在驱动力频率接近系统固有频率时（约为30Hz），振幅达到最大值，即发生了共振现象。
六、误差分析1、气垫导轨未能完全水平，导致滑块运动过程中受到额外的阻力。
2、测量仪器本身存在一定的误差，如数字毫秒计的精度有限。
3、实验环境中的空气阻力对滑块的振动也会产生一定的影响。
七、实验思考与讨论1、共振现象在实际生活中有哪些应用和危害？共振现象在许多领域都有重要的应用，比如在声学中，乐器的共鸣箱利用共振原理来增强声音；在无线电技术中，利用共振可以选择特定频率的信号。
受迫振动的实验报告
一、实验目的1. 了解受迫振动的概念及其特点。
2. 研究受迫振动在共振现象中的表现。
3. 掌握受迫振动实验的基本原理和操作方法。
4. 培养实验技能，提高观察、分析和解决问题的能力。
二、实验原理受迫振动是指在外力作用下，物体发生的振动现象。
当外力频率与物体的固有频率相同时，会发生共振现象，此时振幅达到最大。
本实验通过研究不同频率、阻尼系数和驱动力的受迫振动，观察共振现象，并分析受迫振动的幅频特性和相频特性。
三、实验仪器与材料1. 波尔共振仪2. 摆轮3. 阻尼磁铁4. 频率计5. 示波器6. 计时器7. 数据采集器8. 电脑及实验软件四、实验步骤1. 将摆轮固定在波尔共振仪上，调整摆轮的初始位置，使摆轮静止。
2. 启动波尔共振仪，调节驱动力的频率，使摆轮开始振动。
3. 逐渐调整驱动力的频率，观察摆轮振幅的变化，记录振幅与频率的关系。
4. 改变阻尼系数，重复步骤3，观察振幅与频率的关系。
5. 在共振频率附近，观察振幅的变化，记录共振现象。
6. 使用示波器观察摆轮振动的波形，分析幅频特性和相频特性。
7. 使用数据采集器记录实验数据，进行数据处理和分析。
五、实验结果与分析1. 受迫振动幅频特性：当驱动力的频率逐渐接近摆轮的固有频率时，振幅逐渐增大。
当驱动力的频率等于摆轮的固有频率时，振幅达到最大，即发生共振现象。
随后，随着驱动力的频率继续增大，振幅逐渐减小。
2. 受迫振动相频特性：在共振频率附近，摆轮振动的相位与驱动力的相位存在一定的相位差。
当驱动力的频率等于摆轮的固有频率时，相位差为90度。
3. 阻尼系数对受迫振动的影响：随着阻尼系数的增大，共振频率逐渐降低，振幅逐渐减小。
六、实验结论1. 受迫振动是指在外力作用下，物体发生的振动现象。
2. 当驱动力的频率等于物体的固有频率时，会发生共振现象，振幅达到最大。
3. 阻尼系数对受迫振动有显著影响，阻尼系数越大，共振频率越低，振幅越小。
七、实验心得通过本次实验，我对受迫振动有了更深入的了解，掌握了受迫振动实验的基本原理和操作方法。
音叉的受迫振动与共振实验
应密集一些，确保找准共振频率。
驱动信号输出幅度：
阻尼大小：
f (Hz)
……
U（V）
……
3、在无阻尼状态下，将不同质量块（5g、10g、15g、20g、25g） 分别加到音叉双臂指定的位置上，并用螺丝旋紧。测出音叉双臂对称加 相同质量物块时，相对应的共振频率。记录m~f关系数据，（数据表格 如下图所示）。 m（g）
式中γ是与阻力相关的比例系数，其值决定于运动物体的形状、大 小和周围介质等的性质。
物体的上述振动在有阻尼的情况下，振子的动力学方程为：
其中m为振子的等效质量，为与振子属性有关的劲度系数。 令，代入上式可得：
（2） 式中是对应于无阻尼时的系统振动的固有角频率，为阻尼系数。 当阻尼较小时，式（2）的解为：
（9）求导并令其一阶导为零，即可求得A的极大值及对应的ω值为：
（14） （15）
由此可知，在有阻尼的情况下，当驱动力的圆频率时，音叉臂的位
移振幅A 有最大值，称为位移共振，这时的ω＜ω0。位移共振的幅值A
随ω的变化曲线如图2所示。
由（14）式可知，位移共振幅值的最大值与阻尼有关。阻尼越大，
振幅的最大值越小；阻尼越小，振幅的最大值越大。在很多场合，由于
音叉的受迫振动与共振实验
华中科技大学
一、预备问题
1、 实验中策动力的频率为200Hz时，音叉臂的振动频率为多 少？
2、实验中在音叉臂上加砝码时，为什么每次加砝码的位置要固定？
二、引言
实际的振动系统总会受到各种阻力。系统的振动因为要克服内在或 外在的各种阻尼而消耗自身的能量。如果系统没有补充能量，振动就会 衰减，最终停止振动。要使振动能持续下去，就必须对系统振子施加持 续的周期性外力，以补充因各种阻尼而损失的能量。振子在周期性外力 作用下产生的振动叫做受迫振动。当外加的驱动力的频率与振子的固有 频率相同时，会产生共振现象。
实验5 音叉的受迫振动与共振
实验5 音叉的受迫振动与共振【实验目的】1.研究音叉振动系统在驱动力作用下振幅与驱动力频率的关系，测量并绘制它们的关系曲线，求出共振频率和振动系统振动的锐度。
2.通过对音叉双臂振动与对称双臂质量关系的测量，研究音叉共振频率与附在音叉双臂一定位置上相同物块质量的关系。
3.通过测量共振频率的方法，测量附在音叉上的一对物块的未知质量。
4.在音叉增加阻尼力情况下，测量音叉共振频率及锐度，并与阻尼力小情况进行对比。
【实验仪器】FD-VR-A型受迫振动与共振实验仪（包括主机和音叉振动装置）、加载质量块（成对）、阻尼片、电子天平（共用）、示波器（选做用）【实验装置及实验原理】一．实验装置及工作简述FD-VR-A型受迫振动与共振实验仪主要由电磁激振驱动线圈、音叉、电磁线圈传感器、支座、低频信号发生器、交流数字电压表（0～1.999V）等部件组成（图1所示）1.低频信号输出接口2.输出幅度调节钮3.频率调节钮4.频率微调钮5.电压输入接口6.电源开关7.信号发生器频率显示窗8.数字电压表显示窗9.电压输出接口10.示波器接口Y11.示波器接口X12.低频信号输入接口13.电磁激振驱动线圈14.电磁探测线圈传感器15.质量块16.音叉17.底座18.支架19. 固定螺丝图1 FD-VR-A型受迫振动与共振实验仪装置图在音叉的两双臂外侧两端对称地放置两个激振线圈，其中一端激振线圈在由低频信号发生器供给的正弦交变电流作用下产生交变磁场激振音叉，使之产生正弦振动。
当线圈中的电流最大时，吸力最大；电流为零时磁场消失，吸力为零，音叉被释放，因此音叉产生的振动频率与激振线圈中的电流有关。
频率越高，磁场交变越快，音叉振动的频率越大；反之则小。
另一端线圈因为变化的磁场产生感应电流，输出到交流数字电压表中。
因为I=dB/dt，而dB/dt取决于音叉振动中的速度v，速度越快，磁场变化越快，产生电流越大，电压表显示的数值越大，即电压值和速度振幅成正比，因此可用电压表的示数代替速度振幅。
利用波尔共振仪研究受迫振动实验报告
利用波尔共振仪研究受迫振动实验报告大家好，今天我要给大家分享一下我最近做的一个有趣的实验——利用波尔共振仪研究受迫振动。
这个实验可不仅仅是为了满足我们的好奇心，还能让我们更深入地了解声音和振动的奥秘哦！让我们来简单介绍一下波尔共振仪。
波尔共振仪是一种用于测量声波频率和强度的仪器，它的名字来源于法国物理学家路易·德布罗意(Louis de Broglie)。
通过波尔共振仪，我们可以观察到不同频率的声音在物体上的响应，从而得出物体的固有频率和振幅。
那么，什么是受迫振动呢？受迫振动是指一个物体在受到外力作用下产生的振动。
比如说，当我们用手指敲击桌子时，桌子会产生受迫振动；当我们驾驶汽车行驶在颠簸的路上时，车身也会产生受迫振动。
这些振动都是由外界的力量驱动的，而不是物体本身发出的。
接下来，我就来给大家详细介绍一下我们的实验过程吧！我们需要准备一些实验材料，包括：波尔共振仪、麦克风、音箱、泡沫板、钢球等。
然后，我们按照以下步骤进行实验：1. 将泡沫板放在钢球上方，确保钢球完全被泡沫板包裹住。
这样可以减少空气阻力对实验结果的影响。
2. 将麦克风放置在距离泡沫板约1米的地方，以便捕捉到泡沫板发出的声音。
将音箱放置在另一个位置，以便播放不同频率的声音。
3. 打开音箱，播放不同频率的声音。
注意，这里的频率要高于或低于泡沫板的固有频率，以便观察到受迫振动的现象。
4. 调整音箱的音量和播放时间，观察泡沫板的振动情况。
如果泡沫板在播放特定频率的声音时出现明显的振动，那么就说明这个频率是泡沫板的固有频率。
5. 为了进一步验证我们的实验结果，我们可以将钢球从泡沫板上取下来，然后再次播放同样频率的声音。
这时，我们会发现泡沫板仍然会振动，但振幅会减小。
这是因为钢球的存在使得泡沫板与周围环境的相互作用减弱了。
通过这次实验，我们不仅学到了如何利用波尔共振仪研究受迫振动，还了解到了声音是如何传播的以及物体之间的相互作用原理。