浙江省北仑中学2013-2014学年高一上学期期中考试数学(7-10班)试题及答案
高中浙江省宁波市北仑中学高一上学期期中数学(2-10班)试题
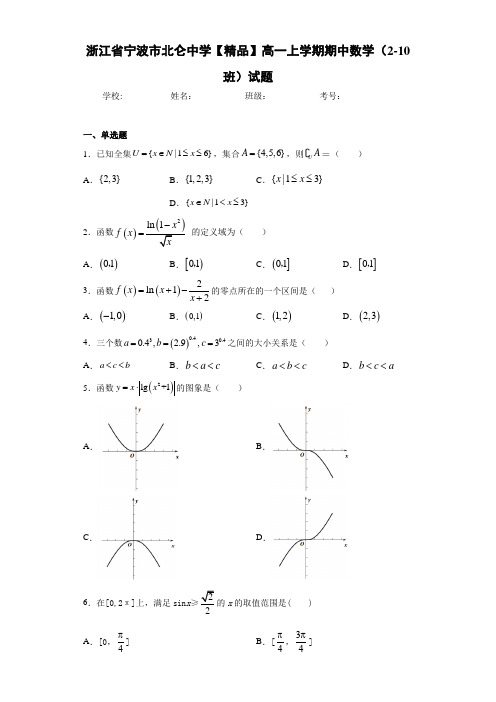
浙江省宁波市北仑中学【精品】高一上学期期中数学(2-10班)试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知全集{|16}U x N x =∈≤≤,集合{4,5,6}A =,则UA( )A .{2,3}B .{1,2,3}C .{|13}x x ≤≤D .{|13}x N x ∈<≤2.函数()2ln 1x f x -=的定义域为( )A .()01,B .[)01,C .(]01,D .[]01,3.函数()()2ln 12f x x x =+-+的零点所在的一个区间是( ) A .()1,0-B .()0,1C .()1,2D .()2,34.三个数()0.430.40.4, 2.9,3a b c ===之间的大小关系是( ) A .a c b <<B .b a c <<C .a b c <<D .b c a <<5.函数()2lg +1y x x =⋅的图象是( )A .B .C .D .6.在[0,2π]上,满足sin x ≥2的x 的取值范围是( ) A .[0,4π] B .[4π,34π]C .[4π,2π] D .[34π,π] 7.设函数()()0,1xf x a a a =>≠,若()122019+++9f x x x =,则()()()122019222f x f x f x ⋅=( )A .3B .9C .27D .818.设函数()1,1,x f x x ⎧=⎨-⎩为有理数为无理数,则下列结论错误的是( )A .()f x 的值域为{}1,1-B .()f x 是非奇非偶函数C .对于任意x ∈R ,都有()()1f x f x +=D .()f x 不是单调函数9.在实数的原有运算法则中,补充定义新运算“⊕”如下:当a b ≥时,a b a ⊕=;当a b <时,2a b b ⊕=,已知函数()()()[]()1222,2f x x x x x =⊕-⊕∈-,则满足()()13f m f m +≤的实数的取值范围是( )A .1,2⎡⎫+∞⎪⎢⎣⎭B .1,22⎡⎤⎢⎥⎣⎦C .12,23⎡⎤⎢⎥⎣⎦D .21,3⎡⎤-⎢⎥⎣⎦10.给出定义:若1122m x m -<≤+(其中m 为整数),则m 叫做离实数x 最近的整数,记作{}x ,即{}=x m .设函数(){}f x x x =-,二次函数2()g x ax bx =+,若函数()y f x =与()y g x =的图象有且只有一个公共点,则,a b 的取值不可能...是( ) A .4,1a b =-= B .2,1a b =-=- C .4,1a b ==- D .5,1a b ==二、双空题 11.(1)12.55(0.64)-=_________;(2)7log 22lg5lg 47++=_________.12.函数221()3x xy -=的值域是________,单调递增区间是_____;13.已知扇形的周长为40,当它的圆心角为____时,扇形的面积最大,最大面积为____. 14.若函数()f x 是幂函数,且满足()()432f f =,则()2f = __________,函数()()2g x f x ax a =-+过定点__________.三、填空题15.函数()()22log 3f x x ax =-++在()2,4是单调递减的,则a 的取值范围是________.16.已知()312=-+xf x ,若关于x 的方程2[()](2)()20f x a f x a -++=有三个实根,则实数a 的取值范围是_____.17.已知0a >时,对任意0x >,有2()()0x a x bx a -+-≥恒成立,则ab的取值范围是_________________.四、解答题18.已知集合231{|230},{|log ,27},9A x x xB y y x x =+-<==<<2{|(1)220,}C x x m x m m R =----<∈ .(1)求AB ;(2)若()C AB ⊆ ,求实数m 的取值范围.19.已知函数()(1)(3)x x f x a a =-+(1a >) (1)求函数()f x 的值域;(2)若[2,1]x ∈-时,函数()f x 的最小值为5-,求a 的值和函数()f x 的最大值.20.已知()()()3sin sin 2sin f ππαααπα⎛⎫--+ ⎪⎝⎭=--. (1)若tan 2α=,求()sin 2cos 3f ααα+的值;(2)若163312f πππαα⎛⎫⎛⎫-=--<<- ⎪ ⎪⎝⎭⎝⎭,求5cos +cos 63ππαα⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭的值.21.已知函数()221x x af x +=+.(1)若()f x 为奇函数,求a 的值;(2)在(1)的条件下,判断()f x 在R 上的单调性并用定义证明; (3)若对任意的,[0,1]m n ∈,总有2()()f m f n >成立,求a 的取值范围. 22.已知a R ∈,()()2log 1f x ax =+. (1)若0a <,求()2f x的值域;(2)若关于x 的方程()()()22log 4250f x a x a x ⎡⎤--+-=⎣⎦的解集中恰有一个元素,求实数a 的取值范围;(3)当0a >时,对任意的1,3t ⎛⎫∈+∞ ⎪⎝⎭,()2f x在[],1t t +上的最大值与最小值的差不超过2,求a 的取值范围.参考答案1.B 【解析】 【分析】求出全集U 中的元素,根据补集定义求解。
2013-2014学年高一数学上学期期中试卷(4-11班)及答案(新人教A版 第143套)

宁波效实中学二○一三学年度第一学期高一期中数学试卷说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共100分. 第Ⅰ卷(选择题 共30分)一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中只有一项是符合题目要求的. 1.已知函数()f x =A .(,1)-∞B .(,1]-∞C .(1,)+∞D .[1,)+∞2.已知集合{|2}S x x =<,2{|340}T x x x =--≤,则()R S T =ðA .(2,4)B .[2,4]C .(,4)-∞D . (,4]-∞3.在区间(,0)-∞上为增函数的是A .1=yB .21x y +=C .122---=x x yD . 21xy x-=- 4.设函数221,1()2,1,x x f x x x x ⎧-≤⎪=⎨+->⎪⎩则1(2)f f ⎛⎫⎪⎝⎭的值为A .18B .89C .1516D .2716-5.若函数()f x = 3442++-mx mx x 的定义域为R ,则实数m 的取值范围是 A .(,)-∞+∞ B .3[0,)4 C .3(,)4+∞ D .3(0,)46.设,a b 是非零实数,若a b <,则下列不等式一定成立的是k*s@5%uA .22a b <B .22ab a b <C .2211ab a b<D .b aa b< 7.已知函数25,1,()11, 1.x ax x f x x x ⎧-+<⎪=⎨+≥⎪⎩在定义域R 上单调,则实数a 的取值范围为 A .(,2]-∞B .[2,)+∞C .[4,)+∞D . [2,4]8.已知集合23{|0,(1,1)}2A x x x k x =--=∈-,若集合A 有且仅有一个元素,则实数k 的取值范围是A .159[,){}2216--B .15(,)22C .95[,)162-D .9[,)16-+∞ 9.已知{},,,,,a ab Max a b b a b ≥⎧=⎨<⎩若函数{}2()|4|,f x Max x x x =-则函数()f x k*s@5%uA .有最小值为0,有最大值为4B .无最小值,有最大值为4C .有最小值为0,无最大值D .无最值10.若0,0,22a b a b >>+=,则下列不等式:○11ab ≤;22≤;○3222a b +≥; ○43383a b +≥;○5112a b+≥.对一切满足条件的,a b 成立的是 A .○1○2○4B .○1○2○5C .○1○4○5D .○2○3○4第Ⅱ卷(非选择题 共70分)二、填空题:本大题共7小题,每小题3分,共21分.11.已知函数()f x =()2f a =,则实数a = ▲ .12.已知集合2{|230}M x x x =--=,{|20}N x ax =-=.若N M ⊆,则实数a 取值构成的集合为 ▲ .13.关于x 的不等式2440x mx -+≥对任意[1,)x ∈+∞恒成立,则实数m 的取值范围为 ▲ .14.已知条件:{}1⇐{}||23|1M x Z x x ⊆∈-<+,则满足条件的集合M 有 ▲ 个.15.函数222331x x y x x -+=-+的值域为 ▲ .16.若关于x 的不等式|23||21|x x a ++-≤有解,则实数a 的取值范围为 ▲ .17. 已知22()53196|53196|f x x x x x =-++-+,则(1)(2)(50f f f +++=▲ .三、解答题:本大题共6小题,共49分. 解答应写出文字说明,证明过程或演算步骤. 18.已知定义在R 上的偶函数()f x .当0x ≥时,2()1x f x x -+=-且(1)0f =. (Ⅰ)求函数()f x 的解析式并画出函数的图象; (Ⅱ)写出函数()f x 的值域.19.已知集合2{|230}A x x x =-->,集合4{|2}2B x x x =≤--. (Ⅰ)求A ,B ; (Ⅱ)求A B 及()R C A B .20.已知定义域为(1,1)-的函数2()1xf x x =+.(Ⅰ)判断函数()f x 奇偶性并加以证明; (Ⅱ)判断函数()f x 的单调性并用定义加以证明; (Ⅲ)解关于x 的不等式(1)()0f x f x -+<.xyO21.已知集合{}22|280A x x ax a =--<,{}22|5(1)4,B x x x m x m R =-=--∈.(Ⅰ)若12(,)A x x =且2115x x -=,求实数a 的值; (Ⅱ)若存在实数m 使得B A ⊆,求实数a 范围.22.已知定义在R 上的奇函数()f x .当0x <时,2()2f x x x =+. (Ⅰ)求函数()f x 的解析式;(Ⅱ)问:是否存在实数,()a b a b ≠,使()f x 在[,]x a b ∈时,函数值的集合为11[,]b a?若存在,求出,a b ;若不存在,请说明理由.附加题:已知*,,N a b c ∈,方程2=0ax bx c ++在区间(1,0)-上有两个不同的实根,求a b c ++的最小值.宁波效实中学二○一三学年度第一学期高一期中数学参考答案11、7 12、{0,2,}3- 13、 (,1]-∞ 14、 3 15、5[,3]316、 [4,)+∞ 17、66018、(I)2,[0,1)(1,)1()0,{1,1}2,(,1)(1,0)1x x x f x x x x x -+⎧∈+∞⎪-⎪=∈-⎨⎪+⎪-∈-∞--+⎩;图象如图: (II)值域为(,2](1,)-∞--+∞u19、(I )(,1)(3,)A =-∞-+∞,[0,2)[4,)B =+∞;(II )[4,)AB =+∞, ()[1,3][4,)RC AB =-+∞。
浙江省北仑中学高一数学上学期期中试题(新疆部)新人教A版

浙江省北仑中学2013-2014学年高一数学上学期期中试题(新疆部)新人教A 版2、cos 24cos36cos66cos54︒︒︒︒-的值为 ( )A 、 0B 、12 C 、2 D 、 12-3、下列函数中,最小正周期是2π的是( ) A 、2sin y x = B 、sin cos y x x = C 、tan 2xy = D 、cos 41y x =+ 4、若平面四边形ABCD 满足0,()0,AB CD AB AD AC +=-•=u u u r u u u r r u u u r u u u r u u u r,则该四边形一定是( )A 、直角梯形B 、矩形C 、菱形D 、正方形5、ABC ∆的三个内角为A B C 、、,cos 2cos 2B CA ++的最大值是 ( ) A 、3B 、0.5C 、1D 、1.56、若||1,||6,()2==•-=a b a b a ,则a 与b 的夹角为( ) A 、6π B 、3π C 、4π D 、2π 7、在△ABC 中,D 、E 、F 分别BC 、CA 、AB 的中点,点M 是△ABC 的重心,则 -+等于( ) A 、OB 、MD 4C 、MF 4D 、ME 48、定义运算⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡df ce bf ae f e d c b a ,如⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡1514543021.已知πβα=+,2πβα=-,则=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡ββααααsin cos sin cos cos sin ( ) A 、00⎡⎤⎢⎥⎣⎦B 、01⎡⎤⎢⎥⎣⎦C 、10⎡⎤⎢⎥⎣⎦D 、11⎡⎤⎢⎥⎣⎦9、已知P 1(2,3),P 2(-1,4),且12P P 2PP =u u u r u u u r,点P 在线段P 1P 2的延长线上,则P 点的坐标为( )A 、(34,-35)B 、(-34, 35) C 、(4,-5) D 、(-4,5)10、 设3120,sin ,cos()2513παβααβ<<<=-=,则sin β的值为( )A 、6516 B 、6533 C 、6556 D 、656311、函数2cos()cos()44y x x ππ=-+是( ) A 、最小正周期为π的奇函数 B 、最小正周期为π的偶函数C 、最小正周期为2π的奇函数 D 、最小正周期为2π的偶函数 12、向量(cos ,sin )θθ=a ,向量1)=-b 则|2|-a b 的最大值,最小值分别是( )A 、0,24 B、4,、16,0 D 、4,0 二、填空题(共6题,每小题3分)13、已知i 为一单位向量,向量a 与i 之间的夹角是120o,而a 在i 方向上的投影为-2,则|=|a .14、已知α是第二象限的角,4tan(2)3πα+=-,则tan α= 15、若向量(2,1),(1,m),(1,2)=-=-=-a b c ,若()||+a b c ,则m =16、已知锐角,αβ满足sin 510α=β=,则α+β= 17、已知02x π<<,化简:2lg(cos tan 12sin ))]lg(1sin 2)24x x x x x π•+-+--+= 18、在ABC ∆中,M 是线段BC 的中点,AM=3,BC=10,则AB AC •u u u r u u u r=三、解答题(共6大题,共84分)19、(10分)计算:(1)51tan1251tan12ππ+- (220、(12分)设e 1,2e 是两个相互垂直的单位向量,且2(2)=-+a e e 1,12λ=-b e e . (1)若||a b ,求λ的值;(2)若⊥a b ,求λ的值。
浙江省北仑中学2013-2014学年高一上学期期中考试化学试题 Word版含答案(1班).pdf

27.工业上冶炼冰铜(mCu2O·nFeS)可得到粗铜,再以粗铜为原料制备硫酸铜晶体。
(1)气体A中的大气污染物可选用下列试剂中的
(填序号)吸收。
a.浓H2SO4
b.浓HNO3
c. NaOH溶液
d.氨水
(2)用稀H2SO4 浸泡熔渣B,取少量所得溶液,滴加
(填物质名称)溶液后呈红色,说明溶液中存在Fe3+,检
C.非金属氧化物一定是酸性氧化物 D.酸性氧化物一定是非金属氧化物
3.下列各组离子在指定的溶液中一定能大量共存的是
()
A.碱性溶液中:K+、Ba2+、Cl-、NO3-
B.酸性溶液中:Na+、Fe2+、NO3-、SO42-
C.能与Al反应生成H2的溶液:Mg2+、K+、NO3-、Cl-
5.下列关于金属冶炼的说法正确的是
()
A.金属冶炼的本质是将化合态金属还原为游离态,冶炼方法由金属的活泼性决定
B.Cu的湿法冶炼是将金属钠投入到CuSO4溶液中,从而置换出铜
C.Fe通常采用热还原法冶炼,加入石灰石的目的是除去过量的碳
D.由于Al的活泼性强,故工业上采用电解熔融AlCl3的方法生产Al
B.0.1mol H2O2催化完全分解(二氧化锰作催化剂),转移电子数为0.1 NA
()
C.100mL 0.1mol/L的H2SO3溶液中,含有的离子数约为0.03 NA
D.1 mol C12发生化学反应,转移的电子数必为2NA
19.有一混合物的水溶液,只可能含有以下离子中的若干种:K+、NH4+ 、Mg2+、Ba2+、Cl-、CO32 -、SO42
B.上述方法的缺点是由于CO2增多,会大大提高空气的酸度
ห้องสมุดไป่ตู้
浙江省北仑中学2013-2014学年高一上学期期中考试化学(7-8班)试题及答案

可能用到的相对原子质量:H 1 He 4 C 12 N 14 O 16 Na 23 P31 S 32 Cl 35.5K 39 Ca 40 Zn 65 Ag 108 Ba 137一、单项选择题:(每小题2分,共48分)1.下列化学反应中,不属于四种基本反应类型但属于氧化还原反应的是A .Cu 2(OH)2CO 3=2CuO+ H 2O+CO 2↑B .NaOH+HCl = NaCl+H 2OC .2Na 2O 2 + 2H 2O = 4NaOH + O 2↑D .4Fe(OH)2+O 2+2H 2O=4Fe(OH)32.13153I 是常规核裂变产物之一,可以通过测定大气或水中13153I 的含量变化来检测核电站 是否发生放射性物质泄漏。
下列有关13153I 的叙述中错误的是A .13153I 的原子核外电子数为78B .13153I 的质子数为53C .13153I 的化学性质与12753I 几乎相同D .13153I 的原子核内中子数多于质子数3.原子结构模型的演变图中,⑴为道尔顿实心球式原子模型 ⑵为卢瑟福行星运转式原子模型 ⑶为汤姆生葡萄干面包式原子模型 ⑷为近代量子力学原子模型⑸为玻尔轨道式原子模型。
其中符合历史演变顺序的一组排列是A .⑴⑶⑵⑸⑷ B .⑴⑵⑶⑷⑸ C .⑴⑸⑶⑵⑷ D .⑴⑶⑸⑷⑵ 4.下列仪器常用于物质分离的是① ② ③ ④ ⑤ ⑥ ⑦A .③⑤⑦B .②③⑤C .②⑤⑦D .①②⑥5.英国的两名科学家安德烈·海姆和康斯坦丁·诺沃肖洛夫因为在石墨烯方面的“突破性实验”获得了2010年的诺贝尔物理学奖。
石墨烯是由碳原子按六边形晶格整齐排布而成的,下列关于石墨烯的说法正确的是A .石墨烯是新发明的一种化合物B .石墨烯属于盐C .石墨烯和石墨互为同素异形体D .石墨烯和石墨互为同位素6.下列溶液中Cl -浓度与50 mL 0.1 mol·L -1 MgCl 2溶液中Cl -浓度相等的是A .50 mL 0.1 mol·L -1的NaCl 溶液B .50 mL 0.1 mol·L -1的FeCl 3溶液C .25 mL 0.2 mol·L -1的CaCl 2溶液D .75 mL 0.2 mol·L -1 NH 4Cl 溶液7.设N A 代表阿伏伽德罗常数,下列说法正确的是A .22.4LNe 含有N A 个Ne 分子B .0.1mol/LNa 2SO 4溶液中有0.2N A 个Na +C .25℃,1标准大气压下,22gCO 2中含有0.5N A 个二氧化碳分子D .标准状况下,N A 个水分子所占的体积约为22.4L8.在下列条件下,两种气体的分子数一定相等的是A .同质量,不同密度的N 2和C 2H 4B .同温度、同体积的O 2和N 2C .同体积、同密度的CO 和CH 4D .同压强、同体积的N 2和O 29.下列一定是纯净物的是A .金刚石和石墨混合B .汽油C .含Fe 元素的质量分数为70%的铁红(Fe 2O 3)D .不含杂质的盐酸10.已知R 2-核内共有N 个中子,R 的质量数为A,mgR 2-中含电子的物质的量为A .A)N A (m -mol B .A )2N A (m +-molC.mA )2NA(+-mol D.A )2NA(m--mol11.在盛有碘水的三只试管中分别加入煤油、四氯化碳和酒精,充分振荡后静置,出现如图所示的现象,有关说法正确的是A.○1中加了四氯化碳,○2中加了煤油,○3中加了酒精B.○1中加了煤油,○2中加了四氯化碳,○3中加了酒精C.○1中加了酒精,○2中加了煤油,○3中加了四氯化碳D.○1中加了四氯化碳,○2中加了酒精,○3中加了煤油12.在K2CO3样品中含Na2CO3、KNO3、Ba(NO3)2中的一或二种杂质,将13.8 g样品溶于足量水中得到澄清溶液,再加入过量CaCl2溶液,可得9.0 g沉淀,则原样品中含有的杂质会是A.肯定有Na2CO3,没有Ba(NO3)2B.肯定有KNO3,没有Ba(NO3)2,可能还有Na2CO3 C.肯定没有Na2CO3,Ba(NO3)2D.无法判断何种为肯定或否定的杂质13.某一溶液中仅含有Na+、Mg2+、Cl-、SO42-四种离子,其中Na+和Mg2+的个数比为4∶5,则Cl-和SO42-的个数比可能为:①8∶3 ②1∶3 ③4∶1 ④3∶2 ,其中正确的是A.只有①B.只有①②④C.只有②④D.①②③④14.等质量的CH4和NH3相比较,下列结论错误的是A.它们的分子个数比为17:16 B.相同状况下它们所占的体积比为17:16C.它们的氢原子个数比为17:12 D.它们的原子个数比为17:1615.下列实验操作中正确的是A.蒸发操作时,应使混合物中的水分完全蒸干后,才能停止加热B.蒸馏时,温度计水银球靠近蒸馏烧瓶的底部, 且冷却水从冷凝管的下口通入上口流出C.分液操作时,分液漏斗中下层液体从下口放出,上层液体从上口倒出D.向1 mol·L-1氯化铁溶液中加入少量的NaOH溶液制取氢氧化铁胶体16.某研究性学习小组欲用化学方法测量一个不规则容器的体积。
浙江省北仑中学2011-2012学年高一下学期期中考试数学试题(7-10班)

(供7、8、9、10班用)一、选择题(每小题5分,共50分,有且只有一个答案正确)。
1.sin12π= ( )A123 62- 62+2.在等差数列}{n a 中,836a a a +=,则=9S ( ) A 0 B 1 C 1- D 以上都不对3. △ABC 中,已知()()a b c b c a bc +++-=,则A 的度数等于 ()A .120B .60C .150D .304. 在等比数列{}n a 中,117a a ⋅=6,144a a +=5,则1020a a 等于 ( )A .32B .23C .23或32D .﹣32或﹣235.在直角ABC ∆中,CD 是斜边AB 上的高,则下列等式不成立的是 ( )A.2AC AC AB=⋅B.2BC BA BC =⋅C.2AB AC CD =⋅D.22()()AC AB BA BC CD AB⋅⨯⋅=6.函数2)cos[2()]y x x ππ=-+是 ( )A .周期为4π的奇函数 B .周期为4π的偶函数 C .周期为2π的奇函数 D .周期为2π的偶函数7.设向量a ,b 满足:||3=a ,||4=b ,0⋅=a b .以a ,b ,-a b 的模为边长构成三角形,则它的边与半径为1的圆的公共点个数最多为 ( )A .3 B.4 C .5 D .68.下列各式中,值为12的是 ( ) A.1515sin cos B.221212cos sin ππ- C.22251225tan .tan .- 1302cos + 9.ABC ∆的三个内角为A B C 、、,cos 2cos2B CA ++的最大值是________ ( ) A .3 B.0.5 C .1D .1.510.已知数列{n a }的前n 项和1111[2()][2(1)()]22n n n S a b n --=---+(1,2,),n =其中a 、b 是非零常数,则存在数列{n x }、{n y }使得 ( )A .}{,n n n n x y x a 其中+=为等差数列,{n y }为等比数列B .}{,n n n n x y x a 其中+=和{n y }都为等差数列C .}{,n n n n x y x a 其中⋅=为等差数列,{n y }都为等比数列D .}{,n n n n x y x a 其中⋅=和{n y }都为等比数列二、填空题:请把答案填在题中横线上(每小题4分,共28分).11.向量(1,2)=a ,(2,3)=-b .若向量c 满足()//+c a b ,()⊥+c a b ,则c =_______.12. 若点O 是ABC △的外心,且0OA OB CO ++=,则ABC △的内角C 为_________. 13.若-2π<α<-23π,则2)cos(1πα--=_________.14.已知数列{}n a 满足11a =,1n n a a --=(2)n ≥,则n a =________15. 在锐角ABC ∆中,1,2,BC B A ==则AC 的取值范围为 .16.已知数列{}n a 满足:1a =m (m 为正整数),1,231,nn n n n a a a a a +⎧⎪=⎨⎪+⎩当为偶数时,当为奇数时。
浙江省北仑中学高一数学上学期期中考试试题(2、3、4、5、6班)【会员独享】

北仑中学2011学年第一学期高一年级期中考试数学试卷(供2-6班)一、选择题(本题共10小题,每题5分,共50分) 1.给出下列关系:①R ∈21②R ∉2 ③|-3|+∈N ④Q ∈-|3|,其中正确的个数为( )(A )1 (B )2 (C )3 (D )42.下列各组函数中:①y=x 与y=(x )2②y=x 与y=2x ③y=x 2+1与y=t 2+1 ④y=112+-x x 与y=x -1.表示同一函数的组数是( )(A )1 (B )2 (C )3 (D )43.若0<a <1,则不等式(a -x)(x -a1)>0的解是( ) (A )a <x<a 1 (B )a 1<x<a (C )x>a 1或x<a (D )x<a1或x>a4.∆ABC 中,若sinA+cosA= 127,那么∆ABC 是( )(A )锐角三角形 (B )直角三角形(C)钝角三角形(D)等边三角形 5.若(cos )cos 2f x x =,(sin15)f =( )()A 12 ()B 12- ()C ()D 6.设有n 个样本12,,,n x x x ,其标准差为x s ,另有n 个样本12,,,n y y y ,且35k k y x =+(1,2,,)k n =,其标准差为y s ,则下列关系正确的是( )()A 35y x s s =+ ()B 3y x s s = ()C y x s = ()D 5y x s =+7.根据函数y=x 和y=x1的图象,判断下列四个曲线中,哪一个是y=x -x 1的图象( )8、按如下程序框图,若输出结果为170,则判断框内应补充的条件为( )A.5i > B. 7i ≥ C.9i >D.9i ≥9.下列函数中,值域是(0,+ ∞)的函数是 ( )A y=x 2-x+1 B xy -⎪⎭⎫ ⎝⎛=151 C 1321+=-xy D y=|log 2x 2|10.函数2()1|12|,()21,f x x g x x x =--=-+,定义⎩⎨⎧=)()()(x g x f x F )()()()(x g x f x g x f <≥,则方程12)(=⋅xx F 的实根的个数是( ) (A ) 1 (B )2 (C )3 (D )4二、填空题(本大题共7小题,每小题4分,共28分,把答案填在答题卷中的相应位置上) 11.函数)2(log 21-=x y 的定义域是 .12.某工厂生产A 、B 、C 三种不同型号的产品,产品数量之比依次为2:3:5.现用分层抽样方法抽出一个容量为n 的样本,样本中A 种型号产品有16件,那么此样本的容量n = . 13.若lgx+lgy=2lg(x -2y),则yx2log 的值的集合是 . 14.已知f(x) 为奇函数, 定义域为R, 当x >0 时,f(x)=lg(x+1), 则当x<0时,f(x) 的表达式为 .15.已知角α终边过点(5,12)(0)P a a a -<,则sin cos αα+的值为 . 16.一种产品的年产量原来是a 件,在今后的m 年内,计划使年产量平均每年比上一年增加p %.写出年产量y 随经过年数x 变化的函数关系式________________________________________.17.定义在R 上的奇函数f(x)的图象经过点(-4,0),且在(0,+∞)上单调递减,则不等式f(x)≥0的解集为________________________________.三、解答题(本大题共5小题,共72分,解答应写出文字说明,证明过程或演算步骤) 18.奇函数f(x)在其定义域(-21,21)上是减函数,并且f(1-sin α)+f(1-sin 2α)<0,求角α的取值范围。
浙江省北仑中学2013-2014学年高一上学期期中考试地理(9-10班)试题及答案

一、选择题(本大题有36小题,每题只有一个正确答案,每题2分,共72分。
请将正确答案写在答题卷上)1.下列有关太阳外部圈层与其活动的组合正确的是A.日冕层——黑子B.色球层——耀斑C.光球层——日珥D.光球层——太阳风2.北京和上海两地的自转角速度和线速度比较,正确的叙述是A.两地的角速速度和线速度都相同B.两地的角速度和线速度都不同C.线速度相同,角速度都不同D.角速度相同,线速度北京小于上海3.下列自然现象与太阳辐射无关..的是A.生物的活动B.大气和水体的运动C.煤、石油的形成D.火山的爆发4.在地球表面上,决定太阳直射最北和最南界线的是A.地球的自转B.地球的球体形状C.地球在宇宙中的位置D.黄赤交角的大小5.某海轮在赤道上沿180°经线向正北方向发射炮弹,炮弹将落在A.180°经线以东B.180°经线C.东半球D.180°经线以西6.当晨昏圈与经线圈重合时,下列说法正确的是A.地球位于近日点附近B.极圈上的正午太阳高度为0°C.地球公转速度越来越慢D.全球各地昼夜平分7.当北京时间2013年1月1日8:00时,全球未进入2013年的地区有A.正好一半地区B.多一半的地区C.少一半的地区D.不能确定北京时间2005年1月18日3时16分,中国南极科考队到达了海拔4093米的南极冰盖的最高点(80°22′0″S、77°21′11″E),回答8~9题。
8.中国科学家登上南极内陆冰盖最高点时,当地的区时是A.3时16分B.0时16分C.23时16分D.3时0分9.考察队员在南极内陆冰盖最高点插上五星红旗,红旗向A.东南方向飘动B.东北方向飘动C.西南方向飘动D.西北方向飘动2007年9月21日,日本探测船“地球”号在东京以南太平洋一处水深2500米的海洋开始钻探,从海底向下钻入7000米深处,盼能揭示气候暖化秘密,寻找有助于解释生命起源的微生物及了解地震成因。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
.设集合A=},41|{<<x x ,集合B =},032|{2≤--x x x 则A∩()R C B =(▲) A .(1,4) B .(3,4) C.(1,3) D .(1,2)∪(3,4). 2.下列四组函数中,表示相同函数的一组是(▲) A .2()lg ,()2lg f x x g x x == B
.()()f x g x =
=C .21(),()11x f x g x x x -=
=+- D .1()2,()2x
x f x g x -⎛⎫
== ⎪⎝⎭
3.设a=3
1
3,b=2
13,c=lo 3
g 2
1
则它们的大小关系(▲)A .c b a << B .c a b << C .a b c << D .a c b <<4.函数1||2)(+-=x x f 的图像大致为(▲)
5.已知函数⎩
⎨⎧<≥+=0|,|0
,12)(x x x x x f ,且3)(0=x f ,则实数0x 的值为 (▲)
A . 3-
B . 1
C . 3-或1
D . 3-或1或3 6.函数()||f x x x x =+,R x ∈是 (▲)
A .偶函数
B .奇函数
C .既不是奇函数也不是偶函数
D .既是奇函数又是偶函数
7.已知函数()(01)x
f x a a a =>≠且在区间[-2,2]上的值不大于2,则函数2()lo
g g a a =的值域是(▲) A .1
1[,0)
(0,]22- B .11(,)(0,]22-∞- C .11[,]22- D .11
[,0)[,)22
-+∞ 8.2
()log (1)(01)a f x x ax a a =-+>≠且满足:对任意实数21,x x ,当2
21a
x x ≤
<时,总有12()()<0f x f x -,那么a 的取值范围是(▲)
A . (0,2)
B .(0,1)
C . (0,1)(1,2)
D . (1,2)
9.若函数(1)y f x =+是偶函数,则下列说法不正确...
的是(▲)A .()y f x =图象关于直线1x =对称 B .(1)y f x =+图象关于y 轴对称C .必有(1)(1)f x f x +=--成立 D .必有(1)(1)f x f x +=-成立
10.已知函数23()2f x ax x =-
的最大值不大于1
6,又当11,42x ⎡⎤∈⎢⎥⎣⎦
时,1()8f x ≥,则a 的值
为 (▲ )
A . 1
B .1-
C .
34 D . 7
8
二、填空题(本大题共7小题,每小题4分,共28分) 11.函数)13lg(13)(2++-=
x x
x x f 的定义域是__▲__.
12.函数()f x 满足:(1)(3),f x x x x R +=+∈,则()f x 的最小值为 ▲ . 13.若集合2{|210,}A x ax x a R =-+≤∈是单元素集,则=a ▲. 14.函数y=215
log (34)x x +- 的单调递减区间是 ▲ .
15.函数1()(1)1m
f x x =-+的图象恒过定点 ▲ .16.已知函数21,0
()1,0
x x f x x ⎧+≥=⎨<⎩,则满足不等式)2()1(2x f x f >-的x 的范围_▲__.
17.设2
||
()2x f x x =+,对于实数12,x x ,给出下列条件:①120x x +>.,②120x x +<,
③2212
x x >,④12||x x >;其中能使12()()f x f x >恒成立的是 ▲ .(写出所有答案)
三、解答题(本大题共5题,共72分) 18.(本题满分14分) ⑴求值:22
lg52lg 2lg5lg 20(lg 2)++⋅+;
⑵求值:11
1
11
2
00.253
3
4
73(0.0081)3()81(3)100.02788-
----⎡⎤⎡
⎤-⨯⨯+-⨯⎢⎥
⎢⎥⎣
⎦⎣⎦.
19.(本题满分14分)
已知集合22{|(23)30,,}B x x m x m m x R m R =--+-≤∈∈,2{|280,}A x x x x R =--≤∈, ⑴若A ∩B =[2,4],求实数m 的值; ⑵设全集为R ,若A
R C B ,求实数m 的取值范围.
20.(本题满分14分)
已知函数32()32x x x x
f x ---=+.
⑴判断()f x 的奇偶性;
⑵判断并证明()f x 的单调性,写出()f x 的值域. 21.(本题满分15分)
函数)43lg(2x x y +-=的定义域为M ,函数124)(+-=x x x f (M x ∈). ⑴求函数)(x f 的值域;
⑵当M x ∈时,关于x 方程)(241R b b x x ∈=-+有两不等实数根,求b 的取值范围 . 22.(本题满分15分)
已知函数R a x a x
a x x f ∈∈+--=],6,1[,9
||)(.
⑴若6a =,写出函数)(x f 的单调区间,并指出单调性;
⑵若函数)(x f 在],1[a 上单调,且存在0[1,]x a ∈使0()2f x >-成立,求a 的取值范围; ⑶当)6,1(∈a 时,求函数)(x f 的最大值的表达式)(a M .
北仑中学2013年第一学期高一年级期中考试数学试题答题卷
一、选择题(本题10小题,每小题5分,共50分,每小题给出的四个选项中,只有一项是
符合题目要求的)
二、填空题(本大题共7小题,每小题4分,共28分)
11. 12. 13. 14.
15. 16. 17.
三、解答题(本大题共5题,共72分)18.(本题满分14分)
解:
19.(本题满分14分)
解:
20.(本题满分14分)
解:
21.(本题满分15分)解:
22.(本题满分15分)解:
解:(1)2⨯lg5+2⨯lg2+lg5⨯(1+lg2)+2)2(lg =2+lg5+lg2⨯(lg5+lg2)=3
(2)
1
210112()100.303333
--+-⨯= 19.(本题满分14分)
解: (1). A:[-2,4];B:[m-3,m] ]4,2[=⋂B A 可知m=5
(2)B 的补集为),()3,(+∞⋃--∞m m ;A:[-2,4],因为A 是B 补集的真子集, 所以m-3>4或者m<-2,即m>7或m<-2 20.(本题满分14分)
解:解:(Ⅰ)3223161
()3223161x x x x x x x x x x f x ---⋅--===+⋅++
所以6116()(),6116
x x
x
x
f x f x x R -----===-∈++,则()f x 是奇函数. (3分) (Ⅱ) 61(61)22
()1616161
x x x x x
f x -+-===-+++在R 上是增函数,(1分) 证明如下:任意取12,x x ,使得:1212660x x
x x >∴>>
则12211212222(66)
()()06161(61)(61)
x x x x x x f x f x --=-=>++++
所以12()()f x f x >,则()f x 在R 上是增函数. (4分)
20261x <<+2()1(1,1)61
x f x ∴=-∈-+,则()f x 的值域为(1,1)- (3分)
21.(本题满分15分)
解:(1). 0432
>+-x x 解得13<>x x 或 M={13<>x x 或};
124)(+-=x x x f ;令t x =2 208,2)(2<<>-=t t t t t f 或
所以值域为)0,1[),48(-⋃+∞
(2). )(241R b b x x ∈=-+有两不等实数根,数形结合b )0,1(-∈。
