Sukriye Ruhi
Itoh-Tsujii Inversion Algorithm

Itoh-Tsujii Inversion AlgorithmJorge GuajardoCommunication Security Group(COSY),Ruhr-Universit¨a t Bochum,44780Bochum,Germany,Email:guajardo@June25,2003Originally introduced in[5],the Itoh and Tsujii algorithm(ITA)is an exponentiation-based algorithm for inversion infinitefields which reduces the complexity of computing the inverse of a non-zero element in GF(2n),when using a normal basis representation,from n−2multiplications in GF(2n)and n−1cyclic shifts using the binary exponentiation method to at most2 log2(n−1) multiplications in GF(2n)and n−1cyclic is also applicable to finitefields with a polynomial basis representation.For the discussion that follows,it is important to point out that there are several possibilities to represent elements of afinitefield.Thus,in general,given an irreducible polynomial P(x) of degree m over GF(q)and a rootαof P(x)(i.e.P(α)=0),one can represent an element A∈GF(q m),q=p n and p prime,as a polynomial inα,i.e.,as A=a m−1αm−1+a m−2αm−2+···+a1α+a0with a i∈GF(q).The set{1,α,α2,...,αm−1}is then said to be a polynomial basis(or standard basis)for thefinitefield GF(q m)over GF(q)(see also extensionfield).Another type of basis is called a normal basis.Normal bases are of the form{β,βq,βq2,...,βq m−1}for an appropriate elementβ∈GF(q m).Then,an element B∈GF(q m)can be represented as B=b m−1βq m−1+b m−2βq m−2+···+b1βq+b0βwhere b i∈GF(q).It can be shown that for anyfield GF(q)and any extensionfield GF(q m),there exists always a normal basis of GF(q m) over GF(q)(see[6,Theorem2.35]).Notice that(βq i)q k=βq i+k=βq i+k mod m which follows from the fact thatβq m≡β(see also Fermat’s little theorem).Thus,raising an element B∈GF(q m) to the q-th power can be easily accomplished through a cyclic shift of its coordinates,i.e.,B q= (b m−1βq m−1+b m−2βq m−2+···+b1βq+b0β)q=b m−2βq m−1+b m−3βq m−2+···+b0βq+b m−1β,where we have used the fact that in anyfield of characteristic p,(x+y)q=x q+y q,where q=p n.Now,we can show how to compute the multiplicative inverse of A∈GF(2n),A=0,according to the binary method for exponentiation.From Fermat’s little theorem we know that A−1≡A2n−2 can be computed asA2n−2=A2·A22···A2n−1This requires n−2multiplications and n−1cyclic shifts.Notice that because we are working over afield of characteristic two(seefinitefield),squaring is a linear operation.In addition,if a normal basis is being used to represent the elements of thefield,we can compute A2for any A∈GF(2n) with one cyclic shift.Itoh and Tsujii proposed in[5]three algorithms.Thefirst two algorithms describe addition chains for exponentiation-based inversion infields GF(2n)while the third one describes a method based on subfield inversion.Thefirst algorithm is only applicable to values of n such that n=2r+1,for some positive r,and it is based on the observation that the exponent2n−2can be re-written as (2n−1−1)·2.Thus if n=2r+1,we can compute A−1≡(A22r−1)2.Furthermore,we can re-write122r−1as22r−1= 22r−1−1 22r−1+ 22r−1−1 (1) Equation(1)and the previous discussion lead to Algorithm1.Notice that Algorithm1performs Algorithm1Multiplicative inverse computation in GF(2n)with n=2r+1[5,Theorem1] Input:A∈GF(2n),A=0,n=2r+1Output:C=A−1C←Afor i=0to r−1doD←C22i{NOTE:2i cyclic shifts}C←C·Dend forC←C2Return(C)r=log2(n−1)iterations.In every iteration,one multiplication and i cyclic shifts,for0≤i<r,are performed which leads to an overall complexity of log2(n−1)multiplications and n−1cyclic shifts.Example1.Let A∈GF(217),A=0.Then according to Algorithm1we can compute A−1with the following addition chain:A2·A=A3A3 221·A3=A15A15 222·A15=A255A255 223·A255=A65535A65535 2=A131070A quick calculation verifies that217−2=131070.Notice that in accordance with Algorithm1we have performed four multiplications in GF(217)and,if using a normal basis,we would also require 24=16cyclic shifts.Algorithm1can be generalized to any value of n[5].First,we write n−1asn−1=ti=12k i,where k1>k2>···>k t(2)Using the fact that A−1≡(A2n−1−1)2and(2),it can be shown that the inverse of A can be written as:(A2n−1−1)2= (A22k t−1) A22k t−1−1 ···(A22k2−1)(A22k1−1)22k2 22k3··· 22k t 2(3)2An important feature of(3)is that in computing A22k1−1all other quantities of the form A22k i−1 for k i<k1have been computed.Thus,the overall complexity of(3)can be shown to be:#MUL= log2(n−1) +HW(n−1)−1#CSH=n−1(4) where HW(·)denotes the Hamming weight of the operand,i.e.,the number of ones in the binary representation of the operand(see also cyclic codes),MUL refers to multiplications in GF(2n),and CSH refers to cyclic shifts over GF(2)when using a normal basis.Example2.Let A∈GF(223),A=0.Then according to(2)we can write n−1=22=24+22+2 where k1=4,k2=2,and k3=1.It follows that we can compute A−1≡A223−2with the following addition chain:A22−1=A2·AA24−1= A3 22·A3A28−1= A15 24·A15A216−1= A255 28·A255A223−2= A22−1· A24−1· A216−1 24 22 2The above addition chain requires6multiplications and22cyclic shifts which agrees with the com-plexity of(4).In[5],the authors also notice that the previous ideas can be applied to extensionfields GF(q m), q=2n.Although this inversion method does not perform a complete inversion,it reduces inversion in GF(q m)to inversion in GF(q).It is assumed that subfield inversion can be done relatively easily, e.g.,through table look-up or with the extended Euclidean algorithm.These ideas are summarized in Theorem1.The presentation here follows[4]general than[5]as a subfield of the form GF(2n)is not required,rather we allow for general subfields GF(q).Theorem1[5,Theorem3]Let A∈GF(q m),A=0,and r=(q m−1)/(q−1).Then,the multiplicative inverse of an element A can be computed asA−1=(A r)−1A r−1.(5) Computing the inverse through Theorem1requires four steps:Step1Exponentiation in GF(q m),yielding A r−1.Step2Multiplication of A and A r−1,yielding A r∈GF(q).Step3Inversion in GF(q),yielding(A r)−1.Step4Multiplication of(A r)−1A r−1.3Steps2and4are trivial since both A r,in Step2,and(A r)−1,in Step4,are elements of GF(q)[6]. Both operations can,in most cases,be done with a complexity that is well below that of one single extensionfield multiplication.The complexity of Step3,subfield inversion,depends heavily on the subfield GF(q).However,in many cryptographic applications the subfield can be small enough to perform inversion very efficiently,for example,through table look-up[3,2],or by using the Euclidean algorithm(see also inversion infinitefields).What remains is Step1,exponentiation to the(r−1)th power in the extensionfield GF(q m).First,we notice that the exponent can be expressed in q-adic representation asr−1=q m−1+···+q2+q=(1···110)q(6)This exponentiation can be computed through repeated raising of intermediate results to the q-th power and multiplications.The number of multiplications in GF(q m)can be minimized by using the addition chain in(3).Thus,computing A r−1requires[5]:#MUL= log2(m−1) +HW(m−1)−1#q−EXP=m−1(7)where q-EXP refers to the number of exponentiations to the q-th power in GF(q).Example3.Let A∈GF(q19),A=0,q=p n for some prime p.Then,using the q-adic representation of r−1from(6)and the addition chain from(3),we canfind an addition chain to compute A r−1=A q18+q17+···+q2+q as follows.First,we write m−1=18=24+2where k1=4,and k2=1. Then,A r−1=(A q16+q15+···+q2+q)q2·(A q2+q)and we can compute A q16+q15+···+q2+q asA q2=(A q)qA q2+q=A q·A q2A 4i=1q i= A q2+q q2·A q2+qA 8i=1q i= A 4i=1q i q4·A 4i=1q iA 16i=1q i= A 8i=1q i q8· A 8i=1q iNotice that in computing A q16+q15+···+q2+q,we have computed A q2+q.The complexity to compute A r−1(and,thus,the complexity to compute A−1if the complexity of multiplication and inversion in GF(q)can be neglected)in GF(q19)is found to be5multiplications in GF(q19)and18expo-nentiations to the q-th power in agreement with(7).We notice that[5]assumes a normal basis representation of thefield elements of GF(q m), q=2n,in which the exponentiations to the q-th power are simply cyclic shifts of the m coefficients that represent an individualfield element.In polynomial(or standard)basis,however,these exponentiations are,in general,considerably more expensive.Reference[4]takes advantage offinitefield properties and of the algorithm characteristics to improve on the overall complexity of the ITA in polynomial basis.The authors make use of two facts:(i)the algorithm performs alternating multiplications and several exponentiations to the q-th power in a row and(ii)raising an element A∈GF(q),q=p n,to the q e-th power is a linear operation in GF(q m),since q is a power of thefield characteristic.4In general,computing A q e has a complexity of m(m−1)multiplications and m(m−2)+1= (m−1)2additions in GF(q)[4].This complexity is roughly the same as one GF(q m)multiplication, which requires m2subfield multiplications if we do not assume fast convolution techniques(e.g.,the Karatsuba algorithm for multiplication).However,in polynomial basis representation computing A q e,where e>1,can be shown to be as costly as a single exponentiation to the q th power. Thus,[4]performs as many subsequent exponentiations to the q th power in one step between multiplications as possible,yielding the same multiplication complexity as in(7),but a reduced number of q e-exponentiations.This is summarized in Theorem2.Theorem2[4,Theorem2]Let A∈GF(q m).One can compute A r−1where r−1=q+q2+···+ q(m−1)with no more than#MUL= log2(m−1) +HW(m−1)−1#q e-EXP= log2(m−1) +HW(m−1)operations,where#MUL and#q e-EXP refer to multiplications and exponentiations to the q e th power in GF(q m),respectively.We would like to stress that Theorem2is just an upper bound on the complexity of this exponentiation.Thus,it is possible tofind addition chains which yield better complexity as shown in[1].In addition,we see from Theorem2that Step1of the ITA algorithm requires about as many exponentiations to the q e th power as multiplications in GF(q m)if a polynomial basis representation is being used.In the discussion earlier in this section it was established that raising an element A∈GF(q m)to the q e th power is roughly as costly as performing one multiplication in GF(q m). Hence,if it is possible to make exponentiations to the q e th power more efficient,considerable speed-ups of the algorithm can be expected.Three classes offinitefields are introduced in[4]for which the complexity of these exponentiations is in fact substantially lower than that of a general multiplication in GF(q m).These are:•Fields GF((2n)m)with binaryfield polynomials.•Fields GF(q m),q=p n and p an odd prime,with binomials asfield polynomials.•Fields GF(q m),q=p n and p an odd prime,with binary equally spacedfield polynomials (ESP),where a binary ESP is a polynomial of the form x sm+x s(m−1)+x s(m−2)+···+x2s+ x s+1.References[1]Jae Wook Chung,Sang Gyoo Sim,and Pil Joong Lee.Fast Implementation of Elliptic CurveDefined over GF(p m)on CalmRISC with MAC2424Coprocessor.In C¸etin K.Ko¸c and Christof Paar,editors,Workshop on Cryptographic Hardware and Embedded Systems—CHES2000, volume LNCS1965,pages57–70,Berlin,August17-18,2000.Springer-Verlag.[2]E.De Win,A.Bosselaers,S.Vandenberghe,P.De Gersem,and J.Vandewalle.A fast softwareimplementation for arithmetic operations in GF(2n).In Kim,K.and Matsumoto,T.,editor, Advances in Cryptology—Asiacrypt’96,volume LNCS1233,pages65–76.Springer-Verlag, 1996.5[3]J.Guajardo and C.Paar.Efficient Algorithms for Elliptic Curve Cryptosystems.In B.Kaliski,Jr.,editor,Advances in Cryptology—CRYPTO’97,volume LNCS1294,pages342–356,Berlin, Germany,August1997.Springer-Verlag.[4]J.Guajardo and C.Paar.Itoh-Tsujii Inversion in Standard Basis and Its Application in Cryp-tography and Codes.Design,Codes,and Cryptography,25(2):207–216,February2002.[5]T.Itoh and S.Tsujii.A Fast Algorithm for Computing Multiplicative Inverses in GF(2m)UsingNormal rmation and Computation,78:171–177,1988.[6]R.Lidl and H.Niederreiter.Finite Fields,volume20of Encyclopedia of Mathematics and itsApplications.Cambridge University Press,Cambridge,Great Britain,second edition,1997.6。
《星星索》歌曲介绍

《星星索》歌曲介绍
《星星索》是一首印尼苏门答腊中部地区巴达克人的船歌。
巴达克的主要分布有苏门答腊中部和北部山区,大多数聚居在多巴湖的周围。
他们主要从事农业,这里湖水清澈,风和日丽,阳光明媚,巴达克人经常在湖上泛舟歌唱。
“星星索”(Sing Sing So)是划船时为船浆起落做节奏伴衬的哼唱声,歌曲由此得名。
“星星索”是象声,并无具体意思,与汉语歌曲中的“呼尔嗨哟”之类的同理。
因此这首歌的英文名字也就应该叫“Sing sing so”。
这首歌实际上也是一首优美的情歌,表达对心爱姑娘的深切思念。
曲调缓慢、悠扬,带有哀伤色彩,每句节奏前紧后松,唱法柔和、松弛。
全曲节奏徐缓而带有摇晃感,歌声委婉、抒情,深沉、真挚。
全曲以固定音型“星星索”作为伴唱。
语用身份理论与方法(武汉1)

14th International Pragmatics Conference, 2015
Panels: Bamberg, Narrative, narrative identity, and using narrative to investigate identity [4 parts] Burdelski & Cekaite, affect, social action, and identity in adult-child and childchild interaction [2 parts] Tanabe & Hale, Pragmatics of interaction: Identity and adjustment Parts of panels: Antonio Garcí a-Gómez, Emotional Persuasion: Teen girls‘ performance of sexual identity in online conflict interaction Pilar Garces-Conejos Blitvich, Conflictual micro-strategies of identity negotiation: The Latino transnational identity and citizen discourse Lili Gong, Identity construction via teasing in Chinese entertaining TV interviews: A positioning perspective Hsi-Yao Su, Politeness, Identity, and Language Ideologies: Discursively constructed contrasts between ―the polite Taiwanese‖ and ―the rude Chinese‖ among Taiwanese in China Olga Denti, Authenticity and identity construction in tourism apps Lecture session: Identity construction [4 sessions]
AS-PS02 AS-PS02A 安裝說明说明书
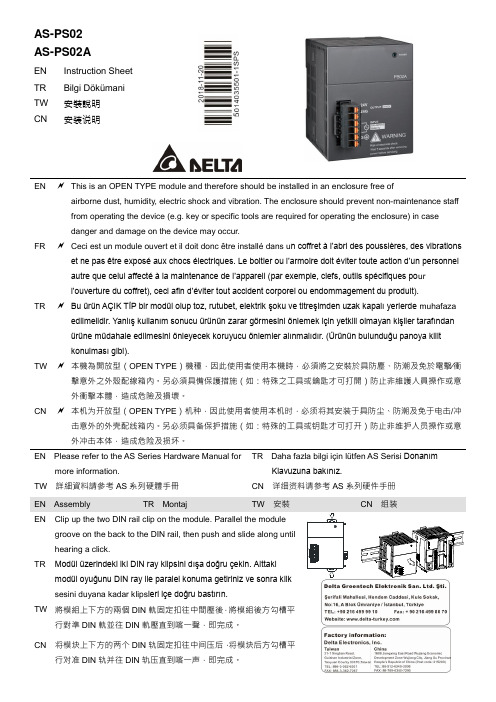
AS-PS02AS-PS02AEN Instruction SheetTR Bilgi DökümaniTW安裝說明CN安装说明EN This is an OPEN TYPE module and therefore should be installed in an enclosure free of airborne dust, humidity, electric shock and vibration. The enclosure should prevent non-maintenance staff from operating the device (e.g. key or specific tools are required for operating the enclosure) in casedanger and damage on the device may occur.FR Ceci est un module ouvert et il doit donc être installé dans u n coffret à l’abri des poussières, des vibrations et ne pas être exposé aux chocs électriques. Le boitier ou l’armoire doit éviter toute action d’un personnel autre que celui affecté à la maintenance de l’appareil (par exemple, clefs, outils spécifiques po url’ouverture du coffret), ceci afin d’éviter tout accident corporel ou endommagement du produit).TR Bu ürün AÇIK TİP bir modül olup toz, rutubet, elektrik şoku ve titreşimden uzak kapalı yerlerde muhafaza edilmelidir. Yanlış kullanım sonucu ürünün zarar görmesini önlemek için yetkili olmayan kişiler tarafındanürüne müdahale edilmesini önleyecek koruyucu önlemler alınmalıdır. (Ürünün bulunduğu panoya kilitkonulması gibi).TW 本機為開放型(OPEN TYPE)機種,因此使用者使用本機時,必須將之安裝於具防塵、防潮及免於電擊∕衝擊意外之外殼配線箱內。
NBA篮球运动员尤素夫·努尔基奇介绍尤素夫.努尔基奇

尤素夫·努尔基奇,波黑职业篮球运发动,司职中锋,下面是WTT的NBA篮球运发动尤素夫·努尔基奇介绍,希望对你有用!NBA篮球运发动尤素夫·努尔基奇简介尤素夫·努尔基奇(Jusuf Nurkic),1994年8月23日出生于波斯尼亚和黑塞哥维那图兹拉(Tuzla,Bosnia and Herzegovina),波黑职业篮球运发动,司职中锋,效力于NBA 波特兰开拓者队。
尤素夫·努尔基奇于20__年通过选秀进入NBA,先后效力于丹佛掘金队和开拓者队,20__-15赛季入选最正确新秀阵容第二阵容。
NBA篮球运发动尤素夫·努尔基奇早年经历1994年8月23日,尤素夫·努尔基奇出生于波斯尼亚和黑塞哥维那。
20__-14赛季,尤素夫·努尔基奇效力于克罗地亚联赛的萨格勒布塞德维达队(Cedevita Zagreb),因犯规问题场均仅上场16.6分钟,得到11.7分、5.7个篮板、1.1次抢断和0.8个盖帽。
NBA篮球运发动尤素夫·努尔基奇NBA生涯效力掘金20__年NBA选秀,尤素夫·努尔基奇在首轮第16位被芝加哥公牛队选中,随即被交易至丹佛掘金队。
20__年8月1日,掘金官方宣布正式签下尤素夫·努尔基奇,合同为期四年价值847万美元,其中20__-17、20__-18球队选项。
20__年2月10日,雷霆队中锋史蒂文·亚当斯因伤缺席20__年全明星新秀挑战赛,NBA官方指定尤素夫·努尔基奇顶替亚当斯参加这场比赛。
2月13日,努尔基奇因为个人原因放弃参加新秀挑战赛。
20__年5月19日,NBA官方公布了20__-15赛季最正确新秀阵容,尤素夫·努尔基奇入选最正确新秀阵容第二阵容。
20__-15赛季,尤素夫·努尔基奇代表掘金队出战62场常规赛比赛,场均得到6.9分和6.2个篮板。
苏约克100%纯天然苏打水

苏约克100%纯天然苏打水苏约克纯天然苏打水产于新疆乌恰县托云乡,地处帕米尔山东沿,天山南沿,喀喇昆仑山北麓,是中国版图的最边缘、最西陲,同时也是亚欧大陆的中心,是古丝绸之路的必经地带。
苏约克拉纯天然苏打水泉眼是目前中国境内唯一真正的天然含汽含苏打的自涌泉,泉水性质与生命起源水相同,含有单细胞藻类和对人体有益的多种稀有矿物元素,能平衡人体所需各种矿物质,同时游离态矿物质能人体更容易吸收,是一款具有减肥和美容功效、健胃护肝、控制三高、解酒等的纯天然含汽含苏打的高钙饮用水。
苏约克通过国家技术监督局颁发的QS认证、HACCP食品安全管理体系认证、IS090010:2000国家质量管理体系认证。
品牌介绍“苏约克”,为当地少数民族柯尔克孜族语言的音译,“苏约克”中的“苏”意为“水”,“约克”意为“没有”,整体意为“没有水的地方”。
柯尔克孜族有着辉煌的文化艺术成就,是一个古老的民族,在“西域”这样一个古来就烽火纷争的地方长盛不衰,足以证明他们的智慧和力量。
“没有水的地方”并非没有水,而是告诫我们,珍惜水资源,否则重蹈南疆部分绿洲的覆辙。
当我们过分享受大地母亲的给予的时候,应时刻提醒自己不能过分贪婪挥霍以免遭受大自然的反噬。
以“苏约克”之名,传播南疆地域文化,传达保护大自然,珍惜水资源的理念。
苏打水功效1、苏打水呈弱碱性。
但是我们每天吃很多肉类、鱼类,都是酸性食物,造成人体内环境也是弱酸性。
因此,需要进行酸碱平衡。
苏打水PH值是调节酸碱平衡的"黄金水""肝脏水""贵族水"2、中和胃酸,缓解胃痛及不适。
吃甜食或胃酸分泌过多,都会导致胃痛或不适。
此时,饮用苏打水,可以中和胃酸,缓解胃痛及不适,效果立竿见影。
3、改善消化系统,促进免疫机能。
坚持每天喝苏打水,增加肠道的蠕动,有助于肠道肌肉的松弛。
4、痛风病人的苏打水保养法:痛风病人主要是由于血液中的尿酸浓度增高,尿酸结晶增加并堆积在组织中,从而引起红、肿、热、痛等发炎症状。
尼科西亚景点

尼科西亚景点下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help yousolve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts,other materials and so on, want to know different data formats and writing methods, please pay attention!尼科西亚,是塞浦路斯的首都和最大城市,也是一个融合了古老历史和现代化文明的城市。
九年级英语国家与首都匹配单选题50题

九年级英语国家与首都匹配单选题50题1.Which city is the capital of France?A.LondonB.ParisC.BerlinD.Rome答案:B。
法国是一个充满浪漫气息的国家,拥有丰富的文化遗产和艺术成就。
巴黎是法国的首都,也是世界著名的时尚之都、艺术之都和文化之都。
伦敦是英国的首都,柏林是德国的首都,罗马是意大利的首都。
2.Which city is the capital of the United Kingdom?A.ParisB.WashingtonC.LondonD.Moscow答案:C。
英国是一个历史悠久的国家,在世界历史上有着重要的地位。
伦敦是英国的首都,也是世界著名的金融中心和文化名城。
巴黎是法国的首都,华盛顿是美国的首都,莫斯科是俄罗斯的首都。
3.Which city is the capital of Germany?A.ParisB.MadridC.BerlinD.Rome答案:C。
德国是一个高度发达的工业国家,拥有世界领先的科技和制造业。
柏林是德国的首都,也是德国的政治、文化和经济中心。
巴黎是法国的首都,马德里是西班牙的首都,罗马是意大利的首都。
4.Which city is the capital of Italy?A.ParisB.LondonC.RomeD.Berlin答案:C。
意大利是一个充满艺术和文化气息的国家,拥有丰富的历史遗产和美食文化。
罗马是意大利的首都,也是世界著名的历史文化名城。
巴黎是法国的首都,伦敦是英国的首都,柏林是德国的首都。
5.Which city is the capital of Spain?A.ParisB.LondonC.MadridD.Berlin答案:C。
西班牙是一个充满热情和活力的国家,拥有丰富的自然风光和文化遗产。
马德里是西班牙的首都,也是西班牙的政治、文化和经济中心。
巴黎是法国的首都,伦敦是英国的首都,柏林是德国的首都。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Self-politeness in managing rapport sensitive acts:The case of compliment responses in TurkishŞükriye RuhiMiddle East Technical University, Ankara, TurkeyThe maxim and the face-management approaches (Leech 1983; Brown and Levinson 1987) to linguistic politeness have received extensive criticism and current academic debate is flourishing with studies that propose extensions of the models or alternative frameworks (e.g., Spencer-Oatey 2000; Eelen 2001). A central issue raised in discussions is the definition of politeness as a technical term. As underscored by Eelen, a promising approach to conceptualising politeness (in his terminology, Politeness 2) is to investigate people’s evaluations of (im)politeness (i.e., Politeness 1).Despite the significance of this proposal, most current research on compliment response has not addressed this issue (e.g., Yu 2003). This is unfortunate since discrepancies have emerged in interpretations of the theories, especially when the face-management approach is the locus of debate. To illustrate, returns are positive politeness strategies in Chen (1993) whereas they feature as negative politeness in Henderson (1996). As this is central to politeness theory, this speech act thus warrants further scrutiny.With these considerations in mind, this paper presents a qualitative study on naturally occurring compliment responses in Turkish for the purpose of unravelling conceptualisations of (im)politeness (i.e., Politeness 1). The study dwells on responses that are theoretically problematic and shows that interlocutors are as much concerned about their own standing in communication as they are about others in the sense that they are sensitive to self-presentational issues. These concerns critically involve the speaker’s sense of personal/social worth, his/her relation to the addressee, and perceived communicative intentions. The data reveal that these aspects of interaction are discursively contested when they conflict with the complimentee’s evaluation. Samples (1)-(3) illustrate how complimentees challenge either the assessment of self in the compliment (1 and 2) or the motivation for the compliment (sample 3). (‘Cer’ stands for ‘Complimenter’; ‘Cee’ stands for Complimentee’)(1) Cer I think these freckles give you a charming air. They makeyou more attractive→Cee Oh don’t speak nonsense! I don’t want an air like that.What’s more I don’t want frecklesCer OK my dear! Be calm. I just told you what I thinkreaction)(noCee(2) Cer You’re very beautiful today again my lady→Cee Thank you. It’s my usual style my dearCer Oh! We’re very modest![we refers to the complimentee] Cee Of course I’m both beautiful and modest(3) Cer You know what I really like you a lot→Cee What do you want again? Tell me go on tell me let’s seeThese findings show that the maxim and the face-management approaches give precedence to politeness in the sense of displaying deference, solidarity, and non-imposition at the expense of the speaker’s concerns for self-presentation.The paper argues that politeness theory needs to incorporate a notion of self-politeness, defined as the individual’s need to present self as one who displays self-confidence, assertiveness, and individuality besides demonstrating consideration for the alter’s needs (Ruhi, ms.) and that defining politeness as showing consideration toward others may not reflect real life discourse. The study thus corroborates Eelen’s (2001) claim that politeness theory needs to account for speaker evaluation of (im)politeness so that a model of communicative events also needs to take into its scope conflictual discourse (Spencer-Oatey 2000). To accommodate for the findings of the data analysis, the paper looks into the rapport management model of communication proposed in Spencer-Oatey to discuss how face and sociality rights concerns of interlocutors interact to produce (im)politeness in discourse. Finally, the paper demonstrates how a relevance-theoretic approach to utterance interpretation (Sperber and Wilson [1986]1995) has much to offer by way of explaining how (im)politeness emerges in discourse. ReferencesBrown, Penelope & Stephen C. Levinson. 1987. Politeness: Some universals in language u s age. Cambridge: CUP.Chen, Rong. 1993. Responding to compliments: A contrastive study of politeness strategies between American English and Chinese speakers. Journal of Pragmatics 20: 49-75.Eelen, Gino. 2001. A critique of politeness theories. Manchester: St. Jerome's Press.Henderson, Anita. 1996. Compliments, compliment responses, and politeness in an African-American community. In J. Arnold, R. Blake, B. Davidson, S. Schwenter, and J. Solomon (eds.), Sociolinguistic variation: Data, theory and analysis, selected papers from NWAV 23 at Stanford. Stanford, CA: Center for Language and Information. 195-208.Holmes, Janet. 1993. New Zealand women are good to talk to: an analysis of politeness strategies in interaction. Journal of Pragmatics 20: 91-116.Leech, Geoffrey. 1983. Principles of pragmatics. London: Longman.Ruhi, Şükriye, ms. Politeness in compliment responses: A perspective from naturally occurring exchanges in Turkish.Spencer-Oatey, Helen. 2000. Rapport management: a framework for analysis. In H.Spencer-Oatey (ed.), Culturally speaking: Managing rapport through talk across cultures. London: Continuum. 11–46.Sperber, Dan & Deirdre Wilson. [1986]1995. Relevance: Communication and cognition. Oxford: Blackwell.Yu, Ming-chung. 2003. On the universality of face: evidence from Chinese compliment response behavior. Journal of Pragmatics 35: 1679-1710.。
