电网络理论习题解
电网络理论1-66
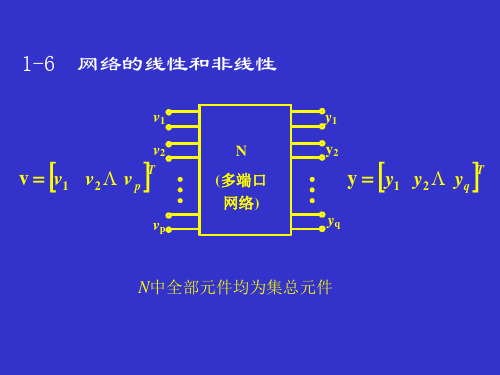
1-7
网络的时不变性和时变性
v (t )
y (t )
时不变网络
u( t )
u( t )
0
(a)
t
性质:
dv( t ) ˆ (t ) v dt
u(t-T)
dy( t ) ˆ (t ) y dt
0 u(t-T ) 0 T
(a)
t
0
T
(b)
t
ˆ ( t ) v( t )dt v
t
ˆ ( t ) y( t )dt y
t
(b)
t
1-7
网络的时不变性和时变性
传统型时不变网络的定义:若一个网络中不含任何非源时变 网络元件,则称该网络为时不变的。
结论:不含时变网络元件的网络是端口型时不变网络。
1-8
网络元件及网络的无源性和有源性
传统的无源网络:若一个网络仅由无源网络元件构成, 则该网络是无源的。 端口型无源网络:设 n 端口网络于 to 时刻贮存的能量为 W(to) ,在 to 至 t 时间内从电源传送至 n 端口网络的能量为 t W ( t o , t ) uT ( )i( )d 式中 u( t )、i( t ) W ( t o ,t ) , t
o
分别为n端口网络的端口电压向量和端口电流向量。如果 对所有的初始时刻to,对所有的 t t o ,以及对所有的容许 信号向量偶 (u( t ), i( t )),均有
W ( t o ) W ( t o , t ) W ( t o ) uT ( )i( )d 0
to t
i +
1-6
网络的线性和非线性1 qFra biblioteku –
电力网络分析计算试题及答案 可编辑

3.1 电网结构如图3—11所示,其额定电压为10KV 。
已知各节点的负荷功率及参数:MVA j S )2.03.0(2+=,MVA j S )3.05.0(3+=,MVA j S )15.02.0(4+=Ω+=)4.22.1(12j Z ,Ω+=)0.20.1(23j Z ,Ω+=)0.35.1(24j Z试求电压和功率分布。
解:(1)先假设各节点电压均为额定电压,求线路始端功率。
0068.00034.0)21(103.05.0)(22223232232323j j jX R U Q P S N +=++=++=∆0019.00009.0)35.1(1015.02.0)(22224242242424j j jX R U Q P S N +=++=++=∆则: 3068.05034.023323j S S S +=∆+=如图所示简单系统,额定电压为110KV 双回输电线路,长度为80km ,采用LGJ-150导线,其单位长度的参数为:r=Ω/km ,x=Ω/km,b=km S /106-⨯。
变电所中装有两台三相110/11kV 的变压器,每台的容量为15MVA,其参数为:5.3%,5.10%,128P 5.40K 0===∆=∆o K I U kW kW P 。
母线A的实际运行电压为117kV ,负荷功率:MVA j S MVA j S LDc LDb 1520,1230+=+=。
当变压器取主抽头时,求母线c 的电压。
解 (1)计算参数并作出等值电路。
输电线路的等值电阻、电抗和电纳分别为由于线路电压未知,可用线路额定电压计算线路产生的充电功率,并将其等分为两部分,便得var65.2var 1101038.42121242M M U B Q N c B -=⨯⨯⨯-=-=∆-将B Q ∆分别接于节点A 和b ,作为节点负荷的一部分。
两台变压器并联运行时,它们的等值电阻、电抗及励磁功率分别为kVkV某一额定电压为10kV 的两端供电网,如图所示。
国家电网考试之电网络分析理论:第二章补充内容

1 1 x1 0 求 H X 0, 1 1 x1 0
T
B 1,1
2019/4/22
25
x1 x2
0 -1 -1 0 H 0 , 1 1 X 0 X B 0 1 1 0
的
解:①求特征根:
1 5 I A 2 3
I A 4 3 10
2
2 3
2
2
I A 0
1 2 j3 , 2 1
2019/4/22
6
②求特征量 i I A 0 1 5 I A 2 3
A 2 1 2
I A1 0
I A2 1
2019/4/22
28
1 对2×2阵 x2 x1 取 1 1 成立!? I A2 1 1 12 1
1 1 x1 1 1 1 x 1 2
P AP J
1
2 1 I A 1 4
1 A1 ,2 1 ,2 0
AP PJ
1 2 3
A1, A2 1,1 2
A1 1
·
的相图
轾 2 过 Z (0) = 犏 犏 2 臌
解:①求特征根
轾 l +1 - 2 [l I - A] = 犏 犏 l - 1 臌5 l I - A = l - 1 + 10 = l + 9 l I- A = 0 l 1 = j3 l 2 = l 1
电工网络考试试题及答案

电工网络考试试题及答案一、单项选择题(每题2分,共20分)1. 电路中电阻的单位是欧姆,其符号为:A. ΩB. VC. AD. S答案:A2. 交流电路中,瞬时值表达式为i(t)=10sin(314t+π/4)A,该电流的频率为:A. 50HzB. 60HzC. 100HzD. 120Hz答案:A3. 电路中,电感L和电容C串联后接在交流电路中,若电路的谐振频率为f0,则有:A. f0 = 1/(2π√(LC))B. f0 = 2π√(LC)C. f0 = 1/(2πL)D. f0 = 2πC答案:A4. 在三相电路中,星形接法的线电压与相电压的关系是:A. 相电压是线电压的√3倍B. 线电压是相电压的√3倍C. 相电压等于线电压D. 线电压等于相电压答案:B5. 电路中,一个电阻R1与一个电感L串联,接在直流电源上,若电路达到稳态后,电感表现为:A. 短路B. 开路C. 电阻D. 电容答案:A6. 电路中,一个电阻R和一个电容C并联,接在交流电源上,若电源频率增加,则电路的总阻抗:A. 增加B. 减少C. 保持不变D. 先增加后减少答案:B7. 电路中,一个理想变压器的原边绕组有N1匝,副边绕组有N2匝,若原边电压为U1,则副边电压U2为:A. U2 = U1 * (N2/N1)B. U2 = U1 * (N1/N2)C. U2 = N2 * U1D. U2 = N1 * U1答案:A8. 电路中,一个二极管正向导通时,其两端电压降约为:A. 0.7VB. 0.3VC. 1.5VD. 2.5V答案:A9. 电路中,一个晶体三极管处于放大状态时,其基极电流IB与集电极电流IC的关系是:A. IC = βIBB. IC = αIBC. IC = 1/βIBD. IC = 1/αIB答案:A10. 电路中,一个理想运算放大器构成的反相放大电路,若输入电压为Vi,输出电压为Vo,则有:A. Vo = -βViB. Vo = βViC. Vo = -αViD. Vo = αVi答案:A二、多项选择题(每题3分,共15分)11. 电路中,以下哪些元件属于被动元件:A. 电阻B. 电感C. 电容D. 二极管答案:ABC12. 电路中,以下哪些元件属于有源元件:A. 电阻B. 电感C. 晶体三极管D. 运算放大器答案:CD13. 电路中,以下哪些因素会影响电路的谐振频率:A. 电感LB. 电容CC. 电源频率D. 电阻R答案:ABC14. 电路中,以下哪些情况会导致电路的功率因数降低:A. 电路中存在纯电阻负载B. 电路中存在纯电感负载C. 电路中存在纯电容负载D. 电路中存在非线性负载答案:BCD15. 电路中,以下哪些因素会影响理想变压器的变比:A. 原边绕组匝数B. 副边绕组匝数C. 电源电压D. 负载电阻答案:AB三、填空题(每题2分,共20分)16. 电路中,欧姆定律表达式为V=____R,其中V表示电压,I表示电流,R表示电阻。
电网络分析理论第3、4章练习题(2)

1. (10%)已知题2图中四端网络a N 的不定导纳阵为44)(⨯=ij ia y Y , b N 的H 参数为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡21218421U I I U ,求a N 、b N 对应节点相联后的不定导纳矩阵。
2. (10分)已知题2图中四端网络a N 的不定导纳阵为44)(⨯=ij ia y Y , b N 的H '参数为112231122I U U I ⎡⎤⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,求a N 、b N 对应节点相联后的不定导纳矩阵。
3. (15%)求题1图所示三端口网络的Y 参数矩阵,并叙述判断多端口网络无源性的方法。
222题图22题图题1图4. (15%)已知四端口网络Na 的不定导纳阵为44)(⨯=ij iay Y ,求增加C ,G后的不定导纳阵。
题2图5. (15%)图示两线性网络1N 和2N ,其节点方程(设均以大地为参考节点)分别为列出下列三种情况下的节点电压方程或改进节点电压方程 (1) 将节点对①-④,②-⑤用阻抗为零的导线联接;(7分)(2) 将节点对①-④,②-⑤用联线联接,设每根联接线的阻抗为l Z :(7分) (3) 将节点对①-④,②-⑤下图所示的互感元件联接。
(6分)6. (15%)试列写题3图所示网络的改进节点方程。
题3图7. (20%)图(a )为桥T 型网络,当在1、2端加上电导G 时,求1)改变后的网络图(b )的不定导纳阵'i Y ;2)求图(c )桥T 型二端口网络的短路导纳阵。
8. (15%)建立图示动态电路的s 域改进节点方程(MNA )方程(设电路中动态元件的初始储能为零)9. (15%)列出图示电路的混合参数方程。
L 2142I 1 α U 110. (20%)图示两线性网络1N 和2N ,其节点方程(设均以大地为参考节点)分别为现将节点对①-④,②-⑤用联接线相联,问当:(1) 忽略联接线的阻抗,(2)设每根联接线的阻抗为l Z 时,网络方程如何变化。
电网络习题答案

习 题1-8 图示二端口由两个线性电阻器(无源元件)和一个理想流控电流源 (有源元件)组成。
试证明:在某些参数值下,它可以是无源二端口。
证明:⎩⎨⎧-=-==21222122111)(r i r i r i i u r i u ββ⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡∴21221210i i r r r u u β 吸收功率:[]⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=-+=+=21222121221222121221122)(i i r r r r i i r i i r i r i i u i u t p βββ R 阵对称正定,即4)(,0,0222121r r r r r β>>>时,该二端口是无源的。
1-9 设互易n 端口有混合参数矩阵H ,求H 应满足的条件。
解:法一:n 端口划分成两部分,a ,b[][]Tk Tk I I I U U U 2121,,==a a I U [][]Tn k k Tn k k I I I U U U 2121,,++++==b b I U⎩⎨⎧+=+=⇒⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡bbb a ba b bab a aa a b a bb baab aa b a U H I H I U H I H U U I H H H H I U图 1-8设[][])()((1)(1)I U I U22,是n 端口的两个任意容许偶,若互易[][](1)T(2)(2)T(1)I U I U =[][][]⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡=(2)b bb (2)a ba (2)a(1)bT T (1)b ab (1)a aa (2)b (2)a (1)bT (1)aT (2)T(1)U H I H I U)U H I (H I I UUIU []⎥⎦⎤⎢⎣⎡++=(2)b bb (2)a ba (2)a(1)bT T ab(1)bT T aa(1)aT U H I H I UHUH I)1()(21 (2)b bb (1)b T (2)a ba T ab (1)b T )(a T aa )(a U H U I H H U I H I +++=[][][][]⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡==(2)b (2)bab (2)a aa T(1)bbb (1)aba (1)a T (2)b (2)a(1)bT (1)aT (2)T(1)(1)T(2)U U H I H )U H I(H I U U IIUIIU )2( (2)b bb T (1)b T (2)b ba T ab (1)a T (2)a aa (1)a U H U )U H (H I I H I +++=对比(1)(2)式得:⎩⎨⎧==bbbb T aaaa H H H H T⎩⎨⎧-=⇒=+-=⇒=+baTab ba T ab Tabba ba T ab H H 0H H H H 0H H 法二:⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡b a bb ba ab aab a U I H H H H I U 转成Z 阵:⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡----b a 1bb ba 1bb 1bbab ba 1bbab aa b a I I H H H H H H H H H U U T Z Z =)1( ba 1bb ab aa T ba 1bb ab T aa H H H H )H H (H H ---=-∴ )2()( 1bb ab ba 1bb H H H H --=-T )3()( ba 1bb 1bb ab H H H H ---=T )4()( 1bb 1bb H H --=T 由(4)得:)5( Tbb bb H H =将(5)代入(2)或(3),得:)6( Tab ba H H -=把(6)代入(1)得:ba 1bb ab aa T ab T ba 1bb T aa H H H H H )H (H H ---=-ba 1bb ab aa ba 1bb ab T aa H H H H H H H H ---=-∴ aa T aa H H =∴ 得证1-10 设x 是输入,y 是输出,它们可以是n 端口的电流或电压。
电网络理论

2-5 列写图所示网络节点电压方程的矩阵形式。
acI 1/wc画出网络的有向图,对节点和支路进行编号。
节点d 为参考节点,其关联矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=110010101011000101A支路导纳矩阵、电压源和电流源列向量分别为:[])/1/(1/1)/1/(1)/(1)/1/(1diag 6623344551b C R R C R L R L C C Y ωωωωωω++++=,,,,,T⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=0000.-0.s5s U UT⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=0.000..s6s1s I I I根据T=A AY Y b n 可求得节点导纳矩阵为:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++++++++++++++++=2665566556655665544111441n 1/11/11/11-/11-0/11-/11-/11/111-0-1R C R L C C R L C C R L C C R L C L R C C C L R C Y ωωωωωωωωωωωωωωωωωω根据s b .s .n .AY -U I A I =可求得节点等效电流源列向量为:⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡+++=s 55s6s 55s1s1.n ./11../11-.-.U L C I U L C I I I ωωωω所以节点电压方程的矩阵形式为:⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡+++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡++++++++++++++++s 55s6s 55s1s1c b a 2665566556655665544111441./11../11-.-....1/11/11/11-/11-0/11-/11-/11/111-0-1U L C I U L C I I U U U R C R L C C R L C C R L C C R L C L R C C C L R C ωωωωωωωωωωωωωωωωωωωωωω2-8 网络如图所示,参考方向已选定,如果选取支路4、5、6为树,且已知电源的角频率为ω,列写网络的割集方程的矩阵形式。
电网络理论习题解

UI 7n 3
Is1 G1Us1 U s7
1
0
I2
0
0 1 I5
0
6. 列写题图 5 所示网络以两条 5电阻支路为撕裂支路的撕裂结点方程。
文案大全
实用标准文档
1
1
+ 10V
1 10A
1 1
5
5
6V +
1
1
+
2
10V
10A
题图 5
1
1
1
+
6V
习题 3
1.利用不定导纳矩阵计算题图 1 所示二端口网络的短路导纳矩阵。
考虑初值时上式中 U's(s) = Us(s)+LTiL(0−)−uC(0−)/s
本题中 LTiL(0−) = [0 0 0 0 L5iL5(0−) 0 0]T,uC(0−)/s = [0 0 0 0 0 uC6(0−)/s uC7(0−)/s]T
U1(s) 0 g U2 (s) g 0
U U
题图 2
实用标准文档
(1) 将 VCVS 变换为 VCCS,2、3 端接地,1 端接电源 u1,计算得
Y11
g1(g2 sC) g1 g2 sC
Y21
g1(g2 Ag3 sC) g1 g2 sC
Y31
g1
Ag1g 3 g2 sC
1、3 端接地,2 端接电源 u2,计算得
Y12 = −Y11
g1
0
Y i'
0
0
g1
g 2 g3 sC g3 g 2 sC
0 g3 Ag 3 g 3 Ag 3
0
g1
g 2 Ag 3 sC
Ag 3 g1 g 2 sC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
阅前提示:以下习题答案仅供参考,未经仔细核实,定有不少谬误,如有发现,请及时指正,谢谢!习题11. 一个非线性电阻元件的电压、电流分别为:u(t) = cos ωt ,i(t) = cos4ωt(u 、i 参考方向一致)。
求该电阻元件的构成关系。
i(t) = cos4ωt = 8cos 4ωt -8cos 2ωt+1 = 8u 4(t)-8u 2(t)+12.二端元件的电压、电流分别为u(t) = 2cost ,i(t) = 0.5-cost ,试确定元件类型(即属于电阻、电感、电容等中的哪一类),并论证其无源性。
i(t) = 0.5-cost = 0.5-0.5u(t)0T d )cos 5.0(cos 2d )(i )(u )t ,t (W TT0<-=ττ-τ=τττ=⎰⎰电阻,有源。
3.有两个二端元件,其电压、电流关系方程分别为dt)t (di )t (2i u(t) (2) dt du(t)2u(t)i(t) )1(2== 试确定各元件类型,并论证各元件的无源性。
(1)因为dt du dt dq i 2==,所以q = u 2+A ,A 为常数,电容元件。
)t (u 32d d du u 2u d )(i )(u )t (W 3t t =ττ⨯=τττ=⎰⎰∞-∞-,当u<0时,W(t)<0,有源。
(2)因为dtdi 32dt d u 3=ψ=,所以ψ = 32i 3+A ,电感元件。
0)t (i 21id d di i 2d )(i )(u )t (W 4t 2t ≥=τ⨯τ=τττ=⎰⎰∞-∞-,无源。
4.如题图1所示二端口电路,其中非线性电阻r 的构成关系为u r = i r 3。
此二端口是有源的还是无源的。
p = u 1i 1+u 2i 2 = i = (i 1R 1+u R )i 1+(i 2R 2+u R )i 2 = i 12R 1+i 22R 2+i R 4≥00pd d )()()t (W tt=≥τ=τττ=⎰⎰∞-∞-i u ,无源。
5.图1.23中对四种线性受控源给出了其一种零泛器模型。
证明各含零泛器电路与对应受控源间的等效性。
6. 图1.16给出了用运放和电阻元件实现的CNIC 和VNIC 的电路。
试证明各含运放电路与对应的负阻抗变换器间的等效性。
题图1习题21. 对题图1所示有向图:(1)若以节点④为参考节点,写出关联矩阵A ;(2)若选树T(1,2,3,4,5),写出基本割集矩阵Q f 和基本回路矩阵B f 。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------=1 1 1 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 1 0 0 1 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 11 10 9 8 7 6 5 4 3 2 1 A⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---------=1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 1 1 0 0 0 1 0 0 0 1 0 1 1 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0 1 1 1 0 0 0 11 10 9 8 7 6 5 4 3 2 1 f B⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----= 0 0 0 1 1 1 1 0 0 0 0 1 0 0 1 0 1 0 1 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 1 11 10 9 8 7 6 5 4 3 2 1 f Q2. 已知图G 对应于某一树的基本割集矩阵如下,(1)试写出对应于同一树的基本回路矩阵;(2)作出对应的有向图。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--------=0 1 1 0 0 0 1 0 0 0 00 0 1 1 1 0 0 1 0 0 01 1 0 1 1 0 0 0 1 0 00 0 0 1 1 1 0 0 0 1 01 0 0 0 0 1 0 0 0 0 1f Q ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡------=-= 0 0 1 0 1 1 0 1 0 0 1 1 0 0 0 0 1 1 1 0 0 1 1 1 0 0 0 0 1 1 5 4 3 2 1 T l t Q B基本回路矩阵:B f = [B t 1l ]网络图如右所示,图中红线表示的是树枝。
3. 若考虑网络中电感和电容的初始值不为0,试写出矩阵表示的网络VCR 方程。
图2.11(a)电路中,电感、电容的初值分别为i L5(0−)、u C6(0−)和u C7(0−),求支路电压向量U b (s)。
1③题图1 ①② ③ ⑤ ⑥设初值向量i L (0−),u C (0−),变换为s 域的电压源L T i L (0−),u C (0−)/s ,L 为支路电感向量。
支路电压向量 U b (s) = Z b (s)[I b (s)+I s (s)]−U 's (s) 支路电流向量 I b (s) = Y b (s)[U b (s)+U 's (s)]−I s (s) 考虑初值时上式中 U 's (s) = U s (s)+L T i L (0−)−u C (0−)/s本题中L T i L (0−) = [0 0 0 0 L 5i L5(0−) 0 0]T ,u C (0−)/s = [0 0 0 0 0 u C6(0−)/s u C7(0−)/s]T⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---------=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----0 0 0 0 0 )0(i s 1)0(u C )0(u C )s (U G 1 0 0 0 1 0 1 0 1 0 0 1 1 0 0 0 1 0 1 1 0 0 0 0 1 1 0 1 0 0 0 0 G g g 0 C s /sL 1 0 0 0 g sC 0 0 G 0 g 0 )s (U )s (U )s (U )s (U )s (U )s (U )s (U 5L 6C 67C 7s 413657476543214. 用导纳矩阵法求题图2所示网络的支路电压向量。
作出网络图,以结点5为参考结点,取树(1、3、4、6、8),列出矩阵。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡= 1- 0 0 1- 0 0 0 0 0 1- 0 0 0 0 0 1- 1 0 0 0 0 1- 1- 0 0 0 1- 0 1- 1 0 0 0 0 0 0 1 0 1 1 8 7 6 5 4 3 2 1 A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡= 0 1 1- 0 1 0 0 1-1- 0 1- 1 0 1- 0 0 0 0 0 0 1- 1- 1 0 87 6 5 4 3 2 1 f B ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1/R 1/R 1/R 1/sL 1/sL sC C s C s 87654321b Y0 0 (s)I s1题图2[]TC3C2s Ts8s1s 0 0 0 0 0 s )0(U s )0(U 0 (s)I - 0 0 0 0 0 0 I (s)⎥⎦⎤⎢⎣⎡--==--U I)s ( )s ( )s ()s ( )s ()s (s b 1f b s 1f b b U 0AY B AY I 0A B AY U ⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=--5. 在题图3所示电路中,以I 5和I 2为直接求解的支路电流,列写改进结点方程。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----==0 1 0 0 0 1 10 1 1 0 1 0 0 1 0 1 1 0 0 1 ] [5 2 7 6 4 3 1 x E 0A A A A Y 0 = diag[G 1 G 2 G 4 G 6] Y x = diag[G 2 G 5]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+=31141610n G G 0 G 0 G 0 G 0 G G )s (Y ⎥⎦⎤⎢⎣⎡-=0 0 G G G 0 )s (522T x x A YI s (s) = [−I s1 0 0 0]T ,U s (s) = [U s1 0 0 −U s6]T⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++--=1s 1s16s 61s 11s 0n U G I 0 U G U G I )s (I改进结点方程⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡++--=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--+-----+0 0U U G I 0U G U G I I I I U U U 1 0 0 0 0 G 0 1 0 G G 0 0 0 0 0 1 1 0 1 0 G G 0 G 0 1 1 0 G 0 1 0 1 G 0 G G 7s 1s 1s16s 61s 11s 5273n 2n 1n 52231141616. 列写题图5所示网络以两条5Ω电阻支路为撕裂支路的撕裂结点方程。
题图3习题31.利用不定导纳矩阵计算题图1所示二端口网络的短路导纳矩阵。
图示电路原始不定导纳矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-----+---+=2122212222111111'i sC sC G G sC sC G G 0 0 sC 0 sC G G sC 0 G sC G Y 消除不可及端子4得三端网络不定导纳矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----+------+=442224422441244224422221442114412442114421211'i Y G G Y C s G Y C s G Y C s G Y C s sC G Y C s C s G Y C s G Y C s C s G Y C s sC G Y ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-+-----+=442222144211442114421211i Y C s sC G Y C s C s G Y C s C s G Y C s sC G Y2.题图2所示网络,试求:(1) 根据不定导纳矩阵的定义求三端网络的不定导纳矩阵;(2) 用首先形成网络的原始不定导纳矩阵的方法,求三端网络的不定导纳矩阵。
210V题图5Ω6V 122'题图12(1) 将VCVS 变换为VCCS ,2、3端接地,1端接电源u 1,计算得sCg g )sC g (g Y 212111+++= sCg g )sC Ag g (g Y 2132121++++-=sCg g g Ag Y 213131++=1、3端接地,2端接电源u 2,计算得 Y 12 = −Y 11311131122g Y g Ag Y Y +-= 3111332g Y g Ag Y -=矩阵第3列可由1、2列相加取负可得 Y 13 = 0 Y 23 = Y 21+Y 22 Y 33 = −Y 31+Y 32⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211i Y Y Y Y Y Y Y Y Y Y (2) 将VCVS 变换为VCCS :i 23 = −Ag 3u 43=Ag 3u 34,原始不定导纳矩阵为 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++---+-----+-++-=sC g g 0 sC g g Ag Ag g g 0 sC Ag g Ag g sC g g 0 g 0 0 g 2121333332333211'i Y 消除不可及端子4可得三端网络不定导纳矩阵⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-++-+-+++-++++-+--=3344233443133443223244321442144211i Ag g Y )sC g (Ag g Y g Ag Ag g Y )sC Ag g )(sC g (sC g g Y )sC Ag g (g 0 Y )sC g (g Y g g Y3.题图3所示一个不含独立源的线性三端网络,其输出端3开路。
