离散数学( 第10讲习题课2)
离散数学课后习题答案(第二章)

(3) 寻求下列各式的真假值。 A) (∀x)( P( x) ∨ Q( x)) ,其中 P( x) : x = 1, Q( x) : x = 2 ,且论域是 {1, 2} B) (∀x)( P → Q( x)) ∨ R( a) , 其中 P : 2 > 1, Q( x) : x ≤ 3, R( x) : x > 5 而 a : 5 , 论域是 {−2,3, 6} 解:a) (x)(P(x)∨Q(x))⇔(P(1)∨Q(1))∧(P(2)∨Q(2)), 但 P(1)为 T,Q(1)为 F,P(2)为 F,Q(2)为 T, 所以(x)(P(x)∨Q(x))⇔(T∨F)∧(F∨T) ⇔T。 b) (x)(P→Q(x))∨R(a)⇔ ((P→Q(−2))∧(P→Q(3))∧(P→Q(6)))∨R(a) 因为 P 为 T,Q(−2)为 T,Q(3)为 T,Q(6)为 F,R(5)为 F, 所以(x)(P→Q(x))∨R(a)⇔((T→T)∧(T→T)∧(T→F))∨F⇔ F (4) 对下列谓词公式中的约束变元进行换名。 A) ∀x∃y ( P ( x, z ) → Q ( y ) � S ( x, y ) B) (∀xP( x) → ( R( x) ∨ Q( x))) ∧ ∃xR( x)) → ∃zS ( x, z) 解:a)(u)(v)(P(u,z)→Q(v))S(x,y) b)(u)(P(u)→ (R(u)∨Q(u))∧(v)R(v))→(z)S(x,z) (5) 对下列谓词公式中的自由变元进行代入。 A) (∃yA( x, y ) → ∀xB ( x, z )) ∧ ∃x∀zC ( x, y , z ) B) (∀yP( x, y ) ∧ ∃zQ( x, z )) ∨ ∀xR( x, y) 解:a)((y)A(u,y)→(x)B(x,v))∧(x)(z)C(x,t,z) b)((y)P(u,y)∧(z)Q(u,z))∨(x)R(x,t) 习题 2-5 (1)考虑以下赋值,论域:
离散数学习题课-命题逻辑

练习1:判断推理是否正确
1. 判断下面推理是否正确: (1) 前提:PQ, Q 结论:P 解 推理的形式结构: (PQ)QP 方法一:等值演算法 (PQ)QP ((PQ)Q)P (PQ)QP ((PQ)(QQ))P PQ 易知10是成假赋值,不是重言式,所以推理不正确.
14
练习3:求公式的主范式
已知命题公式A中含3个命题变项P, Q, R,并知 道它的成真赋值为001, 010, 111, 求A的主析取 范式和主合取范式,及A对应的真值函数. 解: P Q R A P Q R A 0 0 0 0 1 0 0 0 0 0 1 1 0 1 1 1 1 A的主析取范式为m1 m2 m7 A的主合取范式为M0 M3 M4 M5 M6
7
习题课-命题逻辑(2)
基本要求 深刻理解等值式的概念 牢记基本等值式的名称及它们的内容 熟练地应用基本等值式及置换规则进行等 值演算 理解简单析取式、简单合取式、析取范式、 合取范式的概念 深刻理解极小项、极大项的概念、名称及 下角标与成真、成假赋值的关系,并理解 简单合取式与极小项的关系
2
练习1
判断下列语句是否为命题: 是 1. 十是一个整数. 2. 北京是一个村庄. 是 否 3. 请勿吸烟! 是 4. 雪是黑色的. 是 5. 今天是7号. 是 6. 1+101=110. 否 7. 您吃饭了吗? 8. 我学英语或法语. 是 是 9. 如果天气好,我就去散步. 10. 我不给所有自己替自己理发的人理发,但却给 所有自己不替自己理发的人理发。 否
26
练习2:构造证明
2. 在系统P中构造下面推理的证明: 如果今天是周六,我们就到颐和园或圆明园玩. 如果颐和园游人太多,就不去颐和园. 今天是周 六,并且颐和园游太多. 所以, 我们去圆明园或 动物园玩. 证明: (1) 设 P:今天是周六,Q:到颐和园玩, R:到圆明园玩,S:颐和园游人太多 T:到动物园玩 (2) 前提:P(QR), SQ, P, S 结论:RT
离散数学练习题2 答案
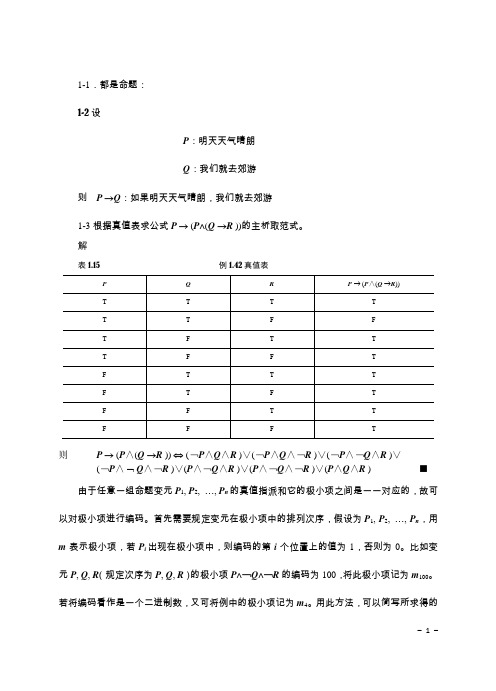
1-1.都是命题:1-2设P:明天天气晴朗Q:我们就去郊游则P →Q:如果明天天气晴朗,我们就去郊游1-3根据真值表求公式P → (P∧(Q →R ))的主析取范式。
解表1.15 例1.42真值表则P → (P∧(Q →R )) ⇔ (﹁P∧Q∧R )∨(﹁P∧Q∧﹁R )∨(﹁P∧﹁Q∧R )∨⌝(﹁P∧Q∧﹁R )∨(P∧﹁Q∧R )∨(P∧﹁Q∧﹁R )∨(P∧Q∧R ) ■由于任意一组命题变元P1, P2, …, P n的真值指派和它的极小项之间是一一对应的,故可以对极小项进行编码。
首先需要规定变元在极小项中的排列次序,假设为P1, P2, …, P n,用m表示极小项,若P i出现在极小项中,则编码的第i个位置上的值为1,否则为0。
比如变元P, Q, R(规定次序为P, Q, R)的极小项P∧﹁Q∧﹁R的编码为100,将此极小项记为m100。
若将编码看作是一个二进制数,又可将例中的极小项记为m4。
用此方法,可以简写所求得的给定公式的主析取范式。
P → (P∧(Q →R )) ⇔m0∨m1∨m2∨m3∨m4∨m5∨m7(规定P, Q, R的次序为P, Q, R)公式P → (P∧(Q →R ))的主析取范式。
解P → (P∧(Q →R ))⇔﹁P∨(P∧(﹁Q∨R ))⇔ (﹁P∨P)∧(﹁P∨﹁Q∨R)⇔ (﹁P∨﹁Q∨R )⇔ (﹁P∨﹁Q∨R )1-4试证明(﹁P →Q )∧(P →R )∧(﹁Q∨S ) ⇒S∨R。
证明(1)﹁P →Q P(2)﹁Q∨S P(3)Q →S T, (2), E16(4)﹁P →S T, (1), (3), I13(5)﹁S →P T, (4), E18(6)P →R P(7)﹁S →R T, (5),(6), I13(8)﹁﹁S∨R T, (7),E16(9)S∨R T, (8), E11-5如果迈克有电冰箱,则或者他卖了洗衣机,或者他向别人借了钱。
离散数学第10章习题答案

第10章习题答案1.解 (1)设G 有m 条边,由握手定理得2m =∑∈Vv v d )(=2+2+3+3+4=14,所以G 的边数7条。
(2)由于这两个序列中有奇数个是奇数,由握手定理的推论知,它们都不能成为图的度数列。
(3) 由握手定理得∑∈Vv v d )(=2m =24,度数为3的结点有6个占去18度,还有6度由其它结点占有,其余结点的度数可为0、1、2,当均为2时所用结点数最少,所以应由3个结点占有这6度,即图G 中至多有9个结点。
2.证明 设1v 、2v 、…、n v 表示任给的n 个人,以1v 、2v 、…、n v 为结点,当且仅当两人为朋友时其对应的结点之间连一条边,这样得到一个简单图G 。
由握手定理知∑=nk kv d 1)(=3n 必为偶数,从而n 必为偶数。
3. 解 由于非负整数列d =(d 1,d 2,…,d n )是可图化的当且仅当∑=ni i d 1≡0(mod 2),所以(1)、(2)、(3)、(5)能构成无向图的度数列。
(1)、(2)、(3)是可简单图化的。
其对应的无向简单图如图所示。
(5)是不可简单图化的。
若不然,存在无向图G 以为1,3,3,3度数列,不妨设G 中结点为1v 、2v 、3v 、4v ,且d(1v )=1,d(2v )=d(3v )=d(4v )=3。
而1v 只能与2v 、3v 、4v 之一相邻,设1v 与2v 相邻,于是d(3v )=d(4v )=3不成立,矛盾。
4.证明 因为两图中都有4个3度结点,左图中每个3度结点均与2个2度结点邻接,而右图中每个3度结点均只与1个2度结点邻接,所以这两个无向图是不同构的。
5. 解 具有三个结点的所有非同构的简单有向图共16个,如图所示,其中(8)~(16)为其生成子图。
6. 解 (1)G 的所有子图如图所示。
(1)(3)(5)(6)(9)(10)(13)(14)(2)图(8)~(18)是G 的所有生成子图。
离散数学课后习题答案二

习题3.71. 列出关系}6|{=×××Î><+d c b a d c b a d c b a 且,,,,,,Z 中所有有序4元组。
组。
解}6|{=×××Î><+d c b a d c b a d c b a 且,,,,,,Z ,2,1,3,1,3,1,2,1,2,3,1,1,3,2,1,1,1,1,1,6,1,1,6,1,1,6,1,1,6,1,1,1{><><><><><><><><=><><><><><><><><2,1,1,3,3,1,1,2,1,2,1,3,1,3,1,2,1,1,2,3,1,1,3,2,1,2,3,1,1,3,2,12. 列出二维表3.18所表示的多元关系中所表示的多元关系中所有所有5元组。
假设不增加新的5元组,找出二维表3.18所有的主键码。
所有的主键码。
表3.18 航班信息航空公司航空公司 航班航班 登机口登机口 目的地目的地 起飞时间起飞时间 Nadir 112 34 底特律底特律 08:10 Acme 221 22 丹佛丹佛 08:17 Acme 122 33 安克雷奇安克雷奇 08:22 Acme 323 34 檀香山檀香山 08:30 Nadir 199 13 底特律底特律 08:47 Acme 222 22 丹佛丹佛 09:10 Nadir 32234底特律底特律09:44解 略3. 当施用投影运算5,3,2p 到有序5元组><d c b a ,,,时你能得到什么?时你能得到什么? 解 略4. 哪个投影运算用于除去一个6元组的第一、第二和第四个分量?元组的第一、第二和第四个分量? 解 略5. 给出分别施用投影运算4,2,1p 和选择运算Nadir 航空公司=s 到二维表3.18以后得到的表。
离散数学习题课带答案

(4)某些汽车比所有的火车都慢,但至少有一列火车比每辆 汽车快 C(x):x是汽车;H(x):x是火车;S(x,y): x比y慢 x(C(x)∧y(H(y)→S(x,y)))∧z(H(z)∧y(C(y) →S(y,z)))
(5)对任何整数x和y,x≤y且y≤x是x=y的充要条件 I(x):x是整数;E(x,y):x=y;G(x,y):x>y xy(I(x)∧I(y)→(G(x,y)∧G(y,x)↔ E(x,y)))
(6)若m是奇数,则 2m 不是奇数 O(x):x是奇数; f(x,y)= x×y O(m) → O(f(2,m)
T⑸ E
⑺ (D∨E)→P
P
⑻ (D∨E)∨P
T⑺E
⑼ (D∧E)∨P
T⑻ E
⑽ (D ∨P) ∧(E∨P) T ⑼ E
⑾ D∨P
T⑽ I
⑿ D→P
T ⑾E
⒀A→P
T ⑹⑿ I
2.附加前提 ⑴A ⑵ A∨B ⑶ (A∨B)→(C∧D) ⑷ C∧D ⑸D ⑹ D∨E ⑺ (D∨E)→P ⑻P ⑼ A→P
2.如果D∨E 为 F,则 前件 (A→(B∨C) )∧(D∨E)∧((D∨E)→A) 为F。
∴(A→(B∨C) )∧(D∨E)∧((D∨E)→A)B∨C
四. 等价公式的证明方法 方法1:用列真值表。(不再举例) 方法2:用公式的等价变换.(用置换定律) (1) 证明 ((A∧B)→C)∧(B→(D∨C))(B∧(D→A))→ C 左式((A∧B)∨C)∧(B∨(D∨C)) ((A∨B)∨C)∧(B∨(D∨C)) ((B ∨A)∨C)∧((B∨D)∨C) ((B ∨A)∧(B∨D))∨C (B ∨(A∧D))∨C (B∧(A∨D))∨C (B∧(D→A))→C
离散数学 第10讲习题课.ppt

规则
2020/1/29
计算机学院
5
掌握与量词相关的基本等价式和基本蕴涵式 能熟练地运用US、ES、UG、EG规则进行推理
2020/1/29
计算机学院
6
语句的符号化
1、将下列命题翻译成谓词公式 ① 每个有理数都是实数,但是并非每个实数都是有理数,
T,10),11)I
13) ~(y)(Q(y)∧R(c,y))
T,4),E
14) (y)~(Q(y)∧R(c,y))
T,13),E
15) ~(Q(b)∧R(c,b))
US,14)
16) (Q(b)∧R(c,b))∧~(Q(b)∧R(c,b)) US,14)
17) □
2020/1/29
计算机学院
22
2020/1/29
计算机学院
P US(1) P US(3) P US(5) T(6)E
25
(8) Q(x)~C(x)
T(2)(7)I
(9) N(x)~C(x)
T(4)(7)I
(10)(Q(x)~C(x))(N(x)~C(x))
T(8)(9)E
(11) C(x)(~Q(x)~N(x))
7) R(x,f(x))
T,2)
8) Q(f(x))∧R(x,f(x))
T,6),7),I
9) (y)(Q(y)∧R(x,y))
EG,8)
10)(y)(P(y)∧R(x,y))(y)(Q(y)∧R(x,y)) CP,1),9)
11)(x)((y)(P(y)∧R(x,y))(y)(Q(y)∧R(x,y)))
离散数学习题课2

第二章谓词逻辑
1、在一元谓词逻辑中,分别在(a)(b)(c)时将下面命题符号化并讨论命题的真值:
1)凡是整数都能被2整除
2)有的整数能被2整除
其中(a):个体域为整数集合;(b):个体域为偶数集合;(c)个体域为实数集合2、在一元谓词逻辑中将下面命题符号化
1)所有的整数,不是负整数,就是正整数,或者是0
2)有的实数是有理数,有的实数是无理数
3)发明家都是聪明的并且勤劳的。
王进是发明家。
所以王进是聪明的并且是勤劳的。
4)实数不都是有理数
5)】
6)不存在能表示成分数的有理数
7)不存在最大的自然数
3、求下列公式的前束范式
1)()()()(,) x F x y G x y ∀→∀
2)()()()(,) x F x x G x y ∀→∀
3)()()()(,) x F x x G x y ∀→∃
4)()(()(,))(()()()(,)) x F x G x y y H y z L y z ∀→→∃→∃
4、人都喜欢吃蔬菜,但不是所有的人都喜欢吃鱼。
所以,存在喜欢吃蔬菜而不喜欢吃鱼
的人。
F(x):x为人;G(x):x喜欢吃蔬菜;H(x):x喜欢吃鱼
5、没有白色的乌鸦。
北京鸭是白色的。
因此,北京鸭不是乌鸦。
F(x):x是乌鸦;H(x):
x是北京鸭;G(x):x是白色的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机学院
20
例4
证明:(x)(P(x)Q(x)) (x)((y)(P(y)∧R(x,y))(y)(Q(y)∧R(x,y)))。
1.采用反证法: 1) ~(x)((y)(P(y)∧R(x,y))
(y)(Q(y)∧R(x,y))) 2) (x)~((y)(P(y)∧R(x,y))
(y)(Q(y)∧R(x,y))) 3) ~((y)(P(y)∧R(c,y))
(7) Q(c)R(c)
T,(4),(6),I
(8)(x)(P(x)→(R(x)S(x))) P
(9) P(c)→(R(c)S(c))
US,(8)
(10) R(c)S(c)
T,(4),(9),I
2020/4/22
计算机学院
17
例2(续3)
(11)(R(c)→S(c))∧(S(c)→R(c)) T,(10),E
F
2020/4/22
计算机学院
11
④ 每个懂得人性本质的作家都很高明。不能刻划人们内心世界的 诗人都不是真正的诗人。莎士比亚创作了哈姆雷特。没有一个 不懂得人性本质的作家能够刻划人们的内心世界。只有真正的 诗人才能创作哈姆雷特。因此,莎士比亚是一个高明的作家。
A(x):x是懂得人性本质的作家 B(x):x是真正的诗人 C(x):x能刻划人们内心世界
结论:(x)(T(x)~P(x))
即证明:(x)(S(x)∧(y)(T(y)L(x,y))),
(x)(y)((S(x)∧P(y))~L(x,y))
(x)(T(x)~P(x))
2020/4/22
计算机学院
19
证明:
1) (x)(S(x)∧(y)(T(y)L(x,y))) P
2) S(c)∧(y)(T(y)L(c,y))
s(x):x的直接后继;
有
EQUAL(x,y):x=y
① (x)(y)[EQUAL(y,s(x))∧
(z)[EQUAL(z,s(x))→EQUAL(y,z)]]
且仅有
2020/4/22
计算机学院
13
② ~(x)[EQUAL(0,s(x))
0以外的任何
③ (x)[~EQUAL(x,0)
自然数
→(y)[EQUAL(y,p(x))∧(z)[EQUAL(z,p(x))
ES,1)
3) P(f(x))
T,2)
4) (x)(P(x)Q(x))
P
5) P(f(x))Q(f(x))
US,4)
6) Q(f(x))
T,3),5),I
7) R(x,f(x))
T,2)
8) Q(f(x))∧R(x,f(x))
T,6),7),I
9) (y)(Q(y)∧R(x,y))
EG,8)
10)(y)(P(y)∧R(x,y))(y)(Q(y)∧R(x,y)) CP,1),9)
可满足式(Why?)
2020/4/22
计算机学院
10
② 诚实的人都讲实话。小林不是诚实的,因而 小林不讲实话。
A(x):x是诚实的人 B(x):x讲实话 a:小林
(x)( A(x) → B(x) )∧ ~A(a)→ ~B(a)
F ③ 好货不便宜。小王买的衣服很贵,所以小王
买的是优质衣服。
A(x):x不便宜 B(x):x是好货 a:小王买的衣服 (x)( B(x)→ A(x))∧A(a)→B(a)
全总个体域的概念 ▪ 能准确理解约束变元(量)和自由变元的概念 ▪ 掌握约束变元的改名规则和自由变元的代入
规则
2020/4/22
计算机学院
5
▪ 掌握与量词相关的基本等价式和基本蕴涵式 ▪ 能熟练地运用US、ES、UG、EG规则进行推
理
2020/4/22
计算机学院
6
语句的符号化
▪ 1、将下列命题翻译成谓词公式 ① 每个有理数都是实数,但是并非每个实数都是有理数,
11)(x)((y)(P(y)∧R(x,y))(y)(Q(y)∧R(x,y)))
EG,10)
2020/4/22
计算机学院
23
例5
所有的有理数都是实数;所有的无理数也是实 数;虚数不是实数。因此,虚数既不是有理数也 不是无理数。 解:设Q(x):x是有理数;R(x):x是实数; N(x): x是无理数; C(x):x是虚数; (x)(Q(x)R(x), (x)(N(x)R(x)) (x)(C(x) ~R(x)) (x)(C(x)(~Q(x)~N(x))
有些实数是有理数。 A(x):x是实数 B(x):x是有理数 (x)(B(x)→A(x))∧(x)(A(x)→B(x))
∧(x)(A(x)∧B(x)) ② 直线a和b平行当且仅当a和b不相交。
A(x):x是直线 F(x,y):x与y平行
G(x,y):x与y相交 (a)(b)(A(a)∧A(b)→
(F(a,b)G(a,b)))
2020/4/22
计算机学院
15
例2(续1)
解:设P(x):x是报考研究生的大学毕业生; Q(x):x参加研究生入学考试; R(x):x被推荐为免试生; S(x):x学习成绩优秀。
则原论断可符号化为: (x)(P(x)→(Q(x)R(x)), (x)(P(x)→(R(x)S(x))), (x)(P(x)∧S(x)), ~(x)(P(x)→S(x))
C(x):x是质数
(x)(A(x)→B(x)C(x))
2020/4/22
计算机学院
8
⑤ 凡是存钱的人都想有利息,如果没有利息, 人们就不会存钱。
A(x):x是存钱的人 F(x,y):x想有y P:存钱没有利息 Q: 人们不存钱 a: 利息 (x)(A(x)→F(x,a))∧(P→Q)
2020/4/22
冯伟森
Email:fws365@ 2020年4月22日星期三
2020/4/22
计算机学院
2
第二章
一、基本概念 全总个体域(全论域)、全称量词、存在量
词、特性谓词、指导(作用)变元、辖域 (作用域)、约束变元、自由变元、约束变 元的改名规则、自由变元的代入规则、常量 符号、变量符号、函数符号、谓词符号、谓 词公式、公式的解释、永真公式(重言式) 、 永假公式(矛盾式,不可满足公式)、
(x)(P(x)∧Q(x))
2020/4/22
计算机学院
16
例2(续2)
证明:(1) ~(x)(P(x)→S(x))
P
(2) (x)(P(x)∧~S(x)) (3) P(c)∧~S(c)
T,(1),E ES,(2)
(4) P(c)
T,(3),I
(5) (x)(P(x)→(Q(x)R(x)) P
(6) P(c)→(Q(c)R(c)) US,(5)
D(x):x很高明 P(x,y):x创作了y a:莎士比亚 b:哈姆雷特
T
2020/4/22
计算机学院
12
例1
将下列三条自然公理翻译成谓词公式:
① 每个自然数有且仅有一个直接后继;
② 没有任何自然数以0为其直接后继;
③ 对0以外的任何自然数,有且仅有一个直接先行。
解:设个体域D为自然数
令p(x):x的直接先行;
(y)(Q(y)∧R(c,y))) 4) (y)(P(y)∧R(c,y))∧
~(y)(Q(y)∧R(c,y)) 5) (y)(P(y)∧R(c,y))
P(附加)
T,1),E
ES,2)
T,3),E T,4),I
2020/4/22
计算机学院
21
例4(续1)
6) P(b)∧R(c,b)
ES,5)
7) P(b)
8) (S(c)∧P(x))~L(c,x)
US,7)
9) S(c)(P(x)~L(c,x))
T,8),E
10)P(x)~L(c,x)
T,3),8),E
11)L(c,x)~P(x)
T,10),E
12)T(x)~P(x)
T,5),11),E
13)(x)(T(x)~P(x))
US,12)
2020/4/22
ES,1)
3) S(c)
说明:该结论明显T,2),I
4) (y)(T(y)L(c,y是))一个错误的结论,T,2),I
5) T(x)L(c,x)
原因在于有一个错US,4)
6) (x)(y)((S(x)∧P误(y的))假设~,L(但x,推y)理)
P
7) (y)((S(c)∧P(y))~是L正(c确,y的பைடு நூலகம்)。 US,6)
15) ~(Q(b)∧R(c,b))
US,14)
16) (Q(b)∧R(c,b))∧~(Q(b)∧R(c,b)) US,14)
17) □
2020/4/22
计算机学院
22
例4(续2)
x是自由变元
2.采用CP规则的直接证明法:
1) (y)(P(y)∧R(x,y))
P(附加前题)
2) P(f(x))∧R(x,f(x))
计算机学院
9
▪ 2、把下列语句符号化,并确定相应谓词公式 是永真式、可满足式,还是矛盾式。
① 如果两个数的积等于0,那么至少其中一个数
为0,数x-1不等于0,所以数x-1和数x+1的
积也不等于0。
A(x):x=0,f(x,y)=xy
xy[A(f(x,y))→(A(x)∨A(y))]∧
~A(x-1)→ ~A(f(x-1,x+1))
2020/4/22
计算机学院
24
(1)(x)(Q(x)R(x)) (2) Q(x)R(x) (3)(x)(N(x)R(x)) (4) N(x)R(x) (5)(x)(C(x)~R(x)) (6) C(x)~R(x) (7) R(x)~C(x)
