一种改进的空间平滑MUSIC算法
MUSIC及其改进算法的研究与实现
MUSIC及其改进算法的研究与实现黄丽薇;陈慧琴;陈玉林【摘要】研究了用于阵列信号处理领域的重要分支,即信号到达角估计的几种MUSIC算法.阐述了经典MUSIC算法、前后向空间平滑MUSIC算法、改进MUSIC算法的原理.采用Matlab进行的仿真表明,经典MUSIC算法对于非相干信源的到达角估计具有良好的性能,但不能用于相干信源的到达角估计;前后向空间平滑MUSIC算法使可估计信源数减小、计算复杂度较高;改进MUSIC算法性能最好,不影响非相关信源的估计,也无明显计算量增加.几种算法在到达角估计中有各自的优缺点.【期刊名称】《电子科技》【年(卷),期】2015(028)003【总页数】4页(P55-57,75)【关键词】MUSIC;空间平滑MUSIC;改进MUSIC;到达角估计【作者】黄丽薇;陈慧琴;陈玉林【作者单位】东南大学成贤学院,江苏南京 210088;东南大学成贤学院,江苏南京210088;东南大学成贤学院,江苏南京 210088【正文语种】中文【中图分类】TN957阵列信号处理是信号处理的重要分支，信号到达角(DOA)估计是阵列信号的重要部分［1－2］。
经典MUSIC算法［3］基于接收信号的协方差矩阵分解，对于非相干信源的到达角估计具有良好的性能。
前/后向空间平滑算法［4］和改进MUSIC(MMUSIC)算法［5］可以实现相干信源的到达角估计。
1 经典MUSIC算法1.1 经典MUSIC原理考虑M元均匀线阵，有N个窄带信源平面波入射，信源方向为θ1，θ2，…，θN。
S(k)=［s1(k)，…，sN(k)］T，si(k)为第i个信源的复振幅。
阵列的导向矢量a(θi)=［1，e－jωi，…，e－j(M－1)ωi］T，i=1，…，N，A=，d 为阵元间距，λ 为载波波长。
n(k)=［n1(k)，…，nM(k)］T，ni(k)为零均值、方差σ2的白噪声，与信源不相关。
第k次快拍，得到的数据为X(k)=AS(k)+n(k)，k=1，2，…，K，K 为快拍次数。
空间平滑music算法原理
空间平滑music算法原理引言：空间平滑music算法是一种用于音频信号处理的算法，主要用于音乐声音的平滑处理，以提升听感和音质。
本文将介绍空间平滑music算法的原理和应用，以及其在音频处理领域的重要性。
一、空间平滑music算法概述空间平滑music算法，全称为Spatial Smoothing Multiple Signal Classification algorithm，是一种基于多信号分类的空间平滑算法。
该算法通过对音频信号进行空间平滑处理，消除噪音和杂音，提高音频信号的质量和清晰度。
二、空间平滑music算法原理空间平滑music算法基于多个传感器（如麦克风）接收到的音频信号，通过对这些信号进行空间平滑处理，提取出目标音频信号。
其原理主要包括以下几个步骤：1. 采集音频信号：使用多个传感器同时采集音频信号，得到多个信号源的混合信号。
2. 构建空间协方差矩阵：将采集到的音频信号进行分析，计算得到信号源之间的空间协方差矩阵。
该矩阵表示了信号源之间的相关性和空间分布。
3. 估计噪声子空间：通过对空间协方差矩阵进行特征值分解，得到特征值和特征向量。
通过选取特征值较小的特征向量，可以估计出信号源的噪声子空间。
4. 构建空间平滑矩阵：根据估计的噪声子空间，构建空间平滑矩阵，用于对混合信号进行平滑处理。
空间平滑矩阵的构建可以通过正交投影等方法实现。
5. 信号源估计：将空间平滑矩阵应用于混合信号，可以得到对目标信号源的估计。
通过对估计信号源的处理，可以得到音频信号的平滑输出。
三、空间平滑music算法的应用空间平滑music算法在音频处理领域具有广泛的应用。
以下是一些常见的应用场景：1. 音乐制作：在音乐制作过程中，空间平滑music算法可以用于去除录音中的噪音和杂音，提高音频的质量和清晰度。
2. 语音识别：在语音识别系统中，空间平滑music算法可以用于增强语音信号，提高语音识别的准确性和稳定性。
空间平滑算法
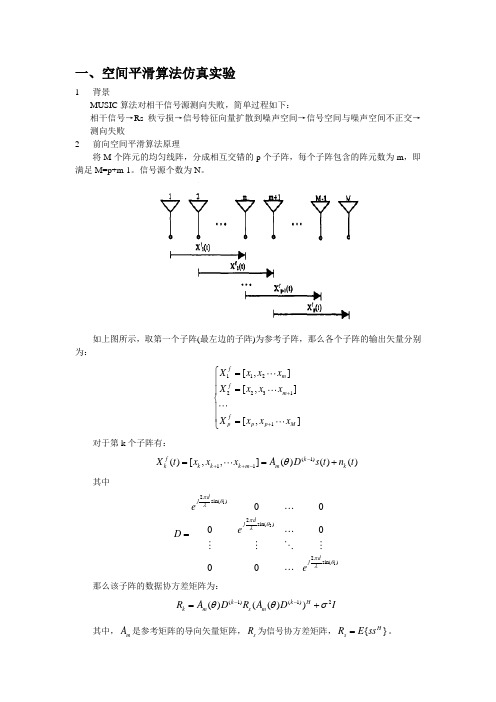
一、空间平滑算法仿真实验1背景MUSIC 算法对相干信号源测向失败，简单过程如下：相干信号→Rs 秩亏损→信号特征向量扩散到噪声空间→信号空间与噪声空间不正交→测向失败2 前向空间平滑算法原理将M 个阵元的均匀线阵，分成相互交错的p 个子阵，每个子阵包含的阵元数为m ，即满足M=p+m-1。
信号源个数为N 。
如上图所示，取第一个子阵(最左边的子阵)为参考子阵，那么各个子阵的输出矢量分别为：11222311[,][,][,]f m fm f pp p M X x x x X x x x X x x x ++⎧=⎪=⎪⎨⎪⎪=⎩ 对于第k 个子阵有：(1)11()[,,]()()()f k k k k k m m k X t x x x A D s t n t θ-++-==+其中1212sin()2sin()2sin()0000djdj dj e eD eπθλπθλπθλ=那么该子阵的数据协方差矩阵为：(1)(1)2()(())k k H k m s m R A D R A D I θθσ--=+其中，m A 是参考矩阵的导向矢量矩阵，s R 为信号协方差矩阵，{}Hs R E ss =。
前向空间平滑技术是通过求各个子阵协方差矩阵的均值来实现的，即取前向平滑修正的协方差矩阵为11pfk k R R p ==∑可以证明，当满足m>N ，p>N 时，前向空间平滑数据协方差矩阵f R 是满秩的。
即可以通过特征分解求得相应的信号子空间和噪声子空间。
3 实验仿真仿真条件：均匀直线阵；阵元个数8；信号个数3；子阵阵元个数5；半径波长比0.5； 方位角[75,125,160]；信噪比[10,20,10]dB 。
未使用空间平滑算法：020406080100120140160180-8-6-4-2024未使用空间平滑算法:sn=3;M=8;方位角：75,125,160；距离波长比：0.5方位角空间谱/d b使用向空间平滑算法：子阵阵元数 > 相干信号个数020406080100120140160180-101020304050方位角空间谱/d b使用向空间平滑算法：子阵阵元数 < 相干信号个数20406080100120140160180-9-8-7-6-5-4-3-2-101使用向空间平滑算法：sn=3;M=8;子阵阵元数2;子阵阵元个数:7方位角空间谱/d b使用向空间平滑算法：子阵阵元数 = 相干信号个数020406080100120140160180-10102030405060方位角空间谱/d b结论：子阵阵元数必须大于等于相干信号，空间平滑算法有效。
低信噪比中MUSIC算法的研究
低信噪比中MUSIC算法的研究引言在无线通信系统中，信号受到噪声的干扰是一个普遍存在的问题。
在低信噪比环境下，如何准确地估计信号的到达角度成为了研究的重点。
MUSIC（Multiple Signal Classification）算法是一种常用的高精度角度估计算法，它在低信噪比环境下具有较好的性能。
本文主要介绍低信噪比中MUSIC算法的原理、实现以及相关研究进展。
一、MUSIC算法原理MUSIC算法是一种基于谱分析的方位估计算法。
其基本思想是将接收到的信号通过空间滤波器变换到空间域，然后通过计算信号在子空间中的谱能量分布来确定信号的到达角度。
具体步骤如下：1.构建传感器阵列：MUSIC算法需要在接收端构建一个由N个传感器组成的均匀线性阵列。
2.接收信号预处理：接收到的信号需要经过预处理，例如采样、滤波等操作。
3.构建协方差矩阵：将N个传感器接收到的信号构成一个接收数据矩阵X，假设其协方差矩阵为R=XX^H。
4.特征值分解：对协方差矩阵进行特征值分解，得到特征值以及对应的特征向量。
5.构建谱估计矩阵：根据特征值和特征向量构建谱估计矩阵P，其中谱估计矩阵的维度为M-L，M为信号源数量，L为噪声子空间的维数。
6.估计信号的到达角度：通过计算谱估计矩阵的特征向量，得到信号的到达角度。
二、低信噪比中MUSIC算法实现在低信噪比环境下，传统的MUSIC算法可能无法准确估计信号的到达角度，因为噪声会导致子空间的降低，使得信号与噪声的区分度较小。
因此，需要对传统的MUSIC算法进行改进，以提高其在低信噪比环境下的性能。
1. 噪声子空间降维：在低信噪比环境下，噪声对子空间的影响较大，因此需要对噪声子空间进行降维处理。
一种常见的方法是使用快速主成分分析（Fast PCA）算法对协方差矩阵进行分解，将噪声子空间的维数减小，从而提高信号与噪声的区分度。
2. 噪声机制建模：在低信噪比环境下，需要对噪声进行准确的建模。
一种方法是使用噪声空间投影（Noise Subspace Projection）技术，通过将接收信号投影到噪声子空间中去除噪声的影响。
MUSIC方法仿真
MUSIC方法仿真MUSIC (MUltiple SIgnal Classification) 是一种常用于音频信号处理和频谱分析的方法，它可以用于估计信号源的方向和频率。
MUSIC方法是一种高分辨率的频谱估计方法，它可以对多个信号源进行分辨。
MUSIC方法的核心思想是通过计算接收信号的空间相关矩阵的特征向量，从而推断信号源的位置和频率。
具体而言，MUSIC方法首先通过阵列接收的信号来估计信号源的波达方向。
然后，根据不同的波达方向假设，计算接收信号的空间相关矩阵。
接下来，通过对空间相关矩阵进行特征分解，可以得到空间谱估计，从而得到信号源的角度。
最后，通过对角线位置较低的特征值进行峰值检测，可以得到信号源的频率。
MUSIC方法的一个重要特点是它可以实现高分辨率的频率估计。
这是因为MUSIC方法采用了特征向量分解的思想，不需要对信号进行加窗处理，在保留了较高分辨率的同时，能够准确估计信号源的频率。
另外，MUSIC方法对于信号源的数量没有限制，它能够处理多个信号源的同时估计。
这使得MUSIC方法在音频信号处理和频谱分析中得到了广泛的应用。
MUSIC方法的应用非常广泛，特别是在音频信号处理领域。
例如，在音频指纹识别中，MUSIC方法可以用于估计音频信号中存在的多个音频源的频率和方向。
在语音识别中，MUSIC方法可以用于分析和识别多个讲话者的语音信号。
此外，MUSIC方法还可以用于音频信号的定位和追踪，例如在无线通信中，可以通过MUSIC方法估计信号源的位置，从而实现无线通信系统的定位和导航。
总之，MUSIC方法是一种高分辨率的频谱估计方法，可以用于音频信号处理和频谱分析。
它能够估计信号源的方向和频率，并且可以处理多个信号源的同时估计。
MUSIC方法在音频信号处理和频谱分析中有着广泛的应用，可以用于音频指纹识别、语音识别、无线通信等领域。
music算法的直观解释
music算法的直观解释一、简介Music算法是一种用于音乐信号处理的算法，它通过对音乐信号进行特征提取和分析，从而实现对音乐的理解和创作。
该算法由美国科学家PaulE.Jacobs及其研究团队开发，并在音乐信号处理领域得到了广泛应用。
二、基本原理Music算法通过分析音乐信号的频率、振幅、时长等特征，对音乐的结构和情感进行分析和建模。
该算法基于音频信号的时域和频域分析，通过计算音频信号的傅里叶变换，将音频信号从时域转换到频域，从而实现对音频信号的频率成分的分析。
三、主要步骤1.音频信号采集：使用麦克风或其他音频采集设备采集音乐信号。
2.预处理：对音频信号进行噪声消除、音量调整等预处理操作，以提高算法的准确性。
3.傅里叶变换：将音频信号从时域转换到频域，以便于分析频率成分。
4.特征提取：从频域分析中提取音乐信号的特征，如频率、振幅、时长等。
5.模型训练：使用提取的特征对音乐的结构和情感进行分析和建模，建立音乐分类模型。
6.音乐创作：根据分类模型，使用算法生成符合音乐风格和情感的音乐片段。
四、优势与局限Music算法在音乐信号处理方面具有以下优势：1.准确性高：通过对音乐信号的全面分析，能够准确提取音乐的结构和情感特征。
2.高效性：Music算法能够快速处理大量音乐数据，并生成符合要求的音乐片段。
3.可扩展性：Music算法可以与其他音乐算法相结合，实现更复杂和多样化的音乐创作。
然而，Music算法也存在一定的局限：1.依赖训练数据：Music算法的性能受训练数据的质量和数量影响较大。
2.无法处理复杂音乐风格：Music算法在处理复杂音乐风格时可能存在一定难度。
3.缺乏个性化：目前Music算法生成的曲目往往是按照一定规则生成的，缺乏个性化和情感表达。
五、未来发展随着人工智能技术的不断发展，Music算法在音乐信号处理领域的应用前景广阔。
未来研究方向包括：1.提高算法的泛化能力：通过改进模型架构和优化训练方法，提高Music算法对不同音乐风格的适应能力。
MUSIC算法原理
MUSIC算法原理MUSIC (Multiple Signal Classification) 算法是一种用于频谱估计和波束形成的高分辨率算法。
它最早由Schmidt在 1986 年提出，用于空间谱估计。
MUSIC 算法的基本原理是将接收到的信号进行空间谱分解，并通过计算特征向量对信号源进行定位。
1.接收到的信号通过阵列天线进行采样，得到信号向量。
信号向量表示每个阵列元素接收到的信号振幅。
2.构建协方差矩阵。
协方差矩阵表示接收到的信号之间的相关性。
协方差矩阵可以通过信号向量的内积进行计算。
3.对协方差矩阵进行特征分解。
特征分解可以得到协方差矩阵的特征值和特征向量。
4.根据特征值和特征向量，计算谱估计。
谱估计是通过将信号向量投影到特征向量的子空间中，得到信号源的空间谱。
特征值较大的特征向量对应的子空间贡献较大，而特征值较小的特征向量则表示噪音。
5.根据谱估计结果，确定信号源的角度。
当信号源角度为0度时，谱估计结果最大，此时信号源沿阵列法线方向；而当信号源角度不为0度时，谱估计结果较小。
MUSIC算法的核心思想是通过计算信号的空间谱，从而实现高分辨率的信号源定位。
它可以处理多路径传播和相干信号，对于不同角度的信号源能够实现较好的角度分辨率。
MUSIC算法广泛应用于雷达、无线通信、声纳等领域。
1.高分辨率：MUSIC算法可以实现较好的信号源定位效果，通过计算信号的空间谱，可以对信号源进行准确的角度估计。
2.对多路径传播和相干信号有较好的处理能力：MUSIC算法可以通过计算协方差矩阵的特征值和特征向量，对多路径传播和相干信号进行分离和定位。
3.算法简单：MUSIC算法的步骤相对简单，容易实现和理解。
它不需要复杂的参数估计和信号模型，只需进行简单的矩阵运算即可得到信号源的定位结果。
1.阵列结构需知：MUSIC算法对阵列结构要求较高，需要事先知道阵列几何结构的具体信息，如阵列元素之间的距离、阵列元素的位置等。
music算法本质原理
music算法本质原理
Music算法本质上是一种信号频率估计的多重分类算法，利用微弱生命体信号子空间与噪声子空间的正交性构造空间谱函数，通过谱峰搜索，确定心跳和呼吸信号的频率。
MUSIC算法的核心是对阵列输出信号的二阶矩Ry进行特征值分解，利用特征向量构建两个正交的子空间，即信号子空间和噪声子空间。
对Ry进行特征分解，即是使得图册中的公式成立。
大特征值对应的特征向量组成的空间Us为信号子空间，小特征值对应的特征向量组成的空间Un为噪声子空间。
将噪声特征向量作为列向量，组成噪声特征矩阵，并张成M-D维的噪声子空间Un，噪声子空间与信号子空间正交。
而Us的列空间向量恰与信号子空间重合，所以Us的列向量与噪声子空间也是正交的，由此，可以构造空间谱函数。
在空间谱域求取谱函数最大值，其谱峰对应的角度即是来波方向角的估计值。
均匀面阵的music算法
均匀面阵的music算法
均匀面阵的MUSIC算法是一种常用的信号处理技术，用于估计信号源的方向或位置。
以下是该算法的基本步骤：
1. 接收阵列布置：选择均匀平面阵列作为接收阵列，确保阵列的几何形状符合所需的定位要求。
2. 采集信号数据：在已布置好的接收阵列上，采集来自信号源的信号数据，并进行预处理，如去除噪声、增强信号质量等。
3. 构建协方差矩阵：使用传感器数据，构建接收阵列的协方差矩阵。
协方差矩阵反映了传感器之间的相互关系和接收到的信号特性。
4. MUSIC算法实施：利用MUSIC算法对协方差矩阵进行分解和分析，以估计信号源的方向或位置。
该算法通过空间谱估计方法，将信号源的DOA （方向到达）与干扰噪声进行区分。
5. 信号源定位：根据MUSIC算法的结果，确定信号源在空间中的位置或方向。
对于均匀平面阵，可以直接获得信号源的方向角度。
需要注意的是，MUSIC算法的实施涉及到信号处理、谱估计和空间波束形成等关键技术。
在实际应用中，还需要考虑传感器间距离、阵列元素数目、信噪比以及接收阵列的校准和校验等方面的因素。
以上是均匀面阵的MUSIC算法的基本步骤，如需了解更多信息，建议咨询专业人士或查阅相关书籍文献。
MUSIC算法原理
MUSIC 算法基本原理信号模型MUSIC 算法是针对多元天线阵列测向问题提出的，用含M 个阵元的阵列对()M K K <个目标信号进行测向，以均匀线阵为例，假设天线阵元在观测平面内是各向同性的，阵元的位置示意图如图1所示。
d图1 均匀线阵示意图来自各远场信号源的辐射信号到达天线阵列时均可以看作是平面波，以第一个阵元为参考，相邻阵元间的距离为d ，若由第k 个辐射元辐射的信号到达阵元1的波前信号为)(t S k ，则第i 个阵元接收的信号为()()()c /sin 1j ex p 0k k k d i t S a θω-- (1)其中，k a 为阵元i 对第k 个信号源信号的响应，这里可取1=k a ，因为己假定各阵元在观察平面内是无方向性的，0ω为信号的中心频率，c 为波的传播速度，k θ表示第k 个信号源的入射角度，是入射信号方向与天线法线的夹角。
计及测量噪声（包括来自自由空间和接收机内部的）和所有信号源的来波信号，则第i 个阵元的输出信号为()()()()()t n d i t S a t x i k Kk k k i +--=∑=c /sin 1j ex p 01θω (2)式中，)(t n i 为噪声，标号i 表示该变量属于第i 个阵元，标号k 表示第k 个信号源。
假定各阵元的噪声是均值为零的平稳白噪声过程，方差为2σ，并且噪声之间不相关，且与信号不相关，则有()()()t t t N AS X += (3)式中，T21)](,),(),([)(t x t x t x t M =X 为M 维的接收数据向量 T 21)](,),(),([)(t S t S t S t K =S 为K 维信号向量)](,),(),([21K θθθa a a A =为K M ⨯维的阵列流形矩阵T )1(j j ]e ,,e ,1[)(00k k M k τωτωθ---= a 为M 维的方向向量，sin k k d θτ=T 21)](,),(),([)(t n t n t n t M =N 为M 维的噪声向量算法原理由于各阵元的噪声互不相关，且也与信号不相关，因此接收数据)(t X 的协方差矩阵为()(){}t t E H XX R = (4)其中，上标H 表示共轭转置，即 I APA R 2H σ+= (5)P 为空间信号的协方差矩阵()(){}t t E H S S P = (6)由于假设空间各信号源不相干，并设阵元间隔小于信号的半波长λ，即2λ≤d ，0c π2λ=，这样矩阵A 将有如下形式⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=---------D θM λd θM λd θM λd D d d d sin )1(π2j 2sin )1(π2j 1sin )1(π2j sin π2j 2sin π2j 1sin π2j e e e e e e 1 1 1 θλθλθλA (7) 矩阵A 是范德蒙德阵，只要j i θθ≠)(j i ≠，它的列就相互独立。
MUSIC算法在空间谱估计中应用的仿真分析
２ 前后 向空 间平 滑 ）
采用前 向平 滑可 以解 决相 干源 的问题 ，但 是有 效阵元 损失 太多 ，为 了尽 量减 少这种 损 失 ， 以采用前 后 向组合 的平 滑技 术 。这种 算 法利用 了均匀线 阵 的旋 转 不变 性 ， 图 １ 可 对 中划
分 的Ｌ 个ｍ元 子阵的相关 矩 阵 的ＭＬ 估计 进行 前后 向平 滑 ， 前后 向空 间平 滑的协 方差矩 阵为 ：
源下的 空间谱 估计 算 法进 行 了对 比分析 。仿 真 结果表 明 ，在 快拍数 一定 的情 况下 ，当阵元
数较 多 、信噪 比较 高的情 况下ＭＵｓｃ算法可 以获得较 高的谱 分辨 率 ；采 用子 阵平滑技 术 ， Ｉ
可 以 解 决信 号 相 干 导 致 的 信 号 源 数 目错 误 估 计 的 问题 。
图３ 阵 元 数 为 ６ 时 的 谱 估 计 ４
・
１ ８・
ＭＵ ｌ 算 法在 空间谱 估计 中应用 的仿真分析 ＳＣ
０八 一科技
可 以看 出 ，在阵元 数 为３ 的情况 下 ，已无 法 有效 分辨 出３ 方 向的 目标 ，而 阵元 数增 ２ 个
加 到６ 时 ，可 以清 晰地分 辨 出３ 方 向的 目标 。 ４ 个
２２ 相 干信 号源下 ＭＵ Ｃ谱估计 ． ＳＩ
当信 号相干 时 ，相 干 的几 个信号 源就会合 并成 一个 信号 ，到达 阵列 的独 立信 号源 就会 减 少 ，阵列协方 差矩 阵会 降秩 ，矩 阵 中的大特 征值 个数 将少 于 实际信 号源 数Ｐ在 空 间谱 曲 ，
线 上不 呈现 峰值 ，从 而不能 正确得 到信号 的Ｄ Ａ 计 。 Ｏ估 对 于相干 信号 的Ｄ Ａ Ｏ 估计 ，其 核心 就是 如何把 协方 差矩 阵 的秩恢 复到 等于信 号 源数Ｐ ， 这 种处 理被称 为解相 干 ，然 后采用 独立信 号源 的方法来 进行 空 间谱估计 。空 间平滑技 术就
DOA估计的一种改进MUSIC算法
Ｍ ＳＣ算 法将会 因为信 号高 相关性 而 失效 。 ＵＩ ＭＵ Ｉ 法结 合空 间平 滑技术 ＿ 可适用 于 相关 ＳＣ算 ２ Ｊ
信 号源 的 Ｄ Ａ估 计 。然 而 ， Ｏ 由于信 号协 方差 矩 阵 的
Ａｂ ｔａ ｔ Ａｎ ｍｐ ｏ ｅ ｓ ｔａ ｓ ｏｈｎ ｔｃ ｎ ｑ ｅ ｏ ｉｅ ｔ ｎ ｏ ｒｉａ ｓｉ ｔｏ ｉ ｐ ｏ ｏ ｅ ｓｒ ｃ ： ｉ ｒｖ ｄ ｐａｉｌ ｍｏ ｔｉｇ ｅ ｈ ｉｕ ｆｒ ｄｒ ｃｉ ｆ ａｒｖ ｌｅ ｔｍａｉｎ ｓ ｒｐ ｓ ｄ，ｉ Ｓ Ｓ ｏ ａ ｎ ｃ ｄｆｅｅ ｃ ａ ｄ ｏ ｔ ｅ ｃ ｖ ｄａ ｅ ｉ ｒ ｎ ｅ ｎ Ｕ ｉｅａｉｅ ｓ ａｉｌｓ ｏ ｔｉｇ． ｒｔ ａｍｏ ｅ ｆａｒ ｙ ａ ｔｎ ｅ ｅｖ ｉｎ ｌｉ ｅ ｃ ｂ ｔｒ ｔ ｐ ｔ ｍｏ ｈ ｎ Ｆｉ ｌ ｖ ａ ｓ ｙ． ｄ ｌｏ ｒａ ｅ ｎａｒ ｃ ｉｅ ｓｇ ａ ｓｄ ｓ ｒ ｅｄ， ｅ ＵＳ Ｃ ａｇ ｒｔｍ ｓｒ ｖｅ ｄ， ｒ ｂｅ ｘｓｉ ｇｉ ｎ ｉ ｈ ｔ ｎＭ Ｉ ｌｏ ｈ ｉ ｅ ｉｗｅ ｐ ｏ ｌｍｓｅ ｉｔｎ ｎ ｉ Ｓ ｌ ｏ ｆ ￣ ｒ ｏｎｅ ｕｔ ａ ｆ ｃｉｅ Ｓ ａｇ ｆｌ ｎ ａｅ ｐ ｉｔｄ ｏ ， ｉ ｎ ｎ ｅ ｅ ｔ ｍｅｈ ｄ ｔ ｏｖ ｈｓ ｐ ｏ ｅ ｉ ｏ ｓ ｄ． ｉａｌ ｓｍｕａ ｏ ｅ ｕｔ ｒ ｖ ｅ ｅ ｅ ｔｖ ｎ ｓ ｆｔｅ ｖ ｔ ｏ ｏ ｓ ｌｅ ｔ ｉ ｒｂｌｍ ｓｐｒｐ ｅ Ｆ ｎ ｌｙ， ｉ ｌｔ ｎ ｒ ｓ ｌ ｐ ｏ ｅ ｔ ｆ ｃｉｅ ｅ ｓ ｏ ｏ ｉ ｓ ｈ ｈ ｉ ｒｖ ｄ ａｇ ｒｔｍ ． ｍｐ ｏ ｅ ｌｏ ｈ ｉ Ｋｅ ｒ ｓ： ｙ ｗｏ ｄ ＤＯＡ ｓｉ ｔ ｎ； ｏ ａ ｉ ｃ ｆｅ ｅ ｃ ｉｅａｉｅ ｓ ａ ａ ｍｏ ｔｉｇ ｅｔ ｍａｉ ｃ ｖ ｒａ ｅｄｉ ｒｎ ｅ；ｔｒ ｔ ｐ ｔ ｌｓ ｏ ｎ ｏ ｎ ｖ ｉ ｈ
信源数目过估计下相干信号的修正MUSIC算法分析
中 图 分 类 号 ： Ｎ １． Ｔ ９１７ 文 献 标 志码 ： Ａ
Ｐｅ ｆ ｒ ａ ｃ ａ ｙ ｉ ｆｔ ｏ ｉｉ ｄ Ｍ ＵＳ Ｃ ｒ ｏ ｍ ｎ ｅ Ａｎ ｌｓｓｏ ｈｅ Ｍ ｄ ｅ ｆ Ｉ
２９ ５ ７部 队 ， 北 涞 水 ３６ 河 ０４０） ７ １０
摘 要 ： 简 要 介 绍 阵 列 信 号 处 理 中 广 泛 采 用 的 ＭＵＳＣ算 法 的 基 础 上 ， 析 了 信 源 数 目过 估 计 情 况 下 的 在 Ｉ 分 ＭＵＳＣ算 法 测 向 性 能 ． 对 信 源 数 目过 估 计下 ＭＵＳＣ谱 会 出现 虚假 信 号 的 问 题 ， 出 了 一 种 适 合 于 相 干 信 Ｉ 针 Ｉ 提
（ｐ ｔ ｌ ｍｏ ｔｉｇ Ｌ 是 一 种最 常用 的 解相 干 预 ｓ ａｉ ｏ ｈｎ ）４ ａｓ ］
ｖ １估 计 中 ， ｃ ｍｉｔ提 出 的基 于空 间协 方 差 矩 ａ） Ｓｈ ｄ
阵 特征值 分解 的 ＭＵＳＣ 算法 最 具 有 代 表 性 （ Ｉ 其
估计 方 差 接 近 Ｃ ａ ｒ ｏ下 界 ）１。跟 常 规 的 ｒｍｅ— Ｒａ Ｌ ］
Ｋｅ ｒ ｓ： ｒ ａ ｉ ａ ｏｃ ｓ ｉ ｙ ｗｏ ｄ ａ ｒ ｙ ｓｇｎ ｌｐｒ ｅ ｓｎｇ；ｃ ｈｅ ｅｎ ｉ ｏ ｒ ｔｓｇｎａ ｏｕｒｅ Ｍ Ｕ ＳＩ ａｇｏｒｔ ｍ ｌｓ ｃ ｓ； Ｃ ｌ ｉｈ
秩 降低 ，导致 无 法 正 确 地 划 分 信 号 子 空 间 和 噪
２ Ｎ ｏ ３５ ｎ ｔ Ｈ ｅ ｅ ｉ ｈｕ ４１ ．９ ６７ Ｕ ｉ ， ｂ ｉＬａ ｓ ｉ０７ ００． ｉ ） Ｃｈ ｎａ
MUSIC算法综述
MUSIC 算法综述姓名：罗 涛 学号：06010120510 导师：张守宏1．引 言在阵列信号处理的许多应用中,需要准确估计空间信号源的方向及空间分布,通常称为“空间谱”。
传统的处理方法是利用天线波束作空域扫描,其缺点是分辨能力受到由阵列孔径大小决定的所谓瑞利限的限制。
一旦两个信号源处于波束之内时便无法分辨。
后来提出“超角分辨”技术,即可以突破瑞利限的限制,实现对处于同一波束内的信号源的分离。
在这些方法中,比较典型的有基于空间协方差矩阵特征值分解的一类算法,如Ｓｃｈｍｉｄｔ提出的多重信号分类(ＭＵＳＩＣ)法[1]、ｍｉｎ ｎｏｒｍ法以及Ｒｏｙ提出的基于旋转不变技术的信号参数估计方法(ＥＳＰＲＩＴ)[2]等。
它们利用空间协方差矩阵的特征向量来构造信号子空间与噪声子空间,由于它们相互正交或信号矢量经旋转后空间参数不变,因此可确定信号的波达方向。
但是,这些方法都是建立在不相干信号模型基础之上的。
对于有相干信号存在的情况,信号矢量将有可能落入噪声子空间中,导致空间协方差矩阵发生秩亏损,因此在这种情况下,基于空间协方差矩阵特征值分解的方法将会失效。
而多径相干信号在雷达、通信、声纳信号处理的应用中是很常见的。
如在雷达测高或低角跟踪的应用中,目标直接回波与地面反射波是强相关的;类似的例子还有通信中基站与移动台之间的信号传输,因此,在多径信号存在的情况下,如何进行高分辨处理是一个重要的研究课题。
目前已提出不少方法来解决这一问题[3～5,7]。
但这些方法大多是基于空间平滑技术来纠正协方差矩阵,然后应用ＭＵＳＩＣ等正交化方法进行处理。
当然高分辨技术还有最大似然(ＭＬ)方法等,但其运算量过大,难以实时实现,故这里不作考虑。
综上所述,上述方法都是基于空间协方差矩阵的特征值分解来构造信号子空间与噪声子空间的,只不过是采用空间平滑或降维等措施来解决空间协方差矩阵的秩亏损问题。
针对以上情况,本文也从另一个角度出发,寻求另一种矩阵,这种矩阵同样具有空间谱的特征,但却不受信号相关性的影响,从而可对多径相关信号作出正确的分离。
MUSIC算法性能研究综述
MUSIC算法性能研究综述作者：田航来源：《科技资讯》2019年第27期摘; 要：智能天线的核心技术之一是波达方向（Direction of Arrival，DOA）估计，其在无线通信中具有重要作用。
多重信号分类（Multiple Signal Classification，MUSIC）算法是经典的DOA估计算法，但因其对于相干及小信噪比信號无法分辨、计算量大等缺陷，故有许多改进算法被提出。
该文从MUSIC算法基础分析入手，分别从阵元数目、阵元间距等参数方面、相干信号方面以及在定位应用方面等几个方面对近几年MUSIC算法的研究进展进行了综述，并对MUSIC算法的研究趋势进行展望。
关键词：智能天线; MUSIC算法; 阵元; 阵列信号处理中图分类号：TN92 ; ;文献标识码：A 文章编号：1672-3791（2019）09（c）-0005-02Schmidt等人在1979年提出了多重信号分类（Multiple Signal Classification， MUSIC）算法。
该算法开辟了空间谱估计算法的新纪元，推动了特征结构算法的兴起和发展[1]。
在此之前，相关算法都是直接处理阵列接收到的数据协方差矩阵，MUSIC算法的基本思想则是特征分解任意阵列输出数据的协方差矩阵，从而得到与信号分类相对应的信号子空间和与信号分量相正交的噪声子空间，接着构造两个子空间的正交空间谱函数，从而通过搜索谱峰检测出信号的波达方向（Direction of Arrival，DOA）[2]。
1; 经典MUSIC算法测向原理1.1 一般阵列数学模型在适当的信号数学模型的基础上，能够对空间谱估计算法进行合理的推导以及参数的正确估计，因此，建立一个与实际情况相符的数学模型至关重要。
在空间谱估计算法中，线性阵列和圆形阵列是两种最常用的天线阵列。
大多数文献中提到的算法原理都是基于均匀线阵的模型，其原因在于线性阵列结构简单，推导容易，算法易于实现。
《脉冲噪声环境下相干循环平稳信源的DOA估计》范文
《脉冲噪声环境下相干循环平稳信源的DOA估计》篇一一、引言在无线通信和信号处理领域，方向到达（Direction of Arrival，DOA）估计是关键技术之一。
然而，在脉冲噪声环境下，特别是当存在相干循环平稳信源时，DOA估计的准确性常常受到挑战。
本文旨在探讨脉冲噪声环境下相干循环平稳信源的DOA估计问题，提出一种改进的算法以提高估计精度和稳定性。
二、背景与相关研究DOA估计是利用接收到的信号来确定信号源的方向。
在传统的DOA估计方法中，如MUSIC（Multiple Signal Classification）算法和ESPRIT（Estimation of Signal Parameters via Rotational Invariance Techniques）算法，通常假设信号源是非相干的。
然而，在实际应用中，信号源往往具有相干性，特别是在脉冲噪声环境下。
因此，如何准确估计相干循环平稳信源的DOA成为一个亟待解决的问题。
三、问题描述与挑战在脉冲噪声环境下，相干循环平稳信源的DOA估计面临诸多挑战。
首先，脉冲噪声具有突发性、高能量和低概率的特点，使得传统DOA估计方法容易受到干扰。
其次，相干信源之间存在空间相关性，导致信号的协方差矩阵出现秩亏现象，从而影响DOA估计的准确性。
此外，循环平稳性也会对DOA估计产生影响，使得传统方法难以有效提取信号特征。
四、改进算法与实现针对上述问题，本文提出一种改进的DOA估计算法。
该算法利用循环平稳特性对信号进行预处理，以抑制脉冲噪声的影响。
在此基础上，采用一种基于空间平滑技术的协方差矩阵重构方法，以解决秩亏问题。
此外，还结合了MUSIC算法和ESPRIT算法的优点，实现更准确的DOA估计。
具体实现步骤如下：1. 对接收到的信号进行循环平稳预处理，以消除脉冲噪声的影响。
2. 利用空间平滑技术对协方差矩阵进行重构，以解决秩亏问题。
3. 采用MUSIC算法或ESPRIT算法对预处理后的信号进行DOA估计。
空间平滑music算法
空间平滑music算法
空间平滑music算法是一种用于估计信号源方向的高分辨率算法。
它
通过对接收到的信号进行频谱分析，提取出信号源的频率信息，并利
用空间滤波技术将干扰信号和噪声降低到最小，从而实现对信号源方
向的准确估计。
这个算法的基本思想是将接收到的信号作为一个多维向量，然后通过
矩阵分解和空间滤波等技术来提取出信号源的方向信息。
具体来说，
首先需要将接收到的信号进行离散傅里叶变换，得到频域数据。
然后，通过构造一个特定的矩阵来描述各个接收器之间的关系，并对其进行
矩阵分解，得到一个特定维数的子空间。
在这个子空间中，可以利用
特定的空间滤波器来降低噪声和干扰信号对估计结果产生的影响。
与传统方法相比，空间平滑music算法具有更高的精度和更好的鲁棒性。
它可以处理多个信号源和复杂环境下的估计问题，并且不需要事
先知道各个信号源之间的距离和强度等信息。
因此，在无线通信、雷
达探测、声波成像等领域都有广泛的应用。
不过，空间平滑music算法也存在一些问题。
例如，它需要大量的计
算资源和存储空间来处理高维数据，并且对信号源的数量和分布情况
有一定限制。
此外，由于该算法是基于频率分析的，因此对于非平稳
信号或多径传播等复杂情况可能会出现较大误差。
总之，空间平滑music算法是一种高精度、鲁棒性强的信号源方向估计方法。
它在多个领域都有广泛应用，并且仍在不断发展和完善中。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第34卷第5期Vol .34 No .5周口师范学院学报Journal of Zhoukou Normal University 217年9月 Sept . 2017一种改进的空间平滑M U S I C 算法申莹，魏山林，张利红，姚遥(周口师范学院物理与电信工程学院，河南周口 466001)摘要：经典M U S I C 算法无法有效的对相干信号源进行解相干，如何有效的对相干信号源进行解相干成为目前到来角估计研究的一个热点.笔者通过研究传统M U I S C 算法和平滑空间算法，提出一种改进的空间平 滑M U S I C 算法，以解决多目标相干信号进入到阵列的解相干问题.通过大量的仿真证明改进空间平滑算法 理论的正确性和解相干的有效性，并与M U S C 算法和传统空间平滑算法相比较，深入分析了改进空间平滑 算法具有可靠的解相干性能.关键词：空间平滑；M U S C ;相干信号源；到来角中图分类号：T N 911文献标志码：A文章编号：1671 - 9476(2017)05 - 0043 - 03D O I ： 10.134 50/j.c n k i.jz k n u.2017.05.012多重信号分类算法（M U S I C )[1]是1 979年Schm idtR O 等人提出来的.在特定的信道环境下，M U S I C 算法具有很高的估计精度、分辨力和 稳健性.目前对M U S I C 算法的研究工作主要集中 在如下几个方面[2]: (D M U S I C 算法的理论与性能 分析；（2) M U S I C 算法的推广应用及性能；（3)存 在模型误差时的M U S I C 算法性能影响.在这些研 究中，相干信号源的研究一直是研究的热点，并涌 现出了大量的研究成果，如奇异值分解算法[3]、加 权空间平滑算法[4]、空间平滑算法[5]等.空间平滑能有效地对相干信号进行解相干，计 算量小易于实现，对相干信号的到来角（D O A )估 计具有很好的性能，但是以牺牲有效阵元数来实现 的.前向平滑和后向平滑技术具有类似的D O A 估 算性能，在阵元数亏损上较严重，但计算量小，前后 向平滑技术（F B M U S I C )具有亏损阵元数小、估算 性能较好的特点，但计算量相对前向平滑计算量 大.笔者针对前向平滑和前后向平滑技术的亏损阵 元数和计算量，提出一种计算量较小、亏损阵元数 较少和性能接近前后向平滑算法的改进空间平滑 算法，称为环形M U S I C 算法，简称C M U S I C 算法.收稿日期：20170227;修回日期：0170418基金项目：河南省科技攻关项目（N o. 162102210312);周口师范学院教育教学改革研究项目（N O .J 2016050);周口师范学院 校本项目资助（N O.Z K N U B 3201710)作者简介：申莹（987 —），女，河南焦作人，硕士，主要研究方向：电子通信技术.1均匀线性阵列模型设均匀线性阵列的阵元数为M ,阵元间隔半个波长心背景噪声是均值为0,方差为V 的高斯 白噪声，人射信号数为D .在窄带情况下，均匀的 线性阵列的第m 个阵元接收到的数据模型为：D (^) ={〇k )nk (^t ) +n m (k = 1那么，输出的数据矩阵模型为：X =A S +N .其中，X (t )=[尤 1 (t )，尤 2 (t )，…，尤 m (〇 ]为 M X 1 阵列，S (t ) = [h (0，(0，…，;；D (0 ] 1，A = [a (01)，a (心），…，<，（0d ) ] 1 为 M X D 阵列，a (d ,) =[1, e -^，…，e - (M-1) « ] T ，凡.=2T ^s n (0j )/A .对数据矩阵做协方差处理得到，其中 R s =[S S H ]2经典的空间谱估计经典M U S I C 算法的数学模型如上，对任意的阵列数据进行协方差处理，将R x 进行特征值分 解，得协方差矩阵：R x =U s S s 邱+〜抑，U s 是信号特征值对应的特征向量张成的信号子空间，是噪声特征值向量对应的噪声子空间.如果信号源相互独立，所有的信号子空间向量能够与44周口师范学院学报217年9月噪声子空间向量相互正交.根据最小优化搜索，可 在1<々<M- + 1时子阵列数据模型以求得D O A.即M U S I C算法公式为：表示为：1⑵a H (d)U NUHa(d)空间平滑技术原理是将均匀线性阵（M个阵元）均 匀分成相互交错的P个子阵列P=M-ot+1 ,每 个子阵列包含<M)个阵元，并且重叠前移. 将最左边的子阵列作为参考子阵，则对第6(1 <々<P)个子阵列而言，其数据模型：x t(t) =[x k，x k+l，…，x k+m-1]=A D(k-l)s(^t) +nk t).K t =A T(t—1：)R s(D^—1)) H A H +。
2/ 为此时的协方差矩阵，其中变量和前向平滑相同.在M—m+2<k <M时，根据子阵列数据模型，可以得到此时的协方差矩阵为:Kk =A K SA H +，其中导向矢量A为：X k t) = [^k，Xk+1，*…，X k+m—1]=(k,)(3)A T(k—1) ^J)+nk t)式中 A = [a^)，a(02)，…，a(0D)] 1是 K X D 矩阵，a队）=[1，e—册，…，e—(M—丄）”T，了=如忍（6—別，e—逆2,…，e—(—1)D)•子阵列的协方差为：K k=A T(k—1)K S (T(—1))H A H+ff21，T k 为T的k次方幂.对所有的子阵列求平均和，得阵 列的协方差：R f =1M—m +1M—m+1E R-1= 1(4)当相干信号同时进人到接收天线阵时，相干信号就很可能进人到不同的子阵列中，从而将相干信号恢复为相互独立的信号.若满足讲>0,则当P>D 时r a n k R f}=D[]，能检测的相干源信号数为M2.前后向空间平滑技术对阵列进行一次前向平滑和一次后向平滑，获得的子阵列协方差求平均和.前后向平滑技术的阵列协方差矩阵为：R f R f +R b2(5)其中R b为前后向平滑协方差矩阵.天线阵元数牺牲量远远小于前向平滑或后向平滑的阵元牺牲数.在最大解相干信源数上提高到2M/3个.但显然前后向平滑算法的计算量比单个的前向平滑或后向平滑的计算量增加了一倍.3 改进空间平滑解相干改进空间平滑解相干算法原理和前向平滑解相干算法类似，将M元阵列分成M个具有m阵元 的子阵列，每个子阵列相互重叠前移.在平移到阵列最后一个阵元时，子阵列继续向前平移，但后续重叠的数据是从第一个阵元的数据，直到最后一个阵元数据和从第一个阵元数据到第m — 1个阵元数据组成的一个子阵列为止.即所有子阵列的数据模型为：X1 (t)=X1，X2，…，Xm]，X2t)=2 ^X3，…？X m+1]，*…，X M—m^)=[X M—m，X M—m+1，…》X M—1]，X M—m+1 ^)=[^ M—m+1，X M—m+2，…，X M]a1(01)… a1(d D)a2(01)… a2(d D)A=a m—(M—k)—1(01)a k(01)a m—(M—k)—1((d)a k (0 d)(6)_aM(01)… a m(0D)_可以证明当m >D时，有rank{R} =D,需要的最小阵元数为m,亏损阵元数为（M—m +1)D/M，显然，改进平滑的阵元亏损比较小；由于去相关能力依赖于子阵列数和信号源到达角的正弦差(sin(i —si(),其中-乒/7].正弦差值越小，去 相关效果越好；子阵列数越多去相关能力越强.从环形平滑子阵列的平滑形式可以知道，环形平滑的子阵列数大于单向平滑但小于前后向平滑数，由此 可以分析出，改进平滑算法的去相关能力大于前向平滑算法.4仿真与性能分析仿真设阵列元数为8的间隔半个波长的均匀线性阵列，子阵列元数为5,窄带相干信号源数为3,快拍数设置为1024.背景噪声为均值为0,方差 为2的高斯白噪声.假设3个相干信号源分别从40°, 0°和一 40°方 向进人到阵列.图1〜图3分别是信噪比为一15 d B，一5 d B和15 d B时仿真得到的到来角估计空间谱.分析图1〜图3,可以看到在信噪比极低(一15 dB)的情况下，C M U S I C算法、M U S I C算法和前后向平滑算法都不能有效的对相干源信号到来角进行正确的估计.在信噪比较低（一 5 dB)时，显然 M U S I C算法还是无法估计到来角，而改进平滑M U S I C算法和前后向平滑M U S I C算法已经能够正确的估计相干信号源的到来角了.在信噪比较高（15 dB)时，三种算法都能估计信号到来角，但 对于M U S I C算法而言仍然无法达到完全分辨到来角的要求.图4是在信噪比为15d B时，到来角 方向为40°、0°和一 10°.对于小角度的分辨力，改进第34卷第5期申莹，等：一种改进的空间平滑M U S I C算法 4 5平滑M U S I C算法和前后向平滑M U S I C算法可以完全分辨出来，但M U S I C算法已经无法有效的对小角度相干信号进行分辨.由以上分析可得，计算量较小的改进平滑算法和前后向平滑算法具有接近的分辨力.图 3 信噪比15d B算法仿真结果为了进一步对比改进算法在D O A估计中具有较好的性能，假设相干信号源个数为2个，采用 20阵元的均匀线性阵列接收.对前后平滑、前向平滑和改进平滑算法的计算复杂度进行仿真如图5.分析图5,随着子阵列阵元数增加，三种算法的计算复杂度都很快加大.但在子阵列阵元数比较小时，改进平滑算法的复杂度远远低于前后向平滑算法的复杂度，根据空间平滑算法分辨力依赖于子阵列数原理，可知在子阵列阵元数较少时，改进平滑算法具有较低的算法复杂度和较高的到来角分辨力.5结论改进平滑算法具有更低的阵元亏损和较低的计算量，能极大的将相干信号恢复到独立的信号.与一般的M U S I C算法相比，改进平滑算法具有较好的分辨力和较高的稳健性，尤其是在低信噪比条件下解相干时表现的更具优势.相比前后向平滑M U S I C算法，环形平滑M U S I C算法也具有相同的性能，但具有更小的阵元亏损和更低的计算复杂度.参考文献：[l]S c h m id t R. M u ltip le e m itte r lo c a tio n and sig n a l p a ra m ete r c s tim a tio n J j]. \KK K,1986, 34(3)：276 — 280.[]王永良，陈辉，彭应宁，等.空间谱估计理论与算法[M].北京：清华大学出版社，2004.[3]高世伟，保铮.利用数据矩阵分解实现对空间相关信号源的超分辨处理[].通信学报，1988,9(1) 41 — 13.[4]吴向东，马仑，梁中华.一种改进的加权空间平滑算法J J].数据采集与处理，2015,30(4):824 —829.[5]陈辉，王永良.基于空间平滑的矩阵分解算法[].信号处理，2002,24(8)424 —327.[6]刘德树，罗景涛，张建云.空间谱估计及其应用[M].合肥：中国科技大学出版社，1 997.[7]田孝华，周易建.无线电定位理论与技术[M].北京：国防工业出版社，2011.。