山东省淄博市淄博区金山中学2015届初中数学毕业班上学期期中质量检测试题 新人教版
山东省淄博市淄博区金山中学2015届九年级上学期期中质量检测物理试卷

2014—2015学年度第一学期期中质量检测初三物理试题一、选择题(选择题内容在第4页至第6页上,每个小题只有一个正确选项,请将正确答案填在下方的答题框中)二、理解与应用16.一只小虫跌落在小李的新铅笔上,小李突发奇想,驱赶小虫从铅笔的左端爬到右端用时9s,并用刻度尺测量铅笔的长度,如图所示。
则刻度尺的分度值是_____,铅笔的长度是_____ cm;小虫爬行的平均速度约是____ m/s。
17.空中,加油机正在给战斗机加油,以加油机为参照物,战斗机是_________的,以地面为参照物,战斗机是_________的。
(选填“静止”或“运动”)18.中国好声音第三季亚军帕尔哈提弹奏吉他时不断用手指去控制琴弦长度,这样做的目的是为了改变声音的;琴声是通过传播到现场观众耳中的,观众在听音乐时都要把手机关机或把铃声调成振动,目的是为了在(选填“声源处”、“传播过程中”或“人耳处”)减弱噪声。
19. 光在空气中的传播速度为m/s;雷雨天,总是先看到闪电后听到雷声,原因是;若小明看到闪电后4s才听到了雷声,则打雷处距离小明m。
20.如图,舞蹈“千手观音”给观众留下了深刻的印象。
观众看不见领舞者邰丽华身后站着的其他舞蹈者,这是因为光是沿传播的;电视观众看到“千手观音”身上绚丽的霞光是由色光的三原色--红、绿、以不同比例混合而成的。
21.一只小鸟在离湖面10米的上空飞行,若湖深为5米,则小鸟在湖里所成的像与它的距离是________m,它在湖里所成的像是由光的_______(填“反射”或“折射”)形成的_______(填“实”或“虚”)像。
22.小明同学用如图所示的装置研究光的反射规律,其中有一个可折转的光屏。
光屏在实验中的作用是 、 ;实验时,光屏应 放置。
23.魔术是深受同学们喜爱的节目,其中包含着许多科学原理。
图甲是某同学自制的一只魔术箱,表演时他将开口的方形空箱面展示给观众,把纸币从空箱顶端的投币口投入,结果纸币“不翼而飞”。
【数学】2014-2015年山东省淄博市淄川区七年级上学期期中数学试卷与解析PDF

2014-2015学年山东省淄博市淄川区七年级(上)期中数学试卷(五四学制)一、精心选一选(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请选出你认为唯一正确的答案,填到后面的表格中,每小题3分,计36分).1.(3分)在△ABC中,∠B=40°,∠C=80°,则∠A的度数为()A.30°B.40°C.50°D.60°2.(3分)下列轴对称图形中,对称轴条数最多的是()A.等腰三角形B.60°的角C.长方形D.等边三角形3.(3分)如图,AD,BE,CF依次是△ABC的高、中线和角平分线,下列表达式中错误的是()A.AE=CE B.∠ADC=90°C.∠CAD=∠CBE D.∠ACB=2∠ACF4.(3分)如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定()A.△ABD≌△ACD B.△ABE≌△ACE C.△BED≌△CED D.△ABE≌△EDC 5.(3分)如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则()A.BC>PC+AP B.BC<PC+AP C.BC=PC+AP D.BC≥PC+AP6.(3分)以下面每组中的三条线段为边的三角形中,是直角三角形的是()A.5cm,12cm,13cm B.5cm,8cm,11cmC.5cm,13cm,11cm D.8cm,13cm,11cm7.(3分)下列条件:①两角及一边分别相等;②两边及其夹角分别相等;③两边及一边所对的角分别相等;④两角及其夹边分别相等.其中能判定两个三角形全等的个数是()A.1个 B.2个 C.3个 D.4个8.(3分)如图,在△ABC中,AB=AC,BD=BC,AD=DE=BE,那么∠A等于()A.30°B.36°C.45°D.54°9.(3分)若几个能唯一确定一个三角形的量称为三角形的“基本量”.下列各组量中一定能成为三角形的基本量的是()A.三个内角B.两条边与一个内角C.周长和两条边D.面积与一条边10.(3分)如图,在△ABC中,AB=AC,BD⊥AC,则下列说法正确的是()A.∠DBC=∠BAC B.∠DBC=∠ABC C.∠ABD=∠BAC D.∠ABD=∠BAD 11.(3分)如图所示,有一块直角三角形纸片,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE 的长为()A.1cm B.1.5cm C.2cm D.3cm12.(3分)已知一等腰三角形的腰长为5,底边长为4,底角为β.满足下列条件的三角形不一定与已知三角形全等的是()A.两条边长分别为4,5,它们的夹角为βB.两个角是β,它们的夹边为4C.三条边长分别是4,5,5D.两条边长是5,一个角是β二、细心填一填(本题共8小题,满分24分,只要求填写最后结果,每小题填对得4分)13.(3分)如图,两个正方形的面积分别是64和49,则AC的长为.14.(3分)一个三角形的两边长分别为1和2,第三边长为整数,则这个三角形的周长为.15.(3分)将一个边长为4的正方形截取一个角,剩下的四边形如图所示,则这个四边形的周长是.16.(3分)如图,点P是△ABC内一点,∠ABC=80°,∠1=∠2,则∠BPC=度.17.(3分)如图,AB与CD相交于点O,∠D=∠B=90°,要使△AOD与△COB全等,还需要添加一个条件,你认为添加的条件可以是.(只添加一个条件即可)18.(3分)如图,是用七巧板拼成一个图形,其中③、⑥、①板的面积分别为S③,S⑥,S①,则S③:S⑥:S①=.19.(3分)如图所示,点C为直线BE上一点,△ABC≌△ADC,∠DCF=∠ECF,则AC和CF的位置关系是.20.(3分)已知等腰△ABC中,AD⊥BC于点D,且AD=BC,则△ABC底角的度数为.三、耐心做一做,相信你能写出正确的解答过程(共52分,注意审题要细心,书写要规范和解答要完整)21.(12分)如图,在10×10的方格中有一个四边形和两个三角形(所有顶点都在方格的格点上)(1)请你画出三个图形关于直线MN的对称图形;(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数.22.(8分)如图,在正方形网格中,每个小正方形的边长都是1,△ABC的顶点均在格点上,试判断△ABC是否为直角三角形?为什么?23.(10分)如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C 作CF∥AB交DE延长线于点F.求证:AD=CF.24.(10分)如图,某隧道的截面是一个半径为4.2米的半圆形,一辆高3.6米,宽3米的卡车能通过隧道吗?为什么?25.(10分)如图,AD∥BC,AE=CF,AD=BC,点E,F在直线AC上,试猜想线段DE与BF有何关系,并说明你的猜想.26.(10分)如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.AC=6,BC=8,∠CAE:∠BAE=1:2,(1)求∠B度数;(2)求ACE的周长;(3)求CE的长.2014-2015学年山东省淄博市淄川区七年级(上)期中数学试卷(五四学制)参考答案与试题解析一、精心选一选(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请选出你认为唯一正确的答案,填到后面的表格中,每小题3分,计36分).1.(3分)在△ABC中,∠B=40°,∠C=80°,则∠A的度数为()A.30°B.40°C.50°D.60°【解答】解:∠A=180°﹣∠B﹣∠C=180°﹣40°﹣80°=60°.故选:D.2.(3分)下列轴对称图形中,对称轴条数最多的是()A.等腰三角形B.60°的角C.长方形D.等边三角形【解答】解:在等腰三角形有1条对角线,60°的角有1条对角线,长方形有2条对角线、等边三角形有3条对角线,故对称轴条数最多的是等边三角形.故选:D.3.(3分)如图,AD,BE,CF依次是△ABC的高、中线和角平分线,下列表达式中错误的是()A.AE=CE B.∠ADC=90°C.∠CAD=∠CBE D.∠ACB=2∠ACF【解答】解:A、BE是△ABC的中线,所以AE=CE,故本表达式正确;B、AD是△ABC的高,所以∠ADC=90,故本表达式正确;C、由三角形的高、中线和角平分线的定义无法得出∠CAD=∠CBE,故本表达式错误;D、CF是△ABC的角平分线,所以∠ACB=2∠ACF,故本表达式正确.故选:C.4.(3分)如图,△ABC中,AB=AC,BE=EC,直接使用“SSS”可判定()A.△ABD≌△ACD B.△ABE≌△ACE C.△BED≌△CED D.△ABE≌△EDC 【解答】解:根据AB=AC,BE=EC,AE=AE可以推出△ABE≌△AACE,理由是SSS,其余△ABD≌△ACD,△BED≌△CED不能直接用SSS定理推出,△ABE和△EDC 不全等,故选:B.5.(3分)如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则()A.BC>PC+AP B.BC<PC+AP C.BC=PC+AP D.BC≥PC+AP【解答】解:∵点P在线段AB的垂直平分线上,∴PA=PB.∵BC=PC+BP,∴BC=PC+AP.故选:C.6.(3分)以下面每组中的三条线段为边的三角形中,是直角三角形的是()A.5cm,12cm,13cm B.5cm,8cm,11cmC.5cm,13cm,11cm D.8cm,13cm,11cm【解答】解:因为只有A满足:52+122=132,故选A.7.(3分)下列条件:①两角及一边分别相等;②两边及其夹角分别相等;③两边及一边所对的角分别相等;④两角及其夹边分别相等.其中能判定两个三角形全等的个数是()A.1个 B.2个 C.3个 D.4个【解答】解:①两角及一边分别相等;能根据AAS判定两个三角形全等,故选项正确;②两边及其夹角分别相等;能根据SAS判定两个三角形全等,故选项正确;③两边及一边所对的角分别相等;不能判定两个三角形全等,故选项错误;④两角及其夹边分别相等;能根据ASA判定两个三角形全等,故选项正确.综上所述,①②④正确.故选:C.8.(3分)如图,在△ABC中,AB=AC,BD=BC,AD=DE=BE,那么∠A等于()A.30°B.36°C.45°D.54°【解答】解:设∠A=x°∵AB=AC,BD=BC∴∠ABC=∠C=∠BDC=90°﹣∠DBC=∠A=x°∵AD=DE=BE∴∠A=∠AED=2∠EBD=2∠EDB∴∠EBD=∵∠ABC=∠C∴90°﹣=x°+∴x=45°即∠A等于45°.故选:C.9.(3分)若几个能唯一确定一个三角形的量称为三角形的“基本量”.下列各组量中一定能成为三角形的基本量的是()A.三个内角B.两条边与一个内角C.周长和两条边D.面积与一条边【解答】解:根据能唯一确定一个三角形的量称为三角形的“基本量”,得只有知道周长和两边时,第三边已经确定,已知三边一定能组成唯一三角形.故选:C.10.(3分)如图,在△ABC中,AB=AC,BD⊥AC,则下列说法正确的是()A.∠DBC=∠BAC B.∠DBC=∠ABC C.∠ABD=∠BAC D.∠ABD=∠BAD 【解答】解:在△ABC中,AB=AC∴∠ABC=∠C=(180°﹣∠A)=90°﹣∠A∵BD⊥AC,∴∠DBC=90°﹣∠C=90°﹣(90°﹣∠A)=∠A故选项A正确,故选:A.11.(3分)如图所示,有一块直角三角形纸片,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE 的长为()A.1cm B.1.5cm C.2cm D.3cm【解答】解:在Rt△ABC中,AB===5根据折叠的性质可知:AE=AB=5∵AC=4∴CE=AE﹣AC=1即CE的长为1故选:A.12.(3分)已知一等腰三角形的腰长为5,底边长为4,底角为β.满足下列条件的三角形不一定与已知三角形全等的是()A.两条边长分别为4,5,它们的夹角为βB.两个角是β,它们的夹边为4C.三条边长分别是4,5,5D.两条边长是5,一个角是β【解答】解:A、两条边长分别为4,5,它们的夹角为β,可以利用“边角边”证明三角形与已知三角形全等,故本选项错误;B、两个角是β,它们的夹边为4,可以利用“角边角”证明三角形与已知三角形全等,故本选项错误;C、三条边长分别是4,5,5,可以利用“边边边”证明三角形与已知三角形全等,故本选项错误;D、两条边长是5,角β如果是底角,则顶角为(180°﹣2β),则转化为“角边角”,利用ASA证明三角形与已知三角形全等;当角β如果是顶角时,底角为(180°﹣β)÷2,此时两三角形不一定全等.故本选项正确.故选:D.二、细心填一填(本题共8小题,满分24分,只要求填写最后结果,每小题填对得4分)13.(3分)如图,两个正方形的面积分别是64和49,则AC的长为故答案为17.【解答】解:∵两个正方形的面积分别是64和49,∴AB=BD=8,DC=7,根据勾股定理得:AC===17.14.(3分)一个三角形的两边长分别为1和2,第三边长为整数,则这个三角形的周长为5.【解答】解:设第三边为x,根据三角形的三边关系,得:2﹣1<x<2+1,即1<x<3,∵x为整数,∴x的值为2.三角形的周长为1+2+2=5.故答案为:5.15.(3分)将一个边长为4的正方形截取一个角,剩下的四边形如图所示,则这个四边形的周长是14.【解答】解:根据勾股定理得:EC====5,C四边形ABCE=AB+BC+CE+EA=4+4+5+1=14.故答案为14.16.(3分)如图,点P是△ABC内一点,∠ABC=80°,∠1=∠2,则∠BPC=100度.【解答】解:∵∠ABC=80°,∠1=∠2∴在△ABC中,∠BPC=180°﹣∠2﹣∠PBC=180°﹣∠1﹣(∠ABC﹣∠1)=180°﹣∠1﹣∠ABC+∠1=180°﹣∠ABC=180°﹣80°=100°,故答案为:100.17.(3分)如图,AB与CD相交于点O,∠D=∠B=90°,要使△AOD与△COB全等,还需要添加一个条件,你认为添加的条件可以是DO=BO.(只添加一个条件即可)【解答】解:DO=BO,理由是:∵AB与CD相交于点O,∵在△AOD和△COB中∴△AOD≌△COB,故答案为:DO=BO.18.(3分)如图,是用七巧板拼成一个图形,其中③、⑥、①板的面积分别为S③,S⑥,S①,则S③:S⑥:S①=1:2:4.【解答】解:由分析可知:S3:S5:S7:S4:S1:S6:S2=1:1:2:2:2:4:4,所以图③、⑥、①板的面积分别是:S③=;S⑥=;S①=,所以S③:S⑥:S①=1:2:4.故答案为:1:2:4.19.(3分)如图所示,点C为直线BE上一点,△ABC≌△ADC,∠DCF=∠ECF,则AC和CF的位置关系是垂直.【解答】解:∵△ABC≌△ADC,∴∠ACD=∠BCD,∵∠DCF=∠ECF,∴∠DCF=∠DCE,∴∠ACD+∠DCF=(∠BCD+∠DCE)=×180°=90°,∴∠ACF=90°,∴AC⊥CF,∴AC和CF的位置关系是垂直.故答案为:垂直.20.(3分)已知等腰△ABC中,AD⊥BC于点D,且AD=BC,则△ABC底角的度数为15°或45°或75°.【解答】解:分四种情况进行讨论:①当AB=AC时,∵AD⊥BC,∴BD=CD,∵AD=BC,∴AD=BD=CD,∴底角为45度;②当AB=BC时,∵AD=BC,∴AD=AB,∴∠ABD=30°,∴∠BAC=∠BCA=75°,∴底角为75度.③当AC=BC时,∵AD=BC,AC=BC,∴AD=AC,∴∠C=30°,∴∠BAC=∠ABC=(180°﹣30°)=75°;④点A是底角顶点,且AD在△ABC外部时,∵AD=BC,AC=BC,∴AD=AC,∴∠ACD=30°,∴∠BAC=∠ABC=×30°=15°,故答案为15°或45°或75°.三、耐心做一做,相信你能写出正确的解答过程(共52分,注意审题要细心,书写要规范和解答要完整)21.(12分)如图,在10×10的方格中有一个四边形和两个三角形(所有顶点都在方格的格点上)(1)请你画出三个图形关于直线MN的对称图形;(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数.【解答】答:(1)所画图形如下所示:(2)这个整体图形共有4条对称轴.22.(8分)如图,在正方形网格中,每个小正方形的边长都是1,△ABC的顶点均在格点上,试判断△ABC是否为直角三角形?为什么?【解答】解:由勾股定理可得:AC==;BC==;AB==,∴AC2+BC2=AB2,∴△ABC是直角三角形.23.(10分)如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C 作CF∥AB交DE延长线于点F.求证:AD=CF.【解答】证明:∵CF∥AB,∴∠1=∠F,∠2=∠A,∵点E为AC的中点,∴AE=EC,在△ADE和△CFE中∴△ADE≌△CFE(AAS),∴AD=CF.24.(10分)如图,某隧道的截面是一个半径为4.2米的半圆形,一辆高3.6米,宽3米的卡车能通过隧道吗?为什么?【解答】解:如图所示:当OB=1.5m,则AB===m∵3.62=12.96<15.39,∴一辆高3.6米,宽3米的卡车能通过隧道.25.(10分)如图,AD∥BC,AE=CF,AD=BC,点E,F在直线AC上,试猜想线段DE与BF有何关系,并说明你的猜想.【解答】解:∵AD∥BC,∴∠DAC=∠BCA,∴∠DAE=∠BCF,∵在△ADE和△BCF中,,∴△ADE≌△BCA(SAS)∴DE=BF,∠E=∠F,∴DE∥BF,∴线段DE与BF平行且相等.26.(10分)如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.AC=6,BC=8,∠CAE:∠BAE=1:2,(1)求∠B度数;(2)求ACE的周长;(3)求CE的长.【解答】解:(1)如图,由题意得:∠B=∠BAE;∵∠CAE:∠BAE=1:2,∴设∠CAE=α,则∠B=∠BAE=2α;∴∠B+∠BAC=90°,即5α=90°,∴α=18°,∠B=2α=36°.(2)由题意得:AE=BE,∴AE+EC+AC=BE+EC+AC=BC+AC=14,即△ACE的周长为14.(3)设BE=AE=λ,则EC=8﹣λ;由勾股定理得:λ2=(8﹣λ)2+62,解得:λ=,∴CE=.。
2015年山东省淄博市中考数学试题及解析

2015年山东省淄博市中考数学试卷一.选择题(每小题4分,四个选项只有一个是正确的)1.(4分)(2015?淄博)下列计算正确的是()224633236238A.B.C.D.a+a=a a÷a=a a?a=a (a)=a2.(4分)(2015?淄博)如图,是由四个相同的正方体组合而成的两个几何体,则下列表述正确的是()A.图甲的主视图与图乙的左视图形状相同图甲的左视图与图乙的俯视图形状相同B.图甲的俯视图与图乙的俯视图形状相同C.D.图甲的主视图与图乙的主视图形状相同二.填空题(共5小题,满分20分)3.(4分)(2015?淄博)计算﹣的结果是.4.(4分)(2015?淄博)如图,在⊙O中,=,∠DCB=28°,则∠ABC=度.张后,放回1,5.随机抽取,4张看上去无差别的卡片,上面分别写着23,4分)5.(4(2015?淄博)有.张,则第二次抽出的数字能够整除第一次抽出的数字的概率是并混合在一起,再随机抽取1,BDC=90°D在等边三角形ABC的内部,∠淄博)如图,等腰直角三角形.(4分)(2015?BDC 的顶点6则分割出的这两个等腰三角形的顶角分别分割成两个等腰三角形,△D作一条直线将ABD连接AD,过点度.是2x+8.当x=m时,二次函数y=2x+yy,满足,y?(4.7(分)2015淄博)对于两个二次函数y+2的12112 1函数值为5,且二次函数y有最小值3.请写出两个符合题意的二次函数y的解析式(要求:22写出的解析式的对称轴不能相同).三.解答题(共7小题,共52分)×.淄博)计算:)(+8.(5分)(2015?9.(5分)(2015?淄博)在学校组织的社会实践活动中,甲、乙两人参加了射击比赛,每人射击七次,命中的环数如表:序号一二三四五六七7 8 8 6 9 8 10 甲命中的环数(环)5 10678 10 10 乙命中的环数(环)根据以上信息,解决一下问题:(1)写出甲、乙两人命中环数的众数;2(2)已知通过计算器求得=8,s≈1.43,试比较甲、乙两人谁的成绩更稳定?甲10.(8分)(2015?淄博)在直角坐标系中,一条直线经过A(﹣1,5),P(﹣2,a),B(3,﹣3)三点.(1)求a的值;(2)设这条直线与y轴相交于点D,求△OPD的面积.11.(8分)(2015?淄博)如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点P是AB上的一个动点(点P与点A、B不重合),矩形PECF的顶点E,F分别在BC,AC上.(1)探究DE与DF的关系,并给出证明;(2)当点P满足什么条件时,线段EF的长最短?(直接给出结论,不必说明理由)12.(8分)(2015?淄博)为充分利用雨水资源,幸福村的小明家和相邻的爷爷家采取了修建蓄水池、屋收集雨水的做法.已知小明和爷爷家的屋顶收集雨水的面积、蓄水池的容积和蓄水池已有水的量如表:小明爷爷120160屋顶收集雨水面积m350 13 蓄水池容积(m)334 11.5 蓄水池已有水量(m)气象预报即将会下雨,为了收集尽可能多的雨水,下雨前需从爷爷家的蓄水池中抽取多少立方米的水注入小明家的蓄水池?13.(9分)(2015?淄博)如图,在△ABC中,点P是BC边上任意一点(点P与点B,C不重合),平行四边形AFPE的顶点F,E分别在AB,AC上.已知BC=2,S=1.设BP=x,平行四边形AFPE的面ABC△积为y.(1)求y与x的函数关系式;(2)上述函数有最大值或最小值吗?若有,则当x取何值时,y有这样的值,并求出该值;若没有,请说明理由.2是圆上异于PBC为直径作⊙O,点是线段(2015?淄博)如图,点B,CAD的三等分点,以分)14.(9 ,PD.,,C的任意一点,连接PA,PBPCB APB的值;PB=PC时,求tan)当(1∠的值.?APBtan∠DPC∠的任意一点时,求,上异于)当(2P是BCtan32015年山东省淄博市中考数学试卷参考答案与试题解析一.选择题(每小题4分,四个选项只有一个是正确的)1.(4分)(2015?淄博)下列计算正确的是()224663332823B..DCA..+aa=a ?a÷a=aa a=a (a=a)考点:同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.分析:根据同底数幂的除法和乘法、幂的乘方和同类项计算即可.633解答:,正确;=a÷a :解A、a236,错误;a=a)B、(235=a,错误;?aC、a222,错误;D+a 、a=2a故选A点评:此题考查同底数幂的除法和乘法、幂的乘方和同类项,关键是根据法则进行计算.2.(4分)(2015?淄博)如图,是由四个相同的正方体组合而成的两个几何体,则下列表述正确的是()甲的主视图与图乙的左视图形状相同A.图甲的左视图与图乙的俯视图形状相同B.图 C .图甲的俯视图与图乙的俯视图形状相同甲的主视图与图乙的主视图形状相同.D图单组合体的三视图.:考点简分析:分别画出图甲、图乙的三视图即可作出判断.:图甲的三视图如下:解解答:图乙的三视图如下: 4因此图甲的左视图与图乙的俯视图形状相同,B.故选:本题主要考查了三视图,能够根据实物画出三视图是解决问题的关键.点评:20分)二.填空题(共5小题,满分.﹣淄博)计算的结果是3.(4分)(2015?式的加减法.考点:分据同分母分式加减运算法则计算即可,最后要注意将结果化为最简分式.分析:根解答:=解:原式==,故答案为:.点评:题考查了分式的加减,归纳提炼:分式的加减运算中,如果是同分母分式,那么分本母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.度.ABC=28中,?淄博)如图,在⊙O=,∠DCB=28°,则∠2015(4.4分)(周角定理;圆心角、弧、弦的关系考分析:;然后根据同弧或等弧所对的圆周角相等,由,可得首先根据= ABC=28度,据此解答即可.∠DCB=28°,可得∠解答:,解:∵=∴;°,DCB=28又∵∠度.∴∠ABC=28 故答案为:28.点评:题主要考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆此 5或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.(分)张后,放回.随机抽取513,4,(2015?淄博)有4张看上去无差别的卡片,上面分别写着2,45..并混合在一起,再随机抽取1张,则第二次抽出的数字能够整除第一次抽出的数字的概率是种,,P(第二次抽出的数字能够整除第一次抽出的数字)=∴故答案为:.点评:所求情况数与总情况数之比.得到第二次=考查概率的求法;用到的知识点为:概率取出的数字能够整除第一次取出的数字的情况数是解决本题的关键.,°的内部,∠BDC=90BDC的顶点D在等边三角形ABC6.(4分)(2015?淄博)如图,等腰直角三角形则分割出的这两个等腰三角形的顶角分别分割成两个等腰三角形,△ABD,过点D作一条直线将连接AD 度.是120,150腰直角三角形;等腰三角形的性质;等边三角形的性质.考点:等分析:利用全等三角形的判定和,据等边三角形和等腰直角三角形的性质得出∠ABD=15°根,再利用等腰三角形解答即可.性质得出∠BAD=30°BDC=90°,的顶点:∵等腰直角三角形BDCD在等边三角形ABC 的内部,∠解答:解°,﹣DBC=60°45°=15∴∠ABD=∠ABC﹣∠ACD中,在△ABD与△,),≌△ACD(SAS∴△ABD °,BAD=∠CAD=30∴∠分割成两个等腰三角形,则分割出的这两个等腰三角ABDD作一条直线将△∴过点,°=120°°180=150°;°﹣30﹣30°﹣15°形的顶角分别是180﹣°15150 120,故答案为:点评:题考查等腰三角形的性质,关键是根据等边三角形和等腰直角三角形的性质得出此.°∠ABD=15 627.(4分)(2015?淄博)对于两个二次函数y,y,满足y+y=2x+2x+8.当x=m时,二次函数y的121212x+)y=(y=x+3,函数值为5,且二次函数y有最小值3.请写出两个符合题意的二次函数y的解析式22222+3(要求:写出的解析式的对称轴不能相同).考点:二次函数的性质.专放型分析知x=时,二次函的函数值,且二次函有最小,故抛物线顶点坐标为,设出顶点式求解即可解答:答案不唯一例如=+2y=(x+)+3.222故答案为:y=x+3,y=(x+)+3.22点评:2考查了二次函数的性质,二次函数y=ax+bx+c(a≠0)的顶点坐标是(﹣,).三.解答题(共7小题,共52分)8.(5分)(2015?淄博)计算:(+)×.考次根式的混合运算分析:首先应用乘法分配律,可得(+)×=×+×;然后根据二次根)×的值是多式的混合运算顺序,先计算乘法,再计算加法,求出算式(+少即可.解答:解:(+)××=×+=1+9=10点评:此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.9.(5分)(2015?淄博)在学校组织的社会实践活动中,甲、乙两人参加了射击比赛,每人射击七次,命中的环数如表:序号一二三四五六七7 8 8 6 9 8 10 甲命中的环数(环)5 10678 10 10 乙命中的环数(环)根据以上信息,解决一下问题:(1)写出甲、乙两人命中环数的众数;2(2)已知通过计算器求得=8,s≈1.43,试比较甲、乙两人谁的成绩更稳定?甲考点:方差;众数.分析:(1)根据众数的定义解答即可;(2)根据已知条件中的数据计算出乙的方差和平均数,再和甲比较即可.解答:解:(1)由题意可知:甲的众数为8,乙的众数为10;7==8,(2)乙的平均数2=﹣8)2]102+(﹣8)2+…乙的方差为:S+(10≈3.71.=[(5﹣8)乙2,s≈1.43∵得=8,∴甲乙的平均成绩一样,而甲的方差小于乙的方差∴甲的成绩更稳定.点评:题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组本数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.3)三点.,﹣2,a),B(3110.(8分)(2015?淄博)在直角坐标系中,一条直线经过A(﹣,5),P(﹣a的值;(1)求OPD的面积.(2)设这条直线与y轴相交于点D,求△定系数法求一次函数解析式;一次函数图象上点的坐标特征考)利用待定系数法解答解析式即可分析的坐标,再利用三角形面积公式解答即可)得出直线轴相交于,)代入)设直线的解析式y=kx+,(解答:可得:,,解得:所以直线解析式为:y=﹣2x+3,)代入y=﹣2x+3中,把P(﹣2,a 得:a=7;,,7)(2)由(1)得点P的坐标为(﹣2 ,x=0,则y=3令,3)所以直线与y轴的交点坐标为(0,=.的面积所以△OPD 此题考查一次函数问题,关键是根据待定系数法解解析式.点评:上是D是AB的中点,点PABC=90分)11.(8(2015?淄博)如图,△ABC是等腰直角三角形,∠°,点上.BC,AC分别在B的一个动点(点P与点A、不重合),矩形PECF的顶点E,F 的关系,并给出证明;与DF)探究(1DE EF的长最短?(直接给出结论,不必说明理由))当点(2P满足什么条件时,线段:考点全等三角形的判定与性质;等腰直角三角形;矩形的性质.分析:的中点得D是AB°△1()连接CD,首先根据ABC是等腰直角三角形,∠C=90,点是等腰直角三角形,,CD⊥AD然后根据四边形PECF是矩形得到△APE,到CD=AD ,,证得≌△△从而得到DCEDAFDE=DFDE;DF⊥8同时最,从而得到当DE和DFDFDE=DF,DE⊥,得到EF=DE=DF(2)根据D重合线段EF 最短.短时,EF最短得到此时点P与点DE⊥DF,解:(1)DE=DF,解答:证明:连接CD,是AB的中点,∵△ABC是等腰直角三角形,∠C=90°,点D ⊥AD,∴CD=AD,C∵四边PEC是矩形,CB,FP∴CE=FP,∥APE是等腰直角三角形,∴△AF=PF=EC,∴°,∴∠DCE=∠A=45 DAF,∴△DCE≌△,CDE∴DE=DF,∠ADF=∠,∵∠CDA=90°,∴∠EDF=90°;DE=DF,DE⊥DF∴,,DE⊥DF(2)∵DE=DF DF,∴EF=DE= EF最短,∴当DE和DF同时最短时,时,二者最短,DF⊥AC,DE⊥AB∴当重合,∴此时点P与点D P与点D重合时,线段EF最短.∴点点评:等腰直角三角形及矩形的性质,解题的关键是题考查了全等三角形的判定与性质、本能够证得两个三角形全等,难度不大.淄博)为充分利用雨水资源,幸福村的小明家和相邻的爷爷家采取了修建蓄水池、屋顶2015?(12.(8分)收集雨水的做法.已知小明和爷爷家的屋顶收集雨水的面积、蓄水池的容积和蓄水池已有水的量如表:爷爷家小明家2160 120 屋顶收集雨水面积(m)313 50 蓄水池容积(m)311.5 34 )蓄水池已有水量(m 气象预报即将会下雨,为了收集尽可能多的雨水,下雨前需从爷爷家的蓄水池中抽取多少立方米的水注入小明家的蓄水池?分式方程的应用.考点:分析:题意可知:屋顶收集雨水面积的比等于所收集雨水体积的比,由此设出未知数,列由出方程解答即可.x立方米的水注入小明家的蓄水池,由题意得下雨前需从爷爷家的蓄水池中抽取解解答::,= ,解得:x=69是所列方程的根.经检验:x=6 6答:下雨前需从爷爷家的蓄水池中抽取立方米的水注入小明家的蓄水池.点评:利用底面积的比与体积的比相同联立方程是解决问题此题考查分式方程的实际运用,的关键.,平行C不重合)P与点B,△ABC中,点P是BC边上任意一点(点分)13.(9(2015?淄博)如图,在的面,平行四边形AFPE=1.设BP=xAB,AC上.已知BC=2,S四边形AFPE的顶点F,E分别在ABC△y.积为的函数关系式;y与x)求(1有这样的值,并求出该值;若没有,请说y)上述函数有最大值或最小值吗?若有,则当x取何值时,(2 明理由.似三角形的判定与性质;二次函数的最值;平行四边形的性质考分析,得出面积比等于相BABF ∽PC,证)由平行四边形的性质得出2的函数关系x),即可得出y与=比的平方,得出S=,同理:S(PEC△△BFP式;1)中函数关系式化成顶点式,即可得出结果.0得出y有最大值,把((2)由﹣<AFPE是平行四边形,(1)∵四边形解答:解:,PF∴∥CA ,BFP∽△BAC∴△2(),∴= ,S=1∵ABC△,S=∴BFP△2(S,=同理:)PEC △﹣y=1﹣,∴﹣;+xy=∴;理由如下:(2)上述函数有最大值,最大值为2 0,﹣<,)(y=∵﹣+x=﹣x﹣1+ 有最大值,∴y.有最大值,最大值为∴当x=1时,y 点评:题考查了平行四边形的性质、相似三角形的判定与性质、二次函数的最值;熟练掌本握平行四边形的性质,证明三角形相似得出关系式是解决问题的关键.1014.(9分)(2015?淄博)如图,点B,C是线段AD的三等分点,以BC为直径作⊙O,点P是圆上异于B,C的任意一点,连接PA,PB,PC,PD.PB=PC时,求tan∠APB(1)当的值;是上异于B,C的任意一点时,求tan∠APB?tan(2)当P∠DPC的值.考等三角形的判定与性质;圆周角定理;解直角三角形分析:(1)首先过点B作BE∥PC,与PA交于点E,根据AB=BC,可得,推得EB=PB;然后根据BC是⊙O的直径,求tan∠APB的值是多少即可.(2)首先过点A作AE∥PC,与PB的延长线交于点E,然后根据全等三角形判定的方法,判断出△ABE△CBP,即可判断出BE=BP,AE=CP;最后推得tan∠APB=,tan∠DPC=,据此求出tan∠APB?tan∠DPC的值是多少即可.解答:解:(1)如图1,过点B作BE∥PC,与PA交于点E,,∵AB=BC,∴,,∴EB=,PB= ∵∴EB=PB,∵BC是⊙O的直径,∴∠BPC=90°,∠PBE=90°,∴tan∠APB=.(2)如图2,过点A作AE∥PC,与PB的延长线交于点E,11的直径是B,AEP=9∴BPC=9中ABCB△△CBP,∴△ABE ,AE=CP,∴BE=BP,∴tan∠APB=DPC=tan∠,∴DPC=?tan,∠tan∴∠APB.tan即∠APB?tan∠DPC的值为点评:)此题主要考查了全等三角形的判定,要熟练掌握,解答此题的关键是要明确:(1SAS2:SSS﹣﹣三条边分别对应相等的两个三角形全等.②判定定理判定定理①1:﹣﹣两角及3:ASA判定定理﹣﹣两边及其夹角分别对应相等的两个三角形全等.③﹣﹣两角及其中一个角AAS4其夹边分别对应相等的两个三角形全等.④判定定理:﹣﹣斜边与直角边对应相等的对边对应相等的两个三角形全等.⑤判定定理5:HL 的两个直角三角形全等.)此题还考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在2(同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.)此题还考查了解直角三角形问题,要熟练掌握,解答此题的关键是要明确解直3(角三角形时要用到的关系.12。
山东省淄博市淄博区金山中学2014-2015学年八年级上学期期中质量检测

2014-2015学年度第一学期期中质量检测初二语文试题说明:本试题共8页,五个大题,22个小题,满分120分,考试时间120分钟。
第Ⅰ卷(选择题)一、基础知识积累与运用(共12分)1.下列加点字的注音有误的一项是()(2分)A.归省.(xǐnɡ) 蓦.(mù) 然颦蹙.(cù) 彷徨.(huánɡ)B.撺.(cuān) 掇冗.(rǒnɡ) 杂惊鸿.(hónɡ) 踌.(chóu) 躇C.凫.(fú) 水羁.(jī) 绊矫.(jiǎo) 健重荷.(hè)D.晦.(huì) 暗徘.(pái) 徊筹.划(chóu) 深邃.(suì)2.下列词语有错别字的一项是()(2分)A.叹为观止浑身解数妇孺皆知慷慨淋漓B.鸦鹊无声金碧辉煌锋芒必露拈轻怕重C.叱咤风云参差不齐迥乎不同杂乱无章D.尽态极妍鲜为人知漠不关心义愤填膺3. 下列句子中,没有语病的一项是( ) (2分)A. 国家反恐工作领导小组决定,以新疆为主战场,其他省市区积极配合,开展为期一年的严厉打击暴力恐怖活动专项行动。
B. 雾霾过后抓紧治霾,才有可能避免不会陷人周而复始的雾霾困扰之中。
C. 我们不能不否认,读那些文字粗糙内容单薄的消遣读物应该有所节制。
D. 这些老年人在晚会上舞姿翩翩,谁能相信他们不是年过花甲的老人呢?4. 下列句子中,加点成语使用有误的一项是()(2分)A.好一个安塞腰鼓!每一个舞姿都使人战栗在浓烈的艺术享受中,使人叹为观止....。
B.去年秋天,俄罗斯首都莫斯科发生了一起危言耸听....的恐怖袭击事件。
C.在荒山僻谷中,兰草仍然生机勃勃....,奋发向上,散发出缕缕清香,不因沦落深山而自抛。
D.一个很大很大的困难,除以13亿,就会变得微不足道....;一个很小很小的爱心,乘以13亿,就会聚成爱的海洋。
5. 下列关于作家、作品的表述,错误的一项是()(2分)A.《社戏》选自《呐喊》,题材小说,作者鲁迅。
山东省淄博市淄博区金山中学2014-2015学年八年级数学上学期期中质量检测试题_新人教版
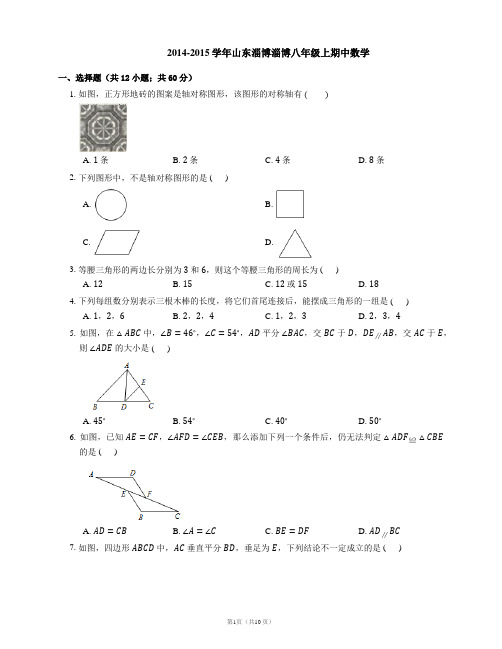
2014-2015学年山东淄博淄博八年级上期中数学一、选择题(共12小题;共60分)1. 如图,正方形地砖的图案是轴对称图形,该图形的对称轴有A. 条B. 条C. 条D. 条2. 下列图形中,不是轴对称图形的是 ( )A. B.C. D.3. 等腰三角形的两边长分别为和,则这个等腰三角形的周长为 ( )A. B. C. 或 D.4. 下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是 ( )A. ,,B. ,,C. ,,D. ,,5. 如图,在中,,,平分,交于,,交于,则的大小是 ( )A. B. C. D.6. 如图,已知,,那么添加下列一个条件后,仍无法判定的是 ( )A. B. C. D.7. 如图,四边形中,垂直平分,垂足为,下列结论不一定成立的是 ( )A. B. 平分C. D.8. 如图所示,有两棵树,一棵高米,另一棵高米,两树相距米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行 ( )A. 米B. 米C. 米D. 米9. 下列四组线段中,可以构成直角三角形的是 ( )A. ,,B. ,,C. ,,D. ,,10. 如图,将沿直线折叠后,使得点与点重合,已知,的周长为,则的长为 ( )A. B. C. D.11. 下列图形:其中所有轴对称图形的对称轴条数之和为 ( )A. B. C. D.12. 如图,中,,,,将折叠,使点与的中点重合,折痕为,则线段的长为 ( )A. B. C. D.二、填空题(共5小题;共25分)13. 若等腰三角形的一个内角为,则它的顶角为.14. 等腰三角形的周长为,其一边长为,则另外两边的长为.15. 如图,已知,,要使,则应添加的一个条件为.(答案不唯一,只需填一个).16. 已知为等边三角形,为中线,延长至,使,连接,则.17. 如图,圆柱形玻璃杯,高为,底面周长为,在杯内离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁到达蜂蜜所在位置的最短距离为.三、解答题(共7小题;共91分)18. 已知,如图,和都是等腰直角三角形,,为边上一点.求证:.19. 两个城镇、与两条公路、位置如图所示,电信部门需在处修建一座信号反射塔,要求发射塔到两个城镇、的距离必须相等,到两条公路,的距离也必须相等,那么点应选在何处?请在图中,用尺规作图找出所有符合条件的点.(不写已知、求作、作法,只保留作图痕迹)并结合实际说明你选择点位置的原因.20. 如图,已知线段及,只用直尺和圆规,求作,使,,(要求保留作图痕迹,不写作法)21. 如图,在中,,点是的中点,点在上.(1)求证:;(2)如图,若的延长线交于点,且,垂足为,,原题设其它条件不变.求证:.22. 如图,在等边三角形中,点,分别在边,上,,过点作,交的延长线于点.(1)求的度数;(2)若,求的长.23. 如图,小华想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小华在河岸边选取点,在点的对岸选取一个参照点,测得;小华沿河岸向前走选取点,并测得.请根据以上数据,用你所学的数学知识,帮小华计算小河的宽度(精确到整数).(提示:过点作于点,)24. 如图,在中,,点是上任意一点,过点分别向,引垂线,垂足分别为,,是边上的高.(1),,的长之间存在着怎样的数量关系?并加以证明;(2)若在底边的延长线上,(1)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.答案第一部分1. C2. C3. B 【解析】当等腰三角形的腰长为时,它的三边长为,,,由于,所以这个三角形不存在.当等腰三角形的腰长为时,它的三边长为,,,满足任意两边之和大于第三边,所以这个三角形存在,它的周长为.4. D5. C6. A7. C8. B 【解析】如图,作于点,连接.根据题意可得:(米),米,所以(米).9. D 10. C11. B 【解析】第一个图形是轴对称图形,有条对称轴;第二个图形是轴对称图形,有条对称轴;第三个图形是轴对称图形,有条对称轴;第四个图形是轴对称图形,有条对称轴;则所有轴对称图形的对称轴条数之和为.12. C 【解析】设.,.为中点,,.,.,,即..第二部分13. 或14. ,或,.15.16.【解析】是等边三角形,为中线,,,,.,,,.17. .【解析】沿过的圆柱的高剪开,得出矩形.过作于,作关于的对称点,连接交于,连接.则就是蚂蚁到达蜂蜜的最短距离.,,.,.在中,由勾股定理得:.第三部分18. 因为和都是等腰直角三角形,所以,因为,所以,所以.在和中,所以,所以19.(1)作出线段的垂直平分线;(2)作出角的平分线(条);它们的个交点,是所求作的点.因为发射塔离两个城镇、的距离越近,信号越强烈,所以,结合实际,点的位置应选在处更好.20. 如图所示:所以为所求作的三角形.21. (1),是的中点,.在和中..(2),,为等腰直角三角形..,是的中点,,.在和中,.22. (1)是等边三角形,.,.,..(2),,是等边三角形,.,,.23. 由题意得,,,,可得.所以.所以.在中,,可得.,可得.答:小华家门前的小河的宽度约为.24. (1).连接.则.即.,.(2)若在底边的延长线上,(1)中的结论不成立.但有.理由:连接.则.即.,.即.同理当在底边的延长线上时,则有,方法同上.。
2015-2016淄博初中各年级期中考试初一期中

A B C D 2015-2016学年度第一学期期中学业水平检测初 一 数 学 试 题第Ⅰ卷 选择题一.选择题(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填在下面的表格中)2.下列哪一个图形经过折叠可以得到正方体( ).3.下列四个图中,是三棱锥的表面展开图的是( ).4.一个数的平方是它的相反数,这个数为( ).A .0或1 B. 0或-1 C. 1 D. -1A B C DA B C D5.负数是指 ( ).A. 把某个数的前边加上“-”号B. 不大于0的数C. 除去正数的其他数D. 小于0的数6.若数轴上A 、B 两点所对应的有理数分别为a 、b ,且B 在A 的右边,则a -b 一定( ) A. 大于零 B. 小于零 C. 等于零D. 无法确定7. 下列结论正确的是( )A. 若|x | = |y |,则x =- yB. 若x =-y ,则 |x | = |y |C. 若|a |<|b |,则a <bD. 若a <b ,则 |a | <|b | 8.如果0,0,0a b a b +<><,那么下列关系式中正确的是( ).A.a b b a -->>>B.a a b b -->>>C.b a b a -->>>D.a b b a -->>> 9.按括号内的要求,用四舍五入法,对1022.0099取近似值,其中正确的是有( )个. ①1022.01(精确到0.001) ② 0.1022万(精确到个位) ③1020(精确到十位) ④ 1022.010(精确到千分位) A .1 B. 2 C. 3 D. 410.有理数a 等于它的倒数,有理数b 等于它的相反数,则a 2003+b 2003的值是( ) A .-1 B. 1 C. 0D. ±111.小明将一个直角三角板(如图1)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是( )A B C D 12.观察下列算式:21=2 , 22=4 , 23=8 , 24=16 25=32 , 26=64 , 27=128 ,28=256根据上述算式中的规律,你认为810的末位数是( ). A .2 B. 4 C. 6 D. 81图第Ⅱ卷 非选择题二.填空题(本题共8小题,请将最后结果填写在空格处)13.木星的赤道半径约为71400000m ,用科学计数法表示为__________m. 14.如图,甲是从_________面看到的图乙的图形. 15.已知21,4==y x ,且xy <0,则y x 的值等于______16.一个平面去截球,截面的形状一定是 17.2(12)a -与|3b -4|是互为相反数,则ab =_________. 18.在横线上填上“>”或者“<”. (1)11____43-- (2)57___79-- (3)32(2)____(3)--- (4)0___0.5-19.下列各数:—(+2),—32,315231200124------,)(,,)(中,负数有_____个.20.将一张长方形的纸对折,如图所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕,如果对折n 次,可以得到 条折痕.三.解答题(本大题共7小题,解答要写出必要的文字说明、求解过程或演算步骤) 21.直接写出得数(1) (17)13-+= (2)9(5)--=(3) 21(8)4-⨯= (4)51217⎛⎫÷- ⎪⎝⎭=第一次对折第二次对折第三次对折22.计算下列各题,能用简便运算的尽量使用简便运算 (1)1233(3)2(5)84545-++-+; (2)3235(5)()32(2)()54-⨯--÷-⨯+;(3)314(3)(1)8()232--⨯--⨯-⨯--;(4)52)4121132(⨯---23. 画出数轴,将下列各数表示在数轴上,并用“<”连接. 2-,|3|-,0, (1)--,23-, 1.7524. 如图所示图形表面分别标上字母A ----F ,问这个正方体各个面上的字母对面各是什么字母?ECDBAC F DA25.一个几何体由大小相同的小正方体搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在这个位置小正方体的个数,请你画出从正面和从左面看到的这个几何体的形状图.26.王先生手中持有四支股票,每只股票的详细信息如下表所示,(单位:元)27. 如图,将一个边长为1的正方形纸片分割成7个部分,部分②是部分①面积的一半,部分③是部分②面积的一半,依次类推. (1)阴影部分的面积是多少?(2)受此启发,你能求出23456111111222222+++++的值吗?【选作题】 (本题不计入总分)我们平常用的数都是十进制数,例如:8321=8×103+3×102+2×101+1×100,表示十进制的数要用十个数码(又叫做数字)0、1、2、3、4、5、6、7、8、9,而在计算机中用的是二进制,它只有两个数码:0、1来表示.如二进制中101=1×22+0×21+1×20等于十进制中的数5,再如10110=1×24+0×23+1×22+1×21+0×20等于十进制中的数22,同学们你看出其中的规律了吗?试一试你的能力吧: 二进制中101011等于十进制中多少呢?(说明20=1)。
数学7上淄川2014-2015期中

2014-2015学年度七年级第一学期期中学业水平考试数学试题2014.11(时间120分满分:120分)注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将学校、姓名、考证号、座号填写在答题卡和试卷规定的位置上,并核对监考教师粘贴的考号条形码是否与本人信息一致。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能写在试卷上。
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置上,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;需要在答题卡上作图时,可用2B 铅笔,但必须把所画线条加黑。
4.答案不能使用涂改液、胶带纸、修正带修改。
不按以上要求作答的答案无效,不允许使用计算器。
一、精心..选一选(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请选出你认为唯一正确.......的答案,填到后面的表格中,每小题3分,计36分)。
1.在△ABC中,∠B=40°,∠C=80°,则∠A等于(D)A.30°B. 40°C.50°D. 60°解:∠A=180°-∠B-∠C=180°-40°-80°=60°。
故选D2.下列轴对称图形中,对称轴条数最多的是(D)A. 等腰三角形B. 60°的角C. 长方形D. 等边三角形【考点】确定轴对称图形的对称轴条数及位置【分析】等腰三角形有一条对称轴,即底边上的高所在的直线;60°的角有一条对称轴,即角的平分线;长方形由2条对称轴,即过对边中点的直线;等边三角形有3条对称轴,即三边上的高所在的直线。
【解答】在等腰三角形、60°的角、长方形、等边三角形中对称轴条数最多的是等边三角形。
故选D【点评】根据各图形的特征及对称轴的意义即可确定对称轴的条数及位置。
山东省淄博市2015年中考数学真题试题(含扫描答案)

中考衣食住用行衣:中考前这段时间,提醒同学们出门一定要看天气,否则淋雨感冒,就会影响考场发挥。
穿着自己习惯的衣服,可以让人在紧张时产生亲切感和安全感,并能有效防止不良情绪产生。
食:清淡的饮食最适合考试,切忌吃太油腻或者刺激性强的食物。
如果可能的话,每天吃一两个水果,补充维生素。
另外,进考场前一定要少喝水!住:考前休息很重要。
好好休息并不意味着很早就要上床睡觉,根据以往考生的经验,太早上床反而容易失眠。
考前按照你平时习惯的时间上床休息就可以了,但最迟不要超过十点半。
用:出门考试之前,一定要检查文具包。
看看答题的工具是否准备齐全,应该带的证件是否都在,不要到了考场才想起来有什么工具没带,或者什么工具用着不顺手。
行:看考场的时候同学们要多留心,要仔细了解自己住的地方到考场可以坐哪些路线的公交车?有几种方式可以到达?大概要花多长时间?去考场的路上有没有修路堵车的情况?考试当天,应该保证至少提前20分钟到达考场。
绝密★启用前试卷类型A 淄博市2015年初中学业水平测试数学试题1819 20 21 22 23 24 分数第I 卷选择题答案栏题号 1 2 3 4 5 6 7 8 9 10 11 12 答案第Ⅰ卷(选择题 共48分)一、选择题(本大题共12小题,每小题选对得3分,共48分。
) 1.31-的倒数是A .3-B .31-C .31 D .32.下列计算结果正确的是A .923)(a a =-B .632a a a =⋅ C .22)21(21-=-- D .1)2160(cos 0=-ο3.在下列四个图案中既是轴对称图形,又是中心对称图形的是A .B .C .D .4.2010年4月20日晚,“支援青海玉树抗震救灾义演晚会”在莱芜市政府广场成功举行,热心企业和现场观众踊跃捐款31083.58元.将31083.58元保留两位有效数字可记为 A .3.1×106元 B .3.11×104元 C .3.1×104元 D .3.10×105元 5.如图,数轴上A 、B 两点分别对应实数a 、b ,则下列结论正确的是A .0>abB .0>-b aC .0>+b aD .0||||>-b a 6.右图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是A. B. C. D. 7.已知反比例函数xy 2-=,下列结论不正确...的是 A .图象必经过点(-1,2) B .y 随x 的增大而增大 C .图象在第二、四象限内 D .若x >1,则y >-2 8.已知圆锥的底面半径长为5,侧面展开后得到一个半圆,则该圆锥的母线长为A .2.5B .5C .10D .15y10 -1 a b BA (第5题图) (第6题图)9.二次函数c bx ax y ++=2的图象如图所示,则一次函数a bx y +=的 图象不经过 A .第一象限 B .第二象限 C .第三象限D .第四象限10.已知⎩⎨⎧==12y x 是二元一次方程组⎩⎨⎧=-=+18my nx ny mx 的解,则n m -2的算术平方根为A .4B .2C . 2D . ±211.一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是A .2B . 3C .1D .12 12.在一次自行车越野赛中,甲乙两名选手行驶的路程y (千米) 随时间x (分)变化的图象(全程)如图,根据图象判定下 列结论不正确...的是 A .甲先到达终点B .前30分钟,甲在乙的前面C .第48分钟时,两人第一次相遇D .这次比赛的全程是28千米第Ⅱ卷(非选择题 共72分)二、填空题(本大题共5小题,只要求填写最后结果,每小题填对得4分,共20分)13.分解因式:=-+-x x x 232 .14.有一组数据如下:2,3,a ,5,6,它们的平均数是4,则这组数据的方差是 . 15.某公司在2009年的盈利额为200万元,预计2011年的盈利额将达到242万元,若每年比上一年盈利额增长的百分率相同,那么该公司在2010年的盈利额为________万元. 16.在平面直角坐标系中,以点)3,4(A 、)0,0(B 、)0,8(C 为顶点的三角形向上平移3个单位,得到△111C B A (点111C B A 、、分别为点C B A 、、的对应点),然后以点1C 为中心将△111C B A 顺时针旋转︒90,得到△122C B A (点22B A 、分别是点11B A 、的对应点),则点2A 的坐标是 . 17.已知:3212323=⨯⨯=C ,1032134535=⨯⨯⨯⨯=C ,154321345646=⨯⨯⨯⨯⨯⨯=C ,…, 观察上面的计算过程,寻找规律并计算=610C .三、解答题(本大题共7小题,共52分,解答要写出必要的文字说明、证明过程或推演步骤) 18.(本题满分5分)先化简,再求值:24)2122(+-÷+--x xx x ,其中34 +-=x .得分 评卷人得分 评卷人O 14 12 1096 86 66 30 x /y /千米 AB C D(第12题图)乙甲19.(本题满分7分) 2010年5月1日,第41届世博会在上海举办,世博知识在校园迅速传播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A :不了解,B :一般了解,C :了解较多,D :熟悉).请你根据图中提供的信息解答以下问题: (1)求该班共有多少名学生;(2)在条形统计图中,将表示“一般了解”的部分补充完整;(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;(4)从该班中任选一人,其对世博知识的了解程度为“熟悉”的概率是多少?20.(本题满分7分)2009年首届中国国际航空体育节在莱芜雪野举办,期间在市政府广场进行了热气球飞行表演.如图,有一热气球到达离地面高度为36米的A 处时,仪器显示正前方一高楼顶部B 的仰角是37°,底部C 的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)(参考数据:,75.037tan ,80.037cos ,60.037sin ≈︒≈︒≈︒73.13≈)21.(本题满分8分)在Rt △ACB 中,∠C =90°,AC =3cm ,BC =4cm ,以BC 为直径作⊙O 交AB 于点D .(1)求线段AD 的长度;(2)点E 是线段AC 上的一点,试问当点E 在什么位置时,直线ED 与⊙O 相切?请说明理由.得分评卷人得分评卷人得分评卷人A B C D人数 5 10 15 20 25(第19题图)A10% B 30% D C OD CB AB AC(第20题图)22.(本题满分9分)小明家的蓄水池容积为50m 3,现在有水34m 3 ,收集水的面积为160m 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8题 第6题第5题山东省淄博市淄博区金山中学2015届初中数学毕业班上学期期中质量检测试题本试题共包含三道大题24个小题,满分120分,检测时间120分钟.一、选择题(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填在下面的表中.每小题3分,满分36分,错选、不选或选出的答案超过一个,均记0分.)1.已知反比例函数y =k x的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是 A .(-6,1) B .(1,6) C .(2,-3) D .(3,-2)2.下列图形中既是轴对称图形,又是中心对称图形的是A .等边三角形B .平行四边形C .正方形D .正五边形3.二次函数y =ax 2+bx +c (a ≠0)的大致图象如图,关于该二次函数,下列说法错误的是A .函数有最小值B .对称轴是直线x =12 C .当x <12,y 随x 的增大而减小 D .当-1<x <2时,y >04.已知一个布袋里装有2个红球,3个白球和a 个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为13,则a 等于 A .1 B .2 C .3 D .45.如图,△ABC 的边AC 与⊙O 相交于C 、D 两点,且经过圆心O ,边AB 与⊙O 相切,切点为B .已知∠A =30°,则∠C 的大小是A .30° B.45°C .60° D.40°6.如图,线段AB 是⊙O 的直径,弦CD 丄AB ,∠CAB =20°,则∠AOD 等于A .160° B.150° C.140° D.120°7.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m 2)与体积V (单位:m 3)满足函数关系式k Vρ=(k 为常数,k ≠0),其图象如图所示,则k 的值为A .-9B .-4C .4D .98.如图,正方形OABC 的两边OA 、OC 分别在x 轴、y 轴上,点D (5,3)在边AB 上,以C 为中心,把△CDB 旋转90°,则旋转后点D 的对应点D ′的坐标是第3题1 -1第11题 第15题 第17题 第16题 第12题A .(2,10)B .(-2,0)C .(2,10)或(-2,0)D .(10,2)或(-2,0)9.一元二次方程x 2-4x +5=0的根的情况是A .有两个不相等的实数根B .有两个相等的实数根C .只有一个实数根D .没有实数根10.要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛.设比赛组织者应邀请x 个队参赛,则x 满足的关系式为A .12x (x +1)=28B .12x (x -1)=28 C .x (x +1)=28 D .x (x -1)=2811.已知二次函数y =ax 2+bx +c (a ≠0)的图象如图,且关于x 的一元二次方程ax 2+bx +c -m =0没有实数根,有下列结论:①b 2-4ac >0;②abc <0;③m >2.其中,正确结论的个数是A .0B .1C .2D .312.如图,半径为2cm ,圆心角为90°的扇形OAB 中,分别以OA 、OB 为直径作半圆,则图中阴影部分的面积为A .(2π-1)cm 2B .(2π+1)cm 2 C . 1cm 2 D .2πcm 2二、填空题(每小题4分,共20分)13.抛物线y =x 2-2x +3的顶点坐标是 .14.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为 .15.如图,A 、B 两点在双曲线y =4x上,分别经过A 、B 两点向轴作垂线段,已知 S 阴影=1,则S 1+S 2= .16.如图,在2×2的正方形网格中有9个格点,已经取定点A 和B ,在余下的7个点中任取一点C ,使△ABC 为直角三角形的概率是.17.如图,△ABC 绕点A 顺时针旋转45°得到△AB ′C ′,若∠BAC =90°,AB =AC则图中阴影部分的面积等于 .三、解答题(第18、19、20题每题8分,第21、22、23、24题每题10分,满分64分)评 价 评 卷 人18.商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.(1)若他去买一瓶饮料,则他买到奶汁的概率是;(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶汁的概率.19.将油箱注满k升油后,轿车行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=ka(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式;(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?20.如图,已知二次函数y=a(x-h)2O(0,0),A(2,0).(1)写出该函数图象的对称轴;(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?21.在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=4.(1)试在图中作出△ABC以点A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.第21题22.如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.(1)求二次函数的解析式;(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.第22题23.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连接CD.(1)求证:∠A=∠BCD;(2)若M为线段BC上的一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.第23题24.实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=kx(k>0)刻画(如图所示).(1)根据上述数学模型计算:①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?②当x=5时,y=45,求k的值.(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.第24题2014—2015学年度上学期期中质量检测初四数学试题参考答案友情提示:解题方法只要正确,可参照得分.一、选择题(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项填在下面的表中.每小题3分,满分36分,错选、不选或选出的答案超过一个,均记0分.)二、填空题(每小题4分,共20分)13.(1,2); 14.3π; 15.6; 16.47; 171.三、解答题(第18、19、20题每题8分,第21、22、23、24题每题10分,满分64分)18.解:(1)14;…………………4分(2)画树状图得:……………6分∵共有12种等可能的结果,他恰好买到雪碧和奶汁的有2种情况,∴他恰好买到雪碧和奶汁的概率为:212=16.……………………8分19.解:(1)由题意得:a=0.1,S=700,代入反比例函数关系式S=ka中,解得:k=Sa=70,………………………………3分所以所求函数关系式为S=70a;………………………………4分(2)将a=0.08代入S=70a得:S=70a =700.08=875(千米)………………………………7分所以该轿车可以行驶875千米. ………………………………8分第20题第21题20.解:(1)∵二次函数y =a (x -h )2O (0,0),A (2,0).∴抛物线的对称轴为直线x =1; ………………………………4分(2)点A ′是该函数图象的顶点.理由如下:如图,作A ′B ⊥x 轴于点B ,∵线段OA 绕点O 逆时针旋转60°到OA ′,∴OA ′=OA =2,∠A ′OA =60°,…………………5分 在Rt△A ′OB 中,∠OA ′B =30°,∴OB =12OA ′=1,∴A ′B………………………6分 ∴A ′点的坐标为(1,………………7分∵二次函数y =a (x -h )2O (0,0),A (2,0) ∴二次函数y =a (x -h )2的解析式为y =x -1)2∴点A ′为抛物线y =x -1)2分21.解:(1)作对△AB 1C 1得3分;(2)如图所示,A (0,1),C (-3,1);每个坐标作对得1分,全对得2分;(3)作对△A 2B 2C 2得3分,B 2(3,-5),C 2(3,-1).对一个坐标得1分,全对得5分.22.解:(1)∵二次函数y =ax 2+bx +c 的图象过A (2,0),B (0,-1)和C (4,5)三点,∴421016415a b a b +-=⎧⎨+-=⎩,第22题第23题∴a =12,b =-12,c =-1,……………3分∴二次函数的解析式为y =12x 2-12x -1;…4分(2)当y =0时,得12x 2-12x -1=0;解得x 1=2,x 2=-1, ……………6分∴点D 的坐标为(-1,0);………8分(3)图象如图, 当一次函数的值大于二次函数的值时,x 的取值范围是-1<x <4.………10分23.(1)证明:∵AC 为直径,∴∠ADC =90°, ……………2分∴∠A +∠ACD =90°,∵∠ACB =90°,∴∠DCB +∠ACD =90°,∴∠DCB =∠A ; ……………5分(2)当MC =MD (或点M 是BC 的中点)时,直线DM 与⊙O 相切;…6分 解:连接DO , ……………7分∵DO =CO ,∴∠1=∠2, ……………8分∵DM =CM ,∴∠4=∠3, ……………9分∵∠2+∠4=90°,∴∠1+∠3=90°, ∴直线DM 与⊙O 相切.………10分24.解:(1)①y =-200x 2+400x =-200(x -1)2+200, ………………3分∴喝酒后1时血液中的酒精含量达到最大值,最大值为200(毫克/百毫升); …………………4分②∵当x =5时,y =45,∴k=xy=45×5=225;…………………5分(2)不能驾车上班;…………………6分理由:∵晚上20:00到第二天早上7:00,一共有11小时,∴将x=11代入y=225x,则y=22511>20,…………………9分∴第二天早上7:00不能驾车去上班.………………10分。
