2020版高考数学理科人教B版一轮复习课时规范练1集合的概念与运算

合集下载

2020届高考一轮复习理科数学(人教版)练习：第1讲集合的概念与运算

第1讲集合的概念与运算1．(2016·全国卷Ⅰ)设集合A ＝{x |x 2－4x ＋3<0}，B ＝{x |2x －3>0}，则A ∩B ＝(D)A ．(－3，－32)B ．(－3，32) C ．(1，32) D ．(32，3) (1)先化简集合A ，B ，再利用交集定义求解．因为x 2－4x ＋3<0，所以1<x <3，所以A ＝{x |1<x <3}．因为2x －3>0，所以x >32，所以B ＝{x |x >32}．所以A ∩B ＝{x |32<x <3}．故选D. 2．(2016·山东卷)设集合A ＝{y |y ＝2x ，x ∈R }，B ＝{x |x 2－1＜0}，则A ∪B ＝(C)A ．(－1,1)B ．(0,1)C ．(－1，＋∞)D ．(0，＋∞)由已知得A ＝{y |y ＞0}，B ＝{x |－1＜x ＜1}，则A ∪B ＝{x |x ＞－1}．故选C.3．(2018·武汉调研测试)已知集合M ＝{x |x 2＝1}，N ＝{x |ax ＝1}，若N ⊆M ，则实数a 的取值集合为(D)A ．{1}B ．{－1，1}C ．{1，0}D ．{1，－1，0}M ＝{x |x 2＝1}＝{－1，1}，又N ⊆M ，则N ＝{－1}，{1}，∅满足条件，所以a ＝1，－1，0，即实数a 的取值集合为{1，－1，0}．4．(2018·佛山一模)已知全集U ＝R ，集合A ＝{0，1，2，3，4}，B ＝{x |x 2－2x ＞0}，则图中阴影部分表示的集合为(A)A ．{0，1，2}B ．{1，2}C ．{3，4}D ．{0，3，4}因为B ＝{x |x 2－2x ＞0}＝{x |x ＞2或x ＜0}，所以∁U B ＝{x |0≤x ≤2}，所以图中阴影部分表示的集合为A ∩(∁U B )＝{0，1，2}．5．(2018·合肥高三质量检测)设集合A ＝{1，2，3}，B ＝{4，5}，M ＝{x |x ＝a ＋b ，a ∈A ，b ∈B }，则集合M 中元素个数为(B)A ．3B ．4C ．5D ．6因为M ＝{5，6，7，8}，所以M 中元素的个数为4.6．(2016·天津卷)已知集合A ＝{1,2,3,4}，B ＝{y |y ＝3x －2，x ∈A }，则A ∩B ＝ {1,4} .因为集合B 中，x ∈A ，所以当x ＝1时，y ＝3－2＝1；当x ＝2时，y ＝3×2－2＝4；当x ＝3时，y ＝3×3－2＝7；当x ＝4时，y ＝3×4－2＝10.即B ＝{1,4,7,10}．又因为A ＝{1,2,3,4}，所以A ∩B ＝{1,4}．7．设U ＝{0,1,2,3}，A ＝{x |x 2＋mx ＝0，x ∈U }，若∁U A ＝{1,2}，则实数m ＝－3 .因为∁U A ＝{1,2}，所以A ＝{0,3}，所以m ＝－3.8．已知M ＝{x |－2≤x ≤5}，N ＝{x |a ＋1≤x ≤2a －1}．(1)若a ＝3时，则M ∪(∁R N )＝ R ；(2)若N ⊆M ，则实数a 的取值范围为 (－∞，3] .(1)当a ＝3时，N ＝{x |4≤x ≤5}，所以∁R N ＝{x |x <4或x >5}．所以M ∪(∁R N )＝R .(2)①当2a －1<a ＋1，即a <2时，N ＝∅，此时满足N ⊆M .②当2a －1≥a ＋1，即a ≥2时，B ≠∅，由N ⊆M ，得⎩⎪⎨⎪⎧a ＋1≥－2，2a －1≤5，所以2≤a ≤3. 综上，实数a 的取值范围为(－∞，3]．9．已知集合A ＝{x |y ＝lg(x －x 2)}，B ＝{x |x 2－cx <0，c >0}，若A ⊆B ，则实数c 的取值范围是(B)A ．(0,1]B ．[1，＋∞)C ．(0,1)D ．(1，＋∞)由x －x 2>0，得0<x <1，所以A ＝(0,1)，由x 2－cx <0，且c >0，得0<x <c ，所以B ＝(0，c )，因为A ⊆B ，所以c ≥1.10．(2018·福州期末)已知集合A ＝[1，＋∞)，B ＝{x ∈R |12a ≤x ≤2a －1}，若A ∩B ≠∅，则实数a 的取值范围是(A)A ．[1，＋∞) B ．[12，1] C ．[23，＋∞) D ．(1，＋∞) 因为A ∩B ≠∅，所以⎩⎪⎨⎪⎧2a －1≥1，2a －1≥12a ，解得a ≥1. 即实数a 的取值范围是[1，＋∞)．11．(2018·北京卷)设集合A ＝{(x ，y )|x －y ≥1，ax ＋y ＞4，x －ay ≤2}，则(D)A ．对任意实数a ，(2，1)∈AB ．对任意实数a ，(2，1)∉AC ．当且仅当a ＜0时，(2，1)∉AD ．当且仅当a ≤32时，(2，1)∉A 若点(2，1)∈A ，则不等式x －y ≥1显然成立，且同时要满足⎩⎨⎧≤->+,22,412a a 即⎪⎩⎪⎨⎧≥>,0,23a a 解得a >32.即点(2，1)∈A ⇒a >32，其等价命题为a ≤32⇒点(2，1)∉A 成立． 12．(2019·海南二校联考)某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱乒乓球运动但不喜爱篮球运动的人数为__7__人．设全集U 为某班30人，集合A 为喜爱篮球运动的15人，集合B 为喜爱乒乓球运动的10人，如图．设两者都喜欢的人数为x 人，则只喜爱篮球的有(15－x )人，只喜爱乒乓球的有(10－x )人，由此可得(15－x)＋(10－x)＋x＋8＝30，解得x＝3.所以10－x＝7，即所求人数为7人．感谢您的下载!快乐分享，知识无限！由Ruize收集整理！。

2020版高考数学一轮复习课时规范练1集合的概念与运算理北师大版 (4)

课时规范练4 简单的逻辑联结词、全称量词与存在量词基础巩固组1.命题“存在实数x0,使x0>1”的否定是()A.对任意实数x,都有x>1B.不存在实数x0,使x0≤1C.对任意实数x,都有x≤1D.存在实数x0,使x0≤12.下列特称命题中真命题的个数为()①存在实数x0,使+2=0;②有些角的正弦值大于1;③有些函数既是奇函数又是偶函数.A.0B.1C.2D.33.设命题p:存在x0∈(0,+∞),x0+>3;命题q:任意x∈(2,+∞),x2>2x,则下列命题为真的是()A.p且(q)B.(p)且qC.p且qD.(p)或q4.若定义域为R的函数f(x)不是偶函数,则下列命题一定为真命题的是()A.任意x∈R,f(-x)≠f(x)B.任意x∈R,f(-x)=-f(x)C.存在x0∈R,f(-x0)≠f(x0)D.存在x0∈R,f (-x0)=-f(x0)5.若命题“存在x0∈R,+(a-1)x0+1<0”是真命题,则实数a的取值范围是()A.[-1,3]B.(-1,3)C.(-∞,-1]∪[3,+∞)D.(-∞,-1)∪(3,+∞)6.已知命题p:对任意x∈R,总有2x>x2;q:“ab>1”是“a>1,b>1”的充分不必要条件,则下列命题为真命题的是()A.p且qB.(p)且qC.p且(q)D.(p)且(q)7.(2018北京十四中月考,6)下列命题正确的是()A.“x<1”是“x2-3x+2>0”的必要不充分条件B.若给定命题p:存在x∈R,使得x2+x-1<0,则p:任意x∈R,均有x2+x-1≥0C.若p且q为假命题,则p,q均为假命题D.命题“若x2-3x+2=0,则x=2”的否命题为“若x2-3x+2=0,则x≠2”8.已知命题p:任意x∈R,x3<x4;命题q:存在x0∈R,sin x0-cos x0=-,则下列命题为真命题的是()A.p且qB.(p)且qC.p且(q)D.(p)且(q)9.(2018湖南长郡中学一模,2)下列判断正确的是()A.若命题p为真命题,命题q为假命题,则命题“p且q”为真命题B.命题“若xy=0,则x=0”的否命题为“若xy=0,则x≠0”C.“sin α=”是“α=”的充分不必要条件D.命题“对任意x∈R,2x>0成立”的否定是“存在x0∈R,≤0成立”10.已知命题“任意x∈R,x2-5x+a>0”的否定为假命题,则实数a的取值范围是.11.已知命题p:任意x∈[0,1],a≥e x;命题q:存在x0∈R,使得+4x0+a=0.若命题“p且q”为真命题,则实数a的取值范围是.12.下列结论:①若命题p:存在x0∈R,tan x0=2,命题q:任意x∈R,x2-x+>0,则命题“p且(q)”是假命题;②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是=-3;③“设a,b∈R,若ab≥2,则a2+b2>4”的否命题为“设a,b∈R,若ab<2,则a2+b2≤4”.其中正确结论的序号为.综合提升组13.(2018河南郑州三模,2)下列命题中,正确的是()A.存在x0∈R,sin x0+cos x0=B.复数z1,z2,z3∈C,若(z1-z2)2+(z2-z3)2=0,则z1=z3C.“a>0,b>0”是“≥2”的充要条件D.命题“存在x∈R,x2-x-2≥0”的否定是“任意x∈R,x2-x-2<0”14.若命题p:函数y=x2-2x的递增区间是[1,+∞),命题q:函数y=x-的递增区间是[1,+∞),则()A.p且q是真命题B.p或q是假命题C.p是真命题D.q是真命题15.已知命题p:关于x的不等式ax2+ax+1>0的解集为全体实数,则实数a∈(0,4);命题q:“x2-3x>0”是“x>4”的必要不充分条件,则下列命题正确的是()A.p且qB.p且(q)C.(p)且qD.(p)且(q)16.已知命题p:存在x0∈R,-mx0=0,q:任意x∈R,x2+mx+1≥0,若p或(q)为假命题,则实数m的取值范围是()A.(-∞,0)∪(2,+∞)B.[0,2]C.RD.⌀创新应用组17.(2018河北衡水中学十模,5)下面四个命题中,假命题是()A.“若a≤b,则2a≤2b”的否命题B.“任意a∈(0,+∞),函数y=a x在定义域内递增”的否定C.“π是函数y=sin x的一个周期”或“2π是函数y=sin 2x的一个周期”D.“x2+y2=0”是“xy=0”的必要条件18.将不等式组的解集记为D,有下面四个命题:p1:任意(x,y)∈D,x+2y≥-2;p2:存在(x,y)∈D,x+2y≥2;p3:任意(x,y)∈D,x+2y≤3;p4:存在(x,y)∈D,x+2y≤-1.其中的真命题是.参考答案课时规范练4 简单的逻辑联结词、全称量词与存在量词1.C特称命题的否定为全称命题,所以将“存在”改为“任意”,将“x>1”改为“x≤1”.故选C.2.B因为x2+2≥2,所以①是假命题;因为任意x∈R均有|sin x|≤1,所以②是假命题;f(x)=0既是奇函数又是偶函数,③是真命题.故选B.3.A命题p:存在x0∈(0,+∞),x0+>3,是真命题,例如取x0=4;命题q:任意x∈(2,+∞),x2>2x,是假命题,例如取x=4时,x2=2x.则命题为真的是p且(q).故选A.4.C不是偶函数是对偶函数的否定,定义域为R的偶函数的定义:任意x∈R,f(-x)=f(x),这是一个全称命题,所以它的否定为特称命题:存在x0∈R,f(-x0)≠f(x0).故选C.5.D因为命题“存在x0∈R,+(a-1)x0+1<0”等价于+(a-1)x0+1=0有两个不等的实根,所以Δ=(a-1)2-4>0,即a2-2a-3>0,解得a<-1或a>3.故选D.6.D命题p:对任意x∈R,总有2x>x2,它是假命题,例如取x=2时,2x与x2相等.q:由a>1, b>1⇒ab>1;反之不成立,例如取a=10,b=.∴“ab>1”是“a>1,b>1”的必要不充分条件,即q是假命题.∴真命题是(p)且(q).故选D.7.B因为x2-3x+2>0,所以x>2或x<1,因此“x<1”是“x2-3x+2>0”的充分不必要条件,故A项错误;命题p:存在x∈R,使得x2+x-1<0的否定为:任意x∈R,均有x2+x-1≥0,故B项正确;若p且q为假命题,则p,q至少有一个为假命题,故C项错误;命题“若x2-3x+2=0,则x=2”的否命题为“若x2-3x+2≠0,则x≠2”,故D项错误.故选B.8.B由x3<x4,得x<0或x>1,∴命题p为假命题;由sin x-cos x=sin=-,得x-=+2kπ(k∈Z),即x=+2kπ(k∈Z),∴命题q为真命题,∴(p)且q为真命题.9.D对A项,若命题p为真,命题q为假,则“p且q”为假,故A错;对B项,因否命题是既否定条件也否定结论,故B错;对C项,“sin α=”是“α=”的必要不充分条件,故C错;对D项,根据全称命题的否定,换量词否结论,故选项正确.故选D.10. 由“任意x∈R,x2-5x+a>0”的否定为假命题,可知原命题必为真命题,即不等式x2-5x+a>0对任意实数x恒成立.设f(x)=x2-5x+a,则其图像恒在x轴的上方,所以Δ=25-4×a<0,解得a>.故实数a的取值范围为.11.[e,4]由命题“p且q”是真命题,得命题p,q都是真命题.由任意x∈[0,1],a≥e x,得a≥e;由存在x0∈R,使+4x0+a=0,知Δ=16-4a≥0,得a≤4,因此e≤a≤4.12.①③在①中,命题p是真命题,命题q也是真命题,故“p且(q)”为假命题是正确的;在②中,l1⊥l2⇔a+3b=0,而=-3能推出a+3b=0,但a+3b=0推不出=-3,故②不正确;在③中,“设a,b∈R,若ab≥2,则a2+b2>4”的否命题为“设a,b∈R,若ab<2,则a2+b2≤4”,所以③正确.13.D选项A中,因sin x+cos x的最大值为,故A错;选项B中,由(z1-z2)2+(z2-z3)2=0,得不出z1=z2,z2=z3,所以也得不出z1=z3;选项C中,a<0,b<0, +≥2也成立,故C错;由特称命题的否定知,D 正确.14.D因为函数y=x2-2x的递增区间是[1,+∞),所以p是真命题;因为函数y=x-的递增区间是(-∞,0)和(0,+∞),所以q是假命题.所以p且q为假命题,p或q为真命题,p为假命题,q为真命题.15.C命题p:当a=0时,不等式ax2+ax+1>0化为1>0,满足条件,当a≠0时,由不等式ax2+ax+1>0的解集为全体实数,得解得0<a<4,所以实数a∈[0,4),因此p是假命题.命题q:由x2-3x>0,解得x>3或x<0.所以“x2-3x>0”是“x>4”的必要不充分条件,即q是真命题.由以上可得(p)且q是真命题.故选C.16.B由p或(q)为假命题,知p为假命题,q为真命题.由e x-mx=0,得m=.设f(x)=,则f' (x)==,当x>1时,f'(x)>0,此时函数递增;当0<x<1时,f'(x)<0,此时函数递减;当x<0时,f'(x)<0,此时函数递减,∴当x=1时,f(x)=取得极小值f(1)=e,∴函数f(x)=的值域为(-∞,0)∪[e,+∞),∵p是假命题,∴0≤m<e.当命题q为真命题时,有Δ=m2-4≤0,即-2≤m≤2.∴m的取值范围是0≤m≤2.17.D对A项,“若a≤b,则2a≤2b”的否命题是“若a>b,则2a>2b”,A是真命题;对B项,“任意a∈(0,+∞),函数y=a x在定义域内单调递增”的否定为“存在a0∈(0,+∞),函数y=a x在定义域内不单调递增”,正确,例如a=时,函数y=在R上单调递减,B为真命题;对C项,“π是函数y=sin x的一个周期”,不正确,“2π是函数y=sin 2x的一个周期”正确,根据“或”命题的定义可知,C为真命题;对D项,“x2+y2=0”⇒“xy=0”,反之不成立,因此“x2+y2=0”是“xy=0”的充分不必要条件,D 是假命题,故选D.18.p1,p2画出题中不等式组所表示的平面区域如图阴影部分所示.作直线l0:y=-x,平移l0,当直线经过点A(2,-1)时,x+2y取最小值,此时(x+2y)min=0.故p1:任意(x,y)∈D,x+2y≥-2为真.p2:存在(x,y)∈D,x+2y≥2为真.。

2020版高考数学一轮复习课时规范练1集合的概念与运算理北师大版 (52)

课时规范练52 随机抽样基础巩固组1.(2018云南昆明模拟,3)某地区想要了解居民生活状况,先把居民按所在行业分为几类,然后每个行业抽取的居民家庭进行调查,这种抽样方法是()A.简单随机抽样B.系统抽样C.分类抽样D.分层抽样2.对一个容量为N的总体抽取容量为n的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为p1,p2,p3,则()A.p1=p2<p3B.p2=p3<p1C.p1=p3<p2D.p1=p2=p33.(2018江西重点中学联考,1)要从已编号(1~70)的70枚最新研制的某型导弹中随机抽取7枚来进行发射试验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的7枚导弹的编号可能是()A.5,10,15,20,25,30,35B.3,13,23,33,43,53,63C.1,2,3,4,5,6,7D.1,8,15,22,29,36,434.(2018豫北豫南名校联考,4)某校高三年级共有800名学生,学号为1~800号,现用系统抽样抽出样本容量为n的样本;从小号到大号抽出的第1个数为8号,第6个数为168,则抽取的第3个数是()号A.64B.72C.80D.885.某学院A,B,C三个专业共有1 200名学生,为了调查这些学生勤工俭学的情况,拟采用分层抽样的方法抽取一个容量为120的样本.已知该学院的A专业有380名学生,B专业有420名学生,则在该学院的C专业应抽取的学生人数为()A.30B.40C.50D.606.某班级有男生20人,女生30人,从中抽取10人作为样本,恰好抽到了4名男生、6名女生,则下列命题正确的是()A.该抽样可能是简单随机抽样B.该抽样一定不是系统抽样C.该抽样中女生被抽到的概率大于男生被抽到的概率D.该抽样中女生被抽到的概率小于男生被抽到的概率7.(2018黑龙江大庆考前模拟,15)假设要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋中抽取60袋牛奶进行检验,利用随机数表抽样时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第8行第7列开始向右读,请你写出抽取检测的第5袋牛奶的编号.(下面摘取了随机数表第7行至第9行)8442 1753 3157 2455 0688 7704 7447 6721 7633 5025 8392 1206 766301 6378 5916 9556 6719 9810 5071 7512 8673 5807 4439 5238 793321 1234 2978 6456 0782 5242 0744 3815 5100 1342 9966 0279 548.(2018河北衡水中学模拟,13)用系统抽样法(按等距离的规则)从160部智能手机中抽取容量为20的样本,现将这160部智能手机随机地从001~160编号,按编号顺序平分成20组:001~008号,009~016号,017~024号,…153~160号,若第9组与第10组抽出的号码之和为140,则第1组中用抽签的方法确定的号码是.综合提升组9.(2018江西南昌模拟,3)某学校老师中,O型血有36人、A型血有24人、B型血有12人,现需要从这些老师中抽取一个容量为n的样本.如果采用系统抽样和分层抽样方法抽取,都不用剔除个体;如果样本容量减少一个,则在采用系统抽样时,需要在总体中剔除2个个体,则样本容量n可能为()A.12B.8C.6D.410.某企业三个分厂生产同一种电子产品,三个分厂产量分布如图所示,现在用分层抽样方法从三个分厂生产的该产品中共抽取100件做使用寿命的测试,则第一分厂应抽取的件数为;由所得样品的测试结果计算出一、二、三分厂取出的产品的使用寿命平均值分别为1 020小时、980小时、1 030小时,估计这个企业所生产的该产品的平均使用寿命为小时.11.(2018东莞二模,13)某机构对某镇的学生的身体素质状况按年级段进行分层抽样调查,得到了如下表所示的数据,则=.12.(2018第二次全国大联考,14)现有20~30岁若干人、30~40岁30人、40~50岁30人共3类人群组成的一个总体.若抽取一个容量为10的样本来分析拥有自住房的比例.如果采用系统抽样和分层抽样方法抽取,不用剔除个体,则总体容量n的值可能是.(写出n的所有可能值)创新应用组13.某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270,使用系统抽样时,将学生统一随机编号为1,2,…,270,并将整个编号依次分为10段,如果抽得号码有下列四种情况:①7,34,61,88,115,142,169,196,223,250;②5,9,100,107,111,121,180,195,200,265;③11,38,65,92,119,146,173,200,227,254;④30,57,84,111,138,165,192,219,246,270.关于上述样本的下列结论中,正确的是()A.②③都不能为系统抽样B.②④都不能为分层抽样C.①④都可能为系统抽样D.①③都可能为分层抽样14.(2018重庆八中模拟,13)2018年俄罗斯世界杯将至,本地球迷协会统计了协会内180名男性球迷和60名女性球迷在观察场所(家里、酒吧、球迷广场)上的选择,制作了如图所示的条形图,用分层抽样的方法从中抽取48名球迷进行调查,则其中选择在酒吧观赛的女球迷人数为人.参考答案课时规范练52 随机抽样1.D由题意,对居民进行职业分类,再进行等量抽取,属于分层抽样.故选D.2.D由随机抽样的原则可知简单随机抽样、分层抽样、系统抽样都必须满足每个个体被抽到的概率相等,即p1=p2=p3,故选D.3.B根据系统抽样的定义则编号间距为70÷7=10,则满足条件的是3,13,23,33,43,53,63,故选B.4.B由系统抽样的特点得8+(6-1)×k=168,k=32.所以抽取的第3个数为8+(3-1)×32=72,故选B.5.B由题知C专业有学生1 200-380-420=400(名),故C专业应抽取的学生人数为120×=40.6.A本题看似是一道分层抽样的题,实际上每种抽样方法都可能出现这个结果,故B不正确.根据抽样的等概率性知C,D不正确.7.175找到第8行第7列的数开始向右读,符合条件的是785,667,199,507,175.故答案为175.8.002由系统抽样法知抽取的20个样本的编号可视为公差为8的等差数列,设首项为a1,又a9+a10=140,所以2a1+17×8=140,所以a1=2,所以第1组中用抽签的方法确定的号码是002.9.C因为采用系统抽样和分层抽样方法抽取,都不用剔除个体,所以样本容量n为36+24+12=72的约数;因为36∶24∶12=3∶2∶1,所以样本容量n为3+2+1=6的倍数,因此舍去B,D;因为如果样本容量减少一个,则在采用系统抽样时,需要在总体中剔除2个个体,所以样本容量n为72-2=70的约数加1,故选C.10.50 1 015第一分厂应抽取的件数为100×50%=50;该产品的平均使用寿命为1020×0.5+980×0.2+1 030×0.3=1 015(小时).11.37 500由分层抽样的特点,得==,即x=750, =50,则=37 500.12.100,150,300根据条件易知,总体容量为n,设总体中的20~30岁的人数为x(x∈N+),则n=x+30+30=x+60.当样本容量为10时,系统抽样间隔为=∈N+,所以x+60是10的倍数.分层抽样的抽样比为=,求得20~30岁、30~40岁、40~50岁的抽样人数分别为x×=、30×=、30×=,所以x+60应是300的约数,所以x+60可能为75,100,150,300.根据“x+60是10的倍数”以及“x+60可能为75,100,150,300”可知,x+60可能为100,150,300,所以x可能为40,90,240.经检验,发现当x分别为40,90,240时,分别为4,6,8,都符合题意.综上所述,x可能为40,90,240,所以n可能为100,150,300.故答案为100,150,300.13.D因为③可能为系统抽样,所以选项A不对;因为②为分层抽样,所以选项B不对;因为④不为系统抽样,所以选项C不对,故选D.14.4总球迷有180+60=240人,家里的女性球迷有120×25%=30人,球迷广场女性有80×12.5%=10人,所以在酒吧观赛的女球迷是60-30-10=20人,抽样中,选择在酒吧观赛的女球迷人数有×48=4人.。

2020版高考数学理科人教B版一轮温习课时标准练1集合的概念与运算

课时标准练1集合的概念与运算基础巩固组1.(2018厦门外国语学校一模,2)已知集合A={x|y=lg(x-1)},B={x||x|<2},则A∩B=()A.(-2,0)B.(0,2)C.(1,2)D.(-2,2)2.已知全集U=R,集合A={x|x<-2或x>2},则∁U A=()A.(-2,2)B.(-∞,-2)∪(2,+∞)C.[-2,2]D.(-∞,-2]∪[2,+∞)3.(2018百校联盟四月联考,1)设集合A={-1,0,1,2},B={y|y=2x,x∈A},则A∪B中元素的个数为()4.设集合S={x|(x-2)(x-3)≥0},T={x|x>0},则S∩T=()A.[2,3]B.(-∞,2]∪[3,+∞)C.[3,+∞)D.(0,2]∪[3,+∞)5.(2018北京101中学3月模拟,1)已知集合A={x|x(x-2)<0},B={x|ln x>0},则A∩B是()A.{x|x>0}B.{x|x>2}C.{x|1<x<2}D.{x|0<x<2}6.设集合U={1,2,3,4},集合A={x∈N|x2-5x+4<0},则∁U A等于()A.{1,2}B.{1,4}C.{2,4}D.{1,3,4}7.(2018山东济南二模,1)设全集U=R,集合A={x|x-1≤0},集合B={x|x2-x-6<0},那么以下图中阴影部份表示的集合为()A.{x|x<3}B.{x|-3<x≤1}C.{x|x<2}D.{x|-2<x≤1}8.已知全集U=R,A={0,1,2,3},B={y|y=2x,x∈A},则(∁U A)∩B=()A.(-∞,0)∪(3,+∞)B.{x|x>3,x∈N}C.{4,8}D.[4,8]9.(2018宁夏银川一中一模,2)设集合A={(x,y)|x2+y2=1},B={(x,y)|y=3x},则A∩B的子集的个数是()10.已知集合A={x|x(x-4)<0},B={0,1,5},则A∩B=.11.已知集合A={x|log2x≤2},B={x|x<a},若A⊆B,那么实数a的取值范围是.12.已知集合M={1,2,3,4},那么集合P={x|x∈M,且2x∉M}的子集的个数为.综合提升组13.已知集合A={x|x2-2x-3≤0},B={x|x<a},若A⊆B,那么实数a的取值范围是()A.(-1,+∞)B.[-1,+∞)C.(3,+∞)D.[3,+∞)14.(2018河北衡水中学十模,1)已知全集U=Z,A={0,1,2,3},B={x|x2=2x},则A∩(∁U B)=()A.{1,3}B.{0,2}C.{0,1,3}D.{2}15.已知全集U=R,集合A={x|x(x+2)<0},B={x||x|≤1},那么如图阴影部份表示的集合是()A.(-2,1)B.[-1,0]∪[1,2)C.(-2,-1)∪[0,1]D.[0,1]16.已知集合A={x|4≤2x≤16},B=[a,b],若A⊆B,那么实数a-b的取值范围是.创新应用组17.已知集合A={x|x<a},B={x|1<x<2},且A∪(∁R B)=R,那么实数a的取值范围是()≤1<1≥2>218.假设集合A={x|x2+4x+k=0,x∈R}中只有一个元素,那么实数k的值为.课时标准练1集合的概念与运算由题意,可知A={x|x>1},B={x|-2<x<2},∴A∩B={x|1<x<2},表示为区间即(1,2),应选C.因为A={x|x<-2或x>2},因此∁U A={x|-2≤x≤2}.应选C.,1,2,4},因为A={-1,0,1,2},B={12,1,2,4,A∪B中元素的个数为6.因此A∪B=-1,0,12由(x-2)(x-3)≥0,解得x≥3或x≤2,因此S={x|x≤2或x≥3}.因为T={x|x>0},因此S∩T={x|0<x≤2或x≥3},应选D.由题意,集合A={x|x(x-2)<0}={x|0<x<2},B={x|ln x>0}={x|x>1},因此A∩B={x|1<x<2}.应选C.集合U={1,2,3,4},集合A={x∈N|x2-5x+4<0}={x∈N|1<x<4}={2,3},因此∁U A={1,4},应选B.由题意可得A={x|x≤1},B={x|-2<x<3},∴A∩B={x|-2<x≤1}.应选D.∵全集U=R,A={0,1,2,3},B={y|y=2x,x∈A}={1,2,4,8},∴(∁U A)∩B={4,8},应选C.∵圆x2+y2=1和指数函数y=3x的图象有两个不同的交点,记为A1、A2,则A∩B的子集应为⌀,{A1},{A2},{A1,A2}共四种,应选A.10.{1}A={x|x(x-4)<0}=(0,4),因此A∩B={1}.11.(4,+∞)由log2x≤2,得0<x≤4,即A={x|0<x≤4},而B={x|x<a},由于A⊆B,则a>4.由题意,得P={3,4},因此集合P的子集有22=4(个).由题意,A=[-1,3],B=(-∞,a),∵A⊆B,∴a>3,∴a的取值范围是(3,+∞).∵全集U=Z,A={0,1,2,3},B={x|x2=2x},∴∁U B={x|x∈Z,且x≠0,且x≠2},∴A∩(∁U B)={1,3}.应选A.由题意可知阴影部份对应的集合为(∁U(A∩B))∩(A∪B).∵A={x|-2<x<0},B={x|-1≤x≤1},∴A∩B={x|-1≤x<0},A∪B={x|-2<x≤1},∴∁U(A∩B)={x|x<-1或x≥0},∴(∁U(A∩B))∩(A∪B)={x|0≤x≤1或-2<x<-1}.应选C.16.(-∞,-2]集合A={x|4≤2x≤16}={x|22≤2x≤24}={x|2≤x≤4}=[2,4].因为A⊆B,因此a≤2,b≥4.因此a-b≤2-4=-2.故实数a-b的取值范围是(-∞,-2].∵A∪(∁R B)=R,∴B⊆A,∴a≥2,应选C.由题意知x2+4x+k=0有两个相等的实根,∴Δ=16-4k=0,解得k=4.。

2020年数学新高考一轮复习(理)集合

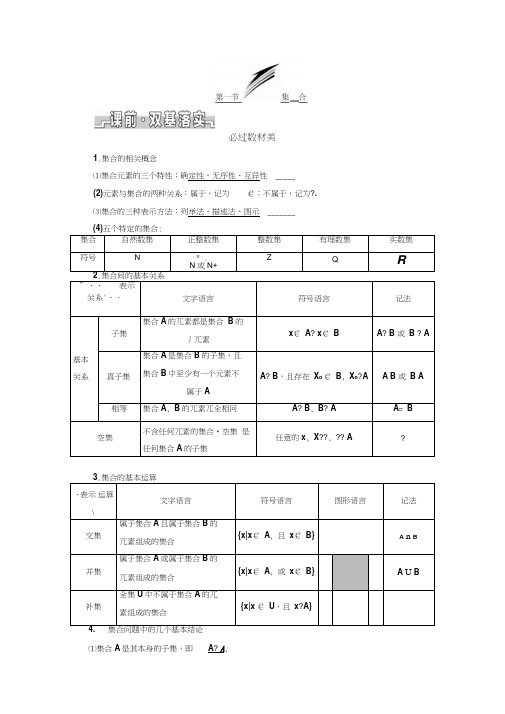
必过数材美1.集合的相关概念⑴集合元素的三个特性：确定性、无序性、互异性 _____(2)元素与集合的两种关系：属于，记为€；不属于，记为?.⑶集合的三种表示方法：列举法、描述法、图示 _______集合自然数集正整数集整数集有理数集实数集符号N* .N或N+Z Q R”、、表示关系'、、文字语言符号语言记法基本关系子集集合A的兀素都是集合B的丿兀素x€ A? x€ B A? B 或B ? A 真子集集合A是集合B的子集，且集合B中至少有一个元素不属于AA? B，且存在X o € B, X o?A A B 或B A 相等集合A, B的兀素兀全相冋A? B, B? A A= B空集不含任何兀素的集合•空集是任何集合A的子集任意的x, X??, ?? A?、表示运算\文字语言符号语言图形语言记法交集属于集合A且属于集合B的兀素组成的集合{x|x€ A, 且x€ B}A n B并集属于集合A或属于集合B的兀素组成的集合{x|x€ A, 或x€ B} A U B补集全集U中不属于集合A的兀素组成的集合{x|x € U，且x?A}(2) 子集关系的传递性，即A? B, B? C? A? C;(3) A U A= A A A= A, A U ? = A, A A ?= ?, ?u U= ?, ? U?= U.(4) A A B= A? A? B, A U B = B? A? B.[小题体验]1. 已知集合A= {1,2} ,B = {x|O v x V 5,x€ N},则满足A? C? B的集合C的个数为()A. 1B. 2C . 3D . 4答案：D2. _________________________________________________________________ 已知集合A = {1,2,3}, B = {2,4,5}，则集合A U B中元素的个数为______________________________.答案：53. (2018 江苏高考)已知集合A= {0,1,2,8} , B= { —1,1,6,8},那么A A B = __________ .解析：A A B= {0,1,2,8} A { —1,1,6,8}= {1,8}.答案：{1,8}必过易措关1.认清集合元素的属性(是点集、数集或其他情形)和化简集合是正确求解集合问题的两个先决条件.2•解题时注意区分两大关系：一是元素与集合的从属关系；二是集合与集合的包含关系.3•易忘空集的特殊性，在写集合的子集时不要忘了空集和它本身.4. 运用数轴图示法易忽视端点是实心还是空心.5. 在解决含参数的集合问题时，要注意检验集合中元素的互异性，否则很可能会因为不满足“互异性”而导致解题错误.[小题纠偏]1. (2019 浙江名校联考)已知？R M = {x|ln|x|> 1} ,N = iy y=f，x>0 仁则M U N =( )A. (0, e]B. [—e,+s )C. ( — m,—e]U (0,+s )D. [ —e, e]解析：选 B 由ln|x|> 1 得|x|>e,「. M = [ —e, e]. N = (0,+ m),「. M U N= [ —e, + m).故选B.2. 若集合A = {x|—2<x w 5}, B= {x|m+ 1 < x< 2m—1}，且B? A,则由m 的可能取值组成的集合为_________ .解析：当m+ 1>2m—1,即m v2 时，B= ?,满足B? A;若?,且满足B? A，如图所示,"m+ 1 < 2m—1, "m> 2,则fm+ 1 > —2, 即f m> —3, 所以2< m< 3.故m v 2或2< m< 3,即所求集合、2m- 1 < 5, [m W 3,为{m|m W 3}.答案：{m|m w 3}3.已知集合A = {0, x+ 1, x2—5x}，若—4 € A,则实数x的值为 ____________解析：T — 4 € A,「. x + 1 = — 4 或x2—5x=— 4./• x=—5或x = 1 或x= 4.若x = 1,贝U A = {0, 2,—4}，满足条件；若x = 4,贝U A = {0, 5,—4}，满足条件；若x =—5,贝U A= {0, —4,50}，满足条件.所以x = 1或x= 4或—5.答案：1或4或—5考点一集合的基本概念基础送分型考点一一自主练透［题组练透］1.下列命题正确的有（）①很小的实数可以构成集合；②（易错题）集合｛y|y= x2—1｝与集合｛（x, y）|y= x2—1｝是同一个集合；③1, 2, 4, — 2 , 0.5这些数组成的集合有5个元素；④集合｛（x, y）|xy w 0, x, y€ R｝是指第二和第四象限内的点集.A. 0个B. 1个C . 2个D . 3个解析：选A 由题意得，①不满足集合的确定性，故错误；②两个集合，一个是数集,1一个是点集，故错误；③中—= 0.5，出现了重复，不满足集合的互异性，故错误；④不仅仅表示的是第二、四象限的点，还可表示原点，故错误.综上，没有正确命题，故选 A.r “2.已知a> 0, b € R,若a, 4, b = ｛a—b,0, a｝,则a + b的值为（）C. 6D. 8B. 4C. 6D. 8解析：选B 由已知得a丰0，则-=0，所以b= 0，于是a2= 4,即a = 2或a=—2,因a为a>0，所以a= 2,故a2+ b2= 22+ 02= 4.3. 若集合A ={x€ R|ax2—3x+ 2 = 0}中只有一个元素，贝V a等于()9 9A_ B _A. 2B.89C. 0D. 0 或8解析：选D 若集合A中只有一个元素，则方程ax2—3x+ 2= 0只有一个实根或有两个相等实根.当a= 0时，x= 3，符合题意.当a丰 0 时，由△= (—3)2 —8a= 0,得a= 9,8所以a的值为0或9.84. _______________________________________ (易错题)(20佃江西重点中学协作体联考)设集合A= {1,2,3} , B= {2,3,4} , M = {x|x =ab, a€ A, b€ B}，贝U M中的元素个数为.解析：结合题意列表计算M中所有可能的值如下：观察可得：M = {2,3,4,6,8,9,12}，据此可知M中的元素个数为7.答案：7［谨记通法］与集合中的元素有关问题的求解策略(1) 确定集合的兀素是什么，即集合是数集还是点集.(2) 看这些元素满足什么限制条件.(3) 根据限制条件列式求参数的值或确定集合中元素的个数，但要注意检验集合是否满足元素的互异性.考点二集合间的基本关系重点保分型考点一一师生共研［典例引领］1.已知集合M = {1,2,3,4}，则集合P = {x|x€ M且2x?M}的子集有（）A. 8个B. 4个C . 3个 D . 2个解析：选B 由题意，得P ={3,4}，所以集合P 的子集有22= 4个.2•已知集合 A = {x|x 2+ x — 2 = 0}, B = {x|ax = 1}，若 B ? A ,贝V a =（）1A • — Q 或 1B . 2 或—1 1C . — 2或1或0D . — Q 或1或0解析：选 D 集合 A = {x|x 2+ x — 2= 0} = {— 2,1}•当 x =— 2 时，一2a = 1，解得 a =— 1亍当x = 1时，a = 1;又因为B 是空集时也符合题意，这时 a = 0,故选D.［由题悟法］集合间基本关系的两种判定方法和一个关键「區三殛蔭g藝赴至殛垂殛关垂］咄廷三丽癒孫丽企菊蒜葫蒔页丨元盍（或圉形}中寻找关聚L __________ ___ ______________________________________________________________________________ _ __ _____________ If 「殛基君电iff耳融施不X采：署融奮矣紊:［即时应用］1•集合{a , b, c , d , e}的真子集的个数为（）A . 32B . 31C . 30D . 29解析：选B 因为集合有5个元素，所以其子集的个数为 25= 32个，其真子集的个数为 2s — 1= 31 个.2.已知集合 A = {x| — 1v x v 3}, B = {x|— m v x v m}，若 B ? A ,贝U m 的取值范围为解析：当m W 0时，B = ?，显然B ? A. 当m >0时， ■/ A = {x|— 1 v x v 3}.当B ? A 时，在数轴上标出两集合，如图，—m > — 1, ••• mW 3,••• 0v mW 1.—m v m.综上所述m 的取值范围为（一8,1］. 答案：（—3 1］两种方一个-1 -m 013考点三集合的基本运算题点多变型考点一一多角探明［锁定考向］集合运算多与解简单的不等式、函数的定义域、值域相联系，考查对集合的理解及不等式的有关知识；有些集合题为抽象集合题或新定义型集合题，考查学生的灵活处理问题的能力.常见的命题角度有： ⑴集合的运算；(2) 利用集合运算求参数； (3) 新定义集合问题.［题点全练］角度一：集合的运算1. (2018 北京高考)已知集合 A = {x||x|v 2}, B = {- 2,0,1,2}，则 A A B =( )B. {- 1,0,1}C. {-2,0,1,2} 解析：选 A•/ A = {x||x|v 2} = {x|- 2v x v 2}, B = {-2,0,1,2},••• A A B = {0,1}.故选 A.2. (2018 全国卷 I )已知集合 A = {x|x 2- x - 2>0}，则？R A =( )C . {x|x v- 1}U {x|x >2}D . {x|x w- 1}U {x|x >2}解析：选 B •/ x 2- x - 2>0,「. (x - 2)(x + 1)>0, /• x > 2 或 x v - 1，即卩 A = {x|x > 2 或 x v - 1}. 则？R A = {x|- 1 w x < 2}.故选 B. 角度二：利用集合运算求参数 3. (2019浙江联盟校联考)已知集合 -1v x v 2}，则实数a 的值为()B . 2解析：选 B 因为 P = {x|- 1 v x v 1}, Q = {x|0v x v a},所以当 a w 1 时，P U Q = {x|- 1v x v 1}，不符合题意；当 a > 1 时，P U Q = {x|- 1 v x v a},结合 P U Q = {x| — 1v x v 2}，可得 a = 2.角度三：新定义集合问题4.如果集合 A , B ，同时满足 A U B = {1,2,3,4}, A A B = {1}, A M {1} , B ^ {1}，就称有序集对(A , B)为“好集对”.这里有序集对 (A , B)是指当A M B 时，(A , B)和(B , A)是不同的集对，那么“好集对”一共有( )个( )A • {0,1}D • {-1,0,1,2A . {x|- 1 v x v 2}B . {x|- 1< x < 2}P = {x|- 1 v x v 1}, Q J= {x|0v x v a},若 P U Q = {x|A. 5个B. 6个C . 7个D . 8个解析：选B 因为A U B= {1,2,3,4} , A n B= {1}, A丰{1} , B^ {1}，所以当A= {1,2}时, B= {1,3,4};当A= {1,3}时，B= {1,2,4};当A= {1,4}时，B= {1,2,3};当A= {1,2,3}时，B = {1,4};当A= {1,2,4}时，B= {1,3};当A = {1,3,4}时，B= {1,2}.所以满足条件的“好集对” 一共有6个，故选B.［通法在握］解集合运算问题4个技巧［演练冲关］1. (2019浙江十校联盟适考)已知集合A= {x|1v x v 4} , B = {x € Z|x2—6x v 0}，则(? R A) n B =( )A. {1,4}B. {4,5}C. {1,4,5}D. {2,3}解析：选C 法一：由x2—6x v 0 可得0v x v 6,所以B= {1,2,3,4,5}，又？R A= {x|x< 1 或x> 4}，所以(?R A)n B = {1,4,5}.法二：因为求的是(?R A)n B,故排除D，又1,5 € ?R A,1 , 5€ B,故选C.2. (2019 长沙模拟)已知集合A= {1,2,3} , B={x|x2—3x + a = 0, a€ A}，若A n B M ?, 则a的值为()A. 1B. 2C . 3D . 1 或2解析：选B 当a= 1时，x2—3x+ 1 = 0,无整数解，贝U A n B= ?;当a= 2时，B = {1,2}, A n B= {1,2}M ?；当a= 3时，B= ?, A n B = ?.因此实数a= 2.3. (2019 杭州高三四校联考)设集合A = {x|(x—3)(x—a)= 0, a€ R}, B= {x|(x—1)(x —4)= 0}，贝U A U B的子集个数最多为()A. 2B. 4D. 16解析：选D 由题意可知，要使A U B 的子集个数最多，则需A U B 中的元素个数最多,C . {x|0< x < 1 或 x > 2}D . {x|0< x < 1 或 x >2}解析：选 D 因为 A = {x|O W x w 2}, B = {y|y > 1}, A U B = {x|x > 0}, A n B = {x|1v x < 2}, 所以 A B = ?A U B (A n B)= {x|0< x w 1 或 x > 2}，故选 D.一抓基础，多练小题做到眼疾手快 1.（2019浙江考前热身联考 )已知集合 M — {x|y = 2x — x 2}, N — {x|— 1 v x v 1}，则 M U N =()A. [0,1)B . (— 1,2)C.(—1,2] D . ( — s, 0] U (1,+s )解析：选C 法一：易知M ― {x|0w x w 2}，又 N — {x| — 1v x v 1}，所以 M U N = (— 1,2] '故选C.法二：取 x = 2,贝 U 2€ M ，所以 2€ M U N ，排除 A 、B ;取 x = 3,贝 U 3? M,3 ?N ，所以 3?M U N ，排除D ，故选C.2.(2019 浙江三地联考)已知集合 P = {x||x |v 2}, Q = {x|— 1 w x w 3},贝U P n Q =()A . [— 1,2)B . (— 2,2)C . (— 2,3]D . [ — 1,3]解析：选 A 由凶 v 2,可得一2v x v 2,所以 P = {x|— 2v x v 2}，所以 P n Q = [— 1,2). 3.(2018嘉兴期末测试)已知集合P = {x|x v 1}, Q= {x|x >0}，则()5.已知集合 A = {x|x 》3} ,B = {x|x > m},且A U B = A,则实数 m 的取值范围是 ___________ . 解析：C . P ?? R Q 解析：选DD . ?R P ? Q由已知可得？R P — [1,+ s ），所以？R P ? Q 故选A . P ? QB . Q? P 此时1, 3,且4，即集合 A = {3,a}, B = {1,4}, A U B = {1,3,4 , a}，故 A U B 的子集最多有24= 16个.4.如图所示的 Venn 图中，A , B 是非空集合，定义集合 A B 为阴影部分表示的集合•若x , y € R, A ={x|y = 2x — x 2}, B ={y|y = 3x ,x > 0}，贝U A B 为（ A . {x|O v x v 2}B . {x|1 v x < 2}...Fr=T A ^Q 12§ 云456*因为集合 A = {x|x > 3}, B = {x|x > m},且A U B = A ,所以B ? A ,如图所示，所以m > 3. 答案：［3,+R )二保咼考，全练题型做到咼考达标1.(2019 杭州七校联考)已知集合 A = {x|x 2> 1} , B = {x|(x 2— 1)(x 2-4)= 0}，则集合 A A B 中的元素个数为()A . 1B . 2C . 3D . 4解析：选 B A = {x|x v — 1 或 x > 1}, B = {— 2, — 1,1,2} , A A B = {— 2,2}，故选 B. 2. (2019 浙江六校联考)已知集合 U = {x|y = 3 x}, A = {x|y = Iog 9x}, B = {y|y =— 2x }则 A A (?u B)=()A . ?B . RC . {x|x > 0}D . {0}解析：选C由题意得，U = R, A = {x|x > 0}，因为y =— 2x < 0,所以B = {y|y v 0}，所以?U B = {x|x > 0}，故 A A (?U B) = {x|x > 0}.故选 C.3. (2019 永康模拟)设集合 M = {x|x 2— 2x — 3 >0}, N = {x|— 3< x < 3}，则( )A . M ? NB . N ? MC . M U N = RD . M A N = ?解析：选 C 由 x 2— 2x — 3 > 0,解得 x > 3 或 x < — 1,所以 M = {x|x < — 1 或 x > 3}, 所以M U N = R .4. (2019宁波六校联考)已知集合A = {x|x 2— 3x <0}, B = {1, a},且A A B 有4个子集, 则实数a 的取值范围是()B . (0,1) U (1,3) D . ( — s, 1) U (3,+^ )解析：选B •/ A A B 有4个子集，••• A A B 中有2个不同的元素，二a € A ,A a 2— 3a< 0,解得0< a < 3且a M 1，即实数a 的取值范围是（0,1） U （1,3），故选B.A . (0,3) C . (0,1) 5.（2018镇海中学期中）若集合M = x y = lg ,N = {x|x < 1}，贝U M U N =()(0,1) B . (0,2) ( — s, 2)D . (0 ,+s )解析：选C 集合M = x y = lg ：={x|0< x < 2}, N = {x|x < 1}. M U N = {x|x < 2}=(— a, 2).故选 C.6•设集合 A = {x|x 2— x — 2W 0}, B = {x|x v 1,且 x € Z }，则 A H B = _______ .解析：依题意得 A = {x|(x + 1)(x — 2)W 0} = {x|— 1 W x < 2}，因此 AH B = {x|— 1< x v 1, x € Z}= { — 1,0}.答案：{ — 1,0}7.(2018 嘉兴二模)已知集合 A = {x|— 1W x W 2},B = {x|x 2— 4x W 0}，则 A U B= ________ A H (?R B) = ______ .解析：因为 B = {x|x 2— 4x W 0} = {x|0W x W 4},所以 A U B = {x|— 1 W x W 4};因为？R B = {x|xv 0 或 x > 4}，所以 A H (?R B) = {x|— 1W x v 0}.答案：{x|— 1 W x W 4} {x|— 1 W x v 0}8•设集合 A = {(x , y)|y >|x — 2|, x > 0}, B = {(x , y)|y W — x + b}, A H B 丰 (1)b 的取值范围是 _________ ;⑵若(x , y) € A H B ,且x + 2y 的最大值为9，贝U b 的值是 _________ 解析：由图可知，当y =— x 往右移动到阴影区域时，才满足条件，所以b > 2;要使z = x + 2y 取得最大值，则过点(0, b),有0 + 2b = 9? _9 =2.9答案：(1)[2 ,+a ) (2号9•已知集合 A = {x|4W 2x W 16}, B = [a , b ]，若 A ? B ,则实数解析：集合 A = {x|4W 2" W 16} = {x|22W 2x W 24}= {x|2W x W 4} =[2,4]，因为 A ? B ,所以 a W 2, b > 4，所以a — b W 2 — 4 =— 2,即实数 a — b 的取值范围是(一^，― 2].答案：( — a, — 2]r [1 一 x10.已知集合 A = {x|(x + 2m)(x — m + 4)v 0}，其中 m € R ,集合 B = c x ~~r> > 0： X 十2 (1)若B ? A ,求实数m 的取值范围；(2)若A H B = ?，求实数m 的取值范围.当A M ?时,4①当一2m v m — 4,即卩 m >3时，A = {x|— 2m v x v m — 4},4a —b 的取值范围是解：(1)集合ix 巳 > 0 x + 2={x|— 2 v x v 1}.当A =?时, m = 4,不符合题意.又因为B ? A ,( 5 ( 4m > 3,m > 3, 所以< 2m < 2即t “所以m > 5.| - 2m < - 2, 1m > 1, | | m — 4> 1,m > 5,4②当一2m > m — 4,即卩 m v 4时，A = {x|m — 4v x v — 2m},3又因为B ? A ,5①当一2m v m — 4,1 卩 m >3时，A = {x|— 2m v x v m — 4},3 又因为 A A B = ?，所以一2m 》1或者 m —4 W — 2, 1 4即m W — 一或者m W 2,所以4v m W 2.2 3②当一2m > m — 4,1 卩 m v 3时，A = {x|m — 4v x v — 2m}, 又因为 A A B = ?，所以 m — 4》1或者一2m W — 2,4即m > 5或者m > 1,所以1 W m v 4.3综上所述，实数 m 的取值范围为[1,2]. 三上台阶，自主选做志在冲刺名校所以4 m V 3, —2m > 1,m — 4< — 2,即 m - 2, m W 2,1所以m W —-.综上所述，实数 m 的取值范围为一R,— 2 u [5,+^). (2)由(1)知，B = {x|— 2 v x v 1}. 当A = ?时，m = 3,符合题意.4当A M ?时，m ^孑3a = 1,B .— 1 D . i解析：选B •/ S = {a , b , c , d}，由集合中元素的互异性可知当a = 1时，b =— 1,c 21•对于复数 a , b , c , d ,若集合 S = {a , b , c , d}具有性质“对任意 x , y € S,必有xy € S ”，则当b 2= 1,L 2= b时，b + c + d 等于(=—1 ,「• c = ±，由"对任意 x , y € S ,必有 xy € S ” 知 ± € S ,「. c = i , d =— i 或 c =— i , d =i ,••• b + c + d = (— 1) + 0=— 1.2.对于集合 M , N ，定义 M — N = {x|x € M ，且 x ?N}, M ® N = (M — N)U (N — M),设___ 13.已知函数f(x)=J x —3 — i --- 的定义域为集合 A ,且B = {x €Z |2V xV 10} , C = -- {x\J 7 — x € R |x v a 或 x > a +1}.(1) 求：A 和(?R A)Q B ;(2) 若A U C = R,求实数a 的取值范围. 解：⑴要使函数f(x)= x — 3—1_-,7 — x应满足x — 3 > 0,且7— x > 0,解得3< x V 7 , 则 A = {x|3< x v 7},得到？R A = {x|x v 3 或 x > 7},而 B = {x € Z |2V x v 10} = {3,4,5,6,7,8,9}, 所以(?R A)A B = {7,8,9}.(2)C = {x € R |x v a 或 x > a + 1},要使 A U C = R , 则有 a > 3,且 a + 1v 7,解得 3< a v 6. 故实数a 的取值范围为[3,6).4. (2018浙江吴越联盟第二次联考 )已知集合 M = {0,1,2,3,4} , N = {2,4,6} , P = M n N ,则P 的子集有 _________ 个.解析：集合 M = {0,1,2,3,4} , N = {2,4,6} , P = M n N = {2,4}，则 P 的子集有?, {2} , {4}, {2,4}，共 4 个.答案：4A = x x >— 4, x € R4,B = {x|x v 0, x € R }，贝V A ® B =(C.一oo, B.—9 U [0,+o ) D.一oo,9 U(o ,解析：选C 依题意得 A — B = {x|x >0 , x € R }, 9B — A = x x V — ； , x € R F ,故 A ® B4 A.4, 09,0[0 , + o ).故选 C.。

2020版高考数学人教版理科一轮复习课时作业：1 集合 Word版含解析

课时作业1集合一、选择题1．(2021·全国卷Ⅲ)集合A＝{x|x－1≥0} ,B＝{0,1,2} ,那么A∩B ＝(C)A．{0} B．{1}C．{1,2} D．{0,1,2}解析：由题意知,A＝{x|x≥1} ,那么A∩B＝{1,2}．2．设集合M＝{x|x2＝x} ,N＝{x|lg x≤0} ,那么M∪N＝(A) A．[0,1] B．(0,1]C．[0,1) D．(－∞ ,1]解析：M＝{x|x2＝x}＝{0,1} ,N＝{x|lg x≤0}＝{x|0<x≤1} ,M∪N＝[0,1]．3．全集U＝{x∈Z|0<x<8} ,集合M＝{2,3,5} ,N＝{x|x2－8x＋12＝0} ,那么集合{1,4,7}为(C)A．M∩(∁U N) B．∁U(M∩N)C．∁U(M∪N) D．(∁U M)∩N解析：由得U＝{1,2,3,4,5,6,7} ,N＝{2,6} ,M∩(∁U N)＝{2,3,5}∩{1,3,4,5,7}＝{3,5} ,M∩N＝{2} ,∁U(M∩N)＝{1,3,4,5,6,7} ,M ∪N＝{2,3,5,6} ,∁U(M∪N)＝{1,4,7} ,(∁U M)∩N＝{1,4,6,7}∩{2,6}＝{6} ,应选C.4．(2021·唐山统一考试)假设全集U＝R,集合A＝{x|x2－5x－6<0} ,B＝{x|2x<1} ,那么图中阴影局部表示的集合是(C)A ．{x |2<x <3}B ．{x |－1<x ≤0}C ．{x |0≤x <6}D ．{x |x <－1}解析：由x 2－5x －6<0 ,解得－1<x <6 ,所以A ＝{x |－1<x <6}．由2x <1 ,解得x <0 ,所以B ＝{x |x <0}．又题图中阴影局部表示的集合为(∁U B )∩A ,∁U B ＝{x |x ≥0} ,所以(∁U B )∩A ＝{x |0≤x <6} ,应选C.5．(2021·莱州一中模拟)集合A ＝{x ∈N |x 2＋2x －3≤0} ,B ＝{C |C ⊆A } ,那么集合B 中元素的个数为( C )A ．2B ．3C ．4D ．5解析：A ＝{x ∈N |(x ＋3)(x －1)≤0}＝{x ∈N |－3≤x ≤1}＝{0,1} ,共有22＝4个子集 ,因此集合B 中元素的个数为4 ,应选C.6．设集合A ＝⎩⎨⎧⎭⎬⎫(x y )|x 24＋y 216＝1 ,B ＝{(x ,y )|y ＝3x } ,那么A ∩B 的子集的个数是( A )A ．4B ．3C ．2D ．1解析：∵A 对应椭圆x 24＋y 216＝1上的点集 ,B 对应指数函数y ＝3x上的点集 ,画出椭圆和指数函数的图象(图略)可知 ,两个图象有两个不同交点 ,故A ∩B 有2个元素 ,其子集个数为22＝4.应选A.7．(2021·长沙模拟)集合A ＝{1,2,3} ,B ＝{x |x 2－3x ＋a ＝0 ,a ∈A } ,假设A ∩B ≠∅ ,那么a 的值为( B )A ．1B ．2C ．3D ．1或2解析：当a ＝1时 ,x 2－3x ＋1＝0 ,无整数解 ,那么A ∩B ＝∅. 当a ＝2时 ,B ＝{1,2} ,A ∩B ＝{1,2}≠∅. 当a ＝3时 ,B ＝∅ ,A ∩B ＝∅.因此实数a ＝2.8．设全集U ＝R ,函数f (x )＝lg(|x ＋1|－1)的定义域为A ,集合B ＝{x |cosπx ＝1} ,那么(∁U A )∩B 的元素个数为( B )A ．1B ．2C ．3D ．4解析：由|x ＋1|－1>0 ,得|x ＋1|>1 ,即x <－2或x >0 ,∴A ＝{x |x <－2或x >0} ,那么∁U A ＝{x |－2≤x ≤0}；由cosπx ＝1 ,得πx ＝2k π ,k ∈Z ,∴x ＝2k ,k ∈Z ,那么B ＝{x |x ＝2k ,k ∈Z }．∴(∁U A )∩B ＝{x |－2≤x ≤0}∩{x |x ＝2k ,k ∈Z }＝{－2,0} ,∴(∁U A )∩B 的元素个数为2.二、填空题9．设全集为R ,集合A ＝{x |x 2－9<0} ,B ＝{x |－1<x ≤5} ,那么A ∩(∁R B )＝{x |－3<x ≤－1}．解析：由题意知 ,A ＝{x |x 2－9<0}＝{x |－3<x <3} ,∵B ＝{x |－1<x ≤5} ,∴∁R B ＝{x |x ≤－1或x >5}．∴A ∩(∁R B )＝{x |－3<x <3}∩{x |x ≤－1或x >5}＝{x |－3<x ≤－1}． 10．设A ,B 是非空集合 ,定义A *B ＝{x |x ∈A ∪B ,且x ∉A ∩B } ,M ＝{y |y ＝－x 2＋2x,0<x <2} ,N ＝{y |y ＝2x －1,x >0} ,那么M *N ＝⎝ ⎛⎦⎥⎤0 12∪(1 ,＋∞)．解析：M ＝{y |y ＝－x 2＋2x,0<x <2}＝(0,1] ,N ＝{y |y ＝2x －1 ,x >0}＝12 ,＋∞ ,M ∪N ＝(0 ,＋∞) ,M ∩N ＝⎝ ⎛⎦⎥⎤12 1 ,所以M *N ＝⎝ ⎛⎦⎥⎤0 12∪(1 ,＋∞)． 11．集合U ＝R ,集合M ＝{x |x ＋2a ≥0} ,N ＝{x |log 2(x －1)<1} ,假设集合M ∩(∁U N )＝{x |x ＝1或x ≥3} ,那么a 的取值为－12.解析：由log 2(x －1)<1 ,得1<x <3 ,那么N ＝(1,3) , ∴∁U N ＝{x |x ≤1或x ≥3}．又M ＝{x |x ＋2a ≥0}＝[－2a ,＋∞) ,M ∩(∁U N )＝{x |x ＝1或x ≥3} ,∴－2a ＝1 ,解得a ＝－12.12．某网店统计了连续三天售出商品的种类情况：第|一天售出19种商品 ,第二天售出13种商品 ,第三天售出18种商品；前两天都售出的商品有3种 ,后两天都售出的商品有4种 ,那么该网店(1)第|一天售出但第二天未售出的商品有16种； (2)这三天售出的商品最|少有29种．解析：(1)如图1所示 ,第|一天售出但第二天未售出的商品有19－3＝16(种)；(2)如图2所示 ,这三天售出的商品最|少有19＋13－3＝29(种)．13．(2021·山东济南外国语学校段考)集合A ＝{x |y ＝x －1} ,A ∩B ＝∅ ,那么集合B 不可能是( D )A ．{x |4x <2x ＋1}B ．{(x ,y )|y ＝x －1}C.⎩⎨⎧⎭⎬⎫y|y ＝sin x －π3≤x ≤π6 D ．{y |y ＝log 2(－x 2＋2x ＋1)} 解析：集合A ＝{x |y ＝x －1}＝{x |x ≥1} ,对于选项A ,{x |4x <2x ＋1}＝{x |x <1} ,满足A ∩B ＝∅；对于选项B ,集合为点集 ,满足A ∩B ＝∅；对于选项C ,{|yy ＝sin x ,－π3≤x ≤π6}＝⎩⎨⎧⎭⎬⎫y|－32≤y ≤12 ,满足A ∩B ＝∅；对于选项D ,{y |y ＝log 2(－x 2＋2x ＋1)}＝{y |y ＝log 2[－(x －1)2＋2]}＝{y |y ≤1} ,A ∩B ＝{1}≠∅ ,应选D.14．集合A ＝{y |y ＝x 12,0≤x ≤1} ,B ＝{y |y ＝kx ＋1 ,x ∈A } ,假设A ⊆B ,那么实数k 的取值范围是( D )A ．k ＝－1B ．k <－1C ．－1≤k ≤1D ．k ≤－1解析：∵A ＝{y |y ＝x 12,0≤x ≤1}＝{y |0≤y ≤1} ,∴B ＝{y |y ＝kx ＋1 ,x ∈A }＝{y |y ＝kx ＋1,0≤x ≤1} ,又∵A ⊆B ,∴⎩⎨⎧k ×0＋1≤0k ×1＋1≥1或⎩⎪⎨⎪⎧k ×0＋1≥1 k ×1＋1≤0解得k ≤－1.∴实数k 的取值范围为k ≤－1.尖子生小题库 - -供重点班学生使用普通班学生慎用15．(2021·贵阳市摸底考试)点集Ω＝{(x ,y )|0≤x ≤e,0≤y ≤e} ,A ＝{(x ,y )|y ≥e x ,(x ,y )∈Ω} ,在点集Ω中任取一个元素a ,那么a ∈A 的概率为( B )A.1eB.1e 2C.e －1eD.e 2－1e 2解析：如图 ,根据题意可知Ω表示的平面区域为正方形BCDO ,面积为e 2 ,A 表示的区域为图中阴影局部 ,面积为⎠⎛01(e －e x )d x ＝(e x －e x )|10＝(e －e)－(－1)＝1,根据几何概型可知a ∈A 的概率P ＝1e 2.应选B.16．假设数集A ＝{a 1 ,a 2 ,… ,a n }(1≤a 1<a 2<…<a n ,n ≥2)具有性质P ：对任意的i ,j (1≤i ≤j ≤n ) ,a i a j 与a ja i 两数中至|少有一个属于A ,那么称集合A 为 "权集〞．那么( B )A ．{1,3,4}为 "权集〞B ．{1,2,3,6}为 "权集〞C ． "权集〞中元素可以有0D ． "权集〞中一定有元素1 解析：对于A ,由于3×4与43均不属于数集{1,3,4} ,故A 不正确；对于B ,选1,2时 ,有1×2属于{1,2,3,6} ,同理取1,3 ,取1,6 ,取2,3时也满足 ,取2,6时 ,有62属于{1,2,3,6} ,取3,6时 ,有63属于{1,2,3,6} ,所以B 正确；由 "权集〞定义知1≤a 1<a 2<…<a n 且a ja i 需要有意义 ,故不能有0 ,故C 不正确；如集合{2,4} ,符合 "权集〞定义 ,但不含1 ,所以D 不正确．。

2020高考数学一轮复习课时规范练1集合的概念与运算理新人教B版

【2019最新】精选高考数学一轮复习课时规范练1集合的概念与运算理新人教B版基础巩固组1.(2017北京,理1)若集合A={x|-2<x<1},B={x|x<-1或x>3},则A∩B=()A.{x|-2<x<-1}B.{x|-2<x<3}C.{x|-1<x<1}D.{x|1<x<3}2.已知集合A={x|(x-1)(x-2)(x-3)=0},集合B={x|y=},则集合A∩B的真子集的个数是( )A.1B.2C.3D.43.(2017山东青岛模拟,理1)已知全集I=R,集合A={y|y=log2x,x>2},B={x|y=},则( )A.A⊆BB.A∪B=AC.A∩B=⌀D.A∩(∁IB)≠⌀4.(2017山东潍坊一模,理1)已知集合A={x|x=2n,n∈N+},B={x|≤2},则A∩B=()A.{2}B.{2,4}C.{2,3,4}D.{1,2,3,4}5.若集合S={x|(x-2)(x-3)≥0},T={x|x>0},则S∩T=()A.[2,3]B.(-∞,2]∪[3,+∞)C.[3,+∞)D.(0,2]∪[3,+∞)6.(2017安徽安庆二模,理1)已知集合U={1,2,3,4},集合A={x∈N|x2-5x+4<0},则∁UA 等于( )A.{1,2}B.{1,4}C.{2,4}D.{1,3,4}7.(2017山西太原三模,理2)已知全集U=R,集合A={x|x(x+2)<0},B={x||x|≤1},则如图阴影部分表示的集合是( )A.(-2,1)B.[-1,0]∪[1,2)C.(-2,-1)∪[0,1]D.[0,1] 〚导学号21500501〛8.(2017山西太原二模,理2)已知全集U=R,A={0,1,2,3},B={y|y=2x,x∈A},则(∁UA)∩B=()A.(-∞,0)∪(3,+∞)B.{x|x>3,x∈N}C.{4,8}D.[4,8] 〚导学号21500502〛9.已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x-y∈A},则B中所含元素的个数为.10.(2017江苏,1)已知集合A={1,2},B={a,a2+3}.若A∩B={1},则实数a的值为.11.已知集合A={x|0<log4x<1},B={x|x≤2},则A∩B=.12.已知集合M={1,2,3,4},则集合P={x|x∈M,且2x∉M}的子集的个数为.综合提升组13.(2017全国Ⅲ,理1)已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中元素的个数为( )A.3B.2C.1D.014.(2017山东潍坊二模,理1)若集合M={x|x2-x<0},N={y|y=ax(a>0,a≠1)},R表示实数集,则下列选项错误的是( )A.M∩(∁RN)=⌀B.M∪N=RC.(∁RM)∪N=RD.M∩N=M15.已知全集U=R,集合A={x|0≤x≤2},B={y|1≤y≤3},则(∁UA)∪B=()A.(2,3]B.(-∞,1]∪(2,+∞)C.[1,2)D.(-∞,0)∪[1,+∞)16.已知集合A={x|4≤2x≤16},B=[a,b],若A⊆B,则实数a-b的取值范围是.创新应用组17.(2017浙江名校联考)已知集合A={x|x<a},B={x|1<x<2},且A∪(∁RB)=R,则实数a 的取值范围是( )A.a≤1B.a<1C.a≥2D.a>2 〚导学号21500503〛18.(2017河南平顶山模拟改编)已知集合A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0},若(∁RB)∩A=⌀,则a= .参考答案课时规范练1 集合的概念与运算1.A A∩B={x|-2<x<-1},故选A.2.C 化简集合得A={1,2,3},集合B={x|x≥2},所以A∩B={2,3},则A∩B的真子集有⌀,{2},{3}.故选C.3.A 因为当x>2时,y=log2x>1,所以A=(1,+∞).又因为B=[1,+∞),所以A⊆B,A∪B=B,A∩B=A,A∩(∁IB)=⌀,故选A.4.B ∵A={x|x=2n,n∈N+}={2,4,6,…},B={x|≤2}={x|0≤x≤4},∴A∩B={2,4},故选B.5.D 由(x-2)(x-3)≥0,解得x≥3或x≤2,所以S={x|x≤2或x≥3}.因为T={x|x>0},所以S∩T={x|0<x≤2或x≥3},故选D.6.B ∵集合U={1,2,3,4},集合A={x∈N|x2-5x+4<0}={x∈N|1<x<4}={2,3},∴∁UA={1,4},故选B.7.C 由题意可知阴影部分对应的集合为(∁U(A∩B))∩(A∪B).∵A={x|-2<x<0},B={x|-1≤x≤1},∴A∩B={x|-1≤x<0},A∪B={x|-2<x≤1},即∁U(A∩B)={x|x<-1或x≥0},∴(∁U(A∩B))∩(A∪B)={x|0≤x≤1或-2<x<-1},故选C.8.C ∵全集U=R,A={0,1,2,3},B={y|y=2x,x∈A}={1,2,4,8},∴(∁UA)∩B={4,8},故选C.9.10 由x∈A,y∈A,x-y∈A,得(x,y)可取值如下:(2,1),(3,1),(4,1),(5,1),(3,2),(4,2),(5,2),(4,3),(5,3),(5,4),故集合B中所含元素的个数为10.10.1 由已知得1∈B,2∉B,显然a2+3≥3,所以a=1,此时a2+3=4,满足题意,故答案为1.11.(1,2] ∵0<log4x<1,∴log41<log4x<log44,即1<x<4,∴A={x|1<x<4}.∵B={x|x≤2},∴A∩B={x|1<x≤2}.12.4 由题意,得P={3,4},所以集合P的子集有22=4(个).13.B A表示圆x2+y2=1上所有点的集合,B表示直线y=x上所有点的集合,易知圆x2+y2=1与直线y=x相交于两点,故A∩B中有2个元素.14.B ∵集合M={x|x2-x<0}={x|0<x<1},N={y|y=ax(a>0,a≠1)}={y|y>0},∴M∩(∁RN)={x|0<x<1}∩{y|y≤0}=⌀,故A正确;M∪N=(0,+∞),故B错误;(∁RM)∪N={x|x≤0或x≥1}∪{y|y>0}=R,故C正确;M∩N={x|0<x<1}∩{y|y>0}={x|0<x<1}=M,故D正确.故选B.15.D 因为∁UA={x|x>2或x<0},B={y|1≤y≤3},所以(∁UA)∪B=(-∞,0)∪[1,+∞).16.(-∞,-2] 集合A={x|4≤2x≤16}={x|22≤2x≤24}={x|2≤x≤4}=[2,4].因为A⊆B,所以a≤2,b≥4.所以a-b≤2-4=-2.故实数a-b的取值范围是(-∞,-2].17.C ∵A∪(∁RB)=R,∴B⊆A,∴a≥2,故选C.18.1 ∵(∁RB)∩A=⌀,∴A⊆B.又A={0,-4},且B中最多有2个元素,∴B=A={0,-4},∴∴a=1.。

2020版高考数学一轮复习课时规范练1集合的概念与运算理北师大版 (7)

课时规范练7 函数的奇偶性与周期性基础巩固组1.函数f(x)= -x的图像关于()A.y轴对称B.直线y=-x对称C.坐标原点对称D.直线y=x对称2.(2018河北衡水中学月考,6)下列函数中,与函数y=-2x的定义域、单调性与奇偶性均一致的函数是()A.y=sin xB.y=x2C.y=D.y=3.已知偶函数f(x)在区间[0,+∞)内递增,则满足f(2x-1)<f的x的取值范围是()A. B.C. D.4.(2018湖南长郡中学三模,6)已知f(x)为奇函数,函数f(x)与g(x)的图像关于直线y=x+1对称,若g(1)=4,则f(-3)=()A.-2B.2C.-1D.45.已知函数f(x)是定义在R上的奇函数,且满足f(x+2)=f(x).若当x∈[0,1)时,f(x)=2x-,则f(lo)的值为()A.0B.1C.D.-6.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0)(x1≠x2),都有<0,则下列结论正确的是()A.f(0.32)<f(20.3)<f(log25)B.f(log25) <f(20.3)<f(0.32)C.f(log25)<f(0.32)<f(20.3)D.f(0.32)<f(log25)<f(20.3)7.已知函数f(x)为奇函数,当x>0时,f(x)=x2-x,则当x<0时,函数f(x)的最大值为()A.-B.C. D.-8.已知定义域为R的函数f(x)在(8,+∞)内为减函数,且函数y=f(x+8)为偶函数,则()A.f(6) >f(7)B.f(6)>f(9)C.f(7)>f(9)D.f(7)>f(10)9.已知f(x)是定义在R上的偶函数,且f(x+4)=f(x-2).若当x∈[-3,0]时,f(x)=6-x,则f(919)=.10.已知f(x)是奇函数,g(x)=,若g(2)=3,则g(-2)=.11.已知定义在R上的函数f(x),对任意实数x有f(x+4)=-f(x)+2,若函数f(x-1)的图像关于直线x=1对称,f(-1)=2,则f(2 017)=.综合提升组12.(2018湖南长郡中学四模,9)下列函数既是奇函数又在(-1,1)上是减函数的是()A.y=tan xB.y=x-1C.y=lnD.y= (3x-3-x)13.已知偶函数f(x)满足f(x)=x3-8(x≥0),则{x|f(x-2)>0}=()A.{x|x<-2或x>4}B.{x|x<0或x>4}C.{x|x<0或x>6}D.{x|x<-2或x>2}14.已知奇函数f(x)的定义域为R,若f(x+1)为偶函数,且f(1)=2,则f(4)+f(5)的值为()A.2B.1C.-1D.-215.已知定义在R上的奇函数f(x)满足:f(x+1)=f(x-1),且当-1<x<0时,f(x)=2x-1,则f(log220)等于()A.B.-C.-D.创新应用组16.(2018安徽宿州三模,8)已知函数y=f(x)为R上的偶函数,且满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=1-x2.下列四个命题:p1:f(1)=0;p2:2是函数y=f的一个周期;p3:函数y=f(x-1)在(1,2)上递增;p4:函数y=f(2x-1)的递增区间为,k∈Z.其中真命题为()A.p1,p2B.p2,p3C.p1,p4D.p2,p417.(2018河南六市联考一,12)已知定义在R上的奇函数f(x)满足:f(x+2e)=-f(x)(其中e=2.718),且在区间[e,2e]上是减函数,令a=,b=,c=,则f(a),f(b),f(c)的大小关系为()A.f(b)>f(a)>f(c)B.f(b)>f(c)>f(a)C.f(a)>f(b)>f(c)D.f(a)>f(c)>f(b)参考答案课时规范练7 函数的奇偶性与周期性1.C∵f(-x)=- +x=-=-f (x),且定义域为(-∞,0)∪(0,+∞),∴f(x)为奇函数.∴f(x)的图像关于坐标原点对称.2.D函数y=-2x的定义域为R,但在R上递减.函数y=sin x和y=x2的定义域都为R,且在R上不单调,故不合题意;函数y=的定义域为(-∞,0)∪(0,+∞),不合题意;函数y=的定义域为R,且在R上递减,且奇偶性一致,故符合题意.故选D.3.A由于函数f(x)在区间[0,+∞)内递增,且f(x)为偶函数,则由f(2x-1)<f,得-<2x-1<,解得<x<.故x的取值范围是.4.A由题意设P(1,4)关于y=x+1的对称点为P'(a,b),则解得则P'(3,2)在函数y=f(x)的图像上,故f(3)=2,则f(-3)=-2.故选A.5.A因为函数f(x)是定义在R上的奇函数,所以f(lo4)=f(-log2)=f=-f.又因为f(x+2)=f(x),所以f=f=-=0.所以f(lo4)=0.6.A∵对任意x1,x2∈(-∞,0),且x1≠x2,都有<0,∴f(x)在(-∞,0)内是减少的,又f(x)是R上的偶函数,∴f(x)在(0,+∞)内是增函数.∵0<0.32<20.3<log25,∴f(0.32)<f(20.3)<f(log25).故选A.7.B法一设x<0,则-x>0,所以f(-x)=x2+x,又函数f(x)为奇函数,所以f(x)=-f(-x)=-x2-x=-+,所以当x<0时,函数f(x)的最大值为.故选B.法二当x>0时,f(x)=x2-x=-,最小值为-,因为函数f(x)为奇函数,所以当x<0时,函数f(x)的最大值为.故选B.8.D由y=f(x+8)为偶函数,知函数f(x)的图像关于直线x=8对称.又因为f(x)在(8,+∞)内是减少的,所以f(x)在(-∞,8)内是增加的.可画出f(x)的草图(图略),知f(7)>f(10).9.6由f(x+4)=f(x-2)知,f(x)为周期函数,且周期T=6.因为f(x)为偶函数,所以f(919)=f(153×6+1)=f(1)=f(-1)=61=6.10.-1∵g(2)==3,∴f(2)=1.又f(-x)=-f(x),∴f(-2)=-1,∴g(-2)===-1.11.2由函数y=f(x-1)的图像关于直线x=1对称可知,函数f(x)的图像关于y轴对称,故f(x)为偶函数.由f(x+4)=-f(x)+2,得f(x+4+4)=-f(x+4)+2=f(x),∴f(x)是周期T=8的偶函数,∴f(2017)=f(1+252×8)=f(1)=f(-1)=2.12.C y=tan x是奇函数,在(-1,1)上是增加的;y=x-1是奇函数,在(-1,0)上是减少的,在(0,1)上是减少的,y=ln=ln是奇函数且在(-1,1)上是减少的;y= (3x-3-x)是奇函数,在(-1,1)上是增加的;故选C.13.B∵f(x)是偶函数,∴f(x-2)>0等价于f(|x-2|)>0=f(2).∵f(x)=x3-8在[0,+∞)内是增加的,∴|x-2|>2,解得x<0或x>4.14.A∵f(x+1)为偶函数,f(x)是奇函数,∴f(-x+1)=f(x+1),f(x)=-f(-x),f(0)=0,∴f(x+1)=f(-x+1)=-f(x-1),∴f(x+2)=-f(x),f(x+4)=f(x+2+2)=-f(x+2)=f(x),则f(4)=f(0)=0,f(5)=f(1)=2,∴f(4)+f(5)=0+2=2.故选A.15.D由f(x+1)=f(x-1),得f(x+2)=f[(x+1)+1]=f(x),∴f(x)是周期为2的周期函数.∵log232>log220>log216,∴4<log220<5,∴f(log220)=f(log220-4)=f=-f.∵当x∈(-1,0)时,f(x)=2x-1,∴f=-,故f(log220)=.16.C∵f(x+2)=-f(x),当x=-1时,f(1)=-f(-1)=-f(1),∴f(1)=0,故p1正确;∵f(x+2)=-f(x),∴f(x+4)=-f(x+2)=f(x),∴y=f(x)的周期为4,y=f的周期为=8,故p2错;∵当x∈[0,1]时,f(x)=1-x2,∴f(x)在区间[0,1]上递减,∴函数y=f(x-1)在(1,2)上递减,故p3错;∵当x∈[0,1]时,f(x)=1-x2,当x∈[-2,-1]时,x+2∈[0,1],∴f(x)=-f(x+2)=-[1-(x+2)2]=(x+2)2-1,∴f(x)在[-2,-1]递增,从而f(x)在[-2,0]递增,在[0,2]上递减,又f(x)是周期为4的函数,∴f(x)的增区间为[4k-2,4k],即4k-2≤2x-1≤4k,∴2k-≤x≤2k+,∴y=f(2x-1)的递增区间为,k∈Z,故p4正确,故选C.17.A∵f(x)是R上的奇函数,满足f(x+2e)=-f(x),∴f(x+2e)=f(-x),∴f(x)的图像关于直线x=e对称,∵f(x)在区间[e,2e]上是减少的,∴f(x)在区间[0,e]上是增加的,令y=,则y'=,∴y=在(0,e]上递增,在(e,+∞)递减.∴b=>=c>0,a-b=-==<0,a-c=-==>0,∴a>c.∴0<c<a<b<e,∴f(b)>f(a)>f(c).。

2020版高考数学一轮复习课时规范练1集合的概念与运算理北师大版 (62)

课时规范练62 离散型随机变量的均值与方差基础巩固组1.(2018辽宁辽南模拟,6)某地区一模考试数学成绩X服从正态分布N(90,σ2),且P(X<70)=0.2.从该地区参加一模考试的学生中随机抽取10名学生的数学成绩,数学成绩在[70,110]的人数记作随机变量ξ.则ξ的方差为()A.2B.2.1C.2.4D.32.已知随机变量X+η=8,若X~B(10,0.6),则Eη,Dη分别是()A.6和2.4B.2和2.4C.2和5.6D.6和5.63.(2018浙江杭州模拟,6)已知0<a<,随机变量ξ的分布列如下:当a增大时()A.Eξ增大,D(ξ)增大B.Eξ减小,D(ξ)增大C.Eξ增大,D(ξ)减小D.Eξ减小,D(ξ)减小4.(2018浙江绍兴模拟,7)若随机变量ξ满足E(1-ξ)=4,D(1-ξ)=4,则下列说法正确的是()A.Eξ=-4,Dξ=4B.Eξ=-3,Dξ=3C.Eξ=-4,Dξ=-4D.Eξ=-3,Dξ=45.已知随机变量ξ的分布列为若Eξ=,则Dξ等于()A. B. C. D.6.(2018重庆三诊,6)记5个互不相等的正实数的平均值为,方差为A,去掉其中某个数后,记余下4个数的平均值为,方差为B,则下列说法中一定正确的是()A.若,则A<BB.若,则A>BC.若,则A<BD.若,则A>B7.(2018浙江教育绿色评价联盟,12)若随机变量ξ的分布列为:若Eξ=,则x+y=,Dξ=.8.(2018广东肇庆模拟,7)已知5台机器中有2台存在故障,现需要通过逐台检测直至区分出2台故障机器为止.若检测一台机器的费用为1 000元,则所需检测费的均值为()A.3 200B.3 400C.3 500D.3 600综合提升组9.(2018浙江金华模拟,7)随机变量ξ的分布列如下:其中a,b,c成等差数列,则Dξ的最大值为()A. B. C. D.10.(2018广东模拟,6)不透明袋子中装有大小、材质完全相同的2个红球和5个黑球,现从中逐个不放回地摸出小球,直到取出所有红球为止,则摸取次数X的均值是()A. B. C. D.创新应用组11.2017年5月,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.为发展业务,某调研组准备从国内n(n∈N+)个人口超过1 000万的超大城市和8个人口低于100万的小城市中随机抽取若干个对扫码支付情况进行统计,若一次抽取2个城市全是小城市的概率为.(1)求n的值;(2)若一次抽取4个城市,则:①假设取出小城市的个数为X,求X的分布列和均值;②若取出的4个城市是同一类城市,求全为超大城市的概率.12.小张举办了一次抽奖活动.顾客花费3元钱可获得一次抽奖机会.每次抽奖时,顾客从装有1个黑球,3个红球和6个白球(除颜色外其他都相同)的不透明的袋子中依次不放回地摸出3个球,根据摸出的球的颜色情况进行兑奖.顾客中一等奖、二等奖、三等奖、四等奖时分别可领取的奖金为a 元、10元、5元、1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况:A:1个黑球2个红球;B:3个红球;C:恰有1个白球;D:恰有2个白球;E:3个白球,且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖、中二等奖、中三等奖、中四等奖、不中奖.(1)通过计算写出中一至四等奖分别对应的情况(写出字母即可);(2)已知顾客摸出的第一个球是红球,求他获得二等奖的概率;(3)设顾客抽一次奖小张获利X元,求变量X的分布列;若小张不打算在活动中亏本,求a的最大值.参考答案课时规范练62 离散型随机变量的均值与方差1.C由正态分布知,每个人数学成绩在[70,110]的概率为(0.5-0.2)=0.6,所以10个学生数学成绩在[70,110]的人数服从二项分布B(10,0.6),所以方差为10×0.6×(1-0.6)=2.4,故选C.2.B由已知随机变量X+η=8,所以有η=8-X.因此,求得Eη=8-EX=8-10×0.6=2,Dη=(-1)2DX=10×0.6×0.4=2.4.3.A Eξ=-+a,当a增大时,Eξ也增大,Dξ也增大.4.D随机变量ξ满足E(1-ξ)=4,D(1-ξ)=4,则1-Eξ=4,(-1)2Dξ=4,据此可得Eξ=-3,Dξ=4.5.B由分布列的性质得x+y=,又Eξ=,所以+2x+3y=,解得x=,y=.故Dξ=1-2×+2-2×+3-2×=.6.A根据平均值与方差的定义,可以确定当=时,则去掉的那个数就是,那么就有A= [(x1-)2+(x2-)2+(x3-)2+(x4-)2+0],B= [(x1-)2+(x2-)2+(x3-)2+(x4-)2],所以可以得到A<B,而当<时.对于所去掉的那个数对平均数的差距不明确.故选A.7. ∵Eξ=,∴由随机变量ξ的分布列,知∴x+y=,x=,y=,Dξ=-1-2×+0-2×+1-2×+2-2×=.8.C设检测的机器的台数为x,则x的所有可能取值为2,3,4.P(x=2)==,P(x=3)==,P(x=4)==,所以E(x)=2×+3×+4×=3.5,所以所需的检测费用的均值为1 000×3.5=3 500.9.A∵a,b,c成等差数列,∴2b=a+c,∵a+b+c=1,∴b=,c=-a,∴Eξ=-a+c=-2a+,Dξ=-1+2a-2×a+2a-2×b+1+2a-2×-a=-4a2+a+=-4a-2+≤.则Dξ的最大值为.10.D当X=k时,第k次取出的必然是红球,而前k-1次中,有且只有1次取出的是红球,其余次数取出的皆为黑球,故P(X=k)==,于是得到X的分布列为:X 2 3 4 5 6 7P故EX=2×+3×+4×+5×+6×+7×=.11.解 (1)共n+8个城市,取出2个的方法总数是,其中全是小城市的情况有种,故全是小城市的概率是==,∴(n+8)(n+7)=210,∴n=7.(2)①X=0,1,2,3,4.P(X=0)==;P(X=1)==;P(X=2)==;P(X=3)==;P(X=4)==.故X的分布列为X0 1 2 3 4PEX=0×+1×+2×+3×+4×=.②若抽取的4个城市全是超大城市,共有=35种情况,若抽取的4个城市全是小城市,共有=70种情况,故所求概率为==.12.解 (1)P(A)===,P(B)==,P(C)===,P(D)===,P(E)===,∴P(B)<P(A)<P(E)<P(C)<P(D),∴中一至四等奖分别对应的情况是B,A,E,C.(2)记事件F为顾客摸出的第一个球是红球,事件G为顾客获得二等奖,则P(G|F)==.(3)X的可能取值为3-a,-7,-2,2,3,则分布列为:X3-a-7 -2 2 3P由题意得,若要不亏本,则×(3-a)+×(-7)+×(-2)+×2+×3≥0,解得a≤194,即a的最大值为194.。

2020版高考数学一轮复习课时规范练1集合的概念与运算理北师大版 (47)

课时规范练47 直线与圆、圆与圆的位置关系基础巩固组1.(2018贵州凯里一中二模,4)直线y=x-和圆x2+y2-4x+2y-20=0的位置是()A.相交且过圆心B.相交但不过圆心C.相离D.相切2.( 2018陕西西安八校联考,3)若过点A(3,0)的直线l与曲线(x-1)2+y2=1有公共点,则直线l斜率的取值范围为()A.(-)B.C.-D.3.(2018重庆巴蜀中学月考,7)已知直线l:y=-ax+a是圆C:(x-2)2+(y-1)2=4的一条对称轴,过点A 作圆C的一条切线,切点为B,则|AB|=()A.4B.6C. D.24.已知圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是2,则圆M与圆N:(x-1)2+(y-1)2=1的位置关系是()A.内切B.相交C.外切D.相离5.(2018北京,理7)在平面直角坐标系中,记d为点P(cos θ,sin θ)到直线x-my-2=0的距离.当θ,m变化时,d的最大值为()A.1B.2C.3D.46.已知圆C:x2+y2-2x+4y=0关于直线3x-ay-11=0对称,则圆C中以,-为中点的弦长为()A.1B.2C.3D.47.直线y=-x+m与圆x2+y2=1在第一象限内有两个不同的交点,则m的取值范围是()A.(,2)B.(,3)C. D.1,8.(2018安徽淮南一模,16)过动点P作圆:(x-3)2+(y-4)2=1的切线PQ,其中Q为切点,若|PQ|=|PO|(O为坐标原点),则|PQ|的最小值是.9.设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若|AB|=2,则圆C的面积为.10.(2018湖南长郡中学一模,14)若过点(1,1)的直线与圆x2+y2-6x-4y+4=0相交于A,B两点,则|AB|的最小值为.综合提升组11.(2018辽宁丹东模拟)圆心为(2,0)的圆C与圆x2+y2+4x-6y+4=0相外切,则圆C的方程为()A.x2+y2+4x+2=0B.x2+y2-4x+2=0C.x2+y2+4x=0D.x2+y2-4x=012.(2018湖南衡阳一模,12)若对圆x2+y2=1上任意一点P(x,y),|3x-4y+a|+|3x-4y-9|的取值与x,y 无关,则实数a的取值范围是()A.a≤-5B.-5≤a≤5C.a≤-5或a≥5D.a≥513.已知圆C:x2+y2=4,过点A(2,3)作圆C的切线,切点分别为P,Q,则直线PQ的方程为.14.(2018云南昆明应性检测,20)已知圆O:x2+y2=4上一动点A,过点A作AB⊥x轴,垂足为B点,AB 中点为P.(1)当A在圆O上运动时,求点P的轨迹E的方程;(2)过点F(-,0)的直线l与E交于M,N两点,当|MN|=2时,求线段MN的垂直平分线方程.创新应用组15.已知圆心为C的圆满足下列条件:圆心C位于x轴正半轴上,与直线3x-4y+7=0相切,且被y轴截得的弦长为2,圆C的面积小于13.(1)求圆C的标准方程;(2)设过点M(0,3)的直线l与圆C交于不同的两点A,B,以OA,OB为邻边作平行四边形OADB.是否存在这样的直线l,使得直线OD与MC恰好平行?如果存在,求出l的方程;若不存在,请说明理由.16.已知圆O:x2+y2=4,点A(-,0),B(,0),以线段AP为直径的圆C1内切于圆O,记点P的轨迹为C2.(1)证明:|AP|+|BP|为定值,并求C2的方程;(2)过点O的一条直线交圆O于M,N两点,点D(-2,0),直线DM,DN与C2的另一个交点分别为S,T,记△DMN,△DST的面积分别为S1,S2,求的取值范围.参考答案课时规范练47 直线与圆、圆与圆的位置关系1.A x2+y2-4x+2y-20=0可化简为(x-2)2+(y+1)2=25,故圆心为(2,-1),半径r=5.将(2,-1)代入y=x-中,3×2-4×(-1)-10=0,满足直线方程,故直线过圆心且与圆相交.故选A.2.D设直线l的方程为y=k(x-3),代入圆的方程中,整理得(k2+1)x2-(6k2+2)x+9k2=0,则Δ=4(1-3k2)≥0,解得-≤k≤,故选D.3.B∵直线l:y=-ax+a是圆C:(x-2)2+(y-1)2=4的一条对称轴,∴y=-ax+a过圆心C(2,1),∴1=-2a+a,解得a=-1,∴直线l的方程为y=x-1,A点坐标为(-4,-1),|AC|2=36+4=40,由勾股定理可得,|AB|2=|AC|2-r2=40-4=36,|AB|=6,故选B.4.B圆M的方程可化为x2+(y-a)2=a2,故其圆心为M(0,a),半径R=a.所以圆心到直线x+y=0的距离d==a.所以直线x+y=0被圆M所截弦长为2=2=a,由题意可得a=2,故a=2.圆N的圆心N(1,1),半径r=1.而|MN|==,显然R-r<|MN|<R+r,所以两圆相交.5.C设P(x,y),则x2+y2=1.即点P在单位圆上,点P到直线x-my-2=0的距离可转化为圆心(0,0)到直线x-my-2=0的距离加上(或减去)半径,所以距离最大为d=1+=1+.当m=0时,d max=3.6.D∵圆C:x2+y2-2x+4y=0关于直线3x-ay-11=0对称,∴直线3x-ay-11=0过圆心C(1,-2),∴3+2a-11=0,解得a=4,∴,-即为(1,-1),点(1,-1)到圆心C(1,-2)的距离d==1,圆C:x2+y2-2x+4y=0的半径r==,∴圆C中以,-为中点的弦长为2=2=4.故选D.7.D当直线经过点(0,1)时,直线与圆有两个不同的交点,此时m=1;当直线与圆相切时,有圆心到直线的距离d==1,解得m=(切点在第一象限),所以要使直线与圆在第一象限内有两个不同的交点,则1<m<.8. 设P(x,y),则x2+y2=(x-3)2+(y-4)2-1,即3x+4y=12,所以点P的运动轨迹是直线3x+4y=12,所以d min=,则|PQ|min==.9.4π圆C的方程可化为x2+(y-a)2=2+a2,直线方程为x-y+2a=0,所以圆心坐标为(0,a),半径r2=a2+2,圆心到直线的距离d=.由已知()2+=a2+2,解得a2=2,故圆C的面积为π(2+a2)=4π.10.4圆x2+y2-6x-4y+4=0的圆心为(3,2),半径r==3,点(1,1)与圆心(3,2)间的距离d==,所以|AB|的最小值|AB|min=2=2=4.11.D圆x2+y2+4x-6y+4=0,即(x+2)2+(y-3)2=9的圆心为(-2,3),半径为3.设圆C的半径为r.由两圆外切知,圆心距为=5=3+r.所以r=2,圆C的方程为(x-2)2+y2=4,即x2+y2-4x=0.故选D.12.D由x2+y2=1可知-5≤3x-4y≤5,令3x-4y=t,则|t+a|+|t-9|的取值与x,y无关,需-a≤t≤9,∴[-5,5]⫋[-a,9],所以a≥5.13.2x+3y-4=0以O(0,0),A(2, 3)为直径端点的圆的方程为x(x-2)+y(y-3)=0,即x2+y2-2x-3y=0,与圆C:x2+y2=4相减得2x+3y-4=0,故直线PQ的方程为2x+3y-4=0.14.解 (1)设P(x,y),则A(x,2y).将A(x,2y)代入x2+y2=4得点P的轨迹E的方程为+y2=1(y≠0).(2)由题意可设直线l方程为x=my-,由得(m2+4)y2-2my-1=0.所以所以|AB|=|y1-y2|===2.所以m=±.当m=时,中点纵坐标y0==,代入x=my-1得中点横坐标x0=-,斜率为k=-.故线段MN的垂直平分线方程为2x+y+=0.当m=-时,同理可得MN的垂直平分线方程为2x-y+=0.所以线段MN的垂直平分线方程为2x+y+=0或2x-y+=0.15.解 (1)设圆C:(x-a)2+y2=r2(a>0),由题意知解得a=1或a=.又S=πr2<13,∴a=1,∴圆C的标准方程为(x-1)2+y2=4.(2)当斜率不存在时,直线l为x=0,不满足题意.当斜率存在时,设直线l:y=kx+3,A(x1,y1),B(x2,y2),又l与圆C相交于不同的两点,联立得消去y得(1+k2)x2+(6k-2)x+6=0.∴Δ=(6k-2)2-24(1+k2)=12k2-24k-20>0,解得k<1-或k>1+.x1+x2=-,y1+y2=k(x1+x2)+6=,=+=(x1+x2,y1+y2),=(1,-3),假设∥,则-3(x1+x2)=y1+y2,解得k=∉-∞,1-∪1+,+∞,假设不成立,∴不存在这样的直线l.16.解 (1)证明:设AP的中点为E,切点为F,连接OE,EF(图略),则|OE|+|EF|=|OF|=2,故|BP|+|AP|=2(|OE|+|EF|)=4.∴点P的轨迹是以A,B为焦点,长轴长为4的椭圆.其中,a=2,c=,b=1,则C2的方程是+y2=1.(2)设直线DM的方程为x=my-2(m≠0).∵MN为圆O的直径,∴∠MDN=90°,∴直线DN的方程为x=-y-2,由得(1+m2)y2-4my=0,∴y M=,由得(4+m2)y2-4my=0,∴y S=,∴=,∴=.∵|DM|=|y M-0|,|DS|=|y S-0|,|DN|=|y N-0|,|DT|=|y T-0|,又∵△DMN,△DST都是有同一顶点的直角三角形, ∴=·=·.设s=1+m2,则s>1,0<<3,∴=4-1+∈4,.。

2020版高考数学一轮复习课时规范练1集合的概念与运算理北师大版 (63)

课时规范练63 坐标系与参数方程基础巩固组1.已知曲线C:=1,直线l:(t为参数).(1)写出曲线C的参数方程,直线l的普通方程;(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.2.(2019届广东珠海9月摸底,22)在直角坐标系xOy中,直线l过定点P(1,-)且与直线OP垂直.以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ-2cos θ=0.(1)求曲线C的直角坐标方程和直线l的参数方程;(2)设直线l与曲线C交于A、B两点,求的值.3.(2018河南一模,22)在直角坐标系xOy中,已知直线l1:(t为参数),l2:(t为参数),其中α∈0,,以原点O为极点,x轴非负半轴为极轴,取相同长度单位建立极坐标系,曲线C的极坐标方程为ρ-4cos θ=0.(1)写出l1,l2的极坐标方程和曲线C的直角坐标方程;(2)设l1,l2分别与曲线C交于点A,B,点A,B都不是坐标原点,求|AB|的值.4.(2018江西师大附中三模,22)在直角坐标系xOy中,曲线C1:(θ为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,直线l:ρsin(α-θ)=2sin α.其中α为直线l的倾斜角(α≠0)(1)求曲线C1的普通方程和直线l的直角坐标方程;(2)直线l与x轴的交点为M,与曲线C1的交点分别为A,B,求|MA|·|MB|的值.5.(2018湖北5月冲刺,22)在直角坐标系xOy中,直线l经过点P(,0),倾斜角为,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2sin θ.(1)求直线l的参数方程;(2)若A点在直线l上,B点在曲线C上,求|AB|的最小值.6.(2018河南郑州摸底)以平面直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,-5),点M的极坐标为4,,若直线l过点P,且倾斜角为,圆C以M为圆心,4为半径.(1)求直线l的参数方程和圆C的极坐标方程;(2)试判定直线l圆C的位置关系.综合提升组7.(2018广西钦州第三次质检,22)在平面直角坐标系xOy中,直线l经过点P(-3,0),其倾斜角为α,以原点O为极点,以x轴非负半轴为极轴,与坐标系xOy取相同的长度单位,建立极坐标系,设曲线C 的极坐标方程为ρ2-2ρcos θ-3=0.(1)若直线l与曲线C有公共点,求倾斜角α的取值范围;(2)设M(x,y)为曲线C上任意一点,求x+y的取值范围.8.(2018重庆西南大学附中模拟)已知平面直角坐标系xOy中,过点P(-1,-2)的直线l的参数方程为(t为参数),l与y轴交于点A,以该直角坐标系的原点O为极点,x轴的非负半轴为极轴建立极坐标系.曲线C的极坐标方程为ρsin2θ=m cos θ(m>0),直线l与曲线C交于M、N两点.(1)求曲线C的直角坐标方程和点A的一个极坐标;(2)若=3,求实数m的值.创新应用组9.(2018河北衡水中学押题一)已知直线l的参数方程为(t为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cos θ,直线l与圆C交于A,B两点.(1)求圆C的直角坐标方程及弦AB的长;(2)动点P在圆C上(不与A,B重合),试求△ABP的面积的最大值.10.(2018湖南长沙模拟二)在直角坐标系xOy中,直线l的方程是x=2,曲线C的参数方程为(α为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.(1)求直线l和曲线C的极坐标方程;(2)射线OM:θ=β其中0<β≤与曲线C交于O,P两点,与直线l交于点M,求的取值范围.参考答案课时规范练63 坐标系与参数方程1.解 (1)曲线C的参数方程为(θ为参数).直线l的普通方程为2x+y-6=0.(2)曲线C上任意一点P(2cos θ,3sin θ)到直线l的距离为d=|4cos θ+3sin θ-6|,则|PA|==|5sin(θ+α)-6|,其中α为锐角,且tan α=.当sin(θ+α)=-1时,| PA|取得最大值,最大值为.当sin(θ+α)=1时,|PA|取得最小值,最小值为.2.解 (1)曲线C的直角坐标方程为y2=2x,直线l的参数方程为(t为参数).(2)设点A、B对应的参数分别为t1、t2,将直线l与曲线C的方程联立得t2-8t+4=0,(*)可知t1,t2是(*)式的两根,则故t1、t2同正.+=+===2.3.解 (1)l1,l2的极坐标方程为θ1=α(ρ∈R),θ2=α+ (ρ∈R).曲线C的极坐标方程为ρ-4cos θ=0,即为ρ2-4ρcos θ=0,利用ρ2=x2+y2,x=ρcos θ,得曲线C的直角坐标方程为(x-2)2+y2=4.(2)因为ρ1=4cos α,ρ2=4cosα+,所以|AB|2=+-2ρ1ρ2cos=16cos2α+cos2α+-cos αcosα+=16cos2α+(cos α-sin α)2-cos α(cos α-sin α)=8,所以|AB|的值为2.4.解 (1)曲线C1的普通方程为(x-1)2+y2=4,直线l的直角坐标方程为x sin α-y cos α=2sin α.(2)直线l与x轴的交点为M(2,0),直线l的参数方程可设为(t为参数),将直线l的参数方程代入圆C1的方程(x-1)2+y2=4,得t2+2t cos α-3=0,故|MA|·|MB|=|t1·t2|=3.5.解 (1)直线l的参数方程为(t为参数),即(t为参数).(2)由(t为参数),得x-y-3=0.由ρ=2sin θ得ρ2=2ρsin θ,即x2+y2-2y=0,即x2+(y-1)2=1.所以曲线C是以点Q(0,1)为圆心,1为半径的圆.又点Q到直线l:x-y-3=0的距离为d==2.故|AB|的最小值为2-1=1.6.解 (1)直线l的参数方程为(t为参数),则(t为参数),M点的直角坐标为(0,4),圆C的方程为x2+(y-4)2=16,且代入得圆C极坐标方程为ρ=8sin θ.(2)直线l的普通方程为x-y-5-=0,圆心M到直线l的距离为d==>4,∴直线l与圆C相离.7.解 (1)将曲线C的极坐标方程ρ2-2ρcos θ-3=0化为直角坐标方程为x2+y2-2x-3=0,直线l的参数方程为(t为参数),将参数方程代入x2+y2-2x-3=0,整理得t2-8t cos α+12=0.∵直线l与曲线C有公共点,∴Δ=64cos2α-48≥0,∴cos α≥,或cos α≤-.∵α∈[0,π),∴α的取值范围是0,∪,π.(2)曲线C的方程x2+y2-2x-3=0可化为(x-1)2+y2=4,其参数方程为(θ为参数),∵M(x,y)为曲线上任意一点,∴x+y=1+2cos θ+2sin θ=1+2sinθ+,∴x+y的取值范围是[1-2,1+2 ].8.解 (1)∵ρsin2θ=m cos θ,∴ρ2sin2θ=mρcos θ,∴y2=mx(m>0),A点坐标为(0,-1),其一个极坐标为A1,π.(2)将(t为参数),代入y2=mx,得t2-(4+m)t+m+4=0.∵=3,∴t1=3t2.∴∴m=.9.解 (1)由ρ=4cosθ得ρ2=4ρcos θ,所以x2+y2-4x=0,所以圆C的直角坐标方程为(x-2)2+y2=4.将直线l的参数方程代入圆C:(x-2)2+y2=4,并整理得t2+2t=0,解得t1=0,t2=-2.所以直线l被圆C截得的弦AB的长为|t1-t2|=2.(2)直线l的普通方程为x-y-4=0.圆C的参数方程为(θ为参数),可设圆C上的动点P(2+2cos θ,2sin θ),则点P到直线l的距离d==2cosθ+-.当cosθ+=-1时,d取最大值,且d的最大值为2+.所以S△ABP≤×2×(2+)=2+2.即△ABP的面积的最大值为2+2.10.解 (1)∵∴直线l的极坐标方程是ρcos θ=2,由消参数得x2+(y-2)2=4,∴曲线C的极坐标方程是ρ=4sin θ.(2)将θ=β分别代入ρ=4sin θ,ρcos θ=2,得|OP|=4sin β,|OM|=,∴=sin 2β.∵0<β≤,∴0<2β≤,∴0<sin 2β≤,∴的取值范围是0,.。

2020版高考数学一轮复习课时规范练1集合的概念与运算理北师大版 (64)

课时规范练64 不等式选讲基础巩固组1.(2018河南最后一次模拟,23)已知函数f(x)=|2x+4|+|2x-a|.(1)当a=6时,求f(x)≥12的解集;(2)已知a>-2,g(x)=x2+2ax+,若对于x∈-1, ,都有f(x)≥g(x)成立,求a的取值范围.2.(2018湖南长沙模拟二,23)已知函数f(x)=|x-1|,关于x的不等式f(x)<3-|2x+1|的解集记为A.(1)求A;(2)已知a,b∈A,求证:f(ab)>f(a)-f(b).3.(2018安徽淮南二模,23)已知函数f(x)=|x-2|-|x+1|.(1)解不等式f(x)+x>0.(2)若关于x的不等式f(x)≤a2-2a的解集为R,求实数a的取值范围.4.(2018河北衡水中学三轮检测,23)已知函数f(x)=|ax-1|-(a-2)x.(1)当a=3时,求不等式f(x)>0的解集;(2)若函数f(x)的图像与x轴没有交点,求实数a的取值范围.综合提升组5.已知函数f(x)=|x-a|.(1)当a=-2时,解不等式f(x)≥16-|2x-1|;(2)若关于x的不等式f(x)≤1的解集为[0,2],求证:f(x)+f(x+2)≥2.6.(2018河南南阳模拟,23)已知函数f(x)=|x-2a+1|+|x+2|,g(x)=3x+1.(1)当a=1时,求不等式f(x)≤g(x)的解集;(2)x∈[-2,a),f(x)≥g(x),求a的取值范围.7.已知函数f(x)=|2x+1|,g(x)=|x+1|,不等式f(x)≤g(x)+1的解集为A.(1)求A;(2)证明:对于任意的a,b∈∁R A,都有g(ab)>g(a)-g(-b)成立.创新应用组8.已知函数f(x)=|x-2|-|x|+m(m∈R).(1)若m=0,解不等式f(x)≥x-1;(2)若方程f(x)=-x有三个不同的解,求实数m的取值范围.9.(2018安徽安庆热身考,23)若关于x的不等式|3x+2|+|3x-1|-t≥0的解集为R,记实数t的最大值为a.(1)求a的值;(2)若正实数m,n满足4m+5n=a,求y=的最小值.参考答案课时规范练64 不等式选讲1.解 (1)当a=6时,f(x)=|2x+4|+|2x-6|,f(x)≥12等价于|x+2|+|x-3|≥6,因为|x+2|+|x-3|=所以或或解得x≥或x≤-,所以解集为.(2)当a>-2时,且x∈-1,时,f(x)=2x+4-(2x-a)=4+a,所以f(x)≥g(x),即4+a≥g(x).又g(x)=x2+2ax+的最大值必为g(-1),g之一,所以即解得-≤a≤,所以a的取值范围为-,.2.解 (1)由f(x)<3-|2x+1|,得|x-1|+|2x+1|<3,即或或解得-1<x≤-或-<x<1,所以,集合A={x∈R|-1<x<1}.(2)证明∵a,b∈A,∴-1<ab<1,∴f(ab)=|ab-1|=1-ab,f(a)=|a-1|=1-a,f(b)=|b-1|=1-b,∵f(ab)-[f(a)-f(b)]=1-ab-1+a+1-b=(1+a)(1-b)>0,∴f(ab)>f(a)-f(b).3.解 (1)不等式f(x)+x>0可化为|x-2|+x>|x+1|.当x<-1时,-(x-2)+x>-(x+1),解得x>-3,即-3<x<-1;当-1≤x≤2时,-(x-2)+x>x+1,解得x<1,即-1≤x<1;当x>2时,x-2+x>x+1,解得x>3,即x>3.综上所述:不等式f(x)+x>0的解集为{x|-3<x<1或x>3}.(2)由不等式f(x)≤a2-2a可得|x-2|-|x+1|≤a2-2a,∵|x-2|-|x+1|≤|x-2-x-1|=3,∴a2-2a≥3,即a2-2a-3≥0.解得a≥3或a≤-1.故实数a的取值范围是a≥3或a≤-1.4.解 (1)当a=3时,不等式可化为|3x-1|-x>0,即|3x-1|>x.∴3x-1<-x或3x-1>x,即x<或x>.即不等式f(x)>0的解集是x.(2)当a>0时,f(x)=要使函数f(x)与x轴无交点,只需即1≤a<2.当a=0时,f(x)=2x+1,函数f(x)与x轴有交点.当a<0时,f(x)=要使函数f(x)与x轴无交点,只需此时a无解.综上可知,当1≤a<2时,函数f(x)与x轴无交点.5.(1)解当a=-2时,不等式为|x+2|+|2x-1|≥16,当x≤-2时,原不等式可化为-x-2-2x+1≥16,解得x≤-,当-2<x≤时,原不等式可化为x+2-2x+1≥16,解得x≤-13,不满足,舍去;当x>时,原不等式可化为x+2+2x-1≥16,解得x≥5.综上不等式的解集为x或x≥5.(2)证明f(x)≤1即|x-a|≤1,解得a-1≤x≤a+1,而f(x)≤1的解集是[0,2],所以解得a=1,从而f(x)=|x-1|.于是证明f(x)+f(x+2)≥2,即证|x-1|+|x+1|≥2,因为|x-1|+|x+1|=|1-x|+|x+1|≥|1-x+x+1|=2,所以|x-1|+|x+1|≥2,所以原不等式得证.6.解 (1)当a=1时,f(x)=|x-1|+|x+2|,①当x≤-2时,f(x)=-2x-1,由-2x-1≤3x+1,知此时无解;②当-2<x<1时,f(x)=3,由3≤3x+1,解得≤x<1;③当x≥1时,f(x)=2x+1,由2x+1≤3x+1,解得x≥1,综上所述,不等式的解集为x.(2)当x∈[-2,a)时,f(x)=|x-2a+1|+x+2≥3x+1,即|x-2a+1|≥2x-1.①当-2<a≤时,2x-1<0,|x-2a+1|≥2x-1恒成立;②当a>,x∈-2,时,2x-1<0,|x-2a+1|≥2x-1恒成立;x∈,a时,|x-2a+1|2≥(2x-1)2恒成立,即3x2+2(2a-3)x-4a(a-1)≤0恒成立,令g(x)=3x2+2(2a-3)x-4a(a-1),g(x)的最大值只可能是g或g(a),g≤0,g(a)=3a2-2a≤0,得0≤a≤.又a>,所以<a≤.综上所述,a的取值范围是a.7.(1)解不等式f(x)≤g(x)+1,即|x+1|-|2x+1|+1≥0.当x<-1时,不等式可化为-x-1+(2x+1)+1≥0,解得x≥-1,∴x无解;当-1≤x≤-,不等式可化为x+1+(2x+1)+1≥0,解得x≥-1,∴-1≤x≤-;当x>-时,不等式可化为x+1-(2x+1)+1≥0,解得x≤1,∴-<x≤1.∴不等式f(x)≤g(x)+1的解集A={x|-1≤x≤1}.(2)证明∵g(a)-g(-b)=|a+1|-|-b+1|≤|a+1-(-b+1)|=|a+b|,∴要证g(ab)>g(a)-g(-b)成立,只需证|ab+1|>|a+b|,即证|ab+1|2>|a+b|2,也就是证明a2b2+2ab+1>a2+2ab+b2成立,即证a2b2-a2-b2+1>0,即证(a2-1)(b2-1)>0.∵A={x|-1≤x≤1},a,b∈∁R A,∴|a|>1,|b|>1,a2>1,b2>1,∴(a2-1)(b2-1)>0成立.从而对于任意的a,b∈∁R A,都有g(ab)>g(a)-g(-b)成立.8.解 (1)因为m=0,所以f(x)=|x-2|-|x|,有或或解得,x∈⌀或0≤x≤1或x<0.所以不等式f(x)≥x-1的解集为(-∞,1].(2)因为f(x)=|x-2|-|x|+m,所以方程f(x)=-x有三个不同的解等价于函数g(x)=|x-2|-|x|的图像与直线y=-x-m有三个不同的交点,作图可知,当直线y=-x-m经过点A(0,2)时,m=-2;当直线y=-x-m经过点B(2,-2)时,m=0.所以实数m的取值范围是(-2,0).9.解 (1)由题意得|3x+2|+|3x-1|≥t对x∈R恒成立,又|3x+2|+|3x-1|=|3x+2|+|1-3x|≥3,∴t≤3.∴a=3.(2)由(1)得4m+5n=3,且m,n>0,∴3y=+(4m+5n)=+[(m+2n)+(3m+3n)]=5++≥5+2=9.当且仅当=且4m+5n=3,即m=n=时等号成立.∴y≥3,即y=+的最小值为3.。

2020版高考数学一轮复习课时规范练1集合的概念与运算理北师大版 (12)

课时规范练12 函数与方程基础巩固组1.下列图像表示的函数中能用二分法求零点的是()2.设f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内的近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在()A.(1,1.25)B.(1.25,1.5)C.(1.5,2)D.不能确定3.已知函数f(x)=-log3x,若实数x0是方程f(x)=0的解,且x0<x1,则f(x1)的值()A.恒为负B.等于零C.恒为正D.不大于零4.(2018新疆乌鲁木齐一模)函数f(x)=e x+2x-3的零点所在的一个区间是()A. B.C. D.5.已知f(x)=|tan x|,则函数y=f(x)+log4x-1的图像与x轴的交点个数是()A.1B.2C.3D.46.已知x0是f(x)=的一个零点,x1∈(-∞,x0),x2∈(x0,0),则()A.f(x1)<0,f(x2)<0B.f(x1)>0,f(x2)>0C.f(x1)>0,f(x2)<0D.f(x1)<0,f(x2)>07.若f(x)是奇函数,且x0是y=f(x)+e x的一个零点,则-x0一定是下列哪个函数的零点()A.y=f(-x)e x-1B.y=f(x)e-x+1C.y=e x f(x)-1D.y=e x f(x)+18.(2018北京西城区一模)函数f(x)=2x+log2|x|的零点个数为()A.0B.1C.2D.39.(2018陕西榆林一模)直线y=x与函数f(x)=的图像恰有三个公共点,则实数m的取值范围是.10.已知函数f(x)=若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是.11.函数f(x)=有两个不同的零点,则实数a的取值范围为.综合提升组12.(2018陕西西安模拟)设函数f(x)=若关于x的方程[f(x)]2-af(x)=0恰有三个不同的实数解,则实数a的取值范围为()A.(0,1]B.(0,1)C.[1,+∞)D.(-∞,1)13.已知f(x)是定义在R上的奇函数,且当x∈(0,+∞)时,f(x)=2 016x+log2 016x,则函数f(x)的零点个数是()A.1B.2C.3D.414.已知函数f(x)=|2x-2|+b的两个零点分别为x1,x2(x1>x2),则下列结论正确的是()A.1<x1<2,x1+x2<2B.1<x1<2,x1+x2<1C.x1>1,x1+x2<2D.x1>1,x1+x2<115.(2018河北衡水中学考前仿真,7)已知函数f(x)=则函数g(x)=2f[f(x)]-1的零点个数为()A.3B.4C.5D.6创新应用组16.(2018河北衡水中学押题二,12)已知函数f(x)=ax3-3x2+1,若f(x)存在三个零点,则a的取值范围是()A.(-∞,-2)B.(-2,2)C.(2,+∞)D.(-2,0)∪(0,2)17.(2018湖南衡阳八中一模,10)已知函数f(x)=若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则x3(x1+x2)+的取值范围是()A.(-1,+∞)B.(-1,1]C.(-∞,1)D.[-1,1)参考答案课时规范练12 函数与方程1.C A中图像表示的函数没有零点,因此不能用二分法求零点;B中函数的图像不连续;D中函数在x轴下方没有图像.故选C.2.B由f(1.25)<0,f(1.5)>0可得方程f(x)=0的根落在区间(1.25,1.5)内,故选B.3.A f(x)=-log3x在(0,+∞)内递减,若f(x0)=0,则当x0<x1时,一定有f(x1)<0,故选A.4.C观察各选项,∵f(0)=e0-3<0,f=-4<0,f=-2<0,f(1)=e-1>0,f=>0,∴零点所在的一个区间为,故选C.5.C由f(x)+log4x-1=0,得f(x)=-log4x+1,作出函数y=f(x),y=-log4x+1的大致图像,因两个函数图像有3个交点.故y=f(x)+log4x-1的图像与x轴的交点个数为3,故选C.6.C如图,在同一平面直角坐标系下作出函数y=,y=-的图像,由图像可知当x∈(-∞,x0)时,>-,当x∈(x0,0)时,<-,所以当x1∈(-∞,x0),x2∈(x0,0)时,有f(x1)>0,f(x2)<0,选C.7.C由已知可得f(x0)=-,则·f(x0)=-1,f(-x0)=1,故-x0一定是y=e x f(x)-1的零点.8.C函数f(x)=2x+log2|x|的零点个数,即为函数y=-2x的图像和函数y=log2|x|的图像的交点个数.如图所示,交点个数为2.故选C.9.[-1,2)直线y=x与射线y=2(x>m)有一个交点A(2,2),且与抛物线y=x2+4x+2在(-∞,m]上的部分有两个交点B、C.由解得B(-1,-1),C(-2,-2).∵抛物线y=x2+4x+2在(-∞,m]上的部分必须包含B、C两点,且点A(2,2)一定在射线y=2(x>m)上,才能使y=f(x)图像与y=x有3个交点,∴实数m的取值范围是-1≤m<2.10.(0,1)因为函数g(x)=f(x)-m有3个零点,所以f(x)-m=0有3个根,所以y=f(x)的图像与直线y=m有3个交点.画出函数y=f(x)的图像,由抛物线顶点为(-1,1),可知实数m的取值范围是(0,1).11. 由于当x≤0时,f(x)=|x2+2x-1|的图像与x轴只有1个交点,即只有1个零点,故由题意知只需方程2x-1+a=0有1个正根即可,变形为2x=-2a,结合图形(图略)得-2a>1⇒a<-.12.A关于x的方程[f(x)]2-af(x)=0的解为f(x)=0或f(x)=a,而函数f(x)的图像如图所示,由图像可知,方程f(x)=0只有一解x=1,而原方程有三解,所以方程f(x)=a有两个不为1的相异的解,即0<a≤1.13.C作出函数y=2 016x和y=-log2 016x的图像如图所示,可知函数f(x)=2 016x+log2 016x在x∈(0,+∞)内存在一个零点.∵f(x)是定义在R上的奇函数,∴f(x)在x∈(-∞,0)内只有一个零点.又f(0)=0,∴函数f(x)的零点个数是3,故选C.14.A函数f(x)=|2x-2|+b有两个零点,即y=|2x-2|与y=-b的图像有两个交点,交点的横坐标就是x1,x2(x2<x1),在同一坐标系中画出y=|2x-2|与y=-b的图像(如下),可知1<x1<2.当y=-b=2时,x1=2,两个函数图像只有一个交点,当y=-b<2时,由图可知x1+x2<2.15.C由g(x)=0,得2f[f(x)]-1=0,令f(x)=z,得2f(z)=1,则f(z)=,当z≤0时,=,得z=0;当z>0时,|ln z|=,解得z=或z=,作出函数y=f(x)的图像,如下图所示,直线y=0与y=f(x)的图像只有一个交点.∵y=>,∴直线y=和直线z=与y=f(x)的图像分别有2个交点,3条直线与y=f(x)的图像共5个交点,即函数g(x)=2f[f(x)]-1有5个零点,故选C.16.D∵函数f(x)=ax3-3x2+1在R上存在三个零点,∴f(x)的极大值与极小值异号,很明显a≠0,由题意可得:f'(x)=3ax2-6x=3x(ax-2),则由f'(x)=0可得x1=0,x2=,由题意得不等式:f(x1)f(x2)=-+1<0,即:>1,a2<4,-2<a<2.综上,可得a的取值范围是(-2,0)∪(0,2).17.B作出函数f(x)=的图像如下,由图可知,x1+x2=-2,-log2x3=log2x4,即x3·x4=1,当x=0时,f(0)=1,当-log2x3=1时,x3=.故方程f(x)=a有四个不同的解时,对应的x3∈,又x3(x1+x2)+=-2x3+,其在x3∈上是减少的,∴-2+1<-2x3+≤-1+2,即-1<-2x3+≤1.∴x3(x1+x2)+∈(-1,1].故选B.。

2020届一轮复习人教B版集合及其运算学案

集合及其运算一、知识梳理：（阅读教材必修1第2页—第14页）1、集合的含义与表示（1）、一般地，我们把研究对象统称为元素，把一些元素组成的总体叫做集合；（2）、集合中的元素有三个性质: 确定性，无序性，互异性；（3）、集合中的元素与集合的关系属于和不属于，分别用和表示；（4）、几个常用的集合表示法数集自然数集正整数集整数集有理数集实数集表示法R Z Q R2、集合间的基本关系表示文字语言符号语言关系相等集合A与集合B中的所有A= B元素相同子集A中任意元素均为B中元素ABA B真子集A中任意元素均为B中元素，且B中至少有一个元素不属于A空集空集是任何集合的子集，φ是任何非空集合的真子集3、集合的基本运算交集并集补集符号表示图形表示意义4、常用结论（1）、集合A中有n个元素，则集合A的子集有个；真子集有个；（2）、并集：AB= B，AA=A；A=A ；ABA；AB=B（3）、交集：AB=AB；AA=A；A；=A；（4）、补集：A=; A=U二、题型探究[探究一]、集合的概念例1：已知A={2，} ,若aA，由6-aA，求实数a的值。

解：若a=2，6-a=4，a=4，6-a=2，a=6，6-a=0.根据集合元素的确定性，综上可得，a ＝ 2，4。

【小结】集合元素的确定性和互异性是解决问题的理论依据。

确定性是入手点，互异性是检验结论的工具。

例2：已知集合P={x|x=2k+1,k} , Q={x|x=2k-1,k} , R={ x|x=4K } , M={ x|x=4K } , N={ x|x=4K },则（ A ）（A ）P=Q=R （B ） P=Q= M （C ）Q=R=M （D ） R=Q= N [探究二]、集合间的基本关系例3：下列命题：（1）.空集没有子集；（2）.任何一个集合至少有两个子集；（3）.空集是任何集合的真子集；（4）.若空集是集合A 的真子集，则A 不是空集。

其中正确的是 A.0个 B.1个 C.2 个 D.3个例4：已知集合p={},集合Q={},若,那么的值是A.1B.-1C.1或-1D.0或-1或1 [探究三]、集合的运算例5: （15年安徽文科）设全集{}123456U =，，，，，，{}12A =，，{}234B =，，，则()U AC B =( B )（A ）{}1256，，，（B ）{}1 （C ）{}2 （D ）{}1234，，，例6: (2018年新课标2文科) 已知集合{}|12A x x =-<<,{}|03B x x =<<,则A B =（ A ）A ．()1,3-B ．()1,0-C ．()0,2D ．()2,3 三、方法提升：1、集合元素的性质:在解题时经常用到集合元素的互异性，一方面利用集合元素的互异性能顺利地找到解题的切入点，另一方面在解答完毕之时，注意检验集合中的元素是否满足互异性,以确保答案正确。

2020届高考数学一轮复习人教B版集合的含义与表示课时作业

第2课时集合的表示学习目标 1.掌握用列举法表示有限集.2.理解描述法格式及其适用情形.3.学会在集合不同的表示法中作出选择和转换．知识点一列举法思考要研究集合，要在集合的基础上研究其他问题，首先要表示集合．而当集合中元素较少时，如何直观地表示集合？答案把它们一一列举出来．梳理把集合中的元素一一列举出来，并用花括号“{ }”括起来表示集合的方法叫做列举法．适用于元素较少的集合．知识点二描述法思考能用列举法表示所有大于1的实数吗？如果不能，又该怎样表示？答案不能．表示集合最本质的任务是要界定集合中有哪些元素，而完成此任务除了一一列举，还可用元素的共同特征(如都大于1)来表示集合，如大于1的实数可表示为{x ∈R |x ＞1}．梳理描述法常用以表示无限集或元素个数较多的有限集．表示方法是在花括号内画一竖线，竖线前写元素的一般符号及取值(或变化)范围，竖线后写元素所具有的共同特征．1.{}1＝1.(×)2.{}，＝{}x ＝1，y ＝2.(×)3.{}x ∈R |x >1＝{}y ∈R |y >1.(√)4.{}x |x 2＝1＝{}－1，1.(√)类型一用列举法表示集合例1 用列举法表示下列集合．(1)小于10的所有自然数组成的集合；(2)方程x 2＝x 的所有实数根组成的集合．考点用列举法表示集合题点用列举法表示数集解(1)设小于10的所有自然数组成的集合为A，那么A＝{0,1,2,3,4,5,6,7,8,9}．(2)设方程x2＝x的所有实数根组成的集合为B，那么B＝{0,1}．反思与感悟(1)集合中的元素具有无序性、互异性，所以用列举法表示集合时不必考虑元素的顺序，且元素不能重复，元素与元素之间要用“，”隔开．(2)元素个数少且有限时，全部列举，如{1,2,3,4}．跟踪训练1 用列举法表示下列集合．(1)由所有小于10的既是奇数又是素数的自然数组成的集合；(2)由1～20以内的所有素数组成的集合．考点用列举法表示集合题点用列举法表示数集解(1)满足条件的数有3,5,7，所以所求集合为{3,5,7}．(2)设由1～20以内的所有素数组成的集合为C，那么C＝{2,3,5,7,11,13,17,19}．类型二用描述法表示集合例2 试用描述法表示下列集合．(1)方程x2－2＝0的所有实数根组成的集合；(2)由大于10小于20的所有整数组成的集合．考点用描述法表示集合题点用描述法表示有限数集解(1)设方程x2－2＝0的实数根为x，并且满足条件x2－2＝0，因此，用描述法表示为A ＝{x∈R|x2－2＝0}．(2)设大于10小于20的整数为x，它满足条件x∈Z，且10<x<20.因此，用描述法表示为B＝{x∈Z|10<x<20}．引申探究用描述法表示函数y＝x2－2图象上所有的点组成的集合．解{(x，y)|y＝x2－2}．反思与感悟用描述法表示集合时应注意的四点(1)写清楚该集合中元素的代号；(2)说明该集合中元素的性质；(3)所有描述的内容都可写在集合符号内；(4)在描述法的一般形式{x∈I|p(x)}中，“x”是集合中元素的代表形式，I是x的范围，“p(x)”是集合中元素x的共同特征，竖线不可省略．跟踪训练2 用描述法表示下列集合．(1)方程x2＋y2－4x＋6y＋13＝0的解集；(2)平面直角坐标系中坐标轴上的点组成的集合．考点用描述法表示集合题点用描述法表示点集解(1)方程x2＋y2－4x＋6y＋13＝0可化为(x－2)2＋(y＋3)2＝0，解得x＝2，y＝－3.所以方程的解集为{(x，y)|x＝2，y＝－3}．(2)坐标轴上的点(x，y)的特点是横、纵坐标中至少有一个为0，即xy＝0，故坐标轴上的点的集合可表示为{(x，y)|xy＝0}．类型三集合表示的综合应用命题角度1 选择适当的方法表示集合例3 用适当的方法表示下列集合．(1)由x＝2n,0≤n≤2且n∈N组成的集合；(2)抛物线y＝x2－2x与x轴的公共点的集合；(3)直线y＝x上去掉原点的点的集合．考点集合的表示综合题点用适当的方法表示集合解(1)列举法：{0,2,4}；或描述法{x|x＝2n,0≤n≤2且n∈N}．(2)列举法：{(0,0)，(2,0)}．(3)描述法：{(x，y)|y＝x，x≠0}．反思与感悟用列举法与描述法表示集合时，一要明确集合中的元素；二要明确元素满足的条件；三要根据集合中元素的个数来选择适当的方法表示集合．跟踪训练3 若集合A＝{x∈Z|－2≤x≤2}，B＝{y|y＝x2＋2000，x∈A}，则用列举法表示集合B＝________.考点集合的表示综合题点用另一种方法表示集合答案{2000,2001,2004}解析由A＝{x∈Z|－2≤x≤2}＝{－2，－1,0,1,2}，所以x2∈{0,1,4}，x2＋2000的值为2000,2001,2004，所以B＝{2000,2001,2004}．命题角度2 新定义的集合例4 在整数集Z中，被5除所得余数为k的所有整数组成一个“类”，记为[k]，即[k]＝{}5n＋k|n∈Z，k＝0,1,2,3,4，给出如下四个结论：①2016∈[1]；②－3∈[3]；③若整数a，b属于同一“类”，则a－b∈[0]；④若a－b∈[0]，则整数a，b属于同一“类”．其中，正确结论的个数是( )A．1B．2C．3D．4考点用描述法表示集合题点用描述法表示与余数有关的整数集合答案 C解析由于[k]＝{5n＋k|n∈Z|，对于①，2016除以5等于403余1，∴2016∈[1]，∴①正确；对于②，－3＝－5＋2，被5除余2，∴②错误；对于③，∵a，b是同一“类”，可设a＝5n1＋k，b＝5n2＋k，则a－b＝5(n1－n2)能被5整除，∴a－b∈[0]，∴③正确；对于④，若a－b∈[0]，则可设a－b＝5n，n∈Z，即a＝5n＋b，n∈Z，不妨令b＝5m＋k，m∈Z，k＝0,1,2,3,4，则a＝5n＋5m＋k＝5(m＋n)＋k，m∈Z，n∈Z，∴a，b属于同一“类”，∴④正确，则正确的有①③④，共3个．反思与感悟命题者以考试说明中的某一知识点为依托，自行定义新概念、新公式、新运算和新法则，做题者应准确理解应用此定义，在新的情况下完成某种推理证明或指定要求．跟踪训练4 定义集合运算：A※B＝{t|t＝xy，x∈A，y∈B}，设A＝{1,2}，B＝{0,2}，则集合A※B中的所有元素之和为________．考点集合的表示综合题点用另一种方法表示集合答案 6解析由题意得t＝0,2,4，即A※B＝{0,2,4}，又0＋2＋4＝6，故集合A※B中的所有元素之和为6.。

北师版高考理科数学一轮总复习课课时规范练1 集合的概念与运算

课时规范练1 集合的概念与运算基础巩固组1.(新高考Ⅱ,1)已知集合A={-1,1,2,4},B={x||x-1|≤1},则A∩B=()A.{-1,2}B.{1,2}C.{1,4}D.{-1,4}答案:B解析:B={x|0≤x≤2},则A∩B={1,2}.故选B.2.(福建模拟预测)设集合A={-2,-1,1,2,3},B={y|y=log2|x|,x∈A},则集合B元素的个数为( )A.2B.3C.4D.5答案:B解析:当x=±2时,y=1;当x=±1时,y=0;当x=3时,y=log23,故集合B共有3个元素.故选B.3.(河南郑州二模)已知集合A={x|x2=2x},集合B={x∈Z|0<x<3},则A∪B=( )A.{2}B.{0,1,2}C.{x|0<x<3}D.{x|0≤x<3}答案:B解析:x2=2x,解得x=2或x=0,所以A={0,2},B={1,2},所以A∪B={0,1,2},故选B.4.(广东广州三模)若a∈{1,3,a2},则a的可能取值有( )A.0B.0,1C.0,3D.0,1,3答案:C解析:若a=0,则a∈{1,3,0},符合题设;若a=1时,显然不满足集合中元素的互异性,不符合题设;若a=3时,则a∈{1,3,9},符合题设.∴a=0或a=3均可以.故选C.5.(湖南师大附中二模)已知集合A={x∈N|1<x<log2k},集合A中至少有2个元素,则( )A.k≥16B.k>16C.k≥8D.k>8答案:D解析:因为集合A中至少有2个元素,所以log2k>3,解得k>8,故选D. 6.(山东实验中学模拟预测)设全集U={-2,-1,0,1,2},A={-2,-1},B={-2,-1,0,1},则(∁U A)∩B=()A.{-2,-1}B.{0,1}C.{-1,0,1}D.{-2,-1,0,1}答案:B解析:由题意知,∁U A={0,1,2},则(∁U A)∩B={0,1},故选B.综合提升组7.某校高三(1)班有50名学生,春季运动会上,有15名学生参加了田赛项目,有20名学生参加了径赛项目,已知田赛和径赛都参加的有8名同学,则该班学生中田赛和径赛都没有参加的人数为( )A.27B.23C.15D.7答案:B解析:设由高三(1)班50名学生组成的集合为U,参加田赛项目的学生组成的集合为A,参加径赛项目的学生组成的集合为B,由题意集合A有15个元素,B有20个元素,A∩B中有8个元素,所以A∪B有15+20-8=27(个)元素.所以该班学生中田赛和径赛都没有参加的人数为50-27=23.8.(湖北华中师大一附中模拟)若集合A∪B=B∩C,则下列对于集合A,B,C 的关系中一定正确的是( )A.A⊆B⊆CB.B⊆C⊆AC.C⊆B⊆AD.B⊆A⊆C答案:A解析:由于A⊆A∪B=B∩C⊆B,同理知B⊆C,故A⊆B⊆C,故选A.9.设集合A={x|y=√x-2},B={y|y=√x-2},C={(x,y)|y=√x-2},则下列集合不为空集的是( )A.A∩BB.A∩CC.B∩CD.A∩B∩C答案:A解析:∵y=√x-2,∴x-2≥0,解得x≥2,则A=[2,+∞),又y=√x-2≥0,∴B=[0,+∞),C={(x,y)|y=√x-2},集合C中包含的元素为函数y=√x-2上点的坐标,则A∩B=[2,+∞),A∩C=⌀,B∩C=⌀,A∩B∩C=⌀.10.(江苏海安高级中学二模)设全集U={x|={x|x2-x<0},N={∪(∁)U N)=(A.(0,1)B.[0,1)C.(1,+∞)D.[0,+∞)答案:B解析:由x2-x<0,即x(={x|x2-x<0}={x|0<x<1},因为N={x|x≥1},U={x|x≥0},所以∁U N={x|0≤∪(∁U N)={x|0≤x<1},故选B.创新应用组11.(湖南岳阳一中一模)定义集合A,B的一种运算:A B={x|x=a2-b,a∈A,b∈B},若A={-1,0},B={1,2},则A B中元素的个数为( )A.1B.2C.3D.4答案:C解析:因为A B={x|x=a2-b,a∈A,b∈B},A={-1,0},B={1,2},所以AB={0,-1,-2},故集合A B中的元素个数为3,故选C.①若A具有性质P,则A可以是有限集;②若A1,A2具有性质P,且A1∩A2≠⌀,则A1∩A2具有性质P;③若A1,A2具有性质P,则A1∪A2具有性质P.答案:①②解析:对于①,取集合A={0,1}具有性质P,故A可以是有限集,故①正确;对于②,取x,y∈A1∩A2,则x∈A1,x∈A2,y∈A1,y∈A2,又A1,A2具有性质P,∴x+y∈A1,xy∈A1,x+y∈A2,xy∈A2,∴x+y∈A1∩A2,xy∈A1∩A2,所以A1∩A2具有性质P,故②正确;对于③,取A1={x|x=2k,k∈Z},A2={x|x=3k,k∈Z},2∈A1∪A2,3∈A1∪A2,但2+3∉A1∪A2,故③错误.。