河南省扶沟县中考数学第一轮复习 二次函数的应用 教案 人教新课标版【教案】
中考数学一轮复习 第12课时 二次函数(1)教案

二次函数最值和单调性,二次函数的最值和增减性的应用
教学方法:
自主探究合作交流讲练结合
教学媒体:
电子白板
【教学过程】:
一、知识梳理
1.二次函数:一般地,自变量x和因变量y之间存在如下关系:一般式:__________(a≠0,a、b、c为常数),则称y为x的二次函数。
2.二次函数的解析式三种形式。
3.二次函数的平移
问题3(1)已知抛物线 ,将抛物线c平移得到抛物线c′,如果两条抛物线,关于直线x=1对称,那么下列说法正确的是( )
A.将c沿x轴向右平移 个单位得到c′B.将c沿x轴向右平移4个单位得到c′
C .将c沿x轴向右平移 个单位得到c′D.将c沿x轴向右平移6个单位得到c′
(2)将抛物线y=(x+m)2向右平移2个单位后,对称轴是y轴,那么m的值 是 .
C.对称轴是直线x=﹣1,最小值是2 D.对称轴是直线x=﹣1,最大值2
2.(20 17•台湾)已知坐标平面上有两个二次函数y=a(x+1)(x﹣7),y=b (x+1)(x﹣15)的图形,其中a、b为整数.判断将二次函数y=b(x+1)(x﹣15)的图形依下列哪一种方式平移后, 会使得此两图形的对称轴重叠( )
(1)一般式:已知抛物线上的三点,通常设解析式为________________
(2)顶点式:已知抛物线顶点坐标(h, k),通常设抛物线解析式为_______________求出表达式后化为一般形式.
(3)交点式:已知抛物线 与x轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________求出表达式后化为一般形式.
③图象不经过第一象限;④当x>2时,y随x的增大而减小.
二次函数中考复习专题教案

二次函数中考复习专题教案一、教学目标1. 理解二次函数的定义、性质及图像;2. 掌握二次函数的求解方法,包括顶点式、标准式和一般式;3. 能够运用二次函数解决实际问题,提高数学应用能力;4. 培养学生的逻辑思维能力和团队合作精神。
二、教学内容1. 二次函数的定义与性质二次函数的定义:函数f(x) = ax^2 + bx + c(a≠0);二次函数的图像:开口方向、顶点、对称轴、单调区间。
2. 二次函数的图像与性质图像特点:开口方向、顶点、对称轴;性质:单调性、最值。
3. 二次函数的求解方法顶点式:f(x) = a(x h)^2 + k;标准式:f(x) = ax^2 + bx + c;一般式:ax^2 + bx + c = 0。
4. 实际问题求解应用二次函数解决几何问题;应用二次函数解决物理问题;应用二次函数解决生活中的问题。
5. 二次函数的综合应用二次函数与其他函数的结合;二次函数与方程组的结合;二次函数与不等式的结合。
三、教学过程1. 复习导入:回顾一次函数和指数函数的相关知识,为二次函数的学习打下基础;2. 知识讲解:分别讲解二次函数的定义、性质、图像与求解方法;3. 案例分析:分析实际问题,引导学生运用二次函数解决实际问题;4. 课堂练习:布置练习题,巩固所学知识;四、教学评价1. 课堂表现:观察学生在课堂上的参与程度、提问回答等情况;2. 练习完成情况:检查学生完成练习题的情况,巩固所学知识;3. 课后作业:布置课后作业,检查学生对知识的掌握程度;4. 小组讨论:评估学生在小组讨论中的表现,培养团队合作精神。
五、教学资源1. PPT课件:展示二次函数的相关概念、性质、图像等;2. 练习题:提供不同难度的练习题,巩固所学知识;3. 实际问题案例:提供与生活相关的实际问题,引导学生运用二次函数解决;4. 教学视频:讲解二次函数的求解方法和解题技巧。
六、教学策略1. 案例分析:通过分析具体案例,让学生了解二次函数在实际问题中的应用;2. 数形结合:利用图形展示二次函数的性质,加深学生对二次函数的理解;3. 小组讨论:鼓励学生进行小组讨论,培养团队合作精神和沟通能力;4. 分层教学:针对不同学生的学习水平,给予相应的指导和辅导;5. 激励评价:及时给予学生鼓励和评价,提高学生的学习积极性。
初中数学《二次函数的应用》教案

初中数学《二次函数的应用》教案2.3二次函数的应用教学目标设计1.知识与技能:通过本节学习,巩固二次函数y=ax2+bx+c (a0)的图象与性质,理解顶点与最值的关系,会用顶点的性质求解最值问题。
能力训练要求1、能够分析实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题的最大(小)值发展学生解决问题的能力,学会用建模的思想去解决其它和函数有关应用问题。
2、通过观察图象,理解顶点的特殊性,会把实际问题中的最值转化为二次函数的最值问题,通过动手动脑,提高分析解决问题的能力,并体会一般与特殊的关系,培养数形结合思想,函数思想。
情感与价值观要求1、在进行探索的活动过程中发展学生的探究意识,逐步养成合作交流的习惯。
2、培养学生学以致用的习惯,体会体会数学在生活中广泛的应用价值,激发学生学习数学的兴趣、增强自信心。
教学方法设计由于本节课是应用问题,重在通过学习总结解决问题的方法,故而本节课以“启发探究式”为主线开展教学活动,解决问题以学生动手动脑探究为主,必要时加以小组合作讨论,充分调动学生学习积极性和主动性,突出学生的主体地位,达到“不但使学生学会,而且使学生会学”的目的。
为了提高课堂效率,展示学生的学习效果,适当地辅以电脑多媒体技术。
教学过程导学提纲设计思路:最值问题又是生活中利用二次函数知识解决最常见、最有实际应用价值的问题之一,它生活背景丰富,学生比较感兴趣,对九年级学生来说,在学习了一次函数和二次函数图象与性质以后,对函数的思想已有初步认识,对分析问题的方法已会初步模仿,能识别图象的增减性和最值,但在变量超过两个的实际问题中,还不能熟练地应用知识解决问题,而面积问题学生易于理解和接受,故而在这儿作此调整,为求解最大利润等问题奠定基础。
从而进一步培养学生利用所学知识构建数学模型,解决实际问题的能力,这也符合新课标中知识与技能呈螺旋式上升的规律。
目的在于让学生通过掌握求面积最大这一类题,学会用建模的思想去解决其它和函数有关应用问题,此部分内容既是学习一次函数及其应用后的巩固与延伸,又为高中乃至以后学习更多函数打下坚实的理论和思想方法基础。
河南省扶沟县年中考数学第一轮复习统计与概率教案人教新课标版
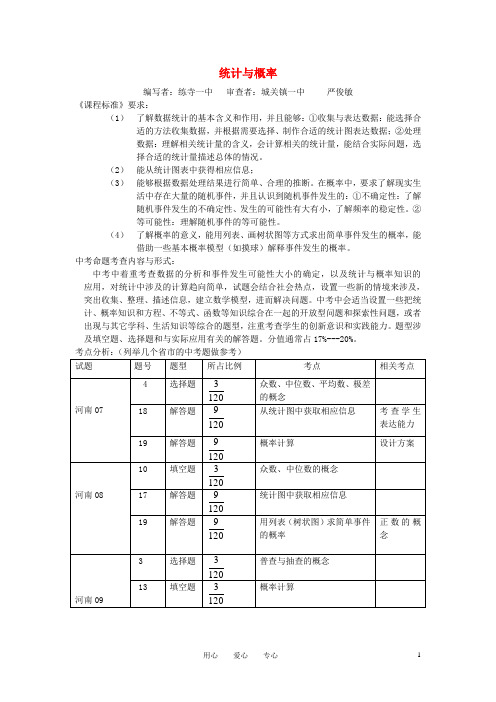
统计与概率编写者:练寺一中审查者:城关镇一中严俊敏《课程标准》要求:(1)了解数据统计的基本含义和作用,并且能够:①收集与表达数据:能选择合适的方法收集数据,并根据需要选择、制作合适的统计图表达数据;②处理数据:理解相关统计量的含义,会计算相关的统计量,能结合实际问题,选择合适的统计量描述总体的情况。
(2)能从统计图表中获得相应信息;(3)能够根据数据处理结果进行简单、合理的推断。
在概率中,要求了解现实生活中存在大量的随机事件,并且认识到随机事件发生的:①不确定性:了解随机事件发生的不确定性、发生的可能性有大有小,了解频率的稳定性。
②等可能性:理解随机事件的等可能性。
(4)了解概率的意义,能用列表、画树状图等方式求出简单事件发生的概率,能借助一些基本概率模型(如摸球)解释事件发生的概率。
中考命题考查内容与形式:中考中着重考查数据的分析和事件发生可能性大小的确定,以及统计与概率知识的应用,对统计中涉及的计算趋向简单,试题会结合社会热点,设置一些新的情境来涉及,突出收集、整理、描述信息,建立数学模型,进而解决问题。
中考中会适当设置一些把统计、概率知识和方程、不等式、函数等知识综合在一起的开放型问题和探索性问题,或者出现与其它学科、生活知识等综合的题型,注重考查学生的创新意识和实践能力。
题型涉及填空题、选择题和与实际应用有关的解答题。
分值通常占17%---20%。
第一节统计知识梳理有关概念:总体、个体、样本、样本容量,普查、抽样调查。
整理数据:三种统计图、频数分布表、频率分布直方图。
分析数据:集中趋势(平均数、众数、中位数)、波动大小(极差、方差、标准差)、分布规律(频数分布表,频率分布直方图)。
处理数据:(思想)用样本估计总体。
典型例题分析一、考查基本概念例1、九、4班某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):50、20、50、30、50、25、135,这组数据的众数和中位数分别是() A 、50,20 B 、50,30 C 、50,50 D、135,50解析:本题主要考查一组数的众数和中位数,将这组数据按从小到大排列为:20,25,30,50,50,50,135,易知众数和中位数分别是50,50,故选C。
中考数学一轮复习《二次函数》教学设计(精品)

二次函数复习教学设计学情分析:(1)学生对函数概念理解不全面,不深刻,不善于结合情境建立函数模型;对二次函数的图象性质理解肤浅,特别是函数的增减性和对称性;不会从已知条件提取信息,准确作出函数图象,或从函数图像获取信息来解决问题;对待定系数法求函数解析式中,不能准确设函数的类型,计算不过关,数形结合思想、函数方程思想、转化与化归意识不强。
(2)思考缺乏条理性,对函数综合性问题无从下手,有畏难情绪。
设计思想本节课安排三个活动,第一个活动是复习教学的启动,以小组讨论形式,让学生回顾二次函数的基础知识,梳理考点,第二个活动是学生先独立思考例题后再小组讨论,例1是围绕二次函数主干知识和思想方法,用问题串的形式训练,是作为函数基础复习第一层次,目的是让学生较为全面地梳理二次函数基础知识,并获得成功体验,树立信心,激发进一步探究的热情。
第三个开放性活动,根据函数图像编写中考题,对运用二次函数图象及性质的能力要求较高,是第一层次的拓展和深化,目的是让学生掌握二次函数的考点及考查类型,丰富数学活动经验,为后续二次函数综合题的探究做好铺垫,打好基础。
教学目标:1.了解二次函数的知识结构框架,进一步巩固二次函数概念2.掌握用待定系数法求二次函数的解析式;3.掌握二次函数的图像性质,并灵活运用二次函数的图像性质解决问题;4.通过探究进一步体会函数的一般研究方法及数形结合等思想,提高分析问题、解决问题的能力。
教学重点:二次函数的图像及性质。
教学难点:二次函数的知识结构框架的建立以及二次函数图像性质的灵活运用。
教学过程一、引入二、小组讨论1.二次函数包含哪些知识点?2.请用框架图或表格形式把知识点罗列出。
三、小组展示四、命题分析二次函数是海南中考必考的内容之一,常与几何知识综合作为压轴题出现。
二次函数考查有以下特点:考点一:二次函数解析式的确定;考点二:二次函数图象的性质(二次函数的开口方向、顶点、对称轴、增减性、最大(或最小)值等;考点三:二次函数图象的平移;考点四:二次函数与一元二次方程、不等式的关系;考点五:二次函数与几何图形的综合运用。
九年级数学上册《二次函数的应用》教案、教学设计

-通过动画展示二次函数图像的平移、伸缩等变换,使学生直观地感受图像的性质。
3.设计具有梯度的问题,引导学生逐步深入地掌握二次函数的知识。
-从简单的二次函数图像识别,到求解实际问题中的二次函数,逐步提高问题的难度。
4.采用小组合作、讨论交流的学习方式,促进学生之间的思维碰撞,共同解决难题。
5.学会运用二次函数的知识,解决生活中的实际问题,提高数学应用能力。
(二)过程与方法
在本章节的学习过程中,学生将通过以下方法培养数学思维与解决问题的能力:
1.通过小组合作、讨论交流,培养学生的合作意识和团队精神。
2.利用数形结合的方法,引导学生观察、分析二次函数的图像,培养学生直观想象和逻辑推理能力。
5.反思与总结:
-请同学们在作业本上写下本节课的学习心得,包括对二次函数的理解、学习过程中的困惑以及解题方法的总结。
-教师在批改作业时,应及时给予反馈,鼓励学生持续反思,不断提高。
4.通过小组合作,培养学生互相尊重、团结协作的品质,增强集体荣誉感。
5.引导学生认识到数学知识在实际生活中的重要性,培养学生的社会责任感和使命感。
二、学情分析
九年级的学生已经具备了一定的数学基础,掌握了线性方程、不等式等知识,对于函数的概念也有初步的理解。在此基础上,学生对二次函数的学习将面临以下挑战:
-完成课后作业中的基础题,旨在让学生通过实际操作,加深对二次函数图像特征的理解。
2.提高作业:
-选做课本第chapter页的提高题,涉及二次函数在实际问题中的应用,如最值问题、面积计算等,以提升学生解决问题的能力。
-设计一道综合性的应用题,要求学生运用本节课所学知识,结合生活实际,解决实际问题。
河南省扶沟县年中考数学第一轮复习数与式教案人教新课标版

九年级第一轮复习------数与式第一部分《数学课程标准》的考查要求一、实数1.在具体环境中,理解实数及其运算的意义。
2.能用数轴上的点表示实数,会比较实数的大小。
3.借助数轴理解相反数和绝对值的意义,会求相反数与绝对值。
4.了解平方根,算术平方根,立方根,无理数和实数,近似数,有效数字的概念。
会求某些数(非负数)的平方根与某些数的立方根。
5.会估算一个无理数的范围。
6.能运用实数及其运算法则解决简单的实际问题。
二、代数式1.会根据实际问题列代数式,理解代数式的含义,能理解一些简单代数式的实际背景或几何意义,体会数学与现实世界的联系。
2.理解合并同类项和去括号法则,并会进行运算。
3.会求代数式的值,能解释值的实际意义,能根据代数式的值推断代数式反映的规律。
4.根据数量关系或图形关系寻找规律,分析,归纳,总结两变量间的关系。
5.整式加减在运算时要注意同类项的识别和合并同类项的方法;在整式的乘除运算中要注意理解和区分幂的运算性质,记住乘法公式,理解其特点和应用范围。
6.弄清因式分解与整式乘法的区别,并加强对基本类型的练习。
会用提公因式法,公式法进行因式分解。
7.会利用分式的基本性质进行约分和通分。
会进行简单的分式加,减,乘,除运算。
第二部分考点分析作者:刘瑞莲严俊敏省份题号 题型 分值 考点 相关的其它考点 所占比例 2007年河南1 选择题 3 乘方的意义 15%2 选择题 3分式的定义 7 填空题 3 相反数的概念 8 填空题 3 整式的运算 12 填空题 3 实数的意义 13 填空题 3 数的规律探究题 2008年河南1 选择题 3绝对值的意义 14% 2 选择题 3 科学记数法的概念7 填空题 3 实数 16 解答题 8 分式的运算 2009年河南1 选择题 3相反数的概念 14% 7 填空题 3 平方根的意义 9 填空题 3 代数式的运算 16 解答题 8 分式的运算 分式的定义2009年北京1 选择题 4 相反数的概念18% 2 选择题 4科学记数法的概念7 选择题 4 因式分解 13 解答题 5 实数的运算 16 解答题 5 整式的运算 整体思想 2009年天津1 选择题 3实数的运算特殊三角函数值10% 3 选择题 3 绝对值的意义,二次根式 乘方的意义,非负数 11 填空题 3 二次根式的运算 12 填空题 3 分式的意义,分式的运算一元二次方程2009年重庆 1 选择题 4 相反数的概念 19% 2 选择题 4幂的运算 11 填空题 4科学记数法的概念 17 解答题 6 实数的运算 21 解答题 10 实数的运算 2009年河北1 选择题2 乘方的意义 18% 2 选择题 2 乘方的意义 4 选择题 2幂的运算,整式的运算 7 选择题 2 实数的意义及相关概念概率 13 填空题 3 实数的意义 16 填空题 3 倒数的意义 19 解答题 8 分式的运算 2009年山东 1 选择题 3实数的运算 14% 2 选择题 3幂的运算 13 填空题 4科学记数法的概念 18 解答题 7分式的运算数与式是初中数学的基础,中考着重对基本概念和计算能力的考查,题型以选择、填空及简单的解答题为主。
(名师整理)最新中考数学专题复习《二次函数的应用》精品教案

1中考数学人教版专题复习:二次函数的应用一、考点突破1. 掌握二次函数的对称轴求法;2. 理解二次函数的最值与其开口方向和对称轴的关系;3. 会分析自变量有一定取值范围的二次函数最值的求法。
二、重难点提示重点:会求二次函数的最值。
难点:当自变量有一定取值范围时,求二次函数的最值。
考点精讲1. 二次函数的最值求法(1)当自变量的取值范围为全体实数时,二次函数2(0)y ax bx c a =++≠在自变量x 取任意实数时的最值情况:24ac-b 024b a x a a>=-当时,函数在处取得最小值,无最大值;24ac-b 024b a x a a<=-当时,函数在处取得最大值,无最小值;【重要提示】自变量x 取任意实数。
(2)当自变量的取值范围不为全体实数时,二次函数2(0)y ax bx c a =++≠的自变量x ,不能取遍任意实数时的最值情况。
需作出函数在所给范围内的图象,观察图象的最高点和最低点,由此得到函数的最大值、最小值及函数取到最值时相应自变量x 的值。
2. 实际问题中的二次函数最值(1)二次函数与几何图形的面积最值问题; (2)二次函数与销售问题中的利润最值问题。
典例精析例题1 崇左市政府大楼前广场有一喷水池,水从地面喷出,喷出水的路径是一条抛物线。
如果以水平地面为x 轴,建立如图所示的平面直角坐标系,水在空中划出的曲线是抛物线y =-x 2+4x (单位:米)的一部分。
则水喷出的最大高度是多少?思路分析:根据题意,可以得到喷水的最大高度,就是水在空中划出的抛物线y=-x2+4x的顶点坐标的纵坐标,利用配方法或公式法,求得其顶点坐标的纵坐标,即为本题的答案。
答案:∵水在空中划出的曲线是抛物线y=-x2+4x,∴喷水的最大高度,就是水在空中划出的抛物线y=-x2+4x的顶点坐标的纵坐标,∴y=-x2+4x=-(x-2)2+4,∴顶点坐标为:(2,4),∴喷水的最大高度为4米,故答案为4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《二次函数》的应用教学目标:1.使学生掌握二次函数模型的建立,并能运用二次函数的知识解决实际问题。
2.能够分析和表示不同背景下实际问题中变量之间的二次函数关系,获得用数学方法解决实际问题的经验,感受数学模型、思想在实际问题中的应用价值。
重点难点:重点:利用二次函数的知识解决实际问题,并对解决问题的策略进行反思。
难点:将实际问题转化为函数问题,并利用函数的性质进行决策。
教学过程:一、例题精析,引导学法,指导建模1.何时获得最大利润问题。
例:重庆市某区地理环境偏僻,严重制约经济发展,丰富的花木产品只能在本地销售,区政府对该花木产品每投资x 万元,所获利润为P=-150(x -30)2+10万元,为了响应我国西部大开发的宏伟决策,区政府在制定经济发展的10年规划时,拟开发此花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元,若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路,且5年修通,公路修通后,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每投资x 万元可获利润Q=-4950(50-x)2+1945(50-x)+308万元。
(1)若不进行开发,求10年所获利润最大值是多少?(2)若按此规划开发,求10年所获利润的最大值是多少?(3)根据(1)、(2)计算的结果,请你用一句话谈谈你的想法。
学生活动:投影给出题目后,让学生先自主分析,小组进行讨论。
教师活动:在学生分析、讨论过程中,对学生进行学法引导,引导学生先了解二次函数的基本性质,并学会从实际问题中抽象出二次函数的模型,借助二次函数的性质来解决这类实际应用题。
教师精析:(1)若不开发此产品,按原来的投资方式,由P=-150(x -30)2+10知道,只需从50万元专款中拿出30万元投资,每年即可获最大利润10万元,则10年的最大利润为M 1=10×10=100万元。
(2)若对该产品开发,在前5年中,当x=25时,每年最大利润是:P =-150(25-30)2+10=9.5(万元) 则前5年的最大利润为M 2=9.5×5=47.5万元设后5年中x 万元就是用于本地销售的投资。
则由Q =-4950 (50-x)+1945(50-x)+308知,将余下的(50-x 万元全部用于外地销售的投资.才有可能获得最大利润; 则后5年的利润是: M 3=[-150(x -30)2+10]×5+(-4950x 2+1945x +308)×5=-5(x -20)2+3500 故当x =20时,M3取得最大值为3500万元。
∴ 10年的最大利润为M =M 2+M 3=3547.5万元(3)因为3547.5>100,所以该项目有极大的开发价值。
强化练习:某公司试销一种成本单价为500元/件的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看做—次函数y=kx+b的关系,如图所示。
(1)根据图象,求一次函数y=kx+b的表达式,(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元,①试用销售单价x表示毛利润S;②试问销售单价定为多少时,该公司可获得最大利润?最大利润是多少?此时的销售量是多少?分析:(1)由图象知直线y=kx+b过(600,400)、(700,300)两点,代入可求解析式为y=-x+1000(2)由毛利润S=销售总价-成本总价,可得S与x的关系式。
S=xy-500y=x·(-x+1000)-500(-x+100)=-x2+1500x-500000=-(x-750)2+62500 (500<x<800)所以,当销售定价定为750元时,获最大利润为62500元。
此时,y=-x+1000=-750+1000=250,即此时销售量为250件。
2.最大面积是多少问题。
例:某广告公司设计一幅周长为12米的矩形广告牌,广告设计费为每平方米1000元,设矩形的边长为x,面积为S平方米。
(1)求出S与x之间的函数关系式;(2)请你设计一个方案,使获得的设计费最多,并求出这个设计费用;(3)为了使广告牌美观、大方,要求做成黄金矩形,请你按要求设计,并计算出可获得的设计费是多少?(精确到元) (参与资料:①当矩形的长是宽与(长+宽)的比例中项时,这样的矩形叫做黄金矩形,②5≈2.236)学生活动:让学生根据已有的经验,根据实际几何问题中的数量关系,建立恰当的二次函数模型,并借助二次函数的相关知识来解决这类问题。
教师精析:(1)由矩形面积公式易得出S=x·(6-x)=-x2+6x(2)确定所建立的二次函数的最大值,从而可得相应广告费的最大值。
由S=-x2+6x=-(x-3)2+9,知当x=3时,即此矩形为边长为3的正方形时,矩形面积最大,为9m2,因而相应的广告费也最多:为9×1000=9000元。
(3)构建相应的方程(或方程组)来求出矩形面积,从而得到广告费用的大小。
设设计的黄金矩形的长为x米,则宽为(6-x)米。
则有x2=6·(6-x)解得x1=-3-3 5 (不合题意,舍去),x2=-3+35。
即设计的矩形的长为(35,3)米,宽为(9-35)米时,矩形为黄金矩形。
此时广告费用约为:1000(35-3)(9-35)≈8498(元)二、课堂小结:让学生谈谈.通过本节课的学习,有哪些体验,如何将实际问题转化为二次函数问题,从而利用二次函数的性质解决最大利润问题,最大面积问题。
三、作业: P28,复习题C组13~15题。
课后反思:二次函数的应用综合体现了二次函数性质的应用,同时,这类综合题与其他学过的知识有着密切的联系,最大利润问题,最大面积问题是实际生活中常见的问题,综合性强,解题的关键在于如何建立恰当的二次函数模型,建立正确的函数关系式,这一点应让学生有深刻的体会。
二次函数的应用专题训练1.某公司生产的A 种产品,它的成本是2元,售价为3元,年销售量为100万件,为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x(十万元)时,产品的年销售量将是原销售量的y 倍,且y =-110x 2+35x +1,如果把利润看成是销售总额减去成本费和广告费。
(1)试写出年利润S(十万元)与广告费x(十万元)的函数关系式.(2)如果投入广告费为10~30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增次?(3)在(2)中,投入的广告费为多少万元时,公司获得的年利润最大?是多少?2.如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可使用长度a =10米)。
(1)如果所围成的花圃的面积为45平方米,试求宽AB 的长;(2)按题目的设计要求,能围成面积比45平方米更大的花圃吗?如果能,请求出最大面积,并说明围法,如果不能请说明理由.3、(2009年重庆市江津区)某商场在销售旺季临近时 ,某品牌的童装销售价格呈上升趋势,假如这种童装开始时的售价为每件20元,并且每周(7天)涨价2元,从第6周开始,保持每件30元的稳定价格销售,直到11周结束,该童装不再销售。
(1)请建立销售价格y (元)与周次x 之间的函数关系;(2)若该品牌童装于进货当周售完,且这种童装每件进价z (元)与周次x 之间的关系为12)8(812+--=x z , 1≤ x ≤11,且x 为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?4、(2009年重庆市江津区)如图,抛物线c bx x y ++-=2与x 轴交与A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y 轴与C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P ,使△PBC 的面积最大?,若存在,求出点P 的坐标及△PBC 的面积最大值.若没有,请说明理由.5、(2009年滨州)某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:(1)若设每件降价x 元、每星期售出商品的利润为y 元,请写出y 与x 的函数关系式,并求出自变量x 的取值范围;(2)当降价多少元时,每星期的利润最大?最大利润是多少?(3)请画出上述函数的大致图象.6、(2009年黄冈市)新星电子科技公司积极应对2008年世界金融危机,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y (万元)与销售时间第x (月)之间的函数关系式(即前x 个月的利润总和y 与x 之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA 、曲线AB 和曲线BC ,其中曲线AB 为抛物线的一部分,点A 为该抛物线的顶点,曲线BC 为另一抛物线252051230y x x =-+-的一部分,且点A ,B ,C 的横坐标分别为4,10,12(1)求该公司累积获得的利润y (万元)与时间第x (月)之间的函数关系式;(2)直接写出第x 个月所获得S (万元)与时间x (月)之间的函数关系式(不需要写出计算过程);(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?7、(2009武汉)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.(1)求y与x的函数关系式并直接写出自变量x的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?8、(2009年广西南宁)如图14,要设计一个等腰梯形的花坛,花坛上底长120米,下底长180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.(1)用含x的式子表示横向甬道的面积;(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?图149、(2009年鄂州)24、如图所示.某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米。
