专题14 直线与圆(命题猜想)-2017年高考数学(文)命题猜想与仿真押题(原卷版)
09直线与圆(高考押题)-2017年高考数学(文)考纲解读与热点难点突破含解析

1.已知直线l:x+ay-1=0(a∈R)是圆C:x2+y2-4x-2y+1=0的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|=()A.2 B.4错误!C.6 D.2错误!【答案】C【解析】圆C的标准方程为(x-2)2+(y-1)2=4,圆心为C(2,1),半径为r=2,因此2+a×1-1=0,所以a=-1,从而A(-4,-1),|AB|=错误!=错误!=6。
2.已知圆x2+y2+mx-错误!=0与抛物线y=错误!x2的准线相切,则m=( )A.±2错误!B.±错误!C.错误!D。
错误!【答案】B【解析】抛物线的准线为y=-1,将圆化为标准方程得错误!2+y2=错误!,圆心到准线的距离为1=错误!⇒m=±3。
3.若动点A,B分别在直线l1:x+y-7=0和l2:x +y-5=0上运动,则AB的中点M到原点的距离最小值为( )A。
错误! B.2错误!C.3 2 D.4错误!【答案】C4.一条光线从点(-2,-3)射出,经y轴反射后与圆(x+3)2+(y-2)2=1相切,则反射光线所在直线的斜率为( )A.-错误!或-错误!B.-错误!或-错误!C.-错误!或-错误!D.-错误!或-错误!【答案】D5.两圆x2+y2+2ax+a2-4=0和x2+y2-4by-1+4b2=0恰有三条公切线,若a∈R,b∈R且ab≠0,则错误!+错误!的最小值为()A.1 B.3C。
错误! D.错误!【答案】A【解析】x2+y2+2ax+a2-4=0,即(x+a)2+y2=4,x2+y2-4by-1+4b2=0,即x2+(y-2b)2=1,依题意可得,两圆外切,则两圆心距离等于两圆的半径之和,则a2+2b2=1+2=3,即a2+4b2=9,所以错误!+错误!=错误!错误!=错误!错误!≥错误!错误!=1,当且仅当错误!=错误!即a=±错误!b时取等号,故选A.6.已知圆的方程为(x-1)2+(y-1)2=9,点P (2,2)是该圆内一点,过点P的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是( )A.3错误!B.4错误!C.57 D.6错误!【答案】D【解析】依题意,圆的最长弦为直径,最短弦为过点P垂直于直径的弦,所以|AC|=2×3=6。
2017年高考数学(文)黄金易错点:专题14-直线和圆(含答案)

1.已知圆M :x 2+y 2-2ay =0(a >0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是( )A .内切B .相交C .外切D .相离答案 B解析 ∵圆M :x 2+(y -a )2=a 2,2.已知点A (2,3),B (-3,-2),若直线kx -y +1-k =0与线段AB 相交,则k 的取值范围是( )A .34,2]B .(-∞,34]∪2,+∞) C .(-∞,1]∪2,+∞) D .1,2]答案 B解析 直线kx -y +1-k =0恒过点P (1,1),k P A =3-12-1=2,k PB =-2-1-3-1=34; 若直线kx -y +1-k =0与线段AB 相交,结合图象(图略)得k ≤34或k ≥2,故选B. 3.若方程(x -2cos θ)2+(y -2sin θ)2=1(0≤θ<2π)的任意一组解(x ,y )都满足不等式y ≥33x ,则θ的取值范围是( )A .π6,7π6] B .5π12,13π12] C .π2,π] D .π3,π] 答案 D 解析 根据题意可得,方程(x -2cos θ)2+(y -2sin θ)2=1(0≤θ<2π)的任意一组解(x ,y )都满足不等式y ≥33x ,表示方程(x -2cos θ)2+(y -2sin θ)2=1(0≤θ<2π)在y =33x 的左上方(包括相切), ∴⎩⎪⎨⎪⎧ |2sin θ-33×2cos θ|1+13≥1,2sin θ>33×2cos θ,∴sin ⎝⎛⎭⎫θ-π6≥12,∵0≤θ<2π,∴θ∈π3,π],故选D. 4.已知点P (x ,y )在直线x +2y =3上移动,当2x +4y 取得最小值时,过点P 引圆(x -12)2+(y +14)2=12的切线,则此切线段的长度为________. 答案 625.已知a ∈R ,方程a 2x 2+(a +2)y 2+4x +8y +5a =0表示圆,则圆心坐标是______________.半径是________.答案 (-2,-4) 5解析 由已知方程表示圆,则a 2=a +2,。
2017年高考数学理试题分类汇编:直线与圆
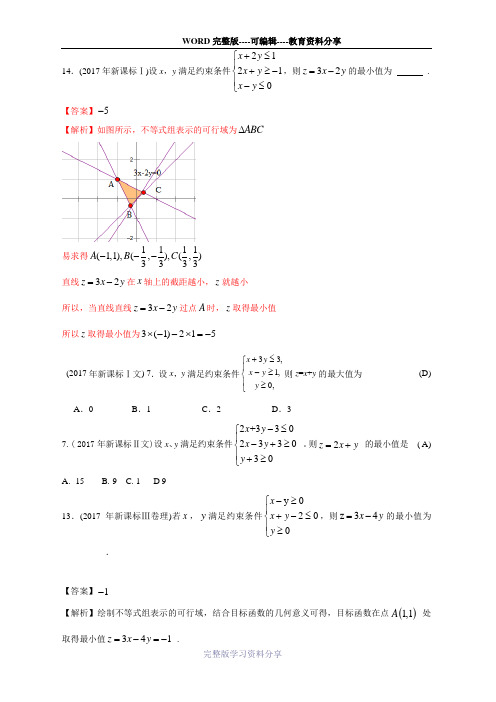
14.(2017年新课标Ⅰ)设x ,y 满足约束条件21210x y x y x y +≤⎧⎪+≥-⎨⎪-≤⎩,则32z x y =-的最小值为 .【答案】5-【解析】如图所示,不等式组表示的可行域为ABC ∆易求得1111(1,1),(,),(,)3333A B C ---直线32z x y =-在x 轴上的截距越小,z 就越小 所以,当直线直线32z x y =-过点A 时,z 取得最小值 所以z 取得最小值为3(1)215⨯--⨯=-(2017年新课标Ⅰ文) 7.设x ,y 满足约束条件33,1,0,x y x y y +≤⎧⎪-≥⎨⎪≥⎩则z =x +y 的最大值为 (D)A .0B .1C .2D .37. ( 2017年新课标Ⅱ文)设x 、y 满足约束条件2+330233030x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩。
则2z x y =+ 的最小值是 ( A)A. -15B.-9C. 1 D 913.(2017年新课标Ⅲ卷理)若x ,y 满足约束条件y 0200x x y y -≥⎧⎪+-≤⎨⎪≥⎩,则z 34x y =-的最小值为__________.【答案】1-【解析】绘制不等式组表示的可行域,结合目标函数的几何意义可得,目标函数在点()1,1A 处取得最小值341z x y =-=- .5. ( 2017年新课标Ⅱ卷理)设x ,y 满足约束条件2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩,则2z x y =+的最小值是( )A .15-B .9-C .1D .9 【答案】A4.(2017年浙江卷)若x ,y 满足约束条件03020x x y x y ≥⎧⎪+-≥⎨⎪-≤⎩,则z =x +2y 的取值范围是A .[0,6]B .[0,4]C .[6,+∞]D .[4,+∞]【答案】D【解析】可行域为一开放区域,所以直线过点(2,1)时取最小值4,无最大值,选D.(2017年江苏卷) 13.在平面直角坐标系xOy 中,(12,0),(0,6),A B -点P 在圆22:50O x y +=上,若20,PA PB ⋅≤则点P 的横坐标的取值范围是 ▲ .(2017年北京卷理) (4)若x ,y 满足32x x y y x ≤⎧⎪+≥⎨⎪≤⎩,,, 则x + 2y 的最大值为(A )1 (B )3 (C )5 (D )9 【答案】D【解析】如图,画出可行域,2z x y =+表示斜率为12-的一组平行线,当过点()3,3C 时,目标函数取得最大值max 3239z =+⨯=,故选D.(2017年江苏卷) [选修4-1:几何证明选讲](本小题满分10分)如图,AB 为半圆O 的直径,直线PC 切半圆O 于点C ,AP ⊥PC ,P 为垂足. 求证:(1)PAC CAB ∠=∠; (2)2AC AP AB =⋅.【选修4-1:几何证明选讲】(本小题满分10分)【解析】(1)因为PC 是圆O 的切线,所以PCA CBA =∠∠,又AP ⊥PC ,所以90PAC PCA +=︒∠∠,因为B 为半圆O 的直径,所以90CAB CBA +=︒∠∠,所以PAC CAB ∠=∠. (2)由(1)可得PAC CAB △∽△,所以PA AC CA AB=,所以2·AC AP AB =. 5.( 2017年全国Ⅲ卷文)设,x y 满足约束条件3260,0,0,x y x y +-≤⎧⎪≥⎨⎪≥⎩则z x y =-的取值范围是()A. []3,0-B.[]3,2-C.[]0,2 D []0,3 【答案】选B【解析】由题意,画出可行域,端点坐标 ()0,0O ,()0,3A ,()2,0B . 在端点,A B 处分别取的最小值与最大值. 所以最大值为2,最小值为3-. 故选B20( 2017年全国Ⅲ卷文)在直角坐标系xOy 中,曲线22-+=mx x y 与x 轴交于B A ,两点,点C 的坐标为(0,1)。
广州市普通高中2017届高三第一次模拟数学备考试题精选:直线和圆

广州市普通高中2017届高三第一次模拟数学备考试题精选:直线和圆1、过点(1,0)且与直线220x y --=平行的直线方程是 A .210x y +-= B .210x y -+= C .220x y +-= D .210x y --= 【答案】D【解析】设所求的平行直线方程为20x y c -+=,因为直线过点(1,0),所以10c +=,即1c =-,所以所求直线方程为210x y --=,选D.2、已知01cos sin 2=-+θθa a 与01cos sin 2=-+θθb b (b a ≠).直线MN 过点),(2a a M 与点),(2b b N ,则坐标原点到直线MN 的距离是 . 【答案】1【解析】由01cos sin 2=-+θθa a 与01cos sin 2=-+θθb b (b a ≠),可知,点),(2a a M 和),(2b b N 是直线sin cos 10y x θθ+-=上的两个点,所以直线MN 的方程为sin cos 10y x θθ+-=,所以原点到直线MN 的距离1d ==。
3、在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为11(,)P x y ,22(,)Q x y 两点之间的“折线距离”.则原点)0,0(O 与直线05=-+y x 上一点),(y x P 的“折线距离”的最小值是 ▲ .【解析】设(,)P x y ,直线05=-+y x 与坐标轴的交点坐标为A B ,直线的斜率为1k =-。
过P 做PM x ⊥于M ,则原点)0,0(O 与直线05=-+y x 上一点),(y x P 的“折线距离”为d OM MP =+,因为PMA 为等腰三角形,所以PM MA =,由图象可知d OM MP OM MA OA =+=+≥=M 在OA 的内部,所以原点)0,0(O 与直线05=-+y x 上一点),(y x P 的“折线距离”的最小距离为。
-2017年高考文科数学真题汇编:直线和圆老师版(可编辑修改word版)

学科教师辅导教案学员姓名 年 级 高三 辅导科目数 学授课老师课时数 2h第次课授课日期及时段2017 年月日:—:历年高考试题集锦——直线和圆1.(2012 辽宁文)将圆 x 2+y 2 -2x-4y+1=0 平分的直线是( C ) (A )x+y-1=0(B ) x+y+3=0 (C )x-y+1=0 (D )x-y+3=02.(2012 浙江文)设 a ∈R ,则“a =1”是“直线 l 1:ax+2y=0 与直线 l 2 :x+(a+1)y+4=0 平行的( A ) A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件3.(2014 湖南文)若圆C : x 2 + y 2 = 1 与圆C : x 2 + y 2 - 6x - 8 y + m = 0 外切,则 m = ( C )12A .21B .19C .9D . -114.(2012 ft 东文)圆(x + 2)2 + y 2 = 4 与圆(x - 2)2 + ( y -1)2 = 9 的位置关系为( B ) (A)内切(B)相交(C)外切(D)相离5.(2013 江西文)若圆 C 经过坐标原点和点(4,0),且与直线 y=1 相切,则圆 C 的方程是 。
【答案】(x - 2)2 + ( y + 3)2 =25246.(2012 安徽文)若直线 x - y +1 = 0 与圆(x - a )2 + y 2 = 2 有公共点,则实数 a 取值范围是(C )( A ) [-3, -1] (B ) [-1, 3] (C ) [-3,1] (D ) (-∞, -3] [1, +∞)7.(2013 安徽文)直线 x + 2 y - 5 + 5 = 0 被圆 x 2 + y 2 - 2x - 4 y = 0 截得的弦长为(C )(A )1 (B )2(C )4(D ) 4 68.(2014 安徽文)过点 P (- 3,-1)的直线 l 与圆 x 2 + y 2 = 1有公共点,则直线 l 的倾斜角的取值范围是( D )A (. 0, ]B (. 0, ] C.[0, ] D.[0, ] 6 3 6 39.(2012 福建文)直线 x + 3y - 2 = 0 与圆 x 2 + y 2 = 4 相交于 A , B 两点,则弦 AB 的长度等于( B )A . 2 5B . 2 3C . 3D .133 3 3 2 22 4 5 5广东文) 10(2012在平面直角坐标系 xOy 中,直线3x + 4 y - 5 = 0 与圆 x 2 + y 2 = 4 相交于 A , B 两点, 则弦 AB 的长等于(B )(A ) ) 3 (B )2 (C )(D )1已知点 M (a ,b )在圆O : x 2 + y 2 = 1 外, 则直线 ax + by = 1 与圆 O 的位置关系是( B )(A) 相切(B) 相交(C) 相离(D) 不确定已知圆 x 2 + y 2 + 2x - 2 y + a = 0 截直线 x + y + 2 = 0 所得弦的长度为4,则实数 a 的值为(B )A. - 2 B. - 4 C. - 6 D. - 813.(2013 天津文)已知过点 P (2,2)的直线与圆(x -1)2+y 2=5 相切,且与直线 ax -y +1=0 垂直,则 a 等于(1C ) A .-21B.1C .2 D.2【简解】圆心为 O (1,0),由于 P (2,2)在圆(x -1)2+y 2=5 上,∴P 为切点,OP 与 P 点处的切线垂直. 2-0∴K OP = =2,又点 P 处的切线与直线 ax -y +1=0 垂直.∴a =K OP =2,选 C.2-114.(2014 ft 东文)圆心在直线 x - 2 y = 0 上的圆C 与 y 轴的正半轴相切,圆C 截 x 轴所得弦的长为2 ,则圆C 的标准方程为 (x - 2)2 + ( y -1)2 = 4 。
高考物理 命题猜想与仿真押题 专题14 电学实验仿真押题(含解析)-人教版高三全册物理试题

电学实验仿真押题1.要测量某种合金的电阻率.图1(1)假设合金丝长度为L ,直径为D ,阻值为R ,如此其电阻率ρ=________. 用螺旋测微器测合金丝的直径如图1甲所示,读数为________mm.(2)图乙是测量合金丝阻值的原理图,S 2是单刀双掷开关.根据原理图在图丙中将实物连线补充完整. (3)闭合S 1,当S 2处于位置a 时,电压表和电流表的示数分别为U 1=1.35V ,I 1=0.30A ;当S 2处于位置b 时,电压表和电流表的示数分别为U 2=0.92V ,I 2=0.32A.根据以上测量数据判断,当S 2处于位置________(选填“a 〞或“b 〞)时,测量相对准确,测量值R x =________Ω.(结果保存两位有效数字) 答案 (1)πRD 24L 0.650 (2)见解析图 (3)b 2.9解析 (1)金属丝电阻:R =U I =ρL S =ρL πD22,如此电阻率:ρ=πRD24L;图示螺旋测微器可知,其示数为:0.5mm +15.0×0.01mm=0.650mm ; (2)实物连线图如下列图:(3)根据ΔU U 1=1.35-0.921.35≈0.32,而ΔI I 1=0.32-0.300.30≈0.07, 可知,使用电流表外接法测量相对准确,即S 2处于位置b , 根据欧姆定律,如此有:R x =0.920.32Ω≈2.9Ω2.如图4甲所示的金属工件,横截面外方内圆,外边长约为1cm 、内径约为0.5cm 、长度约为40cm. (1)某同学用游标卡尺测出横截面外边长如图乙所示,其读数a =__________cm.(2)应选用________来测量工件内径d ,选用________来测量工件长度L .(选填“毫米刻度尺〞、“游标卡尺〞或“螺旋测微器〞)(3)为了测出该金属工件的电阻率,该同学设计了如图丙所示的电路,请按设计的电路完成实物图丁的连线. (4)实验测得工件两端电压为U ,通过的电流为I ,写出该金属电阻率的表达式ρ=________.(用a 、d 、L 、U 、I 等字母表示)图4答案 (1)1.02 (2)游标卡尺 毫米刻度尺 (3)连线图见解析 (4)U 4a 2-πd 24IL解析 (1)游标卡尺读数a =1cm +0.1mm×2=1.02cm(2)应选用游标卡尺来测量工件内径d ,选用毫米刻度尺来测量工件长度L . (3)连线图如下列图.(4)因为R =U I =ρL S =ρL a 2-14πd2,解得ρ=U 4a 2-πd 24IL .3.某学习小组研究一个标有“3.6V1.8W〞的小电珠的伏安特性曲线,可供选用的器材如下: ①电流表A ,量程0~0.6A ,内阻约为0.2Ω; ②电压表V ,量程0~15V ,内阻约为15kΩ; ③滑动变阻器R ,阻值范围0~10Ω; ④学生电源E ,电动势为4V ,内阻不计; ⑤开关S 与导线假设干.图7(1)该学习小组中的某同学设计了如图7甲所示的电路进展测量,请按照图甲所示的实物图帮该同学将图乙中的电路图补充完整.(2)该同学在实验中发现,由于电压表的量程较大而造成读数误差很大,因而影响了测量结果.于是又从实验室找来一只量程为I g =100μA、内阻R g =1000Ω的灵敏电流计,想把该灵敏电流计改装成量程为5V 的电压表,如此需串联一个阻值为________Ω的电阻.(3)该同学用改装后的电压表进展实验,得到电流表读数I1和灵敏电流计读数I2如下表所示.请在图丙中的坐标纸上画出I1-I2图线.I1(A)00.190.300.370.430.460.480.49I2(μA)010203040506070(4)假设将该小电珠接在如图丁所示的电路中,如此该小电珠消耗的电功率约为________W.(电源的电动势为E=3.0V,内阻r=1.5Ω,定值电阻R0=4.5Ω,结果保存两位有效数字.提示:可作出该小电珠在此电路中的I-U图象帮助求解.)答案(1)如下列图(2)49000(3)如下列图(4)0.354.某同学设计了一个如图8甲所示的实验电路,用以测定电源的电动势和内阻,使用的实验器材为:待测一节干电池、电流表A(量程0.6A,内阻小于1Ω)、电流表A1(量程0.6A,内阻不知)、电阻箱(0~99.99Ω)、滑动变阻器(0~10Ω)、单刀双掷开关、单刀单掷开关各一个与导线假设干.考虑到干电池的内阻较小,电流表的内阻不能忽略.图8(1)该同学按图甲连线,闭合开关K,将开关S与C接通,通过调节滑动变阻器和电阻箱,读取电流表A的示数为0.20A、电流表A1的示数为0.60A、电阻箱(如图乙)的示数为________Ω,如此电流表A的内阻为________Ω.(2)利用图甲所示电路测定电源的电动势和内阻的实验步骤:①请同学们按图甲所示电路在图丙中的实物上完成实验所需的线路连接; ②断开开关K ,调节电阻箱R ,将开关S 接D ,记录电阻箱的阻值和电流表示数; ③重复实验步骤②进展屡次测量.(3)图丁是由实验数据绘出的1I-R 图象,由此求出干电池的电动势E =________V 、内阻r =________Ω.(计算结果保存两位有效数字) 答案 (1)0.10 0.20 (2)如下列图(3)1.5 0.25解析 (1)电阻箱的读数为0.10Ω;根据串并联电路的规律可知,流过电阻箱的电流I =0.60A -0.20A =0.40A ;电压U =0.10×0.40V=0.040V ,如此电流表内阻R A =0.0400.20Ω=0.20Ω (2)根据原理图可得出对应的实物图,连线如下列图;(3)将电流表内阻等效为电源内阻,根据闭合电路欧姆定律可知,I =Er ′+R,变形可得:1I =R E +r ′E,根据图象可知,1E =3.0-0.34.0V -1=0.675V -1,解得E ≈1.5V;r ′E =0.3A -1,解得r ′=0.45Ω;如此可知,电源内阻r =0.45Ω-0.20Ω=0.25Ω.5.有一个电压表V ,其内阻为30 kΩ、量程约25 V ~35 V ,共有30个均匀小格,但刻度数值已经模糊.为了测量其量程并重新刻度,现提供如下器材选用: 标准电压表V 1:量程0~3 V ,内阻为3 kΩ 标准电压表V 2:量程0~6 V ,内阻为1 kΩ 电流表A :量程0~3 A ,内阻未知 滑动变阻器R :总阻值1 kΩ 稳压电源E :30 V ,内阻不能忽略 电键、导线假设干(1)根据上述器材,有一位同学设计了如下列图的实验电路图,请指出此电路中测量局部存在的问题:________.(2)请设计一个合理的电路图,画在方框内,将所选用的器材用相应的符号表示(要求测量多组数据,并尽可能提高测量的准确度);选用记录数据中任一组,写出计算量程的表达式U g =________;式中各字母的意义是:________.答案 (1)电流表量程太大,电压表与电流表串联时实际流过电流表的电流太小,电流表的指针偏转不明显 (2)电路图如下列图300U 1N;N 为V 表指针所指格数,U 1为V 1表读数.解析 (1)此电路设计存在的问题:电流表A 的量程太大,电压表的内阻较大,电压表与其串联时实际流过电流表的电流太小,即电流表的指针偏转不明显.(2)由题意可知,待测电压表内阻,如此将两表串联接入电路,两表中的电流相等,由标准电表可求得电流值,通过计算可求得待测电压表的量程;因两电压表阻值较大,而滑动变阻器阻值较小,故滑动变阻器采用分压接法;故电路如答案图所示;由欧姆定律可求得,通过两电压表的电流为:I =U 13 000, 如此待测电压表两端的电压为:I ×30 000=10U 1 此时指针指示的格数为N ,如此有:N30×U m =10U 1;解得量程为:U g =300U 1N,其中N :直流电压表V 指针所指格数,U 1:标准电压表V 1的读数.6.要测量一只量程的电压表的内阻,所备器材如下: A .待测电压表V(量程3 V ,内阻约几千欧) B .电流表A(量程3 A ,内阻0.01 Ω) C .定值电阻R (阻值2 kΩ,额定电流50 mA) D .蓄电池E (电动势略小于3 V ,内阻不计) E .多用电表F .开关K 1、K 2,导线假设干有一同学利用上面所给器材,进展如下实验操作:(1)首先,用多用电表进展粗测,选用×100倍率,操作方法正确.假设这时刻度盘上的指针位置如图甲所示,如此测量的结果是________ Ω.(2)为了更准确地测出此电压表内阻,该同学设计了如下列图的乙、丙实验电路,你认为其中较合理的电路图是________.其理由是_________________________________________________________.(3)在图丁中,根据你选择的电路把实物连接好.(4)用你选择的电路进展实验时,请简述实验步骤:__________________________________________________________;(5)用上述所测量的符号表示电压表的内阻R V=________.答案(1)3 000 (2)丙;乙图中电流表的示数太小,误差太大.丙图中R的阻值与电压表阻值接近,误差小.(3)实物图连接如下列图:(4)实验步骤:①闭合K1,再闭合K2,读得电压表示数U1;再断开K2,读得电压表示数U2.②U2U1-U2R7.测定一卷阻值约为30 Ω的金属漆包线的长度,实验室提供如下器材:A.电流表A:量程0.6 A,内阻R A约为20 ΩB.电压表V:量程15 V,内阻R V约为4 kΩC.学生电源E:可提供0~30 V直流电压D.滑动变阻器R1:阻值范围0~10 ΩE.滑动变阻器R2:阻值范围0~500 ΩF.电键S与导线假设干(1)为了较准确地测量该漆包线的电阻,滑动变阻器应选择________(选填“R1〞或“R2〞),并将方框中的电路图补画完整.(2)根据正确的电路图进展测量,某次实验中电压表与电流表的示数如图,如此电压表的示数U 为________V ,电流表的示数I 为________A.(3)这种漆包线金属丝的直径为d ,材料的电阻率为ρ,如此这一卷漆包线的长度L =________(用U 、I 、d 、ρ表示).答案 (1)R 1 图见解析 (2)13.5、0.46 (3)πd 2U 4ρI解析 (1)题目中给出的电源电压为30 V ,而给出的电压表量程为15 V ,为了便于控制,采用滑动变阻器分压接法,故滑动变阻器选小电阻D (R 1); 电路图如下列图:(2)电压表量程为15 V ,故最小分度为0.5 V ,故读数为13.5 V ,电流表量程为0.6 A ,最小分度为0.02 A ,如此指针示数为:0.46 A ;(3)由电阻定律可知:R L =U I =ρL S =ρLπd22漆包线的长度:L =πd 2U4ρI8.甲、乙两位同学要测量一未知电阻R x 的阻值(阻值约1 kΩ),实验室提供的器材如下: A .待测电阻R xB .电源E :电动势约为3 VC.电流表A1:量程为5 mA,内阻r1不超过10 ΩD.电流表A2:量程为1 mA,内阻r2为50 ΩE.滑动变阻器R:最大阻值为50 ΩF.电阻箱R′:阻值0~9 999.9 ΩG.开关、导线假设干(1)由于没有电压表,甲同学利用电流表A2和电阻箱改装成一个量程为3 V的电压表,如此电流表A2应与电阻箱________(填“串联〞或“并联〞),电阻箱的阻值应为________ Ω.用○V表示A2改装后的电压表,在测量R x的以下实验电路中误差较小的是________.(2)为测量电阻R x,乙同学设计了如下电路,实验中只要保持滑动变阻器的滑片P位置固定,无论怎样调节电阻箱,分压电路的输出电压变化都很小.他的操作步骤如下:A.将滑动变阻器的滑片P放在最左端,闭合开关S;B.将电阻箱的阻值调节到零,调节滑动变器,使电流表A2的指针达到满偏;C.保持滑动变阻器的滑片不动,调节电阻箱,使电流表的指针达到半偏;D.读出电阻箱的示数,记为R0;E.断开开关,整理器材.请你根据量与测量量,写出待测电阻R x 的表达式________.该测量值与真实值相比________(填“偏大〞或“偏小〞).答案 (1)串联 2 950 B (2)R 0-r 2 偏大(2)根据串并联规律,当电流表满偏时应有:I A2=UR x +r 2①电流表半偏时应有12I A2=UR x +r 2+R 0②联立以上两式解得R x =R 0-r 2由于以上实验是在认为变阻器的输出电压不变的情况下得出的,实际上当电阻箱从零变大后,由电路动态分析可知变阻器的输出电压应变大,所以当电流表半偏时, ②式应为:12I A2=U ′R x +r 2+R 0③即U <U ′,比拟①③两式可得R x +r 2<R 0,所以R x <R 0-r 2,即测量值偏大.9.实际电流表有内阻,可等效为理想电流表与电阻的串联.测量实际电流表G 1内阻r 1的电路如图甲所示.供选择的仪器如下:①待测电流表G 1(0~5 mA ,内阻约300 Ω); ②电流表G 2(0~10 mA ,内阻约100 Ω); ③定值电阻R 1(300 Ω); ④定值电阻R 2(10 Ω);⑤滑动变阻器R 3(0~1 000 Ω); ⑥滑动变阻器R 4(0~20 Ω); ⑦干电池(1.5 V); ⑧开关S 与导线假设干.(1)定值电阻应选______,滑动变阻器应选______.(在空格内填写序号) (2)用连线连接如图乙所示的实物图.(3)测量多组电流表G 1、G 2的读数I 1、I 2,以I 2为纵坐标,I 1为横坐标,作出相应图线,如图丙所示.根据I 2-I 1图线的斜率k 与定值电阻(选定),写出待测电流表内阻的表达式________________________________________________________________________.(3)根据串、并联电路规律可知:I 2=I 1+I 1r 1R 1=R 1+r 1R 1I 1,所以k =R 1+r 1R 1,所以r 1=(k -1)R 1. 答案:(1)③ ⑥ (2)见解析图 (3)r 1=(k -1)R 110. (1)某同学用螺旋测微器测量一段粗细均匀的金属丝的直径,如下列图,直径d 为________mm.(2)该同学用多用电表测量其电阻阻值约为5 Ω,现用伏安法进一步准确测量其电阻,备有以下器材:直流电源E:电动势约4.5 V,内阻很小;直流电流表A1:量程0~3 A,内阻约0.025 Ω;直流电流表A2:量程0~0.6 A,内阻约0.125 Ω;直流电压表V:量程0~3 V,内阻约3 kΩ;滑动变阻器R1:最大阻值为50 Ω;开关、导线假设干.①在可选择的器材中应选用的电流表是________.(选填“A1〞或“A2〞)②仅从实验原理上看实验电路电阻的测量值________真实值.(选填“大于〞“小于〞或“等于〞)③如下列图实物连接图,还有两根导线没有连接,请补充完整.答案:(1)4.487(±0.002)(2)①A2②小于③如下列图11.为测定一节干电池(电动势约1.5 V,内阻约1.0 Ω)的电动势和内阻,实验室备有电流计G(满偏电流为3 mA,内阻为25 Ω)、定值电阻R0=0.126 Ω、开关和假设干导线与以下器材:A.量程0~3 V,内阻约1 000 Ω的电压表B.量程0~15 V,内阻约1 500 Ω的电压表C.总阻值为10 Ω、额定电流为2 A的滑动变阻器D.总阻值为100 Ω、额定电流为1 A的滑动变阻器(1)因电流计量程太小,需将R0与电流计________以扩大量程.(2)电压表应选择________;滑动变阻器应选择________.(填代号)(3)请在虚线框内完成实验电路图.(4)根据所画出的电路图,分析引起该实验系统误差的主要原因是________________________________________________________________________.答案:(1)并联(2)A C (3)如下列图(4)由于电压表的分流作用造成改装后电流表读数总是比电池实际输出电流小12.(1)某研究小组的同学为了测量某一电阻R x的阻值,甲同学先用多用电表进展粗测.使用多用电表欧姆挡时,将选择开关置于适宜的挡位后,必须先将两表笔短接,再进展________,使指针指在欧姆刻度的“0〞处.假设该同学将选择旋钮置于“×1〞位置,指针在刻度盘上停留的位置如图甲所示,如此所测量的电阻值为________Ω.(2)为进一步准确测量该电阻,实验台上摆放有以下器材:A.电流表(量程15 mA,内阻未知)B.电流表(量程0.6 A,内阻未知)C.电阻箱(最大电阻99.99 Ω)D.电阻箱(最大电阻999.9 Ω)E.电源(电动势3 V,内阻1 Ω)F.单刀单掷开关2只G.导线假设干乙同学设计的电路图如图乙所示,现按照如下实验步骤完成实验:①调节电阻箱,使电阻箱有适宜的阻值R1,仅闭合S1,使电流表指针有较大的偏转且读数为I;②调节电阻箱,保持开关S1闭合,闭合开关S2,调节电阻箱的阻值为R2,使电流表读数仍为I.a.根据实验步骤和实验器材规格可知,电流表应选择________,电阻箱应选择 ________.(填器材前字母) b.根据实验步骤可知,待测电阻R x=________(用题目所给测量量表示).(3)利用以上实验电路,闭合S2,调节电阻箱R,可测量出电流表的内阻R A,丙同学通过调节电阻箱R,读出多组R和I值,作出了1I-R图象如图丙所示.假设图象中纵轴截距为 1 A-1,如此电流表内阻R A=________Ω.答案:(1)欧姆调零18.0 (2)a.A D b.R2-R1(3)213.利用如图甲所示的电路测量某种电阻丝材料的电阻率,所用电阻丝的电阻约为20 Ω.带有刻度尺的木板上有a和b两个接线柱,把电阻丝拉直后固定在接线柱a和b上.在电阻丝上夹上一个带有接线柱c的小金属夹,沿电阻丝移动金属夹,可改变其与电阻丝接触点P的位置,从而改变接入电路中电阻丝的长度.可供选择的器材还有:电池组E〔电动势为3.0 V,内阻约为1 Ω〕;电流表A1〔量程0~100 mA,内阻约为5 Ω〕;电流表A2〔量程0~0.6 A,内阻约为0.2 Ω〕;电阻箱R〔0~999.9 Ω〕;开关、导线假设干.实验操作步骤如下:A.用螺旋测微器在电阻丝上三个不同的位置分别测量电阻丝的直径.B.将选用的实验器材,按照图甲连接实验电路.C.调节电阻箱使其接入电路中的电阻值较大.D.将金属夹夹在电阻丝上某位置,闭合开关,调整电阻箱的阻值,使电流表满偏,然后断开开关.记录电阻箱的电阻值R和接入电路的电阻丝长度L.E.改变金属夹与电阻丝接触点的位置,闭合开关,调整电阻箱的阻值,使电流表再次满偏.重复屡次,记录每一次电阻箱的电阻值R和接入电路的电阻丝长度L.F.断开开关,整理好器材.〔1〕某次测量电阻丝直径d 时,螺旋测微器示数如图乙所示,如此d =mm ;〔2〕实验中电流表应选择〔选填“A 1〞或“A 2〞〕;〔3〕用记录的多组电阻箱的阻值R 和对应的接入电路中电阻丝长度L 的数 据,绘出了如图丙所示的RL 关系图线,图线在R 轴的截距为R 0,在L 轴的截距 为L 0,再结合测出的电阻丝直径d ,写出电阻丝的电阻率表达式ρ=〔用给定的物理量符号和常数表示〕.〔4〕本实验中,电流表的内阻对电阻率的测量结果〔选填“有〞或 “无〞〕影响.答案 〔1〕0.728~0.732 〔2〕A 1 〔3〕πd 24L 0R 0 〔4〕无14.某学习小组通过实验来研究用电器Z 的导电规律。
直线与圆-高考理科数学压轴题分析详解

重点增分专题十 直线与圆[全国卷3年考情分析](1)圆的方程近几年成为高考全国课标卷命题的热点,需重点关注.此类试题难度中等偏下,多以选择题或填空题形式考查.(2)直线与圆的方程偶尔单独命题,单独命题时有一定的深度,有时也会出现在压轴题的位置,难度较大,对直线与圆的方程(特别是直线)的考查主要体现在圆锥曲线的综合问题上.考点一 直线的方程 保分考点·练后讲评 1.[两直线平行]已知直线l 1:(k -3)x +(4-k )y +1=0与直线l 2:2(k -3)x -2y +3=0平行,则k 的值是( )A .1或3B .1或5C .3或5D .1或2解析:选C 当k =4时,直线l 1的斜率不存在,直线l 2的斜率存在,所以两直线不平行;当k ≠4时,两直线平行的一个必要条件是3-k4-k =k -3,解得k =3或k =5,但必须满足1k -4≠32(截距不等)才是充要条件,经检验知满足这个条件. 2.[两直线垂直]已知直线mx +4y -2=0与2x -5y +n =0互相垂直,垂足为P (1,p ),则m -n +p 的值是( )A .24B .20C .0D .-4解析:选B ∵直线mx +4y -2=0与2x -5y +n =0互相垂直, ∴m -4×25=-1,∴m =10. 直线mx +4y -2=0,即5x +2y -1=0, 将垂足(1,p )代入,得5+2p -1=0,∴p =-2. 把P (1,-2)代入2x -5y +n =0,得n =-12, ∴m -n +p =20,故选B.3.[对称问题]坐标原点(0,0)关于直线x -2y +2=0对称的点的坐标是( ) A.⎝⎛⎭⎫-45,85 B.⎝⎛⎭⎫-45,-85 C.⎝⎛⎭⎫45,-85 D.⎝⎛⎭⎫45,85解析:选A 直线x -2y +2=0的斜率k =12,设坐标原点(0,0)关于直线x -2y +2=0对称的点的坐标是(x 0,y 0),依题意可得⎩⎪⎨⎪⎧x 02-2×y 02+2=0,y 0=-2x 0,解得⎩⎨⎧x 0=-45,y 0=85,即所求点的坐标是⎝⎛⎭⎫-45,85. 4.[两直线的交点与距离]已知直线l 过直线l 1:x -2y +3=0与直线l 2:2x +3y -8=0的交点,且点P (0,4)到直线l 的距离为2,则直线l 的方程为_________________.解析:由⎩⎪⎨⎪⎧ x -2y +3=0,2x +3y -8=0,得⎩⎪⎨⎪⎧x =1,y =2,所以直线l 1与l 2的交点为(1,2).显然直线x =1不符合,即所求直线的斜率存在,设所求直线的方程为y -2=k (x -1),即kx -y +2-k =0,因为P (0,4)到直线l 的距离为2,所以|-4+2-k |1+k 2=2,所以k =0或k =43.所以直线l的方程为y =2或4x -3y +2=0.答案:y =2或4x -3y +2=0[解题方略]1.两直线的位置关系问题的解题策略求解与两条直线平行或垂直有关的问题时,主要是利用两条直线平行或垂直的充要条件,即斜率相等且纵截距不相等或斜率互为负倒数.若出现斜率不存在的情况,可考虑用数形结合的方法去研究或直接用直线的一般式方程判断.2.轴对称问题的两种类型及求解方法考点二 圆的方程 保分考点·练后讲评 [大稳定——常规角度考双基]1.[由圆的方程求参数范围]若方程x 2+y 2+ax +2ay +2a 2+a -1=0表示圆,则实数a 的取值范围是( )A .(-∞,-2) B.⎝⎛⎭⎫-23,0 C .(-2,0)D.⎝⎛⎭⎫-2,23 解析:选D 若方程表示圆,则a 2+(2a )2-4(2a 2+a -1)>0,化简得3a 2+4a -4<0,解得-2<a <23.2.[求圆的标准方程]已知圆C 的圆心在x 轴的正半轴上,点M (0,5)在圆C 上,且圆心到直线2x -y =0的距离为455,则圆C 的标准方程为________. 解析:设C (a,0)(a >0),由题意知|2a |5=455,解得a =2,所以r =22+(5)2=3,故圆C 的标准方程为(x -2)2+y 2=9.答案:(x -2)2+y 2=9[解题方略] 求圆的方程的2种方法几何法 通过研究圆的性质、直线和圆、圆与圆的位置关系,从而求得圆的基本量和方程 代数法 用待定系数法先设出圆的方程,再由条件求得各系数,从而求得圆的方程[小创新——变换角度考迁移]1.[与平面向量交汇]已知圆M :x 2+y 2-2x +a =0,若AB 为圆M 的任意一条直径,且OA ―→·OB ―→=-6(其中O 为坐标原点),则圆M 的半径为( )A. 5B. 6C.7D .2 2解析:选C 圆M 的标准方程为(x -1)2+y 2=1-a (a <1),圆心M (1,0),则|OM |=1,圆的半径r =1-a ,因为AB 为圆M 的任意一条直径,所以MA ―→=-MB ―→,且|MA ―→|=|MB ―→|=r ,则OA ―→·OB ―→=(OM ―→+MA ―→)·(OM ―→+MB ―→)=(OM ―→-MB ―→)·(OM ―→+MB ―→)=OM ―→2-MB ―→2=1-r 2=-6,所以r 2=7,得r =7,所以圆的半径为7,故选C.2.[与概率的交汇]向圆(x -2)2+(y -3)2=4内随机投掷一点,则该点落在x 轴下方的概率为________.解析:如图,连接CA ,CB ,依题意,圆心C 到x 轴的距离为3,所以弦AB 的长为2.又圆的半径为2,所以弓形ADB 的面积为12×23π×2-12×2×3=23π-3,所以向圆(x -2)2+(y -3)2=4内随机投掷一点,则该点落在x 轴下方的概率P =23π-34π=16-34π.答案:16-34π考点三 直线与圆的位置关系 增分考点·广度拓展 [分点研究]题型一 圆的切线问题[例1] (1)(2019届高三·苏州高三调研)在平面直角坐标系xOy 中,已知过点M (1,1)的直线l 与圆(x +1)2+(y -2)2=5相切,且与直线ax +y -1=0垂直,则实数a =________.(2)设点M (x 0,y 0)为直线3x +4y =25上一动点,过点M 作圆x 2+y 2=2的两条切线,切点为B ,C ,则四边形OBMC 面积的最小值为________.[解析] (1)由题意得,直线l 的斜率存在,设过点M (1,1)的直线l 的方程为y -1=k (x-1),即kx -y +1-k =0.因为直线l 与圆(x +1)2+(y -2)2=5相切,所以圆心(-1,2)到直线l 的距离d =|-k -2+1-k |k 2+1=5,整理得k 2-4k +4=0,解得k =2.又直线l 与直线ax +y-1=0垂直,所以-2a =-1,解得a =12.(2)圆心O 到直线3x +4y =25的距离d =259+16=5, 则|OM |≥d =5, 所以切线长|MB |=|OM |2-2≥d 2-2=23,所以S 四边形OBMC =2S △OBM ≥2×12×23×2=46.[答案] (1)12(2)46[变式1] 本例(2)变为:过点A (1,3),作圆x 2+y 2=2的两条切线,切点为B ,C ,则四边形OBAC 的面积为________.解析:由相切可得S 四边形OBAC =2S △OBA ,因为△OAB 为直角三角形,且|OA |=10,|OB |=2, 所以|AB |=22,即S △OBA =12×22×2=2,所以S 四边形OBAC =2S △OBA =4. 答案:4[变式2] 本例(2)变为:设点M (x 0,y 0)为直线3x +4y =25上一动点,过点M 作圆x 2+y 2=2的两条切线l 1,l 2,则l 1与l 2的最大夹角的正切值是________.解析:设一个切点为B ,圆心O 到直线3x +4y =25的距离为d =259+16=5, 则tan ∠OMB =|OB ||MB |≤223,所以tan 2∠OAB =2tan ∠OAB1-tan 2∠OAB=21tan ∠OAB-tan ∠OAB≤24621.故所求最大夹角的正切值为24621. 答案:24621[解题方略] 直线与圆相切问题的解题策略直线与圆相切时利用“切线与过切点的半径垂直,圆心到切线的距离等于半径”建立关于切线斜率的等式,所以求切线方程时主要选择点斜式.过圆外一点求解切线段长的问题,可先求出圆心到圆外点的距离,再结合半径利用勾股定理计算.题型二 圆的弦长问题[例2] 已知圆C 经过点A (-2,0),B (0,2),且圆心C 在直线y =x 上,又直线l :y =kx +1与圆C 相交于P ,Q 两点.(1)求圆C 的方程;(2)过点(0,1)作直线l 1与l 垂直,且直线l 1与圆C 交于M ,N 两点,求四边形PM Q N 面积的最大值.[解] (1)设圆心C (a ,a ),半径为r ,因为圆C 经过点A (-2,0),B (0,2),所以|AC |=|BC |=r ,即(a +2)2+(a -0)2=(a -0)2+(a -2)2=r ,解得a =0,r =2,故所求圆C 的方程为x 2+y 2=4.(2)设圆心C 到直线l ,l 1的距离分别为d ,d 1,四边形PM Q N 的面积为S . 因为直线l ,l 1都经过点(0,1),且l 1⊥l ,根据勾股定理,有d 21+d 2=1.又|P Q |=2×4-d 2,|MN |=2×4-d 21,所以S =12|P Q |·|MN |,即S =12×2×4-d 2×2×4-d 21=216-4(d 21+d 2)+d 21d 2=212+d 21d 2≤212+⎝ ⎛⎭⎪⎫d 21+d 222=212+14=7,当且仅当d 1=d 时,等号成立, 所以四边形PM Q N 面积的最大值为7. [解题方略] 求解圆的弦长的3种方法[多练强化]1.(2018·全国卷Ⅰ)直线y =x +1与圆x 2+y 2+2y -3=0交于A ,B 两点,则|AB |=________.解析:由x 2+y 2+2y -3=0,得x 2+(y +1)2=4.∴圆心C (0,-1),半径r =2.圆心C (0,-1)到直线x -y +1=0的距离d =|1+1|2=2,∴|AB |=2r 2-d 2=24-2=2 2.答案:2 22.已知过点A (0,1)且斜率为k 的直线l 与圆C :(x -2)2+(y -3)2=1交于M ,N 两点,若|MN |=255,则直线l 的方程为________. 解析:直线l 的方程为y =kx +1,圆心C (2,3)到直线l 的距离d =|2k -3+1|k 2+1=|2k -2|k 2+1,由R 2=d 2+⎝⎛⎭⎫|MN |22,得1=(2k -2)2k 2+1+15,解得k =2或12,故所求直线l 的方程为y =2x +1或y =12x +1.答案:y =2x +1或y =12x +13.已知从圆C :(x +1)2+(y -2)2=2外一点P (x 1,y 1)向该圆引一条切线,切点为M ,O 为坐标原点,且有|PM |=|PO |,则当|PM |取最小值时点P 的坐标为________.解析:如图所示,连接CM ,CP .由题意知圆心C (-1,2),半径r = 2.因为|PM |=|PO |,所以|PO |2+r 2=|PC |2,所以x 21+y 21+2=(x 1+1)2+(y 1-2)2,即2x 1-4y 1+3=0.要使|PM |的值最小,只需|PO |的值最小即可.当PO 垂直于直线2x -4y +3=0时,即PO所在直线的方程为2x +y =0时,|PM |的值最小,此时点P 为两直线的交点,则⎩⎪⎨⎪⎧2x -4y +3=0,2x +y =0,解得⎩⎨⎧x =-310,y =35,故当|PM |取最小值时点P 的坐标为⎝⎛⎭⎫-310,35. 答案:⎝⎛⎭⎫-310,35数学建模——直线与圆最值问题的求解[典例] 已知圆O :x 2+y 2=9,过点C (2,1)的直线l 与圆O 交于P ,Q 两点,则当△OP Q 的面积最大时,直线l 的方程为( )A .x -y -3=0或7x -y -15=0B .x +y +3=0或7x +y -15=0C .x +y -3=0或7x -y +15=0D .x +y -3=0或7x +y -15=0[解析] 当直线l 的斜率不存在时,l 的方程为x =2,则P (2,5),Q (2,-5),所以S △OP Q =12×2×25=25,当直线l 的斜率存在时,设l 的方程为y -1=k (x -2)⎝⎛⎭⎫k ≠12,则圆心到直线l 的距离d =|1-2k |1+k 2,所以|P Q |=29-d 2,S △OP Q =12×|P Q |×d =12×29-d 2×d= (9-d 2)d 2≤9-d 2+d 22=92,当且仅当9-d 2=d 2,即d 2=92时,S △OP Q 取得最大值92,因为25<92,所以S △OP Q 的最大值为92,此时4k 2-4k +1k 2+1=92,解得k =-1或k =-7,此时直线l 的方程为x +y -3=0或7x +y -15=0,故选D.[答案] D [素养通路]本题考查了直线与圆的最值问题,结合题目的条件,设元、列式、建立恰当的函数,利用基本不等式模型解决相关的最值问题.考查了数学建模这一核心素养.[专题过关检测]A 组——“6+3+3”考点落实练一、选择题1.“ab =4”是“直线2x +ay -1=0与直线bx +2y -2=0平行”的( ) A .充要条件 B .充分不必要条件 C .必要不充分条件D .既不充分也不必要条件解析:选C 因为两直线平行,所以斜率相等,即-2a =-b 2,可得ab =4,又当a =1,b =4时,满足ab =4,但是两直线重合,故选C.2.已知直线l 1过点(-2,0)且倾斜角为30°,直线l 2过点(2,0)且与直线l 1垂直,则直线l 1与直线l 2的交点坐标为( )A .(3,3)B .(2,3)C .(1,3)D.⎝⎛⎭⎫1,32 解析:选C 直线l 1的斜率k 1=tan 30°=33,因为直线l 2与直线l 1垂直,所以直线l 2的斜率k 2=-1k 1=-3,所以直线l 1的方程为y =33(x +2),直线l 2的方程为y =-3(x -2),联立⎩⎪⎨⎪⎧y =33(x +2),y =-3(x -2),解得⎩⎪⎨⎪⎧x =1,y =3,即直线l 1与直线l 2的交点坐标为(1,3).3.已知圆M :x 2+y 2-2ay =0(a >0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是( )A .内切B .相交C .外切D .相离解析:选B 圆M :x 2+y 2-2ay =0(a >0)可化为x 2+(y -a )2=a 2,由题意,M (0,a )到直线x +y =0的距离d =a 2,所以a 2=a 22+2,解得a =2.所以圆M :x 2+(y -2)2=4,所以两圆的圆心距为2,半径和为3,半径差为1,故两圆相交.4.(2018·全国卷Ⅲ)直线x +y +2=0分别与x 轴,y 轴交于A ,B 两点,点P 在圆(x -2)2+y 2=2上,则△ABP 面积的取值范围是( )A .[2,6]B .[4,8]C .[2,32]D .[22,32]解析:选A 设圆(x -2)2+y 2=2的圆心为C ,半径为r ,点P 到直线x +y +2=0的距离为d ,则圆心C (2,0),r =2,所以圆心C 到直线x +y +2=0的距离为|2+2|2=22,可得d max =22+r =32,d min =22-r = 2. 由已知条件可得|AB |=22,所以△ABP 面积的最大值为12|AB |·d max =6,△ABP 面积的最小值为12|AB |·d min =2.综上,△ABP 面积的取值范围是[2,6].5.已知圆O :x 2+y 2=4上到直线l :x +y =a 的距离等于1的点至少有2个,则实数a 的取值范围为( )A .(-32,32)B .(-∞,-32)∪(32,+∞)C .(-22,22)D .[-32,3 2 ]解析:选A 由圆的方程可知圆心为(0,0),半径为2.因为圆O 上到直线l 的距离等于1的点至少有2个,所以圆心到直线l 的距离d <r +1=2+1,即d =|-a |12+12=|a |2<3,解得a ∈(-32,32).6.在平面直角坐标系中,O 为坐标原点,直线x -ky +1=0与圆C :x 2+y 2=4相交于A ,B 两点,OM ―→=OA ―→+OB ―→,若点M 在圆C 上,则实数k 的值为( )A .-2B .-1C .0D .1解析:选C 法一:设A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧x -ky +1=0,x 2+y 2=4得(k 2+1)y 2-2ky -3=0,则Δ=4k 2+12(k 2+1)>0,y 1+y 2=2k k 2+1,x 1+x 2=k (y 1+y 2)-2=-2k 2+1,因为OM ―→=OA ―→+OB ―→,故M ⎝⎛⎭⎪⎫-2k 2+1,2k k 2+1,又点M 在圆C 上,故4(k 2+1)2+4k 2(k 2+1)2=4,解得k =0. 法二:由直线与圆相交于A ,B 两点,OM ―→=OA ―→+OB ―→,且点M 在圆C 上,得圆心C (0,0)到直线x -ky +1=0的距离为半径的一半,为1,即d =11+k 2=1,解得k =0.二、填空题7.已知直线l :x +my -3=0与圆C :x 2+y 2=4相切,则m =________.解析:因为圆C :x 2+y 2=4的圆心为(0,0),半径为2,直线l :x +my -3=0与圆C :x 2+y 2=4相切,所以2=31+m 2,解得m =±52 .答案:±528.过点C (3,4)作圆x 2+y 2=5的两条切线,切点分别为A ,B ,则点C 到直线AB 的距离为________.解析:以OC 为直径的圆的方程为⎝⎛⎭⎫x -322+(y -2)2=⎝⎛⎭⎫522,AB 为圆C 与圆O :x 2+y 2=5的公共弦,所以AB 的方程为x 2+y 2-⎣⎡⎦⎤⎝⎛⎭⎫x -322+(y -2)2=5-254,化简得3x +4y -5=0,所以C 到直线AB 的距离d =|3×3+4×4-5|32+42=4.答案:49.(2018·贵阳适应性考试)已知直线l :ax -3y +12=0与圆M :x 2+y 2-4y =0相交于A ,B 两点,且∠AMB =π3,则实数a =________.解析:直线l 的方程可变形为y =13ax +4,所以直线l 过定点(0,4),且该点在圆M 上.圆的方程可变形为x 2+(y -2)2=4,所以圆心为M (0,2),半径为2.如图,因为∠AMB =π3,所以△AMB 是等边三角形,且边长为2,高为3,即圆心M 到直线l 的距离为3,所以|-6+12|a 2+9=3,解得a =±3.答案:±3 三、解答题10.已知圆(x -1)2+y 2=25,直线ax -y +5=0与圆相交于不同的两点A ,B . (1)求实数a 的取值范围;(2)若弦AB 的垂直平分线l 过点P (-2,4),求实数a 的值. 解:(1)把直线ax -y +5=0代入圆的方程, 消去y 整理,得(a 2+1)x 2+2(5a -1)x +1=0, 由于直线ax -y +5=0交圆于A ,B 两点, 故Δ=4(5a -1)2-4(a 2+1)>0, 即12a 2-5a >0,解得a >512或a <0,所以实数a 的取值范围是(-∞,0)∪⎝⎛⎭⎫512,+∞. (2)由于直线l 为弦AB 的垂直平分线,且直线AB 的斜率为a , 则直线l 的斜率为-1a,所以直线l 的方程为y =-1a (x +2)+4,即x +ay +2-4a =0,由于l 垂直平分弦AB , 故圆心M (1,0)必在l 上,所以1+0+2-4a =0, 解得a =34,由于34∈⎝⎛⎭⎫512,+∞, 所以a =34.11.已知以点A (-1,2)为圆心的圆与直线l 1:x +2y +7=0相切.过点B (-2,0)的动直线l 与圆A 相交于M ,N 两点.(1)求圆A 的方程;(2)当|MN |=219时,求直线l 的方程. 解:(1)设圆A 的半径为R .因为圆A 与直线l 1:x +2y +7=0相切,所以R =|-1+4+7|5=2 5.所以圆A 的方程为(x +1)2+(y -2)2=20.(2)当直线l 与x 轴垂直时,易知x =-2符合题意; 当直线l 与x 轴不垂直时,设直线l 的方程为y =k (x +2),即kx -y +2k =0.由于|MN |=219,于是⎝ ⎛⎭⎪⎪⎫|-k -2+2k |k 2+12+(19)2=20,解得k =34, 此时,直线l 的方程为3x -4y +6=0.所以所求直线l 的方程为x =-2或3x -4y +6=0.12.在平面直角坐标系xOy 中,直线x -y +1=0截以原点O 为圆心的圆所得的弦长为6.(1)求圆O 的方程;(2)若直线l 与圆O 相切于第一象限,且直线l 与坐标轴交于点D ,E ,当线段DE 的长度最小时,求直线l 的方程.解:(1)因为点O 到直线x -y +1=0的距离为12, 所以圆O 的半径为⎝⎛⎭⎫122+⎝⎛⎭⎫622=2, 故圆O 的方程为x 2+y 2=2.(2)设直线l 的方程为x a +yb =1(a >0,b >0),即bx +ay -ab =0, 由直线l 与圆O 相切,得|-ab |b 2+a2=2,即1a 2+1b 2=12,则|DE |2=a 2+b 2=2(a 2+b 2)⎝⎛⎭⎫1a 2+1b 2=4+2b 2a 2+2a 2b2≥8,当且仅当a =b =2时取等号,此时直线l 的方程为x +y -2=0.B 组——大题专攻补短练1.已知点M (-1,0),N (1,0),曲线E 上任意一点到点M 的距离均是到点N 的距离的3倍.(1)求曲线E 的方程;(2)已知m ≠0,设直线l 1:x -my -1=0交曲线E 于A ,C 两点,直线l 2:mx +y -m =0交曲线E 于B ,D 两点.当CD 的斜率为-1时,求直线CD 的方程.解:(1)设曲线E 上任意一点的坐标为(x ,y ), 由题意得(x +1)2+y 2=3·(x -1)2+y 2,整理得x 2+y 2-4x +1=0,即(x -2)2+y 2=3为所求. (2)由题意知l 1⊥l 2,且两条直线均恒过点N (1,0).设曲线E 的圆心为E ,则E (2,0),设线段CD 的中点为P ,连接EP ,ED ,NP ,则直线EP :y =x -2.设直线CD :y =-x +t ,由⎩⎪⎨⎪⎧y =x -2,y =-x +t ,解得点P ⎝ ⎛⎭⎪⎫t +22,t -22, 由圆的几何性质,知|NP |=12|CD |=|ED |2-|EP |2,而|NP |2=⎝ ⎛⎭⎪⎫t +22-12+⎝ ⎛⎭⎪⎫t -222,|ED |2=3, |EP |2=⎝ ⎛⎭⎪⎫|2-t |22,所以⎝⎛⎭⎫t 22+⎝ ⎛⎭⎪⎫t -222=3-(t -2)22,整理得t 2-3t =0, 解得t =0或t =3,所以直线CD 的方程为y =-x 或y =-x +3.2.在平面直角坐标系xOy 中,点A (0,3),直线l :y =2x -4,设圆C 的半径为1,圆心在l 上.(1)若圆心C 也在直线y =x -1上,过点A 作圆C 的切线,求切线的方程; (2)若圆C 上存在点M ,使|MA |=2|MO |,求圆心C 的横坐标a 的取值范围. 解:(1)因为圆心在直线l :y =2x -4上,也在直线y =x -1上,所以解方程组⎩⎪⎨⎪⎧y =2x -4,y =x -1,得圆心C (3,2),又因为圆的半径为1,所以圆的方程为(x -3)2+(y -2)2=1,又因为点A (0,3),显然过点A ,圆C 的切线的斜率存在, 设所求的切线方程为y =kx +3,即kx -y +3=0, 所以|3k -2+3|k 2+12=1,解得k =0或k =-34,所以所求切线方程为y =3或y =-34x +3,即y -3=0或3x +4y -12=0.(2)因为圆C 的圆心在直线l :y =2x -4上, 所以设圆心C 为(a,2a -4), 又因为圆C 的半径为1,则圆C 的方程为(x -a )2+(y -2a +4)2=1. 设M (x ,y ),又因为|MA |=2|MO |,则有 x 2+(y -3)2=2x 2+y 2,整理得x 2+(y +1)2=4,其表示圆心为(0,-1),半径为2的圆,设为圆D , 所以点M 既在圆C 上,又在圆D 上,即圆C 与圆D 有交点, 所以2-1≤a 2+(2a -4+1)2≤2+1,解得0≤a ≤125,所以圆心C 的横坐标a 的取值范围为⎣⎡⎦⎤0,125. 3.在直角坐标系xOy 中,曲线y =x 2+mx -2与x 轴交于A ,B 两点,点C 的坐标为(0,1),当m 变化时,解答下列问题:(1)能否出现AC ⊥BC 的情况?说明理由;(2)证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值. 解:(1)不能出现AC ⊥BC 的情况,理由如下: 设A (x 1,0),B (x 2,0),则x 1,x 2满足x 2+mx -2=0, 所以x 1x 2=-2. 又C 的坐标为(0,1),故AC 的斜率与BC 的斜率之积为-1x 1·-1x 2=-12,所以不能出现AC ⊥BC 的情况.(2)证明:由(1)知BC 的中点坐标为⎝⎛⎭⎫x 22,12, 可得BC 的中垂线方程为y -12=x 2⎝⎛⎭⎫x -x 22. 由(1)可得x 1+x 2=-m , 所以AB 的中垂线方程为x =-m2.联立⎩⎨⎧x =-m 2,y -12=x 2⎝⎛⎭⎫x -x 22,x 22+mx 2-2=0可得⎩⎨⎧x =-m 2,y =-12.所以过A ,B ,C 三点的圆的圆心坐标为⎝⎛⎭⎫-m 2,-12,半径r =m 2+92. 故圆在y 轴上截得的弦长为2r 2-⎝⎛⎭⎫m 22=3,即过A ,B ,C 三点的圆在y 轴上截得的弦长为定值.4.(2018·广州高中综合测试)已知定点M (1,0)和N (2,0),动点P 满足|PN |=2|PM |. (1)求动点P 的轨迹C 的方程;(2)若A ,B 为(1)中轨迹C 上两个不同的点,O 为坐标原点.设直线OA ,OB ,AB 的斜率分别为k 1,k 2,k .当k 1k 2=3时,求k 的取值范围.解:(1)设动点P 的坐标为(x ,y ), 因为M (1,0),N (2,0),|PN |=2|PM |, 所以(x -2)2+y 2=2·(x -1)2+y 2.整理得,x 2+y 2=2.所以动点P 的轨迹C 的方程为x 2+y 2=2.(2)设点A (x 1,y 1),B (x 2,y 2),直线AB 的方程为y =kx +b .由⎩⎪⎨⎪⎧x 2+y 2=2,y =kx +b消去y ,整理得(1+k 2)x 2+2bkx +b 2-2=0.(*) 由Δ=(2bk )2-4(1+k 2)(b 2-2)>0,得b 2<2+2k 2.① 由根与系数的关系,得x 1+x 2=-2bk 1+k 2,x 1x 2=b 2-21+k 2.②由k 1·k 2=y 1x 1·y 2x 2=kx 1+b x 1·kx 2+bx 2=3,得(kx 1+b )(kx 2+b )=3x 1x 2, 即(k 2-3)x 1x 2+bk (x 1+x 2)+b 2=0.③ 将②代入③,整理得b 2=3-k 2.④由④得b 2=3-k 2≥0,解得-3≤k ≤ 3.⑤ 由①和④,解得k <-33或k >33.⑥ 要使k 1,k 2,k 有意义,则x 1≠0,x 2≠0, 所以0不是方程(*)的根,所以b 2-2≠0,即k ≠1且k ≠-1.⑦ 由⑤⑥⑦,得k 的取值范围为 [-3,-1)∪⎝⎛⎭⎫-1,-33∪⎝⎛⎭⎫33,1∪(1, 3 ].。
专题15 直线与圆(命题猜想)-2017年高考数学(理)命题猜想与仿真押题(解析版)

专题15 直线与圆(命题猜想) 2017年高考数学(理)命题猜想与仿真押题【考向解读】考查重点是直线间的平行和垂直的条件、与距离有关的问题.直线与圆的位置关系特别是弦长问题,此类问题难度属于中低档,一般以选择题、填空题的形式出现. 【命题热点突破一】 直线的方程及应用 1.两条直线平行与垂直的判定若两条不重合的直线l 1,l 2的斜率k 1,k 2存在,则l 1∥l 2⇔k 1=k 2,l 1⊥l 2⇔k 1k 2=-1.若给出的直线方程中存在字母系数,则要考虑斜率是否存在. 2.求直线方程要注意几种直线方程的局限性.点斜式、两点式、斜截式要求直线不能与x 轴垂直.而截距式方程不能表示过原点的直线,也不能表示垂直于坐标轴的直线. 3.两个距离公式(1)两平行直线l 1:Ax +By +C 1=0,l 2:Ax +By +C 2=0间的距离d =|C 1-C 2|A 2+B 2. (2)点(x 0,y 0)到直线l :Ax +By +C =0的距离公式d =|Ax 0+By 0+C |A 2+B 2.例1、【2016高考新课标3理数】已知直线l :30mx y m ++=错误!未找到引用源。
与圆2212x y +=错误!未找到引用源。
交于,A B 两点,过,A B 分别做l 的垂线与x 轴交于,C D 两点,若AB =错误!未找到引用源。
,则||CD =错误!未找到引用源。
__________________. 【答案】4【变式探究】(1)已知直线l 1:(k -3)x +(4-k )y +1=0与l 2:2(k -3)x -2y +3=0平行,则k 的值是( ) A .1或3B .1或5C .3或5D .1或2(2)已知两点A (3,2)和B (-1,4)到直线mx +y +3=0的距离相等,则m 的值为( ) A .0或-12 B.12或-6C .-12或12D .0或12答案 (1)C (2)B解析 (1)当k =4时,直线l 1的斜率不存在,直线l 2的斜率存在,则两直线不平行;当k ≠4时,两直线平行的一个必要条件是3-k 4-k =k -3,解得k =3或k =5.但必须满足1k -4≠32(截距不相等)才是充要条件,经检验知满足这个条件.(2)依题意,得|3m +5|m 2+1=|-m +7|m 2+1.所以|3m +5|=|m -7|. 所以(3m +5)2=(m -7)2, 所以8m 2+44m -24=0. 所以2m 2+11m -6=0. 所以m =12或m =-6.【特别提醒】(1)求解两条直线的平行或垂直问题时要考虑斜率不存在的情况;(2)对解题中可能出现的特殊情况,可用数形结合的方法分析研究. 【变式探究】已知A (3,1),B (-1,2)两点,若∠ACB 的平分线方程为y =x +1,则AC 所在的直线方程为( ) A .y =2x +4 B .y =12x -3C .x -2y -1=0D .3x +y +1=0 答案 C解析 由题意可知,直线AC 和直线BC 关于直线y =x +1对称.设点B (-1,2)关于直线y =x +1的对称点为B ′(x 0,y 0),则有⎩⎪⎨⎪⎧y 0-2x 0+1=-1,y 0+22=x 0-12+1⇒⎩⎪⎨⎪⎧x 0=1,y 0=0,即B ′(1,0).因为B ′(1,0)在直线AC 上,所以直线AC 的斜率为k =1-03-1=12,所以直线AC 的方程为y -1=12(x -3),即x -2y -1=0. 故C 正确.【命题热点突破二】 圆的方程及应用 1.圆的标准方程当圆心为(a ,b ),半径为r 时,其标准方程为(x -a )2+(y -b )2=r 2,特别地,当圆心在原点时,方程为x 2+y 2=r 2. 2.圆的一般方程x 2+y 2+Dx +Ey +F =0,其中D 2+E 2-4F >0,表示以(-D 2,-E 2)为圆心,D 2+E 2-4F2为半径的圆.例2、【2016高考新课标2理数】圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a=( )(A )43-(B )34- (C (D )2 【答案】A【解析】圆的方程可化为22(x 1)(y 4)4-+-=,所以圆心坐标为(1,4),由点到直线的距离公式得:d ,解得43a =-,故选A .【变式探究】(1)若圆C 经过(1,0),(3,0)两点,且与y 轴相切,则圆C 的方程为( ) A .(x -2)2+(y ±2)2=3 B .(x -2)2+(y ±3)2=3 C .(x -2)2+(y ±2)2=4 D .(x -2)2+(y ±3)2=4(2)已知圆M 的圆心在x 轴上,且圆心在直线l 1:x =-2的右侧,若圆M 截直线l 1所得的弦长为23,且与直线l 2:2x -5y -4=0相切,则圆M 的方程为( ) A .(x -1)2+y 2=4 B .(x +1)2+y 2=4 C .x 2+(y -1)2=4 D .x 2+(y +1)2=4答案 (1)D (2)B解析 (1)因为圆C 经过(1,0),(3,0)两点,所以圆心在直线x =2上,又圆与y 轴相切,所以半径r =2,设圆心坐标为(2,b ),则(2-1)2+b 2=4,b 2=3,b =±3,所以选D. (2)由已知,可设圆M 的圆心坐标为(a,0),a >-2,半径为r ,得⎩⎪⎨⎪⎧a +2+32=r 2,|2a -4|4+5=r ,解得满足条件的一组解为⎩⎪⎨⎪⎧a =-1,r =2,所以圆M 的方程为(x +1)2+y 2=4.故选B.【特别提醒】解决与圆有关的问题一般有两种方法:(1)几何法,通过研究圆的性质、直线和圆、圆与圆的位置关系,进而求得圆的基本量和方程;(2)代数法,即用待定系数法先设出圆的方程,再由条件求得各系数. 【变式探究】(1)经过点A (5,2),B (3,-2),且圆心在直线2x -y -3=0上的圆的方程为________________. (2)已知直线l 的方程是x +y -6=0,A ,B 是直线l 上的两点,且△OAB 是正三角形(O 为坐标原点),则△OAB 外接圆的方程是____________________.答案 (1)(x -2)2+(y -1)2=10 (2)(x -2)2+(y -2)2=8(2)设△OAB 的外心为C ,连接OC ,则易知OC ⊥AB ,延长OC 交AB 于点D ,则|OD |=32,且△AOB 外接圆的半径R =|OC |=23|OD |=2 2.又直线OC 的方程是y =x ,容易求得圆心C 的坐标为(2,2),故所求圆的方程是(x -2)2+(y -2)2=8.【命题热点突破三】 直线与圆、圆与圆的位置关系1.直线与圆的位置关系:相交、相切和相离,判断的方法主要有点线距离法和判别式法.(1)点线距离法:设圆心到直线的距离为d ,圆的半径为r ,则d <r ⇔直线与圆相交,d =r ⇔直线与圆相切,d >r ⇔直线与圆相离.(2)判别式法:设圆C :(x -a )2+(y -b )2=r 2,直线l :Ax +By +C =0,方程组⎩⎪⎨⎪⎧Ax +By +C =0,x -a 2+y -b 2=r2消去y ,得关于x 的一元二次方程根的判别式Δ,则直线与圆相离⇔Δ<0,直线与圆相切⇔Δ=0,直线与圆相交⇔Δ>0.2.圆与圆的位置关系有五种,即内含、内切、相交、外切、外离.设圆C 1:(x -a 1)2+(y -b 1)2=r 21,圆C 2:(x -a 2)2+(y -b 2)2=r 22,两圆心之间的距离为d ,则圆与圆的五种位置关系的判断方法如下: (1)d >r 1+r 2⇔两圆外离; (2)d =r 1+r 2⇔两圆外切; (3)|r 1-r 2|<d <r 1+r 2⇔两圆相交; (4)d =|r 1-r 2|(r 1≠r 2)⇔两圆内切; (5)0≤d <|r 1-r 2|(r 1≠r 2)⇔两圆内含. 例3、【2016高考江苏卷】如图,在平面直角坐标系xOy 中,已知以M 为圆心的圆22:1214600M x y x y +--+=及其上一点(2,4)A(1)设圆N 与x 轴相切,与圆M 外切,且圆心N 在直线6x =上,求圆N 的标准方程; (2)设平行于OA 的直线l 与圆M 相交于,B C 两点,且BC OA =,求直线l 的方程;(3)设点(,0)T t 满足:存在圆M 上的两点P 和Q ,使得,TA TP TQ +=,求实数t 的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【考向解读】考查重点是直线间的平行和垂直的条件、与距离有关的问题.直线与圆的位置关系特别是弦长问题,此类问题难度属于中低档,一般以选择题、填空题的形式出现. 【命题热点突破一】 直线的方程及应用 1.两条直线平行与垂直的判定若两条不重合的直线l 1,l 2的斜率k 1,k 2存在,则l 1∥l 2⇔k 1=k 2,l 1⊥l 2⇔k 1k 2=-1.若给出的直线方程中存在字母系数,则要考虑斜率是否存在.2.求直线方程要注意几种直线方程的局限性.点斜式、两点式、斜截式要求直线不能与x 轴垂直.而截距式方程不能表示过原点的直线,也不能表示垂直于坐标轴的直线.3.两个距离公式(1)两平行直线l 1:Ax +By +C 1=0,l 2:Ax +By +C 2=0间的距离d =|C 1-C 2|A 2+B2. (2)点(x 0,y 0)到直线l :Ax +By +C =0的距离公式d =|Ax 0+By 0+C |A 2+B 2.例1、【2016高考新课标3理数】已知直线l :30mx y m ++=错误!未找到引用源。
与圆2212x y +=错误!未找到引用源。
交于,A B 两点,过,A B 分别做l 的垂线与x 轴交于,C D 两点,若AB =错误!未找到引用源。
,则||CD =错误!未找到引用源。
__________________.【变式探究】(1)已知直线l 1:(k -3)x +(4-k )y +1=0与l 2:2(k -3)x -2y +3=0平行,则k 的值是( )A .1或3B .1或5C .3或5D .1或2(2)已知两点A (3,2)和B (-1,4)到直线mx +y +3=0的距离相等,则m 的值为( ) A .0或-12 B. 12或-6C .-12或12D .0或12【特别提醒】(1)求解两条直线的平行或垂直问题时要考虑斜率不存在的情况;(2)对解题中可能出现的特殊情况,可用数形结合的方法分析研究.【变式探究】已知A (3,1),B (-1,2)两点,若∠ACB 的平分线方程为y =x +1,则AC 所在的直线方程为( ) A .y =2x +4 B .y =12x -3C .x -2y -1=0D .3x +y +1=0 【命题热点突破二】 圆的方程及应用 1.圆的标准方程当圆心为(a ,b ),半径为r 时,其标准方程为(x -a )2+(y -b )2=r 2,特别地,当圆心在原点时,方程为x 2+y 2=r 2.2.圆的一般方程x 2+y 2+Dx +Ey +F =0,其中D 2+E 2-4F >0,表示以(-D 2,-E 2)为圆心,D 2+E 2-4F2为半径的圆.例2、【2016高考新课标2理数】圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a=( )(A )43-(B )34- (C (D )2 【变式探究】(1)若圆C 经过(1,0),(3,0)两点,且与y 轴相切,则圆C 的方程为( ) A .(x -2)2+(y ±2)2=3 B .(x -2)2+(y ±3)2=3 C .(x -2)2+(y ±2)2=4 D .(x -2)2+(y ±3)2=4(2)已知圆M 的圆心在x 轴上,且圆心在直线l 1:x =-2的右侧,若圆M 截直线l 1所得的弦长为23,且与直线l 2:2x -5y -4=0相切,则圆M 的方程为( )A .(x -1)2+y 2=4 B .(x +1)2+y 2=4 C .x 2+(y -1)2=4D .x 2+(y +1)2=4【特别提醒】解决与圆有关的问题一般有两种方法:(1)几何法,通过研究圆的性质、直线和圆、圆与圆的位置关系,进而求得圆的基本量和方程;(2)代数法,即用待定系数法先设出圆的方程,再由条件求得各系数.【变式探究】(1)经过点A (5,2),B (3,-2),且圆心在直线2x -y -3=0上的圆的方程为________________. (2)已知直线l 的方程是x +y -6=0,A ,B 是直线l 上的两点,且△OAB 是正三角形(O 为坐标原点),则△OAB 外接圆的方程是____________________.【命题热点突破三】 直线与圆、圆与圆的位置关系1.直线与圆的位置关系:相交、相切和相离,判断的方法主要有点线距离法和判别式法.(1)点线距离法:设圆心到直线的距离为d ,圆的半径为r ,则d <r ⇔直线与圆相交,d =r ⇔直线与圆相切,d >r ⇔直线与圆相离.(2)判别式法:设圆C :(x -a )2+(y -b )2=r 2,直线l :Ax +By +C =0,方程组⎩⎪⎨⎪⎧Ax +By +C =0,x -a 2+y -b2=r2消去y ,得关于x 的一元二次方程根的判别式Δ,则直线与圆相离⇔Δ<0,直线与圆相切⇔Δ=0,直线与圆相交⇔Δ>0.2.圆与圆的位置关系有五种,即内含、内切、相交、外切、外离.设圆C 1:(x -a 1)2+(y -b 1)2=r 21,圆C 2:(x -a 2)2+(y -b 2)2=r 22,两圆心之间的距离为d ,则圆与圆的五种位置关系的判断方法如下:(1)d >r 1+r 2⇔两圆外离; (2)d =r 1+r 2⇔两圆外切; (3)|r 1-r 2|<d <r 1+r 2⇔两圆相交; (4)d =|r 1-r 2|(r 1≠r 2)⇔两圆内切; (5)0≤d <|r 1-r 2|(r 1≠r 2)⇔两圆内含. 例3、【2016高考江苏卷】如图,在平面直角坐标系xOy 中,已知以M 为圆心的圆22:1214600M x y x y +--+=及其上一点(2,4)A(1)设圆N 与x 轴相切,与圆M 外切,且圆心N 在直线6x =上,求圆N 的标准方程; (2)设平行于OA 的直线l 与圆M 相交于,B C 两点,且BC OA =,求直线l 的方程;(3)设点(,0)T t 满足:存在圆M 上的两点P 和Q ,使得,TA TP TQ +=,求实数t 的取值范围。
22(6)(1)1x y -+-=22t -≤≤+【变式探究】(1)已知直线2x +(y -3)m -4=0(m ∈R )恒过定点P ,若点P 平分圆x 2+y 2-2x -4y -4=0的弦MN ,则弦MN 所在直线的方程是( )A .x +y -5=0B .x +y -3=0C .x -y -1=0D .x -y +1=0(2)已知P (x ,y )是直线kx +y +4=0(k >0)上一动点,PA ,PB 是圆C :x 2+y 2-2y =0的两条切线,A ,B 是切点,若四边形PACB 的最小面积是2,则k 的值为( )A .3B.212C .22D .2【特别提醒】 (1)讨论直线与圆及圆与圆的位置关系时,要注意数形结合,充分利用圆的几何性质寻找解题途径,减少运算量.(2)圆上的点与圆外点的距离的最值问题,可以转化为圆心到点的距离问题;圆上的点与直线上点的距离的最值问题,可以转化为圆心到直线的距离问题;圆上的点与另一圆上点的距离的最值问题,可以转化为圆心到圆心的距离问题.【变式探究】(1)已知在平面直角坐标系xOy 中,圆C 的方程为x 2+y 2=-2y +3,直线l 过点(1,0)且与直线x -y +1=0垂直.若直线l 与圆C 交于A 、B 两点,则△OAB 的面积为( )A .1B.2C .2D .2 2(2)两个圆C 1:x 2+y 2+2ax +a 2-4=0(a ∈R )与C 2:x 2+y 2-2by -1+b 2=0(b ∈R )恰有三条公切线,则a +b 的最小值为( )A .-6B .-3C .-32D .3 【高考真题解读】1.【2016高考新课标2理数】圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a=( )(A )43-(B )34- (C (D )2 2.【2016高考上海理数】已知平行直线012:,012:21=++=-+y x l y x l ,则21,l l 的距离___________.3.【2016高考新课标3理数】已知直线l :30mx y m ++=错误!未找到引用源。
与圆2212x y +=错误!未找到引用源。
交于,A B 两点,过,A B 分别做l 的垂线与x 轴交于,C D 两点,若AB =错误!未找到引用源。
,则||CD =错误!未找到引用源。
__________________.4.【2016高考新课标1卷】(本小题满分12分)设圆222150x y x ++-=的圆心为A ,直线l 过点B (1,0)且与x 轴不重合,l 交圆A 于C ,D 两点,过B 作AC 的平行线交AD 于点E .(I )证明EA EB +为定值,并写出点E 的轨迹方程;(II )设点E 的轨迹为曲线C 1,直线l 交C 1于M ,N 两点,过B 且与l 垂直的直线与圆A 交于P ,Q 两点,求四边形MPNQ 面积的取值范围.5.【2016高考江苏卷】(本小题满分16分)如图,在平面直角坐标系xOy 中,已知以M 为圆心的圆22:1214600M x y x y +--+=及其上一点(2,4)A(1)设圆N 与x 轴相切,与圆M 外切,且圆心N 在直线6x =上,求圆N 的标准方程; (2)设平行于OA 的直线l 与圆M 相交于,B C 两点,且BC OA =,求直线l 的方程;(3)设点(,0)T t 满足:存在圆M 上的两点P 和Q ,使得,TA TP TQ +=,求实数t 的取值范围。
22(6)(1)1x y -+-=22t -≤≤+.(2015·新课标全国Ⅰ,14)一个圆经过椭圆x 216+y 24=1的三个顶点,且圆心在x 轴的正半轴上,则该圆的标准方程为________.2.(2015·江苏,10)在平面直角坐标系xOy 中,以点(1,0)为圆心且与直线mx -y -2m -1=0(m ∈R )相切的所有圆中,半径最大的圆的标准方程为________.3.(2015·广东,5)平行于直线2x +y +1=0且与圆x 2+y 2=5相切的直线的方程是( ) A .2x -y +5=0或2x -y -5=0 B .2x +y +5=0或2x +y -5=0 C .2x -y +5=0或2x -y -5=0 D .2x +y +5=0或2x +y -5=04.(2015·新课标全国Ⅱ,7)过三点A (1,3),B (4,2),C (1,-7)的圆交y 轴于M 、N 两点,则|MN |=( )A .2 6B .8C .4 6D .105.(2015·重庆,8)已知直线l :x +ay -1=0(a ∈R )是圆C :x 2+y 2-4x -2y +1=0的对称轴,过点A (-4,a )作圆C 的一条切线,切点为B ,则|AB |=( )A .2B .4 2C .6D .2106.(2015·山东,9)一条光线从点(-2,-3)射出,经y 轴反射后与圆(x +3)2+(y -2)2=1相切,则反射光线所在直线的斜率为( )A .-53或-35B .-32或-23C .-54或-45D .-43或-347.(2014·江西,9)在平面直角坐标系中,A ,B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线2x +y -4=0相切,则圆C 面积的最小值为( )A.45π B.34π C .(6-25)π D.54π8.(2014·陕西,12)若圆C 的半径为1,其圆心与点(1,0)关于直线y =x 对称,则圆C 的标准方程为____________.9.(2014·四川,14)设m ∈R ,过定点A 的动直线x +my =0和过定点B 的动直线mx -y -m +3=0交于点P (x ,y ),则|PA |·|PB |的最大值是________.10.(2014·江苏,11)在平面直角坐标系xOy 中,若曲线y =ax 2+bx(a ,b 为常数)过点P (2,-5),且该曲线在点P 处的切线与直线7x +2y +3=0平行,则a +b 的值是________.11.(2015·广东,20)已知过原点的动直线l 与圆C 1:x 2+y 2-6x +5=0相交于不同的两点A ,B . (1)求圆C 1的圆心坐标;(2)求线段AB 的中点M 的轨迹C 的方程;(3)是否存在实数k ,使得直线L :y =k (x -4)与曲线C 只有一个交点?若存在,求出k 的取值范围;若不存在,说明理由.。
