气体气态、液态体积换算
液氧单位换算.
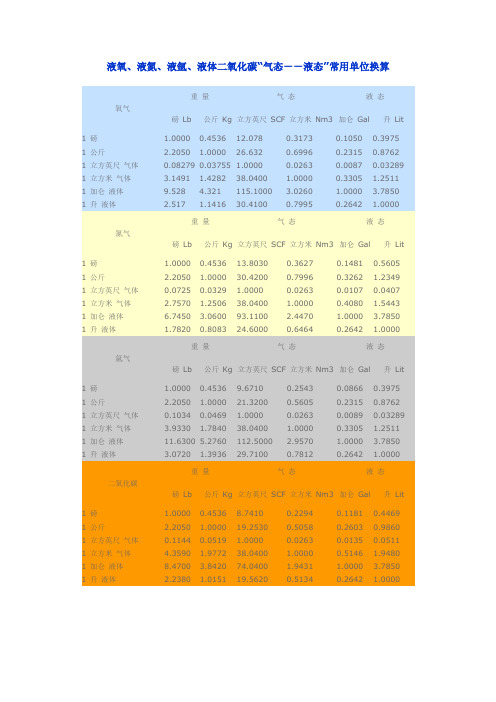
液氧、液氮、液氩、液体二氧化碳“气态－－液态”常用单位换算重量气态液态氧气磅Lb 公斤Kg 立方英尺SCF 立方米Nm3 加仑Gal 升Lit1 磅 1.0000 0.4536 12.078 0.3173 0.1050 0.3975 1 公斤 2.2050 1.0000 26.632 0.6996 0.2315 0.8762 1 立方英尺气体0.08279 0.03755 1.0000 0.0263 0.0087 0.03289 1 立方米气体 3.1491 1.4282 38.0400 1.0000 0.3305 1.2511 1 加仑液体9.528 4.321 115.1000 3.0260 1.0000 3.7850 1 升液体 2.517 1.1416 30.4100 0.7995 0.2642 1.0000重量气态液态氮气磅Lb 公斤Kg 立方英尺SCF 立方米Nm3 加仑Gal 升Lit1 磅 1.0000 0.4536 13.8030 0.3627 0.1481 0.5605 1 公斤 2.2050 1.0000 30.4200 0.7996 0.3262 1.2349 1 立方英尺气体0.0725 0.0329 1.0000 0.0263 0.0107 0.0407 1 立方米气体 2.7570 1.2506 38.0400 1.0000 0.4080 1.5443 1 加仑液体 6.7450 3.0600 93.1100 2.4470 1.0000 3.7850 1 升液体 1.7820 0.8083 24.6000 0.6464 0.2642 1.0000重量气态液态氩气磅Lb 公斤Kg 立方英尺SCF 立方米Nm3 加仑Gal 升Lit1 磅 1.0000 0.4536 9.6710 0.2543 0.0866 0.3975 1 公斤 2.2050 1.0000 21.3200 0.5605 0.2315 0.8762 1 立方英尺气体0.1034 0.0469 1.0000 0.0263 0.0089 0.03289 1 立方米气体 3.9330 1.7840 38.0400 1.0000 0.3305 1.2511 1 加仑液体11.6300 5.2760 112.5000 2.9570 1.0000 3.7850 1 升液体 3.0720 1.3936 29.7100 0.7812 0.2642 1.0000重量气态液态二氧化碳磅Lb 公斤Kg 立方英尺SCF 立方米Nm3 加仑Gal 升Lit1 磅 1.0000 0.4536 8.7410 0.2294 0.1181 0.4469 1 公斤 2.2050 1.0000 19.2530 0.5058 0.2603 0.9860 1 立方英尺气体0.1144 0.0519 1.0000 0.0263 0.0135 0.0511 1 立方米气体 4.3590 1.9772 38.0400 1.0000 0.5146 1.9480 1 加仑液体8.4700 3.8420 74.0400 1.9431 1.0000 3.7850 1 升液体 2.2380 1.0151 19.5620 0.5134 0.2642 1.0000参考以上得出以下：氧气1立方米气态=1.25升液态=0.00125立方米液态1升液态=0.001立方米液态=0.80立方米气态所以：1立方米液态=800立方米气态二氧化碳1立方米气态=1.95升液态=0.00195立方米液态1升液态=0.001立方米液态=0.51立方米气态所以：1立方米液态=510立方米气态以上纯属本人查找资料再加以计算得出，准确性不敢保证，仅供参考。
气体换算成标准状况体积
气体换算成标准状况体积摘要：一、气体换算背景二、标准状况的定义三、气体体积换算公式四、实际应用与意义正文：气体换算成标准状况体积，通常是指将某种气体在非标准状况下的体积，转换为该气体在标准状况下的体积。
这一过程涉及到气体的物质量和温度、压强等参数，需要运用相应的物理化学知识进行计算。
首先，我们需要了解什么是标准状况。
在国际标准下，标准状况是指温度为0 摄氏度（273.15 开尔文），压强为1 个标准大气压（约为101.325 千帕）的状态。
在这种条件下，1 摩尔任何气体的体积为22.4 升。
气体体积换算公式为：V1/T1 = V2/T2，其中V1和T1分别代表非标准状况下的气体体积和温度，V2和T2则代表标准状况下的气体体积和温度。
通过这个公式，我们可以将非标准状况下的气体体积转换为标准状况下的体积。
实际应用中，气体换算成标准状况体积的意义主要体现在以下几个方面：1.为科学研究提供便利：在实验室中，研究者需要对气体的体积进行精确测量。
将气体体积换算成标准状况下的体积，有助于比较不同实验条件下的气体体积，便于数据分析。
2.工业生产优化：在工业生产过程中，气体体积的测量和控制对于生产效率和产品质量具有重要意义。
将气体体积换算成标准状况下的体积，有助于优化生产过程，提高资源利用率。
3.环境监测与分析：在大气污染、温室气体排放等环境问题研究中，需要对气体体积进行监测和分析。
将气体体积换算成标准状况下的体积，有助于更准确地评估环境问题，为政策制定提供科学依据。
总之，气体换算成标准状况体积是一个在科学研究、工业生产、环境监测等领域具有广泛应用价值的课题。
LNG单位换算表
LNG的物理性质LNG是液化天然气（liquefied natural gas）的英文缩写，主要成分是甲烷。
LNG无色、无味、无毒且无腐蚀性，其体积约为同量气态天然气体积的1/625，密度约为水的45%。
●LNG密度：0.425-0.46kg/L●沸点：-162℃●气化后密度：0.6-0.7kg/m3●高热值：41.5-45.3MJ/m3●气液体积比：625:1●辛烷值：130●储存温度：-160~-120℃●操作压力：0~1.0MPaLNG计量单位换算表：以其产生热值的角度来考虑：1L(柴油)≈1.1㎥（天然气）； 1.33L(柴油）≈1.47㎥（天然气）；1kg(LNG)≈1.47㎥（天然气）； 1.33L(柴油)≈1kg(LNG)1L(汽油)≈0.9㎥（天然气）； 1.63L(汽油）≈1.47㎥（天然气）；1.63L(汽油)≈1kg(LNG)LNG在液态与气态时的单位换算：LNG液体状态气体状态T（吨）KG（公斤）㎥（立方米）L(升) ㎥（立方米）1T（吨）=* 1000 2.19 2190 1470 1KG（公斤）= 0.001 * 0.00219 2.19 1.47 1㎥（立方米）= 0.456 456 * 1000 * 1L(升)= 0.000456 0.456 0.001 * 0.6250.68 0.0016 1.6 1 LNG汽车常用车载瓶换算表：（一般有效容积为额定的90%）可装LNG体积（L）可装LNG重量（kg）标准状况下气体体积（m3）1Ｌ 1 0.425 0.62 275Ｌ车载瓶247.5 105 153 335L车载瓶301.5 128 187 375L车载瓶337.5 128 187 450L车载瓶405.0 172 251。
天然气，一立方米，是指气态还是液态？
天然⽓，⼀⽴⽅⽶，是指⽓态还是液态？关于天然⽓体积的⼏个概念漫谈天然⽓在⽇常使⽤过程中，有三种形式，即：液化天然⽓（LNG）、压缩天然⽓（CNG）、管道天然⽓（NG）；平时交流时使⽤的：⼀⽴⽅⽶，⼀般是指⽓态；同时是指该⽓体在标准状态下的体积。
包括压缩天然⽓。
液化天然⽓由于是以液态状态存在的，平时⼀般交流时使⽤的：⼀公⽄（kg）或者⼀吨（T）。
⼀、⽓体体积与标准状态⽓体分⼦之间的间距是很⼤的，所以它们之间的作⽤⼒很弱，不管把⽓体放到多⼤的体积的容积中，⽓体总是可以充满整个容器所以容器的体积就是⽓体的体积，当然随着体积的改变⽓压也是要改变的。
为了表征⽓体的体积就得引进标准状态下的⽓体体积这个概念。
关于⽓体体积和质量的计算⽅法，牵涉的知识太多，理想⽓体状态⽅程是基础 由 pV=nRT 得 pV=mRT/M 得出 m= pVM/RT=（p×V×M）÷【8.314×（273.15+t℃）】 m 质量 单位Kg p ⽓体压强 单位Pa V ⽓体体积 单位m M ⽓体摩尔质量 t ⽓体温度 单位℃标况下天然⽓⽴⽅，1 Nm³ 就是20摄⽒度，⼀个⼤⽓压下的 1个⽴⽅。
⼆、商业活动中⽓体体积的交易⽐如说⼀台撬车⽔容积为18⽴⽅⽶，实际加⽓可以到3000-4000⽅⽓。
这⾥⽓体被压缩到18⽴⽅的容器⾥⾯了，但是压⼒到了200公⽄左右，释放后可以到3000-4000N ⽴⽅。
如果分的仔细点，⽴⽅⽶就是⼯况下的计量，⽐如以上例⼦的，加压到200公⽄左右，天然⽓只有18⽴⽅⽶了。
⼯况和标况的换算是根据PV= nRT ⽓体⽅程来换算的。
三、对于液化天然⽓讨论体积时要⽤到⽓化率的概念，也就是⽓化后标准状态下的体积。
液氧_换算工作表
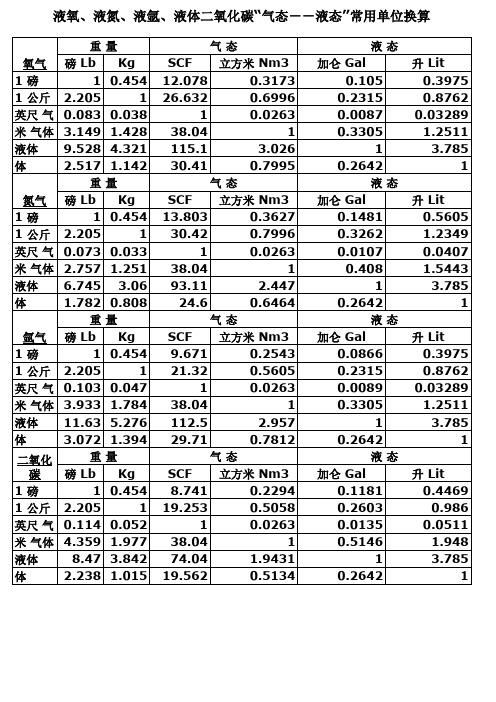
重 量公斤 立方英尺 气 态 氧气 磅 Lb Kg SCF 立方米 Nm3 1磅 1 0.454 12.078 0.3173 1 公斤 2.205 1 26.632 0.6996 立方 英尺 气 0.083 0.038 1 0.0263 1 立方 米 加仑 3.149 1.428 38.04 1 1 气体 液体 115.1 3.026 1 升 液 9.528 4.321 体 2.517 1.142 30.41 0.7995 重 量公斤 立方英尺 气 态 氮气 磅 Lb Kg SCF 立方米 Nm3 1磅 1 0.454 13.803 0.3627 公斤 1 30.42 0.7996 1 立方 2.205 英尺 气 1 0.0263 1 立方 0.073 0.033 米 加仑 2.757 1.251 38.04 1 1 气体 液体 液 6.745 3.06 93.11 2.447 1升 体 1.782 0.808 24.6 0.6464 重 量公斤 立方英尺 气 态 氩气 1磅 公斤 1 立方 英尺 气 1 立方 米 加仑 1 气体 液体 液 1升 体 二氧化 碳 1磅 1 公斤 立方 英尺 气 1 立方 米 加仑 1 气体 液体 1升液 体 磅 Lb 1 2.205 0.103 3.933 11.63 3.072 重 磅 Lb 1 2.205 0.114 4.359 8.47 2.238 Kg SCF 立方米 Nm3 0.454 9.671 0.2543 1 21.32 0.5605 0.047 1 0.0263 1.784 38.04 1 5.276 112.5 2.957 1.394 29.71 0.7812 量公斤 立方英尺 气 态 Kg SCF 立方米 Nm3 0.454 8.741 0.2294 1 19.253 0.5058 0.052 1 0.0263 1.977 38.04 1 3.842 74.04 1.9431 1.015 19.562 0.5134 液态 加仑 Gal 0.105 0.2315 0.0087 0.3305 1 0.2642 液态 加仑 Gal 0.1481 0.3262 0.0107 0.408 1 0.2642 液态 加仑 Gal 0.0866 0.2315 0.0089 0.3305 1 0.2642 液态 加仑 Gal 0.1181 0.2603 0.0135 0.5146 1 0.2642 升 Lit 0.3975 0.8762 0.03289 1.2511 3.785 1 升 Lit 0.5605 1.2349 0.0407 1.5443 3.785 1 升 Lit 0.3975 0.8762 0.03289 1.2511 3.785 1 升 Lit 0.4469 0.986 0.0511 1.948 3.785 1
气体的状态计算和理想气体定律
气体的状态计算和理想气体定律一、气体的状态计算1.气体的基本状态参数–压力（P）：气体对容器壁的垂直压力，单位为帕斯卡（Pa）–体积（V）：气体占据的空间大小，单位为立方米（m³）–温度（T）：气体分子的平均动能大小，单位为开尔文（K）–物质的量（n）：气体中分子数目的多少，单位为摩尔（mol）2.气体的状态方程–理想气体状态方程：PV = nRT•P：气体压强•V：气体体积•n：气体的物质的量•R：理想气体常数，8.314 J/(mol·K)•T：气体的绝对温度3.气体状态变化计算–等压变化：PV/T = 常数–等容变化：P/T = 常数–等温变化：PV = 常数二、理想气体定律1.玻意耳定律（Boyle’s Law）–一定量的气体在恒温条件下，压强与体积成反比，即PV = 常数。
2.查理定律（Charles’s Law）–一定量的气体在恒压条件下，体积与温度成正比，即V/T = 常数。
3.盖·吕萨克定律（Gay-Lussac’s Law）–一定量的气体在恒容条件下，压强与温度成正比，即P/T = 常数。
4.理想气体状态方程（ combines laws）–PV/T = 常数，这是由玻意耳定律、查理定律和盖·吕萨克定律组合而成的。
5.理想气体的概念–理想气体是一种理想化的物理模型，假设气体分子之间无相互作用力，体积可以忽略不计，气体分子运动的速率分布符合麦克斯韦-玻尔兹曼分布。
三、实际气体与理想气体的区别1.实际气体：在现实生活中存在的气体，受到分子间相互作用力的影响，体积不能忽略不计。
2.理想气体：是一种理想化的物理模型，假设气体分子之间无相互作用力，体积可以忽略不计。
四、气体的饱和蒸汽压与相变1.饱和蒸汽压：在一定温度下，液体与其饱和蒸汽之间达到动态平衡时的蒸汽压强。
2.相变：气体与液体、固体之间的相互转化。
如水的沸腾（液态→气态）和凝固（液态→固态）。
初中化学气体的压强与体积变化的数值计算方法
初中化学气体的压强与体积变化的数值计算方法化学中，气体是一种常见的物质状态。
在研究气体行为时，我们经常需要计算气体的压强和体积的变化。
这篇文章将介绍初中化学中气体的压强与体积变化的数值计算方法。
一、气体的压强变化计算方法气体的压强是指气体分子对容器壁的冲击力，单位通常使用帕斯卡（Pa）或者标准大气压（atm）。
计算气体的压强变化涉及到以下公式：1. 理想气体状态方程：PV = nRT其中，P为气体的压强（单位为Pa或者atm），V为气体的体积（单位为升），n为气体的摩尔数（单位为摩尔），R为气体常数（单位为J/mol·K或者L·atm/mol·K），T为气体的绝对温度（单位为开尔文）。
2. 气压差产生的压强变化：ΔP = ρgh其中，ΔP为压强的变化量（单位为Pa或者atm），ρ为液体的密度（单位为千克/立方米或者gram/升），g为重力加速度（单位为米/秒²或者厘米/秒²），h为液体的高度（单位为米或者厘米）。
二、气体的体积变化计算方法气体的体积变化通常涉及到以下公式：1. 气体体积与摩尔数的关系：V/n = V₁/n₁ = V₂/n₂其中，V为气体的体积（单位为升），n为气体的摩尔数（单位为摩尔），V₁和n₁为初始状态下的体积和摩尔数，V₂和n₂为最终状态下的体积和摩尔数。
2. 理想气体体积与温度的关系：V₁/T₁ = V₂/T₂其中，V为气体的体积（单位为升），T为气体的绝对温度（单位为开尔文），V₁和T₁为初始状态下的体积和温度，V₂和T₂为最终状态下的体积和温度。
三、案例分析现在我们通过一个简单的案例来应用上述的计算方法。
假设一个气体在初始状态下的体积为2 L，摩尔数为0.02 mol，在温度为300 K下，求气体在最终状态下的压强和体积。
根据理想气体状态方程PV = nRT，我们可以先计算气体的压强：P = nRT/V= (0.02 mol)(8.31 J/mol·K)(300 K)/(2 L)= 249.3 J/L≈ 249.3 Pa接下来，我们可以利用理想气体体积与温度的关系计算气体的体积变化：V₁/T₁ = V₂/T₂(2 L)/(300 K) = V₂/(350 K)解方程得到：V₂ = 2 L × (350 K)/(300 K)≈ 2.33 L综上所述，初始体积为2 L，摩尔数为0.02 mol的气体，在温度为300 K下，最终的压强约为249.3 Pa，最终的体积约为2.33 L。
气体气态液态体积换算
气体气态液态体积换算 The following text is amended on 12 November 2020.理想气体状态方程（克拉伯龙方程）：标准状态是指0℃（273K），1atm= kPa的状态下。
V=nRTV：标准状态下的气体体积；n：气体的摩尔量；R：气体常量、比例系数；molKT：绝对温度；273KP：标准大气压；V=nRT=n273/或V=nRT=n273/1另可以简便计算：V=V0ρMV：标准状态下的气体体积；V0：气体液态体积；ρ：液化气体的相对密度；M：分子量。
氮的标准沸点是-195.8℃,液体密度（-195.8℃），1m3液氮可汽化成氮气1*（808/28）*= 标立二氧化碳液体密度（-79℃），1m3液态二氧化碳可汽化成二氧化碳1*（1560/）*=794 标立氯的标准沸点是-34℃,液体密度， 1m 3液氯可汽化成氯气 1*（1470/）*= 标立液态氧气体体积膨胀计算在标准状态下0℃，，1摩尔气体占有22.4升体积，根据液态气体的相对密度，由下式可计算出它们气化后膨胀的体积：4.221000⨯⨯⨯=Md v V oo V — 膨胀后的体积（升） v o — 液态气体的体积（升） d o — 液态气体的相对密度（水=1） M — 液态气体的分子量将液氧的有关数据代入上式，由d o =，M=32得oo oo v v Md v V 7984.2210003214.14.221000=⨯⨯⨯=⨯⨯⨯=即液氧若发生泄漏则会迅速气化，其膨胀体积为原液态体积为798倍。
b. 液氧爆破能量模拟计算：液氧处于过热状态时，液态介质迅速大量蒸发，使容器受到很高压力的冲击，产生暴沸或扩展为BLEVE 爆炸，其爆破能量是介质在爆破前后的熵、焓的函数。
1)计算过程(1)容器爆破能量计算公式E L=[(i1－i2)－(s1－s2)T b]m式中：E L——过热状态下液体的爆破能量 KJ；i1——爆破前饱和液体的焓 KJ/kg；i2——在大气压力下饱和液体的焓 KJ/kg；s1——爆破前饱和液体的熵KJ/(kg·k)；s2——在大气压力下饱和液体的熵KJ/(kg·k)；m——饱和液体的质量 kg；T b——介质在大气压下的沸点 k(2)30m3液氧储罐的爆破能量本项目液氧贮存在1个容积为30m3/的储罐内，液氧最大储存量为34290kg，液氧沸点；假设事故状态下储罐内液氧的的温度为95K，则爆破能量：E= [ -将爆破能量换算成TNT能量q，1kg TNT平均爆炸能量为4500kJ/kg，故q=E／4500=1186091／4500=264 (kg)(4)求出爆炸的模拟比α即得α=3=×(264)1/3=(5)查得各种伤害、破坏下的超压值表5-4 冲击波超压对人体及建筑物伤害破坏作用表(6)求出在1000kg TNT爆炸试验中的相当距离R0根据相关数据查得：Δp=时 R0=56；Δp=时 R0=43；Δp=时 R0=32；Δp=时 R0=23；Δp=时 R0=17；(7)求出发生爆炸时各类伤害半径R1=R0×α=56×≈35.8m；R2=R0×α=43×≈27.5m；R3=R0×α=32×≈20.5m；R4=R0×α=23×≈14.7m；R5=R0×α=17×≈10.9m；2)事故后果预测小结按照单罐物理性爆炸事故后果预测，如果一台30m3的低温液氧储罐爆炸，其各类伤害、损失半径见表5-5。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
理想气体状态方程（克拉伯龙方程）：
标准状态是指0℃（273K），1atm=101.3 kPa的状态下。
V=nRT
V：标准状态下的气体体积；
n：气体的摩尔量；
R：气体常量、比例系数；8.31441J/mol•K
T：绝对温度；273K
P：标准大气压；101.3kPa
V=nRT=n•8.31441•273/101.3
或V=nRT=n•0.082•273/1
另可以简便计算：V=V0•ρ•22.4/M
V：标准状态下的气体体积；
V0：气体液态体积；
ρ：液化气体的相对密度；
M：分子量。
氮的标准沸点是-195.8℃,液体密度0.808（-195.8℃），1m3液氮可汽化成氮气
1*（808/28）*22.4=646.4 标立
二氧化碳液体密度1.56（-79℃），
1m3液态二氧化碳可汽化成二氧化碳
1*（1560/44.01）*22.4=794 标立
氯的标准沸点是-34℃,液体密度1.47， 1m 3液氯可汽化成氯气
1*（1470/70.9）*22.4=464.4 标立
液态氧气体体积膨胀计算
在标准状态下0℃，0.1MPa ，1摩尔气体占有22.4升体积，根据液态气体的相对密度，由下式可计算出它们气化后膨胀的体积：
4.221000⨯⨯⨯=
M
d v V o
o V — 膨胀后的体积（升） v o — 液态气体的体积（升） d o — 液态气体的相对密度（水=1） M — 液态气体的分子量
将液氧的有关数据代入上式，由d o =1.14，M=32得
o
o o
o v v M
d v V 7984.22100032
14.14.221000=⨯⨯⨯=⨯⨯⨯=
即液氧若发生泄漏则会迅速气化，其膨胀体积为原液态体积为798倍。
b. 液氧爆破能量模拟计算：
液氧处于过热状态时，液态介质迅速大量蒸发，使容器受到很高压力的冲击，产生暴沸或扩展为BLEVE 爆炸，其爆破能量是介质在爆破前后的熵、焓的函数。
1)计算过程
(1)容器爆破能量计算公式 E L =[(i 1－i 2)－(s 1－s 2)T b ]m
式中：E L ——过热状态下液体的爆破能量 KJ ；
i1——爆破前饱和液体的焓KJ/kg；
i2——在大气压力下饱和液体的焓KJ/kg；
s1——爆破前饱和液体的熵KJ/(kg·k)；
s2——在大气压力下饱和液体的熵KJ/(kg·k)；
m——饱和液体的质量kg；
T b——介质在大气压下的沸点k
(2)30m3液氧储罐的爆破能量
本项目液氧贮存在1个容积为30m3/1.84Mpa的储罐内，液氧最大储存量为34290kg，液氧沸点90.188K；假设事故状态下储罐内液氧的的温度为95K，则爆破能量：
E= [ (167.2-125.4) -(1.73-1.65)×90.188]×34290=1186091KJ
(3)将爆破能量换算成TNT能量q，1kg TNT平均爆炸能量为4500kJ/kg，故q=E／4500=1186091／4500=264 (kg)
(4)求出爆炸的模拟比α
即得α=0.1q1/3=0.1×(264)1/3=0.64
(5)查得各种伤害、破坏下的超压值
表5-4 冲击波超压对人体及建筑物伤害破坏作用表
(6)求出在1000kg TNT爆炸试验中的相当距离R0
根据相关数据查得：
Δp=0.02时R0=56；
Δp=0.03时R0=43；
Δp=0.05时R0=32；
Δp=0.10时R0=23；
Δp=0.20时R0=17；
(7)求出发生爆炸时各类伤害半径
R1=R0×α=56×0.64≈35.8m；
R2=R0×α=43×0.64≈27.5m；
R3=R0×α=32×0.64≈20.5m；
R4=R0×α=23×0.64≈14.7m；
R5=R0×α=17×0.64≈10.9m；
2)事故后果预测小结
按照单罐物理性爆炸事故后果预测，如果一台30m3的低温液氧储罐爆炸，其各类伤害、损失半径见表5-5。
表5-5 冲击波超压对人体及建筑物伤害破坏作用半径表
综上，液氧若发生泄漏则会迅速气化，其膨胀体积为原液态体积为798倍；发生爆炸（30m3液氧）的冲击波超压破坏作用数据见表4-6。
计算可见，如氧罐发生物理爆炸，对50米外的丙烷气站人员及设备不会造成太大的影响。