弹性模量资料
常用材料弹性模量及泊松比

(《钢结构设计规范》GB 50017━2003表3、4、3统一取弹性模量206000MPa 。
泊松比约为0。
3 )(有限元材料库得参数为:45号钢密度7890kg/m3,泊松比0.269,杨氏模量209000G P。
)(HT200,弹性模量为135GP a,泊松比为0、27)(HT200 密度:7、2-7。
3,弹性模量:70-80; 泊松比0。
24—0、25 ;热膨胀系数 加热: 10冷却—8)(用灰铸铁 HT 200,根据资料可知其密度为7340kg /m3,弹性模量为120GPa ,泊松比为0。
25)(HT200,弹性模量E=1.22e 11 Pa, 泊松比λ=0。
25,密度ρ=7800 k g/m 3) ( HT200 122 /0。
3 /7。
2 ×10 — 6)(材料H T200,密度为7。
8103 kg / m 3 ,弹性模量为 145 GPa,泊松比为0。
3) ( H T200,其弹性模量 E=140GPa,泊松 比μ=0、25,密度ρ=7.8×10 3 kg /m 3) (模具材料为灰口铸铁 HT200,C —3.47%,Si —2。
5%,密度 7210 kg / m3 ,泊松比 0.27、)(箱体材料为HT200,其性能参数为:弹性模量E=1.4×10 11 Pa,泊松比μ=0。
3,密度为ρ=7.8×10 3 k g.m —3 )(模型材料H T200,其主要物理与机械性能参数如下:密度7。
25 t /m 3 ,弹性模量126 GPa, 泊松比0。
3)(垫板得材料采用 HT200, 材料相关参数查表可 得, 弹性模量 E = 1120 ×10 5 N /mm 2 , 泊松比 μ= 0125, 密度ρ=712 ×10 - 9 t /m m 3)表58—23,常用材料得弹性模量,泊松比与线胀系数灰铸铁(HT150、HT200) 70~80 0。
(整理)弹性模量、压缩模量、变形模量

E--弹性模量Es--压缩模量Eo--变形模量在工程中土的弹性模量要远大于压缩模量和变形模量,而压缩模量又大于变形模量。
但在勘察报告中却只提供变形模量,在模拟计算的时侯我们要用弹性模量。
变形模量的定义在表达式上和弹性模量是一样的E=σ/ε,对于变形模量ε是指应变,包括弹性应变εe和塑性应变εp,对于弹性模量而言,ε就是指εe。
压缩模量指的是侧限压缩模量,通过固结试验可以测定。
如果土体是理想弹性体,那么E=Es(1-2μ^2/(1-μ))=E0。
在土体模拟分析时,如果时一维压缩问题,选用Es;如果是变形问题,一般用E0;如果是瞬时变形,或弹性变形用E。
土的变形模量与压缩模量的关系土的变形模量和压缩模量,是判断土的压缩性和计算地基压缩变形量的重要指标。
为了建立变形模量和压缩模量的关系,在地基设计中,常需测量土的側压力系数ξ和側膨胀系数μ。
側压力系数ξ:是指側向压力δx与竖向压力δz之比值,即:ξ=δx/δz土的側膨胀系数μ(泊松比):是指在側向自由膨胀条件下受压时,测向膨胀的应变εx与竖向压缩的应变εz之比值,即μ=εx/εz根据材料力学广义胡克定律推导求得ξ和μ的相互关系,ξ=μ/(1-μ)或μ=ε/(1+ε)土的側压力系数可由专门仪器测得,但側膨胀系数不易直接测定,可根据土的側压力系数,按上式求得。
在土的压密变形阶段,假定土为弹性材料,则可根据材料力学理论,推导出变形模量E0和压缩模量Es之间的关系。
,令β=则Eo=βEs当μ=0~0.5时,β=1~0,即Eo/Es的比值在0~1之间变化,即一般Eo小于Es。
但很多情况下Eo/Es 都大于1。
其原因为:一方面是土不是真正的弹性体,并具有结构性;另一方面就是土的结构影响;三是两种试验的要求不同;μ、β的理论换算值土的种类μβ碎石土0.15~0.20 0.95~0.90砂土0.20~0.25 0.90~0.83粉土0.23~0.31 0.86~0.72粉质粘土0.25~0.35 0.83~0.62粘土0.25~0.40 0.83~0.47注:E0与Es之间的关系是理论关系,实际上,由于各种因素的影响,E0值可能是βEs值的几倍,一般来说,土愈坚硬则倍数愈大,而软土的E0值与βEs 值比较弹性模量的数值随材料而异,是通过实验测定的,其值表征材料抵抗弹性变形的能力。
常用材料弹性模量及泊松比

167
23
20CrMnTi
212
209
203
197
187
177
24
25Cr12wMoV
216
211
205
198
189
178
25
214
212
205
199
190
178
26
30CrMnSiA
196
—
177
167
162
157
27
30CrMnSiNi2A
207
204
200
—
—
—
28
35CrMo
181
11
4Cr13
215
210
202
194
184
173
12
4Cr10Si2Mo
206
211
207
202
196
168
13
9Cr18
200
—
—
—
—
—
14
0Cr18Ni9
199
—
—
—
—
—
15
1Cr18Ni9
180
—
170
164
—
—
16
0Cr17Ni2
193
—
—
164
—
148
17
12Cr1MoV
214
211
4
25#
198
196
191
185
164
—
5
45#
209
207
202
196
186
174
常用材料弹性模量及泊松比
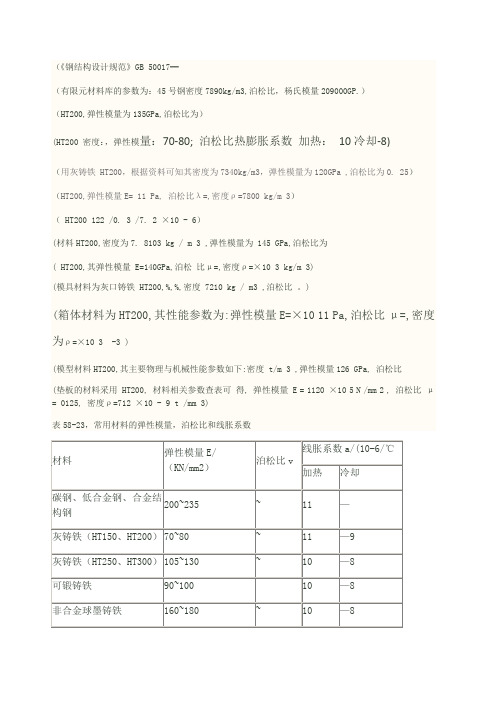
(《钢结构设计规范》GB 50017━(有限元材料库的参数为:45号钢密度7890kg/m3,泊松比,杨氏模量209000GP.)(HT200,弹性模量为135GPa,泊松比为)(HT200 密度:,弹性模量:70-80; 泊松比热膨胀系数加热:10冷却-8)(用灰铸铁 HT200,根据资料可知其密度为7340kg/m3,弹性模量为120GPa ,泊松比为0. 25)(HT200,弹性模量E= 11 Pa, 泊松比λ=,密度ρ=7800 kg/m 3)( HT200 122 /0. 3 /7. 2 ×10 - 6)(材料HT200,密度为7. 8103 kg / m 3 ,弹性模量为 145 GPa,泊松比为( HT200,其弹性模量 E=140GPa,泊松比μ=,密度ρ=×10 3 kg/m 3)(模具材料为灰口铸铁 HT200,%,%,密度 7210 kg / m3 ,泊松比。
)(箱体材料为HT200,其性能参数为:弹性模量E=×10 11 Pa,泊松比μ=,密度为ρ=×10 3 -3 )(模型材料HT200,其主要物理与机械性能参数如下:密度 t/m 3 ,弹性模量126 GPa, 泊松比(垫板的材料采用 HT200, 材料相关参数查表可得, 弹性模量 E = 1120 ×10 5 N /mm 2 , 泊松比μ= 0125, 密度ρ=712 ×10 - 9 t /mm 3)表58-23,常用材料的弹性模量,泊松比和线胀系数常用弹性模量及泊松比━━━━━━━━━━━━━━━━━━名称弹性模量E 切变模量G 泊松比μ GPa GPa──────────────────镍铬钢 206合金钢 206碳钢 196-206 79铸钢 172-202球墨铸铁 140-154 73-76灰铸铁 113-157 44白口铸铁 113-157 44冷拔纯铜 127 48轧制磷青铜 113 41轧制纯铜 108 39轧制锰青铜 108 39铸铝青铜 103 41冷拔黄铜 89-97 34-36 轧制锌 82 31硬铝合金 70 26轧制铝 68 25-26铅 17 7玻璃 55 22混凝土 14-23纵纹木材横纹木材橡胶电木尼龙可锻铸铁 152拔制铝线 69大理石 55花岗石 48 石灰石 41 尼龙1010夹布酚醛塑料石棉酚醛塑料高压聚乙烯低压聚乙烯聚丙烯。
弹性模量定义与公式

弹性模量之宇文皓月创作开放分类:基本物理概念工程力学物理学自然科学“弹性模量”的一般定义是:应力除以应变,即弹性变形区的应力-应变曲线的斜率:其中λ是弹性模量,【stress应力】是引起受力区变形的力,【strain应变】是应力引起的变更与物体原始状态的比,通俗的讲对弹性体施加一个外界作用,弹性体会发生形状的改变称为“应变”。
资料在弹性变形阶段,其应力和应酿成正比例关系(即胡克定律),其比例系数称为弹性模量。
弹性模量的单位是达因每平方厘米。
“弹性模量”是描述物质弹性的一个物理量,是一个总称,包含“杨氏模量”、“剪切模量”、“体积模量”等。
所以,“弹性模量”和“体积模量”是包含关系。
编辑摘要中文名:弹性模量其他外文名:Elastic Modulus 定义:应力除以应变类型:定律•6单位指标定义/弹性模量编辑混凝土弹性模量测定仪图册弹性模量modulusofelasticity,又称弹性系数,杨氏模量。
弹性资料的一种最重要、最具特征的力学性质。
是物体变形难易程度的表征。
用E暗示。
定义为理想资料在小形变时应力与相应的应变之比。
根据分歧的受力情况,分别有相应的拉伸弹性模量(杨氏模量)、剪切弹性模量(刚性模量)、体积弹性模量等。
它是一个资料常数,表征资料抵抗弹性变形的能力,其数值大小反映该资料弹性变形的难易程度。
对一般资料而言,该值比较稳定,但就高聚物而言则对温度和加载速率等条件的依赖性较明显。
对于有些资料在弹性范围内应力-应变曲线不符合直线关系的,则可根据需要可以取切线弹性模量、割线弹性模量等人为定义的法子来代替它的弹性模量值。
线应变/弹性模量编辑弹性模量图册对一根细杆施加一个拉力F,这个拉力除以杆的截面积S,称为“线应力”,杆的伸长量dL除以原长L,称为“线应变”。
线应力除以线应变就等于杨氏模量E=( F/S)/(dL/L)剪切应变:对一块弹性体施加一个侧向的力f(通常是摩擦力),弹性体会由方形酿成菱形,这个形变的角度a称为“剪切应变”,相应的力f除以受力面积S称为“剪切应力”。
常用材料的弹性模量及泊松比数据表

常用材料的弹性模量及泊松比数据表(S)序号材料名称弹性模量\E\Gpa 切变模量\G\Gpa 泊松比\μ1 镍铬钢、合金钢206 79.38 0.25~0.32 碳钢196~206 79 0.24~0.283 铸钢172~202 - 0.34 球墨铸铁140~154 73~76 -5 灰铸铁、白口铸铁113~157 44 0.23~0.276 冷拔纯铜127 48 -7 轧制磷青铜113 41 0.32~0.358 轧制纯铜108 39 0.31~0.349 轧制锰青铜108 39 0.3510 铸铝青铜103 41 -11 冷拔黄铜89~97 34~36 0.32~0.4212 轧制锌82 31 0.2713 硬铝合金70 26 -14 轧制铝68 25~26 0.32~0.3615 铅17 7 0.4216 玻璃55 22 0.2517 混凝土14~23 4.9~15.7 0.1~0.1818 纵纹木材9.8~12 0.5 -19 横纹木材0.5~0.98 0.44~0.64 -20 橡胶0.00784 - 0.4721 电木 1.96~2.94 0.69~2.06 0.35~0.3822 尼龙28.3 10.1 0.423 可锻铸铁152 - -24 拔制铝线69 - -25 大理石55 - -26 花岗石48 - -27 石灰石41 - -28 尼龙1010 1.07 - -29 夹布酚醛塑料4~8.8 - -30 石棉酚醛塑料 1.3 - -31 高压聚乙烯0.15~0.25 - -32 低压聚乙烯0.49~0.78 - -33 聚丙烯 1.32~1.42 - -Q235等属于碳素结构钢,35#、45#等属于优质碳素钢,强度较高,塑性和韧性都比碳素钢好。
屈服强度:是弹性变形的极限也叫屈服点。
增加应力到一定程度时成为塑性变形,也就是变弯了。
每种钢的屈服强度是不一样的镍铬钢、合金钢的弹性模量是206GPa碳钢的弹性模量为196~206GPa,计算时一般取206GPa铸钢的弹性模量为172~202Gpa(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
常用材料弹性模量及泊松比完整版

(模具材料为灰口铸铁 HT200,%,%,密度 7210 kg / m3 ,泊松比。)
(箱体材料为HT200,其性能参数为:弹性模量E=×10 11 Pa,泊松比μ=,密度为ρ=×10 3-3 )
(模型材料HT200,其主要物理与机械性能参数如下:密度t/m 3 ,弹性模量126 GPa, 泊松比
205
198
189
178
25
28CrNiMoV
214
212
205
199
190
178
26
30CrMnSiA
196
—
177
167
162
157
27
30CrMnSiNi2A
207
204
200
—
—
—
28
35CrMo
213
209
205
199
181
177
29
40Cr
211
208
202
195
186
177
30
40CrNiMo
加热
冷却
碳钢、低合金钢、合金结构钢
200~235
~
11
—
灰铸铁(HT150、HT200)
70~80
~
11
—9
灰铸铁(HT250、HT300)
105~130
~
10
—8
可锻铸铁
90~100
10
—8
非合金球墨铸铁
160~180
~
10
—8
青铜
85
17
常用材料弹性模量及泊松比(参照类别)

197
191
183
174
7
08AL
214
212
206
200
192
179
8
1Cr13
217
—
206
198
189
179
9
2Cr13
228
214
208
200
189
180
10
3Cr13
219
210
202
196
181
11
4Cr13
215
210
202
194
184
173
12
4Cr10Si2Mo
206
211
207
轧制锌 82 31 0.27
硬铝合金 70 26
轧制铝 68 25-26 0.32-0.36
铅 17 7 0.42
玻璃 55 22 0.25
混凝土 14-23 4.9-15.7 0.1-0.18
纵纹木材 9.8-12 0.5
横纹木材 0.5-0.98 0.44-0.64
橡胶 0.00784 0.47
0.24~0.26
10
—8
可锻铸铁
90~100
0.25
10
—8
非合金球墨铸铁
160~180
0.28~0.29
10
—8
青铜
85
0.35
17
—15
黄铜
80
0.36~0.37
18
—16
铝合金
69
0.32~0.36
21
—20
镁铝合金
40
0.25~0.30
25.5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弹性模量
一般地讲,对弹性体施加一个外界作用力,弹性体会发生形状的改变(称为“形变”),“弹性模量”的一般定义是:单向应力状态下应力除以该方向的应变。
材料在弹性变形阶段,其应力和应变成正比例关系(即符合胡克定律),其比例系数称为弹性模量。
弹性模量的单位是达因每平方厘米。
“弹性模量”是描述物质弹性的一个物
对一根细杆施加一个拉力F,这个拉力除以杆的截面积S,称为“线应力”,杆的伸长量dL除以原长L,称为“线应变”。
线应力除以线应变就等于杨氏模量E=( F/S)/(dL/L)
剪切应变:
编辑
对一块弹性体施加一个侧向的力f(通常是摩擦力),弹性体会由方形变成菱形,这个形变的角度a称为“剪切应变”,相应的力f除以受力面积S称为“剪切应力”。
剪切应力除以
对弹性体施加一个整体的压强p,这个压强称为“体积应力”,弹性体的体积减少量(-dV)除以原来的体积V称为“体积应变”,体积应力除以体积应变就等于体积模量: K=P/(-
dV/V)
在不易引起混淆时,一般金属材料的弹性模量就是指杨氏模量,即正弹性模量。
单位:E(弹性模量)兆帕(MPa)
意义
弹性模量是工程材料重要的性能参数,从宏观角度来说,弹性模量是衡量物体抵抗弹性变形能力大小的尺度,从微观角度来说,则是原子、离子或分子之间键合强度的反映。
凡影响键合强度的因素均能影响材料的弹性模量,如键合方式、晶体结构、化学成分、微观组织、温度等。
因合金成分不同、热处理状态不同、冷塑性变形不同等,金属材料的杨氏模量值会有5%或者更大的波动。
但是总体来说,金属材料的弹性模量是一个对组织不敏感的力学性能指标,合金化、热处理(纤维组织)、冷塑性变形等对弹性模量的影响较小,温度、加载速率等外在因素对其影响也不大,所以一般工程应用中都把弹性模量作为常数。
弹性模量可视为衡量材料产生弹性变形难易程度的指标,其值越大,使材料发生一定弹性变形的应力也越大,即材料刚度越大,亦即在一定应力作用下,发生弹性变形越小。
弹性模量E是指材料在外力作用下产生单位弹性变形所需要的应力。
它是反映材料抵抗弹
又称杨氏模量,弹性材料的一种最重要、最具特征的力学性质,是物体弹性变形难易程度的表征,用E表示。
定义为理想材料有小形变时应力与相应的应变之比。
E以σ单位面积上承受的力表示,单位为N/m^2。
模量的性质依赖于形变的性质。
剪切形变时的模量称为剪切模量,用G表示;压缩形变时的模量称为压缩模量,用K表示。
模量的倒数称为柔量,用J表示。
拉伸试验中得到的屈服极限σs和强度极限σb,反映了材料对力的作用的承受能力,而延伸率δ或截面收缩率ψ,反映了材料塑性变形的能力。
为了表示材料在弹性范围内抵抗变形的难易程度,在实际工程结构中,材料弹性模量E的意义通常是以零件的刚度体现出来的,这是因为一旦零件按应力设计定型,在弹性变形范围内的服役过程中,是以其所受负荷而产生的变形量来判断其刚度的。
一般按引起单位应变的负荷为该零件的刚度,例如,在拉压构件中其刚度为:EA0
式中A0为零件的横截面积。
由上式可见,要想提高零件的刚度E A0,亦即要减少零件的弹性变形,可选用高弹性模量的材料和适当加大承载的横截面积,刚度的重要性在于它决定了零件服役时稳定性,对细长杆件和薄壁构件尤为重要。
因此,构件的理论分析和设计计算来说,弹性模量E是经常要用到的一个重要力学性能指标。
单位指标
编辑
材料的抗弹性变形的一个量,材料刚度的一个指标。
钢材的弹性模量E=2.06e11Pa=206GPa (e11表示10的11次方)
它只与材料的化学成分有关,与温度有关。
与其组织变化无关,与热处理状态无关。
但是与材料缠绕形状有一定关系,比如将一根弹模已知的钢丝绕成一根弹簧,则弹模会改变,或者多根钢丝捻制成绞线,把他当成一个整体来检测弹性模量,其整体弹模与材料本身的弹模是不一样的。
各种钢的弹性模量差别很小,金属合金化对其弹性模量影响也很小。
1兆帕(MPa)=145磅/英寸2(psi)=10.2千克力/平方厘米(kgf/cm²)=10巴(bar)=9.8大气压(atm)
1磅/英寸2(psi)=0.006895兆帕(MPa)=0.0703千克力/平方厘米(kgf/cm²)=0.0689巴(bar)=0.068大气压(atm)
1巴(bar)=0.1兆帕(MPa)=14.503磅/英寸2(psi)=1.0197千克力/平方厘米
(kgf/cm²)=0.987大气压(atm)
1大气压(atm)=0.101325兆帕(MPa)=14.696磅/英寸2(psi)=1.0333千克力/平方厘米kgf/cm²)=1.0133巴(bar)。
