结构力学课后习题答案
结构力学课后习题答案(2)
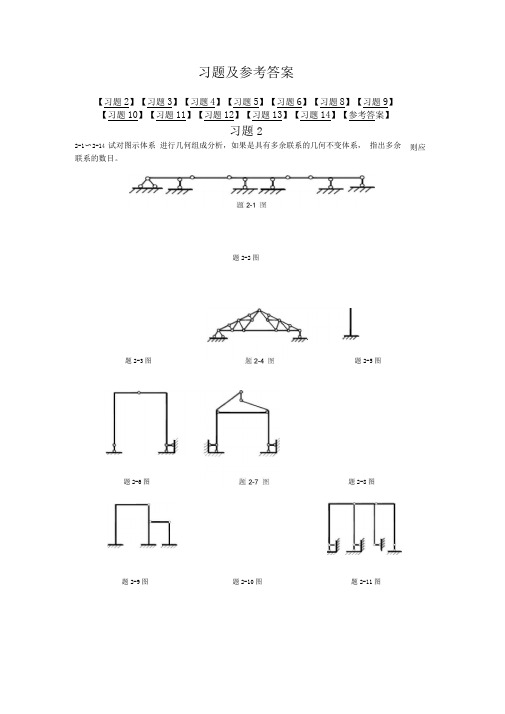
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1〜2-14 试对图示体系进行几何组成分析，如果是具有多余联系的几何不变体系，指出多余则应联系的数目。
题2-2图题2-3图题2-5图题2-6图题2-8图题2-9图题2-10图题2-11图题4-1图4-2 作图示刚架的M 图。
3-1 试作图示多跨静定梁的M 及Q 图。
习题(a)1.5m 1 2m I2.5m | 1.5m l 4.5m题3-1(b)3-2 试不计算反力而绘出梁的M 图。
4m40kN(a) 5kN/mM(b )4-1 作图示刚架的M 、Q 、N 图。
2kN /m2kN • m (a)2kN 题3-2习题4(b ) (c )4-3 4-4 4-54m(a)(d)作图示三铰刚架的M图。
M=4Pa2a(b)4kN4m 4m(c)珂10kN/m4m(e)题4-2图CE0.5m ]m2J 0.5m7mB7m(a)题4-3作图示刚架的M图。
(a)I 盒lUlUUW已知结构的M图，试绘出荷载。
10kN/m1.5m题4-4图urm*~ G3mC7.35m 7.35m(b)m6Nn m220kN40kN/m4m(b)C_PaPaPaa4-6 检查下列刚架的M图，并予以改正。
5-15-2 题4-5图(b)P(d)(e) (f)(c)题4-6图习题5图示抛物线三铰拱轴线方程4 f1kN/mx)x，(h)试求D截面的内力。
20kN10m题5-1图K15m j 5ml=30m带拉杆拱，拱轴线方程 y ，求截面的弯矩。
题5-3图习题66-1 判定图示桁架中的零杆。
6-2 6-3 6-4 6-5 用结点法计算图示桁架中各杆内力。
(b) (c)m题6-2用截面法计算图示桁架中指定各杆的内力。
3m [ 3m3m I 3m题6-3试求图示组合结构中各链杆的轴力并作受弯杆件的用适宜方法求桁架中指定杆内力。
结构力学力法习题答案
结构力学力法习题答案结构力学力法习题答案结构力学是一门研究物体在受力作用下的变形和破坏规律的学科。
在学习结构力学的过程中，习题是必不可少的一部分。
通过解答习题，我们可以更好地理解和应用力学原理，提高解决实际问题的能力。
下面，我将为大家提供一些结构力学力法习题的详细解答，希望对大家的学习有所帮助。
习题一：一根悬臂梁的长度为L，截面为矩形，宽度为b，高度为h，材料的弹性模量为E。
在悬臂梁的自重和外力作用下，求悬臂梁的最大弯矩和最大挠度。
解答：首先，我们需要根据悬臂梁的几何形状和受力情况，绘制出受力图。
在这个问题中，悬臂梁受到自重和外力的作用，自重作用在悬臂梁的重心处，外力作用在悬臂梁的端点处。
根据受力图，我们可以得到悬臂梁在端点处的反力和弯矩分布。
接下来，我们可以根据结构力学的基本原理，利用力平衡和力矩平衡的方程，求解出悬臂梁的最大弯矩和最大挠度。
在这个问题中，我们可以利用弯矩-曲率关系，得到最大弯矩的表达式。
然后，我们可以利用悬臂梁的边界条件，求解出最大挠度的表达式。
习题二：一根悬臂梁的长度为L，截面为圆形，直径为d，材料的弹性模量为E。
在悬臂梁的自重和外力作用下，求悬臂梁的最大弯矩和最大挠度。
解答：与习题一类似，我们需要绘制出悬臂梁的受力图，根据受力图求解出悬臂梁的最大弯矩和最大挠度。
在这个问题中，悬臂梁的截面为圆形，因此我们需要利用圆形截面的惯性矩和弯矩-曲率关系，求解出最大弯矩的表达式。
习题三：一根梁的长度为L，截面为矩形，宽度为b，高度为h，材料的弹性模量为E。
梁的两端固定，受到均布载荷q的作用，求梁的最大弯矩和最大挠度。
解答：在这个问题中，梁的两端固定，因此我们需要考虑边界条件对梁的受力和变形的影响。
首先，我们需要绘制出梁的受力图，根据受力图求解出梁的最大弯矩。
然后，我们可以利用梁的边界条件，求解出最大挠度的表达式。
通过以上三个习题的解答，我们可以看到，在结构力学的学习中，我们需要灵活运用力学原理，结合具体的问题，综合考虑几何形状、材料性质和边界条件等因素，才能得到准确的解答。
南京航空航天大学 飞行器结构力学 课后习题答案 第1章
第一章 弹性力学基础1-1 上端悬挂、下端自由的等厚度薄板，其厚度为1，容重为ρ。
试求在自重作用下的位移分量表达式。
解：如图1-1建立坐标系.利用x σ沿y 方向均匀分布及x 方向的力平衡条件0=∑x 可得，⎪⎩⎪⎨⎧==-= x l xyy x 00)(τσρσ 又因为1()()x y u u l x x E Eρσσ∂=-=-∂ )()(1x l Eu u E y vx y --=-=∂∂ρσσ 积分得)()21(12y f x lx u +-=Eρ)()(2x f y x l uv +--=Eρ又由对称性 0)(020=⇒==x f v y 由 2110()2xy u v f y uy y x Eτρ∂∂=+=⇒=-∂∂ 综上所述有2221)21(uy Ex lx u ρρ--=Ey x l uv )(--=Eρ1-2 写出图1-2所示平面问题的应力边界条件。
解：上表面为力边界，100＝，＝，＝，m l q lxl X --=Y 。
代入x xy xy y l m Xl m Yσττσ⎧+=⎪⎨+=⎪⎩ 中得到上表面的边界条件为00=--=xy y x q lxl τσσ；＝；下表面为自由边，边界条件为000==xy y x τσσ；＝；侧面为位移边界。
1-3 矩形板厚为1。
试用应力函数22A xy ϕ=求解。
（并画出面力分布图）解：应力函数22A xy ϕ=满足应力函数表示的变形协调方程，可以作为解。
在无体力的情况下，矩形板的应力为22x Ax yϕσ∂==∂220y x ϕσ∂==∂2xy Ay x yϕτ∂=-=-∂∂根据应力边界条件公式x xy xy y l m X l m Yσττσ+=+=各边的应力边界为a d 边： 0,1l m == 20A X A y h Y ⎧=-=-⎪⎨⎪=⎩ c b 边： 0,1l m ==- 20A X A y hY ⎧==-⎪⎨⎪=⎩a b 边： 1,0l m =-= 0X Y A y⎧=⎪⎨=⎪⎩c d 边： 1,0l m == X A x A lY A y⎧==⎪⎨=-⎪⎩根据以上各边的应力边界条件，可画出矩形板的面力分布图如图1-3a 。
南京航空航天大学结构力学课后习题答案
第三章能量原理（习题解答）3-1写出下列弹性元件的应变能和余应变能的表达式。
（a ）等轴力杆；（b ）弯曲梁；（c ）纯剪矩形板。
解：（a ）等轴力杆 应变能 余应变能其中L 为杆的长度，f 为杆的截面积，△为杆的变形量，E 为材料的弹性模量。
（b ） 弯曲梁 应变能 余应变能（c ） 纯剪矩形板 应变能 余应变能3-2求图3-2所示桁架的应变能及应变余能，应力一应变之间的关系式为 (a) E (b)E,_解：取节点2进行受力分析，如图3-2a 所示 根据平衡条件，有U BdV fl dV联立（1）、（2）、（3）、（4）,得到桁架的应变能为 联立（1）、（2）、（3）、（5）,得到桁架的余应变能为(a ) E 时N 1 cos45 N 3COS 45N 1 si n45 N 3 sin 45PN 1p1BN1、2N巳P N 1 1f 13N 3f 3N ±3N 31Ef 1Ef 3 U v AdVfld(1)(2)(3) (4) (5)Nj 联立（1）、（2）、（4）、（6）,得到桁架的应变能为 联立（1）、（2）、（5）、（6）,得到桁架的应变能为3-3 一种假想的材料遵循如下二维的应力一应变规律 其中E 、G 和 是材料常数。
导出用这种材料做成的二维物体的应变能密度解：应变能密度 余应变能密度 总应变能密度 而 所以应变能密度为3-4试用虚位移原理或最小位能原理确定题3-4图所示平面桁架的节点 o的位置和各杆内力。
各杆材料相同，弹性常数为 E 。
P 1 104N ，P 2 5 103 N ，各杆截面积 f 1 1.5cm 2， f 2. 2cm 2，o-2 杆:系统位能 令 0,则——0，—— 0 ,从而：uv解得由N 旦^ ，得l3-5 试用最小位能原理导出承受均布载荷 q 的弯曲等截面梁（图3-5）的 平衡方程式。
解：由教科书例3-2知 悬臂梁的边界条件为： 在 x 0 处，w 0， dw 0dx在x l 处，剪力Q 0，弯矩M 0 又知u z 业（直法线假设）dx(b )3cm 2。
结构力学课后答案-第6章--力法
习题6-1试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g)所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定II去掉复铰，可减去2（4-1）=6个约束，沿I-I截面断开，减去三个约束，故为9次超静定沿图示各截面断开，为21次超静定I II 刚片I与大地组成静定结构，刚片II只需通过一根链杆和一个铰与I连接即可，故为4次超静定(h)6-2试回答：结构的超静定次数与力法基本结构的选择是否有关？力法方程有何物理意义？6-3试用力法计算图示超静定梁，并绘出M 、F Q 图。
(a)解：上图=l1M pM 01111=∆+p X δ其中：EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EI l F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61F PA2l 3l 3B2EIEIC题目有错误，为可变体系。
+pF p lF 32X 1=1M 图p Q X Q Q +=11p F 21⊕p F 21(b)解：基本结构为：l1M 3l l2M l F p 21pM l F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδp M X M X M M ++=2211pQ X Q X Q Q ++=22116-4试用力法计算图示结构，并绘其内力图。
(a)l2l 2l2lABCD EI =常数F Pl 2E FQ 图F PX 1X 2F P解：基本结构为：1M pM 01111=∆+p X δpM X M M +=11(b)解：基本结构为：EI=常数qACEDB4a 2a4a4a20kN/m3m6m6mAEI 1.75EIB CD 20kN/mX 1166810810计算1M ，由对称性知，可考虑半结构。
结构力学章节习题及参考答案
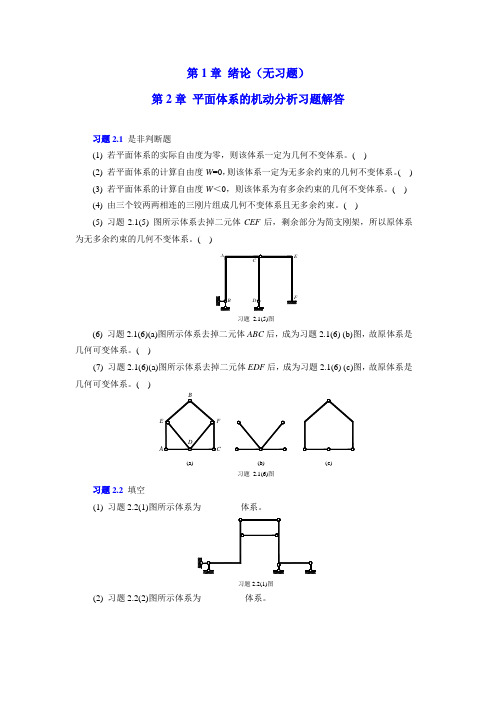
第1章绪论（无习题）第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零，则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0，则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W＜0，则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。
( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后，成为习题2.1(6) (b)图，故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后，成为习题2.1(6) (c)图，故原体系是几何可变体系。
()(a)(b)(c)习题2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题 2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题2.2(5)图(6) 习题2.2(6)图所示体系为_________体系，有_________个多余约束。
习题2.2(6)图(7) 习题2.2(7)图所示体系为_________体系，有_________个多余约束。
习题2.2(7)图习题2.3对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用内力图特征绘制某受弯杆段的弯矩图时，必须先求出该杆段两端的端弯矩。
(完整版)!完整的结构力学答案-同济大学朱慈勉!
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度，并分析体系的几何构造。
(a )ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(Ⅱ Ⅲ)舜变体系`ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)2-3 试分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(Ⅱ Ⅲ)几何不变W=3×3 - 2×2 – 4=1>0可变体系ⅠⅡⅢ（ⅠⅡ）（ⅠⅢ）（ⅡⅢ）几何不变2-4 试分析图示体系的几何构造。
(a)（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）ⅠⅡⅢ几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系ⅢⅠⅡ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）几何不变(d)（ⅠⅡ）ⅢⅠⅡ（ⅡⅢ）（ⅠⅢ）二元杆有一个多余约束的几何不变体ⅠⅡⅢ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）舜变体系(f)ⅠⅡⅢ（ⅠⅢ）（ⅡⅢ）（ⅠⅡ）无多余约束内部几何不变ⅠⅡⅢ（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）二元体(h)ⅠⅡⅢ（ⅠⅢ）（ⅠⅡ）（ⅡⅢ）二元体多余约束W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)（ⅠⅢ）ⅠⅡⅢ（ⅠⅡ）（ⅡⅢ）舜变体系(b)ⅠⅡⅢ（ⅠⅡ）（ⅡⅢ）（ⅠⅢ）几何不变同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)4P F a2P F a 2P F a Ｍ4P F Ｑ34P F 2P F(b)ABCaa aaaF P a DEFF P2m6m2m4m2mABCD10kN2kN/m４2020M Q10/326/3４10(c)21018018040M1560704040Q(d)3m2m2mA B CEF15kN 3m3m4m20kN/mD 3m2m2m2mA2m 2m2mABCD E FG H 6kN ·m4kN ·m 4kN2m7.5514482.524MQ3-3 试作图示刚架的内力图。
结构力学课后习题答案
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】「习题11】【习题12】【习题13】【习题14】【参考答衆】习题22-1〜2-14试对图示体系进行儿何组成分析，如果是只有多余联系的儿何不变体系，则应指出多余联系的数目。
d5∑° X 厂^τ"βH题2-2图ΓΛ题2-3图题2-5图题2-6图题2-1图H 2-9 图题2-10图题2-11图题2-12图题2-13图习题3试作图示多跨挣定梁的M及Q图。
(a) (b)题3-1图3-2试不计算反力而绘出梁的M图。
题3-2图习题44-1作图示刚架的M、Q、N图。
40fcN 40kN20kNm4-2作图示刚架的M图。
2OkN m SkN mSkXm 40fcN题4-1图4-3作图示三狡刚架的M图。
4-4作图示刚架的M图。
AEmJnIAr lD1题4-2图4-5己知结构的M图•试绘出荷载。
题4-4图3IOkNnlJ^1.5mC(a)题4-3日6erIB9 9题5-1图5-2带拉杆拱，拱轴线方程y= il(l-χ)χ,求截面K 的弯矩。
题5-2图5-3试求图示带拉杆的半圆三狡拱截面K 的内力・4-6检査F 列刚架的M 图，并予以改正。
题4-5图ω∙I ∣ULL∏ ∏ ⅛)题4-6图习题5图示抛物纟戈三铁拱轴线方程y = ff(l-x)x ，试求D 截面的内力。
IkNm15m [ 5m [ ICm 1=3OmC题5-3图习题6 6-1判定图示桁架中的零杆。
题6-1图6-2用结点法计算图示桁架中各杆内力。
(a) FGH月Λ4x4m=16m题6-2图6-3用截面法计算图示桁架中指定各杆的内力。
40kN题6-3图6-4试求图示组介结构中齐链杆的轴力并作受弯杆件的Q图。
2m ] 2m ]lm]lπ⅝] 2m [题6-4图6-5用适宜方法求桁架中指定杆内力。
题6-6图习题88-1试作图示悬臂梁的反力V B 、MB 及内力Q C 、MC 的影响线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
7- 32 习 题 7-1 试确定图示结构的位移法基本未知量数目，并绘出基本结构。 (a) (b) (c)
EI EI EI
2EI 2EI
1个角位移 3个角位移，1个线位移 4个角位移，3个线位移
(d) (e) (f) EI1=∞ EA EI
EI1=∞
3个角位移，1个线位移 2个线位移 3个角位移，2个线位移 (g) (h) (i) k
一个角位移，一个线位移 一个角位移，一个线位移 .
'. 三个角位移，一个线位移 7-2 试回答：位移法基本未知量选取的原则是什么？为何将这些基本未知位移称为关键位移？是否可以将静定部分的结点位移也选作位移法未知量？ 7-3 试说出位移法方程的物理意义，并说明位移法中是如何运用变形协调条件的。 7-4 试回答：若考虑刚架杆件的轴向变形，位移法基本未知量的数目有无变化？如何变化？ 7-5 试用位移法计算图示结构，并绘出其内力图。 (a)
解：（1）确定基本未知量和基本结构 有一个角位移未知量，基本结构见图。
l l
l A B C D i i i
q 7- 34
11r1
1Z3i
4i
2iii
1M图
1pR213ql
216ql
pM图 （2）位移法典型方程 11110prZR （3）确定系数并解方程
iqlZqliZqlRirp24031831,821212111
（4）画M图 2724ql
2524ql
M图
218ql
216ql
(b) 4m 4m
4m A C D B 10kN EI 2EI
2.5kN/m EI .
'. 解：（1）确定基本未知量 1个角位移未知量，各弯矩图如下
11r11Z
1M图3
2EI
EI12EI
590
pM图 （2）位移法典型方程 11110prZR （3）确定系数并解方程
1115,352prEIR 153502EIZ
114ZEI
（4）画M图
()KNmM图2640
147 (c)
6m 6m
9m A B
C
EA=∞ FP 2EI EI EI
D E F EA=∞ 7- 36
解：（1）确定基本未知量 一个线位移未知量，各种M图如下
11r
1M图
11Z27EI227EI
27
EI
1243EI2
243EI1
243EIp
M图
pF1p
R
（2）位移法典型方程 11110prZR （3）确定系数并解方程
1114,243pprEIRF 140243pEIZF
12434ZEI
（4）画M图 .
'. 94pF9
4pF9
2pF
M图
(d)
解：（1）确定基本未知量 一个线位移未知量，各种M图如下
11Z2/25EAa4/25EAa
11r
1M图 2
5EA
11r
1M图
2/25EAa
2
/25EAa
简化
a 2a a 2a a EA EA A B C D
E F
FP FP
EI1=∞ 7- 38
图1pRpFpF
4
5a3
5a
1
5a
pM
（2）位移法典型方程 11110prZR （3）确定系数并解方程
11126/,55pprEAaRF 126055pEAZFa
13aZEA
（4）画M图
图M0.6pFap
Fa
1.2pF0.6pF
(e)
l l EA
A B
C D
EA EA
FP .
'. 解：（1）确定基本未知量 两个线位移未知量，各种M图如下
图11Z 11r
21r
1121
2142 4EArlEArl
1M2EAl
EAl
图21Z 12r22
r
22214EArl
2M2EAl
EAl
图 12 0ppp
RFR
pM
1pRpF000
（2）位移法典型方程 1111221211222200pp
rZrZRrZrZR
（3）确定系数并解方程 7- 40
1112212212221,44214,0ppp
EAEArrrllEArlRFR
代入，解得
121222121212p
p
lZFEAlZFEA
（4）画M图
图 M122212pF
2212pF
1
212pF
7-6 试用位移法计算图示结构，并绘出M图。 (a)
解：（1）确定基本未知量 10kN/m A C
B E
D F
6m 6m
6m
6m EI=常数 .
'. 两个角位移未知量，各种M图如下 23EI13EI23EI
23EI
13EI
1121
21 3rEIrEI
图1M
23EI
23EI
13EI
22116rEI
图2M
13EI1
3EI
1130 0pp
RR
图pM
30
（2）位移法典型方程 1111221211222200pp
rZrZRrZrZR
（3）确定系数并解方程
111221221212,311630,0pp
rEIrrEIrEIRR
代入，解得 1215.47,2.81ZZ （4）画最终弯矩图