最新北师大版八年级下册数学第三章图形的平移和旋转单元测试试题以及答案

合集下载

北师大八年级下《第三章图形的平移与旋转》单元测试(含答案)

第三章图形的平移与旋转一、旋转题1.如图，所给图形中是中心对称图形但不是轴对称图形的是（）A. B. C. D.2.用放大镜将图形放大，应该属于（）A. 平移变换B. 相似变换C. 对称变换D. 旋转变换3.将点M（﹣1，﹣5）向右平移3个单位长度得到点N，则点N所处的象限是（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限4.如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AB=8，将△ABC沿CB向右平移得到△DEF．若四边形ABED 的面积等于8，则平移距离等于（）A. 2B. 4C. 8D. 165.如图，OA=OB=6cm，线段OB从与OA重合的位置开始沿逆时针方向旋转120°，在旋转过程中，设AB的中点为P（当OA与OB重合时，记点P与点A重合），则点P运动的路径长为（）A. 6cmB. 4πcmC. 2πcmD. 3cm6.如图，Rt△ABC中，∠BAC＝90°，∠B＝60°，△AB′C′可以由△ABC绕点A顺时针旋转90°得到（点B′与点B是对应点，点C′与点C是对应点），连结CC′，则∠CC′B′的度数是（）A. 45°B. 30°C. 25°D. 15°7.如图，等腰直角三角形ABC的直角边AB的长为6cm，将△ABC绕点A逆时针旋转15°后得到△AB′C′，AC 与B′C′相交于点H，则图中△AHC′的面积等于（）A. 12﹣6B. 14﹣6C. 18﹣6D. 18+68.如图所示是“福娃欢欢”的五幅图案，②，③，④，⑤哪一个图案可以通过平移图案①得到（）A. ②B. ③C. ④D. ⑤9.如图，在正方形ABCD中，AB=3，点E在CD边上，DE=1，把△ADE绕点A顺时针旋转90°，得到△ABE′，连接EE′，则线段EE′的长为（）A. B. C. 4 D.10.如图，△ABC是等边三角形，D为BC边上的点，∠BAD＝15°，△ABD经旋转后到达△ACE的位置，那么旋转了( ).A. 75°B. 60°C. 45°D. 15°二、填空题11.在等边三角形、正方形、直角三角形、等腰梯形中，既是轴对称图形，又是中心对称图形的是________ .12.在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB'C',则∠B'AC=________.13.如图，△ABC沿射线AC方向平移2cm得到△A′B′C′，若AC=3cm，则A′C=________ cm．14.点P（﹣2，1）向上平移2个单位后的点的坐标为________15.如图，△ABC中，AB=AC，BC=12cm，点D在AC上，DC=4cm．将线段DC沿着CB的方向平移7cm得到线段EF，点E，F分别落在边AB，BC上，则△EBF的周长为________ cm．16.某景点拟在如图的矩形荷塘上架设小桥，若荷塘中小桥的总长为100米，则荷塘周长为________m.三、解答题17.如图所示，有一条宽相等的小路穿过长方形的草地ABCD，若AB=60m，BC=84m，AE=100m，若要硬化这条小路，且每平方米造价50元，则需要多少元钱？18.请把下面的小船图案先向上平移3格，再向右平移4格，最后为这个图案配上一句简短的解说词．19.每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，①把△ABC向上平移5个单位后得到对应的△A1B1C1，画出△A1B1C1，②以原点O为对称中心，再画出与△A1B1C1关于原点O对称的△A2B2C2．参考答案一、旋转题C BD A C D C D A B二、填空题11.正方形12.17°13.114.（﹣2，3）15.1316.200三、解答题17.解：在矩形ABCD中，AF∥EC，又∵AF=EC，∴四边形AECF是平行四边形．在Rt△ABE中，AB=60，AE=100，根据勾股定理得BE=80，∴EC=BC﹣BE=4，所以这条小路的面积S=EC•AB=4×60=240（m2）．240×50=1200元．答：需要1200元钱18.解：如图所示：解说词：两只小船在水中向前滑行19.解：如图所示：。

北师大版八年级数学下册第三章图形的平移与旋转单元测试卷 (含答案)

北师版八年级数学下册图形的平移与旋转单元测试卷（含答案）(时间：40分钟满分：100分)一、选择题(每小题3分，共30分)1.在A，B，C，D四幅图案中，能通过左图平移得到的是(B)A B C D2．下列图形中是中心对称图形的是(B)A B C D3．△ABC在平移过程中，下列说法错误的是(B)A．对应线段一定相等B．对应线段一定平行C．周长和面积保持不变D．对应边中点所连接线段的长等于平移的距离4．在平面直角坐标系中，若将三角形上各点的横坐标都加上5，纵坐标保持不变，则所得图形在原图形的基础上(D)A．向左平移了5个单位长度B．向下平移了5个单位长度C．向上平移了5个单位长度D．向右平移了5个单位长度5.如图，已知图形是中心对称图形，则对称中心是(D)A．点F B．点D C．线段BD的中点D．线段FD的中点6．如图，将△ABC绕点B顺时针旋转，旋转角是∠ABC，则下列说法错误的是(A)A．AC∥BE B．AB＝BD C．BC平分∠ABE D．AC＝DE 7．如图是某公园里一处长方形风景欣赏区ABCD，长AB＝100米，宽BC＝50米，为方便游人观赏，公园特意修建了如图所示的小路(图中非阴影部分)，小路的宽均为2米，那么小明沿着小路的中间，从出口A 到出口B 所走的路线(图中虚线)长为(B)A ．148米B ．196米C ．198米D ．200米8．下列3个图形中，能通过旋转得到右侧图形的有(B)① ② ③A ．①②B ．①③C ．②③ D.①②③9.如图，把△ABC 沿BC 方向平移，得到△A′B′C′，随着平移距离的不断增大，△A′CB 的面积大小变化情况是(C)A ．增大B ．减小C ．不变D ．不确定10．如图，在△OAB 中，OA ＝OB ，∠AOB＝15°，在△OCD 中，OC ＝OD ，∠COD＝45°，且点C 在边OA 上，连接CB ，将线段OB 绕点O 逆时针旋转一定角度得到线段OE ，使得DE ＝CB ，则∠BOE 的度数为(B)A ．15°B ．15°或45°C ．45°D ．45°或60°二、填空题(每小题4分，共20分)11．“绿水青山就是金山银山”，可以用“平移”来解释的是“山”字． 12．平面直角坐标系中，点O 为坐标原点，现有一点A(2，5)，将点A 向下平移5个单位长度，可以得到对应点的坐标A′(2，0)；再将线段OA′顺时针旋转90°，则点A″的坐标为(0，－2__)．13．如图，把三角板的斜边紧靠直尺平移，一个顶点从刻度“5”平移到刻度“10”，则顶点C 平移的距离CC′＝5．14．如图，在平面直角坐标系中，若△ABC 与△A 1B 1C 1关于点D 成中心对称，则对称中心点D 的坐标是(2，－12)．15．如图，在平面直角坐标系xOy中，△OA1B1绕点O逆时针旋转90°，得△OA2B2；△OA2B2绕点O逆时针旋转90°，得△OA3B3；△OA3B3绕点O逆时针旋转90°，得△OA4B4；…；若点A1(1，0)，B1(1，1)，点B2020的坐标是(1，－1)．三、解答题(共50分)16．(12分)如图1，2均为7×6的正方形网格，点A，B，C在格点上．(1)在图1中确定格点D，并画出以A，B，C，D为顶点的四边形，使其为轴对称图形(画一个即可)；(2)在图2中确定格点E，并画出以A，B，C，E为顶点的四边形，使其为中心对称图形(画一个即可)．图1 图2 解：(1)(2)如图所示．(答案不唯一)17．(12分)如图，在等腰Rt△ABC中，BA＝BC，∠ABC＝90°，点D在AC上，将△ABD绕点B沿顺时针方向旋转90°后，得到△CBE.(1)求∠DCE的度数；(2)若AB＝4，CD＝3AD，求DE的长．解：(1)∵△ABC为等腰直角三角形，∴∠BAD＝∠BCD＝45°，由旋转，得∠BA D＝∠BCE＝45°，∴∠DCE＝∠ACB＋∠BCE＝45°＋45°＝90°.(2)∵AB＝BC＝4，∠ABC＝90°，∴AC＝AB2＋BC2＝4 2.∵CD＝3AD, ∴AD＝2，CD＝3 2.由旋转，得AD＝CE＝ 2.∴DE＝CD2＋CE2＝（32）2＋（2）2＝2 5.18．(12分)如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A(1，1)，B(4，1)，C(3，3)．(1)将△ABC向下平移5个单位长度后得到△A1B1C1，请画出△A1B1C1；(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2，请画出△A2B2C2；(3)判断以O，A1，B为顶点的三角形的形状．(无须说明理由)解：(1)如图所示，△A1B1C1即为所求．(2)如图所示，△A2B2C2即为所求．(3)OB＝OA1＝16＋1＝17，A1B＝25＋9＝34.∵OB2＋OA21＝A1B2，∴△OA1B为等腰直角三角形．19．(14分)如图所示，在△ABC中，AD是BC边上的中线．(1)画出与△ACD关于点D成中心对称的三角形；(2)找出与AC相等的线段；(3)探索：在△ABC中，AB＋AC与中线AD之间的关系，并说明理由．解：(1)延长AD至A′，使AD＝A′D，连接A′B，则△A′DB就是与△ADC关于点D成中心对称的三角形．(2)A′B＝AC.(3)AB＋AC＞2AD.理由：∵△ADC与△A′DB关于D点成中心对称，∴AD＝A′D，AC＝A′B.在△ABA′中，AB＋BA′＞AA′，即AB＋AC＞AD＋A′D.∴AB＋AC＞2AD.。

北师大版八年级数学下册《第三章图形的平移与旋转》单元检测题-附答案

北师大版八年级数学下册《第三章图形的平移与旋转》单元检测题-附答案学校:___________班级：___________姓名：___________考号：___________一、单选题1．如左图是新疆维吾尔自治区第十四届运动会的会徽．平移此会徽中的图形，可以得到的是（）A．B．C．D．2．下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．3．在平面直角坐标系中，将点A(3,−2)向右平移4个单位长度后的对应点的坐标是（）A．(−1,−2)B．(7,−2)C．(3,−6)D．(3,2)4．如图，将△ABC沿BC方向平移3cm得到△DEF，若△ABC的周长为14cm，则四边形ABFD的周长为（）A．14cm B．17cm C．20cm D．23cm5．在平面直角坐标系中，以原点为中心，若将点Q(4,5)按逆时针方向旋转90°得到点P，则P的坐标是（）A．(−5,4)B．(−4,−5)C．(−5,−4)D．(5,−4)6．如图，在△ABD中∠BAD=90°，将△ABD绕点A逆时针旋转后得到△ACE，此时点C恰好落在BD边上．若∠BAC=48°，则∠E的度数为（）A．20°B．24°C．28°D．32°7．如图，△ABC的边BC长为5cm．将△ABC向上平移2cm得到△A′B′C′，且BB′⊥BC，则阴影部分的面积为（）A．50cm2B．25cm2C．20cm2D．10cm28．如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上．将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…，若点A(3,0)，B(0,4)，点B2024的坐标为（）A．(12132,0)B．(12144,4)C．(12140,4)D．(12152,0)二、填空题9．在平面直角坐标系中，已知点A(2a−b,−8)与点B(−2,a+3b)关于原点对称，a+b=．10．为了便于游客领略“人从桥上过，如在河中行”的美好意境，某景点拟在如图所示的长方形荷塘上架设小桥．若荷塘周长为600m，且桥宽忽略不计，则小桥总长为m．11．如图，将Rt△ABC沿着点B到C的方向平移到△DEF的位置AB=9，DO=4阴影部分面积为35，则平移距离为．12．在平面直角坐标系中，已知线段AB的两个端点分别是A(1,2),B(2,0)，将线段AB平移后得到线段CD，其中，点A的对应点为点C，若C(3,a),D(b,1)，则a−b的值为．13．如图，将△ABC沿BA方向平移得到△DEF．若DB=15，AE=2则平移的距离为．14．如图，在Rt△ABC中∠ACB=90°，AC=4，BC=5将△ABC绕点A逆时针旋转α(0°<α<90°)得到△ADE，延长BC交ED于点F．若∠EAB=90°，则线段EF的长为．15．如图，在△ABC，∠C=90°，将Rt△ABC绕顶点A顺时针旋转一定角度得到Rt△AB′C′，此时点C的对应点C′恰好落在AB边上，连接BB′，若∠BB′C′=35°，则∠BAC=°．16．如图，△ABC的顶点坐标分别为A(2,4),B(0,1),C(0,4)，将△ABC绕某一点旋转可得到△A′B′C′,△A′B′C′的三个顶点都在格点上，则旋转中心的坐标是．三、解答题17．如图，在4×4的方格中，有4个小方格被涂黑成“L形”．(1)在图1中再涂黑4格，使新涂黑的图形与原来的“L形“关于对称中心点O成中心对称；(2)在图2和图3中再分别涂黑4格，使新涂黑的图形与原来的“L形”所组成的新图形既是轴对称图形又是中心对称图形（两个图各画一种）．18．如图，在△ABC中∠B=40°，∠BAC=80°将△ABC绕点A逆时针旋转一定角度后得到△ADE．(1)求∠E的度数；(2)当AB∥DE时，求∠DAC的度数．19．如图，在12×8的正方形网格中，每个小正方形的边长都是1个单位长度，点A，B，C，O都在格点上．按下列要求画图：(1)画出将△ABC向右平移8个单位长度后的△A1B1C1；(2)画出将△ABC以点O为旋转中心、顺时针旋转90°后的△A2C2B2(3)△A1B1C1与△A2C2B2是否成轴对称？若是，请画出对称轴．20．如图，在△ABC中∠BAC=80°，三个内角的平分线交于点O．(1)∠BOC的度数为________．(2)过点O作OD⊥OB交BC于点D．①探究∠ODC与∠AOC之间的数量关系，并说明理由；②若∠ACB=60°，将△BOD绕点O顺时针旋转α得到△B′OD′(0°<α<90°)，当B′D′所在直线与OC平行时，求α的值．21．如图，在平面直角坐标系中，已知A(−1,0),B(3,0),M为第三象限内一点．(1)若点M(2−a,2a−10)到两坐标轴的距离相等．①求点M的坐标；②若MN∥AB且MN=AB，求点N的坐标．(2)若点M为(n,n)，连接AM,BM．请用含n的式子表示三角形AMB的面积；(3)在（2）的条件下，将三角形AMB沿x轴方向向右平移得到三角形DEF（点A，M的对应点分别为点D，E），若三角形AMB的周长为m，四边形AMEF的周长为m+4，求点E的坐标（用含n的式子表示）．22．如图，在锐角△ABC中∠A=60°，点D，E分别是边AB，AC上一动点，连接BE交直线CD于点F．(1)如图1，若AB>AC，且BD=CE，∠BCD=∠CBE，K为射线CD上一点CK=BE．①求证：BD=BK；②求∠CFE的度数；(2)如图2，若AB=AC，且BD=AE，在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM，连接MF，点N是MF的中点，连接CN．在点D，E运动过程中，猜想线段BF，CF，CN之间存在的数量关系，并证明你的猜想．参考答案1．解：根据平移的性质可知：能由如图经过平移得到的是B．故选：B2．解：A、是中心对称图形，但不是轴对称图形，故不符合题意；B、既是轴对称图形又是中心对称图形，故符合题意；C、是轴对称图形，但不是中心对称图形，故不符合题意；D、是轴对称图形，但不是中心对称图形，故不符合题意；故选B．3．解：将点A(3,−2)向右平移4个单位长度后的对应点的坐标是(3+4,−2)，即(7,−2)故选：B．4．解：由平移的性质得：AD=BE=CF=3cm，AC=DF∵△ABC的周长为14cm∵AB+BC+AC=14cm∵四边形ABFD的周长为AB+BC+CF+DF+AD=AB+BC+AC+CF+AD=14+3+3=20cm．故选：C．5．解：如图，过点Q作QM⊥x轴，过点P作PN⊥x轴∴∠PNO=∠QMO=90°∵Q(4,5)∴OM=4由旋转的性质可知OQ=OP，∠POQ=90°∴∠PON+∠QOM=90°∵∠PON+∠OPN=90°∴∠OPN=∠QOM∴△PON≌△OQM(AAS)∴ON=QM=5，PN=OM=4∵点P在第二象限∴点P的坐标是(−5,4)故选：A．6．解：∵△ABD旋转得到△ACE∵AB=AC，∠ABC=∠ACE，∠E=∠D∵∠BAC=48°∴∠ABD=∠ACD=180°−∠BAC=66°2∵∠BAD =90°∵∠D =180°−∠ABC −∠BAD =24°∵∠E =∠D =24°．故选：B ．7．解：三角形ABC 的边BC 的长为5cm ．将三角形ABC 向上平移2cm 得到三角形A ′B ′C ′，且BB ′⊥BC 则：S △ABC =S △A ′B ′C ′，四边形BCC ′B ′是长方形，BB ′=2∵S 阴影=S △A ′B ′C ′+S 长方形BB ′C ′C −S △ABC =S 长方形BB ′C ′C =BC ×BB ′=5×2=10(cm 2)故选D ．8．解：∵点A(3，0)，B(0，4)∵OA =3，OB =4∵AB =√32+42= 5∵OA +AB 1+B 1C 2=3+5+4=12观察图象可知B 、B 2、B 4…每偶数之间的B 的横坐标相差12个单位长度，点B 2n 的纵坐标为4∵2024÷2=1012∵点B 2024的横坐标为1012×12=12144，点B 2024的纵坐标为4∵点B 2024的坐标为(12144,4)．故选：B ．9．解：依题意可得：{2a −b =−(−2)a +3b =−(−8)∴{a =2b =2∴a +b =2+2=4故答案为：4．10．解：由平移的性质得，小桥总长=长方形周长的一半∵600÷2=300m∵小桥总长为300m ．故答案为：300．11．解：∵Rt △ABC ，沿着点B 到C 点的方向平移到△DEF 的位置∵△ABC≌△DEF∵AB =DE ，S △ABC =S △DEF∵S阴影=S梯形ABEO=35∵AB=9，DO=4∵OE=DE−OH=9−4=5∵12(5+9)×BE=35解得：BE=5，即为平移的距离；故答案为：5．12．解：由题意得，线段AB向右平移2个单位，向上平移1个单位得到线段CD∴2+2=b，2+1=a∴a=3，b=4∴a−b=3−4=−1故答案为：−1．13．解：平移的性质可得：AD=BE又∵DB=15，AE=2∵AD=BE=DB−AE2=6.5即平移的距离为6.5故答案为：6.5．14．解：连接AF∵∠ACB=90°，AC=4，BC=5∵AB=√42+52=√41由旋转的性质得AE=AC，∠E=∠ACB=90°∵∠E=∠ACF=90°∵AF=AF∵Rt△AFE≌Rt△AFC(HL)∵EF=FC，∠EFA=∠CFA∵∠EAB=90°∵DE∥AB∵∠EFA=∠FAB∵∠BFA=∠FAB∵BF=AB=√41∵EF=FC=BF−BC=√41−5故答案为：√41−5．15．解：∵将Rt△ABC绕顶点A顺时针旋转一定角度得到Rt△AB′C′，此时点C的对应点C′恰好落在AB边上∵AB=AB′，∠BC′B′=90°，∠B′AC′=∠BAC∵∠ABB′=∠AB′B而∠BB′C′=35°∵∠ABB′=90°−35°=55°∵∠B′AC′=∠BAC=180°−55°×2=70°．故答案为：70．16．解：如图所示：连接AA′，BB′，然后作AA′，BB′的垂直平分线，这两条垂直平分线交于一点，记为点P，为旋转中心，此时旋转中心的坐标是(−1，0)故答案为：(−1，0)17．解：（1）所求图形，如图所示．（2）所求图形，如图所示．18．（1）解：由旋转可得：∠E=∠C．∵∠B=40°，∠BAC=80°∵∠C=180°−∠B−∠BAC=60°∵∠E=60°．（2）如图1，当DE在AB下方时．由旋转可得：∠D=∠B=40°．∵AB∥DE∵∠BAD=∠D=40°∵∠DAC=∠BAC−∠BAD=80°−40°=40°．如图2，当DE在AB上方时．∵AB∥DE∵∠BAD+∠D=180°∵∠BAD=180°−∠D=180°−40°=140°∵∠DAC=360°−∠BAC−∠BAD=360°−80°−140°=140°．综上所述，∠DAC的度数为40°或140°．19．（1）解：如图,∴△A1B1C1为所求画的三角形；（2）解：如图∴△A2C2B2为所求画的三角形；（3）解：成轴对称，如图∴直线OD为所求画的对称轴．20．（1）解：∵三个内角的平分线交于点O，(∠ABC+∠ACB)∵∠OBC+∠OCB=12∵∠BAC=80°∵∠ABC+∠ACB=180°−∠BAC=100°∵∠OBC+∠OCB=50°∵∠BOC=180°−(∠OBC+∠OCB)=180°−50°=130°故答案为：130°；（2）解：①∠ODC=∠AOC，理由如下：∵三个内角的平分线交于点O，(∠BAC+∠ACB)∵∠OAC+∠OCA=12∵∠BAC+∠ACB=180°−∠ABC∵∠OAC+∠OCA=12(180°−∠ABC)=90°−12∠ABC∵∠AOC=180°−(∠OAC+∠OCA)=180°−(90∘−12∠ABC)=90°+12∠ABC∵OD⊥OB∵∠BOD=90°∵∠ODC=∠BOD+∠OBD=90°+12∠ABC∵∠ODC=∠AOC；②如图∵OC平分∠ACB，∠ACB=60°∵∠OCD=12∠ACB=30°由（1）知∠BOC=130°∵∠BOD=90°∵∠COD=40°∵∠BDO=∠COD+∠OCD=70°由旋转性质可知：∠BDO=∠B′D′O=70°∵B′D′∥OC∵∠COD′=∠B′D′O=70°∵∠DOD′=∠COD′−∠COD=30°，即此时旋转角度α=30°∵α的值为30°．21．（1）解：①∵M(2−a,2a−10)到两坐标轴的距离相等，且在第三象限∵−(2−a)=−(2a−10)∵a=4∵M(−2,−2)；②∵A A(−1,0),B(3,0)∵AB=4∵MN∥AB，MN=AB，M(−2，−2)∵N(−6,−2)或(2,−2)；（2）解：∵M(n,n)在第三象限∵n<0∵三角形AMB的面积为12×4×(−n)=−2n；（3）解：∵△AMB沿x轴方向向右平移得到△DEF ∵BM=EF，AD=ME=BF．∵△AMB的周长为m∵AM+MB+AB=m．∵四边形AMEF的周长为m+4∵AM+ME+EF+AF=m+4，即2ME=4∵解得ME=2∵点E的坐标为(n+2,n)．22．（1）解：①证明：在△BCE与△CBK中{BE=CK ∠BCK=∠CBE BC=CB∵△BCE≌△CBK(SAS)∵CE=BK∵BD=CE∵BD=BK；②由①知：BD=BK，∵∠BKD=∠BDK∵△BCE≌△CBK(SAS)∵∠BKC=∠CEB∵∠BDK=∠CEB∵∠BDK=∠ADC∴∠ADC=∠CEB∵∠CEB+∠AEF=180°∴∠ADF+∠AEF=180°∴∠A+∠EFD=180°∵∠A=60°∴∠EFD=120°∴∠CFE=180°−∠EFD=180°−120°=60°；（2）解：结论：BF+CF=2CN．理由：如图2中∵AB=AC，∠A=60°∴△ABC是等边三角形∴AB=CB=AC，∠A=∠CBD=∠ACB=60°∵AE=BD∴△ABE≌△BCD(SAS)∴∠BCF=∠ABE∴∠FBC+∠BCF=60°∴∠BFC=120°∵∠BFD=60°由旋转可得：AC=CM∵BC=CM，∠BCM=∠ACB+∠ACM=120°如图2中，延长CN到Q，使得NQ=CN，连接FQ∵NM=NF，∠CNM=∠FNQ，CN=NQ∴△CNM≌△QNF(SAS)∴CM=QF，∠MCN=∠NQF∴CM=BC延长CF到P，使得PF=BF∵PF=BF∵△PBF是等边三角形∵∠BPC=60°∴∠PBC+∠PCB=∠PCB+∠FCM=120°∴∠FCM=∠PBC∵∠PFQ=∠FCQ+∠CQF=∠FCQ+∠MCN=∠FCM∵∠PFQ=∠PBC∵PB=PF∴△PFQ≌△PBC(SAS)∴PQ=PC，∠CPB=∠QPF=60°∴△PCQ是等边三角形∴BF+CF=PC=QC=2CN．。

北师大八年级下《第3章图形的平移与旋转》单元测试题含答案试卷分析详解

第三章图形的平移与旋转一、选择题1．点P（-2，-3）向左平移1个单位，再向上平移3个单位，则所得到的点的坐标为（）A.（-3，0）B.（-1，6）C.（-3，-6）D.（-1，0）2..下列说法正确的是（）A.平移不改变图形的形状和大小，而旋转改变图形的形状和大小B.平移和旋转都不改变图形的形状和大小C.图形可以向某方向平移一定距离，也可以向某方向旋转一定距离D.在平移和旋转图形的过程中，对应角相等，对应线段相等且平行3．如图，将边长为4的等边△沿边BC向右平移2个单位得到△，则四边形的周长为（）A.12B.16C.20D.244.如图，在正方形中，，点在上，且，点是上一动点，连接，将线段绕点逆时针旋转90°得到线段.要使点恰好落在上，则的长是（）A.1B.2C.3D.45．如图，在平面直角坐标系中，将点M(2，1)向下平移2个单位长度得到点N，则点N的坐标为()A．(2，－1) B．(2，3) C．(0，1) D．(4，1)第5题图第7题图第8题图6．已知点A(a，1)与点A′(5，b)关于坐标原点对称，则实数a，b的值是() A．a＝5，b＝1 B．a＝－5，b＝1C．a＝5，b＝－1 D．a＝－5，b＝－17．如图，把△ABC绕点C顺时针旋转35°得到△A′B′C，A′B′交AC于点D.若△A′DC＝90°，则△A的度数为()A．45° B．55° C．65° D．75°8．如图，在6×4的方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是(B)A．点M B．点N C．点P D．点Q9．如图所示的四个图案中，既可用旋转来分析整个图案的形成过程，又可用轴对称来分析整个图案的形成过程的图案有()A．4个B．3个C．2个D．1个10．如图，在Rt△ABC中，△C＝90°，△ABC＝30°，AB＝8，将△ABC沿CB方向向右平移得到△DEF.若四边形ABED的面积为8，则平移距离为()A．2 B．4 C．8 D．1611．如图，Rt△ABC向右翻滚，下列说法正确的有()(1)△→△是旋转；(2)△→△是平移；(3)△→△是平移；(4)△→△是旋转．A．1个B．2个C．3个D．4个12．如图，在等边△ABC中，点D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°得到△BAE，连接ED.若BC＝5，BD＝4，则下列结论错误的是()A．AE△BCB．△ADE＝△BDCC．△BDE是等边三角形D．△ADE的周长是9二、填空题1．将点A(2，1)向左平移3个单位长度得到的点B的坐标是________．2．如图，将△ABC绕着点C顺时针方向旋转50°后得到△A′B′C.若△A＝40°，△B′＝110°，则△BCA′的度数是________．第2题图第3题图3．如图，将△ABC沿直线AB向右平移后到达△BDE的位置，若△CAB＝50°，△ABC＝100°，则△CBE的度数为________．4．如图，香港特别行政区区徽由五个相同的花瓣组成，它是以一个花瓣为“基本图案”通过连续四次旋转组成的，这四次旋转中旋转角度最小是________度．第4题图第5题图5．如图，△ABC中，AB＝AC，BC＝12cm，点D在AC上，DC＝4cm，将线段DC沿着CB的方向平移7cm得到线段EF，点E，F分别落在AB，BC上，则△EBF的周长为________cm.6．如图，A，B两点的坐标分别为(－2，0)，(0，1)，将线段AB平移到线段A1B1的位置．若A1(b，1)，B1(－1，a)，则b－a＝________．第6题图第8题图7．在等腰三角形ABC中，△C＝90°，BC＝2cm，如果以AC的中点O为旋转中心，将△ABC旋转180°，点B落在B′处，则BB′的长度为________．8．如图，Rt△ABC中，AC＝5，BC＝12，则其内部五个小直角三角形的周长之和为________．三、解答题1．如图，经过平移，△ABC的顶点移到了点D，作出平移后的△DEF.2．如图，△ABO与△CDO关于O点中心对称，点E，F在线段AC上，且AF＝CE.求证：FD＝BE.3.如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫作格点．△ABC的三个顶点A，B，C都在格点上，将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.(1)在正方形网格中，画出△AB′C′；(2)画出△AB′C′向左平移4格后的△A′B″C″；(3)计算线段AB在变换到AB′的过程中扫过区域的面积．4．如图，在Rt△ABC中，△ACB＝90°，点D，E分别在AB，AC上，CE＝BC，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CF，连接EF.(1)补充完成图形；(2)若EF△CD，求证：△BDC＝90°.5．如图，Rt△ABC中，△ACB＝90°，AC＝3，AB＝5，将△ABC沿AB边所在直线向右平移3个单位，记平移后的对应三角形为△DEF.(1)求DB的长；(2)求此时梯形CAEF的面积．6．如图，4×4网格图都是由16个相同小正方形组成，每个网格图中有4个小正方形已涂上阴影，请在空白小正方形中，按下列要求涂上阴影．(1)在图△中选取2个空白小正方形涂上阴影，使6个阴影小正方形组成一个中心对称图形；(2)在图△中选取2个空白小正方形涂上阴影，使6个阴影小正方形组成一个轴对称图形，但不是中心对称图形．7．两块等腰直角三角形纸片AOB和COD按图△所示放置，直角顶点重合在点O处，AB＝25.保持纸片AOB不动，将纸片COD绕点O逆时针旋转α(0°＜α＜90°)角度，如图△所示．(1)在图△中，求证：AC＝BD，且AC△BD；(2)当BD与CD在同一直线上(如图△)时，若AC＝7，求CD的长．答案一、选择题ABBCA DBBAA CB二、填空题1．(－1，1)2.80°3.30°4.725.136.－57．25cm8.30三、解答题1．解：如图，△DEF即为所求．(8分)2．证明：△△ABO与△CDO关于O点中心对称，△OB＝OD，OA＝OC.△AF＝CE，△OF ＝OE.(3分)在△DOF和△BOE中，OD＝OB，△DOF＝△BOE，OF＝OE，△△DOF△△BOE(SAS)，(6分)△FD＝BE.(8分)3．解：(1)如图所示，△AB ′C ′即为所求．(3分) (2)如图所示，△A ′B ″C ″即为所求．(6分)(3)△AB ＝42＋32＝5，(8分)△线段AB 在变换到AB ′的过程中扫过区域的面积为半径为5的圆的面积的14，即14×π×52＝254π.(10分)4．(1)解：补全图形，如图所示．(4分)(2)证明：由旋转的性质得△DCF ＝90°，DC ＝FC ，△△DCE ＋△ECF ＝90°.(5分)△△ACB＝90°，△△DCE ＋△BCD ＝90°，△△ECF ＝△BCD .△EF △DC ，△△EFC ＋△DCF ＝180°，△△EFC ＝90°.(6分)在△BDC 和△EFC 中，⎩⎪⎨⎪⎧DC ＝FC ，△BCD ＝△ECF ，BC ＝EC ，△△BDC △△EFC (SAS)，△△BDC ＝△EFC ＝90°.(8分) 5．解：(1)△将△ABC 沿AB 边所在直线向右平移3个单位到△DEF ，△AD ＝BE ＝CF ＝3.△AB ＝5，△DB ＝AB －AD ＝2.(3分)(2)过点C 作CG △AB 于点G .在△ACB 中，△△ACB ＝90°，AC ＝3，AB ＝5，△由勾股定理得BC ＝AB 2－AC 2＝4.(6分)由三角形的面积公式得12AC ·BC ＝12CG ·AB ，△3×4＝5×CG ，解得CG ＝125.(8分)△梯形CAEF 的面积为12(CF ＋AE )×CG ＝12×(3＋5＋3)×125＝665.(10分)6．解：(1)如图所示．(5分)(2)如图所示．(10分)7.(1)证明：如图，延长BD 交OA 于点G ，交AC 于点E .(1分)△△AOB 和△COD 是等腰直角三角形，△OA ＝OB ，OC ＝OD ，△AOB ＝△COD ＝90°，△△AOC ＋△AOD ＝△DOB ＋△DOA ，△△AOC ＝△DOB .(3分)在△AOC 和△BOD 中，⎩⎪⎨⎪⎧OA ＝OB ，△AOC ＝△BOD ，OC ＝OD ，△△AOC △△BOD ，△AC ＝BD ，△CAO ＝△DBO .(5分)又△△DBO ＋△OGB ＝90°，△OGB ＝△AGE ，△△CAO ＋△AGE ＝90°，△△AEG ＝90°，△AC △BD .(2)解：由(1)可知AC ＝BD ，AC △BD .△BD ，CD 在同一直线上，△△ABC 是直角三角形．由勾股定理得BC ＝AB 2－AC 2＝252－72＝24.(10分)，△CD ＝BC －BD ＝BC －AC ＝17.。

北师大版八年级下《第三章图形的平移与旋转》测试题(含答案)

第三章图形的平移与旋转一、选择题(本大题共7小题，每小题4分，共28分)1．下列图形中，既是轴对称图形又是中心对称图形的是( )图12．已知△ABC 沿水平方向平移得到△A ′B ′C ′，若AA ′＝3，则BB ′等于( ) A.32B ．3C ．5D ．10 3．已知点A (a ，2018)与点A ′(－2019，b )是关于原点O 的对称点，则a ＋b 的值为( ) A ．1B ．5C ．6D ．44．如图2，△ABC 绕点A 顺时针旋转80°得到△AEF ，若∠B ＝100°，∠F ＝50°，则∠α的度数是( )图2A ．40°B ．50°C ．80°D ．100°5．正方形ABCD 在平面直角坐标系中的位置如图3所示，将正方形ABCD 绕点A 顺时针旋转180°后，点C 的坐标是( )图3A ．(2，0)B ．(3，0)C ．(2，－1)D ．(2，1)6．如图4，将边长为4的等边三角形OAB 先向下平移3个单位长度，再将平移后的图形沿y 轴翻折，经过两次变换后，点A 的对应点A ′的坐标为( )图4A ．(2，3－23)B ．(2，1)C ．(－2，23－3)D ．(－1，23)7．如图5，P 是正方形ABCD 内一点，将△ABP 绕着B 沿顺时针方向旋转到与△CBP ′重合，若PB ＝3，则PP ′的长为( )图5A．2 2 B．3 2C．3 D．无法确定二、填空题(本大题共5小题，每小题4分，共20分)8．有一种拼图游戏是当每一行的小方格铺满后，这一行消失并使玩家得分．若在游戏过程中，已拼好的图案如图6，又出现了一小方格体向下运动，为了使所有图案消失，最简单的操作是将这个小方格体先________时针旋转________°，再向________平移，再向________平移，才能拼成一个完整的图案，从而使图案消失．图69．如图7，将△ABC绕点C顺时针旋转至△DEC，使点D落在BC的延长线上，已知∠A＝27°，∠B＝40°，则∠ACE＝________°.10．已知点A(1，－2)，B(－1，2)，E(2，a)，F(b，3)，若将线段AB平移至EF，点A，E为对应点，则a＋b的值为________．图711.如图8所示，在△ABC中，∠C＝90°，AC＝BC＝5，现将△ABC沿着CB的方向平移到△A′B′C′的位置．若平移的距离为2，则图中阴影部分的面积为________．图812．如图9，在平面直角坐标系中，已知点A(－3，0)，B(0，4)，对△OAB连续作旋转变换，依次得到△1，△2，△3，△4，…，则△2019的直角顶点的坐标为__________．图9三、解答题(本大题共4小题，共52分)13．(12分)如图10，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC和△DEF的顶点都在格点上，结合所给的平面直角坐标系解答下列问题：(1)画出△ABC向上平移4个单位长度后所得到的△A1B1C1；(2)画出△DEF绕点O按顺时针方向旋转90°后所得到的△D1E1F1；(3)△A1B1C1和△D1E1F1组成的图形是轴对称图形吗？如果是，请直接写出对称轴所在直线的函数表达式．图1014．(12分)如图11，将一个直角三角板ACB(∠C＝90°)绕60°角的顶点B顺时针旋转，使得点C旋转到AB的延长线上的点E处，请解答下列问题：(1)三角板旋转了多少度？(2)连接CE，请判断△BCE的形状；(3)求∠ACE的度数．图1115．(14分)在网格中画对称图形．(1)如图12是五个小正方形拼成的图形，请你移动其中一个小正方形，重新拼成一个图形，使得所拼成的图形满足下列条件，并分别画在图13①②③中(只需各画一个，内部涂上阴影)；图12图1①是轴对称图形，但不是中心对称图形；②是中心对称图形，但不是轴对称图形；③既是轴对称图形，又是中心对称图形．(2)请你在图13④的网格内设计一个商标，满足下列要求：①是顶点在格点的凸多边形(不是平行四边形)；②是中心对称图形，但不是轴对称图形；③商标内部涂上阴影．16．(14分)如图14，O是等边三角形ABC内一点，∠AOB＝110°，∠BOC＝α.将△BOC 绕点C按顺时针方向旋转60°得到△ADC，连接OD.(1)求证：△COD是等边三角形；(2)当α＝150°时，试判断△AOD的形状，并说明理由；(3)探究：当α为多少度时，△AOD是等腰三角形？图141．[答案]C2．[解析]B根据平移的定义及性质解题．平移是在平面内，把一个图形沿某个方向移动一定的距离的运动．平移不改变图形的形状和大小，只改变图形的位置．本题中AA′与BB′都是对应点所连的线段，所以BB′＝3.3．[答案]A4．[答案]B5．[答案]B6．[解析]C∵等边三角形OAB的边长为4，∴A(2，23)．∵先向下平移3个单位长度，∴点A的对应点坐标为(2，23－3)．∵再将平移后的图形沿y轴翻折，∴这时点A的对应点A′的坐标为(－2，23－3)．故选C.7．[答案]B8．[答案]顺90右下9．[答案]4610．[答案] －1[解析]∵线段AB平移至EF，即点A平移到点E，点B平移到点F，而A(1，－2)，B(－1，2)，E(2，a)，F(b，3)，∴点A向右平移1个单位长度到点E，点B向上平移1个单位长度到点F，∴线段AB先向右平移1个单位长度，再向上平移1个单位长度得到EF，∴－2＋1＝a，－1＋1＝b，∴a＝－1，b＝0，∴a＋b＝－1＋0＝－1.11．[答案]8[解析]S阴影＝S△A′B′C′－S△BC′D＝252－92＝8.12．[答案] (8076，0)[解析]∵点A(－3，0)，B(0，4)，∴AB＝32＋42＝5，由图可知，每三个三角形为一个循环组依次循环，一个循环组前进的长度为4＋5＋3＝12.∵2019÷3＝673，∴△2019的直角顶点是第673个循环组的第三个三角形的直角顶点．∵673×12＝8076，∴△2019的直角顶点的坐标为(8076，0)．13．解：(1)△A1B1C1如图所示．(2)△D1E1F1如图所示．(3)△A1B1C1和△D1E1F1y＝x或y＝－x－2.14．解：(1)∵∠ABC＝60°ACB绕顶点B 顺时针旋转得到△DEB，∴∠CBE等于旋转角，∴三角板旋转了120°.(2)连接CE，∵直角三角板ACB绕顶点B顺时针旋转得到△DEB，∴BC＝BE，∴△BCE为等腰三角形．(3)∵∠CBE ＝120°，△BCE 为等腰三角形，∴∠BCE ＝12×(180°－120°)＝30°，∴∠ACE ＝∠ACB ＋∠BCE ＝90°＋30°＝120°.15．解：(1)如图①，是轴对称图形，但不是中心对称图形(答案不唯一)；如图②，是中心对称图形，但不是轴对称图形；如图③，既是轴对称图形，又是中心对称图形． (2)16．解：(1)ADC ， ∴CO ＝CD ，∠OCD ＝60°， ∴△COD 是等边三角形． (2)当α＝150°时，△AOD 是直角三角形．理由：∵△BOC ≌△ADC ， ∴∠ADC ＝∠BOC ＝150°. ∵△COD 是等边三角形， ∴∠ODC ＝60°，∴∠ADO ＝∠ADC －∠ODC ＝90°，即△AOD 是直角三角形．(3)①要使OA ＝AD ，需∠AOD ＝∠ADO ， ∵∠AOD ＝360°－110°－60°－α＝190°－α，∠ADO ＝α－60°， ∴190°－α＝α－60°， ∴α＝125°；②要使OA ＝OD ，需∠OAD ＝∠ADO. ∵∠OAD ＝180°－(∠AOD ＋∠ADO)＝180°－(190°－α＋α－60°)＝50°， ∴α－60°＝50°， ∴α＝110°；③要使OD ＝AD ，需∠OAD ＝∠AOD. ∵∠AOD ＝360°－110°－60°－α＝190°－α，∠OAD ＝180°－（α－60°）2＝120°－α2，∴190°－α＝120°－α2，解得α＝140°.综上所述，当α的度数为125°，110°或140°时，△AOD 是等腰三角形．。

北师大版八年级数学下册第三章《图形的平移和旋转》单元综合测试卷(含答案)

北师版八年级数学下册第3章图形的平移与旋转单元综合测试卷(时间90分钟，满分120分)一、选择题（共10小题，3*10=30）1．下列图形变换，不是旋转变换的是()2．如图，下列四个图形中，△ABC经过旋转之后不能得到△A′B′C′的是()3．下列图形中，既是轴对称图形又是中心对称图形的是()4．已知点A的坐标为(1，3)，点B的坐标为(2，1)．将线段AB沿某一方向平移后，点A的对应点的坐标为(－2，1)，则点B的对应点的坐标为()A．(5，3) B．(－1，－2) C．(－1，－1) D．(0，－1)5．下列四张扑克牌图案，属于中心对称图形的是()6. 如图，在△ABC中，∠CAB＝70°.在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使CC′∥AB，则∠BAB′＝()A．30° B．35° C．40° D．50°7．如图，将△ABC沿射线BC向右平移到△DCE的位置，连接AD，则下列结论：①AB∥CD；②AC ＝DE；③AD＝BC；④∠B＝∠ADC；⑤△ACD≌△EDC.其中正确的结论有()A．5个B．4个C．3个D．2个8．如图，在Rt △ABC 中，∠ACB ＝90°，∠A ＝30°，BC ＝2，将△ABC 绕点C 按顺时针方向旋转n°后，得到△EDC ，此时，点D 在AB 边上，斜边DE 交AC 边于点F ，则n 的大小和图中阴影部分的面积分别为( )A ．30，2B ．60，2C ．60，32D ．60，3 9．如图，在△ABC 中，∠CAB ＝75°，在同一平面内，将△ABC 绕点A 旋转到△AB′C′的位置，点C 在B′C′上，使得CC′∥AB ，则∠BAB′等于( )A ．30°B ．35°C ．40°D ．50°10．如图，P 为等边三角形ABC 内的一点，且P 到三个顶点A ，B ，C 的距离分别为3，4，5，则△ABC 的面积为( )A ．9＋2534B ．9＋2532C ．18＋25 3D ．18＋2532二．填空题（共8小题，3*8=24）11．如图，△DEF 是△ABC 沿水平方向向右平移后的对应图形，若∠B ＝31°，∠C ＝79°，则∠D 的度数是________°.12. 如图，已知面积为1的正方形ABCD 的对角线相交于点O ，过点O 任作一条直线分别交AD ，BC 于E ，F ，则阴影部分的面积是______.13．在平面直角坐标系中，点(a ，5)关于原点对称的点的坐标是(1，b ＋1)，则a ＋b 的值为________．14．如图，将等边三角形ABC 绕顶点A 顺时针方向旋转，使边AB 与AC 重合得△ACD ，BC 的中点E 的对应点为F ，则∠EAF 的度数是______．15．已知：如图，在长方形ABCD 中，AB ＝8，BC ＝6，平移长方形ABCD 到长方形A 1B 1C 1D 1，使得与原长方形A 1B 1C 1D 1重合部分的面积是12，则将长方形ABCD 沿着AB 边向右平移________个单位长度，得到长方形A 1B 1C 1D 1．(一种即可)16．如图，在△ABC 中，AC ＝BC ＝8，∠BCA ＝60°，直线AD ⊥BC ，E 是AD 上的一个动点，连接EC ，将线段EC 绕点C 逆时针方向旋转60°得到FC ，连接DF ，则在点E 运动的过程中，DF 的最小值是________．17．如图，在等边三角形ABC 中，点D 是边AC 上一点，连接BD ，将△BCD 绕点B 逆时针旋转60°，得到△BAE ，连接ED ，若BC ＝4.5，BD ＝4，则△ADE 的周长为________．18．如图，直线y ＝－43x ＋4与x 轴、y 轴分别交于A ，B 两点，把△AOB 绕点A 顺时针旋转90°后得到△AO′B′，则点B′的坐标是__________．三．解答题（共7小题， 66分）19．(8分) 如图，每个小方格都是边长为1个单位长度的小正方形．(1)将△ABC 向右平移3个单位长度，画出平移后的△A 1B 1C 1.(2)将△ABC绕点O旋转180°，画出旋转后的△A2B2C2.(3)画出一条直线将△AC1A2的面积分成相等的两部分．20．(8分) 如图，等边三角形ABC经过平移后成为△BDE，其平移的方向为点A到点B的方向，平移的距离是线段AB的长．△BDE能否看成是△ABC经过旋转得到的？如果能，请指出△BDE是△ABC 绕哪一点经过怎样的旋转得到的？并指出点A，B，C的对应点．21．(8分) 如图，将△ABC向右平移7个单位长度，再向下平移6个单位长度，得到△A1B1C1.(1)不画图，直接写出点A1，B1，C1的坐标(点A1，B1，C1分别是点A，B，C的对应点)；(2)求△A1B1C1的面积．22．(10分) 如图所示，三角形ABC三个顶点A，B，C的坐标分别为A(1，2)，B(4，3)，C(3，1)．(1)三角形A1B1C1向右平移4个单位长度，再向下平移3个单位长度，恰好得到三角形ABC，试写出三角形A1B1C1三个顶点的坐标；(2)求△ABC的面积．23．(10分)如图，△ACD，△AEB都是等腰直角三角形，∠CAD＝∠EAB＝90°，∠BAC＝30°，若将△EAC旋转后能与△BAD重合．(1)旋转中心是哪一点？旋转角为多少度？(2)若BD＝5 cm，求EC的长度．24．(10分) 如图1，在△ABC中，AC＝BC，∠A＝30°，点D在AB边上，且∠ADC＝45°.(1)求∠BCD的度数；(2)将图1中的△BCD绕点B顺时针旋转得到△BC′D′，当点D′恰好落在BC边上时，如图2所示，连接C′C并延长交AB于点E.①求∠C′CB的度数；②求证：△C′BD′≌△CAE.25．(12分) 如图①，△ABC和△CEF是两个大小不等的等边三角形，且有一个公共顶点C，连接AF，BE.(1)线段AF和BE有怎样的数量关系？请说明理由．(2)将图①中的△CEF绕点C旋转一定的角度，得到图②，(1)中的结论还成立吗？作出判断并说明理由．参考答案1-5DDBCC 6-10CACAA11. 7012. 1413.－714．60°15. 6(答案不唯一)16. 217．8.518. (7，3)19. 解：(1)(2)(3)如图．20. 解：能，△BDE 可以看成是△ABC 绕点B 按顺时针方向旋转120°得到的，点A ，B ，C 的对应点分别为点E ，B ，D.(答案不唯一)21. 解：(1)A 1(5，－1)，B 1(3，－7)，C 1(9，－3)．(2)S △A 1B 1C 1＝S △ABC ＝6×6－12×6×2－12×6×4－12×4×2＝14. 22. 解：(1)△A 1B 1C 1如图所示，A 1(－3，5)，B 1(0，6)，C 1(－1，4)(2)△A 1B 1C 1的面积＝3×2－12×1×2－12×1×2－12×1×3＝6－1－1－1.5＝6－3.5＝2.5 23. 解：(1)∵将△EAC 逆时针旋转后能与△BAD 重合，∴点A 即为两个三角形的公共顶点，∴旋转中心是点A.∵将△EAC 逆时针旋转后能与△BAD 重合，∴AE 与AB 为对应边．∵∠BAE ＝90°，∴旋转角的度数为90°.(2)由题意知，EC 和BD 是对应线段．根据旋转的性质，可得EC ＝BD ＝5 cm.24. 解：(1)∵AC ＝BC ，∠A ＝30°，∴∠B ＝∠A ＝30°.∵∠ADC ＝45°，∴∠BCD ＝∠ADC －∠B ＝15°(2)①由旋转，得BC ＝BC′＝AC ，∠C′BD′＝∠CBD ＝∠A ＝30°.∴∠CC′B ＝∠C′CB ＝75°②证明：∵∠CEB ＝∠C′CB －∠CBA ＝45°，∴∠ACE ＝∠CEB －∠A ＝15°.∴∠BC′D′＝∠BCD ＝∠ACE.在△C′BD′和△CAE 中，⎩⎪⎨⎪⎧∠BC′D′＝∠ACE ，BC′＝AC ，∠C′BD′＝∠A ，∴△C′BD′≌△CAE(ASA)25. 解：(1)AF ＝BE.理由如下：∵△ABC 和△CEF 是等边三角形，∴AC ＝BC ，CF ＝CE ，∠ACF ＝∠BCE ＝60°.在△AFC 与△BEC 中，⎩⎪⎨⎪⎧AC ＝BC ，∠ACF ＝∠BCE ，CF ＝CE ，∴△AFC ≌△BEC(SAS)．∴AF ＝BE.(2)成立．理由：∵△ABC 和△CEF 是等边三角形，∴AC ＝BC ，CF ＝CE ，∠ACB ＝∠FCE ＝60°.∴∠ACB －∠FCB ＝∠FCE －∠FCB ，即∠ACF ＝∠BCE.在△AFC 与△BEC 中，⎩⎪⎨⎪⎧AC ＝BC ，∠ACF ＝∠BCE ，CF ＝CE ，∴△AFC ≌△BEC(SAS)．∴AF ＝BE.。

北师大版八年级数学下册第三章图形的平移与旋转单元测试题(含答案)

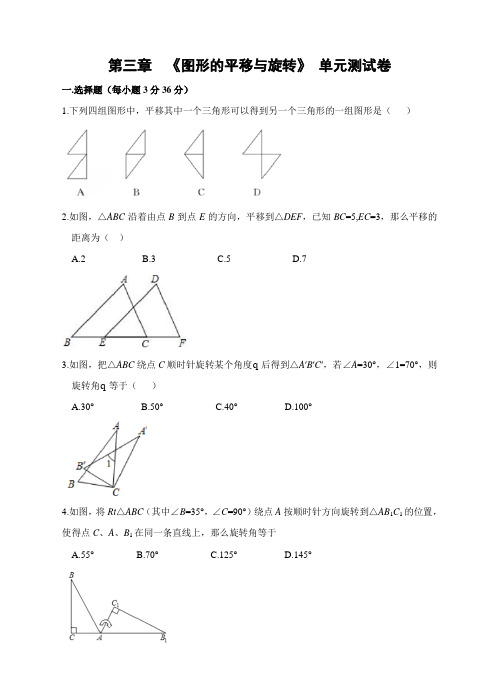
第三章《图形的平移与旋转》单元测试卷一.选择题（每小题3分36分）1.下列四组图形中，平移其中一个三角形可以得到另一个三角形的一组图形是（）2.如图，△ABC沿着由点B到点E的方向，平移到△DEF，已知BC=5,EC=3，那么平移的距离为（）A.2B.3C.5D.73.如图，把△ABC绕点C顺时针旋转某个角度q后得到△A′B′C′，若∠A=30°，∠1=70°，则旋转角q等于（）A.30°B.50°C.40°D.100°4.如图，将Rt△ABC（其中∠B=35°，∠C=90°）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么旋转角等于A.55°B.70°C.125°D.145°5.下列标志既是轴对称图形又是中心对称图形的是（）6.点P（2，3）关于原点对称的点的坐标是（）A.（2，﹣3）B.（﹣2，3）C.（﹣2，﹣3）D.（2，3）7.如图，将△ABC绕着点C顺时针旋转50°后得到△A′B′C.若∠A=40°.∠B′=110°，则∠BCA′的度数是（）.A.110°B.80°C.40°D.30°8.点P（－2，－3）向左平移1个单位，再向上平移3个单位，则所得到的点的坐标为（）A.（－3，0）B.（－1，6）C.（－3，－6）D.（－1，0）9.如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D 的坐标是（）A.（2，10）B.（－2，0）C.（2，10）或（－2，0）D.（10，2）或（－2，0）10.下列图形：线段、角、圆、平行四边形、矩形、正方形中，既是轴对称图形又是中心对称图形的有（）A.6个B.5个C.4个D.3个11.如图，在Rt△ABC中，∠ACB=90º，∠A=30º，BC=2，将△ABC绕点C按顺时针方向旋转n度后，得到△EDC，此时，点D在AB边上，斜边DE交AC边于点F，则n的大小和图中阴影部分的面积分别为（）. A.30，2 B.60，2 C.60，23D.60，312.如图，O 是等边△ABC 内一点，OA =3，OB =4，OC =5，将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO ′，下列结论：①△BO ′A 可以由△BOC 绕点B 逆时针旋转60°得到；②点O 与O ′的距离为4；③∠AOB =150°；④四边形AOBO ′的面积为；⑤AOCAOBS S+=其中正确的结论是（）A. ①②③B.①②③④C.①②③⑤D.①②③④⑤二.填空题（题型注释）13.点P （－2，1）向上平移2个单位后的点的坐标为__________ .14.如图，等腰直角△ABC 中，AC =BC ，∠ACB =90°，点O 分斜边AB 为BO ：OA =1将△BOC 绕C 点顺时针方向旋转到△AQC 的位置，则∠AQC = .15. 如图，在正方形ABCD 中，边AD 绕点A 顺时针旋转角度m （︒<<︒3600m ），得到线段AP ，连接PB ，PC .当△BPC 是等腰三角形时，m 的值为 .16.如图，在平面直角坐标系中，将△ABO 绕点A 顺时针旋转到△AB 1C 1的位置，点B 、O 分别落在点B 1、C 1处，点B 1在x 轴上，再将△AB 1C 1绕点B 1顺时针旋转到△A 1B 1C 2的位置，点C 2在x 轴上，将△A 1B 1C 2绕点C 2顺时针旋转到△A 2B 2C 2的位置，点A 2在x 轴上，依次进行下去….若点A （3，0），B （0，4），则点B 100的坐标为_________.三.解答题（共52分）17.如图，已知△ABC 三个顶点的坐标分别为A （－2，－1），B （－3，－3），C （－1，－3）,（1）、画出△ABC 向右平移三个单位的对应图形△111C B A ,并写出1A 的坐标；（2）、画出△ABC 关于原点O 对称的△222C B A ，并写出2A 的坐标；18.如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC （顶点是网格线的交点）.（1）将△ABC 绕点B 顺时针旋转90°得到△A ′BC ′，请画出△A ′BC ′；（2）求BA边旋转到B A′位置时所扫过图形的面积.19.如图，点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD.已知∠AOB=110°.（1）求证：△COD是等边三角形；（2）当α=150°时，试判断△AOD的形状，并说明理由；（3）探究：当α为多少度时，△AOD是等腰三角形.20.正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF=45°.将△DAE绕点D逆时针旋转90°，得到△DCM.（1）求证：EF=FM；（4分）（2）当AE=1时，求EF的长.（4分）21.已知：如图，在△ABC中，∠BAC=1200，以BC为边向形外作等边三角形△BCD，把△ABD绕着点D按顺时针方向旋转600后得到△ECD，若AB=3，AC=2，求∠BAD的度数与AD 的长.22.如图，C在线段BD上，△ABC和△CDE都是等边三角形，BE与AD有什么关系？请用．旋转的性质证明．．．．．．．你的结论。

八年级数学下册第三章《图形的平移与旋转》单元测试题-北师大版(含答案)

八年级数学下册第三章《图形的平移与旋转》单元测试题-北师大版（含答案）一、单选题（本大题共12小题，每小题3分，共36分)1．今年4月，被称为“猪儿虫”的璧山云巴正式运行．云巴在轨道上运行可以看作是（）A ．对称B ．旋转C ．平移D ．跳跃2．在平面直角坐标系中，点(4,)P m n -，(,2)Q m n -均在第一象限，将线段PQ 平移，使得平移后的点P 、Q 分别落在x 轴与y 轴上，则点P 平移后的对应点的坐标是（）A ．(4,0)-B ．(4,0)C ．(0,2)D ．(0,2)-3．如图，在Rt ABC △中，90ABC ∠=︒，2AB BC =ABC 绕点A 逆时针转60°得到AB C ''△，则BC '的长是（）A 31B ．232C ．32D ．234．如图，将ABC 绕点A 逆时针旋转40︒得到ADE ，AD 与BC 相交于点F ，若80E ∠=︒且AFC 是以线段FC 为底边的等腰三角形，则BAC ∠的度数为（）A ．55︒B ．60︒C ．65︒D ．70︒5．下列命题是真命题的是（）A ．一个角的补角一定大于这个角B ．平行于同一条直线的两条直线平行C ．等边三角形是中心对称图形D ．旋转改变图形的形状和大小6．如图，在△ABC 中，AB =AC ，若M 是BC 边上任意一点，将△ABM 绕点A 逆时针旋转得到△ACN ，点M 的对应点为点N ，连接MN ，则下列结论一定正确的是（）A ．AB AN = B ．AB NC ∥ C ．AMN ACN ∠=∠D ．MN AC ⊥7．如图，点A 的坐标为()0,2，点B 是x 轴正半轴上的一点，将线段AB 绕点A 按逆时针方向旋转60°得到线段AC ．若点C 的坐标为(),3m ，则m 的值为（）A 43B 221C 53D 421 8．以图（1）（以O 为圆心，半径为1的半圆）作为“基本图形”，分别经历如下变换，不能得到图（2）的是（）A ．绕着OB 的中点旋转180°即可 B ．先绕着点O 旋转180°，再向右平移1个单位C ．先以直线AB 为对称轴进行翻折，再向右平移1个单位D ．只要向右平移1个单位9．平面直角坐标系中，O 为坐标原点，点A 的坐标为()5,1-，将OA 绕原点按逆时针方向旋转90︒得OB ，则点B 的坐标为（）A ．()5,1-B ．()1,5--C ．()5,1--D ．()1,5-10．小明把一副三角板按如图所示叠放在一起，固定三角板ABC ，将另一块三角板DEF 绕公共顶点B 顺时针旋转（旋转角度不超过180°）．若两块三角板有一边平行，则三角板DEF 旋转的度数可能是（）A ．15°或45°B ．15°或45°或90°C ．45°或90°或135°D ．15°或45°或90°或135°11．如图，ABC 与A B C '''关于点O 成中心对称，则下列结论不成立的是（）A ．点A 与点A '是对称点B ．BO B O '=C ．AOB A OB ''∠=∠D ．ACB C A B '''∠=∠ 12．如图，已知△ABC 中，∠CAB ＝20°，∠ABC ＝30°，将△ABC 绕A 点逆时针旋转50°得到△AB ′C ′，以下结论：∠BC ＝B ′C ′，∠AC ∠C ′B ′，∠C ′B ′∠BB ′，∠∠ABB ′＝∠ACC ′，正确的有（）A ．∠∠∠B ．∠∠∠C ．∠∠∠D ．∠∠∠二、填空题（本大题共8小题，每小题3分，共24分)13．已知点A （﹣2，b ）与点B （a ，3）关于原点对称，则a ﹣b =______．14．如图．两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B 到C 的方向平移到DEF 的位置，8,3==AB DP ，平移距离为6，则阴影部分的面积为____________．15．如图，边长为2的等边ABO 在平面直角坐标系的位置如图所示，点O 为坐标原点，点A 在x 轴上，以点O 为旋转中心，将ABO 按顺时针方向旋转120°，得到OA B ''△，则点A '的坐标为_____．16．如图，在ABC 中，∠C ＝90°，点D 、E 分别在AC 、BC 上，∠CDE ＝45°，ECD 绕点D 顺时针旋转x 度（45<x <180）到11E C D △，则1BEE ∠等于______度．（用含x 的代数式表示）17．如图，在宽为13米、长为24米的长方形地面上修筑同样宽的道路（图中阴影部分），道路的宽为2米，余下部分种植草坪. 则草坪的面积为__________.18．如图，在平面直角坐标系中，ABC 的顶点A ，B 的坐标分别是()0,2A ，()2,1B -．平移ABC 得到A B C '''，若点A 的对应点A '的坐标为()1,0-，则点B 的对应点B '的坐标是_____________．19．线段MN 是由线段EF 经过平移得到的，若点(1,3)-E 的对应点(4,7)M -，则点(3,2)F --的对应点N 的坐标是____________．20．如图，DEF ∆是由ABC ∆通过平移得到，且点,,,B E C F 在同一条直线上，如果14BF =，6EC =．那么这次平移的距离是_________．三、解答题（本大题共5小题，每小题8分，共40分)21．如图，已知图中A 点和B 点的坐标分别为()2,4-和()2,2-．(1)请在图1中画出坐标轴建立适当的直角坐标系；(2)写出点C 的坐标为______；(3)在y 轴上有点D ．满足20DBC S =△，则点D 的坐标为______；(4)已知第一象限内有两点()4,M m n -，(),3N m n -．平移线段MN 使点M 、N 分别落在两条坐标轴上．则点M 平移后的对应点的坐标是______．22．如图，点A 在射线OX 上，OA a =．如果OA 绕点O 按逆时针方向旋转(0360)<≤︒n n 到OA '，那么点A '的位置可以用(),︒a n 表示．(1)按上述表示方法，若3a =，37n =，则点A '的位置可以表示为______；(2)在（1）的条件下，已知点B 的位置用()3,74︒表示，连接A A '、A B '．求证：A A A B ''=．23．如图，()1,0A ，点B 在y 轴上，将三角形OAB 沿x 轴负方向平移，平移后的图形为三角形DEC ，点C 的坐标为()3,2-．(1)点B 的坐标为_______，点E 的坐标为______；(2)点P 从点O 出发，沿OB BC CD →→移动，若点P 的速度为每秒1个单位长度，运动时间为()0t t >秒． ∠用含t 的式子表示点P 的坐标；∠当t 为多少时，点P 的横坐标与纵坐标互为相反数；∠当三角形AEP 的面积为2时，直接．．写出此时t 的值．24．在平面直角坐标系中，A（－2，4），B（－3，－1），C（0，2）．将∠ABC平移至∠A1B1C1，点A对应点A1（3，3），点B对应点B1，点C对应点C1．(1)画出平移后的∠A1B1C1，并写出B1的坐标；(2)求∠ABC的面积；(3)若存在点D（m，n）使得∠BB1D和∠BB1C面积相等，其中m，n均为绝对值不超过5的整数，则点D的坐标为_________．25．在平面直角坐标系xOy中，对于点A，规定点A的α变换和β变换．α变换：将点A向左平移一个单位长度，再向上平移两个单位长度；β变换：将点A向右平移三个单位长度，再向下平移一个单位长度(1)若对点B进行α变换，得到点（1，1），则对点B进行β变换后得到的点的坐标为．=，求m的值．(2)若对点C（m，0）进行α变换得到点P，对点C（m，0）进行β变换得到点Q，OP OQ(3)点D为y轴的正半轴上的一个定点，对点D进行α变换后得到点E，点F为x轴上的一个动点，对点F进行β变+的最小值为，直接写出点D的坐标．换之后得到点G，若DG EF参考答案1．C2．A3．A4．B5．B6．C7．C8．D9．B10．D11．D12．B13．514．3915．（1316．452x ⎛⎫+ ⎪⎝⎭ 17．242平方米18．()1,3-19．（−6，2）20．421．(1)1(2)（3，2）(3)（0，﹣6）或（0，10）(4)（0，3）或（﹣4，0）22．(1)(3,37°)23．(1)（0，2），（2-，0）(2)∠当点P 在OB 上时，点P 的坐标为（0，t ）；点P 在BC 上时，点P 的坐标（2t -，2）；当点P 在CD 上时，点P 的坐标为（3-，7t -）；∠当t =4时，点P 的横坐标与纵坐标互为相反数；∠t 的值为43或17324．(1)B1的坐标（2，﹣2）(2)6(3)（﹣5，3）或（0，2）或（5，1）或（﹣1，﹣5）25．(1)（5，-2）(2)58m=-(3)（0，32）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

最新八年级下册图形的平移和旋转单元测试试题
知识点一、平移的性质经过平移， _________， __________分别相等，
对应点所连的线段_____________．对应角。

1、在下列生活现象中，不是平移现象的是（）
A.站在运行的电梯上的人
B.左右推动的推拉窗帘
C.小亮荡秋千的运动
D. 坐在直线行驶的列车上的乘客
2、在5×5的方格纸中将图1中的图形N平移后的位置如图2中所示，那么正确的平移方法是：先向（）移动（）格，再向（）移动（）格．
3、如下左图，△ABC经过平移到△DEF的位置，则下列说法：①AB∥DE，AD=CF=BE；②∠ACB=∠DEF；③平移的方向是点C到点E的方向；
④平移距离为线段BE的长.其中说法正确的有（）
A.个
B.2个
C.3个
D.4个
4、如下右图，在等边△ABC中，D、E、F分别是边BC、AC、AB的中点，则△AFE经过平移可以得到（）
A、△DEF
B、△FBD
C、△EDC
D、△FBD和△EDC
5、如图，将△ABE向右平移2cm得△DCF，若△ABE的周长是16cm，则四边形ABFD的周长是___cm．
6、如图，在△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿射线BC 的方向平移2个单位后，得到△A′B′C′，连接A′C，则△A′B′C 的周长为______．
7、在平面直角坐标系中，将点A（1，-2）向上平移3个单位长度，再向左平移2个单位长度，得到点A′，则点A′的坐标是（）A.（-1，1） B.（-1，-2）
C.（-1，2）
D.（1，2）
8、在平面直角坐标系中，将三角形各点的纵坐标都减去3，横坐标保持不变，所得图形与原图形相比。

A.向右平移了3个单位
B.向左平移了3个单位
C.向上平移了3个单位
D.向下平移了3个单位
9、如图，将△PQR向右平移2个单位长度，再向下平移3个单位长度，则顶点P平移后的坐标是（）。

A．（-2，-4)） B．（-2，4）
C．（2，-3） D．（-1，-3）
10、已知点M（3a－9,1－a）将点M向右平移3个单位长度后落在y 轴上，则a= 。

旋转的性质：
1、经过旋转后的图形与原图形的对应线段______，对应角_______
2、对应点到旋转中心的距离。

3、____________________都是旋转角．
4、经过旋转，图形上每一点都绕旋转中心沿相同方向转动了相同角
度
1、下列运动是属于旋转的是( )
A、滾动过程中篮球的滚动
B、钟表的钟摆的摆动
C、气球升空的运动
D、一个图形沿某直线对折过程
2、如图，两块相同的直角三角形完全重合在一起，∠A=30°，AC=10，把上面一块绕直角顶点B逆时针旋转到△A′B′C′的位置，点C′在AC上，A′C′与AB相交于点D，则C′D=（）
3、如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A 旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′=（）。

A．30° B．35°
C．40° D．50°
4、如图，△ABC中，∠C=67°，将△ABC绕点A顺时针旋转后，得到△AB′C′，且C′在边BC上，则∠B′C′B的度数为（）A．56° B．50°
C．46° D．40°
5、如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C 顺时针旋转至△A′B′C，使得点A′恰好落在AB上，则旋转角度为（）
5、如图，在方格纸中的△ABC经过变换得到△DEF，正确的变换是（）
A．把△ABC向右平移6格
B．把△ABC向右平移4格，再向上平移1格
C．把△ABC绕着点A顺时针方向90°旋转，再右平移6格
D．把△ABC绕着点A顺时针方向90°旋转，再右平移6格。

7、如图，把三角形△ABC绕着点C顺时针旋转35°，得到△A′B′C，A′B′交AC于D点．若∠A′DC=90°，则∠A=（）度．
8、如图，在等边三角形ABC中，AB=6，D是BC上一点，且BC=3BD，△ABD绕点A旋转后得到△ACE，则CE的长度为．
9、如图所示，△ABC是等腰直角三角形，BC是斜边，将△ABC绕点A 逆时针旋转后，能与△ACP′重合，如果AP=3，那么PP′的长等于（）。

A、 B.
C. D.
10、在如图所示的单位正方形网格中，△ABC经过平移后得到△A1B1C1，已知在AC上一点P（2.4，2）平移后的对应点为P1，点P1绕点O逆时针旋转180°，得到对应点P2，则P2点的坐标为（）
A．（1.4，－1）B．（1.5，2）
C．（1.6，1） D．（2.4，1）
11、如图，△ABC中，∠C=67°，将△ABC绕点A顺时针旋转后，得到△AB′C′，且C′在边BC上，则∠B′C′B的度数为（）
12、如图，将矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置，旋转角为，若∠1=110°，则∠= 度．
13、、如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点
A的坐标为（2，4），请解答下列问题：
（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标．（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2，并写出点A2的坐标．
14、如图，D为等边△ABC外一点，且BD=CD，∠BDC=120°，点M，N
，
分别在AB，AC上，若BM+CN=MN
求证：（1）∠MDN=60°；
（2）作出△DMN的高DH，并证明DH=BD．
15、已知点M（2a-b,3）与点N（-6，a+b）关于原点中心对称，则
a-b= ．
16、如图，在平面直角坐标系中，已知点A（3，0），B（0，4），记Rt△OAB为三角形①，按图中所示的方法旋转三角形，依次得到三角
形②，③，④，……，则三角形⑤的直角顶点的坐标为；三角形⑩的直角顶点的坐标为；第2018个三角形的直角顶点的
坐标为．
17、【操作发现】
（1）如图1，△ABC为等边三角形，先将三角板中的60°角与∠ACB 重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于
30°），旋转后三角板的一直角边与AB交于点D，在三角板斜边上取
一点F，使CF=CD，线段AB上取点E，使∠DCE=30°，连接AF，EF．
①求∠EAF的度数；
②DE与EF相等吗？请说明理由；
【类比探究】
（2）如图2，△ABC为等腰直角三角形，∠ACB=90°，先将三角板的90°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角
大于0°且小于45°），旋转后三角板的一直角边与AB交于点D，在三角板另一直角边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=45°，连接AF，EF．请直接写出探究结果：
①∠EAF的度数；
②线段AE，ED，DB之间的数量关系．
18、如图，已知ABC
ABA C厘米，8
BC厘米，点D为AB的中△中，10
点．
（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1秒后，BPD
△与△是否全等，请说明理由；
CQP
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使BPD
△全等？
△与CQP
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿ABC
△三边运动，求经过多长时间点P
与点Q第一次在ABC
△的哪条边上相遇？
19、如图，过线段AB的两个端点作射线AM、BN，使AM∥BN，画∠MAB、∠NBA的平分线交于E，按下列要求回答：
（1）∠AEB是什么角？并说明理由。

（2）过点E作一直线交AM于D，交BN于C，观察线段DE、CE，你有
何发现？
（3）无论DC的两端点在AM、BN如何移动，只要DC经过点E，①AD+BC=AB；
②AD+BC=CD谁成立？并说明理由。