编译原理第四章答案
编译原理-第4章 语法分析--习题答案

第4章语法分析习题答案1.判断(1)由于递归下降分析法比较简单,因此它要求文法不必是LL(1)文法。
(× )LL(1)文法。
(× )(3)任何LL(1)文法都是无二义性的。
(√)(4)存在一种算法,能判定任何上下文无关文法是否是LL(1) 文法。
(√)(× )(6)每一个SLR(1)文法都是LR(1)文法。
(√)(7)任何一个LR(1)文法,反之亦然。
(× )(8)由于LALR是在LR(1)基础上的改进方法,所以LALR(× )(9)所有LR分析器的总控程序都是一样的,只是分析表各有不同。
(√)(10)算符优先分析法很难完全避免将错误的句子得到正确的归约。
(√)2.文法G[E]:E→E+T|TT→T*F|FF→(E)|i试给出句型(E+F)*i的短语、简单短语、句柄和最左素短语。
答案:画出语法树,得到:短语: (E+F)*i ,(E+F) ,E+F ,F ,i简单短语: F ,i句柄: F最左素短语: E+F3.文法G[S]:S→SdT | TT→T<G | GG→(S) | a试给出句型(SdG)<a的短语、简单短语、句柄和最左素短语。
答案:画出语法树,得到:短语:(SdG)<a 、(SdG) 、SdG 、G 、a简单(直接)短语:G 、a句柄:G最左素短语:SdG4.对文法G[S]提取公共左因子进行改写,判断改写后的文法是否为LL(1)文法。
S→if E then S else SS→if E then SS→otherE→b答案:提取公共左因子;文法改写为:S→if E then S S'|otherS'→else S|E→bLL(1)文法判定:① 文法无左递归② First(S)={if,other}, First(S')={else, }First(E)={b}Follow(S)= Follow(S')={else,#}Follow(E)={then}First(if E then S S')∩First(other)=First(else S)∩First( )=③First(S')∩Follow(S')={else}不为空集故此文法不是LL(1)文法。
编译基础学习知识原理第4章规范标准答案
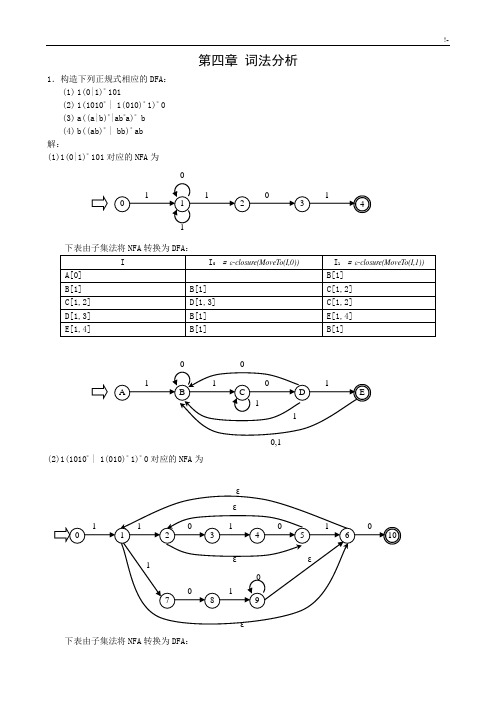
第四章 词法分析1.构造下列正规式相应的DFA :(1) 1(0|1)*101(2) 1(1010* | 1(010)* 1)*(3) a((a|b)*|ab *a)*b(4) b((ab)* | bb)*ab 解:(1)1(0|1)*101对应的NFA 为下表由子集法将NFA 转换为DFA :(2)1(1010* | 1(010)* 1)*0对应的NFA 为下表由子集法将NFA 转换为DFA :(3)a((a|b)*|ab*a)* b (略)(4)b((ab)* | bb)* ab (略)2.已知NFA=({x,y,z},{0,1},M,{x},{z})其中:M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA。
解:根据题意有NFA图如下0,1 下表由子集法将NFA转换为DFA:下面将该DFA最小化:(1)首先将它的状态集分成两个子集:P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F,C等价。
由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D,E不等价(见下步),从而B与C,F可以区分。
有P21={C,F},P22={B}。
(3)区分P1:由于A,E输入0到终态,而D输入0不到终态,所以D与A,E可以区分,有P11={A,E},P12={D}。
(4)由于F(A,0)=B,F(E,0)=F,而B,F不等价,所以A,E可以区分。
(5)综上所述,DFA可以区分为P={{A},{B},{D},{E},{C,F}}。
所以最小化的DFA如下:3.将图4.16确定化:图4.16解:下表由子集法将NFA转换为DFA:14.把图4.17的(a)和(b)分别确定化和最小化:(a) (b)解: (a):可得图(a1),由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价,可将DFA 最小化,即:删除B ,将原来引向B 的引线引向与其等价的状态A ,有图(a2)。
编译原理第4章.doc
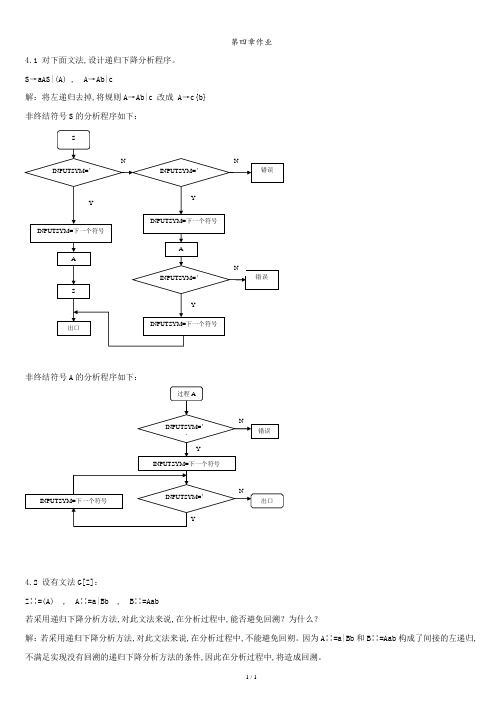
第四章作业4.1 对下面文法,设计递归下降分析程序。
S→aAS|(A) , A→Ab|c解:将左递归去掉,将规则A→Ab|c 改成 A→c{b}非终结符号S的分析程序如下:非终结符号A的分析程序如下:4.2 设有文法G[Z]:Z∷=(A) , A∷=a|Bb , B∷=Aab若采用递归下降分析方法,对此文法来说,在分析过程中,能否避免回溯?为什么?解:若采用递归下降分析方法,对此文法来说,在分析过程中,不能避免回朔。
因为A∷=a|Bb和B∷=Aab构成了间接的左递归,不满足实现没有回溯的递归下降分析方法的条件,因此在分析过程中,将造成回溯。
4.3 若有文法如下,设计递归下降分析程序。
<语句>→<语句><赋值语句>|ε<赋值语句>→ID=<表达式><表达式>→<项>|<表达式>+<项>|<表达式>-<项><项>→<因子>|<项>*<因子>|<项>/<因子><因子>→ID|NUM|(<表达式>)解:首先,去掉左递归(1)<语句>→<语句><赋值语句>|ε改为: <语句>→{<赋值语句>}(3)<表达式>→<项> | <表达式> + <项> | <表达式> - <项> 改为:<表达式>→<项>{(+ | -)<项>}(4)<项>→<因子> | <项> * <因子> | <项> / <因子>改为:<项>→<因子>{(* | /)<因子>}则文法变为:<语句>→{<赋值语句>}<赋值语句>→ID=<表达式><表达式>→<项>{(+ | -)<项>}<项>→<因子>{(* | /)<因子>}<因子>→ID|NUM|(<表达式>)非终结符号 <语句>→{<赋值语句>} 的分析程序如下:非终结符号 <赋值语句>→ID=<表达式> 的分析程序如下:非终结符号<表达式>→<项>{(+ | -)<项>} 的分析程序如下:非终结符号 <项>→<因子>{(* | /)<因子>} 的分析程序如下:非终结符号 <因子>→ID|NUM|(<表达式>) 的分析程序如下:4.4 有文法G[A]:A::=aABe|ε,B::=Bb|b(1)求每个非终结符号的FOLLOW集。
编译原理第4章习题答案

S-> S’ S’->(S)SS’| First( (S)SS’) = { ( } Follow(S)=Follow(S’)= { (, ),$ }
预测分析表
非终结符 S ( S->S’ ) S->S’ $ S->S’
S’
S’->(S)SS’
S’->
S’->
S’->
冲突
仔细分析后,发现该文法 S->S(S)S| 是二义性文法。 二义性文法不可能是LL(1)文法。 例如:( ) ( )
S->aS’ S’->aS’AS’|Ɛ A->+|*
First(S) = First(aS’)={a} First(S’)= First(aS’AS’) ∪ First(Ɛ)= {a} ∪{Ɛ}= {a, Ɛ} First(A) = { +,*}
Follow(S) ={$} 因为 S->aS’,所以把Follow(S)加入到Follow(S’)中。 因为 S’->aS’AS’的第一个S’ ,所以把First(AS’)={+,*}加入到Follow(S’)中。 因为 S’->aS’AS’的第二个S’ ,所以Follow(S)加入到Follow(S’)中。 所以,Follow(S’)= {$, +,*} 对 S’->aS’AS’的A ,当A后面的S’推导出非空时,把First(S’)-{Ɛ}={a}加入到Follow(A)中。 对 S’->aS’AS’的A ,当A后面的S’推导出空时,把Follow(S’)={$,+,*}加入到Follow(A)中。 所以,Follow(A)= {a, +,*,$} 对于S’->aS’AS’|Ɛ,因为First(aS’AS’) ∩Follow(S’)={a} ∩{$,+,*}=空集,所以没有冲突。 对于A->+|*,因为First(+) ∩First(*)={+} ∩{*}=空集,所以没有冲突。 所以该文法是LL(1)文法。
编译原理课后习题答案ch4

注意:本题应该理解为对图(a)进行确定化和对图(b)进行最小化。提供的答案没有对图(a)确 定化。
盛威网()专业的计算机学习网站 14
《编译原理》课后习题答案第四章
第5题 构造一个 DFA,它接收 Σ={0,1}上所有满足如下条件的字符串:每个 1 都有 0 直接跟在 右边。并给出该语言的正规式。 答案: 按题意相应的正规表达式是(0*10)*0*, 或 0*(0 | 10)*0* 构造相应的 DFA, 首先构造 NFA 为
7
《编译原理》课后习题答案第四章
注意:这个题,也可以这样构造 NFA(用最少的ε,但注意不能出错) :
a,b 0 a a 2 a,b 1 a b 3
盛威网()专业的计算机学习网站
8
《编译原理》课后习题答 ε X b A ε F B a C b ε b G b H ε ε D ε E a I b Y
除 X,A 外,重新命名其他状态,令 AB 为 B、AC 为 C、ABY 为 D,因为 D 含有 Y(NFA 的终态),所以 D 为终态。 . X A B C D DFA 的状态图:: 0 . A C A C 1 A B B D B
(2)先构造 NFA: 0 ε X 1 A ε ε F B 1 C 1 0 ε 0 D 1 E 1 0 ε 用子集法将 NFA 确定化 ε X T0=X A T1= ABFL Y CG T2= Y T3= CGJ DH K T4= DH EI T5= ABFKL T6= ABEFIL EJY T7= ABEFGJLY EHY CGK T8= ABEFHLY EY CGI T9= ABCFGJKL DHY T10= ABEFLY T11= CGJI DHJ T12= DHY T13= DHJ EIK T14= ABEFIKL ABEFIKL EJY CG DHJ ?正确 DHJG EI EIK DHY EY DHJ CG K ABEFLY CGJI DHY CGK ABEFHLY ABCFGJKL EY CGI ABEFGJLY EHY CGK ABEFIL Y EJY CG CG DH ABFKL EI DH K Y CGJ ABFL Y CG X A 0 1 1 ε L ε K ε J 0 Y
编译原理第四章参考答案

编译原理第四章参考答案1.1考虑下⾯⽂法G1S->a|^|(T)T->T,S|S消去G1的左递归。
然后对每个⾮终结符,写出不带回溯的递归⼦程序。
答::(1)消除左递归:S->a|^|(T)T-> ST’T’->,S T’|ε(2)first(S)={ a , ^ , ( } first(T)= { a , ^ , ( } first(T’)={ , ε}First(a)={a},First(^)={^},First( (T) )={ ( }S的所有候选的⾸符集不相交First(,ST’)={,} ,First(ε)={ε},T’的所有候选的⾸符集不相交Follow(T’)=Follow(T)={ )}first(T’)∩Follow(T’)={}所以改造后的⽂法为LL(1)⽂法。
不带回溯的递归⼦程序如下:S( ){if (lookahead=’a’) advance;Else if(lookahead=’^’) advance;Else if(lookahead=’(’){advance;T();if(lookahead=’)’) advance;else error();}Else error();}T( ){S( );T’( ):}T’->,S T’|εT’( ){if (lookahead=’,’){advance;T’();}Else if(lookahead=Follow(T’)) advance;Else error;}有⽂法G(S):S→S+aF|aF|+aFF→*aF|*a(1)改写⽂法为等价⽂法G[S’],消除⽂法的左递归和回溯(2)构造G[S’]相应的FIRST和FOLLOW集合;(3)构造G[S’]的预测分析表,以此说明它是否为LL(1)⽂法。
(4)如果是LL(1)⽂法,请给出句⼦a*a+a*a*a的预测分析过程该⽂法为LL(1)⽂法,因为它的预测分析表中⽆冲突项。
编译原理第四章答案
First( A' ) Follow ( A' ) {d , } {), b}
4.4(2)
见课后答案 规则见课本P66
问题?
Select( E gAf ) Select( E c) First( gAf ) Frist(c) {g} {c}
4.2
对下面的文法G: E→TE’ E’→+TE’|ε T→FT’ T’→*FT’|ε F→(E)|id (1)计算这个文法的每个非终结符的FIRST和FOLLOW。 (2)证明这个文法是LL(1)的。 (3)构造它的预测分析表。 (4)构造它的递归下降分析程序。
第四章习题
4.1 4.2 4.3 4.4
4.1
1、考虑下面文法G[A]: A→BCc|gDB B→bCDE|ε C→DaB|ca D→dD|ε E→gAf|c (1)FIRST集和FOLLOW集 (2)是否是LL(1)文法。
4.1(1) First集
First( A) First( BCc) First( gDB) First( B) \ { } First(C ) {g} {b} First( D) \ { } {a} First(ca) {g} {b} {d } {a} {c} {g} {a, b, c, d , g}
E’→ε T→FT ’ T’→ε F→idFra bibliotekE’→ε
T’→ε
4.2(4)
规则见课本P66 见课后答案 E→TE’ T→FT’ F→(E)|id E’→+TE’|ε T’→*FT’|ε
4.3
文法G[S]: S→A A→B|AiB B→C|B+C C→)A*|( 1)改写为LL(1)文法 2)求改写后的文法的每个非终结符的First集和Follow集 3)构造相应的预测分析表
编译原理 龙书答案
第四章部分习题解答Aho:《编译原理技术与工具》书中习题(Aho)4.1 考虑文法S → ( L ) | aL → L, S | Sa)列出终结符、非终结符和开始符号解:终结符:(、)、a、,非终结符:S、L开始符号:Sb)给出下列句子的语法树i)(a, a)ii)(a, (a, a))iii)(a, ((a, a), (a, a)))c)构造b)中句子的最左推导i)S(L)(L, S) (S, S) (a, S) (a, a)ii)S(L)(L, S) (S, S) (a, S) (a, (L)) (a, (L, S)) (a, (S, S)) (a, (a, S) (a, (a, a))iii)S(L)(L, S) (S, S) (a, S) (a, (L)) (a, (L, S)) (a, (S, S)) (a, ((L), S)) (a, ((L, S), S)) (a, ((S, S), S)) (a, ((a, S), S))(a, ((a, a), S)) (a, ((a, a), (L))) (a, ((a, a), (L, S))) (a, ((a, a), (S, S))) (a, ((a, a), (a, S))) (a, ((a, a), (a, a)))d)构造b)中句子的最右推导i)S(L)(L, S) (L, a) (S, a) (a, a)ii)S(L)(L, S) (L, (L)) (L, (L, S)) (L, (L, a)) (L, (S, a)) (L, (a, a)) (S, (a, a)) (a, (a, a))iii)S(L)(L, S) (L, (L)) (L, (L, S)) (L, (L, (L))) (L, (L, (L, S))) (L, (L, (L, a))) (L, (L, (S, a))) (L, (L, (a, a))) (L, (S,(a, a))) (L, ((L), (a, a))) (L, ((L, S), (a, a))) (L, ((L, a), (a,a))) (L, ((S, a), (a, a))) (L, ((a, a), (S, S))) (S, ((a, a), (a,a))) (a, ((a, a), (a, a)))e)该文法产生的语言是什么解:设该文法产生语言(符号串集合)L,则L = { (A1, A2, …, A n) | n是任意正整数,A i=a,或A i∈L,i是1~n之间的整数}(Aho)4.2考虑文法S→aSbS | bSaS |a)为句子构造两个不同的最左推导,以证明它是二义性的S aSbS abS abaSbS ababS ababS aSbS abSaSbS abaSbS ababS ababb)构造abab对应的最右推导S aSbS aSbaSbS aSbaSb aSbab ababS aSbS aSb abSaSb abSab ababc)构造abab对应语法树d)该文法产生什么样的语言?解:生成的语言:a、b个数相等的a、b串的集合(Aho)4.3 考虑文法bexpr→bexpr or bterm | btermbterm→bterm and bfactor | bfactorbfactor→not bfactor | ( bexpr ) | true | falsea)试为句子not ( true or false)构造分析树解:b)试证明该文法产生所有布尔表达式证明:一、首先证明文法产生的所有符号串都是布尔表达式变换命题形式——以bexpr、bterm、bfactor开始的推导得到的所有符号串都是布尔表达式最短的推导过程得到true、false,显然成立假定对步数小于n的推导命题都成立考虑步数等于n 的推导,其开始推导步骤必为以下情况之一bexpr bexpr or btermbexpr btermbterm bterm and bfactorbexpr bfactorbfactor not bfactorbfactor ( bexpr )而后继推导的步数显然<n,因此由归纳假设,第二步句型中的NT推导出的串均为布尔表达式,这些布尔表达式经过or、and、not运算或加括号,得到的仍是布尔表达式因此命题一得证。
编译原理第4章答案
第四章 词法分析1.构造下列正规式相应的DFA :(1) 1(0|1)*101(2) 1(1010*| 1(010)*1)*0 (3) a((a|b)*|ab *a)*b (4) b((ab)*| bb)*ab 解:(1)1(0|1)*101对应的NFA 为下表由子集法将NFA 转换为DFA :(2)1(1010*| 1(010)*1)*0对应的NFA 为 10,1下表由子集法将NFA转换为DFA:(3)a((a|b)*|ab *a)*b (略) (4)b((ab)*| bb)*ab (略)2.已知NFA=({x,y,z},{0,1},M,{x},{z})其中:M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA 。
解:根据题意有NFA 图如下下表由子集法将NFA 转换为DFA :0,1下面将该DFA最小化:(1)首先将它的状态集分成两个子集:P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F,C等价。
由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D,E不等价(见下步),从而B与C,F可以区分。
有P21={C,F},P22={B}。
(3)区分P1:由于A,E输入0到终态,而D输入0不到终态,所以D与A,E可以区分,有P11={A,E},P12={D}。
(4)由于F(A,0)=B,F(E,0)=F,而B,F不等价,所以A,E可以区分。
(5)综上所述,DFA可以区分为P={{A},{B},{D},{E},{C,F}}。
所以最小化的DFA如下:3.将图确定化:1101111解:下表由子集法将NFA 转换为DFA :4.把图的(a)和(b)分别确定化和最小化:(a) (b)解: (a):下表由子集法将NFA 转换为DFA :0,1a可得图(a1),由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价,可将DFA 最小化,即:删除B ,将原来引向B 的引线引向与其等价的状态A ,有图(a2)。
编译原理第四章作业答案
非终结符
FIRSTVT
LASTVT
E
+ * ↑( i
+ * ↑) i
T
* ↑( i
* ↑) i
F
↑( i
↑)i
P
(i
)i
2).关系 1.由#E#,知 # = # ;由(E)知 ( = ) 2.求 < 关系 考察对象:文法中终结符号在前,非终结符号在后的相邻符号对 由#E # < FIRSTVT(E) 由+T + < FIRSTVT(T) 由*F * < FIRSTVT(F) 由↑F ↑< FIRSTVT(F) 由(E ( < FIRSTVT(E)
T→F
F→-P
F→P
P→(E)
P→i
(1) 构造 G 的算符优先矩阵;
(2) 指出 G 不是算符优先文法,即指出具有多重定义的优先矩阵元素;
(3)将 G 改写为算符优先文法。
解:
(1)求每个非终结符号的 FIRSTVT 集和 LASTVT 集
S→E
E→E-T|T
T→T*F|F
F→-P|P
P→(E)|i
Z 11 Z 12 Z 13
(S
A
B ) = (φ (S ) + () [S ] + [])Z 21
Z 22
Z
23
Z 31 Z 32 Z 33
Z 11 Z 12 Z 13 ε φ φ A B φ Z 11 Z 12 Z 13
Z 21
Z 22
Z
23
=
φ
ε
φ
+
ε
φ
φ
Z
21
Z 22
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
First( A' ) Follow ( A' ) {d , } {), b}
4.4(2)
见课后答案 规则见课本P66
问题?
FIRST集: * FIRST()= {a | a…, a∈ VT } 若 ε,ε∈ FIRST() FOLLOW集: FOLLOW(A)={a |S * ...Aa...,a∈VT} 若S...A,则规定 $∈FOLLOW(A)
4.2(2) LL(1)?
1) 不含左递归 2)
E→TE’ T→FT’ F→(E)|id
Follow ( E) Follow ( B) {a, c, d , f , g ,$}
A→BCc|gDB B→bCDE|ε C→DaB|ca D→dD|ε E→gAf|c
4.1(2) LL(1)?
LL(1)文法定义 一个上下文无关文法 G是LL(1)文法, 当 且仅当对 G 中每个非终结符A的任何两 个不同的规则 A→ α | β,满足 SELECT(A→ α)∩SELECT(A→β) = Φ 其中α 、β中至多只有一个能推出ε串。
B→CB'
First
Follow
S
A A' B B' C
{),(}
{),(} {i,ε} {),(} {+,ε} {),(}
{$}
{$,*} {$,*} {i,$,*} {i,$,*} {+,i,$,*}
4.3(3)预测分析表
+ S A I
S→A A→BA' A'→iBA'|ε B'→+CB'|ε C→)A*|(
4.4(1) LL(1)?
1)无左递归
2)
First (( A)) First (aAb) {(} {a} First (eA' ) First (dSA' ) {e} {d } First (dA' ) First( ) {d } { }
Select(C DaB) Select(C ca) First( DaB) Frist(ca) {a, d} {c}
Select( D dD) Select( D ) First(dD) Follow ( D) {d } {a, b, c, f , g ,$}
4.2(2) LL(1)?
左递归的消除: P→Pα|β 改为: P→βP’ P’ →αP’| ε
LL(1)文法要求: (1)文法不含左递归。 (2)对文法中的每一个非终极符 A, 若 A →α1|α2|...|αn, 则 FIRST(αi) FIRST(αj)= (3)对文法中的每一个非终极符 A,若它存在某个候选首 符集包含 ε, 则 FIRST(A) FOLLOW(A)=
E’→ε T→FT ’ T’→ε F→id
E’→ε
T’→ε
4.2(4)
规则见课本P66 见课后答案 E→TE’ T→FT’ F→(E)|id E’→+TE’|ε T’→*FT’|ε
4.3
文法G[S]: S→A A→B|AiB B→C|B+C C→)A*|( 1)改写为LL(1)文法 2)求改写后的文法的每个非终结符的First集和Follow集 3)构造相应的预测分析表
First( B) First(bCDE) { } {b, }
First(C ) First( DaB) First(ca) First( D) \ { } {a} {c} {d , a, c}
First ( D) First (dD) { } {d , }
First
E E’ T T’ F {(,id} {+,ε} {(,id} {*,ε} {(,id}
Follow
{$,)} {$,)} {+,$,)} {+,$,)} {*,+,$,)}
+ E E' T T' F T’→ε
*
( E→TE ’
)
id E→TE ’
$
E’→+T E’ T→FT’
T’→*F T’ F→(E)
3)
First( E ' ) Follow ( E ' ) {, } {$, )} First(T ' ) Follow (T ' ) {*, } {,$,)}
4.2(3) 预测分析表
E→TE’ T→FT’ F→(E)|id
E’→+TE’|ε T’→*FT’|ε
E’→+TE’|ε T’→*FT’|ε
First E E’ T T’ F {(,id} {+,ε} {(,id} {*,ε} {(,id} Follow {$,)} {$,)} {+,$,)} {+,$,)} {*,+,$,)}
First (TE ' ) First ( ) {} { } First (*FT ' ) First ( ) {*} { } First ((E )) Frist (id ) {(} {id }
B→CB'
( S→A
) S→A
*
$
A→BA' A→BA'
A'
B
A'→iB A'
B→CB' B→CB' B'→+C B'
A'→ε
A'→ε
B'
C
B'→ε
C→( C→)A*
B'→ε
B'→ε
4.4
文法G[S]: S→(A)|aAb A→eA'|dSA' A'→dA'|ε 1)LL(1)? 2)递归下降分析程序。
Select( E gAf ) Select( E c) First( gAf ) Frist(c) {g} {c}
4.2
对下面的文法G: E→TE’ E’→+TE’|ε T→FT’ T’→*FT’|ε F→(E)|id (1)计算这个文法的每个非终结符的FIRST和FOLLOW。 (2)证明这个文法是LL(1)的。 (3)构造它的预测分析表。 (4)构造它的递归下降分析程序。
4.1(2) LL(1)?
A→BCc|gDB D→dD|ε
B→bCDE|ε E→gAf|c
C→DaB|ca
Select( A BCc) Select( A gDB) First( BCc) First( gDB) {b, c, d , a} {g}
Select( B bCDE) Select( B ) First (bCDE) Follow ( B) {b} {a, c, d , f , g ,$}
First( E ) {g , c}
A→BCc|gDB B→bCDE|ε C→DaB|ca D→dD|ε E→gAf|c
4.1(1) Follow集
Follow ( A) {$, f }
Follow ( B) First(C ) Follow ( A) Follow (C ) {a, c, d } {$, f } Follow (C ) {a, c, d , f , g ,$}
4.2(1)
解: (1)FIRST和FOLLOW集如下表:
E→TE’ T→FT’ F→(E)|id
E’→+TE’|ε T’→*FT’|ε
First
E E’ T T’ F {(,id} {+,ε} {(,id} {*,ε} {(,id}
Follow
{$,)} {$,)} {+,$,)} {+,$,)} {*,+,$,)}
第四章习题
4.1 4.2 4.3: A→BCc|gDB B→bCDE|ε C→DaB|ca D→dD|ε E→gAf|c (1)FIRST集和FOLLOW集 (2)是否是LL(1)文法。
4.1(1) First集
First( A) First( BCc) First( gDB) First( B) \ { } First(C ) {g} {b} First( D) \ { } {a} First(ca) {g} {b} {d } {a} {c} {g} {a, b, c, d , g}
4.3(1)改成LL(1)文法
S→A A→BA' A'→iBA'|ε B→CB' B'→+CB'|ε C→)A*|(
S→A A→B|AiB B→C|B+C C→)A*|(
左递归的消除: P→Pα|β 改为: P→βP’ P’ →αP’| ε
4.3(2)
S→A A→BA' A'→iBA'|ε B'→+CB'|ε C→)A*|(
Follow (C) {c} First( DE) {c} {d , g , c} {c, d , g}
Follow ( D) First ( B) /{ } Follow ( A) First ( E ) {a} {b} {$, f } {g , c} {a} {a, b, c, f , g ,$}
