六年级下学期数学广角——鸽巢问题
六年级下册数学教案-5.1数学广角——鸽巢问题|人教版(5)

六年级下册数学教案5.1 数学广角——鸽巢问题|人教版 (5)一、教学内容今天我们要学习的是人教版六年级下册数学的第五章第一节《数学广角——鸽巢问题》。
这一节主要让我们了解鸽巢问题的概念,学会用一种全新的思路去解决问题。
我们会通过生活中的实例,了解鸽巢问题的实质,以及如何运用它来解决实际问题。
二、教学目标通过这一节课的学习,我希望同学们能够理解并掌握鸽巢问题的解题思路,能够运用它来解决实际问题。
同时也希望同学们能够提高自己的逻辑思维能力,增强自己的解决问题的能力。
三、教学难点与重点本节课的重点是让学生理解并掌握鸽巢问题的解题思路。
难点在于如何让学生理解并接受这种全新的解决问题的方法。
四、教具与学具准备为了更好地进行课堂教学,我已经准备好了相关的教具和学具,包括PPT、鸽巢模型等。
五、教学过程1. 通过一个实际问题引入:假设有一个鸽巢,里面有n只鸽子,我们要如何计算出最多能有多少只鸽子在同一个鸽巢里?2. 引导学生思考,尝试用自己的方法解决问题。
3. 引导学生发现,当我们解决问题的方法不够科学时,可能会得出错误的结论。
4. 引入鸽巢问题的概念,讲解鸽巢问题的解题思路。
5. 通过例题讲解,让学生理解并掌握鸽巢问题的解题思路。
6. 通过随堂练习,让学生运用所学的知识解决实际问题。
六、板书设计板书设计主要包括鸽巢问题的定义、解题思路等关键信息。
七、作业设计作业题目:1. 如果有5只鸽子,最多能有多少只鸽子在同一个鸽巢里?2. 如果有10只鸽子,最多能有多少只鸽子在同一个鸽巢里?答案:1. 5只鸽子2. 10只鸽子八、课后反思及拓展延伸通过这一节课的学习,我发现同学们对鸽巢问题的理解还有待提高。
在今后的教学中,我需要更加深入地引导同学们理解并掌握鸽巢问题的解题思路,提高他们的解决问题的能力。
同时,我也可以尝试引入更多实际问题,让学生更好地理解鸽巢问题的应用。
重点和难点解析一、实际问题引入在教学过程中,我使用了实际问题引入的方法,这是非常重要的一个步骤。
六下(人教)第五单元数学广角——鸽巢问题(抽屉原理)(附答案)

第五单元数学广角——鸽巢问题(抽屉原理)一、最不利原则:为了保证能完成一件事情,需要考虑在最倒霉(最不利)的情况下,如何能达到目标。
二、抽屉原理:形式1:把n+1个苹果放到n个抽屉中,一定有2个苹果放在一个抽屉里;形式2:把m×n+1个苹果放到n个抽屉中,一定有m+1个苹果放在一个抽屉里。
模块一抽屉原理【例题1】把3个苹果放到两个抽屉中,有()种放法。
【练习1】把4支铅笔放进3个笔筒中,有()种放法。
【例题2】把8个桃子放到7个果盘里,一定有一个果盘里至少放进了()桃子。
【练习2】把7本书放进6个抽屉,不管怎么放,总有一个抽屉里至少放进()本书。
【例题3】五年级一班有28个学生,保证至少有几个同学在同一个月出生?【练习3】在任意25个人中,至少有几个人的星座相同?【例题4】把25个玻璃球最多放进几个盒子里,才能保证至少有一个盒子里有5个玻璃球?【练习4】把17本书最多放到()个空书架上,才能保证至少有一个书架上有5本书。
【例题5】平安路小学组织862名同学去参观甲、乙、丙3处景点。
规定每名同学至少参观一处,最多可以参观两处,至少有多少名同学参观的景点相同?【练习5】中国奥运代表团的173名运动员到超市买饮料,已知超市有可乐、雪碧、芬达、橙汁、味全和矿泉水6种饮料,每人各买两种不同的饮料,那么至少多少人买的饮料完全相同?【例题6】国庆嘉年华共有5项游艺活动,每个学生至多参加2项,至少参加1项。
那么至少有多少个学生,才能保证至少有4个人参加的活动完成相同?【练习6】桂苑小学六年级每名学生都订阅了《数学小灵通》、《小学生作文》、《英语天地》、《科学画报》这4种报刊中的2种,他们当中至少有34名学生订阅的报刊种类相同。
你知道桂苑小学六年级至少有多少名学生吗?【例题7】从1,2,3,……,21这些自然数中,最多可以取出多少个数,使得其中每两个数的差都不等于4?【练习7】1至70这70个自然数中,最多可以取出多少个数,使得其中每两个数的差都不等于6?【例题8】从1,4,7,10,……37,40这14个自然数,至少任取多少个数才能保证其中至少有2个数的和是41?【练习8】从1到50这50个自然数中,至少选出多少个数,才能保证其中一定有两个数的和是50?【例题9】从1到100这100个自然数中,至少选出多少个数才能保证其中一定有两个数的和是7的倍数?如果要保证是6的倍数呢?【练习9】从1至99这99个自然数中任意取出一些数,要保证其中一定有两个数的和是5的倍数,至少要取多少个?【例题10】某省有4千万人口,每个人的头发根数不超过15万根,那么该省中至少有多少人的头发根数一样多?【练习10】49名同学共同参加体操表演,其中最小的8岁,最大的11岁。
人教版六年级下数学数学广角——鸽巢问题

人教版六年级下数学数学广角——鸽巢问题第十二周数学广角——鸽巢问题鸽巣原理是一个重要而又基本的组合原理,在解决数学问题时有非常重要的作用。
鸽巣原理的最简单表达形式是:物体个数÷鸽巣个数=商……余数,至少个数=商+1.举例来说,如果有3个苹果放在2个盒子里,共有四种不同的放法,但无论哪一种放法,都可以说“必有一个盒子放了两个或两个以上的苹果”。
类似的,如果有5只鸽子飞进四个鸽笼里,那么一定有一个鸽笼飞进了2只或2只以上的鸽子。
如果有6封信,任意投入5个信箱里,那么一定有一个信箱至少有2封信。
摸2个同色球的计算方法是:要保证摸出两个同色的球,摸出的球的数量至少要比颜色数多1.物体数=颜色数×(至少数-1)+1.另外,可以使用极端思想:用最不利的摸法先摸出两个不同颜色的球,再无论摸出一个什么颜色的球,都能保证一定有两个球是同色的。
在填空题中,可以通过运用鸽巣原理来解决问题。
例如,鱼岳三小六年级有30名学生是二月份出生的,那么六年级至少有3名学生的生日是在二月份的同一天。
又如,有3个同学一起练投篮,如果他们一共投进16个球,那么一定有1个同学至少投进了6个球。
把6只鸡放进5个鸡笼,至少有2只鸡要放进同1个鸡笼里。
某班有个小书架,40个同学可以任意借阅,小书架上至少要有14本书,才可以保证至少有1个同学能借到2本或2本以上的书。
在解决问题时,我们可以运用鸽巣原理来求解。
例如,六(1)班有50名同学,至少有6名同学是同一个月出生的。
书籍里混装着3本故事书和5本科技书,要保证一次一定能拿出2本科技书,一次至少要拿出4本书。
把16支铅笔最多放入3个铅笔盒里,可以保证至少有1个铅笔盒里的铅笔不少于6支。
在拓展应用中,我们可以通过鸽巣原理来解决更加复杂的问题。
例如,把27个球最多放在4个盒子里,可以保证至少有1个盒子里有7个球。
教师引导学生规范解答:2、假设先取5只,全是红的,不符合题意,要继续取;假设再取5只,5只有全是黄的,这时再取一只一定是蓝色的,这样取5×2+1=11(只)可以保证每种颜色至少有1只。
人教版六年级下册数学第五单元《数学广角》鸽巢问题

人教版六年级下册数学第五单元《数学广角 》
2)如果把158个苹果放进 3个抽屉里,不管怎么放, 总有一个抽屉里至少有几 个苹果?
精品课件
抽屉原理(二)
把 a 个 物 体 放 进 n 个 抽 屉,若a÷n=b……c
(c≠0 ,c<n )
则一定有一个抽屉至少 放了______ 个物体。 精品课件
比一比:两个抽屉原理有 何区别?
“原理1”和“原理2”的区别 是:原理1苹果多,抽屉少,数 量比较接近;原理2虽然也是 苹果多,抽屉少,但是数量相 差较大,苹果个数比抽屉个数 的几倍还多几。
2、从任意5双手套中任取6只,其中至少有2只 恰为一双手套 ,对吗?
3、从数1,2,。。。,10中任取6个数,其中 至少有2个数为奇偶性相同。
4、体育用品仓库里有许多足球、排球和篮球, 某班 50名同学来仓库拿球,规定每个人至少拿 1个球,至多拿2个球,问至少有几名同学所 拿的球种类是一致的?
精品课件
例:把一些铅笔放进3个文具盒中,保证其中 一个文具盒至少有4枝铅笔,原来至少有多少
枝铅笔?至少:只有一个文具盒有 4 枝,
其余都是(4-1)枝
3 +1
3
3
3
3×(4-1)+1=10(枝)
求总数=抽屉×(至少-1)+1
要分的份精数品课件 其中一个多1
鸽巢问题 (二)
六年级下册数学广角鸽巢问题

1
把4支铅笔放进3个笔筒中,不管怎么放,总
有一个笔筒里至少有2 支铅笔。
“总有”和“至少” 是什么意思?
为什么呢?
“总有”就是说“一定有一个笔筒。 “至少”就是说“不少于2支,可能是2支,也可能多于2支”。
第一种:
我们可以摆一摆。
0 0
第二种:
我们可以摆一摆。
0
第三种:
我们可以摆一摆。
0
第四种:
把四种颜色看作4个抽屉,把取出的球看作物品,那 么至少取4+1=5个球可以保证取到两个颜色相同的 球。
5.任意给出3个不同的自然数,其中一定有2个数的和 是偶数,请说明理由。
因为自然数可以分成奇数、偶数两类。把奇数、偶数看作两 个抽屉,把任意给出的3个不同自然数看作3个物品。至少有 一个抽屉里放了两个数。又因为奇数+奇数=偶数,偶数+偶 数=偶数,所以,任意给出3个不同的自然数,其中一定有2个 数的和是偶数。
假如1个鸽笼里飞进1只鸽子,3个鸽笼最多飞进3只 鸽子,还剩下2只鸽子,所以,无论怎么飞,总有1 个鸽笼里至少飞进2只鸽子。
做一做2
我给大家表演一个“魔术”。 一副牌,取出大小王,还剩 52 张牌,你们5 人每人随意 抽一张,我知道至少有2 张 牌是同花色的。
你理解上面扑克牌魔术的道理了吗?
至少有2张牌是同花色。
六年级下册数学广角鸽巢问题
抽屉原理是组合数学中的一个重要原理,它最早由德国数学
家狄里克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原 理又称“狄里克雷原理”。抽屉原理有两个经典案例,一个是把10 个苹果放进9 个抽屉里,总有一个抽屉里至少放了2个苹果,所以这 个原理称作“抽屉原理”;另一个是6 只鸽子飞进5个鸽巢,总有一 个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
六年级下册数学教案-5.1 数学广角——鸽巢问题|人教版 (1)

六年级下册数学教案-5.1 数学广角——鸽巢问题|人教版 (1)教学目标:1. 理解鸽巢原理的基本概念,掌握其在数学中的应用。
2. 能够运用鸽巢原理解决实际问题,提升逻辑思维能力。
3. 培养学生对数学的兴趣,激发探究欲望。
教学内容:1. 鸽巢原理的引入2. 鸽巢原理的定义及证明3. 鸽巢原理的应用4. 练习与拓展教学步骤:一、引入(5分钟)1. 教师通过展示一些生活中的例子,如:10个苹果放入9个篮子,让学生观察并思考,是否会有一个篮子里放入两个或以上的苹果。
2. 学生通过观察和思考,得出结论:必定会有一个篮子里放入两个或以上的苹果。
二、定义及证明(15分钟)1. 教师给出鸽巢原理的定义:如果有n个鸽子,要放入m个巢中(n>m),那么至少有一个巢中会有两个或以上的鸽子。
2. 教师引导学生通过反证法来证明鸽巢原理。
三、应用(15分钟)1. 教师给出一些实际问题,如:有13个学生,要分配到4个小组中,请学生运用鸽巢原理来解决问题。
2. 学生通过运用鸽巢原理,得出结论:至少有一个小组中有4个或以上的学生。
四、练习与拓展(15分钟)1. 教师给出一些练习题,让学生独立完成。
2. 教师对学生的答案进行点评,并引导学生思考更深入的问题。
教学反思:通过本节课的教学,学生对鸽巢原理有了深入的理解,并能够运用其解决实际问题。
在教学过程中,教师应注重引导学生思考,激发学生的探究欲望,提升学生的逻辑思维能力。
同时,教师还应注重培养学生的数学兴趣,使其在学习中感受到数学的魅力。
需要重点关注的细节是“定义及证明”部分。
这部分内容是本节课的核心,理解鸽巢原理的定义和证明过程对于学生掌握鸽巢原理至关重要。
以下是对这个重点细节的详细补充和说明:二、定义及证明(15分钟)1. 鸽巢原理的定义:在数学中,鸽巢原理(也称为狄利克雷抽屉原理)是一个基础且重要的原理。
它的直观表述是:如果有n个鸽子要放入m个巢中,且n>m,那么至少有一个巢中会有两个或以上的鸽子。
六年级下册数学广角鸽巢问题

六年级下册数学广角鸽巢问题
# 一、鸽巢原理(抽屉原理)的基本概念
1. 定义
把多于公式个的物体放到公式个抽屉里,则至少有一个抽屉里的东西不少于两件。
例如:把公式个苹果放到公式个抽屉里,那么至少有一个抽屉里有公式个苹果。
2. 公式表示
如果物体数除以抽屉数有余数,那么至少有一个抽屉里的物体数等于商加上公式。
用字母表示为:物体数公式抽屉数公式(公式),至少数公式。
# 二、典型题目及解析
(一)简单的鸽巢问题
1. 题目
把公式本书放进公式个抽屉,不管怎么放,总有一个抽屉至少放进几本书?
2. 解析
首先计算公式,这里商是公式,余数是公式。
根据鸽巢原理,至少数公式。
也就是说,总有一个抽屉至少放进公式本书。
(二)求物体数的鸽巢问题
1. 题目
一个抽屉里放着若干个玻璃球,要保证有一个抽屉里至少有公式个玻璃球,那么玻璃球的总数至少有多少个?(这里假设抽屉数为公式个)
2. 解析
已知至少数是公式,抽屉数是公式。
根据公式至少数公式,可以推出公式。
那么物体数(玻璃球总数)至少为公式个。
(三)生活中的鸽巢问题
1. 题目
六(1)班有公式名学生,至少有几名学生的生日在同一个月?
2. 解析
一年有公式个月,相当于公式个抽屉,公式名学生相当于物体数。
公式,商是公式,余数是公式。
至少数公式。
所以至少有公式名学生的生日在同一个月。
人教版六年级下数学数学广角——鸽巢问题
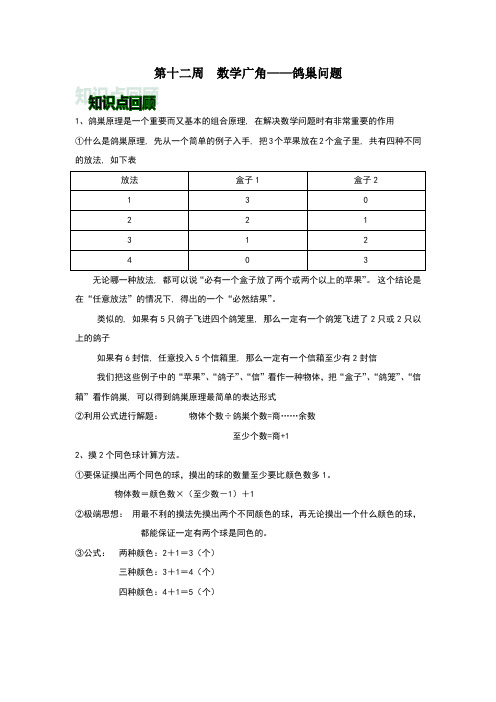
第十二周数学广角——鸽巢问题1、鸽巣原理是一个重要而又基本的组合原理, 在解决数学问题时有非常重要的作用①什么是鸽巣原理, 先从一个简单的例子入手, 把3个苹果放在2个盒子里, 共有四种不同的放法, 如下表无论哪一种放法, 都可以说“必有一个盒子放了两个或两个以上的苹果”。
这个结论是在“任意放法”的情况下, 得出的一个“必然结果”。
类似的, 如果有5只鸽子飞进四个鸽笼里, 那么一定有一个鸽笼飞进了2只或2只以上的鸽子如果有6封信, 任意投入5个信箱里, 那么一定有一个信箱至少有2封信我们把这些例子中的“苹果”、“鸽子”、“信”看作一种物体,把“盒子”、“鸽笼”、“信箱”看作鸽巣, 可以得到鸽巣原理最简单的表达形式②利用公式进行解题:物体个数÷鸽巣个数=商……余数至少个数=商+12、摸2个同色球计算方法。
①要保证摸出两个同色的球,摸出的球的数量至少要比颜色数多1。
物体数=颜色数×(至少数-1)+1②极端思想:用最不利的摸法先摸出两个不同颜色的球,再无论摸出一个什么颜色的球,都能保证一定有两个球是同色的。
③公式:两种颜色:2+1=3(个)三种颜色:3+1=4(个)四种颜色:4+1=5(个)1、填一填:(1)鱼岳三小六年级有30名学生是二月份(按28天计算)出生的,六年级至少有()名学生的生日是在二月份的同一天。
(2)有3个同学一起练习投篮,如果他们一共投进16个球,那么一定有1个同学至少投进了()个球。
(3)把6只鸡放进5个鸡笼,至少有()只鸡要放进同1个鸡笼里。
(4)某班有个小书架,40个同学可以任意借阅,小书架上至少要有()本书,才可以保证至少有1个同学能借到2本或2本以上的书。
学生独立思考解答,集体交流纠正。
2、解决问题。
(1)(易错题)六(1)班有50名同学,至少有多少名同学是同一个月出生的?(2)书籍里混装着3本故事书和5本科技书,要保证一次一定能拿出2本科技书。
一次至少要拿出多少本书?(3)把16支铅笔最多放入几个铅笔盒里,可以保证至少有1个铅笔盒里的铅笔不少于6支?3、拓展应用1、把27个球最多放在几个盒子里,可以保证至少有1个盒子里有7个球?教师引导学生分析:盒子数看作抽屉数,如果要使其中1个抽屉里至少有7个球,那么球的个数至少要比抽屉数的(7-1)倍多1个,而(27-1)÷(7-1)=4...2,因此最多放进4个盒子里,可以保证至少有1个盒子里有7个球。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、把6根铅笔放进5个杯子里,总有一个 杯子里至少放进( 2)根铅笔。
2、把7根铅笔放进6个杯子里,总有一个杯子 里至少放进( 2 )根铅笔? 把8根铅笔放进7个杯子里呢?
把9根铅笔放进8个杯子里呢? ……
把100根铅笔放进99个杯子里呢? ……
3、把5根铅笔放进3个杯子里,总有一 个杯子里至少放进( 2 )根铅笔。
人教版六年级下册——鸽巢问题
游戏规则:
老师宣布开始,4位同学就围着凳 子转圈,老师喊“停”的时候,四个人 每个人都必须坐在凳子上。准备好了 吗?
学习目标
1.理解最简单的“鸽巢问题”及“鸽 巢问题”的一般形式。 2. 让学生采用操作的方法进行枚举 及假设探究“鸽巢问题”。 3.会用“鸽巢问题”解决简单的实 际问题。
总结全课:
认真分析,先找出在每一道题中的“待分物体及 其数量”和“抽屉及其数量”,再平均分。
7只鸽子飞回5个鸽舍,至少有( 2 ) 只鸽子要飞进同一个鸽舍。为什么?
7÷5=1……2
8只鸽子飞回3个鸽舍,至少有( 3 ) 只鸽子要飞进同一个鸽舍。为什么?
8÷3=2……2
1、 三个小朋友同行,其中必有 两个小朋友性别相同,为什么?
相当于“2个抽屉” “两种性别”
相当于“3个待分物体” “三个小朋友”
1、把3根铅笔放进2个杯子里,有几 种方法?试试看。你有什么发现?
2、把4根铅笔放进3个杯子里,不管怎么 放,总有一个杯子里至少放进2根铅笔。 这是为什么?
2、把4根铅笔放进3个杯子里,不管怎么 放,总有一个杯子里至少放进2根铅笔。 这是为什么?
2、把4根铅笔放进3个杯子里,不管怎么 放,总有一个杯子里至少放进2根铅笔。 这是为什么?
2、 从全校学生中任意找 来13位同学,至少有两个人 属相相同,为什么?
“12个属相” 相当 “ 12个抽屉” 于 “13个人” 相当 “13个待分物体”
于
3、一副扑克牌(除去大小王)52张中有四种 花色,从中随意抽5张牌,无论怎么抽,为什 么总有两张牌是同一花色的?
铅笔 杯子 总有一个杯子里至少有 (商+1) 3 ÷ 2 = 1……1 2 4 ÷ 3 = 1……1 2 5 ÷ 4 = 1……1 2 6 ÷ 5 = 1……1 2 10 0 ÷ 9 9 = 1……1 2 ( n+1) ÷n =1 ……1 2 5 ÷ 3 = 1……2 2 5 ÷ 2 = 2……1 3 7 ÷ 2 = 3……1 4 15 ÷ 4 = 3……3 4 a ÷ n = b……c(c≠0) (b+1)
2、把4根铅笔放进3个杯子里,不管怎么 放,总有一个杯子里至少放进2根铅笔。 这是为什么?
2、把4根铅笔放进3个杯子里,不管怎么放, 总有一个杯子里至少放进2根铅笔。这是为什么? 2根以上 2根
不管怎么放,一定有一个杯子里放进了2根或2根以上。
平均分
把4根铅笔放进3个杯子里: 如果每个杯子里先各放1根铅笔,3个杯子中 最多放3根,剩下的1根不管放进哪一个杯子中, 总有一个杯子里至少放进2根铅笔。
3、(1) 把5本书进2个抽屉中,不管怎么放,总有一个 抽屉至少放进3本书。这是为什么?
5÷2=2……1
(3本)
(2) 把7本书进2个抽屉中,结果会怎样? (4本) 7÷2=3……1 (3) 把15本书进4个抽屉中,结果又会怎样? (4本) 15÷4=3……3
拓展资料
“抽屉原理”又称“鸽笼原理”, 最先是由19世纪的德国数学家狄利克 雷提出来的,所以又称“狄里克雷原 理”,也称为“鸽巢原理”。这一原 理在解决实际问题中有着广泛的应用。 “抽屉原理”的应用是千变万化的, 用它可以解决许多有趣的问题,并且 常常能得到一些令人惊异的结果。
