高考物理牛顿运动定律的应用(一)解题方法和技巧及练习题

合集下载

(物理)物理牛顿运动定律的应用练习题含解析

（物理）物理牛顿运动定律的应用练习题含解析一、高中物理精讲专题测试牛顿运动定律的应用1．如图，光滑水平面上静置一长木板A ，质量M =4kg ，A 的最前端放一小物块B （可视为质点），质量m =1kg ，A 与B 间动摩擦因数μ=0.2．现对木板A 施加一水平向右的拉力F ，取g =10m/s 2．则：（1）若拉力F 1=5N ，A 、B 一起加速运动，求A 对B 的静摩擦力f 的大小和方向；（2）为保证A 、B 一起加速运动而不发生相对滑动，求拉力的最大值F m （设最大静摩擦力与滑动摩擦力相等）；（3）若拉力F 2=14N ，在力F 2作用t =ls 后撤去，要使物块不从木板上滑下，求木板的最小长度L【答案】（1）f = 1N ，方向水平向右；（2）F m = 10N 。

（3）木板的最小长度L 是0.7m 。

【解析】【详解】（1）对AB 整体分析，由牛顿第二定律得：F 1=（M +m ）a 1 对B ，由牛顿第二定律得：f =ma 1联立解得f =1N ，方向水平向右；（2）对AB 整体，由牛顿第二定律得：F m =（M +m ）a 2对B ，有：μmg =ma 2联立解得：F m =10N（3）因为F 2＞F m ，所以AB 间发生了相对滑动，木块B 加速度为：a 2=μg =2m/s 2。

木板A 加速度为a 3，则：F 2-μmg =Ma 3解得：a 3=3m/s 2。

1s 末A 的速度为：v A =a 3t =3m/s B 的速度为：v B =a 2t =2m/s 1s 末A 、B 相对位移为：△l 1=2A Bv v t -=0.5m 撤去F 2后，t ′s 后A 、B 共速对A ：-μmg =Ma 4可得：a 4=-0.5m/s 2。

共速时有：v A +a 4t ′=v B +a 2t ′可得：t ′=0.4s 撤去F 2后A 、B 相对位移为：△l 2='2A Bv v t -=0.2m 为使物块不从木板上滑下，木板的最小长度为：L =△l 1+△l 2=0.7m 。

(物理)物理牛顿运动定律的应用练习题及答案及解析

（物理）物理牛顿运动定律的应用练习题及答案及解析一、高中物理精讲专题测试牛顿运动定律的应用1．如图，有一质量为M=2kg的平板车静止在光滑的水平地面上，现有质量均为m=1kg的小物块A和B（均可视为质点），由车上P处开始，A以初速度=2m/s向左运动，同时B 以=4m/s向右运动，最终A、B两物块恰好停在小车两端没有脱离小车，两物块与小车间的动摩擦因数都为μ=0.1，取，求：（1）开始时B离小车右端的距离；（2）从A、B开始运动计时，经t=6s小车离原位置的距离。

【答案】（1）B离右端距离（2）小车在6s内向右走的总距离：【解析】(1)设最后达到共同速度v，整个系统动量守恒，能量守恒解得：，A离左端距离，运动到左端历时，在A运动至左端前，木板静止，，解得B离右端距离(2)从开始到达共速历时，，，解得小车在前静止，在至之间以a向右加速：小车向右走位移接下来三个物体组成的系统以v共同匀速运动了小车在6s内向右走的总距离：【点睛】本题主要考查了运动学基本公式、动量守恒定律、牛顿第二定律、功能关系的直接应用，关键是正确分析物体的受力情况，从而判断物体的运动情况，过程较为复杂.2．如图所示，长木板质量M=3 kg，放置于光滑的水平面上，其左端有一大小可忽略，质量为m=1 kg的物块A，右端放着一个质量也为m=1 kg的物块B，两物块与木板间的动摩擦因数均为μ=0.4，AB之间的距离L=6 m，开始时物块与木板都处于静止状态，现对物块A施加方向水平向右的恒定推力F 作用，取g=10 m/s 2．（1）.为使物块A 与木板发生相对滑动，F 至少为多少？（2）.若F=8 N ，求物块A 经过多长时间与B 相撞，假如碰撞过程时间极短且没有机械能损失，则碰后瞬间A 、B 的速度分别是多少？【答案】（1）5 N （2）v A’=2m/s v B’=8m/s 【解析】【分析】【详解】（1）据分析物块A 与木板恰好发生相对滑动时物块B 和木板之间的摩擦力没有达到最大静摩擦力．设物块A 与木板恰好发生相对滑动时，拉力为F 0，整体的加速度大小为a ，则：对整体： F 0=（2m +M ）a 对木板和B ：μmg =（m +M ）a 解之得： F 0=5N即为使物块与木板发生相对滑动，恒定拉力至少为5 N ；（2）物块的加速度大小为：24A F mga m s mμ-==∕ 木板和B 的加速度大小为：B mga M m=+μ=1m/s 2设物块滑到木板右端所需时间为t ，则：x A -x B =L即221122A B a t a t L -= 解之得：t =2 s v A =a A t=8m/s v B =a B t=2m/sAB 发生弹性碰撞则动量守恒：mv a +mv B =mv a ＇+mv B ＇机械能守恒：12mv a 2+12mv B 2=12mv a ＇2+12mv B ＇2 解得：v A ＇=2m/s v B ＇=8m/s3．如图所示，有1、2、3三个质量均为m =1kg 的物体，物体2与物体3通过不可伸长轻绳连接，跨过光滑的定滑轮，设长板2到定滑轮足够远，物体3离地面高H =5.75m ，物体1与长板2之间的动摩擦因数μ=O .2.长板2在光滑的桌面上从静止开始释放，同时物体1(视为质点)在长板2的左端以v =4m/s 的初速度开始运动，运动过程中恰好没有从长板2的右端掉下．(取g =10m/s²)求： (1)长板2开始运动时的加速度大小；(2)长板2的长度0L ；(3)当物体3落地时，物体1在长板2的位置．【答案】（1）26m /s （2）1m （3）1m 【解析】【分析】【详解】设向右为正方向（1）物体1： -μmg = ma 1 a 1=–μg = -2m/s 2 物体2：T +μmg = ma 2 物体3：mg –T = ma 3 且a 2= a 3由以上两式可得：22g ga μ+==6m/s 2 （2）设经过时间t 1二者速度相等v 1=v +a 1t=a 2t 代入数据解t 1=0．5s v 1=3m/s112v v x t +==1．75m 122v tx ==0．75m 所以木板2的长度L 0=x 1-x 2=1m（3）此后，假设物体123相对静止一起加速 T =2m a mg —T =ma 即mg =3m a 得3g a =对1分析：f 静=ma =3．3N ＞F f =μmg =2N ，故假设不成立，物体1和物体2相对滑动物体1： a 3=μg =2m/s 2 物体2：T —μmg = ma 4 物体3：mg –T = ma 5 且a 4= a 5 得：42g ga μ-==4m/s 2 整体下落高度h =H —x 2=5m 根据2124212h v t a t =+解得t 2=1s物体1的位移23123212x v t a t =+=4m h -x 3=1m 物体1在长木板2的最左端【点睛】本题是牛顿第二定律和运动学公式结合，解题时要边计算边分析物理过程，抓住临界状态：速度相等是一个关键点．4．如图所示，从A 点以v 0=4m/s 的水平速度抛出一质量m =1kg 的小物块（可视为质点），当物块运动至B 点时，恰好沿切线方向进入固定在地面上的光滑圆弧轨道BC ，其中轨道C 端切线水平。

历年高考物理力学牛顿运动定律题型总结及解题方法

历年高考物理力学牛顿运动定律题型总结及解题方法单选题1、现在城市的滑板运动非常流行，在水平地面上一名滑板运动员双脚站在滑板上以一定速度向前滑行，在横杆前起跳并越过杆，从而使人与滑板分别从杆的上方、下方通过，如图所示，假设人和滑板运动过程中受到的各种阻力忽略不计，若运动员顺利地完成了该动作，最终仍落在滑板原来的位置上，则下列说法错误的是（）A．运动员起跳时，双脚对滑板作用力的合力竖直向下B．起跳时双脚对滑板作用力的合力向下偏后C．运动员在空中最高点时处于失重状态D．运动员在空中运动时，单位时间内速度的变化相同答案：B解析：AB．运动员竖直起跳，由于本身就有水平初速度，所以运动员既参与了水平方向上的匀速直线运动，又参与了竖直上抛运动。

各分运动具有等时性，水平方向的分运动与滑板的运动情况一样，运动员最终落在滑板的原位置。

所以水平方向受力为零，则起跳时，滑板对运动员的作用力竖直向上，运动员对滑板的作用力应该是竖直向下，故A正确，不符合题意；B错误，符合题意；C．运动员在空中最高点时具有向下的加速度g，处于失重状态，故C正确，不符合题意；D．运动员在空中运动时，加速度恒定，所以单位时间内速度的变化量相等，故D正确，不符合题意。

故选B。

2、如图所示，物体静止于水平面上的O点，这时弹簧恰为原长l0，物体的质量为m，与水平面间的动摩擦因数为μ，现将物体向右拉一段距离后自由释放，使之沿水平面振动，下列结论正确的是（）A．物体通过O点时所受的合外力为零B．物体将做阻尼振动C．物体最终只能停止在O点D．物体停止运动后所受的摩擦力为μmg答案：B解析：A．物体通过O点时弹簧的弹力为零，但摩擦力不为零，A错误；B．物体振动时要克服摩擦力做功，机械能减少，振幅减小，做阻尼振动，B正确；CD．物体最终停止的位置可能在O点也可能不在O点。

若停在O点摩擦力为零，若不在O点，摩擦力和弹簧的弹力平衡，停止运动时物体所受的摩擦力不一定为μmg，CD错误。

高考物理牛顿运动定律的应用常见题型及答题技巧及练习题(含答案)含解析

高考物理牛顿运动定律的应用常见题型及答题技巧及练习题(含答案)含解析一、高中物理精讲专题测试牛顿运动定律的应用1．如图所示，质量为2kg 的物体在与水平方向成37°角的斜向上的拉力F 作用下由静止开始运动．已知力F 的大小为5N ，物体与地面之间的动摩擦因数μ为0.2，（sin37°=0.6，cos37°=0.8）求：(1)物体由静止开始运动后的加速度大小；(2)8s 末物体的瞬时速度大小和8s 时间内物体通过的位移大小； (3)若8s 末撤掉拉力F ，则物体还能前进多远？【答案】(1)a =0.3m/s 2 (2)x =9.6m (3)x ′=1.44m 【解析】(1)物体的受力情况如图所示：根据牛顿第二定律，得: F cos37°-f =ma F sin37°+F N =mg 又f =μF N联立得：a =cos37(sin 37)F mg F mμ--o o代入解得a =0.3m/s 2(2)8s 末物体的瞬时速度大小v =at =0.3×8m/s=2.4m/s 8s 时间内物体通过的位移大小219.6m 2x at == (3)8s 末撤去力F 后，物体做匀减速运动，根据牛顿第二定律得，物体加速度大小22.0m/s f mg a g m mμμ===='' 由v 2=2a ′x ′得:21.44m 2v x a =''=【点睛】本题关键是多次根据牛顿第二定律列式求解加速度，然后根据运动学公式列式求解运动学参量．2．如图，质量M=4kg 的长木板静止处于粗糙水平地面上，长木板与地面的动摩擦因数μ1=0.1，现有一质量m=3kg 的小木块以v 0=14m/s 的速度从一端滑上木板，恰好未从木板上滑下，滑块与长木板的动摩擦因数μ2=0.5，g 取10m/s 2，求：（1）木块刚滑上木板时，木块和木板的加速度大小；（2）木板长度；（3）木板在地面上运动的最大位移。

高中物理牛顿运动定律的应用试题(有答案和解析)及解析

高中物理牛顿运动定律的应用试题(有答案和解析)及解析一、高中物理精讲专题测试牛顿运动定律的应用1．质量为m =0.5 kg 、长L =1 m 的平板车B 静止在光滑水平面上，某时刻质量M =l kg 的物体A （视为质点）以v 0=4 m/s 向右的初速度滑上平板车B 的上表面，在A 滑上B 的同时，给B 施加一个水平向右的拉力．已知A 与B 之间的动摩擦因数μ=0.2，重力加速度g 取10 m/s 2．试求：（1）如果要使A 不至于从B 上滑落，拉力F 大小应满足的条件；（2）若F =5 N ，物体A 在平板车上运动时相对平板车滑行的最大距离．【答案】(1)1N 3N F ≤≤ (2)0.5m x ∆= 【解析】【分析】物体A 不滑落的临界条件是A 到达B 的右端时，A 、B 具有共同的速度，结合牛顿第二定律和运动学公式求出拉力的最小值．另一种临界情况是A 、B 速度相同后，一起做匀加速直线运动，根据牛顿第二定律求出拉力的最大值，从而得出拉力F 的大小范围．【详解】(1)物体A 不滑落的临界条件是A 到达B 的右端时，A 、B 具有共同的速度v 1，则：222011-22A Bv v v L a a =＋又： 011-=A Bv v v a a 解得：a B =6m/s 2再代入F ＋μMg =ma B 得：F =1N若F <1N ，则A 滑到B 的右端时，速度仍大于B 的速度，于是将从B 上滑落，所以F 必须大于等于1N当F 较大时，在A 到达B 的右端之前，就与B 具有相同的速度，之后，A 必须相对B 静止，才不会从B 的左端滑落，则由牛顿第二定律得：对整体：F =(m ＋M )a 对物体A ：μMg =Ma 解得：F =3N若F 大于3N ，A 就会相对B 向左滑下综上所述，力F 应满足的条件是1N≤F ≤3N(2)物体A 滑上平板车B 以后，做匀减速运动，由牛顿第二定律得：μMg =Ma A 解得：a A =μg =2m/s 2平板车B 做匀加速直线运动，由牛顿第二定律得：F ＋μMg =ma B 解得：a B =14m/s 2两者速度相同时物体相对小车滑行最远，有：v 0－a A t =a B t 解得：t =0.25s A 滑行距离 x A =v 0t －12a A t 2=1516m B 滑行距离：x B =12a B t 2=716m 最大距离：Δx =x A －x B =0.5m 【点睛】解决本题的关键理清物块在小车上的运动情况，抓住临界状态，结合牛顿第二定律和运动学公式进行求解．2．如图所示为货场使用的传送带的模型，传送带倾斜放置，与水平面夹角为37θ=︒，传送带AB 足够长，传送带以大小为2m/s υ=的恒定速率顺时针转动。

高考物理复习：牛顿定律在直线运动中的应用

专题(1)牛顿定律在直线运动中的应用一、大纲解读：本专题的教学要求1、知道机械运动、质点、参考系的概念，能在具体物理问题中正确使用质点模型。

（对相对参考系不作要求）2、能区分位移与路程，理解位移的矢量性。

3、理解速度的概念，知道速度和速率的区别，掌握匀速直线运动的条件、规律，理解图象的物理意义并能应用图象解决实际问题。

4、能用平均速度公式求解、判断实际问题，能正确区分平均速度与瞬时速度。

5、掌握加速度的定义和内涵，能结合实际、灵活运用匀变速直线运动的规律及推论解决问题，会运用图象分析问题。

6、理解牛顿第一定律，理解惯性，了解伽利略的理想实验方法。

7、理解牛顿第三定律，能正确区分作用力、反作用力和平衡力。

8、掌握牛顿第二定律并能正确应用于实际问题，了解牛顿运动定律的适用范围和局限性。

（不要求求解加速度不同的连接体问题）二、重点剖析：本专题重点有：1、速度、位移、加速度的矢量性及运算公式的运用。

2、直线运动中的追及问题，特别要注意追及问题中的临界条件。

3、利用图象（s-t、v-t），从速度、位移的角度分析运动的物理过程并处理相关问题。

4、灵活运用牛顿第二定律和运动学公式分析解决问题。

5、电荷在匀强电场、匀强磁场、电磁场及复合场中的直线运动问题的处理。

本专题难点有：1、运用运动学图象处理实际问题。

2、综合运用牛顿第二定律和运动学公式处理复杂过程问题。

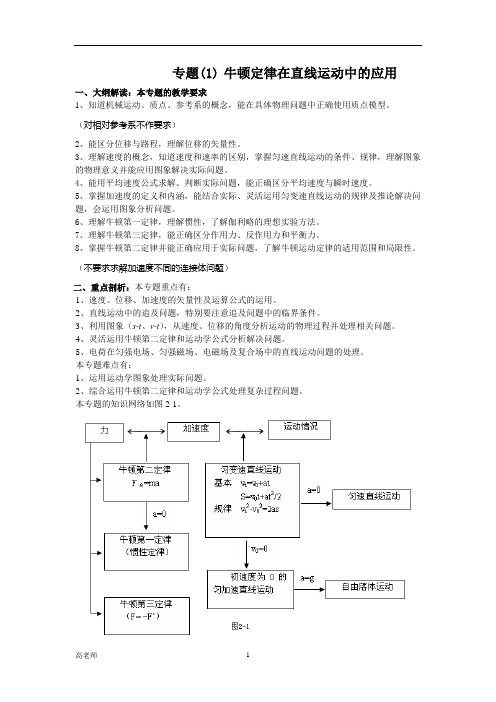
本专题的知识网络如图2-1。

三、考点透视：1、质点、参考系、位移和路程【例题1】关于质点及其位移和路程的说法中正确的是（）A. 位移是矢量，位移的方向即质点运动的方向B. 不论物体的质量多大，只要物体的尺寸跟物体间距相比甚小时，就可以看成质点C.只有低速运动的物体才可看成质点，高速运动的物体不可看作质点D. 物体通过的路程不等，位移可能相同解析：一个实际物体能否看成质点，跟它体积的绝对大小、质量的多少以及运动速度的高低无关，决定于物体的尺寸与物体间距相比的相对大小.例如，地球可称得上是个庞然大物，其直径约为1.28×107 m，质量达到6×1024kg，在太空中绕太阳运动的速度每秒几百米.由于其直径与地球离太阳的距离（约1.5×1011m）相比甚小，因此在研究地球的公转运动时，完全可以忽略地球的形状、大小及地球自身的运动，把它看成一个质点.位移是表示物体位置变化的物理量，它是矢量，其方向由质点初位置指向末位置，其大小是连接质点始、末位置线段的长度。

物理牛顿运动定律的应用练习题20篇及解析

对
B： a2' /
s2
经分析，B 先停止运动，A 最后恰滑至 B 的最右端时速度减为零，故 v2 v2 L 2a1 2a2 ' 2
【详解】
（1）A、B 间恰要相对滑动的临界条件是二者间达到最大静摩擦力，
对 A，由牛顿第二定律可知，加速度 a 1g 2m / s2 ；
对 B，由牛顿第二定律可知， Fmin 2 m M g 1mg Ma ，
/
解得 Fmin 18N
（2）F=20N>18N，二者间会相对滑动，对 B，由牛顿第二定律；
（1）若 A、B 间相对滑动，F 的最小值；
（2）当 F=20N 时，若 F 的作用时间为 2s，此时 B 的速度大小；
/
（3）当 F=16N 时，若使 A 从 B 上滑下，F 的最短作用时间．
【答案】（1） Fmin 18N （2） v2 20m / s （3） t2 1.73s
【解析】
【分析】
（1）对铅块、木板根据牛顿第二定律求解加速度大小；（2）从开始到滑落过程，铅块和木板的位移之差等于 L，求解时间；（3）根据两种临界态：到右端恰好共速以及共速后不能从左侧滑下求解力 F 的范围；【详解】
（1）铅块： 1mg ma1
解得 a1=4m/s2；对木板： 1mg 2 (M m)g Ma2 解得 a2=2m/s2
1 2
a1t12
1 2
a2t12
1.25m
撤掉 F 后：物块相对于木板上滑，加速度仍未 a1=8m/s2，减速上滑
而木板： Mg sin 2 (M m)g cos 1mg cos Ma2
则： a2 12m/s2 ，方向沿斜面向下，减速上滑
由于： Mg sin 1mg cos 2 (M m)g cos

2023年高考物理一轮复习《牛顿运动定律的综合应用(练)》含答案解析

3.2 牛顿运动定律的综合应用1．已知列车向左做直线运动，某同学为了研究列车在水平直轨道上的运动情况，他在列车车厢顶部用细线悬挂一个小球。

某段时间内，细线偏离竖直方向一定角度θ，并相对车厢保持静止，如图所示，重力加速大小为g，则列车在这段时间内（）A．水平向右做匀速直线运动B．列车速度正在变大C．列车加速度的大小为g tanθ，方向水平向右D．加速度的大小为gsinθ，方向水平向左【答案】C【解析】A．对小球受力分析可知小球所受合力方向向右具有向右的加速度，列车与小球相对静止，不可能做匀速直线运动，A错误；B．列车与小球相对静止做匀变速直线运动，列车的运动方向未知可能做匀加速运动也可能做匀减速运动，B 错误；C 、D．小球所受合力方向向右具有向右的加速度，由牛顿第二定律得θ=mg matan得=tana gθC正确，D错误；故选C。

2．如图所示，一足够长的斜面固定在地面上，其倾角为37°。

一质量为1kg的物体（可视为质点）放在斜面上，恰好能保持静止。

现对物体施加一沿斜面向上的外力F，大小为14N，重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8，则下列说法中正确的是（）A ．物体仍静止在斜面上B ．物体将向上做匀加速直线运动，加速度大小为4m/s 2C ．外力F 作用3s 末时，物体的速度为6m/sD ．物体与斜面间的动摩擦因数为0.5【答案】C 【解析】D ．物体放在斜面上，恰好能保持静止，则o osin 37cos37mg mg μ=解得0.75μ=故D 错误；AB ．施加拉力F 后，由牛顿第二定律得o o sin 37cos37F mg mg maμ--=解得22m/s a =施加一沿斜面向上的外力F 时，物体以22m/s 的加速度做匀加速直线运动，故AB 错误；C ．外力F 作用3s 末时，物体的速度为6m/sv at ==故C 正确。

高中物理必修一第四章第五节牛顿运动定律的应用

针对训练1
一质量为m＝2 kg的滑块在倾角为θ＝30°的足够长的固定斜面上在无外力F的情况下以加速度a＝ 2.5 m/s2匀加速下滑.若用一水平向右的恒力F作用于滑块，如图所示，使滑块由静止开始沿斜面向上做匀加速直线运动，在0～2 s时间内沿斜面运动的位移s＝4 m.求：(g取10 m/s2) (1)滑块和斜面之间的动摩擦因数μ；
答案 0.5 30 N
设力F作用时物体的加速度为a1，对物体进行受力分析，由牛顿第二定律可知： F－mgsin 37°－μmgcos 37° ＝ma1，撤去力F后，物体的加速度大小为a2，由牛顿第二定律有 mgsin 37°＋μmgcos 37°＝ma2，根据v－t图像的斜率表示加速度可知a1＝20 m/s2，a2＝10 m/s2，联立解得μ＝0.5，F＝30 N.
(1)滑雪者受到雪面的支持力大小；答案 400 N
滑雪者在雪坡上受力如图所示，建立如图所示的直角坐标系， FN＝mgcos 37°＝400 N.
(2)滑雪者受到的阻力大小. 答案 100 N
由v－t图像可得滑雪者的加速度大小， a＝v2－t v1＝4 m/s2，
根据牛顿第二定律，mgsin 37°－f＝ma，得f＝mgsin 37°－ma＝100 N.
(2)人在离C点多远处停下.
答案 12.8 m
人在水平面上滑行时，水平方向只受到水平面的摩擦力作用.设人在水平面上运动的加速度大小为a′，由牛顿第二定律得μmg＝ma′ 设人到达C时的速度为v，则由匀变速直线运动规律得人在斜坡下滑的过程：v2＝2aL 人在水平面上滑行时：0－v2＝－2a′s 联立解得s＝12.8 m.
(2)t＝3 s时物体的速度大小；
答案 0 t＝3 s时的速度v3＝v1－a2t＝20 m/s－10×2 m/s＝0，即t＝3 s时物体的速度为0.

(物理)物理牛顿运动定律的应用练习题含答案

（物理）物理牛顿运动定律的应用练习题含答案一、高中物理精讲专题测试牛顿运动定律的应用1．传送带与平板紧靠在一起，且上表面在同一水平面内，两者长度分别为L 1＝2.5 m 、L 2＝2 m ．传送带始终保持以速度v 匀速运动．现将一滑块（可视为质点）轻放到传送带的左端，然后平稳地滑上平板．已知：滑块与传送带间的动摩擦因数μ＝0.5，滑块与平板、平板与支持面的动摩擦因数分别为μ1＝0.3、μ2＝0.1，滑块、平板的质量均为m ＝2 kg ，g 取10 m/s 2.求：（1）若滑块恰好不从平板上掉下，求滑块刚滑上平板时的速度大小；（2）若v ＝6 m/s ，求滑块离开平板时的速度大小．【答案】（1）4/m s （2）3.5/m s 【解析】【详解】(1)滑块在平板上做匀减速运动，加速度大小：a 1＝1mgmμ＝3 m/s 2由于μ1mg>2μ2mg故平板做匀加速运动，加速度大小：a 2＝122mg mgmμμ-⨯＝1 m/s 2设滑块滑至平板右端用时为t ，共同速度为v′，平板位移为x ，对滑块： v′＝v －a 1t(1分)L 2＋x ＝vt －12a 1t 2 对平板：v′＝a 2tx ＝12a 2t 2 联立以上各式代入数据解得：t ＝1 s ，v ＝4 m/s. (2)滑块在传送带上的加速度：a 3＝mgmμ＝5 m/s 2若滑块在传送带上一直加速，则获得的速度为： v 1112a L 5 m/s<6 m/s 即滑块滑上平板的速度为5 m/s设滑块在平板上运动的时间为t′，离开平板时的速度为v″，平板位移为x′ 则v″＝v 1－a 1t′ L 2＋x′＝v 1t′－12a 1t′2 x′＝12a 2t′2联立以上各式代入数据解得：t′1＝12s ，t′2＝2 s(t′2>t ，不合题意，舍去) 将t′＝12s 代入v″＝v －a 1t′得：v″＝3.5 m/s.2．如图所示，长木板B 质量为m 2＝1．0 kg ，静止在粗糙的水平地面上，长木板左侧区域光滑．质量为m 3＝1．0 kg 、可视为质点的物块C 放在长木板的最右端．质量m 1＝0．5 kg 的物块A ，以速度v 0＝9 m ／s 与长木板发生正碰（时间极短），之后B 、C 发生相对运动．已知物块C 与长木板间的动摩擦因数μ1＝0．1，长木板与地面间的动摩擦因数为μ2＝0．2，最大静摩擦力等于滑动摩擦力，整个过程物块C 始终在长木板上，g 取10 m ／s 2．（1）若A 、B 相撞后粘在一起，求碰撞过程损失的机械能．（2）若A 、B 发生弹性碰撞，求整个过程物块C 相对长木板的位移．【答案】（1）13.5J （2）2.67m 【解析】（1）若A 、B 相撞后粘在一起，由动量守恒定律得1012()m v m m v =+由能量守恒定律得 22101211()22E m v m m v ∆=-+ 解得损失的机械能 21201213.52()m m v E J m m ∆==+ （2）A 、B 发生完全弹性碰撞，由动量守恒定律得101122m v m v m v =+由机械能守恒定律得222101122111222m v m v m v =+ 联立解得 1210123/m m v v m s m m -==-+， 1201226/m v v m s m m ==+之后B 减速运动，C 加速运动，B 、C 达到共同速度之前，由牛顿运动定律，对长木板： 2231321-()m m g m g m a μμ+-= 对物块C ： 1332m g m a μ=设达到共同速度过程经历的时间为t ，212v a t a t += 这一过程的相对位移为22121211322x v t a t a t m ∆=+-= B 、C 达到共同速度之后，因12μμ<，二者各自减速至停下，由牛顿运动定律，对长木板： 2231323-()m m g m g m a μμ++=对物块C ：1334-m g m a μ=这一过程的相对位移为 2222243()()1223a t a t x m a a ∆=-=-- 整个过程物块与木板的相对位移为 1282.673x x x m m ∆=∆-∆== 点睛：此题是多研究对象、多过程问题，过程复杂，分析清楚物体的运动过程，应用牛顿第二定律、运动学公式、动量守恒定律、机械能守恒定律即可正确解题．3．如图所示，质量为m=2kg 的物块放在倾角为θ=37°的斜面体上，斜面质量为M=4kg ，地面光滑，现对斜面体施一水平推力F ，要使物块m 相对斜面静止，求：（取sin37°=0.6，cos37°=0.8，g=10m/s 2）（1）若斜面与物块间无摩擦力，求m 加速度的大小及m 受到支持力的大小；（2）若斜面与物块间的动摩擦因数为μ=0.2，已知物体所受滑动摩擦力与最大静摩擦力相等，求推力F 的取值．（此问结果小数点后保留一位）【答案】（1）7.5m/s 2；25N （2）28.8N≤F≤67.2N 【解析】【分析】(1)斜面M 、物块m 在水平推力作用下一起向左匀加速运动，物块m 的加速度水平向左，合力水平向左，分析物块m 的受力情况，由牛顿第二定律可求出加速度a 和支持力．(2)用极限法把F 推向两个极端来分析：当F 较小（趋近于0）时，由于μ＜tanθ，因此物块将沿斜面加速下滑；若F 较大（足够大）时，物块将相对斜面向上滑，因此F 不能太小，也不能太大，根据牛顿第二定律，运用整体隔离法求出F 的取值范围．【详解】(1)由受力分析得：物块受重力，斜面对物块的支持力，合外力水平向左．根据牛顿第二定律得： mgtanθ=ma得 a=gtanθ=10×tan37°=7.5m/s 2 m 受到支持力20N=25N cos cos37N mg F θ==︒(2)设物块处于相对斜面向下滑动的临界状态时的推力为F 1，此时物块的受力如下图所示:对物块分析，在水平方向有 Nsinθ﹣μNcosθ=ma 1 竖直方向有 Ncosθ+μNsinθ﹣mg=0 对整体有 F 1=（M+m ）a 1 代入数值得a 1=4.8m/s 2 ，F 1=28.8N设物块处于相对斜面向上滑动的临界状态时的推力为F 2，对物块分析，在水平方向有 N ′sin θ﹣μN′cos θ=ma 2 竖直方向有 N ′cos θ﹣μN ′sin θ﹣mg =0 对整体有 F 2=（M +m ）a 2 代入数值得a 2=11.2m/s 2 ，F 2=67.2N综上所述可以知道推力F 的取值范围为：28.8N≤F ≤67.2N ．【点睛】解决本题的关键能够正确地受力分析，抓住临界状态，运用牛顿第二定律进行求解，注意整体法和隔离法的运用．4．如图所示，质量为M =10kg 的小车停放在光滑水平面上．在小车右端施加一个F =10N 的水平恒力．当小车向右运动的速度达到2.8m/s 时，在其右端轻轻放上一质量m =2.0kg 的小黑煤块（小黑煤块视为质点且初速度为零），煤块与小车间动摩擦因数μ＝0.20．假定小车足够长．（1）求经过多长时间煤块与小车保持相对静止（2）求3s 内煤块前进的位移（3）煤块最终在小车上留下的痕迹长度【答案】(1) 2s (2) 8.4m (3) 2.8m 【解析】【分析】分别对滑块和平板车进行受力分析，根据牛顿第二定律求出各自加速度，物块在小车上停止相对滑动时，速度相同，根据运动学基本公式即可以求出时间．通过运动学公式求出位移．【详解】(1)根据牛顿第二定律，刚开始运动时对小黑煤块有：1N F ma μ=F N -mg =0代入数据解得：a 1=2m/s 2 刚开始运动时对小车有：2N F F Ma μ-=解得：a 2=0.6m/s 2经过时间t ，小黑煤块和车的速度相等，小黑煤块的速度为：v 1=a 1t车的速度为：v 2=v +a 2t解得：t =2s ；(2)在2s 内小黑煤块前进的位移为：21114m 2x a t ==2s 时的速度为：11122m/s 4m/s v a t ==⨯=此后加速运动的加速度为：235m/s 6F a M m ==+ 然后和小车共同运动t 2=1s 时间，此1s 时间内位移为：2212321 4.4m 2x v t a t =+=所以煤块的总位移为：128.4m x x +=(3)在2s 内小黑煤块前进的位移为：21114m 2x a t ==小车前进的位移为：21116.8m 2x v t a t '=+=两者的相对位移为：m 1 2.8x x x '∆=-=即煤块最终在小车上留下的痕迹长度2.8m ．【点睛】该题是相对运动的典型例题，要认真分析两个物体的受力情况，正确判断两物体的运动情况，再根据运动学基本公式求解．5．如图所示，一质量M =40kg 、长L =2.5m 的平板车静止在光滑的水平地面上. 一质量m =10kg 可视为质点的滑块，以v 0=5m/s 的初速度从左端滑上平板车，滑块与平板车间的动摩擦因数μ=0.4，取g=10m/s2.（1）分别求出滑块在平板车上滑行时，滑块与平板车的加速度大小；（2）计算说明滑块能否从平板车的右端滑出.【答案】（1），（2）恰好不会从平板车的右端滑出．【解析】根据牛顿第二定律得对滑块，有，解得对平板车，有，解得．设经过t时间滑块从平板车上滑出滑块的位移为：．平板车的位移为：．而且有解得：此时，所以，滑块到达小车的右端时与小车速度相等，恰好不会从平板车的右端滑出．答：滑块与平板车的加速度大小分别为和．滑块到达小车的右端时与小车速度相等，恰好不会从平板车的右端滑出．点睛：对滑块受力分析，由牛顿第二定律可求得滑块的加速度，同理可求得平板车的加速度；由位移关系可得出两物体位移间相差L时的表达式，则可解出经过的时间，由速度公式可求得两车的速度，则可判断能否滑出．6．图示为仓库中常用的皮带传输装置示意图，它由两台皮带传送机组成，一台水平传送，A、B 两端相距3m ，另一台倾斜，传送带与地面的倾角θ= 37°，C、D 两端相距4.45m，B、C相距很近。

高考物理牛顿运动定律(一)解题方法和技巧及练习题及解析

高考物理牛顿运动定律(一)解题方法和技巧及练习题及解析一、高中物理精讲专题测试牛顿运动定律1．利用弹簧弹射和传送带可以将工件运送至高处。

如图所示，传送带与水平方向成37度角，顺时针匀速运动的速度v ＝4m/s 。

B 、C 分别是传送带与两轮的切点，相距L ＝6.4m 。

倾角也是37︒的斜面固定于地面且与传送带上的B 点良好对接。

一原长小于斜面长的轻弹簧平行斜面放置，下端固定在斜面底端，上端放一质量m ＝1kg 的工件（可视为质点）。

用力将弹簧压缩至A 点后由静止释放，工件离开斜面顶端滑到B 点时速度v 0＝8m/s ，A 、B 间的距离x ＝1m ，工件与斜面、传送带问的动摩擦因数相同，均为μ＝0.5，工件到达C 点即为运送过程结束。

g 取10m/s 2，sin37°＝0.6，cos37°＝0.8，求：（1）弹簧压缩至A 点时的弹性势能；（2）工件沿传送带由B 点上滑到C 点所用的时间；（3）工件沿传送带由B 点上滑到C 点的过程中，工件和传送带间由于摩擦而产生的热量。

【答案】(1)42J,(2)2.4s,(3)19.2J【解析】【详解】（1）由能量守恒定律得，弹簧的最大弹性势能为：2P 01sin 37cos372E mgx mgx mv μ︒︒=++ 解得：E p ＝42J（2）工件在减速到与传送带速度相等的过程中，加速度为a 1，由牛顿第二定律得： 1sin 37cos37mg mg ma μ︒︒+=解得：a 1＝10m/s 2 工件与传送带共速需要时间为：011v v t a -=解得：t 1＝0.4s 工件滑行位移大小为：220112v v x a -= 解得：1 2.4x m L =<因为tan 37μ︒<，所以工件将沿传送带继续减速上滑，在继续上滑过程中加速度为a 2，则有：2sin 37cos37mg mg ma μ︒︒-=解得：a 2＝2m/s 2假设工件速度减为0时，工件未从传送带上滑落，则运动时间为：22vt a = 解得：t 2＝2s工件滑行位移大小为：2 3? 1n n n n n 解得：x 2＝4m工件运动到C 点时速度恰好为零，故假设成立。

物理牛顿运动定律的应用专项习题及答案解析

物理牛顿运动定律的应用专项习题及答案解析一、高中物理精讲专题测试牛顿运动定律的应用1．一长木板置于粗糙水平地面上，木板左端放置一小物块，在木板右方有一墙壁，木板右端与墙壁的距离为4.5m ，如图（a ）所示．0t =时刻开始，小物块与木板一起以共同速度向右运动，直至1t s =时木板与墙壁碰撞（碰撞时间极短）．碰撞前后木板速度大小不变，方向相反；运动过程中小物块始终未离开木板．已知碰撞后1s 时间内小物块的v t -图线如图（b ）所示．木板的质量是小物块质量的15倍，重力加速度大小g 取10m/s 2．求（1）木板与地面间的动摩擦因数1μ及小物块与木板间的动摩擦因数2μ；（2）木板的最小长度；（3）木板右端离墙壁的最终距离．【答案】（1）10.1μ=20.4μ=（2）6m （3）6.5m 【解析】（1）根据图像可以判定碰撞前木块与木板共同速度为v 4m/s = 碰撞后木板速度水平向左，大小也是v 4m/s =木块受到滑动摩擦力而向右做匀减速，根据牛顿第二定律有24/0/1m s m sg sμ-=解得20.4μ=木板与墙壁碰撞前，匀减速运动时间1t s =，位移 4.5x m =，末速度v 4m/s = 其逆运动则为匀加速直线运动可得212x vt at =+ 带入可得21/a m s =木块和木板整体受力分析，滑动摩擦力提供合外力，即1g a μ= 可得10.1μ=（2）碰撞后，木板向左匀减速，依据牛顿第二定律有121()M m g mg Ma μμ++= 可得214/3a m s =对滑块，则有加速度224/a m s =滑块速度先减小到0，此时碰后时间为11t s = 此时，木板向左的位移为2111111023x vt a t m =-=末速度18/3v m s =滑块向右位移214/022m s x t m +== 此后，木块开始向左加速，加速度仍为224/a m s =木块继续减速，加速度仍为214/3a m s =假设又经历2t 二者速度相等，则有22112a t v a t =- 解得20.5t s =此过程，木板位移2312121726x v t a t m =-=末速度31122/v v a t m s =-= 滑块位移24221122x a t m == 此后木块和木板一起匀减速．二者的相对位移最大为13246x x x x x m ∆=++-= 滑块始终没有离开木板，所以木板最小的长度为6m（3）最后阶段滑块和木板一起匀减速直到停止，整体加速度211/a g m s μ==位移23522v x m a==所以木板右端离墙壁最远的距离为135 6.5x x x m ++= 【考点定位】牛顿运动定律【名师点睛】分阶段分析，环环相扣，前一阶段的末状态即后一阶段的初始状态，认真沉着，不急不躁2．如图，光滑水平面上静置一长木板A ，质量M =4kg ，A 的最前端放一小物块B （可视为质点），质量m =1kg ，A 与B 间动摩擦因数μ=0.2．现对木板A 施加一水平向右的拉力F ，取g =10m/s 2．则：（1）若拉力F 1=5N ，A 、B 一起加速运动，求A 对B 的静摩擦力f 的大小和方向；（2）为保证A 、B 一起加速运动而不发生相对滑动，求拉力的最大值F m （设最大静摩擦力与滑动摩擦力相等）；（3）若拉力F 2=14N ，在力F 2作用t =ls 后撤去，要使物块不从木板上滑下，求木板的最小长度L【答案】（1）f = 1N ，方向水平向右；（2）F m = 10N 。

2023届高考物理一轮复习知识点精讲与2022高考题模考题训练专题13牛顿运动定律的运用(解析版)

2023高考一轮知识点精讲和最新高考题模拟题同步训练第三章牛顿运动定律专题13 牛顿第二定律的应用第一部分知识点精讲1. 瞬时加速度问题（1）两类模型（2）. 在求解瞬时加速度时应注意的问题(i)物体的受力情况和运动情况是时刻对应的，当外界因素发生变化时，需要重新进行受力分析和运动分析。

(ii)加速度可以随着力的突变而突变，而速度的变化需要一个积累的过程，不会发生突变。

（3）求解瞬时加速度的步骤2．动力学的两类基本问题第一类：已知受力情况求物体的运动情况。

第二类：已知运动情况求物体的受力情况。

不管是哪一类动力学问题，受力分析和运动状态分析都是关键环节。

（1）解决两类基本问题的方法以加速度为“桥梁”，由运动学公式和牛顿第二定律列方程求解，具体逻辑关系如图：作为“桥梁”的加速度，既可能需要根据已知受力求解，也可能需要根据已知运动求解。

（2）动力学两类基本问题的解题步骤（3）掌握动力学两类基本问题的“两个分析”“一个桥梁”，以及在多个运动过程之间建立“联系”。

（i ）把握“两个分析”“一个桥梁”(ii)找到不同过程之间的“联系”，如第一个过程的末速度就是下一个过程的初速度，若过程较为复杂，可画位置示意图确定位移之间的联系。

3.物体在五类光滑斜面上运动时间的比较第一类：等高斜面(如图1所示)由L ＝12 at 2，a ＝g sin θ，L ＝h sin θ可得t ＝1sin θ 2h g，可知倾角越小，时间越长，图1中t 1＞t 2＞t 3。

第二类：同底斜面(如图2所示)由L ＝12 at 2，a ＝g sin θ，L ＝d cos θ可得t ＝ 4d g sin 2θ，可见θ＝45°时时间最短，图2中t 1＝t 3＞t 2。

第三类：圆周内同顶端的斜面(如图3所示)在竖直面内的同一个圆周上，各斜面的顶端都在竖直圆周的最高点，底端都落在该圆周上。

由2R ·sin θ＝12·g sin θ·t 2，可推得t 1＝t 2＝t 3。

高考物理牛顿运动定律解题技巧及经典题型及练习题(含答案)及解析(1)

高考物理牛顿运动定律解题技巧及经典题型及练习题(含答案)及解析(1)一、高中物理精讲专题测试牛顿运动定律1．如图所示，在倾角为θ = 37°的足够长斜面上放置一质量M = 2kg 、长度L = 1.5m 的极薄平板 AB ，在薄平板的上端A 处放一质量m =1kg 的小滑块(视为质点)，将小滑块和薄平板同时无初速释放。

已知小滑块与薄平板之间的动摩擦因数为μ1=0.25、薄平板与斜面之间的动摩擦因数为μ2=0.5,sin37°=0.6,cos37°=0.8，取g=10m/s 2。

求：(1)释放后，小滑块的加速度a l 和薄平板的加速度a 2; (2)从释放到小滑块滑离薄平板经历的时间t 。

【答案】(1)24m/s ，21m/s ；(2)1s t = 【解析】【详解】（1）设释放后，滑块会相对于平板向下滑动，对滑块m ：由牛顿第二定律有：011sin 37mg f ma -=其中01cos37N F mg =，111N f F μ= 解得：00211sin 37cos374/a g g m s μ=-=对薄平板M ，由牛顿第二定律有：0122sin 37Mg f f Ma +-= 其中002cos37cos37N F mg Mg =+，222N f F μ=解得：221m/s a =12a a >，假设成立，即滑块会相对于平板向下滑动。

设滑块滑离时间为t ，由运动学公式，有：21112x a t =，22212x a t =，12x x L -= 解得：1s t =2．质量为2kg 的物体在水平推力F 的作用下沿水平面做直线运动，一段时间后撤去F ，其运动的图象如图所示取m/s 2，求：（1）物体与水平面间的动摩擦因数；（2）水平推力F 的大小；（3）s内物体运动位移的大小．【答案】（1）0.2；（2）5.6N；（3）56m。

【解析】【分析】【详解】（1）由题意可知，由v-t图像可知，物体在4～6s内加速度：物体在4～6s内受力如图所示根据牛顿第二定律有：联立解得：μ=0.2（2）由v-t图像可知：物体在0～4s内加速度：又由题意可知：物体在0～4s内受力如图所示根据牛顿第二定律有：代入数据得：F=5.6N（3）物体在0～14s内的位移大小在数值上为图像和时间轴包围的面积，则有：【点睛】在一个题目之中，可能某个过程是根据受力情况求运动情况，另一个过程是根据运动情况分析受力情况；或者同一个过程运动情况和受力情况同时分析，因此在解题过程中要灵活处理．在这类问题时，加速度是联系运动和力的纽带、桥梁．3．固定光滑细杆与地面成一定倾角，在杆上套有一个光滑小环，小环在沿杆方向的推力F 作用下向上运动，推力F与小环速度v随时间变化规律如图所示，取重力加速度g＝10m/s2．求：（1）小环的质量m ；（2）细杆与地面间的倾角a ．【答案】（1）m ＝1kg ，（2）a ＝30°．【解析】【详解】由图得：0-2s 内环的加速度a=vt=0.5m/s 2 前2s ，环受到重力、支持力和拉力，根据牛顿第二定律，有：1sin F mg ma α-= 2s 后物体做匀速运动，根据共点力平衡条件，有：2sin F mg α= 由图读出F 1=5.5N ，F 2=5N联立两式，代入数据可解得：m =1kg ，sinα=0.5，即α=30°4．如图甲所示，一长木板静止在水平地面上，在0t =时刻，一小物块以一定速度从左端滑上长木板，以后长木板运动v t -图象如图所示.已知小物块与长木板的质量均为1m kg =，小物块与长木板间及长木板与地面间均有摩擦，经1s 后小物块与长木板相对静止()210/g m s=，求：()1小物块与长木板间动摩擦因数的值； ()2在整个运动过程中，系统所产生的热量．【答案】（1）0.7（2）40.5J 【解析】【分析】()1小物块滑上长木板后，由乙图知，长木板先做匀加速直线运动，后做匀减速直线运动，根据牛顿第二定律求出长木板加速运动过程的加速度，木板与物块相对静止时后木板与物块一起匀减速运动，由牛顿第二定律和速度公式求物块与长木板间动摩擦因数的值．()2对于小物块减速运动的过程，由牛顿第二定律和速度公式求得物块的初速度，再由能量守恒求热量．【详解】()1长木板加速过程中，由牛顿第二定律，得1212mg mg ma μμ-=； 11m v a t =；木板和物块相对静止，共同减速过程中，由牛顿第二定律得 2222mg ma μ⋅=； 220m v a t =-；由图象可知，2/m v m s =，11t s =，20.8t s = 联立解得10.7μ=()2小物块减速过程中，有：13mg ma μ=； 031m v v a t =-；在整个过程中，由系统的能量守恒得2012Q mv = 联立解得40.5Q J =【点睛】本题考查了两体多过程问题，分析清楚物体的运动过程是正确解题的关键，也是本题的易错点，分析清楚运动过程后，应用加速度公式、牛顿第二定律、运动学公式即可正确解题．5．如图所示.在距水平地面高h =0.80m 的水平桌面一端的边缘放置一个质量m =0.80kg 的木块B ，桌面的另一端有一块质量M =1.0kg 的木块A 以初速度v 0=4.0m/s 开始向着木块B 滑动，经过时间t =0.80s 与B 发生碰撞，碰后两木块都落到地面上，木块B 离开桌面后落到地面上的D 点．设两木块均可以看作质点，它们的碰撞时间极短，且已知D 点距桌面边缘的水平距离s =0.60m ，木块A 与桌面间的动摩擦因数μ=0.25，重力加速度取g =10m/s 2．求：(1)木块B 离开桌面时的速度大小； (2)两木块碰撞前瞬间，木块A 的速度大小； (3)两木块碰撞后瞬间，木块A 的速度大小．【答案】(1) 1.5m/s (2) 2.0m/s (3) 0.80m/s 【解析】【详解】(1)木块离开桌面后均做平抛运动，设木块B 离开桌面时的速度大小为2v ，在空中飞行的时间为t ′．根据平抛运动规律有：212h gt =，2s v t '= 解得：2 1.5m/s 2gv sh== (2)木块A 在桌面上受到滑动摩擦力作用做匀减速运动，根据牛顿第二定律，木块A 的加速度：22.5m/s Mga Mμ==设两木块碰撞前A 的速度大小为v ，根据运动学公式，得0 2.0m/s v v at =-=(3)设两木块碰撞后木块A 的速度大小为1v ，根据动量守恒定律有：2Mv Mv mv =+1解得：210.80m/s Mv mv v M-==.6．如图所示,水平面上AB 间有一长度x=4m 的凹槽,长度为L=2m 、质量M=1kg 的木板静止于凹槽右侧,木板厚度与凹槽深度相同,水平面左侧有一半径R=0.4m 的竖直半圆轨道,右侧有一个足够长的圆弧轨道,A 点右侧静止一质量m1=0.98kg 的小木块.射钉枪以速度v 0=100m/s 射出一颗质量m0=0.02kg 的铁钉,铁钉嵌在木块中并滑上木板,木板与木块间动摩擦因数μ=0.05,其它摩擦不计.若木板每次与A 、B 相碰后速度立即减为0,且与A 、B 不粘连,重力加速度g=10m/s 2.求:（1）铁钉射入木块后共同的速度v ;（2）木块经过竖直圆轨道最低点C 时,对轨道的压力大小F N; （3）木块最终停止时离A 点的距离s.【答案】（1）2/v m s = （2）12.5N F N = （3） 1.25L m ∆= 【解析】(1) 设铁钉与木块的共同速度为v ，取向左为正方向，根据动量守恒定律得：0001()m v m m v =+解得：2m v s =；(2) 木块滑上薄板后，木块的加速度210.5ma g s μ==，且方向向右板产生的加速度220.5mgma s Mμ==，且方向向左设经过时间t ，木块与木板共同速度v 运动则：12v a t a t -=此时木块与木板一起运动的距离等于木板的长度22121122x vt a t a t L ∆=--=故共速时，恰好在最左侧B 点，此时木块的速度11m v v a t s'=-=木块过C 点时对其产生的支持力与重力的合力提供向心力，则：'2N v F mg m R-=代入相关数据解得：F N =12.5N.由牛顿第三定律知，木块过圆弧C 点时对C 点压力为12.5N ； (3) 木块还能上升的高度为h ，由机械能守恒有：201011()()2m m v m m gh +=+ 0.050.4h m m =<木块不脱离圆弧轨道，返回时以1m/s 的速度再由B 处滑上木板，设经过t 1共速，此时木板的加速度方向向右，大小仍为a 2，木块的加速度仍为a 1，则：21121v a t a t -=，解得：11t s = 此时2211121110.522x v t a t a t m ∆=--='' 3210.5m v v at s=-=碰撞后，v 薄板=0，木块以速度v 3=0.5m/s 的速度向右做减速运动设经过t 2时间速度为0，则3211v t s a == 2322210.252x v t a t m =-=故ΔL=L ﹣△x'﹣x=1.25m即木块停止运动时离A 点1.25m 远．7．如图所示，在风洞实验室里，粗糙细杆与竖直光滑圆轨AB 相切于A 点，B 为圆弧轨道的最高点，圆弧轨道半径R =1m ，细杆与水平面之间的夹角θ=37°．一个m =2kg 的小球穿在细杆上，小球与细杆间动摩擦因数μ=0.3．小球从静止开始沿杆向上运动，2s 后小球刚好到达A 点，此后沿圆弧轨道运动，全过程风对小球的作用力方向水平向右，大小恒定为40N ．已知g =10m/s 2，sin37°=0.6，cos37°=0.8．求：(1)小球在A 点时的速度大小；(2)小球运动到B 点时对轨道作用力的大小及方向．【答案】(1)8m/s (2)12N 【解析】【详解】(1)对细杆上运动时的小球受力分析，据牛顿第二定律可得：cos sin (sin cos )F mg F mg ma θθμθθ--+=代入数据得：24m/s a =小球在A 点时的速度8m/s A v at ==(2)小球沿竖直圆轨道从A 到B 的过程，应用动能定理得：2211sin37(1cos37)22B A FR mgR mv mv -︒-+︒=- 解得：2m/s B v =小球在B 点时，对小球受力分析，设轨道对球的力竖直向上，由牛顿第二定律知：2N Bv mg F m R-=解得：F N =12N ，轨道对球的力竖直向上由牛顿第三定律得：小球在最高点B 对轨道的作用力大小为12N ，方向竖直向下．8．水平面上固定着倾角θ=37°的斜面，将质量m=lkg 的物块A 从斜面上无初速度释放，其加速度a=3m/s 2。

(物理)物理牛顿运动定律的应用练习题含答案及解析

（物理）物理牛顿运动定律的应用练习题含答案及解析一、高中物理精讲专题测试牛顿运动定律的应用1．如图所示，钉子A 、B 相距5l ，处于同一高度．细线的一端系有质量为M 的小物块，另一端绕过A 固定于B ．质量为m 的小球固定在细线上C 点，B 、C 间的线长为3l ．用手竖直向下拉住小球，使小球和物块都静止，此时BC 与水平方向的夹角为53°．松手后，小球运动到与A 、B 相同高度时的速度恰好为零，然后向下运动．忽略一切摩擦，重力加速度为g ，取sin53°=0.8，cos53°=0.6．求：（1）小球受到手的拉力大小F ；（2）物块和小球的质量之比M :m ；（3）小球向下运动到最低点时，物块M 所受的拉力大小T【答案】（1）53F Mg mg =- （2）65M m = （3）()85mMg T m M =+（4855T mg =或811T Mg =）【解析】【分析】【详解】（1）设小球受AC 、BC 的拉力分别为F 1、F 2 F 1sin53°=F 2cos53° F +mg =F 1cos53°+ F 2sin53°且F 1=Mg 解得53F Mg mg =- （2）小球运动到与A 、B 相同高度过程中小球上升高度h 1=3l sin53°，物块下降高度h 2=2l 机械能守恒定律mgh 1=Mgh 2 解得65M m = （3）根据机械能守恒定律，小球回到起始点．设此时AC 方向的加速度大小为a ，重物受到的拉力为T牛顿运动定律Mg –T =Ma 小球受AC 的拉力T ′=T 牛顿运动定律T ′–mg cos53°=ma解得85mMg T m M =+（）（4885511T mg T Mg ==或）【点睛】本题考查力的平衡、机械能守恒定律和牛顿第二定律．解答第（1）时，要先受力分析，建立竖直方向和水平方向的直角坐标系，再根据力的平衡条件列式求解；解答第（2）时，根据初、末状态的特点和运动过程，应用机械能守恒定律求解，要注意利用几何关系求出小球上升的高度与物块下降的高度；解答第（3）时，要注意运动过程分析，弄清小球加速度和物块加速度之间的关系，因小球下落过程做的是圆周运动，当小球运动到最低点时速度刚好为零，所以小球沿AC方向的加速度（切向加速度）与物块竖直向下加速度大小相等．2．如图所示，倾角α=30°的足够长传送带上有一长L=1.0m，质量M=0.5kg的薄木板，木板的最右端叠放质量为m=0.3kg的小木块.对木板施加一沿传送带向上的恒力F，同时让传送带逆时针转动，运行速度v=1.0m/s。

高中物理第四章用牛顿定律解决问题

第四章 4.6.1用牛顿定律解决问题【学习目标】1．进一步学习对物体的受力情况及运动情况进行分析的方法。

2．掌握应用牛顿运动定律和运动学公式解答有关问题的基本思路和方法。

【学习任务】一、由受力情况确定运动情况例1一木箱装货物后质量为50 kg，木箱与地面间的动摩擦因数为0.2，某人以200 N斜向下的力推箱，推力的方向与水平面成30°角，g取10 m/s2.求：(1)木箱的加速度；(2)第2 s末木箱的速度．解析取木箱为研究对象，木箱受力情况如右图所示，建立直角坐标系xOy，并取加速度a的方向为x轴的正方向．(1)根据牛顿第二定律有X: Fcos 300—F f=maY: F N-Fsin 300-mg=0又有 F f=μF N联立解得：a=代入数据得：a=1.06 m/s2.(2)第2 s末速度为：v2=at=1.06×2 m/s=2.12 m/s.归纳总结：(1)基本思路：首先对研究对象进行受力情况和运动情况分析，把题中所给的情况弄清楚，然后由牛顿第二定律，结合运动学公式进行求解．(2)一般步骤①确定研究对象，对研究对象进行受力分析，并画出物体的受力图．②根据力的合成与分解，求出物体所受的合外力(包括大小和方向)．③根据牛顿第二定律列方程，求出物体运动的加速度．④结合物体运动的初始条件，选择运动学公式，求出所需的运动学量——任意时刻的位移和速度，以及运动轨迹等．【补充学习材料】例1．一个滑雪者从静止开始沿山坡滑下，山坡的倾角θ＝30°，滑雪板与雪地的动摩擦因数是0.04(g取10 m/s2)求：(1)滑雪者加速度的大小；(2)滑雪者5 s内滑下的路程；(3)滑雪者5 s末速度的大小．2 质量为m=10kg的物体静止在水平面上，它们之间的动摩擦系数μ=0.5，现在对物体施加以如图所示的拉力F=100N ,与水平方向夹角θ=37º (sin37º=0.6，g取10m/s2。

物理牛顿运动定律的应用模拟试题及解析

物理牛顿运动定律的应用模拟试题及解析一、高中物理精讲专题测试牛顿运动定律的应用1．如图，质量M=4kg 的长木板静止处于粗糙水平地面上，长木板与地面的动摩擦因数μ1=0.1，现有一质量m=3kg 的小木块以v 0=14m/s 的速度从一端滑上木板，恰好未从木板上滑下，滑块与长木板的动摩擦因数μ2=0.5，g 取10m/s 2，求：（1）木块刚滑上木板时，木块和木板的加速度大小；（2）木板长度；（3）木板在地面上运动的最大位移。

【答案】（1）5m/s 2 2m/s 2（2）14m （3）12m 【解析】【分析】（1）由题意知，冲上木板后木块做匀减速直线运动，木板由静止做匀加速度直线运动，根据牛顿第二定律求解加速度；（2）木块恰好未从木板滑下，当木块运动到木板最右端时，两者速度相等；根据位移关系求解木板的长度；（3）木块木板达到共同速度后将一起作匀减速直线运动，结合运动公式求解木板在地面上运动的最大位移. 【详解】（1）由题意知，冲上木板后木块做匀减速直线运动，初速度 v 0=14m/s ，加速度大小 212a μg 5m /s ==木板由静止做匀加速度直线运动即 ()212μmg μM m g Ma -+=解得 22a 2m /s =（2）木块恰好未从木板滑下，当木块运动到木板最右端时，两者速度相等。

设此过程所用时间为t即 012v v a t v a t =-==木板木块解得 t=2s木块位移 2011x v t a t 18m 2木块=-= 木板位移 221x a t 4m 2木板== 木板长度 L x x 14m =-=木板木块（3）木块木板达到共同速度后将一起作匀减速直线运动，分析得2231v a t 4m /s a μg 1m /s ====共，木板位移 23vx8m 2a ==，共木板总位移 ,x x x 12m =+=木板木板2．如图，光滑绝缘水平面上静置两个质量均为m 、相距为x 0的小球A 和B ，A 球所带电荷量为+q ，B 球不带电。