热力学第二定律4
热力学第二定律(4)
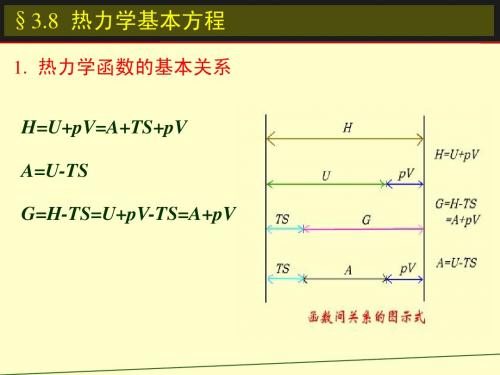
dH TdS Vdp
(3) dA SdT pdV (4)
A(T ,V )
G(T , p)
dG SdT Vdp
适用条件:(1)无相变化和化学变化(恒定组成)的均 相封闭系统发生单纯pVT变化的可逆或不可逆过程(2) 对于化学反应和相变化只适用于非体积功为零的可逆过程 即非体积功为零的恒定组成的封闭系统
解:对理想气体,
pV nRT
p nRT /V
p nR ( )V T V
p nR U ( )T T ( )V p T p 0 V T V
所以,理想气体的热力学能只是温度的函数。
§3.8 热力学基本方程
8、偏微分运算规则: z f ( x, y ) 循环关系式:
=
2U U V S SV V S T V S
S一定时对V 微分 U T ; S V
§3.8 热力学基本方程 (1) dU TdS pdV
§3.8 热力学基本方程 3、热力学方程的简单应用
例:试证明理想气体恒温过程ΔA=ΔG
dT 0 dA pdV A
V2 V1
dT 0 dG Vdp G Vdp nRT ln
p1 p2
V1 pdV nRT ln V2
p2 V nRT ln 1 p1 V2
H G / T 2 T T p
积分:
G2
G1
T2 G H d( ) 2 dT T1 T T
T2 H G2 G1 dT 2 T1 T T2 T1
§3.8 热力学基本方程
第四章热力学第二定律

第四章热力学第二定律主要内容:4.1 自发过程及热力学第二定律4.2 卡诺循环与卡诺定理4.3熵的概念4.4Clausius不等式及熵增加原理4.5 熵变的计算及熵的物理意义4.6 热力学第三定律与规定熵4.7 亥姆霍兹能及吉布斯能4.8 热力学基本方程及麦克斯韦关系式4.9吉布斯自由能及温度、压力的关系§4.1 自发过程及热力学第二定律自发过程热力学第二定律1. 自发过程自发过程无需依靠消耗环境的作用(即不借助外力),就能自动进行的过程。
(1) 焦耳热功当量中功自动转变成热;(2) 气体向真空膨胀;(3) 热量从高温物体传入低温物体;(4) 浓度不等的溶液混合均匀;(5) 锌片与硫酸铜的置换反应等,它们的逆过程都不能自动进行。
当借助外力,系统恢复原状后,会给环境留下不可磨灭的影响。
自发过程的特征:1)自发过程总是单向趋于平衡;2)自发过程均具有不可逆性;3)自发过程具有对环境作功的能力,如配有合适的装置,则可从自发过程中获得可用的功。
如:温度传递;气体流动;系统自发过程达到平衡后,无环境作用系统是不可能自动反方向进行并回到原来状态;自发过程的不可逆性是指自然界中所有自发过程都具有热力学的不可逆性;2. 热力学第二定律克劳修斯(Clausius) 的说法:“不可能把热从低温物体传到高温物体,而不引起其它变化。
”—热传导的不可逆性开尔文(Kelvin)的说法:“不可能从单一热源取出热使之完全变为功,而不发生其它的变化。
”—摩擦生热的不可逆性二者说法是等效的,均指明某种自发过程的逆过程是不能自动进行的重要结论: (1)均指明过程的方向性;(2)自发过程存在内在的联系,可以从某一自发过程的不可逆性,便可以推导出其它自发过程的不可逆性。
理解:♦并非“功可以转变为热,而热不能完全变为功”,而是在不引起其它变化的条件下,热才不能完全转变为功。
如:理想气体等温膨胀。
♦第二类永动机:从单一热源吸热使之完全变为功而不留下任何影响。
(完整版)热力学第二定律.ppt

热力学第二定律的微观实质
从微观上看,任何热力学过程都伴随着大量分子的无序运 动的变化。热力学第二定律就是说明大量分子运动的无序程度 变化的规律。 •功转换为热:大量分子的有序运动向无序运动转化, 是可 能的;而相反的过程,是不可能的。
•热传导:大量分子运动的无序性由于热传导而增大了。 •自由膨胀:大量分子向体积大的空间扩散,无序性增大。
不可能从单一热源吸收热量,使它
Q
完全转变为功而不引起其它变化。
热源
A. 从单一热源吸收热量,使它完全转变为功,一定要引起 其它变化。
特例:等温过程从单一热源吸收热量,并完全用来做功, 必导致系统体积变化。
B. 第二类永动机不可能制成。
η 100% 2.克劳修斯表述
热量不能自动地从低温物体传向高温物体。
讨论: A.没有外界做功,不可能从低温热源将
热量传输到高温热源。 B.第二类永动机不可能制成。
高温热源 Q1 A
Q2 低温热源
热力学第二定律是研究热机效率和制冷系数时提 出的。对热机,不可能吸收的热量全部用来对外 作功;对制冷机,若无外界作功,热量不可能从 低温物体传到高温物体。热力学第二定律的两种 表述形式,解决了物理过程进行的方向问题。
S 0
(孤立系, 自然过程)ห้องสมุดไป่ตู้
§8-6 热力学过程的不可逆性
广义定义:假设所考虑的系统由一个状态出发
经过某一过程达到另一状态,如果存在另一个 过程,它能使系统和外界完全复原(即系统回 到原来状态,同时原过程对外界引起的一切影 响)则原来的过程称为可逆过程;反之,如果 用任何曲折复杂的方法都不能使系统和外界完 全复员,则称为不可逆过程。
各种宏观态不是等几率的。那种宏观态包含的微观态 数多,这种宏观态出现的可能性就大。
第四章热力学第二定律

无限可转换能—机械能,电能
能量转换方向性的 实质是能质有差异 部分可转换能—热能
T T0
不可转换能—环境介质的热力学能
能质降低的过程可自发进行,反之需一定条件—补偿过 程,其总效果是总体能质降低。
q1 q2 wnet
代价
q2 T1 T2
q2
T2 T1
代价
wnet q1 q2
二.热力学第二定律的实质和表述
衡量制冷循环经济性的工作系数称为制冷系数,即
q2 q2 制冷系数可以大于1, w q1 q2 等于1或者小于1
衡量热泵的经济性的工作系数称为供热系数,即
/ q1 q1
供热系数总是大于1
w q1 q2
/ q1 q1 q1 q2 q2 1
w q1 q2
q1 q2
第二节 热力学第二定律 (Second law)
三、两种说法的等价性
克劳修斯说法:不可能把热从
1.违反克劳修斯说法 必然违反开尔文说法
低温物体传到高温物体而不 引起其它变化。
开尔文说法:不可能从单一
高温热源T1
热源取热,使之完全变为有 用功,而不引起其它变化。
Q1
WB
AW Q2
Q2 Q1>Q2
低温热源T2
A-违反Clausius表述 B-Carnot热机
把热能转化为机械能的循环叫正向循环,也叫热 机循环或动力循环,它使外界得到功。
热源
Q1
热机
Q2
冷源
W Q1 Q2
2、逆循环(counterclockwise direction cycle):
把热量从低温热源传给高温热源的循环叫逆 向循环,分为制冷循环和热泵循环,它消耗外界 的功。
§4 卡诺定理

卡诺的伟大就在于,他早在1824 年,即第二定律发 卡诺的伟大就在于,他早在1824 现之前26年就得到了这一“不可能性” 26年就得到了这一 现之前26年就得到了这一“不可能性”,假如年轻的卡诺 不是因病于1832年逝世,他完全可以创立热力学第二定律. 1832年逝世 不是因病于1832年逝世,他完全可以创立热力学第二定律. 事实上,克劳修斯就是从卡诺在证明卡诺定理的破绽 事实上, 中意识到能量守恒定律之外还应有另一条独立的定律。 中意识到能量守恒定律之外还应有另一条独立的定律。 • 卡诺英年早逝,他能在短暂的科学研究岁月中作出不 卡诺英年早逝, 朽贡献是因为他善于采用科学抽象的方法 他善于采用科学抽象的方法, 朽贡献是因为他善于采用科学抽象的方法,他能在错综复 杂的客观事物中建立理想模型。在抽象过程中, 杂的客观事物中建立理想模型。在抽象过程中,把热机效 率的主要特征以纯粹理想化的形式呈现出来, 率的主要特征以纯粹理想化的形式呈现出来,从而揭示了 客观规律。 客观规律。 • 卡诺热机与其他理想模型诸如质点、刚体、理想气体、 卡诺热机与其他理想模型诸如质点、刚体、理想气体、 理想流体、绝对黑体、 理想流体、绝对黑体、理想溶液一样都是经过高度抽象的 理想客体。它能最真实、 理想客体。它能最真实、最普遍地反映出客观事物的基本 特征。 特征。
一、卡诺定理 (1)在相同的高温热源和相同的低温热源之间工作的 (1)在相同的高温热源和相同的低温热源之 在相同的高温热源和相同的低温热源 一切可逆热机,其效率都相等,与工作物质无关。 一切可逆热机,其效率都相等,与工作物质无关。 (2)在相同的高温热源和相同的低温热源之 (2)在相同的高温热源和相同的低温热源之间工作的 在相同 一切不可逆热机, 效率都不可能大于可逆热机的效率。 不可逆热机 一切不可逆热机,其效率都不可能大于可逆热机的效率。 说明:a.此处热源指温度均匀的恒温热源; 说明:a.此处热源指温度均匀的恒温热源; 此处热源指温度均匀的恒温热源 b.在高温热源处吸热,低温热源处放热, b.在高温热源处吸热,低温热源处放热,从而对外 在高温热源处吸热 处放热 作功的可逆机实际均为卡诺机。 作功的可逆机实际均为卡诺机。 由于历史的局限性, 由于历史的局限性,卡诺信奉当时在科学界中据支配 地位的“热质学” 卡诺是在“热质说” 基础上得出卡 地位的“热质学”。卡诺是在“热质说”的基础上得出卡 诺定理的.卡诺定理也可以由热力学第一, 诺定理的.卡诺定理也可以由热力学第一,第二定律得到证 明。 反证法证明卡诺定理: 反证法证明卡诺定理:
热3.热力学第二定律

O
Q2 i = 1+ (2) Q1i
12
由(1) (2)有 有
Q1i Q2 i + =0 T1i T2 i
Q1 i Q 2 i + 循环: 循环:∑ T2 i i = 1 T1 i
n
=0
∑
2n
Q j Tj
j =1
=0
n → ∞: Q j → d Q,T j → T,∑ → ∫
∴
9
w =∞
二. 两种表述的等价性 1. 若克氏表述成立,则开氏表述亦成立. 若克氏表述成立,则开氏表述亦成立. 反证法: 反证法: T1 T1
设开氏表 述不成立 Q1 Q1+Q2 A=Q1 T2 开氏表 述成立 T1 Q1 Q2 等价 T2 克氏表 述成立 则克氏表 Q2 述不成立
A
( 10 2. 若开氏表述成立,则克氏表述也成立.自证) 若开氏表述成立,则克氏表述也成立.自证)
T Q 第二类 永动机
η =1
A=Q
8
开氏表述的另种说法: 开氏表述的另种说法: 不存在第二类永动机
V1 T Q V2 A= Q
思考 左图所示过程是 否违反热力学第二定律? 否违反热力学第二定律?
2. 克氏表述(clausius,1850) : 克氏表述( , ) 热量不能 自动地从低 自动地从低 温物体传向 高温物体 T1(高) Q T2(低)
实际上,昨天的故事!" 一切不可逆过程都是相互沟通的. 实际上,昨天的故事!" 一切不可逆过程都是相互沟通的. 任何一种不可逆过程的表述, 任何一种不可逆过程的表述,都可作为热力学第 二定律的表述! 二定律的表述! 7
§4.3 热力学第二定律
是关于自然过程方向的一 热力学第二定律是关于 热力学第二定律是关于自然过程方向的一 条基本的,普遍的定律. 条基本的,普遍的定律. 热力学第二定律的两种表述: 一. 热力学第二定律的两种表述: 1.开氏表述(Kelvin, 1851): 开氏表述( 开氏表述 , ): 其唯一效果 唯一效果 是热量全部转 是热量全部转 全部 变为功的过程 是不可能的. 是不可能的.
3.4 热力学第二定律(解析版)

第4节热力学第二定律【知识梳理与方法突破】1.热力学第二定律的理解(1)“自发地”过程就是不受外来干扰进行的自然过程,在热传递过程中,热量可以自发地从高温物体传到低温物体,却不能自发地从低温物体传到高温物体。
要将热量从低温物体传到高温物体,必须“对外界有影响或有外界的帮助”,就是要有外界对其做功才能完成。
电冰箱就是一例,它是靠电流做功把热量从低温处“搬”到高温处的。
(2)“不产生其他影响”的含义是发生的热力学宏观过程只在本系统内完成,对周围环境不产生热力学方面的影响。
如吸热、放热、做功等。
(3)热力学第二定律的每一种表述都揭示了大量分子参与的宏观过程的方向性。
如机械能可以全部转化为内能,内能却不可能全部转化为机械能而不引起其他变化,进一步揭示了各种有关热的物理过程都具有方向性。
(4)适用条件:只能适用于由很大数目分子所构成的系统及有限范围内的宏观过程。
而不适用于少量的微观体系,也不能把它扩展到无限的宇宙。
(5)热力学第二定律的两种表述是等价的,即一个说法是正确的,另一个说法也必然是正确的;如一个说法是错误的,另一个说法必然是不成立的。
2.热力学第一定律与第二定律的比较项目热力学第一定律热力学第二定律定律揭示的问题它从能量守恒的角度揭示了功、热量和内能改变量三者间的定量关系它指出自然界中出现的宏观过程是有方向性的机械能和内能的转化当摩擦力做功时,机械能可以全部转化为内能内能不可能在不引起其他变化的情况下全部转化为机械能热量的传递热量可以从高温物体自发地传到低温物体说明热量不能自发地从低温物体传到高温物体表述形式只有一种表述形式有多种表述形式联系两定律都是热力学基本定律,分别从不同角度揭示了与热现象有关的物理过程所遵循的规律,二者相互独立,又相互补充,都是热力学的理论基础3.能量耗散的理解(1)各种形式的能最终都转化为内能,流散到周围的环境中,分散在环境中的内能不管数量多么巨大,它也只能使地球、大气稍稍变暖一点,却再也不能自动聚集起来驱动机器做功了。
热力学第二定律(4)

定义: 熵
dS
Qrev
Tr
比熵 ds
qrev
Tr
于19世纪中叶首先克劳修斯 (R.Clausius)引入,式中S从1865年起称 为entropy,由清华大学刘仙洲教授译成 为“熵”。
熵的物理意义
定义:熵
dS
Qre
T
比熵 ds
qre
T
热源温度=工质温度
可逆时
dS 0 dS 0 dS 0
自发过程的方向性
摩擦生热
功量
100% 发电厂
热量
功量
40%
热量
放热
自发过程具有方向性、条件、限度
热力学第二定律的实质
自然界过程的方向性表现在不同的方面
能不能找出共同的规律性? 能不能找到一个判据?
热力学第二定律
热力学第二律的表述与实质
热二律的表述有 60-70 种
热功转换
1851年 开尔文-普朗克表述 热功转换的角度
Q
Q
p
2 b v
热力学第二定律的数学表达式
任意不可逆循环
Q Q 1 2 可得:
T1 T2
Q2 T2 1 1 Q1 T1
式中δQ2为绝对值: p a 2 b v
δQ2改用代数值:
Q1
T1
Q2
T2
0
1
克劳修斯不等式
热力学第二定律推论之一 卡诺定理给出热机的最高理想 热力学第二定律推论之二 克劳修斯不等式反映过程方向性 定义熵
∴ Q1
’-
Q1 = Q2 - Q2= 0
’
工质循环、冷热源均恢复原状, 外界无痕迹,只有可逆才行, 与原假定矛盾。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ssur
H(268.2K) T
9874 268.2
J
K 1
36.8J
K 1
Siso Ssys Ssur
(35.4 36.8)J K 1 1.40J K 1
Siso 0 自发不可逆过程
例4. 求反应 2C(s) O2 (g) 2CO(g)
dT dT T2 nCp,m (l)
T1
T
H相变 T相变
T2 nCp,m ( s)
T1
T
S S1 S2 S3
dT dT T2 nCp,m (l)
T1
T
H相变 T相变
T2 nCp,m ( s)
T1
T
[(1.0
126.8
ln
278.7 268.2
解:过冷液体的凝固是不可逆过程,需要在相 同始终态间设计一个可逆过程来计算熵变。设 计的可逆过程为
C6H6 (l,268.2K) SC6H6 (s,268.2K)
可逆 S1
加热
可逆
S3 冷却
C6
H
6
(l
,
278.7K)源自S2 可逆过程C6
H
6
(
s,
278.7
K
)
S S1 S2 S3
在298K时反应的标准摩尔熵变 。
r
Sm
(298K
)
2Sm
(CO,
298K
)
S
m
(O2
,
298K
)
2
S
m
(C,
298K
)
(2197.9 205.02 25.69)J mol1 K 1
179.4J mol1 K 1
3.4 亥姆霍兹函数及吉布斯函数
)
(
9916 278.7
)
(1.0 122.6
ln
268.2 278.7
)]J
K
1
35.4J K 1
为了计算环境的熵变,可令苯与268.2K的大热储器接 触,在268.2K苯凝固时,所放出的热量全部由热储器 吸收,由于热储器很大,其温度不变,吸热过程均可 看作是可逆的,所以
(dG)T, p > W '
若是不可逆过程,系统所作的非膨胀功小于Gibbs 自由能的减少值。
如果系统在等温、等压、且不作非膨胀功的条件下,
(dG) T
,
p
,W
'
0
0
或
(dG)T,p,W'0 0
(dG) T
,
p
,W
'
0
0
" "表示可逆,平衡 " "表示不可逆,自发
即自发变化总是朝着Gibbs自由能减少的方向进行,
亥姆霍兹函数及判据 吉布斯函数及判据
3.4.1 亥姆霍兹函数及判据
A def U TS
A 称为Helmholtz自由能(Helmholtz free energy), 是状态函数,具有广度性质。
则 W dA
即:在等温过程中,封闭系统对外所作的功等于 或小于系统Helmholtz自由能的减少值。
3.4.2 吉布斯函数及判据
G def H TS
G 称为Gibbs自由能(Gibbs free energy),是 状态函数,具有广度性质。
W ' dG
W ' dG
等号表示可逆过程
(dG)T , p,R
W
' max
即:等温、等压、可逆过程中,封闭系统对外所作
的最大非膨胀功等于系统Gibbs自由能的减少值。
解法1
S(O2 )
nR ln
V2 V1
0.5R ln
22.4 12.2
S
(N2
)
0.5R
ln
22.4 12.2
mixS S(O2 ) S(N2 ) nR ln 22.4 nR ln 2 > 0 12.2
例3:在273 K时,将一个22.4 dm3 的 盒子用隔板一分为二,
对外做功,E 为正值,所以加“—”号。
(dA) T
,V
,W
'
0
0
或
(dA) T
,V
,W
'
0
0
等号表示可逆过程,小于号表示是一个自发的不
可逆过程,即自发变化总是朝着Helmholtz自由能 减少的方向进行。这就是Helmholtz自由能判据:
(dA)T ,V ,Wf 0 0
" "表示可逆,平衡 " "表示不可逆,自发
R
vap H Tb
44020 J 118.0 J K1 373.15 K
显然 Ssur 118.0 J K1
例3:在273 K时,将一个22.4 dm3 的 盒子用隔板一分为二,
0.5 mol 0.5 mol O2 (g) N2 (g)
求抽去隔板后,两种气体混合过程的熵变?
0.5 mol 0.5 mol O2 (g) N2 (g)
求抽去隔板后,两种气体混合过程的熵变?
解法2
mixS R nB ln xB
B
R
n(O2
)
ln
1 2
n(N2
)
ln
1 2
1.0 mol R ln 2 5.76 J K1
例1. 1.0mol Ag(s)在等容下由273K加热到303K,
这就是Gibbs自由能判据,系统不可能自动发生dG>0
的变化。
因为大部分实验在等温、等压条件下进行,所以这 个判据特别有用。
在等温、等压、可逆电池反应中
rG
W
' max
nEF
式中n为电池反应中电子的物质的量,E为可逆电
池的电动势,F为Faraday常数。 这是联系热力学和电化学的重要公式。因电池
例1:1 mol理想气体在等温下通过:(1)可逆膨 胀,(2)真空膨胀,体积增加到原来的10倍,分别 求其系统和环境的熵变,并判断过程的可逆性。
解:(1) 可逆膨胀
Ssys
Q T
R
Wmax T
nR ln V2 V1
nR ln10 19.14 J K1
Ssys Ssur
Siso 0
过程(1)为可逆过程。
解:(2)真空膨胀 熵是状态函数,始终态相同熵变也相同,所以:
Ssys 19.14 J K1
Ssur 0 (系统未吸热,也未做功)
Siso Ssys Ssur = 19.14 J K1 > 0
(2)为不可逆过程。
例2:求下述过程熵变
H2O(1 mol, l, p ,373.15 K) H2O(1 mol, g ,p ,373.15 K)
已知H2O(l)在汽化时吸热 44.02 kJ
解:当系统得(失)热量时,可以认为环境是以可逆的方式
失(得)热量。由于环境比系统大得多,所以系统发生变化
时,环境的温度不变
Ssys
Q T
解:这是一个p,V,T都发生变化的反应,因知道始终态
的温度和体积,采用先等温后等容的途径
S
S1
S2
nR ln
V2 V1
nCV ,m
ln
T2 T1
[2.0
(8.314
ln
100 25
19.5
ln
600 300
)]J
K
1
50.1J K 1
例3. 在268.2K和100kPa压力下, 1.0mol液态苯 凝固,放热9874J,求苯凝固过程的熵变。已知, 苯熔点278.7K,标准摩尔熔化热为9916J/mol, Cp,m(l) =126.8J/K/mol, Cp,m(s) =122.6J/K/mol 。
根据 W dA
等号表示可逆过程,即:
(dA)T ,R Wmax
在等温、可逆过程中,系统对外所作的最大功等 于系统Helmholtz自由能的减少值,所以把 A 称为 功函(work function)。 若是不可逆过程,系统所作的功小于A的减少值
dA> W
如果系统在等温、等容且不作其他功的条件下
求过程的熵变。已知,在该温度区间内Ag(s)的
CV,m为24.48J/K/mol。 解:
S
dT nC ln T2 nCV ,m
T1 T
T2 V ,m T1
(1.0
24.48
ln
303 273
)J
K
1
2.55J
K
1
例2. 2.0mol 理想气体从300K加热到600K,体积 由25dm3变为100dm3,计算该过程的熵变。已 知,该气体的CV,m为19.5J/K/mol。
