八下数学每日一练:菱形的判定与性质练习题及答案_2020年解答题版
八下数学每日一练:菱形的判定与性质练习题及答案_2020年单选题版

八下数学每日一练:菱形的判定与性质练习题及答案_2020年单选题版答案答案答案2020年八下数学:图形的性质_四边形_菱形的判定与性质练习题~~第1题~~(2019西湖.八下期末) 如图,分别以Rt △ABC 的斜边AB ,直角边AC 为边向外作等边△ABD 和△ACE ,F 为AB 的中点,DE ,AB 相交于点G .连接EF ,若∠BAC =30°,下列结论:①EF ⊥AC ;②四边形ADFE 为菱形;③AD =4AG ;④△DBF ≌△EFA .则正确结论的序号是( )A . ①③B . ②④C . ①③④D . ②③④考点: 线段垂直平分线的判定;全等三角形的判定与性质;等边三角形的性质;直角三角形斜边上的中线;菱形的判定与性质;~~第2题~~(2019嘉兴.八下期末) 如图,将平行四边形纸片ABCD 折叠,使顶点D 恰好落在AB 边上的点M 处,折痕为AN ,那么对于结论:①MN ∥BC ,②MN=AM.下列说法正确的是( )A . ①②都错B . ①对②错C . ①错②对D . ①②都对考点: 平行四边形的性质;菱形的判定与性质;翻折变换(折叠问题);~~第3题~~(2019淮安.八下期中) 下列命题是真命题的是( )A . 四边都相等的四边形是矩形B . 菱形的对角线相等C . 对角线互相垂直的平行四边形是正方形D . 顺次连接矩形各边中点所得的四边形是菱形考点: 菱形的判定与性质;矩形的判定;正方形的判定;~~第4题~~(2019淮安.八下期中) 如图,△ABC 是边长为1的等边三角形,分别取AC ,BC 边的中点D ,E ,连接DE ,作EF ∥AC 得到四边形EDAF ,它的周长记作C ;分别取EF ,BE 的中点D , E , 连接D E , 作E F ∥EF ,得到四边形ED FF ,它的周长记作C 照此规律作下去,则C 等于( ) A . B . C . D .111111*********答案答案答案答案答案答案答案考点: 三角形中位线定理;菱形的判定与性质;~~第5题~~(2019东莞.八下期末) 在四边形ABCD 中,AC =BD .顺次连接四边形ABCD 四边中点E 、F 、G 、H ,则四边形EFGH 的形状是( )A . 矩形B . 菱形C . 正方形D . 不能确定考点: 线段的中点;菱形的判定与性质;~~第6题~~(2019封开.八下期末) 已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A . 当AB=BC 时,四边形ABCD 是菱形B . 当AC=BD 时,四边形ABCD 是正方形C . 当AC ⊥BD 时,四边形ABCD 是菱形 D . 当∠ABC=90°时,四边形ABCD 是矩形考点: 菱形的判定与性质;矩形的判定与性质;~~第7题~~(2019中山.八下期中) 如图,在∠MON 的两边上分别截取OA 、OB ,使OA =OB ;分别以点A 、B 为圆心,OA 长为半径作弧,两弧交于点C ;连接AC 、BC 、AB 、OC .若AB =2cm ,四边形OACB 的面积为4cm2.则OC 的长为( )cmA . 2B . 3C . 4D . 5考点: 菱形的判定与性质;~~第8题~~(2019南.八下期中) 下列判断错误的是( )A . 四个角相等的四边形是矩形B . 对角线垂直的四边形是菱形C . 对角线相等的平行四边形是矩形D . 对角线垂直的平行四边形是菱形考点: 菱形的判定与性质;矩形的判定与性质;~~第9题~~(2018东台.八下期中) 已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A . 当AB=BC 时,它是菱形B . 当AC=BD 时,它是正方形C . 当∠ABC=90°时,它是矩形D . 当AC ⊥BD 时,它是菱形考点: 菱形的判定与性质;矩形的判定;正方形的判定;~~第10题~~(2018深圳.八下期中) 如图,在平行四边形ABCD 中,用直尺和圆规作∠BAD 的平分线AG 交BC 于点E,以点A 为圆心,AB 长为半径画弧交AD 于F,若BF=12,AB=10,则AE 的长为( )A . 16B . 15C . 14D . 13考点: 勾股定理;平行四边形的性质;菱形的判定与性质;2020年八下数学:图形的性质_四边形_菱形的判定与性质练习题答案1.答案:C2.答案:D3.答案:D4.答案:C5.答案:C6.答案:B7.答案:C8.答案:B9.答案:B10.答案:A。
19.2菱形的性质与判定-2020-2021学年八年级数学下册(华师大版)(解析版)

19.2菱形的性质与判定一.选择题(共6小题)1.菱形具有而平行四边形不一定具有的性质是()A.两组对边分别平行B.两组对角分别相等C.对角线互相平分D.对角线互相垂直解:A、不正确,两组对边分别平行;B、不正确,两组对角分别相等,两者均有此性质正确;C、不正确,对角线互相平分,两者均具有此性质;D、菱形的对角线互相垂直但平行四边形却无此性质.故选:D.2.如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于()A.10B.√7C.6D.5解:∵四边形ABCD是菱形,∴OA=12AC,OB=12BD,AC⊥BD,∵AC=8,BD=6,∴OA=4,OB=3,∴AB=√OA2+OB2=5,即菱形ABCD的边长是5.故选:D.3.如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y=kx(x<0)的图象经过顶点B,则k的值为()A.﹣12B.﹣27C.﹣32D.﹣36解:∵A(﹣3,4),∴OA=√32+42=5,∵四边形OABC是菱形,∴AO=CB=OC=AB=5,则点B的横坐标为﹣3﹣5=﹣8,故B的坐标为:(﹣8,4),将点B的坐标代入y=kx得,4=k−8,解得:k=﹣32.故选:C.4.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为()A.1B.2C.3D.4解:作F点关于BD的对称点F′,连接EF′交BD于点P,则PF=PF′.∴EP+FP=EP+F′P.由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.∵四边形ABCD为菱形,周长为12,∴AB=BC=CD=DA=3,AB∥CD,∵AF=2,AE=1,∴DF=DF′=AE=1,∴四边形AEF′D是平行四边形,∴EF′=AD=3.∴EP+FP的最小值为3.故选:C.5.如图,在▱ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定▱ABCD是菱形的只有()A.AC⊥BD B.AB=BC C.AC=BD D.∠1=∠2解:A、正确.对角线垂直的平行四边形的菱形.B、正确.邻边相等的平行四边形是菱形.C、错误.对角线相等的平行四边形是矩形,不一定是菱形.D、正确.可以证明平行四边形ABCD的邻边相等,即可判定是菱形.故选:C.6.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB 长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为()A.16B.15C.14D.13解:连结EF,AE与BF交于点O,如图,∵AO平分∠BAD,∴∠1=∠2,∵四边形ABCD为平行四边形,∴AF∥BE,∴∠1=∠3,∴∠2=∠3,∴AB=EB,同理:AF=BE,又∵AF∥BE,∴四边形ABEF是平行四边形,∴四边形ABEF是菱形,∴AE⊥BF,OB=OF=6,OA=OE,在Rt△AOB中,由勾股定理得:OA=√AB2−OB2=√102−62=8,∴AE=2OA=16.故选:A.二.填空题(共4小题)7.如图,在菱形ABCD 中,对角线AC =6,BD =10,则菱形ABCD 的面积为 30 .解:∵在菱形ABCD 中,对角线AC =6,BD =10,∴菱形ABCD 的面积为:12AC •BD =30.故答案为:30.8.如图,在菱形ABCD 中,过对角线BD 上任一点P ,作EF ∥BC ,GH ∥AB ,下列结论正确的是 ①②④ .(填序号)①图中共有3个菱形;②△BEP ≌△BGP ;③四边形AEPH 的面积等于△ABD 的面积的一半;④四边形AEPH 的周长等于四边形GPFC 的周长.解:∵图中有三个菱形,如菱形ABCD 、菱形HOFD 、菱形BEPG ,∴①正确;∵四边形ABCD 是菱形,∴AB∥DC,AD∥BC,∠ABD=∠CBD,∵EF∥BC,GH∥AB,∴四边形BEPG是平行四边形,∴PE=BG,PG=BE,在△BEP和△PGB中,{BE=PG BP=BP PE=BG∴△BEP≌△PGB(SSS),∴②正确;∵只有当H为AD中点,E为AB中点时,四边形AEPH的面积等于△ABD的面积的一半,∴③错误;∵四边形ABCD是菱形,∴AB∥CD,AD∥BC,∵EF∥BC,GH∥AB,∴AD∥EF∥BC,AB∥GH∥CD,∴四边形AEPH、四边形HPFD、四边形BEPG、四边形PFCG是平行四边形,∴AH=BG=PE,AE=HP=DF,BE=PG=CF,DH=PF=VG,∵四边形ABCD是菱形,∴∠EBP=∠GBP,∵PE∥BG,∴∠EPB=∠GBP,∴∠EBP=∠EPB,∴BE=PE,∴AH=PE=BG=BE=CF=PG,同理AE=HP=DF=PF=CG,∴四边形AEPH的周长=四边形GPFC的周长,∴④正确;故答案为:①②④.9.如图,在菱形ABCD 中,点E 是AB 上的一点,连接DE 交AC 于点O ,连接BO ,且∠AED =50°,则∠CBO = 50 度.解:在菱形ABCD 中,AB ∥CD ,∴∠CDO =∠AED =50°,CD =CB ,∠BCO =∠DCO ,∴在△BCO 和△DCO 中,{CD =CB ∠BCO =∠DCO CO =CO,∴△BCO ≌△DCO (SAS ),∴∠CBO =∠CDO =50°.故答案为50.10.如图,四边形ABCD 是轴对称图形,且直线AC 是对称轴,AB ∥CD ,则下列结论:①AC ⊥BD ;②AD ∥BC ;③四边形ABCD 是菱形;④△ABD ≌△CDB .其中正确的是 ①②③④ (只填写序号)解:因为l 是四边形ABCD 的对称轴,AB ∥CD ,则AD =AB ,∠1=∠2,∠1=∠4,则∠2=∠4,∴AD =DC ,同理可得:AB=AD=BC=DC,所以四边形ABCD是菱形.根据菱形的性质,可以得出以下结论:所以①AC⊥BD,正确;②AD∥BC,正确;③四边形ABCD是菱形,正确;④在△ABD和△CDB中∵{AB=BCAD=DCBD=BD∴△ABD≌△CDB(SSS),正确.故答案为:①②③④.三.解答题(共1小题)11.如图,在▱ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.(1)求证:▱ABCD是菱形;(2)若AB=5,AC=6,求▱ABCD的面积.(1)证明:∵四边形ABCD是平行四边形,∴∠B=∠D,∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°,∵BE=DF,∴△AEB≌△AFD∴AB=AD,∴四边形ABCD是菱形.(2)连接BD交AC于O.∵四边形ABCD是菱形,AC=6,∴AC⊥BD,AO=OC=12AC=12×6=3,∵AB=5,AO=3,∴BO=√AB2−AO2=√52−32=4,∴BD=2BO=8,∴S平行四边形ABCD=12×AC×BD=24.。
2020—2021年人教版初中数学八年级下册菱形的性质与判定专项练习题及答案(精品试题).docx

八年级数学下册菱形性质与判定练习题一选择题:1.下列四边形中不一定为菱形的是()A.对角线相等的平行四边形B.每条对角线平分一组对角的四边形C.对角线互相垂直的平行四边形D.用两个全等的等边三角形拼成的四边形2.下列说法中正确的是()A.四边相等的四边形是菱形B.一组对边相等,另一组对边平行的四边形是菱形C.对角线互相垂直的四边形是菱形D.对角线互相平分的四边形是菱形3.若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是()A.菱形B.对角线互相垂直的四边形C.矩形D.对角线相等的四边形4.菱形的周长为8cm,高为1cm,则菱形两邻角度数比为()A.4:1 B.5:1 C.6:1 D.7:15.四个点A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD=•BC;⑤AD∥BC.这5个条件中任选三个,能使四边形ABCD是菱形的选法有().A.1种B.2种C.3种D.4种6.如图,在菱形ABCD中,AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠CDF=24°,则∠DAB等于()A.100°B.104°C.105°D.110°7.如图,在长方形ABCD中,AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,且△EFG为等腰直角三角形,则EF的长为()A.10B.10C.12D.128.用一条直线将一个菱形分割成两个多边形,若这两个多边形的内角和分别为M 和N,则M+N值不可能是()A.360°B.540°C.630°D.720°9.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为()A.1B.2C.3D.410.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC 的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是()A.4.8B.5C.6D.7.211.如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC 为8,宽AB为4,则折痕EF的长度为()A.5B.3C.2D.312.如图,四边形ABCD,AD与BC不平行,AB=CD.AC,BD为四边形ABCD的对角线,E,F,G,H分别是BD,BC,AC,AD的中点.下列结论:①EG⊥FH;②四边形EFGH 是矩形;③HF平分∠EHG;④EG =(BC﹣AD);⑤四边形EFGH是菱形.其中正确的个数是()A.1个B.2个C.3个D.4个二填空题:13.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E 为垂足,连接DF,则∠CDF的度数=度.14.如图,正△AEF的边长与菱形ABCD的边长相等,点E、F分别在BC、CD上,则∠B的度数是.15.把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重合,折痕为EF.若BF=4,FC=2,则∠DEF的度数是.16.如图,在▱ABCD中,对角线AC、BD相交于点O.如果AC=8,BD=14,AB=x,那么x取值范围是.17.在菱形ABCD中,AE为BC边上的高,若AB=5,AE=4,则线段CE的长为.18.如图,▱ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的长为.三解答题:19.如图,已知△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,求ED.20.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD平分线交BC于点E(尺规作图的痕迹保留在图中了),连EF.(1)求证:四边形ABEF为菱形;(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.21.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF ∥BE交DE的延长线于F,连接CD.(1)求证:四边形BCFE是菱形;(2)在不添加任何辅助线和字母的情况下,请直接写出图中与△BEC面积相等的所有三角形(不包括△BEC).22.如图,已知在菱形ABCD中,F为边BC的中点,DF与对角线AC交于M,过M作ME⊥CD于E,∠1=∠2.(1)若CE=1,求BC的长;(2)求证:AM=DF+ME.23.如图,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P为BD 中点,M为AB中点、N为DE中点,连接PM、PN、MN.(1)试判断△PMN的形状,并证明你的结论;(2)若CD=5,AC=12,求△PMN的周长.参考答案1.A2.A3.D4.B5.D6.B7.B8.C9.C.10.A 11.C 12.C13.答案为:60.14.案为:80°.15.答案为:60.16.答案为:3<x<11.17.【解答】解:当点E在CB的延长线上时,如图1所示.∵AB=5,AE=4,∴BE=3,CE=BC+BE=8;当点E在BC边上时,如图2所示.∵AB=5,AE=4,∴BE=3,CE=BC﹣BE=2.综上可知:CE的长是2或8.故答案为:2或8.18.【解答】解:分两种情况:(1)①当∠BPC=90°时,作AM⊥BC于M,如图1所示,∵∠B=60°,∴∠BAM=30°,∴BM=AB=1,∴AM=BM=,CM=BC﹣BM=4﹣1=3,∴AC==2,∴AB2+AC2=BC2,∴△ABC是直角三角形,∠BAC=90°,∴当点P与A重合时,∠BPC=∠BAC=90°,∴BP=BA=2;②当∠BPC=90°,点P在边AD上,CP=CD=AB=2时,BP===2;(2)当∠BCP=90°时,如图3所示:则CP=AM=,∴BP==;综上所述:当△PBC为直角三角形时,BP的长为2或2或.19.ED=1,提示:延长BE,交AC于F点.20.【解答】(1)证明:由尺规作∠BAF的角平分线的过程可得AB=AF,∠BAE=∠FAE,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠FAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE,∴BE=FA,∴四边形ABEF为平行四边形,∵AB=AF,∴四边形ABEF 为菱形;(2)解:∵四边形ABEF为菱形,∴AE⊥BF,BO=FB=3,AE=2AO,在Rt△AOB中,AO=4,∴AE=2AO=8.21.【解答】(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC,BC=2DE.∵CF∥BE,∴四边形BCFE是平行四边形.∵BE=2DE,BC=2DE,∴BE=BC.∴▱BCFE是菱形;(2)解:①∵由(1)知,四变形BCFE是菱形,∴BC=FE,BC∥EF,∴△FEC与△BEC是等底等高的两个三角形,∴S△FEC=S△BEC.②△AEB与△BEC是等底同高的两个三角形,则S△AEB=S△BEC.③S△ADC=S△ABC,S△BEC=S△ABC,则它S△ADC=S△BEC.④S△BDC=S△ABC,S△BEC=S△ABC,则它S△BDC=S△BEC.综上所述,与△BEC面积相等的三角形有:△FEC、△AEB、△ADC、△BDC.22.【解答】(1)解:∵四边形ABCD是菱形,∴AB∥CD,∴∠1=∠ACD,∵∠1=∠2,∴∠ACD=∠2,∴MC=MD,∵ME⊥CD,∴CD=2CE,∵CE=1,∴CD=2,∴BC=CD=2;(2)证明:如图,∵F为边BC的中点,∴BF=CF=BC,∴CF=CE,在菱形ABCD中,AC平分∠BCD,∴∠ACB=∠ACD,在△CEM和△CFM中,∵,∴△CEM≌△CFM(SAS),∴ME=MF,延长AB交DF的延长线于点G,∵AB∥CD,∴∠G=∠2,∵∠1=∠2,∴∠1=∠G,∴AM=MG,在△CDF和△BGF中,∵,∴△CDF≌△BGF(AAS),∴GF=DF,由图形可知,GM=GF+MF,∴AM=DF+ME.23.略。
八下数学每日一练:菱形的性质练习题及答案_2020年单选题版

八下数学每日一练:菱形的性质练习题及答案_2020年单选题版答案答案答案答案2020年八下数学:图形的性质_四边形_菱形的性质练习题~~第1题~~(2019诸暨.八下期末) 已知:如图,在菱形OABC 中,OC =8,∠AOC =60°,OA 落在x 轴正半轴上,点D 是OC 边上的一点(不与端点O ,C 重合),过点D作DE ⊥AB 于点E ,若点D ,E 都在反比例函数y = (x >0)图象上,则k 的值为( )A . 8B . 9C . 9D . 16考点: 待定系数法求反比例函数解析式;菱形的性质;解直角三角形;~~第2题~~(2019嵊州.八下期末) 如图1,在菱形ABCD 中,∠A=120°,点E 是BC边的中点,点P 是对角线BD 上一动点,设PD 的长度为x ,PE 与PC 的长度和为y ,图2是y 关于x 的函数图象,其中H 是图象上最低点,则a+b 的值为( )A . 7B . 4 +6C . 14D . 6 +9考点: 函数的图象;菱形的性质;轴对称的应用-最短距离问题;相似三角形的判定与性质;解直角三角形;~~第3题~~(2019苍南.八下期末) 如图,正方形ABCD 的边长为3,点EF 在正方形ABCD 内若四边形AECF 恰是菱形连结FB ,DE ,且AF -FB =3,则菱形AECF 的边长为( ).A .B .C . 2D .考点: 勾股定理;菱形的性质;正方形的性质;~~第4题~~(2019余姚.八下期末) 菱形具有而一般矩形不具有的性质是( )A . 对边相等B . 对角线相等C . 对角线互相平分D . 对角线互相垂直考点: 菱形的性质;~~第5题~~(2019南浔.八下期末) 在数学课拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长是1,且一个内角是60°的小菱形拼成的图形,P 是其中4个小菱形的公共顶点,小新在小明的启发下,将该图形沿着过点P 的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )22答案答案答案答案答案 A . 2 B . 3 C . D .考点: 勾股定理;菱形的性质;~~第6题~~(2019天台.八下期末) 如图,在菱形 中,E ,F 分别是 的中点,若∠B =50°,则∠AFE 的度数为( )A . 50°B . 60°C . 65°D . 70°考点: 菱形的性质;~~第7题~~(2019嘉兴.八下期末)如图,在平面直角坐标系xOy 中,已知点A(,0),B(1,1).若平移点A 到点C ,使以点O ,A ,C ,B 为顶点的四边形是菱形,则正确的平移方法是( )A . 向左平移1个单位,再向下平移1个单位 B . 向左平移(2-1个单位,再向上平移1个单位 C . 向右平移 个单位,再向上平移1个单位 D . 向右平移1个单位,再向上平移1个单位考点:坐标与图形性质;菱形的性质;坐标与图形变化﹣平移;~~第8题~~(2019漯河.八下期末) 如图,菱形ABCD 的对角线AC=5,BD=10,则该菱形的面积为( )A . 50B . 25C .D . 12.5考点: 菱形的性质;~~第9题~~(2019双阳.八下期末) 如图,菱形ABCD 的周长为16,面积为12,P 是对角线BD 上一点,分别作P 点到直线AB ,AD 的垂线段PE ,PF ,则PE +PF 等于( )A . 6B . 3C . 1.5D . 0.75考点: 平行四边形的面积;菱形的性质;~~第10题~~(2019莘.八下期中) 如图,四边形ABCD 是菱形,AC=8,DB=6,DH ⊥AB 于H ,则DH 等于( )答案A . B . C . 5 D . 4考点: 菱形的性质;菱形的判定;2020年八下数学:图形的性质_四边形_菱形的性质练习题答案1.答案:C2.答案:C3.答案:A4.答案:D5.答案:D6.答案:C7.答案:D8.答案:B9.答案:B10.答案:A。
八下数学每日一练:菱形的性质练习题及答案_2020年压轴题版
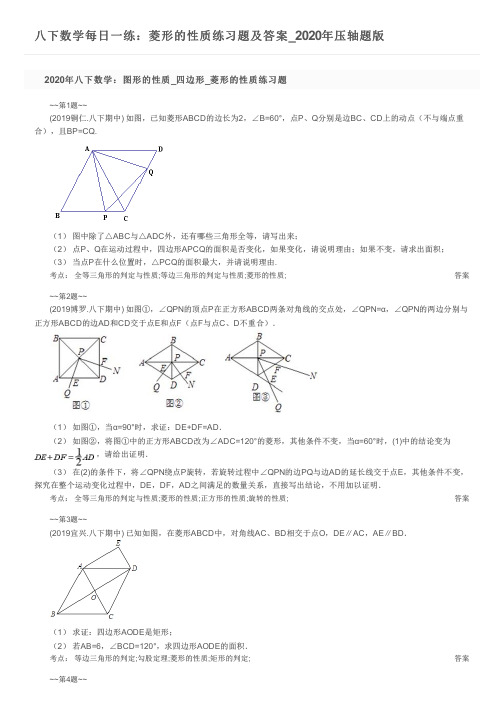
八下数学每日一练:菱形的性质练习题及答案_2020年压轴题版答案答案答案2020年八下数学:图形的性质_四边形_菱形的性质练习题~~第1题~~(2019铜仁.八下期中) 如图,已知菱形ABCD 的边长为2,∠B=60°,点P 、Q 分别是边BC 、CD 上的动点(不与端点重合),且BP=CQ.(1) 图中除了△ABC 与△ADC 外,还有哪些三角形全等,请写出来;(2) 点P 、Q 在运动过程中,四边形APCQ 的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;(3) 当点P 在什么位置时,△PCQ 的面积最大,并请说明理由.考点: 全等三角形的判定与性质;等边三角形的判定与性质;菱形的性质;~~第2题~~(2019博罗.八下期中) 如图①,∠QPN 的顶点P 在正方形ABCD 两条对角线的交点处,∠QPN=α,∠QPN 的两边分别与正方形ABCD 的边AD 和CD 交于点E 和点F (点F 与点C 、D 不重合).(1) 如图①,当α=90°时,求证:DE+DF=AD .(2) 如图②,将图①中的正方形ABCD 改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为,请给出证明.(3) 在(2)的条件下,将∠QPN 绕点P 旋转,若旋转过程中∠QPN 的边PQ 与边AD 的延长线交于点E ,其他条件不变,探究在整个运动变化过程中,DE ,DF ,AD 之间满足的数量关系,直接写出结论,不用加以证明.考点: 全等三角形的判定与性质;菱形的性质;正方形的性质;旋转的性质;~~第3题~~(2019宜兴.八下期中) 已知如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,DE ∥AC ,AE ∥BD .(1) 求证:四边形AODE 是矩形;(2) 若AB=6,∠BCD=120°,求四边形AODE 的面积.考点: 等边三角形的判定;勾股定理;菱形的性质;矩形的判定;~~第4题~~答案答案(2019桂林.八下期末) 如图,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点C 在x 轴的正半轴上,AB边交y 轴于点H ,OC =4,∠BCO =60°.(1) 求点A 的坐标(2) 动点P 从点A 出发,沿折线A ﹣B 一C 的方向以2个单位长度秒的速度向终点C 匀速运动,设△POC 的面积为S ,点P 的运动时间为t 秒,求S 与t 之间的函数关系式(要求写出自变量t 的取值范围);(3) 在(2)的条件下,直接写出当t 为何值时△POC 为直角三角形.考点: 动点问题的函数图象;三角形的面积;勾股定理;菱形的性质;~~第5题~~(2019天河.八下期末) 如图,在菱形ABCD 中,∠A =60°,AD =8,F 是AB 的中点,过点F 作FE ⊥AD , 垂足为E , 将△AEF 沿点A 到点B 的方向平移,得到△A ′E ′F ′.(1) 求EF 的长;(2) 设P ,P ′分别是EF ,E ′F ′的中点,当点A ′与点B 重合时,求证四边形PP ′CD 是平行四边形,并求出四边形PP ′CD 的面积.考点: 等边三角形的判定与性质;含30度角的直角三角形;勾股定理;平行四边形的性质;菱形的性质;2020年八下数学:图形的性质_四边形_菱形的性质练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
八年级下《菱形的性质与判定》练习题及答案

2017年八年级数学下册菱形性质与判定练习题一选择题:1.下列四边形中不一定为菱形的是()A. 对角线相等的平行四边形B. 每条对角线平分一组对角的四边形C.对角线互相垂直的平行四边形D.用两个全等的等边三角形拼成的四边形2∙下列说法中正确的是()A. 四边相等的四边形是菱形B. 一组对边相等,另一组对边平行的四边形是菱形C. 对角线互相垂直的四边形是菱形D. 对角线互相平分的四边形是菱形3∙若顺次连接四边形 ABCD 各边的中点所得四边形是菱形,则四边形4.菱形的周长为8cm,高为1cm,则菱形两邻角度数比为(ABCD- '定是A.菱形B.对角线互相垂直的四边形C. 矩形D. 对角线相等的四边形.5: 1.6: .7: 15.四个点A, B, C, D在同一平面内,从①AB// CD ②AB=CD③AC⊥ BD④AD=?BC⑤AD// BC.这5个条件中任选三个,能使四边形ABCD是菱形的选法有).A.1 种B.2C.3D.46.如图,在菱形ABCD中, AB的垂直平分线EF交对角线AC于点F,垂足为点E,连接DF,若∠ CDF=24 ,则∠A . 100°B . 104°C . 105°.110°7.如图,在长方形ABCD中,AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,且厶EFG为等腰直角三C.12D.12 √28∙用一条直线将一个菱形分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N直不可能是(A.360B.540C.630D.720))9.如图,在周长为12的菱形ABCD 中,AE=1,AF=2,若P 为对角线BD 上一动点,则EP+FP 的最小值为()到矩形的两条对角线AC 和BD 的距离之和是11.如图,把长方形纸片 ABCD 折叠,使其对角顶点 C 与A 重合.若长方形的长BC 为8,宽AB 为4,则折痕EF 的长度 为()A.5B.3C.2D.3 √212.如图,四边形ABCD,AD 与 BC 不平行,AB=CD.AC,BD 为四边形 ABCD 的对角线,E,F,G,H 分别是BD,BC,AC,AD 的中 点•下列结论:①EGL FH;②四边形EFGH 是矩形;③HF 平分∠ EHG ④EG =二(BC- AD :⑤四边形 EFGH 是菱形•其中正确的个数是()A.1个B.2个C.3 个D.4 个填空题:13.如图,在菱形ABCD 中,∠ BAD=80 ,AB 的垂直平分线交对角线 AC 于点F,E 为垂足,连接DF,则∠ CDF 的度数=度.A.1B.2C.3D.410.如图,点 P 是矩形ABCD 的边AD 上的一动点,矩形的两条边AB 、 BC 的长分别是6和8,则点PB.5C.6D.7.2A.4.8GSFCC15.把一张矩形纸片 ABCD按如图方式折叠,使顶点 B和顶点D重合,折痕为EF.若BF=4, FC=2,则∠ DEF的度数是 .16∙如图,在?ABCD中 ,对角线AC BD相交于点O.如果AC=8,BD=14,AB=x,那么X取值范围是______________17. ______________________________________________________________________ 在菱形ABCD中, AE为BC边上的高,若 AB=5 AE=4,则线段CE的长为_______________________________________________18. 如图,?ABCD中,AB=2,BC=4, ∠ B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的三解答题:19. 如图,已知△ ABc中 ,D是BC⅛的中点,AE平分∠ BAC,BE1 AE于 E点,若 AB= 5,AC= 7,求ED.20. 如图,在平行四边形ABC中 ,用直尺和圆规作∠ BAD^分线交BC于点E(尺规作图的痕迹保留在图中了),连EF.(2) AE, BF相交于点Q若BF=6, AB=5求AE的长. (22.21. 如图,在△ ABC 中,D E 分别是 AB AC 的中点,BE=2DE 过点C 作CF// BE 交DE 的延长线于 F,连接CD (1) 求证:四边形BCFE 是菱形; (2)在不添加任何辅助线和字母的情况下,请直接写出图中与△BEC 面积相等的所有三角形(不包括厶 BEC)22. 如图,已知在菱形ABCD^ ,F 为边BC 勺中点,DF 与对角线AC 交于M,过M 乍MELCDf E, ∠仁∠ 2.23. 如图,已知等腰 Rt△ ABC 和厶CDE AC=BC,CD=C,E 连接BE AD, P 为BD 中点,M 为AB 中点、N 为DE 中点, 连接 PM PN MN.(1) 试判断△ PMN 勺形状,并证明你的结论; (2) 若CD=5 AC=12求厶PMN 的周长.BE=3 CE=BC+BE=β当点E 在BC 边上时,如图 2所示. BE=3 CE=BC- BE=2 综上可知:CE 的长是2或8.故答案为:2或8.18. 【解答】解:分两种情况:(1)①当∠ BPC=90时,作 AML BC 于M 如图1所示,τ∠ B=60°,∙∙∙∠ BAM=30 ,二 BM=TAB=1,1.A2.A3.D4.B5.D6.B7.B8.C9.C 13. 答案为:60 . 14. 案为:80°. 15. 答案为:60 . 参考答案.10.A 11.C 12.C16. 答案为:3v X V 11. 17. 【解答】解:当点 E 在CB 的延长线上时,如图 1所示.■/ AB=5 AE=4, ■/ AB=5 AE=4, (2)求证:AM=DF+ME∙ AM= BM= , CM=BC- BM=4- 1=3, =2归,∙ A B+A 6=B 6 , •••△ ABC 是直角三角形,∠ BAC=90 ,•当点 P 与 A 重合时,∠ BPC=/ BAC=90 , ∙ BP=BA=2②当 ∠ BPC=90 ,点 P 在边 AD 上,CP=CD=AB=时,BP=J B C^ _ CP ^ =荷 (2)当 ∠ BCP=90 时,如图 3 所示:则 CP=AM 丹,∙ BPF JBC ?+C P ^=^^;V 四边形 ABC 是平行四边形,• AD// BC, ∙∠ FAE=∠ AEB ∙∠ BAE=Z AEB• AB=BE ∙ BE=FA •四边形ABEf 为平行四边形,V AB=AE •四边形ABEf 为菱形; (2)解:V 四边形 ABE 为菱形,∙ AE L BF, BO= FB=3, AE=2AQ 在 Rt△ AoB^ , AO=4 ∙ AE=2AO=8【解答】(1)证明:v D E 分别是AB AC 的中点,∙ DE// BC BC=2DE v CF// BE,∙∙∙四边形BCFE 是平行四边形.V BE=2DE BC=2DE ∙ BE=BC • ?BCFE 是菱形;(2)解:① v 由(1)知,四变形 BCFE 是菱形,∙ BC=FE BCll EF,• △ FEC 与厶BEC 是等底等高的两个三角形,• ②厶AEB 与厶BEC 是等底同高的两个三角形,贝U S A BE C F Q S A ABC 则它 S A ADC =S A BEC.【解答】(1)解:I 四边形ABC 是菱形,∙ AB// CD ∙∠ 1 = ∠ACDτ∠ 1 = ∠ 2 ,∙∠ ACD=/ 2 ,∙ MC=M P v MEL CD ∙ CD=2CE∙∙∙ CE=I ∙ CD=2 ∙ BC=CD=2(2)证明:如图,∙∙∙ F 为边 BC 的中点,∙∙∙ BF=CF= BC,二 CF=CE综上所述:当△ PBC 为直角三角形时, DBP 的长为2或2 或 ∣.∙ AC =2- 22=W3 ;21. S A FEC =S ABEC.S △ AEB F S Δ③ S A AD(FQ S A ABC FEC △ AEB △ ADC △ BDC△ ④ S A BD (= Q SS A BEC =G S A ABC 则它 S A BDC F S A BEC.在菱形 ABC中,AC平分∠ BCD ∙∙∙∠ACB=∠ ACD 22.CE=CF在厶CEM^n△ CFM中,∙∙∙二J ZAeD ,•••△CEM^△ CFM( SAS ,I Cl=CM• ME=MF 延长 AB交 DF的延长线于点 G,τ AB// CD, ∙∠ G=∠ 2,ΓZG≈Z2∙∙∙∠1 = ∠ 2,∙∙∙∠仁∠ G • AM=MG在厶 CD和△ BGFφ,∙∙∙d朗SZOTK对顶角招等),BFWF•••△CDF^△ BGF( AAS , ∙ GF=DF 由图形可知, GM=GF+MF∙ AM=DF+MEG 5JRP T S-Il ■ «ri!!r-BrB!rBT9B B -CST23.略。
初中数学菱形的判定及性质练习题(附答案)

初中数学菱形的判定及性质练习题 一、单选题 1.如图,正方形ABCD 的边长为4,点E 在对角线BD 上,且22.5BAE ∠=︒,EF AB ⊥,垂足为F ,则EF 的长为( )A. 1B. 2C. 422-D. 324-2.如图,点P 是矩形ABCD 的边AD 上的一个动点,矩形的两条边AB 、BC 的长分别为3和4,那么点P 到矩形的两条对角线AC 、BD 的距离之和是( )A. 125B. 245C. 65D.不确定3.如图,下列条件之一能使平行四边形ABCD 是菱形的为( )①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BDA.①③B.②③C.③④D.①②③4.如图,在菱形ABCD 中, 2AB =,60?BAD ∠=,E 是AB 的中点, P 是对角线AC 上的一个动点,则PE PB +的最小值为( )A. 1B.3C. 2D.55.菱形具有而一般平行四边形不具有的性质是( )A.对边相等B.对角相等C.对角线互相平分D.对角线互相垂直6.如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是( )=A.AB CD=B.AD BC=C.AB BC=D.AC BD=;②7.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB BC⊥中选两个作为补充条件,使ABCD为正方形(如=;④AC BDABC90∠=︒;③AC BD图),现有下列四种选法,你认为其中错误的是( )A.①②B.②③C.①③D.②④AC BD相交于点,O H为AD边的中点,菱形ABCD的周长8.如图,在菱形ABCD中,对角线,为28,则OH的长等于( )A.3.5B. 4C. 7D. 149.下列说法中正确的是( )A.两条对角线垂直的四边形是菱形B.对角线垂直且相等的四边形是正方形C.两条对角线相等的四边形是矩形D.两条对角线相等的平行四边形是矩形10.如图,在△ABC中,点D、E、F 分别在BC、AB、CA上,且DE//CA,DF//BA,则下列三种说法:①如果∠BAC=90°,那么四边形AEDF是矩形;②如果AD 平分∠BAC,那么四边形AEDF 是菱形;③如果AD⊥BC 且AB=AC,那么四边形AEDF 是菱形。
八下数学每日一练:菱形的判定练习题及答案_2020年填空题版

八下数学每日一练:菱形的判定练习题及答案_2020年填空题版答案答案答案2020年八下数学:图形的性质_四边形_菱形的判定练习题~~第1题~~(2016扬州.八下期中) 如图,点E 、F 、G 、H 分别是任意四边形ABCD 中AD 、BD 、BC 、CA 的中点,当四边形ABCD的边至少满足________条件时,四边形EFGH 是菱形.考点: 三角形中位线定理;菱形的判定;~~第2题~~(2018邗江.八下期中) 顺次连接对角线相等的四边形的四边中点,所得的四边形一定是________.考点: 三角形中位线定理;菱形的判定;~~第3题~~(2017北京.八下期末) 如图,在 ABCD 中,对角线AC , BD 相交于点O ,若再增加一个条件,就可得出 ABCD是菱形,则你添加的条件是________考点: 菱形的判定;~~第4题~~(2017怀柔.八下期末) 阅读下面材料:在数学课上,老师提出如下问题:小凯的作法如下:答案答案答案答案答案答案老师说:“小凯的作法正确.”请回答:在小凯的作法中,判定四边形AECF 是菱形的依据是________.考点: 平行四边形的判定与性质;菱形的判定;~~第5题~~(2017长春.八下期末) 如图,在四边形ABCD 中,AB=BC=CD=DA ,对角线AC 与BD 相交于点O ,若不增加任何字母与辅助线,要使四边形ABCD 是正方形,则还需增加一个条件是________.考点: 菱形的判定;正方形的判定;~~第6题~~(2017闵行.八下期末) 如图,在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BD 、CD 、AC 的中点,要使四边形EFGH 是菱形,四边形ABCD 还应满足的一个条件是________.考点: 三角形中位线定理;平行四边形的判定;菱形的判定;~~第7题~~(2017宜兴.八下期中) 如图,在△ABC 中,点D 是BC 的中点,点E ,F 分别在线段AD 及其延长线上,且DE=DF .给出下列条件:①BE ⊥EC ;②BF ∥CE ;③AB=AC;从中选择一个条件使四边形BECF 是菱形,你认为这个条件是________(只填写序号).考点: 菱形的判定;~~第8题~~(2017宜城.八下期末) 如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,请你添加一个适当的条件________使其成为菱形(只填一个即可).考点: 平行四边形的性质;菱形的判定;~~第9题~~(2017老河口.八下期末) 在▱ABCD 中,AB=5,AC=6,当BD=________时,四边形ABCD 是菱形.考点: 平行四边形的性质;菱形的判定;~~第10题~~(2017邵阳.八下期末) 如图,如果要使 ABCD 成为一个菱形,需要添加一个条件,那么你添加的条件是________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八下数学每日一练:菱形的判定与性质练习题及答案_2020年解答题版答案答案答案2020年八下数学:图形的性质_四边形_菱形的判定与性质练习题
~~第1题~~
(2019苏州.八下期中) 如图,在四边形ABCD 中,E 、F 分别是AD 、BC 的中点,G 、H 分别是BD 、AC 的中点且AB=CD,
则EF 与GH 有怎样的关系?请说明你的理由.
考点: 三角形中位线定理;菱形的判定与性质;~~第2题~~
(2019中山.八下期中) 在Rt △ABC 中,∠BAC=90°,D 是BC 的中点,E 是AD 的中点,过点A 作AF ∥BC
交BE 的延长线于点F .
(1) 求证:△AEF ≌△DEB ;
(2) 判断:四边形ADCF 是形,说明理由;
(3) 若AC=4,AB=5,求四边形ADCF 的面积.
考点: 全等三角形的判定与性质;菱形的判定与性质;~~第3题~~
(2019中山.八下期中) 如图,在Rt △ABC 中,∠B=90°,AC=12,∠A=60°.点D 从点C 出发沿CA 方向以每秒2个单位长的速度向A 点匀速运动,同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动,当其中一个点到达终点时
,另一个点也随之停止运动.设点D 、E 运动的时间是t 秒(t >0).过点D 作DF ⊥BC 于点F ,连接DE 、EF .(1) AB 的长是.
(2) 在D 、E 的运动过程中,线段EF 与AD 的关系是否发生变化?若不变化,那么线段EF 与AD 是何关系,并给予证明;若变化,请说明理由.
(3) 四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,说明理由.
考点: 含30度角的直角三角形;平行四边形的判定与性质;菱形的判定与性质;~~第4题~~
(2017.八下期末) 如图,已知四边形ABCD 是矩形,对角线AC 、BD 相交于点O ,CE ∥BD ,DE ∥AC ,CE 与DE 交于点
答案答案E.请探索
CD 与OE 的位置关系,并说明理由.
考点: 菱形的判定与性质;矩形的性质;~~第5题~~
(2017北京
.八下期中) 如图,菱形
中,对角线
,
交于
点,
,
.
求证:四边形
为矩形.
考点: 菱形的判定与性质;矩形的判定;2020年八下数学:图形的性质_四边形
_菱形的判定与性质练习题答案
1.答案:
2.答案:
3.答案:
4.答案:
5.答案:。
