考研数学：无穷级数考点和常考题型分析
无穷级数知识点总结考研
无穷级数知识点总结考研一、无穷级数的概念无穷级数是由无穷多个数的和组成，通常用符号∑表示。
其一般形式为：S = a_1 + a_2 + a_3 + ...... + a_n + ......其中a_n是一个数列，称为级数的通项。
无穷级数是由级数的部分和组成的序列，即S_n = a_1 + a_2 + ...... + a_n，所以求无穷级数的和，就是求该序列的极限，即lim(S_n)。
在实际运用中，我们通常是通过研究级数的部分和的性质，来求级数的和或证明级数的敛散性。
二、无穷级数的敛散性1. 收敛与发散的定义级数的和S = ∑a_n，如果级数的部分和S_n = a_1 + a_2 + ...... + a_n存在极限L，即lim(S_n) = L，那么称级数收敛，其和为L，记作∑a_n = L。
如果级数的部分和S_n的极限不存在，或者极限为无穷大，即lim(S_n) = ±∞，那么称级数发散。
2. 收敛级数的判定（1）正项级数收敛判定对于正项级数∑a_n，即a_n≥0，根据级数的部分和单调递增有界的结论，若存在常数M，使得对一切n始终成立S_n ≤ M，那么级数收敛；如果对于任意的M > 0，总存在n_0，使得对一切n > n_0有S_n > M，那么级数发散。
（2）比较判别法若对于所有的n，总有0 ≤ a_n ≤ b_n，且∑b_n收敛，那么∑a_n也收敛；若对于所有的n，总有a_n ≥ b_n ≥ 0，且∑b_n发散，那么∑a_n也发散；若∑b_n发散，且对于足够大的n，总有a_n＞b_n，则∑a_n发散。
（3）比值判别法若存在常数0 < q < 1及整数n_0，使得当n > n_0时，有a_n_+1/a_n ≤ q，那么级数收敛；若a_n_+1/a_n≥1，那么级数发散；若a_n_+1/a_n不满足以上两个条件，那么比值判别法无法判断级数的敛散性。
考研数学常考题型及解题思路
考研数学常考题型及解题思路考研数学是众多考研学子需要攻克的重要科目之一。
在备考过程中，了解常考题型及掌握相应的解题思路至关重要。
以下将为大家详细介绍考研数学中常出现的题型以及有效的解题方法。
一、函数、极限与连续这部分是考研数学的基础，经常以选择题、填空题和解答题的形式出现。
1、求函数的极限对于简单的函数，直接代入法是常用的。
例如，当函数在某点的定义明确时，可以直接将该点的值代入函数中求解。
对于较为复杂的分式函数，通常采用约分、通分、有理化等方法将其化简，然后再求极限。
当遇到无穷小量乘以有界函数时，其极限为零。
2、函数的连续性要判断函数在某点的连续性，需要先判断函数在该点是否有定义，然后判断函数在该点的极限是否存在，最后判断极限值是否等于函数在该点的函数值。
间断点的类型判断也是常见考点，包括可去间断点、跳跃间断点和无穷间断点等。
二、一元函数微分学这部分在考研数学中占有较大比重。
1、导数的计算利用基本的求导公式是基础，如常见的幂函数、指数函数、对数函数等的求导公式。
对于复合函数，使用链式法则进行求导。
隐函数求导则需要通过方程两边同时对自变量求导来求解。
2、利用导数研究函数的性质通过求导判断函数的单调性和极值。
当导数大于零时，函数单调递增；导数小于零时，函数单调递减。
导数为零的点可能是极值点。
利用二阶导数判断函数的凹凸性。
二阶导数大于零时，函数为凹函数；二阶导数小于零时，函数为凸函数。
三、一元函数积分学1、不定积分的计算熟练掌握基本积分公式是关键。
换元积分法和分部积分法是常用的方法。
换元积分法要注意选择合适的换元方式，分部积分法通常适用于被积函数是两个不同类型函数乘积的情况。
2、定积分的计算与应用计算定积分可以通过牛顿莱布尼茨公式，先求出原函数，然后代入上下限相减。
定积分在几何上可以求图形的面积、旋转体的体积等；在物理上也有广泛的应用。
四、多元函数微分学1、偏导数的计算按照定义分别对每个自变量求偏导。
考研数学微分方程与无穷级数相关解析
考研数学微分方程与无穷级数相关解析“世事洞明皆学问”。
想把一件事做好，就需要用心揣摩其规律、总结其方法。
考研复习亦不例外：除了结合考纲把基础打牢，还需适当总结方法、关注重点。
针对考生需求，以下是高数微分方程与无穷级数部分，供参考。
一、微分方程微分方程可视为一元函数微积分学的应用与推广。
该部分在考试中以大题与小题的形式交替出现，平均每年所占分值在8分左右。
常考的题型包括各种类型微分方程的求解，线性微分方程解的性质，综合应用。
对于该部分内容的复习，考生首先要能识别各种方程类型(一阶：可分离变量的方程、齐次方程、一阶线性方程、伯努利方程(数一、二)、全微分方程(数一);高阶：线性方程、欧拉方程(数一)、高阶可降阶的方程(数一、二))，熟悉其求解步骤，并通过足量练习以求熟练掌握;在此基础上还要具备数学建模的能力——能根据几何或物理背景，建立微分方程。
另外，有几点需提醒考生：1. 解微分方程主要考查考生计算积分的能力，而实际应用则对考生的综合能力提出较高要求，考生需结合练习把“解方程”和“列方程”的能力练好。
2. 非基本类型的方程一般都可通过变量替换化为基本类型。
3. 考生需弄清常见的物理量、几何量与微分、积分的关系。
二、无穷级数级数可视为微积分的综合应用。
该部分是数一、数三的必考内容，分值约占10%。
常考的题型有：常数项级数的收敛性，幂级数的收敛半径和收敛域，幂级数展开，幂级数求和，常数项级数求和以及傅里叶级数。
其中幂级数是重点。
结合考试分析，建议考生从以下方面把握该部分内容：1. 常数项级数理解其收敛的相关概念并掌握各种收敛性判别法。
2. 幂级数考试有三方面的要求：幂级数收敛域的计算，幂级数求和，幂级数展开。
考生应通过一定量训练使自己具备这三方面的能力——给定幂级数，准确计算其收敛半径进而得到收敛域，能求其和函数，能将一个简单函数在指定点展开成幂级数。
3.傅里叶级数考试出现频率和考试要求均较低，掌握傅里叶系数的求法，再了解狄利克雷定理的内容即可。
积分学和无穷级数
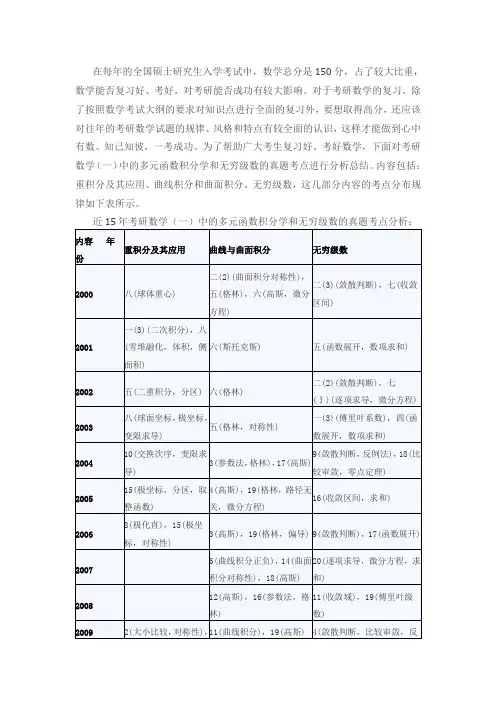
在每年的全国硕士研究生入学考试中，数学总分是150分，占了较大比重，数学能否复习好、考好，对考研能否成功有较大影响。
对于考研数学的复习，除了按照数学考试大纲的要求对知识点进行全面的复习外，要想取得高分，还应该对往年的考研数学试题的规律、风格和特点有较全面的认识，这样才能做到心中有数、知己知彼，一考成功。
为了帮助广大考生复习好、考好数学，下面对考研数学（一）中的多元函数积分学和无穷级数的真题考点进行分析总结。
内容包括：重积分及其应用、曲线积分和曲面积分、无穷级数，这几部分内容的考点分布规律如下表所示。
近15年考研数学（一）中的多元函数积分学和无穷级数的真题考点分析： 内容 年份 重积分及其应用 曲线与曲面积分无穷级数 2000 八(球体重心) 二(2)(曲面积分对称性)，五(格林)，六(高斯，微分方程)二(3)(敛散判断)，七(收敛区间) 2001 一(3)(二次积分)，八(雪堆融化，体积，侧面积)六(斯托克斯)五(函数展开，数项求和) 2002 五(二重积分，分区) 六(格林)二(2)(敛散判断)，七(Ⅰ)(逐项求导，微分方程) 2003 八(球面坐标，极坐标，变限求导)五(格林，对称性)一(3)(傅里叶系数)，四(函数展开，数项求和) 2004 10(交换次序，变限求导) 3(参数法，格林)，17(高斯) 9(敛散判断，反例法)，18(比较审敛，零点定理)2005 15(极坐标，分区，取整函数)4(高斯)，19(格林，路径无关，微分方程) 16(收敛区间，求和) 2006 8(极化直)，15(极坐标，对称性)3(高斯)，19(格林，偏导) 9(敛散判断)，17(函数展开)2007 6(曲线积分正负)，14(曲面积分对称性)，18(高斯) 20(逐项求导，微分方程，求和)2008 12(高斯)，16(参数法，格林) 11(收敛域)，19(傅里叶级数) 2009 2(大小比较，对称性)，12(球面坐标，对称性) 11(曲线积分)，19(高斯) 4(敛散判断，比较审敛，反例法)，16(数项求和，面积)2010 4(定义求和)，12(立体形心)11(参数法，格林)，19(曲面积分，切平面，投影) 18(收敛域，和函数) 201119(交换次序，分部积分，抽象函数) 12(参数法，斯托克斯) 2(收敛域) 201212(曲面积分)，19(格林) 17((收敛域，和函数)) 2013 19(旋转体方程，立体形心) 4(格林，参数法) 3(傅里叶，延拓，周期性)，16(逐项求导，微分方程) 20143(交换次序，直化极) 12(参数法，斯托克斯)，18(高斯，对称性，投影法)19(证数列收敛、级数收敛) 上面表格中数字表示相应年份的试卷中考题的题号，数字后面括号里的文字说明表示该考题涉及的主要考点或主要解题方法。
考研第七章 无穷级数
第八章 无穷级数（数学一和数学三）引 言所谓无穷级数就是无穷多项相加，它与有限项相加有本质不同。
历史上曾经对一个无穷级数问题引起争论。
例如+-++-+-+1)1(1111n历史上曾有三种不同看法，得出三种不同的“和”， 第一种 0)11()11()11(=+-++-+- 第二种 1)11()11()11(1=-------- 第三种 设S n =+-++-+-+ 1)1(1111 则[]S =+-+-- 11111 S S =-1， 12=S ， 21=S这种争论说明对无穷多项相加，缺乏一种正确的认识， （1）什么是无穷多项相加？如何考虑？ （2）无穷多项相加，是否一定有“和”？（3）无穷多项相加，什么情形有结合律，什么情形有交换律等性质。
因此对无穷级数的基本概念和性质需要作详细的讨论。
8.1 常数项级数甲 内容要点一．基本概念与性质 1．基本概念无穷多个数 ,,,,,321n u u u u ，依次相加所得到的表达式+++++=∑∞=n n nu u u u u3211称为数项级数（简称级数）() ,3,2,13211=++++==∑=n u u u u uS n nk kn称为级数的前n 项的部分和。
{}),3,2,1( =n S n 称为部分和数列。
若()S S n n =∞→存在lim ，则称级数∑∞=1n n u 是收敛的，且其和为S ，记以S u n n =∑∞=1若n n S ∞→lim 不存在，则称级数∑∞=1n n u 是发散的，发散级数没有和的概念。
（注：在某些特殊含义下可以考虑发散级数的和，但在基础课和考研的考试大纲中，不作这种要求。
）2．基本性质（1）如果∑∞=1n n u 和∑∞=1n n v 皆收敛，b a ,为常数，则()∑∞=+1n n nbv au收敛，且等于∑∑∞=∞=+11n n n n v b u a（2）在级数中增加或减少或变更有限项则级数的收敛性不变。
考研数学一大题题型归纳
考研数学一大题题型归纳考研数学一是一个比较重要的科目，其中一道大题是题型比较多样且需要综合运用多个知识点的题目。
在这篇文章中，我将归纳一些常见的考研数学一大题题型，帮助考生更好地准备考试。
1. 函数与极限题型这是考研数学一中出现频率较高的题型之一。
经典的题型包括利用函数的性质求函数的特定值、函数的界与连续性、函数的单调性与图像的性质等。
考生需要熟练掌握函数与极限的性质，并灵活应用。
2. 一元函数微分学与高阶导数题型这类题目考查考生对导数概念的理解，要求灵活应用求导法则、高阶导数及其在函数研究中的应用。
常见的题型包括求函数的极值、函数的凹凸区间、函数与导数的关系等。
解题时，考生需要熟悉函数导数的基本概念与性质，并理解函数导数与函数本身的关系。
3. 一元函数积分学题型一元函数积分学也是考研数学一中的重点内容。
常见题型包括利用定积分求曲线下面积、参数方程下的弧长、平均值等。
考生需要掌握定积分的计算方法（换元法、分部积分等），并了解定积分的几何意义与物理应用。
4. 一阶线性微分方程题型一阶线性微分方程是考研数学一的重点内容之一。
这类题目要求考生对微分方程的求解方法有深入的理解，熟悉常微分方程的基本理论与性质，并能够灵活运用。
常见的题型包括求解一阶线性方程、初值问题、变量可分离方程等。
5. 常微分方程数值解题型这类题目考查考生对常微分方程数值解方法的掌握程度。
题型多样，常见包括欧拉法、改进的欧拉法、四阶龙格-库塔法等。
考生需要了解数值解方法的基本原理和步骤，并能够运用具体的数值方法求解常微分方程。
6. 多元函数微分学与积分学题型多元函数微分学与积分学是考研数学一中的难点内容。
考题要求考生熟悉多元函数的偏导数、方向导数、全微分、极值与条件极值等概念与性质，并能够应用到具体的题目中去。
对于多元函数的积分学，考生需要了解多重积分的计算方法（变量代换法、极坐标法、球坐标法等），并能够正确应用。
7. 无穷级数题型无穷级数是考研数学一中的重点内容之一。
7考研数学大纲知识点解析(第七章无穷级数(数学一)和傅里叶级数(数学一))
，
使
，于是
．令
，当 充分大时，有
因为
收敛，所以级数
绝对收敛．
【综合题】（04 年，数学一）设有方程
，其中 为正整数．证明此方程存
在唯一正实根 ，并证明当
时，级数
收敛．
【证明】记
．当
时，
，
故
在
上单调增加．
由于
，根据连续函数的零点存在定理知方程
存在唯一正实根 ，且
．从而当
时，有
，
而正项级数
收敛，所以当
在其收敛域 上可以逐项积分，即
， 且积分后的幂级数的收敛半径与原级数的收敛半径相同．
【函数展开成幂级数】
设
在
点的邻域
存在任意阶导数，则称幂级数
为
在
点处的泰勒级数．
特别地，当
时，称幂级数
【泰勒级数收敛充要条件】设函数
敛于
的充要条件为
，为
的麦克劳林级数．
在
内存在任意阶导数，则其泰勒级数收
，
其中
．
【常见麦克劳林级数】
（A）发散．
（C）绝对收敛． 【答案】（C）．
收敛，则级数 （B）条件收敛． （D）收敛性与 有关．
【解析】由于
，
又级数
与
均收敛，所以由级数的运算性质得级数
收敛，
由正项级数的比较判别法，得级数
绝对收敛．故选（C）．
【例题】（03 年，数学三）
设
，则下列命题正确的是 ．
（A）若
条件收敛，则
与
都收敛．
【解析】因
当
时，因级数
设
，所以收敛半径
．
及
发散，故收敛域为
无穷级数知识点总结专升本
无穷级数知识点总结专升本一、概念无穷级数是由无限多个项组成的级数，其中每个项都是一个数字或者变量的表达式。
无穷级数通常用符号∑表示，其中∑表示总和，表示对所有项进行求和。
无穷级数可以是收敛的，也可以是发散的。
对于收敛的无穷级数，其和可以用极限来表示；对于发散的无穷级数，其和不存在。
二、级数的性质1.级数的部分和级数的部分和是指级数前n项的和，用Sn表示。
当n趋向无穷大时，级数的部分和就是级数的和。
当级数的部分和的极限存在时，级数收敛；当级数的部分和的极限不存在时，级数发散。
2.级数的收敛与发散级数的收敛指的是级数的部分和的极限存在，也就是级数的和存在；级数的发散指的是级数的部分和的极限不存在，也就是级数的和不存在。
3.级数的敛散性级数敛散性指的是级数的收敛性或发散性。
级数的敛散性可以通过级数的部分和的极限是否存在来判断。
4.级数的比较性级数的比较性是指通过级数的部分和与其他级数的部分和进行比较来判断级数的敛散性。
可以通过比较原则、比值原则、根值原则等方法来比较级数的敛散性。
5.级数的运算性质级数满足加法、数乘、绝对收敛、收敛性与级数重新排列等运算性质。
三、收敛级数1.正项级数对于所有项均为非负数的级数，称为正项级数。
正项级数通常采用单调有界数列的性质来判断是否收敛。
2.幂级数幂级数是形式为∑an*x^n的无穷级数，其中an为常数系数，x为自变量。
幂级数通常需要通过收敛半径来判断其收敛性。
3.级数的收敛判别法级数的收敛判别法是用来判断级数是否收敛的方法，包括比较法、审敛法、根值法、比值法、积分法等。
4.级数收敛性的应用无穷级数的收敛性可以应用于数学和物理等领域，如泰勒级数、傅立叶级数等。
四、发散级数1.发散级数的定义对于发散级数而言，其和不存在，无法通过有限项之和来表示。
发散级数可能是几何级数、调和级数、交错级数等。
2.级数的发散判别法级数的发散判别法是用来判断级数是否发散的方法，例如：项数发散法、数值发散法、微分法等。
考研数学考点解析及必考题型总结
考研数学考点解析及必考题型总结考研数学考点分析及和考题型总结考研数学的卷种分三种，分别为数学一、数学二、数学三。
这三个卷中针对的专业不同，须使用数学一的招生专业为工学门类中的力学、机械工程、光学工程、仪器科学与技术、信息与通信工程、控制科学与工程、计算机科学与技术、土木工程、水利工程、测绘科学与技术、交通运输工程、交通运输工程、传播与海洋工程、航空宇航科学与技术、兵器科学与技术、核科学与技术、生物医学工程等20个一级学科中所有的二级学科、专业，授工学学位的管理科学与工程的一级学科。
工学门类中的材料科学与工程、化学工程与技术、地质资源与地质工程、矿业工程、石油与天然气工程、环境科学与工程等一级学科中对数学要求较高的二级学科，专业的选用数学一，对数学要求较高的选用数学二。
专业不同对数学的要求自然不同，从难度看数学一最难，其次是数学二，最后是数学三，从考试范围看，数学一考试范围最多，数学三次之，最后，数学二，三种卷中大部分考试内容是一样的，数一数二数三又各有自己特点和单独考查的内容。
下面跨考教育数学教研室边一老师就数学一单独考查内容进行一一盘点。
一元函数微分学：隐函数求导、曲率圆和曲率半径;一元积分学：旋转体的侧面积、平面曲线的弧长、功、引力、压力、质心、形心等;向量代数与空间解析几何：向量、直线与平面、旋转曲面、球面、柱面、常用的二次曲面方程及其图形、投影曲线方程;多元函数微分学：方向导数和梯度、空间曲线的切线与法平面、曲面的切平面和法线;隐函数存在定理;多元函数积分学：三重积分、第一型曲线积分、第二型曲线积分、第一型曲面积分、第二型曲面积分、格林公式、高斯公式、斯托克斯公式、散度、旋度;无穷级数：傅里叶级数;微分方程：伯努利方程、全微分方程、可降阶的高阶微分方程、欧拉方程。
以上内容为数学一单独考查的内容，是数学一特有的内容，所以这些内容每年必考。
其中：多元函数积分学中曲线曲面积分三重积分几乎每年必考，常与空间解析几何一起考查，尤见于大题，今年(2017年)考查了第一型曲面积分及投影曲线，散度旋度常见于小题。
考研数学假期作业第七章无穷级数(数一数三必做的29题,附详解)
考研数学假期作业第七章无穷级数（数一数三必做29题，附答案） 1.判别无穷级数的收敛性. 2.;3.求级数的和.4.敛散性5.已知，级数收敛，证明级数也收敛.6.判断级数的敛散性7.判断下列级数的敛散性 （1）（2）.（3） （4）8.判定下列级数的收敛性.（1）（2）（3）（4）9.判别级数的收敛性. 10.判定下列级数的收敛性.（1）（2）11. 判定下列级数的收敛性.)1(1 431321211⋅⋅⋅+++⋅⋅⋅+⋅+⋅+⋅n n )122(1∑∞=++-+n n n n ∑∞=++1)2)(1(1n n n n ∑∞=⎪⎭⎫ ⎝⎛-121cos 1n n n 0lim =∞→n n nu ))(1(11n n n u un ∑∞=+-+∑∞=1n n u 111n nni nn n +∞=⎛⎫+ ⎪⎝⎭∑n ∞=11(1)(2)n n n ∞=++∑12(1)2nn n ∞=+-∑121(2ln 1)n nn n n n -∞=++∑∑∞=11sin n n ∑∞=+12)11ln(n n ;!21∑∞=⋅n n n n n ;2)!(122∑∞=n n n 10! 10321102110132⋅⋅⋅++⋅⋅⋅+⋅⋅+⋅+nn ;!21∑∞=⋅n n n n n ;2)!(122∑∞=n n n（1）；（2）.12.判定下列级数的收敛性（1），（2）. 13. 判断的收敛性. 14.判别下列级数是绝对收敛还是条件收敛.（1）(2) 15.判别级数的收敛性. 16.已知级数绝对收敛，级数条件收敛，则（）（A ） （B ）（C ） （D ） 17.设幂级数在处收敛，则此级数在处（ ）. （A ）条件收敛（B ）绝对收敛（C ）发散（D ）收敛性不能确定18. 设幂级数的收敛半径为3，则幂级数的收敛区间_____.19.求幂级数的收敛半径与收敛域. 20.求幂级数的收敛域. 21.求幂级数的收敛半径.22.求幂级数的收敛域.12332n n n ∞=+-∑11(21)2n n n∞=-⋅∑∑∞=-+12)1(2n n n 121n n n n ∞=⎛⎫ ⎪+⎝⎭∑∑∞=--11ln )1(n n nn∑∞=12sin n nna11(1)21nn n ∞=--∑∑∞=+-12)11(21)1(n n nnn 11(1)n n α∞=-∑21(1)nn nα∞-=-∑102α<≤112α<≤312α<≤322α<<1(1)nn n a x ∞=-∑1x =-2x =0nn n a x∞=∑11(1)n nn na x ∞+=-∑∑∞=--11)1(n nn nx ∑∞=0!1n nx n ∑∞=0!n n x n ∑∞=-12)1(n n nnx23.求下列幂级数的和函数.（1）（2）（3）（4） 24.求下列级数的和（1）， （2）， （3）， （4） 25.将函数展开成x 的幂级数.26.将函数展开成x 的幂级数.27.将函数展开成的幂级数.28.将函数展开成(x -1)的幂级数. 29.（1）验证函数满足微分方程；(2)利用(1)的结果求幂级数的和函数.考研数学假期作业第七章无穷级数答案1.判别无穷级数的收敛性.解：,所以这级数收敛,它的和是1.2.;解：.∑∞=+011n n x n 1(1)n n n x n ∞=-∑0(21)n n n x ∞=+∑22121(2)2n nn n x ∞-=-+∑1212n n n ∞=-∑11(21)2nn n ∞=-∑1(1)2nn n n ∞=+∑2(1)(1)2n n n n n ∞=--+∑211)(x x f +=()arcsin f x x =()sin f x x =)4(π-x 341)(2++=x x x f +6!3693()1,,3!9!(3)!n x x x x y x x n =+++++-∞<<+∞'''x y y y e ++=30(3)!nn x n ∞=∑ )1(1 431321211⋅⋅⋅+++⋅⋅⋅+⋅+⋅+⋅n n )1(1 431321211++⋅⋅⋅+⋅+⋅+⋅=n n s n 111)111( )3121()211(+-=+-+⋅⋅⋅+-+-=n n n 1)111(lim lim =+-=∞→∞→n s n n n )122(1∑∞=++-+n n n n nn n n n n n u n ++-+++=++-+=11121122所以,原级数收敛.3.求级数的和. 解：.4.敛散性解：, 原级数发散. 5.已知，级数收敛，证明级数也收敛.解： 因收敛，设其项部分和数列为，则可设其中是的第项部分和,则121121 )11121()231341()121231(+-+++=++-++++++-+++-+=∴n n n n n n s n121lim +-=∞→n n s ∑∞=++1)2)(1(1n n n n )21121(21)2)(1(1+++-=++=n n n n n n u n41s lim )211121(21 )21121121221(21 )21121(21 )514231(21)413221(21 )31221(21n n ==∴+++-=+++-+++-=+++-+++-++-++-=∴∞→s n n n n n n n n s n ∑∞=⎪⎭⎫ ⎝⎛-121cos 1n n n 02121lim 1cos 1lim lim 222≠==⎪⎭⎫ ⎝⎛-=∞→∞→∞→n n n n u n n n n ∴0lim =∞→n n nu ))(1(11n n n u un ∑∞=+-+∑∞=1n n u ))(1(11n n n u un ∑∞=+-+n {}n S lim n n S A →∞=21321112() 3() (1)() (1)n n n n n S u u u u n u u u s n u ++=-+-+++-=--++ n s ∑∞=2n nun 11(1)n n n s u S n u +=--++11lim lim lim(1)n n n n n n s u S n u +→∞→∞→∞∴=--++故级数收敛，其和为.6.判断级数的敛散性解：，所以级数发散. 7.判断下列级数的敛散性 （1）（2）.（3） （4）证（1）因为, 而级数是发散的,根据比较审敛法可知所给级数也是发散的. （2）因为由于，而级数收敛，由比较判别法知收敛 （3）此题无法直接用比较判别法，因随的增加而变化，当为奇数时等于1，当为奇数时等于3，即分母不超过3，因此有。
高数考研试题解析无穷级数的收敛域与收敛半径
高数考研试题解析无穷级数的收敛域与收敛半径无穷级数是数学分析中的一个重要概念，研究它的收敛域和收敛半径是高数考研试题中常见的一种题型。
在本文中，我们将从收敛域和收敛半径的定义入手，通过例题解析的方式来帮助读者更好地理解和应用这一概念。
无穷级数的收敛域是指使得无穷级数收敛的所有实数x的集合，也称为收敛区间。
而收敛半径则是收敛域的长度，记作R。
在解析无穷级数的收敛域和收敛半径时，常用的方法有根值判别法、比值判别法和积分判别法等。
根值判别法是通过计算无穷级数的通项的n次根的极限值来判断收敛域和收敛半径。
对于一个无穷级数∑(aₙxⁿ)，通过计算lim┬(n→∞)(|aₙ|⁄|aₙ₊₁|)的值，当该极限存在且大于0时，收敛半径R=1/lim┬(n→∞)(|aₙ|⁄|aₙ₊₁|)；当该极限不存在或为无穷大时，R=0；当该极限等于无穷时，R=+∞。
比值判别法是通过计算无穷级数的通项的绝对值的n+1项与n项的比值的极限值来判断收敛域和收敛半径。
对于一个无穷级数∑(aₙxⁿ)，通过计算lim┬(n→∞)(|aₙ₊₁|⁄|aₙ|)的值，当该极限存在且大于0时，收敛半径R=1/lim┬(n→∞)(|aₙ₊₁|⁄|aₙ|)；当该极限不存在或为无穷大时，R=0；当该极限等于无穷时，R=+∞。
积分判别法是通过求解无穷级数的通项对应的函数在收敛域上的不定积分的性质来判断收敛域和收敛半径。
对于一个无穷级数∑(aₙxⁿ)，令f(x) = ∑(aₙxⁿ)，如果f(x)在收敛域上连续，则收敛域包含收敛半径R。
为了更好地理解和应用这些方法，我们接下来通过解析一个具体的考研试题来探讨。
【解析示例】考虑无穷级数∑(n!)⁄(nⁿxⁿ)，我们将通过根值判别法、比值判别法和积分判别法来求解它的收敛域和收敛半径。
首先，我们使用根值判别法。
计算通项的n次根的极限值，lim┬(n→∞)(|(n!)⁄(nⁿxⁿ)|⁄|(n+1)!⁄((n+1)ⁿxⁿ₊₁)|)= lim┬(n→∞)((n+1)ⁿ⁺¹⁄nⁿ₊₁) = (1+1/n)ⁿ → 1因此，根值判别法得到的收敛半径为R = 1。
考研无穷级数笔记
⽆无穷级数的总结分成四⼤大部分1.级数的概念与性质2.常数项级数的判敛3.幂级数4.傅⽴立叶级数⼀一.级数的概念与性质及分类1.级数的定义2.部分和的定义3.定义法判敛（适合于任意项的常数项级数）Note：应⽤用于部分和可以容易易得到的情形，救命稻草4.级数的性质：（5个）1.级数收敛于S，则k倍的级数收敛于kS2.级数Un收敛于S，级数Vn收敛于T，则级数Un加减Vn收敛于S加减TNote：1.收敛加减发散等于发散2.发散加减发散等于不不定3.加上或减去或改变前有限项，不不改变级数的敛散性4.收敛级数任意加上括号后级数仍收敛Note：1.加上括号后级数收敛，原级数不不定（反例例）2.加上括号后级数发散，原级数发散（逆否命题）5.级数收敛，Un的极限为0（收敛的必要条件）Note：1.证明2.Un极限为0，级数不不定3.Un极限不不为0，级数发散（逆否命题）5.级数的分类：分成常数项级数与函数项级数，常数项级数分为1.正项级数（Un⾮非负）（可以缺项），2.交错级数（Un>0)（不不可以缺项）；3.任意项级数；函数项级数分为幂级数与傅⽴立叶级数Note：3可能等于1+2（所谓的拆）⼆二.常数项级数的判敛1.正项级数判敛（6种）：（注意Un⾮非负，⽽而且不不⼀一定从前⼏几项开始）1.收敛原则（正项级数⚠，充要条件，要知道证明，在抽象题⽬目中会⽤用到）2.⽐比较判敛法（⽤用收敛原则证明，⽤用法：1.放缩与⾃自⼰己⽐比，2.命题⼈人给出来的）3.⽐比较判敛法的极限形式（四个尺度：等⽐比级数，p级数，（证明调和级数发散）⼴广义p级数（注意还有⼀一个推⼴广），交错p级数）4.⽐比值判别法（注意p⼤大于1，包括∞）5.根值判别法Note：⽐比值与根值有三个注Note1: 注意是极限Note2：⽐比值与根值的判别是收敛的充分⾮非必要条件，也就是说，如果⼀一个正向级数收敛，可能⽐比值和根值的极限不不存在Note3: ⽐比值与根值⽤用在任意项级数上，发散判定（证明）Note ：1在做选择时，还有⼀一种判别法可以考虑，对数判别法（与⽐比值相反）。
无穷级数 考研真题
无穷级数考研真题无穷级数是数学中一个非常重要的概念，也是考研数学中的一个常见考点。
在考研真题中，经常会出现与无穷级数相关的题目，考察学生对该概念的理解和运用能力。
本文将从无穷级数的定义、性质和应用等方面进行探讨。
首先，我们来看一下无穷级数的定义。
无穷级数是由无穷多个数相加而得到的一种数列。
通常用符号∑表示，∑an表示无穷级数的一般形式，其中an为级数的通项。
例如，∑(1/2)^n就是一个无穷级数，其中(1/2)^n为通项。
接下来，我们来讨论无穷级数的性质。
首先是级数的收敛性。
如果无穷级数的部分和数列{Sn}存在有限的极限S，那么我们称该无穷级数是收敛的，记作∑an=S。
反之，如果无穷级数的部分和数列{Sn}不存在有限的极限，那么我们称该无穷级数是发散的。
其次是级数的收敛域。
对于收敛的无穷级数∑an，我们可以通过求和的方式得到一个数S。
但是需要注意的是，这个和S并不一定包含在级数的收敛域内。
级数的收敛域是指所有使得级数收敛的x值构成的集合。
例如，级数∑(1/2)^n在区间(-1,1)内是收敛的，但是在区间[-1,1]的两个端点上是发散的。
再次是级数的运算性质。
对于两个收敛的无穷级数∑an和∑bn，我们可以进行加法、减法和乘法运算。
具体来说，如果两个级数都是收敛的，那么它们的和级数∑(an+bn)、差级数∑(an-bn)和乘积级数∑(an*bn)也都是收敛的。
最后，我们来探讨一下无穷级数的应用。
无穷级数在数学中有广泛的应用，特别是在数学分析和物理学中。
例如，在数学分析中，我们可以通过无穷级数来表示和计算各种函数，如三角函数、指数函数和对数函数等。
在物理学中，无穷级数可以用来描述连续体的离散化模型，如波动方程和热传导方程等。
此外，无穷级数还可以用来研究概率论、数论和微分方程等领域的问题。
综上所述，无穷级数是数学中一个重要的概念，也是考研数学中的一个常见考点。
通过对无穷级数的定义、性质和应用的探讨，我们可以更好地理解和运用这一概念。
数三高数考查重点和题型总结
考研数学三高等数学考察重点及题型总结
章节知识点题型
重要度等
级
第一章函数、极限、
连续等价无穷小代换、洛必达法则、
泰勒展开式
求函数的极限★★★★★函数连续的概念、函数间断点的
类型
判断函数连续性与间断点的类型★★★
第二章一元函数微分学导数的定义、可导与连续之间的
关系
按定义求一点处的导数，可导与连
续的关系
★★★★函数的单调性、函数的极值讨论函数的单调性、极值★★★★闭区间上连续函数的性质、罗尔
定理、拉格朗日中值定理、柯西
中值定理和泰勒定理
微分中值定理及其应用★★★★★
第三章一元函数积分学积分上限的函数及其导数变限积分求导问题★★★★★定积分的应用用定积分计算几何量★★★★
第四章多元函数微积分学隐函数、偏导数、全微分的存在
性以及它们之间的因果关系
函数在一点处极限的存在性，连续
性，偏导数的存在性，全微分存在
性与偏导数的连续性的讨论与它
们之间的因果关系
★★★二重积分的概念、性质及计算二重积分的计算及应用★★★★★
第五章无穷级数级数的基本性质及收敛的必要
条件，正项级数的比较判别法、
比值判别法和根式判别法，交错
级数的莱布尼茨判别法
数项级数敛散性的判别★★★★★
第六章常微分方程一阶线性微分方程、齐次方程，
微分方程的简单应用
用微分方程解决一些应用问题★★★★。
近五年考研数学无穷级数考点分析
第24卷第3期2021年5月高等数学研究STUDIES IN COLLEGE MATHEMATICSVol24,No.3May2021doi:10.3969/j.issn.1008-1399.2021.03.006近五年考研数学无穷级数考点分析王成强（成都师范学院数学学院,四川成都611130）摘要将近五年的考研数学中的无穷级数问题归为四类，并针对每类问题给出简要解答；基于解题体验，分析每类题型中的常考知识点；在所得的分析结果的基础上，提出学习大学数学课程中的级数理论的几点建议.关键词大学数学；考研数学；级数理论中图分类号O173；G642.0文献标识码A文章编号1008-1399（2021）03-0017-05Analysis of Infinite Series Problems in NPEE MathematicsWANG Chengqiang(School of Mathematics,Chengdu Normal University,Chengdu611130,PRC)Abstract Infinite series problems in NPEE mathematics of last five years are classified into four groups, and brief solutions to each group are discussed and summarized.Suggestions are made for learning the series theory. Keywords NPEE mathematics,series theory0引言无穷级数理论是大学数学课程中的重要知识模块'1—2（.与有限个数求和相比，无穷级数更抽象、涉及到的概念更多，与它相关的问题形式更丰富.因此，级数理论一直以来也是大学数学课程中的学习难点•考研数学题中，大多是大学数学教学研究的新近结果,蕴藏着课程教学的发展趋势，有重要的研究价值[3—4].本文将近五年（2016年一2020年）级数理论相关的考题进行归类研究，并据此分析大学数学或高等数学课程中级数理论的学习的侧重点，期望在级数理论的讲授与学习方向引发更多思考•1考题归类解析类型1数项级数的收敛及运算性质收稿日期：2020-04-15修改日期2020-06-28基金项目：成都师范学院校级教改一般项目（2020JG38）；国家自然科学基金青年基金（11701050）；成都师范学院校级重点项目（CS19ZA10）.作者简介：王成强（1985—），男，四川武胜人，博士、副教授•主要研究方向为：数学控制论与数学教育•E-Mail：cqwung@.题1（2018年数学三第4题%若级数'”u”与”—1'仏都绝对收敛，则（）.”=1”（A）'u”4”条件收敛”一1（B）'u”4”绝对收敛”一1(C)'("”+◎”)收敛(D)'("”+◎”)发散”一1”一1解经计算，可验证'丨u”I•I4”I—'('|”u”I)?弘I•于是，由比较判别法，'u”4”绝对收敛.故选项（B）”一1正确，选项（A）错误.因级数'”•1与'1•1都绝对收敛，而'（"”+◎”）发散，故选项（C）错误•”一1因级数'"・1、'丄・1及'（u”+Q都收敛,”一171n~1n71n~1故选项（D）错误•题2（2016年数学三第10题%给定命题：(1)'(u”+u”+1)收敛时,'u”收敛%8高等数学研究2021年5月2)n '% 2n ，n % 2n+%000(3) l im 2+1 > 1 时，'"”发散 n %%2n +%”("U)(4)' 2n+ 9”)收敛时，'u ”与'9”收敛n %%则以上命题中正确的是( $A )$%) 2)$C ) 3 ) 4 )n %%n %)!(B)(2)(3)(D)(l)(4)解 因'((—1)n + ( — 1)n +1 )收敛于零，但级n %%数'(—1)n 发散，故选项(1)错误•另一方面，级n %%数'(—1)n 与'(—1))+1都发散，故选项⑷错!， B )!题3(2019年数学一第3题)设2”3-1单调递增且有界，则下列级数收敛的是()•(B)'(一 卩”n %%(A)' 2n n %%2 一(”)2)(C) ' (1 — 2”) (D) ' ((u ”+1) n %%n +%n %%解 因2” 3-1有界，故：F 〉0,使得对任何正整数”，都有\ $$2n +%)2 — $2n )2 ) \ %\2n +% +2—2F2”+1 — 2”).:” \ (,”十1 一 u ”)因2” 3—1单调有界故收敛，故',n +% —2n 收敛.n %%由比较判别法，'((2)+1) 2 — 2))2)绝对收敛.故n %%选(D).因级数'1 )2 —丄)发散,故选项(A)错nnn %%误.因级数'(一1)”/(2 —丄)发散,故选项(B)错n %%" 1 1 " 1误.因级数'(1 — (—1)/(一#3))%— ' 1n %%n %%发散，故选项(C )错误.题4(2017年数学三第4题) 若级数'(sin 1 — k ln(1 — 1)) n %2 n n收敛，则k —().$A %$B )2$C ) —% $D ) —2解经计算，有1im(sin 1 — k ln(1 — 1) ) / 1 % 1 + k .”(" n n n1若1 + k % 0,则因调和级数'1发散，故级数n %2'(sin — — k in ( 1 ——))发散.于是，只能选择(C ).n %2n n事实上，有lim(sin 1 + ln ( 1 — 1)) / 1 %— £.因级数'1收敛，故'(sin 1 + 1n(1 一 1))收敛.n %2n %2题5(2016年数学一第19题) 已知函数f(")在R 上可导，且f (0) % 1,0 <)(")< 2.设数列{"n3-1 满足"n +1 — f ("”)•证明：(i) 级数'("n +1 — "n )绝对收敛；)—1(ii) 极限lim "” 存在，且 0 V lim ") V 2.”("”("证 (i)由题设，对任何"，存在(介于"n 与")—1 之间)，使得'(.))\ "n — "n 1 \— 2 \ ")— ")1 \.由数学归纳法，对任何”有\ "n +1—"n \— \ "I -"1 \ •因级数'—收敛，故级数'(")+1 —"))绝对收 敛.于是，数列{"n 3—1收敛.(ii)令 A —l i mx ”.因"”十1 — f("”),故 A —f(A ).由Lagrange 中值定理，：$ , R,使得A —1 % f(A)—f (0) - f'$)A ,或等价地，得三一1 %'$)•由题意，有0 V 三一1V 2•解得 1 V A V 2.类型2 幕级数的收敛性质题6(2020年数学一第4题) 设R 是幕级数'$”"”的收敛半径，"是实数，则().(A %'$n"nn %1，\"\ 2R(B %'$n"nn %1， \"\ —R(C %\"\ 2R ， '$n "nn %1(D %\"\ —R ， '$n "n”―1解给定幕级数第24卷第3期王成强：近五年考研数学无穷级数考点分析19'a”("一 "0 )” ! (1)”一1设R 为其收敛半径•级数'”a ” "一"0)”一1与”一1E 弓汁("一"0)”+1的收敛半径都是2.幕级数 ”一1 ” + 1(1)在区间("0 —R,"0 +2)上内闭一致收敛；当I " — "0 I 〉2 时，级数(1)发散；当 I " — "0 I $ R时，级数(1)绝对收敛；当I " — "0 I — R 时，级数(1) 可能(条件或绝对)收敛也可能发散；对",R,若级数(1)条件收敛，则I " —"0 I — R .结合题意，可知选项(A )正确•题7(2020年数学三第4题% 若幕级数的概率分布P ( X — n ) % 1，” , N,y 表示X 除以3的余数,EY — ______•解 EY — '2+1 + 2'— ' 1 % 7题11(2020年数学二第4题％ 设f")—"2ln(1 —").对任何正整数” 2 3,计算f ()(0)— $ ) •'”a ”("一2)”的收敛区间是(一2,6),则幕级数”一1'a 0 $"+1)20 的是$ ) •”一1(A )”!(B) ” !9” —2—2(C )— ( —2)!(D ) ( 一 2)nn解算, 有f (" ) — "2ln (1 —-")%—'——2(A)(—2,6)(B)(—3,1)$C )$—5,3) $D )$—17,15)解 仿照题6的解答可验证选项(B)正确•类型3 幕级数的运算性质题8(2018年数学一第3题% 计算数项级数又由Taylor 级数理论，有f"二'广”0"”，从而!f !0)— ，即 f ”(0)=”打.故选(A ).! —2n —2题12(2018年数学三第18题％知p (一 1 )”2” + 3'(2” + 1)!$A )sin1 +cos1)•$B )2sin1 +cos1$C )2sin1 +2cos1$D )3sin1 +2cos1解经计算，有' $—1)”一02 +3(2” + 1)!8 2'(-1)cos2" (.)—(1 +"%2'a " •”—0求a n •解直接 算, 得cos2"—1 _ & (— 1) ”(1 +")2 ' (2”) !(")” + (1 )1 +"(—1)2”(1 + (—1)”) ”n ! %n -0'((—1)2i(1 +(—D ”) + ( + 1)(—计1)”n -0”!"2”+12sin1 +cos1 •2”+1)!+2' —1)”一0故选(B ).题9(2019年数学一第17题；数学三第18题% 求曲线夕％ e -"sin " ( " 2 0)与"轴之间图形的面积.解直接计算，得I e —"Din "I d " %”%0”"" 气”+1)"I e —"sin "I d "吕 「(”+1)"' —1)”e —"sin "d "”%0”"1' (e —”" + e —(+1)")2 n -01 1 + 1 ( 1 — 1) — e " + 12 1 — e —"十 21 —e -" 一 丿 % 2e " — 2题10(2020年数学三第14题％ 设随机变量X% 'a ”"” •n -0故 a ” ％ (—1)2"—1( + (一 D ”) + ( + 1) (— 1)1 •0!题13(2017年数学一第12题% 幕级数'(—1)n —1n"n —1在区间内(一1,1)的和函数是”一 1S") % .解直接计算，得S") — ' (—1) ”—1”—1%—('(—") ”)%— (—1— ) — ----1----1+" (1+")・题14(2019年数学一第11题% 幕级数'()"”在0, + ")的和函数是S (")—_____•20高等数学研究2021年5月(一 1)”(2))!"n % 'n %0一、,(槡")％ cos 槡". 2n !类型4 以微分方程为工具求幕级数的和函数题15(2016年数学三第19题) 设幕级数'“，1、、“""”十2的和函数为 S (")," , R .n %0 (2 (n+ 2% !!(i) 求S")满足的一阶微分方程；(ii) 求和函数S")的解析表达式.级数'$”"”绝对收敛.故级数' $n "n 的径n %0n %0不小于1.$i )算, 有(1 — ")S ‘(")一 "S ")解 (i)经计算，对任何",R,有S ，(") % "'n %0______±______"2 (卄1)(2) + 1))!!(1—") (e $”"”)一 "S ")n %0(1 — ") ^'(” 十 1 )$”+"” 一 "'$”"”n %0n %0' $n+1)$n +1"n — ' $$n+1)$n +1 +$n )"n+1n %0 n %011"3 +"'n %0___________±___________ 2(”+2)(2(”十2))!严% 1"3 + "S (").(i) 证明级数'$”"”的收敛半径不小于1;n %0(ii) 证明(1 —")S ‘(")一"S") % 0, ", (—1,1), 并求S(")的解析表达式.证 (i)经分析可知，对任何”〉2,有0 V $” V 1.于是，有'\ $”"” \— ' \ " \n .因此，只要 \ " \ V 1,故S(")满足的一阶微分方程是s ，(" ) % 2"3 + "S (").(ii)解法1 经计算可知,S(")也满足e -1"2S'(" ) + (e -1"2) ' S (" ) - 1"3 e -2"2或等价地，满足(e -2"2S(" ) ) ' — 1"3e -1"2.于是 e -2"2S(" ) — 1 — e -1"2 — 2"2 e -1"2，解得S(") % e 1"2 — 1 — 1"2 •解法2 直接计算，有" ] " 1 1V * __________±_________/(”+2) = V *丄—丄/'(2( + 2 ) ) !严'(2”)！严2"% e 2" — 1 — 2"2题16((017年数学三第19题)给定数列{$) 3—0,假设它满足条件：_ 1 _ c_ ("+ 1 ) $)+1 + $)如 ％ 丄,Q1 % U,Q …+2 ———- ,” + 2—'(n + 1 )$”+"” — ' ( n + 2)$”+"n +1 — 0.n %0n %0易知(1 — "S (") — "S (") % 0 等价于(1 — ")e "S ‘ ")+ ( (1 — ")e ")‘S(") % 0 ,或者等价于((1 — ")e "S ( ") % 0.于是，对任何",(一1,1),有(1—") e "S (") % (1 — 0)e 0S (0) % 1,或等价地，有S (")—严——•1 —"题17((020年数学一第17题) 设{” }"—1满足条件：$1 — 1,(" + 1)$”十1 — (n + 1 )$”，证明'$”"”的收敛区间是(一1,1),并求其和函数•n %1证 因 lim— lim 严 f % 1,故'$”"” 的”("a ””("厶％ ~ Li”—1是 —1,1).解法1 令S ( ") — '$”"”•经计算，有n %1S ") % 1 + ' n$”"”-10%2—1 + ' ( n — 1 )$l 1"”-1解'S")是幕级数'$”"”的和函数•n %0 (i)1 + "S ( ") + -^-S ("),等 地, 有(槡1 — "S ( "))' % 槡1 — "S (")S ")2槡1 —"1槡1 —"于是，S (")—槡"S ( " %槡1 —" 槡1 —"—2.第24卷第3期王成强：近五年考研数学无穷级数考点分析21解法2经计算，对任何正整数”，有a””1一1 a1'a_—'~k_ k—2S k—1k—2氏+k)•于是2(—1)”+1”!2考点分析及对学习的启示前一节将近五年的级数理论相关的考研题归为了四类：数项级数的收敛及运算性质类考题,幕级数的收敛性质类考题，幕级数的运算性质类考题，以微分方程为工具求幕级数的和函数类考题.针对每类题型中的每道题都给出了简要解答，其中一些考题的解答与官方参考答案不同，部分考题也给出了基于多视角的解答.数项数的运算性（1—5）涉及发散、条件收敛、绝对收敛等概念及这些概念间的关系，涉及到级数的和、级数的线性运算、对级数加括号、级数的乘积、改变（删除、增加、往后移、往前移、交换顺序）级数中的部分项等运算，涉及到定义法、单调有界定理、比较判别法.d'Alembert比式判别法、Cauchy-Hadamard根式判别法、Leibniz判别等方.数的性（6—7）涉及到的知识点有：幕级数在收敛区间内绝对收敛，在收敛区间的端点（如果存在）处的收敛性要具体问题具体分析，在收敛区间及其端点之外的所有点处都发散；幕级数经求导或不定积分运算所得到的新级数与原级数具有相同的收敛半径.幕级数的运算性质类考题（题8—14）主要涉及考查以常见函数的幕级数展开公式、微分、积分为工具，将函数展开成幕级数或者求幕级数的和函数.以微分方程为工具求幕级数的和函数类考题（题15—17）—般是假设幕级数的系数满足一定的递推关系式，要求确定出幕级数的和函数.此类问题的解答思路通常是，对幕级数求若干次导，利用题设中给出的系数满足的条件，将求导而得到的式子重新整理成关于幕级数和函数的常微分方程,最后通过解方程求得和函数.通过解答题1—17,获得三点体验感受.绝大部分考题都是对基础知识、基本思想与方法的考查.题1与3基本算得上是直接对单调有界收敛定理的应用.题2尽管涉及到数项级数多方面的运算性质，综合性较高，但鉴于其选择题特性，它也算是基础题.题6、7直接考查幕级数的收敛特性.题8—14都只涉及常见幕级数公式的直接应用.少部分考题综合性、创新性、挑战性较高：题4需要带参讨论，有一定的难度；题15—17涉及到幕级数理论与微分方程理论的融合，计算量也非常大，难度极高.对于高难度问题，考研数学试卷通常会通过营造恰当的数学情境，引导考生的思维接近正确答案：题4综合性高，具有一定难度，但以选择题的形式让学生通过代入每个选项的值验证题设条件而完成解答任务；题15—16的难度都较高，但它们都以“在第（i）小问中设置验证型证明题（证明结果暗示第（ii）小问的解答思路）”的形式引导学生经过探索、验证等找到可行的解题思路.综上，考研数学试题重视基础知识、基本思想与方法的考查，设置一定比例的高难度问题，保证试卷的效度与区分度，激励学生提高科学计算能力、转化与划归能力、创新运用所学知识的能力等.受上述分析结果的启发，得到三点关于大学数学课程中级数理论的学习的启示.一是，要系统化掌握的基础知识、基本思想与方法；二是，要研究多年的考研数学试题;三是，要动手推导书本例题的解答步骤，解答课后习题与考研数学试题，并积攒解题.参考文献[1]华东师范大学数学系.数学分析[M].4版.北京：高等教育出版社，2010.[2]同济大学数学系.高等数学[M].6版.北京：高等教育版社20078']王成强.一道有需级数背景的考研极限题的解法研究[J].宁波教育学院学报，2019,21（05）82-85.']王成强.一例递推数列极限考研题的进一步探究[J].宁夏师范学院学报，2019,40（01）:100-103.。
考研数学数学分析常见题型解题技巧分享
考研数学数学分析常见题型解题技巧分享在考研数学中，数学分析是一个重要的考试科目。
掌握数学分析的解题技巧对于考生来说是至关重要的。
本文将介绍几种常见的数学分析题型以及解题技巧，希望对考生有所帮助。
一、极限题型极限是数学分析中的基本概念，很多题目都与极限求解相关。
解决极限问题时，可以运用以下技巧：1. 利用夹逼定理来求解复杂的极限问题。
夹逼定理是极限的一个重要概念，可以帮助我们确定一个函数的极限值。
2. 如果是无穷小量的极限问题，可以使用等价无穷小代换求解。
将原问题转化为一个等价的无穷小量，从而求取极限值。
3. 对于一些特殊的函数极限，可以使用泰勒级数展开来计算。
通过将函数展开为无穷级数的形式，可以简化计算过程。
二、导数和微分题型导数和微分也是数学分析中常见的题型。
在解题时，可以使用以下技巧：1. 利用导数定义求解导数。
导数定义是求解导数的基本方法，将函数进行微小变化，然后求解极限值即可得到导数。
2. 利用导数的四则运算法则来计算导数。
根据导数的基本运算法则，可以将复杂的函数导数运算化简为简单的运算。
3. 对于隐函数求导，可以使用隐函数求导法。
利用隐函数求导法，可以将含有隐函数的导数求解转化为常规的导数求解。
三、积分题型积分是数学分析中的重要内容。
在解决积分题型时，可以运用以下技巧：1. 利用换元法进行积分计算。
通过进行变量代换，可以将复杂的积分问题转化为简单的形式，从而解决积分问题。
2. 利用分部积分法进行积分计算。
分部积分法是积分运算的一种法则，通过对积分进行分部拆解，可以简化积分的计算过程。
3. 对于一些特殊的函数积分，可以使用定积分的性质来计算。
利用定积分的性质和几何意义，可以更加简便地计算积分值。
四、级数题型级数是数学分析中的重要内容之一。
在解决级数题型时，可以使用以下技巧：1. 利用比较判别法来判断级数的敛散性。
比较判别法是判断级数敛散的一种方法，通过将待判断的级数与已知级数进行比较，可以得出级数的敛散性。
数学考研数学分析重点梳理
数学考研数学分析重点梳理一、数列与极限1. 数列的概念与性质数列的定义、数列的极限、数列的有界性等2. 数列极限的判定方法夹逼准则、单调有界准则、卡氏准则等3. 无穷级数无穷级数的概念、收敛性与发散性、常见级数等4. 函数的极限函数的概念、函数极限的定义、函数极限的性质等二、连续函数与一元函数微分学1. 连续函数与间断点连续函数的概念、间断点的分类、连续函数的性质等2. 闭区间上连续函数的性质零点存在性、介值定理、最值定理等3. 一元函数微分学的基本概念导数的定义、函数的可导性、导数的几何意义等4. 导数的计算和应用导数的四则运算法则、高阶导数、隐函数求导、极值问题等三、多元函数微分学1. 多元函数及其图像多元函数的定义、多元函数的图像、多元函数的性质等2. 偏导数与全微分偏导数的定义和计算、全微分的定义、全微分的计算等3. 多元函数的连续性与偏导数存在性多元函数的连续性、混合偏导数的存在性、 Schwarz 定理等4. 多元函数的极值与条件极值二元函数的极值、拉格朗日乘子法、约束条件的处理等四、一元函数积分学1. 不定积分不定积分的定义、基本积分表、换元积分法等2. 定积分定积分的定义、定积分的性质、常用积分公式等3. 定积分的计算方法牛顿－莱布尼茨公式、分部积分法、曲线长度与旋转体体积等4. 应用问题平面向量的应用、物理问题与几何问题等五、多元函数积分学1. 二重积分二重积分的定义、二重积分的计算方法、极坐标下的二重积分等2. 二重积分的应用质量、质心、转动惯量、面积等应用问题3. 三重积分三重积分的定义、三重积分的计算方法、球坐标下的三重积分等4. 三重积分的应用质量、质心、转动惯量、体积等应用问题以上便是数学考研数学分析的重点梳理，希望对你的学习有所帮助。
通过对这些重点知识的掌握和学习，相信你能够顺利应对数学分析的考试。
加油！。
考研数学考前预测重点题型之无穷级数(数一、数三)
考研数学考前预测重点题型之无穷级数（数一、数三）无穷级数是考研数学中数学一和数学三同学必考的内容，这一部分是同学们复习的难点，但是它也是考试的重点. 在考试中，既可以以选择题和填空题的方式进行考查，也可以以解答题的方式进行考查. 要求同学们对于数项级数敛散性的判别，幂级数收敛半径，收敛区间，收敛域的求法，求幂级数的和函数，求函数的幂级数展示式的基本方法掌握到位，不过这一块经常也会出一些比较难的压轴题，比如和数列极限存在性的结合，和微分方程的综合题等等.题型一：判别数项级数的敛散性【例1】设正项级数1ln(1)n n a ∞=+∑收敛，则级数1(1)n ∞=-∑ ) (A) 条件收敛 (B) 绝对收敛 (C) 发散 (D) 敛散性不能确定【难度】中【答案】(B)【解析】由于正项级数1ln(1)n n a ∞=+∑收敛，所以0n a >，且lim 0n n a →∞=， 又因为ln(1)lim 1n n n a a →∞+=，所以1ln(1)n n a ∞=+∑与1n n a ∞=∑有相同的敛散性，即1n n a ∞=∑收敛，故11n n a ∞+=∑也收敛.又()11(1)2n n a a +-=≤+，而()11n n n a a ∞+=+∑收敛，所以由比较判别法可得1(1)n ∞=-∑. 【小结】此题考查了正项级数的比较判别法.抽象型数项级数敛散性的判别经常以选择题的方式进行考查,而出现了正项级数，经常考的是比较判别法.题型二：简单函数的幂级数展开【例2】设21()3n n n S x a x ∞==+∑满足()()2x S x S x e '+=+，求()S x ，并求出n a .【难度】中【解析】已知()()2x S x S x e '+=+且可得(0)3S =，解得1()2()2x x S x e e -=++.001()()2[]2!!n n n n x x S x n n ∞∞==-=++∑∑011(1)22!nn n x n ∞=+-=+∑22200112112232(2)!(2)!(2)!n n n n n n x x x n n n ∞∞∞====+=+=+∑∑∑，(,)x ∈-∞+∞ 因21()3n n n S x a x ∞==+∑，故1(2)!n a n =. 【小结】此题考查了微分方程和幂级数的综合题，但是此题难度不大. 通过微分方程可以求出函数的表达式，进而可以写出对应的幂级数展开式.要求对于常见函数的麦克劳林级数形式记住了.题型三：求幂级数的和函数【例3】求幂级数20(1)1n n n x n ∞=-+∑的和函数.【难度】中 【解析】22(1)2lim 11n n n n n→∞-+⋅=+，故收敛半径为1. 当1x =±时，20(1)1n n n ∞=-+∑发散，故收敛域为(1,1)-. 设20000(1)1()(1)4411n n n n n n n n n S x x n x x x n n ∞∞∞∞====-==+-+++∑∑∑∑， 112001()(1)1(1)nn n n x S x n x x x x ∞∞+==''⎛⎫⎛⎫=+=== ⎪ ⎪--⎝⎭⎝⎭∑∑， 204()41nn S x x x ∞===-∑，301()41n n S x x n ∞==+∑， 14301()()41n n S x xS x x n ∞+===+∑，404()41n n S x x x ∞='==-∑，4()4ln(1)S x x =--， 当0x ≠时，34ln(1)()x S x x --=， 此时22144ln(1)434()ln(1)(1)1(1)x x S x x x x x x x--=--=-----. 当0x =时，(0)1S =. 故2434ln(1),(1,0)(0,1)(1)()1,0x x x x x S x x -⎧--∈-⎪-=⎨⎪=⎩. 【小结】此题考查了幂级数的和函数的计算，属于常规类型的题目，在考试中是同学们要拿分的题目.掌握基本方法，注意细节，考试尽量拿满分.。
考研级数典型例题完美版讲析
常数项级数内容要点一，概念与性质(一)概念 由数列 ,,,,21n u u u 构成的式子=∑∞=1n nu++++n u u u 21称为无穷级数，简称为级数.n u 称为级数的一般项，∑==ni in us 1称为级数的部分和.如果s s n n =∞→lim ,则称级数∑∞=1n nu收敛，s 称为该级数的和.此时记=∑∞=1n nus .否则称级数发散.（二）性质 1, 若∑∞=1n nu收敛，则.11∑∑∞=∞==n n n nu k ku2, 若∑∞=1n n u ,∑∞=1n nv收敛，则().111∑∑∑∞=∞=∞=±=±n n n n n n nv u v u3, 级数增减或改变有限项，不改变其敛散性.4, 若级数收敛，则任意加括号后所成的级数仍收敛. 5(收敛的必要条件), 若∑∞=1n nu收敛，则.0lim =∞→n n u注意：若.0lim ≠∞→n n u 则∑∞=1n nu必发散.而若∑∞=1n nu发散,则不一定.0lim ≠∞→n n u(三) 两个常用级数 1, 等比级数⎪⎩⎪⎨⎧≥<-=∑∞=1,1,10q q qaaq n n2, -p 级数⎩⎨⎧≤>=∑∞=1,1,11p p n n p 二，正项级数敛散性判别法 (一) 比较判别法设∑∑ℜ=∞=11,n nn n vu 均为正项级数，且),2,1( =≤n v u n n ,则∑∞=1n nv收敛⇒∑∞=1n nu收敛；∑∞=1n nu发散⇒∑∞=1n nv发散(二) 极限判别法如果)0(lim +∞≤<=∞→l l nu n n ,则∑∞=1n nu发散；如果对,1>p )0(lim +∞<≤=∞→l l u n n pn ,则∑∞=1n nu则收敛.(三) 比值判别法 设∑∞=1n nu为正项级数，若⎪⎩⎪⎨⎧⇒>⇒=⇒<==+∞→fb cu u n n n 111lim1ρ 二，交错级数收敛性判别法 莱布尼兹判别法：设())0(111>-∑∞=-n n n n u u 为交错级数，如果满足：1, ),2,1(1 =≥+n u u n n 2, 0lim =∞→n n u则此交错级数收敛.三，任意项级数与绝对收敛 （一） 绝对收敛 如果∑∞=1n nu收敛，则称∑∞=1n nu绝对收敛.（二） 条件收敛 如果∑∞=1n nu收敛，但∑∞=1n nu发散,则称∑∞=1n nu条件收敛.（三） 定理 若级数绝对收敛，则该级数必收敛.函数项级数一、 主要内容 1、基本概念函数列（函数项级数）的点收敛、一致收敛、内闭一致收敛、绝对收敛、和函数幂级数的收敛半径、收敛区间、收敛域 2、一致收敛性 A 、 函数列{()}n f x一致收敛性的判断：（1）定义：用于处理已知极限函数的简单函数列的一致收敛性（2）Cauchy 收敛准则：用于抽象、半抽象的函数列的一致收敛性的判断 （3）确界（最大值方法）：||()()||0n f x f x -→（4）估计方法：|()()|0n n f x f x a -≤→（5）Dini-定理：条件1）闭区间[,]a b ；2）连续性；3）关于n 的单调性注、除Cauchy 收敛准则外，都需要知道极限函数，因此，在判断一致收敛性时，一般应先利用点收敛性计算出极限函数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
考研数学：无穷级数考点和常考题型分
析
在研究生入学考试中，高等数学是数一、数二、数三考试的公共内容。
数一、数三均占56%(总分150分)，考察4个选择题(每题4分，共16分)、4个填空题(每题4分，共16分)、5个解答题(总分50分)。
数二不考概率论，高数占78%，考察6个选择题(每题4分，共24分)、4个填空题(每题5分，共20分)、7个解答题(总分72分)。
由高数所占比例易知，高数是考研数学的重头戏，因此一直流传着“得高数者得数学。
”高等数学包含函数、极限与连续、一元函数微分学、一元函数积分学、多元函数微分学、多元函数积分学、常微分方程和无穷级数等七个模块，在梳理分析函数、极限与连续、一元函数微分学、一元函数积分学、多元函数微分学和积分学的基础上，梳理分析无穷级数，希望对学员有所帮助。
无穷级数内容数二考生不要求掌握。
1、考试内容
(1)常数项级数的收敛与发散的概念;(2)收敛级数的和的概念;(2)级数的基本性质与收敛的必要条件;(3)几何级数与级数及其收敛性;(4)正项级数收敛性的判别法;(5)交错级数与莱布尼茨定理;(6)任意项级数的绝对收敛与条件收敛;(7)函数项级数的收敛域与和函数的概念;(8)幂级数及其收敛半径、收敛区间(指开区间)和收敛域;(9)幂级数的和函数;(10)幂级数在其收敛区间内的基本性质;(11)简单幂级数的和函数的求法;(12)初等函数的幂级数展开式;(13)函数的傅里叶(Fourier)系数与傅里叶级数;(14)狄利克雷(Dirichlet)定理;(15)函数的傅里叶级数;(16)函数的正弦级数和余弦级数。
(其中13-16只要求数一考生掌握，数三考试不要求掌握)。
2、考试要求
(1)理解常数项级数收敛、发散以及收敛级数的和的概念，掌握级数的基本性质及收敛的必要条件;(2)掌握几何级数与级数的收敛与发散的条件;(3)掌握正项级数收敛性的比较判别法和比值判别法，会用根值判别法;(4)掌握交错级数的莱布尼茨判别法;(5)了解任意项级数绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系;(6)了解函数项级数的收敛域及和函数的概念;(7) 理解幂级数收敛半径的概念、并掌握幂级数的收敛半径、收敛区间及收敛域的求法;(8)了解幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分)，会求一些幂级数在收敛区间内的和函数，并会由此求出某些数项级数的和;(9)
了解函数展开为泰勒级数的充分必要条件;(10)掌握的麦克劳林(Maclaurin)展开式，会用它们将一些简单函数间接展开成幂级数;(11)了解傅里叶级数的概念和狄利克雷收敛定理，会将定义在上的函数展开为傅里叶级数，会将定义在上的函数展开为正弦级数与余弦级数，会写出傅里叶级数的和函数的表达式.(其中11只要求数一考生掌握，数二、数三考试不要求掌握)
3、常考题型
(1)判定级数的敛散性;(2)求幂级数的收敛域和收敛半径;(3)把函数展开成幂级数;(4)求幂级数的和函数;(5)特殊的常数项级数的求和;(6)把函数展开成傅立叶级数、正弦级数、余弦级数;(6)狄利克雷定理
小提示：目前本科生就业市场竞争激烈，就业主体是研究生，在如今考研竞争日渐激烈的情况下，我们想要不在考研大军中变成分母，我们需要：早开始+好计划+正确的复习思路+好的辅导班（如果经济条件允许的情况下）。
2017考研开始准备复习啦，早起的鸟儿有虫吃，一分耕耘一分收获。
加油！。