【名师推荐】专题10 直线与圆-十年高考(2009-2018)之高三数学分项与解读(浙江专版) Word版含解析
专题17 直线与圆小题综合(教师卷)- 十年(2015-2024)高考真题数学分项汇编(全国通用)
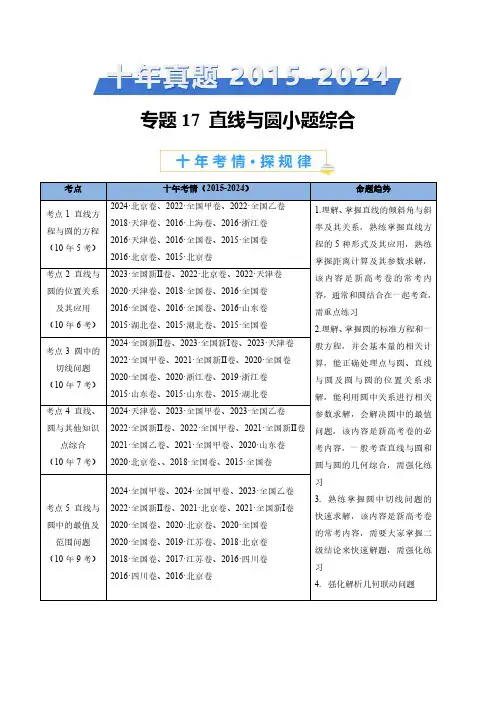
专题17直线与圆小题综合考点十年考情(2015-2024)命题趋势考点1直线方程与圆的方程(10年5考)2024·北京卷、2022·全国甲卷、2022·全国乙卷2018·天津卷、2016·上海卷、2016·浙江卷2016·天津卷、2016·全国卷、2015·全国卷2016·北京卷、2015·北京卷1.理解、掌握直线的倾斜角与斜率及其关系,熟练掌握直线方程的5种形式及其应用,熟练掌握距离计算及其参数求解,该内容是新高考卷的常考内容,通常和圆结合在一起考查,需重点练习2.理解、掌握圆的标准方程和一般方程,并会基本量的相关计算,能正确处理点与圆、直线与圆及圆与圆的位置关系求解,能利用圆中关系进行相关参数求解,会解决圆中的最值问题,该内容是新高考卷的必考内容,一般考查直线与圆和圆与圆的几何综合,需强化练习3.熟练掌握圆中切线问题的快速求解,该内容是新高考卷的常考内容,需要大家掌握二级结论来快速解题,需强化练习4.强化解析几何联动问题考点2直线与圆的位置关系及其应用(10年6考)2023·全国新Ⅱ卷、2022·北京卷、2022·天津卷2020·天津卷、2018·全国卷、2016·全国卷2016·全国卷、2016·全国卷、2016·山东卷2015·湖北卷、2015·湖北卷、2015·全国卷考点3圆中的切线问题(10年7考)2024·全国新Ⅱ卷、2023·全国新Ⅰ卷、2023·天津卷2022·全国甲卷、2021·全国新Ⅱ卷、2020·全国卷2020·全国卷、2020·浙江卷、2019·浙江卷2015·山东卷、2015·山东卷、2015·湖北卷考点4直线、圆与其他知识点综合(10年7考)2024·天津卷、2023·全国甲卷、2023·全国乙卷2022·全国新Ⅱ卷、2022·全国甲卷、2021·全国新Ⅱ卷2021·全国乙卷、2021·全国甲卷、2020·山东卷2020·北京卷、、2018·全国卷、2015·全国卷考点5直线与圆中的最值及范围问题(10年9考)2024·全国甲卷、2024·全国甲卷、2023·全国乙卷2022·全国新Ⅱ卷、2021·北京卷、2021·全国新Ⅰ卷2020·全国卷、2020·北京卷、2020·全国卷2020·全国卷、2019·江苏卷、2018·北京卷2018·全国卷、2017·江苏卷、2016·四川卷2016·四川卷、2016·北京卷考点01直线方程与圆的方程1.(2024·北京·高考真题)圆22260x y x y +-+=的圆心到直线20x y -+=的距离为()A 2B .2C .3D .32【答案】D【分析】求出圆心坐标,再利用点到直线距离公式即可.【详解】由题意得22260x y x y +-+=,即()()221310x y -++=,则其圆心坐标为()1,3-,则圆心到直线20x y -+=()()221323211--+=+-故选:D.2.(2022·全国甲卷·高考真题)设点M 在直线210x y +-=上,点(3,0)和(0,1)均在M 上,则M 的方程为.【答案】22(1)(1)5x y -++=【分析】设出点M 的坐标,利用(3,0)和(0,1)均在M 上,求得圆心及半径,即可得圆的方程.【详解】[方法一]:三点共圆∵点M 在直线210x y +-=上,∴设点M 为(,12)-a a ,又因为点(3,0)和(0,1)均在M 上,∴点M 到两点的距离相等且为半径R ,2222(3)(12)(2)-+-+-=a a a a R ,222694415-++-+=a a a a a ,解得1a =,∴(1,1)M -,5R =M 的方程为22(1)(1)5x y -++=.故答案为:22(1)(1)5x y -++=[方法二]:圆的几何性质由题可知,M 是以(3,0)和(0,1)为端点的线段垂直平分线y=3x-4与直线210x y +-=的交点(1,-1).5R =M 的方程为22(1)(1)5x y -++=.故答案为:22(1)(1)5x y -++=3.(2022·全国乙卷·高考真题)过四点(0,0),(4,0),(1,1),(4,2)-中的三点的一个圆的方程为.【答案】()()222313x y -+-=或()()22215x y -+-=或224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭或()2281691525x y ⎛⎫-+-= ⎪⎝⎭.【分析】方法一:设圆的方程为220x y Dx Ey F ++++=,根据所选点的坐标,得到方程组,解得即可;【详解】[方法一]:圆的一般方程依题意设圆的方程为220x y Dx Ey F ++++=,(1)若过()0,0,()4,0,()1,1-,则01640110F D F D E F =⎧⎪++=⎨⎪+-++=⎩,解得046F D E =⎧⎪=-⎨⎪=-⎩,所以圆的方程为22460x y x y +--=,即()()222313x y -+-=;(2)若过()0,0,()4,0,()4,2,则01640164420F D F D E F =⎧⎪++=⎨⎪++++=⎩,解得042F D E =⎧⎪=-⎨⎪=-⎩,所以圆的方程为22420x y x y +--=,即()()22215x y -+-=;(3)若过()0,0,()4,2,()1,1-,则0110164420F D E F D E F =⎧⎪+-++=⎨⎪++++=⎩,解得083143F D E ⎧⎪=⎪⎪=-⎨⎪⎪=-⎪⎩,所以圆的方程为22814033x y x y +--=,即224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭;(4)若过()1,1-,()4,0,()4,2,则1101640164420D E F D F D E F +-++=⎧⎪++=⎨⎪++++=⎩,解得1651652F D E ⎧=-⎪⎪⎪=-⎨⎪=-⎪⎪⎩,所以圆的方程为2216162055x y x y +---=,即()2281691525x y ⎛⎫-+-= ⎪⎝⎭;故答案为:()()222313x y -+-=或()()22215x y -+-=或224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭或()2281691525x y ⎛⎫-+-= ⎪⎝⎭.[方法二]:【最优解】圆的标准方程(三点中的两条中垂线的交点为圆心)设()()()()0,04,01,14,2A B C D -点,,,(1)若圆过、、A B C 三点,圆心在直线2x =,设圆心坐标为(2,)a ,则()224913,a a a r +=+-⇒=22(2)(3)13x y -+-=;(2)若圆过A B D 、、三点,设圆心坐标为(2,)a,则2244(2)1,a a a r +=+-⇒==的方程为22(2)(1)5x y -+-=;(3)若圆过A C D 、、三点,则线段AC 的中垂线方程为1y x =+,线段AD 的中垂线方程为25y x =-+,联立得47,33x y r ==⇒=,所以圆的方程为224765()()339x y -+-=;(4)若圆过B C D 、、三点,则线段BD 的中垂线方程为1y =,线段BC 中垂线方程为57y x =-,联立得813,155x y r ==⇒=,所以圆的方程为()228169()1525x -y +-=.故答案为:()()222313x y -+-=或()()22215x y -+-=或224765339x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭或()2281691525x y ⎛⎫-+-=⎪⎝⎭.【整体点评】方法一;利用圆过三个点,设圆的一般方程,解三元一次方程组,思想简单,运算稍繁;方法二;利用圆的几何性质,先求出圆心再求半径,运算稍简洁,是该题的最优解.4.(2018·天津·高考真题)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为.【答案】2220x y x +-=【详解】分析:由题意利用待定系数法求解圆的方程即可.详解:设圆的方程为220x y Dx Ey F ++++=,圆经过三点(0,0),(1,1),(2,0),则:01104020F D E F D F =⎧⎪++++=⎨⎪+++=⎩,解得:200D E F =-⎧⎪=⎨⎪=⎩,则圆的方程为2220x y x +-=.点睛:求圆的方程,主要有两种方法:(1)几何法:具体过程中要用到初中有关圆的一些常用性质和定理.如:①圆心在过切点且与切线垂直的直线上;②圆心在任意弦的中垂线上;③两圆相切时,切点与两圆心三点共线.(2)待定系数法:根据条件设出圆的方程,再由题目给出的条件,列出等式,求出相关量.一般地,与圆心和半径有关,选择标准式,否则,选择一般式.不论是哪种形式,都要确定三个独立参数,所以应该有三个独立等式.5.(2016·上海·高考真题)已知平行直线,则12l l 与的距离是.【详解】试题分析:利用两平行线间的距离公式得5d ==.【考点】两平行线间距离公式【名师点睛】确定两平行线间距离,关键是注意应用公式的条件,即,x y 的系数必须相同,本题较为容易,主要考查考生的基本运算能力.6.(2016·浙江·高考真题)已知a R ∈,方程222(2)4850a x a y x y a +++++=表示圆,则圆心坐标是,半径是.【答案】(2,4)--;5.【详解】试题分析:由题意,知22a a =+,12a =-或,当1a =-时,方程为224850x y x y +++-=,即22(2)(4)25x y +++=,圆心为(2,4)--,半径为5,当2a =时,方程为224448100x y x y ++++=,2215()(1)24x y +++=-不表示圆.圆的标准方程.由方程222(2)4850a x a y x y a +++++=表示圆可得a 的方程,解得a 的值,一定要注意检验a 的值是否符合题意,否则很容易出现错误.7.(2016·天津·高考真题)已知圆C 的圆心在x 轴的正半轴上,点M 在圆C 上,且圆心到直线20x y -=的距离为5,则圆C 的方程为.【答案】22(2)9.x y -+=【详解】试题分析:设(,0)(0)C a a >2,3a r ===,故圆C 的方程为22(2)9.x y -+=【考点】直线与圆位置关系【名师点睛】求圆的方程有两种方法:(1)代数法:即用“待定系数法”求圆的方程.①若已知条件与圆的圆心和半径有关,则设圆的标准方程,列出关于a ,b ,r 的方程组求解.②若已知条件没有明确给出圆的圆心或半径,则选择圆的一般方程,列出关于D ,E ,F 的方程组求解.(2)几何法:通过研究圆的性质、直线和圆的位置关系等求出圆心、半径,进而写出圆的标准方程.8.(2016·全国·高考真题)圆2228130+--+=x y x y 的圆心到直线10ax y +-=的距离为1,则=a A .43-B .34-C D .2【答案】A【详解】试题分析:由2228130x y x y +--+=配方得22(1)(4)4x y -+-=,所以圆心为(1,4),因为圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为11=,解得43a =-,故选A.【考点】圆的方程,点到直线的距离公式【名师点睛】直线与圆的位置关系有三种情况:相交、相切和相离.已知直线与圆的位置关系时,常用几何法将位置关系转化为圆心到直线的距离d 与半径r 的大小关系,以此来确定参数的值或取值范围.9.(2015·全国·高考真题)过三点(1,3)A ,(4,2)B ,(1,7)C -的圆交y 轴于M ,N 两点,则MN =A .2B .8C .4D .10【答案】C【详解】由已知得321143AB k -==--,27341CB k +==--,所以1AB CB k k =-,所以AB CB ⊥,即ABC ∆为直角三角形,其外接圆圆心为AC 中点(1,2)-,半径为长为AC52=,所以外接圆方程为22(1)(2)25x y -++=,令0x =,得2y =±,所以MN =C .考点:圆的方程.10.(2016·北京·高考真题)圆(x +1)2+y 2=2的圆心到直线y =x +3的距离为()A .1B .2CD .【答案】C【详解】试题分析:圆心坐标为(1,0)-,由点到直线的距离公式可知d = C.【考点】直线与圆的位置关系【名师点睛】点到直线(即)的距离公式记忆容易,对于知求,很方便.11.(2015·北京·高考真题)圆心为()1,1且过原点的圆的方程是A .()()22111x y -+-=B .()()22111x y +++=C .()()22112x y +++=D .()()22112x y -+-=【答案】D【详解】试题分析:设圆的方程为()()2211(0)x y m m -+-=>,且圆过原点,即()()220101(0)m m -+-=>,得2m =,所以圆的方程为()()22112x y -+-=.故选D.考点:圆的一般方程.考点02直线与圆的位置关系及其应用1.(2023·全国新Ⅱ卷·高考真题)已知直线:10l x my -+=与()22:14C x y -+= 交于A ,B 两点,写出满足“ABC 面积为85”的m 的一个值.【答案】2(112,2,,22--中任意一个皆可以)【分析】根据直线与圆的位置关系,求出弦长AB ,以及点C 到直线AB 的距离,结合面积公式即可解出.【详解】设点C 到直线AB 的距离为d ,由弦长公式得AB =,所以1825ABC S d =⨯⨯=△,解得:5d =或5d =,由d ==5=5=,解得:2m =±或12m =±.故答案为:2(112,2,,22--中任意一个皆可以).2.(2022·北京·高考真题)若直线210x y +-=是圆22()1x a y -+=的一条对称轴,则=a ()A .12B .12-C .1D .1-【答案】A【分析】若直线是圆的对称轴,则直线过圆心,将圆心代入直线计算求解.【详解】由题可知圆心为(),0a ,因为直线是圆的对称轴,所以圆心在直线上,即2010a +-=,解得12a =.故选:A .3.(2022·天津·高考真题)若直线()00x y m m -+=>与圆()()22113x y -+-=相交所得的弦长为m ,则m =.【答案】2【分析】计算出圆心到直线的距离,利用勾股定理可得出关于m 的等式,即可解得m 的值.【详解】圆()()22113x y -+-=的圆心坐标为()1,1圆心到直线()00x y m m -+=>由勾股定理可得2232m ⎛⎫+= ⎪⎝⎭,因为0m >,解得2m =.故答案为:2.4.(2020·天津·高考真题)已知直线80x +=和圆222(0)x y r r +=>相交于,A B两点.若||6AB =,则r 的值为.【答案】5【分析】根据圆的方程得到圆心坐标和半径,由点到直线的距离公式可求出圆心到直线的距离d ,进而利用弦长公式||AB =,即可求得r .【详解】因为圆心()0,0到直线80x -+=的距离4d ==,由||AB =可得6==5r .故答案为:5.【点睛】本题主要考查圆的弦长问题,涉及圆的标准方程和点到直线的距离公式,属于基础题.5.(2018·全国·高考真题)直线1y x =+与圆22230x y y ++-=交于A B ,两点,则AB =.【答案】【分析】方法一:先将圆的方程化成标准方程,求出圆心,半径,再根据点到直线的距离公式以及弦长公式即可求出.【详解】[方法一]:【通性通法】【最优解】弦长公式的应用根据题意,圆的方程可化为22(1)4x y ++=,所以圆的圆心为(0,1)-,且半径是2,弦心距d =AB ==.故答案为:[方法二]:距离公式的应用由221230y x x y y =+⎧⎨++-=⎩解得:01x y =⎧⎨=⎩或21x y =-⎧⎨=-⎩,不妨设(0,1),(2,1)A B --,所以AB =.故答案为:[方法三]:参数方程的应用直线1y x =+的参数方程为0212x y ⎧=+⎪⎪⎨⎪=+⎪⎩,将其代入22230x y y ++-=,可得22112130222t t ⎛⎫⎛⎫++++-= ⎪ ⎪⎝⎭⎝⎭,化简得20t +=,从而120,t t ==-12AB t t =-=.故答案为:【整体点评】方法一:利用圆的弦长公式直接求解,是本题的通性通法,也是最优解;方法二:直接求出弦的端点坐标,再根据两点间的距离公式求出,是求解一般弦长的通性通法,有时计算偏麻烦;方法三:直线参数方程中弦长公式的应用.6.(2016·全国·高考真题)已知直线l:60x +=与圆2212x y +=交于,A B 两点,过,A B 分别作l 的垂线与x 轴交于,C D 两点.则CD =.【答案】4【详解】试题分析:由60x -+=,得6x =-,代入圆的方程,整理得260y -+=,解得12y y ==120,3x x ==-,所以AB ==l 的倾斜角为30︒,由平面几何知识知在梯形ABDC 中,4cos30ABCD ==︒.【考点】直线与圆的位置关系【技巧点拨】解决直线与圆的综合问题时,一方面,要注意运用解析几何的基本思想方法(即几何问题代数化),把它转化为代数问题;另一方面,由于直线与圆和平面几何联系的非常紧密,因此,准确地作出图形,并充分挖掘几何图形中所隐含的条件,利用几何知识使问题较为简捷地得到解决.7.(2016·全国·高考真题)已知直线l:30mx y m ++=与圆2212x y +=交于A ,B 两点,过A ,B 分别作l 的垂线与x 轴交于C ,D两点,若||AB =,则||CD =.【答案】4【分析】由题,根据垂径定理求得圆心到直线的距离,可得m 的值,既而求得CD 的长可得答案.【详解】因为AB =r =()0,0到直线30mx y m ++=的距离为33=,解得m =l的方程,得3y x =+l 的倾斜角为30︒,由平面几何知识知在梯形ABDC 中,4AB CD ==︒.故答案为4【点睛】解决直线与圆的综合问题时,一方面,要注意运用解析几何的基本思想方法(即几何问题代数化),把它转化为代数问题;另一方面,由于直线与圆和平面几何联系得非常紧密,因此,准确地作出图形,并充分挖掘几何图形中所隐含的条件,利用几何知识使问题较为简捷地得到解决.8.(2016·全国·高考真题)设直线2y x a =+与圆C :x 2+y 2-2ay -2=0相交于A ,B两点,若AB =C 的面积为【答案】4π【详解】因为圆心坐标与半径分别为(0,),=C a rd =2232a +=+,解之得22a =,所以圆的面积2(22)4πππ==+=S r ,应填答案4π.9.(2016·山东·高考真题)已知圆()22:200M x y ay a +-=>截直线0x y +=所得线段的长度是则圆M与圆()()22:111N x y -+-=的位置关系是A .内切B .相交C .外切D .相离【答案】B【详解】化简圆()()2221:0,,M x y a a M a r a M +-=⇒=⇒到直线0x y +=的距离d =⇒()221220,2,2a a M r+=⇒=⇒=,又()2121,1,1N r MN r r MN=⇒⇒-<<12r r+⇒两圆相交.选B10.(2015·湖北·高考真题)如图,已知圆C与x 轴相切于点,与y轴正半轴交于两点A,B(B在A 的上方),且2AB=.(Ⅰ)圆C的标准方程为_________;(Ⅱ)圆C在点B处的切线在x轴上的截距为_________.【答案】(Ⅰ)22(1)(2x y-+-=;(Ⅱ)1-.【详解】设点C的坐标为00(,)x y,则由圆C与x 轴相切于点知,点C的横坐标为1,即1x=,半径0r y=.又因为2AB=,所以22211y+=,即0y r=,所以圆C的标准方程为22(1)(2x y-+=,令0x=得:1)B+.设圆C在点B处的切线方程为1)y kx-=,则圆心C到其距离为:d==1k=.即圆C在点B处的切线方程为1)y x=+,于是令0y=可得1x=,即圆C在点B处的切线在x轴上的截距为1-22(1)(2x y-+=和1--考点:本题考查圆的标准方程和圆的切线问题,属中高档题.11.(2015·湖北·高考真题)如图,圆C与x轴相切于点()1,0T,与y轴正半轴交于两点,A B (在的上方),且2AB=.(Ⅰ)圆C的标准方程为;(Ⅱ)过点A任作一条直线与圆22:1O x y+=相交于,M N两点,下列三个结论:①NA MANB MB=;②2NB MANA MB-=;③NB MANA MB+=其中正确结论的序号是.(写出所有正确结论的序号)【答案】22(1)(2)2x y -+-=;①②③【详解】(Ⅰ)依题意,设(1,)C r (r 为圆的半径),因为||2AB =,所以22112r =+,所以圆心(2,C ,故圆的标准方程为()(22122x y -+=.(Ⅱ)因为,M N 在圆22:1O x y +=上,所以可设(cos ,sin ),(cos ,sin )M N ααββ,所以22(cos 0)[sin (21)]NA ββ=-+--2(21)(2sin )β=--22(cos 0)[sin (21)]NB ββ=-+-+2(21)(2sin )β+-所以21NA NB =,同理可得21M AM B,所以NA MA NBMB=,1(21)221NB MA NAMB--=-,22NA MA NB MB +=,故①②③都正确.12.(2015·全国·高考真题)过三点(1,3)A ,(4,2)B ,(1,7)C -的圆交y 轴于M ,N 两点,则MN =A .2B .8C .4D .10【答案】C【详解】由已知得321143AB k -==--,27341CB k +==--,所以1AB CB k k =-,所以AB CB ⊥,即ABC ∆为直角三角形,其外接圆圆心为AC 中点(1,2)-,半径为长为AC52=,所以外接圆方程为22(1)(2)25x y -++=,令0x =,得262y =±,所以46MN =C .考点:圆的方程.考点03圆中的切线问题1.(2024·全国新Ⅱ卷·高考真题)(多选)抛物线C :24y x =的准线为l ,P 为C 上的动点,过P 作22:(4)1A x y +-=⊙的一条切线,Q 为切点,过P 作l 的垂线,垂足为B ,则()A .l 与A 相切B .当P ,A ,B 三点共线时,||PQ =C .当||2PB =时,PA AB⊥D .满足||||PA PB =的点P 有且仅有2个【答案】ABD【分析】A 选项,抛物线准线为=1x -,根据圆心到准线的距离来判断;B 选项,,,P A B 三点共线时,先求出P 的坐标,进而得出切线长;C 选项,根据2PB =先算出P 的坐标,然后验证1PA AB k k =-是否成立;D 选项,根据抛物线的定义,PB PF =,于是问题转化成PA PF =的P 点的存在性问题,此时考察AF 的中垂线和抛物线的交点个数即可,亦可直接设P 点坐标进行求解.【详解】A 选项,抛物线24y x =的准线为=1x -,A 的圆心(0,4)到直线=1x -的距离显然是1,等于圆的半径,故准线l 和A 相切,A 选项正确;B 选项,,,P A B 三点共线时,即PA l ⊥,则P 的纵坐标4P y =,由24P P y x =,得到4P x =,故(4,4)P ,此时切线长PQ ===,B 选项正确;C 选项,当2PB =时,1P x =,此时244P P y x ==,故(1,2)P 或(1,2)P -,当(1,2)P 时,(0,4),(1,2)A B -,42201PA k -==--,4220(1)AB k -==--,不满足1PA AB k k =-;当(1,2)P -时,(0,4),(1,2)A B -,4(2)601PA k --==--,4(2)60(1)AB k --==--,不满足1PA AB k k =-;于是PA AB ⊥不成立,C 选项错误;D 选项,方法一:利用抛物线定义转化根据抛物线的定义,PB PF =,这里(1,0)F ,于是PA PB =时P 点的存在性问题转化成PA PF =时P 点的存在性问题,(0,4),(1,0)A F ,AF 中点1,22⎛⎫ ⎪⎝⎭,AF 中垂线的斜率为114AF k -=,于是AF 的中垂线方程为:2158x y +=,与抛物线24y x =联立可得216300y y -+=,2164301360∆=-⨯=>,即AF 的中垂线和抛物线有两个交点,即存在两个P 点,使得PA PF =,D 选项正确.方法二:(设点直接求解)设2,4t P t ⎛⎫⎪⎝⎭,由PB l ⊥可得()1,B t -,又(0,4)A ,又PA PB =,214t =+,整理得216300t t -+=,2164301360∆=-⨯=>,则关于t 的方程有两个解,即存在两个这样的P 点,D 选项正确.故选:ABD2.(2023·全国新Ⅰ卷·高考真题)过点()0,2-与圆22410x y x +--=相切的两条直线的夹角为α,则sin α=()A .1BCD 【答案】B【分析】方法一:根据切线的性质求切线长,结合倍角公式运算求解;方法二:根据切线的性质求切线长,结合余弦定理运算求解;方法三:根据切线结合点到直线的距离公式可得2810k k ++=,利用韦达定理结合夹角公式运算求解.【详解】方法一:因为22410x y x +--=,即()2225x y -+=,可得圆心()2,0C ,半径r =,过点()0,2P -作圆C 的切线,切点为,A B ,因为PC =PA =可得sin APC APC ∠=∠=,则sin sin 22sin cos 2APB APC APC APC ∠=∠=∠∠=⨯22221cos cos 2cos sin 04APB APC APC APC ⎫∠=∠=∠-∠=-=-<⎪⎪⎝⎭⎝⎭,即APB ∠为钝角,所以()sin sin πsin 4APB APB =-∠=∠=α;法二:圆22410x y x +--=的圆心()2,0C ,半径r =,过点()0,2P -作圆C 的切线,切点为,A B ,连接AB ,可得PC =PA PB ===,因为22222cos 2cos PA PB PA PB APB CA CB CA CB ACB +-⋅∠=+-⋅∠且πACB APB ∠=-∠,则()336cos 5510cos πAPB APB +-∠=+--∠,即3cos 55cos APB APB -∠=+∠,解得1cos 04APB ∠=-<,即APB ∠为钝角,则()1cos cos πcos 4APB APB =-∠=-∠=α,且α为锐角,所以sin α==;方法三:圆22410x y x +--=的圆心()2,0C ,半径r 若切线斜率不存在,则切线方程为0x =,则圆心到切点的距离2d r =>,不合题意;若切线斜率存在,设切线方程为2y kx =-,即20kx y --=,=2810k k ++=,且644600∆=-=>设两切线斜率分别为12,k k ,则12128,1k k k k +=-=,可得12k k -=所以1212tan 1k k k k -==+αsin cos αα=,可得cos =α则2222sin sin cos sin 115+=+=αααα,且()0,πα∈,则sin 0α>,解得sin α=故选:B.3.(2023·天津·高考真题)已知过原点O 的一条直线l 与圆22:(2)3C x y ++=相切,且l 与抛物线22(0)y px p =>交于点,O P 两点,若8OP =,则p =.【答案】6【分析】根据圆()2223x y ++=和曲线22y px =关于x 轴对称,不妨设切线方程为y kx =,0k >,即可根据直线与圆的位置关系,直线与抛物线的位置关系解出.【详解】易知圆()2223x y ++=和曲线22y px =关于x 轴对称,不妨设切线方程为y kx =,0k >,=k =22y y px ⎧=⎪⎨=⎪⎩解得:00x y =⎧⎨=⎩或23p x y ⎧=⎪⎪⎨⎪=⎪⎩,所以483p OP ==,解得:6p =.当k =故答案为:6.4.(2022·全国甲卷·高考真题)若双曲线2221(0)x y m m-=>的渐近线与圆22430x y y +-+=相切,则m =.【分析】首先求出双曲线的渐近线方程,再将圆的方程化为标准式,即可得到圆心坐标与半径,依题意圆心到直线的距离等于圆的半径,即可得到方程,解得即可.【详解】解:双曲线()22210x y m m-=>的渐近线为y x m =±,即0x my ±=,不妨取0x my +=,圆22430x y y +-+=,即()2221x y +-=,所以圆心为()0,2,半径1r =,依题意圆心()0,2到渐近线0x my +=的距离1d ==,解得m =或m =.故答案为:3.5.(2021·全国新Ⅱ卷·高考真题)(多选)已知直线2:0l ax by r +-=与圆222:C x y r +=,点(,)A a b ,则下列说法正确的是()A .若点A 在圆C 上,则直线l 与圆C 相切B .若点A 在圆C 内,则直线l 与圆C 相离C .若点A 在圆C 外,则直线l 与圆C 相离D .若点A 在直线l 上,则直线l 与圆C 相切【答案】ABD【分析】转化点与圆、点与直线的位置关系为222,a b r +的大小关系,结合点到直线的距离及直线与圆的位置关系即可得解.【详解】圆心()0,0C 到直线l的距离2d =若点(),A a b 在圆C 上,则222a b r +=,所以2d r =,则直线l 与圆C 相切,故A 正确;若点(),A a b 在圆C 内,则222a b r +<,所以2d r =,则直线l 与圆C 相离,故B 正确;若点(),A a b 在圆C 外,则222a b r +>,所以2d r =,则直线l 与圆C 相交,故C 错误;若点(),A a b 在直线l 上,则2220a b r +-=即222=a b r +,所以2d r =,直线l 与圆C 相切,故D 正确.故选:ABD.6.(2020·全国·高考真题)若直线l 与曲线yx 2+y 2=15都相切,则l 的方程为()A .y =2x +1B .y =2x +12C .y =12x +1D .y =12x +12【答案】D【分析】根据导数的几何意义设出直线l 的方程,再由直线与圆相切的性质,即可得出答案.【详解】设直线l在曲线y =(0x ,则00x >,函数y =y '=l的斜率k =,设直线l的方程为)0y x x =-,即00x x -+=,由于直线l 与圆2215x y +==两边平方并整理得2005410x x --=,解得01x =,015x =-(舍),则直线l 的方程为210x y -+=,即1122y x =+.故选:D.【点睛】本题主要考查了导数的几何意义的应用以及直线与圆的位置的应用,属于中档题.7.(2020·全国·高考真题)若过点(2,1)的圆与两坐标轴都相切,则圆心到直线230x y --=的距离为()A B C D 【答案】B【分析】由题意可知圆心在第一象限,设圆心的坐标为(),,0a a a >,可得圆的半径为a ,写出圆的标准方程,利用点()2,1在圆上,求得实数a 的值,利用点到直线的距离公式可求出圆心到直线230x y --=的距离.【详解】由于圆上的点()2,1在第一象限,若圆心不在第一象限,则圆与至少与一条坐标轴相交,不合乎题意,所以圆心必在第一象限,设圆心的坐标为(),a a ,则圆的半径为a ,圆的标准方程为()()222x a y a a -+-=.由题意可得()()22221a a a -+-=,可得2650a a -+=,解得1a =或5a =,所以圆心的坐标为()1,1或()5,5,圆心到直线的距离均为1d =;圆心到直线的距离均为25d =圆心到直线230x y --=的距离均为5d ==;所以,圆心到直线230x y --=.故选:B.【点睛】本题考查圆心到直线距离的计算,求出圆的方程是解题的关键,考查计算能力,属于中等题.8.(2020·浙江·高考真题)设直线:(0)l y kx b k =+>与圆221x y +=和圆22(4)1x y -+=均相切,则k =;b =.【答案】33-【分析】由直线与两圆相切建立关于k ,b 的方程组,解方程组即可.【详解】设221:1C x y +=,222:(4)1C x y -+=,由题意,12,C C 1=,1=,所以||4b k b =+,所以0k =(舍)或者2b k =-,解得k b ==【点晴】本题主要考查直线与圆的位置关系,考查学生的数学运算能力,是一道基础题.9.(2019·浙江·高考真题)已知圆C 的圆心坐标是(0,)m ,半径长是r .若直线230x y -+=与圆相切于点(2,1)A --,则m =,r =.【答案】2m =-r =【分析】本题主要考查圆的方程、直线与圆的位置关系.首先通过确定直线AC 的斜率,进一步得到其方程,将(0,)m 代入后求得m ,计算得解.【详解】可知11:1(2)22AC k AC y x =-⇒+=-+,把(0,)m 代入得2m =-,此时||r AC ===【点睛】解答直线与圆的位置关系问题,往往要借助于数与形的结合,特别是要注意应用圆的几何性质.10.(2015·山东·高考真题)一条光线从点()2,3--射出,经y 轴反射后与圆()()22321x y ++-=相切,则反射光线所在直线的斜率为()A .53-或53B .35-或32C .23-或23D .43-或34-【答案】D【详解】由光的反射原理知,反射光线的反向延长线必过点()2,3-,设反射光线所在直线的斜率为k ,则反射光线所在直线方程为:()32y k x +=-,即:230kx y k ---=.又因为光线与圆相切,()()22321x y ++-=1=,整理:21225120k k ++=,解得:43k =-,或34k =-,故选D .考点:1、圆的标准方程;2、直线的方程;3、直线与圆的位置关系.11.(2015·山东·高考真题)过点P (作圆221x y +=的两条切线,切点分别为,A B ,则PA PB ⋅=.【答案】32【详解】如图,连接PO ,在直角三角形PAO中,1,OA PA ==所以,tan APO ∠=,22211tan 1cos 1tan 2APO APB APO --∠∠==+∠,故1322PA PB PA PB cos APB ⋅=⋅∠== .考点:1.直线与圆的位置关系;2.平面向量的数量积.12.(2015·湖北·高考真题)如图,已知圆C 与x 轴相切于点,与y 轴正半轴交于两点A ,B (B 在A的上方),且2AB =.(Ⅰ)圆C 的标准方程为_________;(Ⅱ)圆C 在点B 处的切线在x 轴上的截距为_________.【答案】(Ⅰ)22(1)(2)2x y -+-=;(Ⅱ)12-.【详解】设点C 的坐标为00(,)x y ,则由圆C 与x 轴相切于点知,点C 的横坐标为1,即01x =,半径0r y =.又因为2AB =,所以222011y +=,即02y r =,所以圆C 的标准方程为22(1)(2)2x y -+=,令0x =得:21)B +.设圆C 在点B 处的切线方程为(21)y kx -=,则圆心C 到其距离为:222121k d k -++==+1k =.即圆C 在点B 处的切线方程为(21)y x =+,于是令0y =可得21x =-,即圆C 在点B 处的切线在x 轴上的截距为12-22(1)(2)2x y -+=和12--考点:本题考查圆的标准方程和圆的切线问题,属中高档题.考点04直线、圆与其他知识点综合1.(2024·天津·高考真题)圆22(1)25-+=x y 的圆心与抛物线22(0)y px p =>的焦点F 重合,A 为两曲线的交点,则原点到直线AF 的距离为.【答案】45/0.8【分析】先求出圆心坐标,从而可求焦准距,再联立圆和抛物线方程,求A 及AF 的方程,从而可求原点到直线AF 的距离.【详解】圆22(1)25-+=x y 的圆心为()1,0F ,故12p=即2p =,由()2221254x y y x ⎧-+=⎪⎨=⎪⎩可得22240x x +-=,故4x =或6x =-(舍),故()4,4A ±,故直线()4:13AF y x =±-即4340x y --=或4340x y +-=,故原点到直线AF 的距离为4455d ==,故答案为:452.(2023·全国甲卷·高考真题)已知双曲线2222:1(0,0)x y C a b a b-=>>C 的一条渐近线与圆22(2)(3)1x y -+-=交于A ,B 两点,则||AB =()A B C D 【答案】D【分析】根据离心率得出双曲线渐近线方程,再由圆心到直线的距离及圆半径可求弦长.【详解】由e =222222215c a b b a a a+==+=,解得2ba=,所以双曲线的一条渐近线为2y x =,则圆心(2,3)到渐近线的距离5d =,所以弦长||5AB ===.故选:D3.(2023·全国乙卷·高考真题)设O 为平面坐标系的坐标原点,在区域(){}22,14x y x y ≤+≤内随机取一点,记该点为A ,则直线OA 的倾斜角不大于π4的概率为()A .18B .16C .14D .12【答案】C【分析】根据题意分析区域的几何意义,结合几何概型运算求解.【详解】因为区域(){}22,|14x y x y ≤+≤表示以()0,0O 圆心,外圆半径2R =,内圆半径1r =的圆环,则直线OA 的倾斜角不大于π4的部分如阴影所示,在第一象限部分对应的圆心角π4MON ∠=,结合对称性可得所求概率13π143π4P ⨯==.故选:C.4.(2022·全国新Ⅱ卷·高考真题)图1是中国古代建筑中的举架结构,,,,AA BB CC DD ''''是桁,相邻桁的水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图.其中1111,,,DD CC BB AA 是举,1111,,,OD DC CB BA 是相等的步,相邻桁的举步之比分别为11111231111,0.5,,DD CC BB AAk k k OD DC CB BA ====.已知123,,k k k 成公差为0.1的等差数列,且直线OA 的斜率为0.725,则3k =()A .0.75B .0.8C .0.85D .0.9【答案】D【分析】设11111OD DC CB BA ====,则可得关于3k 的方程,求出其解后可得正确的选项.【详解】设11111OD DC CB BA ====,则111213,,CC k BB k AA k ===,依题意,有31320.2,0.1k k k k -=-=,且111111110.725DD CC BB AA OD DC CB BA +++=+++,所以30.530.30.7254k +-=,故30.9k =,故选:D5.(2022·全国甲卷·高考真题)若双曲线2221(0)x y m m-=>的渐近线与圆22430x y y +-+=相切,则m =.【分析】首先求出双曲线的渐近线方程,再将圆的方程化为标准式,即可得到圆心坐标与半径,依题意圆心到直线的距离等于圆的半径,即可得到方程,解得即可.【详解】解:双曲线()22210x y m m-=>的渐近线为y x m =±,即0x my ±=,不妨取0x my +=,圆22430x y y +-+=,即()2221x y +-=,所以圆心为()0,2,半径1r =,依题意圆心()0,2到渐近线0x my +=的距离1d ==,解得m =或m =.6.(2021·全国新Ⅱ卷·高考真题)抛物线22(0)y px p =>的焦点到直线1y x =+p =()A .1B .2C.D .4【答案】B【分析】首先确定抛物线的焦点坐标,然后结合点到直线距离公式可得p 的值.【详解】抛物线的焦点坐标为,02p ⎛⎫ ⎪⎝⎭,其到直线10x y -+=的距离:d ==解得:2p =(6p =-舍去).故选:B.7.(2021·全国乙卷·高考真题)双曲线22145x y -=的右焦点到直线280x y +-=的距离为.【分析】先求出右焦点坐标,再利用点到直线的距离公式求解.【详解】由已知,3c ==,所以双曲线的右焦点为(3,0),所以右焦点(3,0)到直线280x y +-==.8.(2021·全国甲卷·高考真题)点()3,0到双曲线221169x y -=的一条渐近线的距离为()A .95B .85C .65D .45【答案】A【分析】首先确定渐近线方程,然后利用点到直线距离公式求得点到一条渐近线的距离即可.【详解】由题意可知,双曲线的渐近线方程为:220169x y -=,即340x y ±=,结合对称性,不妨考虑点()3,0到直线340x y +=的距离:95d ==.故选:A.9.(2020·山东·高考真题)(多选)已知曲线22:1C mx ny +=.()A .若m >n >0,则C 是椭圆,其焦点在y 轴上B .若m =n >0,则CC .若mn <0,则C 是双曲线,其渐近线方程为y =D .若m =0,n >0,则C 是两条直线【答案】ACD【分析】结合选项进行逐项分析求解,0m n >>时表示椭圆,0m n =>时表示圆,0mn <时表示双曲线,0,0m n =>时表示两条直线.【详解】对于A ,若0m n >>,则221mx ny +=可化为22111x y m n+=,因为0m n >>,所以11m n<,即曲线C 表示焦点在y 轴上的椭圆,故A 正确;对于B ,若0m n =>,则221mx ny +=可化为221x y n+=,此时曲线C 表示圆心在原点,半径为n的圆,故B 不正确;对于C ,若0mn <,则221mx ny +=可化为22111x y m n+=,此时曲线C 表示双曲线,。
十年高考分类解析与应试策略数学09--第九章 直线、平面、简单几何体(A)

3
面 ABCD 是边长为 3 的正方形,EF∥AB,EF= ,EF 与面 AC 的距离
2
为 2,则该多面体的体积是( )
图 9—6
9
A.
B.5
2
—259—
15
C.6
D.
2
26.(1998 全国,7)已知圆锥的全面积是底面积的 3 倍,那么该圆锥的侧面展开图扇形
的圆心角为( )
A.120°
B.150°
A.V 甲>V 乙且 S 甲>S 乙
B.V 甲<V 乙且 S 甲<S 乙
C.V 甲=V 乙且 S 甲>S 乙
D.V 甲=V 乙且 S 甲=S 乙
10.(2002 北京理,10)设命题甲:“直四棱柱 ABCD-A1B1C1D1 中,平面 ACB1 与对
角面 BB1D1D 垂直”;命题乙:“直四棱柱 ABCD-A1B1C1D1 是正方体”.那么,甲是乙的
1
1
A.
B.
32
2
图 9—5
1
C.
2
1
D.
42
22.(2000 全国理,9)一个圆柱的侧面积展开图是一个正方形,这个圆柱的全面积与侧 面积的比是( )
1 2 A. 2
1 4 B. 4
1 2 C.
1 4 D. 2
23.(1999 全国,7)若干毫升水倒入底面半径为 2 cm 的圆柱形器皿中,量得水面的高 度为 6 cm.若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是( )
12.(2001 上海,15)已知 a、b 为两条不同的直线,α、β为两个不同的平面,且 a⊥
α,
b⊥β,则下列命题中的假命题是( )
A.若 a∥b,则α∥β
高三数学二轮复习《直线圆圆锥曲线》专题讲义

高三数学二轮复习《直线、圆、圆锥曲线》专题讲义专题热点透析解析几何是高中数学的重点内容之一,也是高考考查的热点。
高考着重考查基础知识的综合,基本方法的灵活运用,数形结合、分类整合、等价转化、函数方程思想以及分析问题解决问题的能力。
其中客观题为基础题和中档题,主观题常常是综合性很强的压轴题。
本专题命题的热点主要有:①直线方程;②线性规划;③直线与圆、圆锥曲线的概念和性质;④与函数、数列、不等式、向量、导数等知识的综合应用。
热点题型范例 一、动点轨迹方程问题例1.M (-2,0)和N (2,0)是平面上的两点,动点P 满足: 2.PM PN -= (Ⅰ)求点P 的轨迹方程; (Ⅱ)设d 为点P 到直线l :12x =的距离,若22PM PN =,求PM d 的值。
1.1在平面直角坐标系xOy 中,点P 到两点(0-,,(0的距离之和等于4,设点P 的轨迹为C . (Ⅰ)写出C 的方程;(Ⅱ)设直线1y kx =+与C 交于A ,B 两点.k 为何值时OA ⊥OB ?此时AB 的值是多少?二、圆的综合问题例2、在直角坐标系中,A(a,0)(a>0),B(0,a),C(-4,0),D(0,4),设三角形ABC 的外接圆圆心为E 。
(1)若圆E 与直线CD 相切,求实数a 的值;(2)设点p 在圆E 上,使三角形PCD 的面积等于12的点P 有且只有三个,试问这样的圆E 是否存在?若存在,求出圆E 的标准方程;若不存在,请说明理由。
三、圆锥曲线定义的应用例3. 已知21F F 、为椭圆192522=+y x 的两个焦点,过1F 的直线交椭圆于A 、B 两点,若1222=+B F A F ,则AB =3.1已知双曲线2222:1(0,0)x y C a b a b-->>的两个焦点为:(2,0),:(2,0),F F P -点的曲线C 上.(Ⅰ)求双曲线C 的方程;(Ⅱ)记O 为坐标原点,过点Q (0,2)的直线l 与双曲线C 相交于不同的两点E 、F ,若△OEF 的面积为求直线l 的方程四、圆锥曲线性质问题例5.①已知双曲线22:1916x y C -=的左右焦点分别为12,F F ,P 为C 的右支上一点,且212PF F F =,则12PF F ∆的面积等于( )(A)24 (B)36 (C)48 (D)96②已知1F 、2F 是椭圆的两个焦点,满足120MF MF ⋅=的点M 总在椭圆内部,则椭圆离心率的取值范围是( )A .(0,1)B .1(0,]2 C.(0,2D.2 4.1.设ABC △是等腰三角形,120ABC ∠=,则以A B ,为焦点且过点C 的双曲线的离心率为( )A .221+ B .231+ C . 21+ D .31+4.2.已知F 是抛物线24C y x =:的焦点,A B ,是C 上的两个点,线段AB 的中点为(22)M ,,则ABF △的面积等于五、圆锥曲线中的定值、定点问题例6. 设A 、B 为椭圆22143x y +=上的两个动点。
直线与圆位置关系-十年高考(2009-2018)之高三数学分项与解读(江苏专版)(解析版)
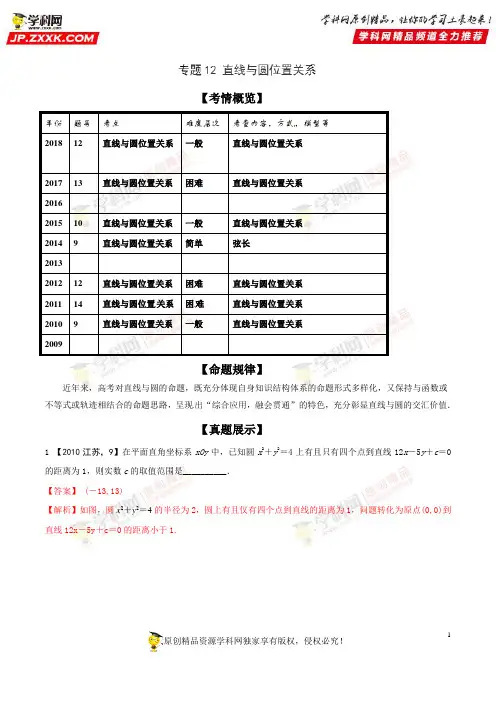
,若直线
上总存在点 ,使得过点 的 【答案】 【解析】 【分析】
的两条切线互相垂直,则实数 的取值范围是_____.
设两个切点分别为 A、B,则由题意可得四边形 PAOB 为正方形,根据圆心 O 到直线 进行求解即可得 的范围. 【详解】
的距离
,
圆心为 ,半径 ,
设两个切点分别为 A、B,则由题意可得四边形 PAOB 为正方形,
【考情概览】
年份 题号 考点
难度层次 考查内容,方式,模型等
2018 12
直线与圆位置关系 一般 [来
直线与圆位置关系
2017 13 2016 2015 10 2014 9 2013 2012 12 2011 14 2010 9 2009
源:学科网ZXXK]
直线与圆位置关系 困难
直线与圆位置关系 一般 直线与圆位置关系 简单
交
于不同的两点 A,B.若 O 是坐标原点,且
,则实数 b权,侵权必究!
4
【答案】
点睛:本题考查向量知识的运用,考查直线与圆的位置关系,考查学生的计算能力,能正确的转化向量的 不等式是解题关键,属于中档题.
2.【江苏省苏州市第五中学校 2018 届高三上学期期初考试数学(文)试题】已知
A B ,则实数 m 的取值范围是
。
原创精品资源学科网独家享有版权,侵权必究!
2
【答案】
1 2
,2
2
5 【2015 江苏高考,10】在平面直角坐标系 xOy 中,以点 (1,0) 为圆心且与直线 mx y 2m 1 0(m R)
相切的所有圆中,半径最大的圆的标准方程为 【答案】 (x 1)2 y2 2.
【解析】由题意得:半径等于 | m 1| m2 1
高三数学-2018年全国高考试题分类解析(直线与圆) 精品

2018年全国高考试题分类解析(直线与圆)一、选择题1.(江西卷)在△OAB 中,O 为坐标原点,]2,0(),1,(sin ),cos ,1(πθθθ∈B A ,则当△OAB 的面积达最大值时,=θ ( )A .6π B .4π C .3π D .2π2.(江西卷) “a =b ”是“直线相切与圆2)()(222=-+-+=b y a x x y ”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件3. (重庆卷)圆(x +2)2+y 2=5关于原点(0,0)对称的圆的方程为( ) (A) (x -2)2+y 2=5; (B) x 2+(y -2)2=5;(C) (x +2)2+(y +2)2=5; (D) x 2+(y +2)2=5。
4 (浙江)点(1,-1)到直线x -y +1=0的距离是 ( )(A)21 (B) 32 (C) 2 (D)25.(浙江)设集合A ={(x ,y )|x ,y ,1-x -y 是三角形的三边长},则A 所表示的平面区域(不含边界的阴影部分)是 ( )6.(天津卷)将直线2x -y +λ=0,沿x 轴向左平移1个单位,所得直线与圆x 2+y 2+2x -4y=0相切,则实数λ的值为 ( ) A .-3或7 B .-2或8 C .0或10 D .1或11 7. (全国卷Ⅰ)在坐标平面上,不等式组⎩⎨⎧+-≤-≥131x y x y 所表示的平面区域的面积为()(A )2(B )23(C )223 (D )28. (全国卷Ⅰ)设直线l 过点)0,2(-,且与圆122=+y x 相切,则l 的斜率是 ( )(A )1±(B )21±(C )33±(D )3±9. (全国卷I)已知直线l 过点),(02-,当直线l 与圆x y x 222=+有两个交点时,其斜率k 的取值范围是 ( )(A )),(2222- (B )),(22- (C )),(4242-(D )),(8181- 10. (全国卷III)已知过点A(-2,m)和B(m ,4)的直线与直线2x+y-1=0平行,则m 的值为( )(A )0 (B )-8 (C )2 (D )10 11.(北京卷)从原点向圆 x 2+y 2-12y +27=0作两条切线,则该圆夹在两条切线间的劣弧长为( ) (A )π (B )2π (C )4π (D )6π12. (辽宁卷)若直线02=+-c y x 按向量)1,1(-=平移后与圆522=+y x 相切,则c 的值为( )A .8或-2B .6或-4C .4或-6D .2或-813. (湖南卷)设直线的方程是0=+By Ax ,从1,2,3,4,5这五个数中每次取两个不同的数作为A 、 B 的值,则所得不同直线的条数是 ( )A .20B .19C .18D .1614.(湖南卷)已知点P (x ,y )在不等式组⎪⎩⎪⎨⎧≥-+≤-≤-022,01,02y x y x 表示的平面区域上运动,则z =x -y 的取值范围是 ( )A .[-2,-1]B .[-2,1]C .[-1,2]D .[1,2] 15.(北京卷)“m =21”是“直线(m +2)x +3my +1=0与直线(m -2)x +(m +2)y -3=0相互垂直”的( ) (A )充分必要条件(B )充分而不必要条件(C )必要而不充分条件(D )既不充分也不必要条件填空题1.(全国卷II)圆心为(1,2)且与直线51270x y --=相切的圆的方程为 . 2.(湖南卷)设直线0132=++y x 和圆03222=--+x y x 相交于点A 、B ,则弦AB 的垂直平分线方程是3.(湖南卷)已知直线ax +by +c =0与圆O :x 2+y 2=1相交于A 、B 两点,且|AB|=3,则⋅=4.(湖北卷)某实验室需购某种化工原料118千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元. 在满足需要的条件下,最少要花费 元.5 (福建卷)15.非负实数x 、y 满足y x y x y x 3,03042+⎩⎨⎧≤-+≤-+则的最大值为6(江西卷)设实数x , y 满足的最大值是则x y y y x y x ,03204202⎪⎩⎪⎨⎧≤->-+≤--7(上海)3.若x,y 满足条件 x+y ≤3y ≤2x ,则z=3x+4y 的最大值是 8(上海)直线y=21x 关于直线x =1对称的直线方程是 9.(上海)将参数方程⎩⎨⎧=+=θθsin 2cos 21y x (θ为参数)化为普通方程,所得方程是10.(山东卷)设x 、y 满足约束条件5,3212,03,0 4.x y x y x y +≤⎧⎪+≤⎪⎨≤≤⎪⎪≤≤⎩则使得目标函数65z x y =+的最大的点(,)x y 是11.(重庆卷文)若y x y x -=+则,422的最大值是 . 12.(重庆文)已知B A ),0,21(-是圆F y x F (4)21(:22=+-为圆心)上一动点,线段AB 的垂直平分线交BF 于P ,则动点P 的轨迹方程为 .解答题1.(广东卷)在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图5所示).将矩形折叠,使A点落在线段DC上. (Ⅰ)若折痕所在直线的斜率为k,试写出折痕所在直线的方程; (Ⅱ)求折痕的长的最大值.XPMN2.(江苏卷) 如图,圆O 1与圆O 2的半径都是1,O 1O 2=4,过动点P 分别作圆O 1、圆O 2的切线PM 、PN (M 、N 分别为切点),使得PM 试建立适当的坐标系,并求动点 P 的轨迹方程.3.(天津卷)某人在一山坡P 处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l 且点P 在直线l 上,l 与水平地面的夹角为a ,tana=1/2试问此人距水平地面多高时,观看塔的视角∠BPC 最大(不计此人的身高)2018年全国高考试题分类解析(直线与圆)参考答案选择题1.4)2()1(22=-+-y x 2. 0323=--y x 3. 21-4. 5005. 96.237. 11 8. 022=-+y x 9. 4)1(22=+-y x 10. (2, 3) 11. 22 12. 13422=+y x 解答题 1.(广东卷).解(I) (1)当0=k 时,此时A 点与D 点重合, 折痕所在的直线方程21=y (2)当0≠k 时,将矩形折叠后A 点落在线段CD 上的点为G(a,1) 所以A 与G 关于折痕所在的直线对称,有k a k ak k OG -=⇒-=-=⋅11,1 故G 点坐标为)1,(k G -,从而折痕所在的直线与OG 的交点坐标(线段OG 的中点)为)21,2(k M -折痕所在的直线方程)2(21kx k y +=-,即222k k kx y ++= 由(1)(2)得折痕所在的直线方程为:k=0时,21=y ;0≠k 时222k k kx y ++= (II )(1)当0≠k 时,折痕的长为2;(1) 当0≠k 时, 折痕所在的直线与坐标轴的交点坐标为)0,21(),21,0(22k k P k N +-+ 23222224)1()21()21(kk k k k PN y +=+-++== 432222/168)1(42)1(3k kk k k k y ⋅+-⋅⋅+=令0/=y 解得22-=k ∴21627max <=PN 所以折痕的长度的最大值2PMN2.(江苏卷)解:如图,以直线12O O 为x 轴,线段12O O 的垂直平分线为y 轴, 建立平面直角坐标系,则两圆心分别为12(2,0),(2,0)O O -. 设(,)P x y ,则2222211(2)1PM O P O M x y =-=++-, 同理222(2)1PN x y =-+-.∵PM ,∴2222(2)12[(2)1]x y x y ++-=-+-,即221230x x y -++=,即22(6)33x y -+=.这就是动点P 的轨迹方程. 3.(天津卷)以OA 所在直线为x 轴,以OB 所在直线为y 轴建立直角坐标系, 直线l 与水平面的夹角为α,tan α=21即l 的斜率为21,又直线l 过A (200,0)点, 所以l 方程为)200(21-=x y ,即02002=--y x 过B ,C 两点作一个圆,圆心为M ,点M 在线段BC 的垂直平分线上。
十年高考真题分类汇编(2010-2019) 数学 专题11直线与圆

十年高考真题分类汇编(2010—2019)数学专题11 直线与圆一、选择题1.(2019·全国2·理T11文T12)设F 为双曲线C:x 2a 2−y 2b2=1(a>0,b>0)的右焦点,O为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P,Q 两点.若|PQ|=|OF|,则C 的离心率为( ) A.√2 B.√3 C.2 D.√5【答案】A【解析】如图,设PQ 与x 轴交于点A,由对称性可知PQ ⊥x 轴. ∵|PQ|=|OF|=c,∴|PA|=c2.∴PA 为以OF 为直径的圆的半径,A 为圆心, ∴|OA|=c 2.∴P c 2,c2.又点P 在圆x 2+y 2=a 2上,∴c 24+c 24=a 2,即c 22=a 2, ∴e2=c 2a 2=2,∴e=√2,故选A.2.(2018·北京·理T7)在平面直角坐标系中,记d 为点P(cos θ,sin θ)到直线x-my-2=0的距离.当θ,m 变化时,d 的最大值为( ) A.1 B.2 C.3 D.4 【答案】C【解析】设P(x,y),则{x =cosθ,y =sinθ,x 2+y 2=1.即点P 在单位圆上,点P 到直线x-my-2=0的距离可转化为圆心(0,0)到直线x-my-2=0的距离加上(或减去)半径,所以距离最大为d=1+2=1+2.当m=0时,d max =3.3.(2018·全国3·理T6文T8)直线x+y+2=0分别与x 轴、y 轴交于A,B 两点,点P 在圆(x-2)2+y 2=2上,则△ABP 面积的取值范围是( ) A.[2,6] B.[4,8]C.[√2,3√2]D.[2√2,3√2]【答案】A【解析】设圆心到直线AB 的距离d=√2=2√2.点P到直线AB的距离为d'.易知d-r≤d'≤d+r,即√2≤d'≤3√2.又AB=2√2,∴S△ABP=12·|AB|·d'=√2d',∴2≤S△ABP≤6.4.(2016·山东·文T7)已知圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是2√2.则圆M与圆N:(x-1)2+(y-1)2=1的位置关系是( )A.内切B.相交C.外切D.相离【答案】B【解析】圆M的方程可化为x2+(y-a)2=a2,故其圆心为M(0,a),半径R=a.所以圆心到直线x+y=0的距离d=√1+1=√22a.所以直线x+y=0被圆M所截弦长为2√R2-d2=2√a2-(√22a)2=√2a,由题意可得√2a=2√2,故a=2.而|MN|=√(1-0)2+(1-2)2=√2,显然R-r<|MN|<R+r,所以两圆相交.5.(2016·全国2·理T4文T6)圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1,则a=( )A.-4B.-3C.√3D.2【答案】A【解析】圆的方程可化为(x-1)2+(y-4)2=4,圆心坐标为(1,4).所以d=2=1,解得a=-43,故选A.6.(2015·全国2·理T7)过三点A(1,3),B(4,2),C(1,-7)的圆交y轴于M,N两点,则|MN|=( )A.2√6B.8C.4√6D.10【答案】C【解析】设圆的方程为x2+y2+Dx+Ey+F=0,将点A,B,C代入,得{D+3E+F+10=0,4D+2E+F+20=0,D-7E+F+50=0,解得{D=-2,E=4,F=-20.则圆的方程为x2+y2-2x+4y-20=0.令x=0得y2+4y-20=0,设M(0,y1),N(0,y2),则y1,y2是方程y2+4y-20=0的两根, 由根与系数的关系,得y1+y2=-4,y1y2=-20,故|MN|=|y1-y 2|=√(y 1+y 2)2-4y 1y 2=√16+80=4√6.7.(2015·全国2·文T7)已知三点A(1,0),B(0,√3),C(2,√3),则△ABC 外接圆的圆心到原点的距离为( ) A.53 B.√213C.2√53D.43【答案】B【解析】由题意知,△ABC 外接圆的圆心是直线x=1与线段AB 垂直平分线的交点为P,而线段AB 垂直平分线的方程为y-√32=√33(x -12),它与x=1联立得圆心P 坐标为(1,2√33),则|OP|=√12+(2√33)2=√213.8.(2015·北京·文T2)圆心为(1,1)且过原点的圆的方程是( ) A.(x-1)2+(y-1)2=1B.(x+1)2+(y+1)2=1 C.(x+1)2+(y+1)2=2D.(x-1)2+(y-1)2=2 【答案】D【解析】圆的半径r=√2 ,标准方程为(x-1)2+(y-1)2=2.9.(2015·广东·理T5)平行于直线2x+y+1=0且与圆x 2+y 2=5相切的直线的方程是( ) A.2x+y+5=0或2x+y-5=0 B.2x+y+√5=0或2x+y-√5=0 C.2x-y+5=0或2x-y-5=0 D.2x-y+√5=0或2x-y-√5=0 【答案】A【解析】设与直线2x+y+1=0平行的直线方程为2x+y+m=0(m ≠1), 因为直线2x+y+m=0与圆x 2+y 2=5相切, 所以√5=√5,|m|=5.故所求直线的方程为2x+y+5=0或2x+y-5=0.10.(2015·山东·理T9)一条光线从点(-2,-3)射出,经y 轴反射后与圆(x+3)2+(y-2)2=1相切,则反射光线所在直线的斜率为( ) A.-53或-35 B.-32或-23 C.-54或-45D.-43或-34【答案】D【解析】如图,作出点P(-2,-3)关于y 轴的对称点P 0(2,-3).由题意知反射光线与圆相切,其反向延长线过点P 0.故设反射光线为y=k(x-2)-3,即kx-y-2k-3=0. ∴圆心到直线的距离d=√1+k=1,解得k=-43或k=-34.11.(2015·重庆·理T8)已知直线l:x+ay-1=0(a ∈R)是圆C:x 2+y 2-4x-2y+1=0的对称轴.过点A(-4,a)作圆C 的一条切线,切点为B,则|AB|=( ) A.2 B.4√2 C.6 D.2√10【答案】C【解析】依题意,直线l 经过圆C 的圆心(2,1),因此2+a-1=0,所以a=-1,因此点A 的坐标为(-4,-1).又圆C 的半径r=2,由△ABC 为直角三角形可得|AB|=√|AC |2-r 2. 又|AC|=2√10,所以|AB|=√(2√10)2-22=6.12.(2014·全国2·文T12)设点M(x 0,1),若在圆O:x 2+y 2=1上存在点N,使得∠OMN=45°,则x 0的取值范围是( ) A.[-1,1] B.[-12,12] C.[-√2,√2] D.[-√22,√22]【答案】A【解析】建立三角不等式,利用两点间距离公式找到x 0的取值范围.如图,过点M 作☉O 的切线,切点为N,连接ON.M 点的纵坐标为1,MN 与☉O 相切于点N. 设∠OMN=θ,则θ≥45°,即sin θ≥√22, 即ON OM ≥√22.而ON=1,∴OM≤√2.∵M 为(x 0,1),∴√x 02+1≤√2,∴x 02≤1,∴-1≤x 0≤1,∴x 0的取值范围为[-1,1].13.(2014·浙江·文T5)已知圆x 2+y 2+2x-2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a 的值是( ) A.-2B.-4C.-6D.-8【答案】B【解析】圆的方程可化为(x+1)2+(y-1)2=2-a,因此圆心为(-1,1),半径r=√2-a .圆心到直线x+y+2=0的距离d=√2=√2,又弦长为4,因此由勾股定理可得(√2)2+(42)2=(√2-a )2, 解得a=-4.故选B.14.(2014·安徽·文T6)过点P(-√3,-1)的直线l 与圆x 2+y 2=1有公共点,则直线l 的倾斜角的取值范围是( ) A.(0,π] B.(0,π] C.[0,π6] D.[0,π3]【答案】D【解析】设过点P 的直线方程为y=k(x+√3)-1,则由直线和圆有公共点知√3k √1+k ≤1,解得0≤k≤√3.故直线l 的倾斜角的取值范围是[0,π3].15.(2014·北京·文T7)已知圆C:(x-3)2+(y-4)2=1和两点A(-m,0),B(m,0)(m>0).若圆C 上存在点P,使得∠APB=90°,则m 的最大值为( ) A.7 B.6 C.5 D.4【答案】B【解析】因为A(-m,0),B(m,0)(m>0),所以使∠APB=90°的点P 在以线段AB 为直径的圆上,该圆的圆心为O(0,0),半径为m.而圆C 的圆心为C(3,4),半径为1. 由题意知点P 在圆C 上,故两圆有公共点. 所以两圆的位置关系为外切、相交或内切, 故m-1≤|CO|≤m+1,即m-1≤5≤m+1,解得4≤m ≤6. 所以m 的最大值为6.故选B.16.(2014·四川·文T9)设m ∈R,过定点A 的动直线x+my=0和过定点B 的动直线mx-y-m+3=0交于点P(x,y),则|PA|+|PB|的取值范围是( ) A.[√5,2√5] B.[√10,2√5] C.[√10,4√5] D.[2√5,4√5]【答案】B【解析】由题意,得A(0,0),B(1,3),因为1×m+m×(-1)=0,所以两直线垂直,所以点P在以AB为直径的圆上,所以PA⊥PB.所以|PA|2+|PB|2=|AB|2=10,设∠ABP=θ,则|PA|+|PB|=√10sin θ+√10cos θ=2√5sin(θ+π4).因为|PA|≥0,|PB|≥0,所以0≤θ≤π2.所以√10≤|PA|+|PB|≤2√5,故选B.17.(2013·重庆·理T7)已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P 为x轴上的动点,则|PM|+|PN|的最小值为( )A.5√2-4B.√17-1C.6-2√2D.√17【答案】A【解析】圆C1,C2的圆心分别为C1,C2,由题意知|PM|≥|PC1|-1,|PN|≥|PC2|-3,∴|PM|+|PN|≥|PC1|+|PC2|-4,故所求值为|PC1|+|PC2|-4的最小值.又C1关于x轴对称的点为C3(2,-3),所以|PC1|+|PC2|-4的最小值为|C3C2|-4=√(2-3)2+(-3-4)2-4=5√2-4,故选A.18.(2013·湖南·理T8)在等腰直角三角形ABC中,AB=AC=4,点P为边AB上异于A,B的一点,光线从点P出发,经BC,CA反射后又回到点P.若光线QR经过△ABC的重心,则AP等于( )A.2B.1C.83D.43【答案】D【解析】以A为原点,AB为x轴,AC为y轴建立直角坐标系如图所示. 则A(0,0),B(4,0),C(0,4).设△ABC的重心为D,则D点坐标为(43,43 ).设P点坐标为(m,0),则P点关于y轴的对称点P1为(-m,0),因为直线BC方程为x+y-4=0,所以P点关于BC 的对称点P2为(4,4-m),根据光线反射原理,P1,P2均在QR所在直线上,∴k P 1D =k P 2D ,即4343+m=43-4+m 43-4, 解得,m=43或m=0.当m=0时,P 点与A 点重合, 故舍去.∴m=43.19.(2012·浙江·理T3)设a ∈R,则“a=1”是“直线l 1:ax+2y-1=0与直线l 2:x+(a+1)y+4=0平行”的( ) A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件 【答案】A【解析】l 1与l 2平行的充要条件为a(a+1)=2×1且a×4≠1×(-1),可解得a=1或a=-2,故a=1是l 1∥l 2的充分不必要条件.20.(2010·安徽·文T4)过点(1,0)且与直线x-2y-2=0平行的直线方程是( ) A.x-2y-1=0 B.x-2y+1=0 C.2x+y-2=0 D.x+2y-1=0 【答案】A【解析】设直线方程为x-2y+c=0,将点(1,0)代入,解得c=-1,故直线方程为x-2y-1=0. 二、填空题1.(2019·江苏·T10)在平面直角坐标系xOy 中,P 是曲线y=x+4x (x>0)上的一个动点,则点P 到直线x+y=0的距离的最小值是 . 【答案】4【解析】当直线x+y=0平移到与曲线y=x+4x 相切位置时,切点Q 即为点P 到直线x+y=0的最小距离的点,有y'=(x +4x )'=1-4x 2=-1(x>0),得x=√2(-√2舍). 此时y=√2√2=3√2,即切点Q(√2,3√2),则切点Q 到直线x+y=0的距离为d=√2+3√2|√1+1=4,即为所求最小值.2.(2019·天津·理T12)设a ∈R,直线ax-y+2=0和圆{x =2+2cosθ,y =1+2sinθ(θ为参数)相切,则a 的值为____.【答案】34【解析】由{x =2+2cosθ,y =1+2sinθ(θ为参数),得(x-2)2+(y-1)2=4, 圆心为(2,1),r=2. 由直线与圆相切,得√2=2,解得a=3.3.(2019·浙江·T 12)已知圆C 的圆心坐标是(0,m),半径长是r.若直线2x-y+3=0与圆C 相切于点A(-2,-1),则m= ,r= . 【答案】-2 √5【解析】由题意知k AC =-12⇒AC:y+1=-12(x+2),把(0,m)代入得m=-2,此时r=|AC|=√4+1=√5. 4.(2018·天津·文T12)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为 . 【答案】x 2+y 2-2x=0【解析】画出示意图如图所示,则△OAB 为等腰直角三角形,故所求圆的圆心为(1,0),半径为1,所以所求圆的方程为(x-1)2+y 2=1,即x 2+y 2-2x=0.5.(2018·全国1·文T15)直线y=x+1与圆x 2+y 2+2y-3=0交于A,B 两点,则|AB|= . 【答案】2【解析】圆的方程可化为x 2+(y+1)2=4,故圆心C(0,-1),半径r=2,圆心到直线y=x+1的距离d=√2=√2,所以弦长|AB|=2√r 2-d 2=2√4-2=2√2.6.(2018·天津·理T12)已知圆x 2+y 2-2x=0的圆心为C, 直线{x =-1+√22t ,y =3-√22t (t 为参数)与该圆相交于A,B两点,则△ABC 的面积为_____________. 【答案】12【解析】圆C 的方程可化为(x-1)2+y 2=1,得圆心为C(1,0),半径为1.由{x =-1+√22t ,y =3-√22t(t 为参数),可得直线的普通方程为x+y-2=0.所以圆心C(1,0)到直线x+y-2=0的距离d=√1+1=√22.所以|AB|=2√1-(√22)2=√2. 所以S △ABC =12·|AB|·d=12×√2×√22=12.7.(2016·全国1·文T15)设直线y=x+2a 与圆C:x 2+y 2-2ay-2=0相交于A,B 两点,若|AB|=2√3,则圆C 的面积为 . 【答案】4π【解析】圆C 的方程可化为x 2+(y-a)2=2+a 2,直线方程为x-y+2a=0, 所以圆心坐标为(0,a),半径r 2=a 2+2,圆心到直线的距离d=√2.由已知(√3)2+a 22=a 2+2,解得a 2=2,故圆C 的面积为π(2+a 2)=4π.8.(2016·上海·理T3)已知平行直线l 1:2x+y-1=0,l 2:2x+y+1=0,则l 1,l 2的距离是 . 【答案】2√55 【解析】d=12√A +B =√2+1=2√55.9.(2016·浙江·文T10)已知a ∈R,方程a 2x 2+(a+2)y 2+4x+8y+5a=0表示圆,则圆心坐标是 ,半径是 .【答案】(-2,-4) 5【解析】由题意,可得a 2=a+2,解得a=-1或2.当a=-1时,方程为x 2+y 2+4x+8y-5=0,即(x+2)2+(y+4)2=25,故圆心为(-2,-4),半径为5;当a=2时,方程为4x 2+4y 2+4x+8y+10=0,(x +12)2+(y+1)2=-54不表示圆.10.(2016·天津·文T12)已知圆C 的圆心在x 轴的正半轴上,点M(0,√5)在圆C 上,且圆心到直线2x-y=0的距离为4√55,则圆C 的方程为 . 【答案】(x-2)2+y 2=9【解析】设圆心C 的坐标为(a,0)(a>0),√5=4√55⇒a=2.又点M(0,√5)在圆C 上,则圆C 的半径r=√22+5=3.故圆C 的方程为(x-2)2+y 2=9.11.(2016·全国3·理T16文T15)已知直线l:mx+y+3m-√3=0与圆x 2+y 2=12交于A,B 两点,过A,B 分别作l 的垂线与x 轴交于C,D 两点.若|AB|=2√3,则|CD|= .【答案】4【解析】因为|AB|=2√3,且圆的半径R=2√3,所以圆心(0,0)到直线mx+y+3m-√3=0的距离为√R 2-(|AB |2)2=3.由√3|2=3,解得m=-√33.将其代入直线l 的方程,得y=√33x+2√3,即直线l 的倾斜角为30°. 由平面几何知识知在梯形ABDC 中, |CD|=|AB |cos30°=4. 12.(2015·江苏·T10)在平面直角坐标系xOy 中,以点(1,0)为圆心且与直线mx-y-2m-1=0(m ∈R)相切的所有圆中,半径最大的圆的标准方程为 . 【答案】(x-1)2+y 2=2【解析】(方法一)设A(1,0).由mx-y-2m-1=0,得m(x-2)-(y+1)=0,则直线过定点P(2,-1),即该方程表示所有过定点P 的直线系方程.当直线与AP 垂直时,所求圆的半径最大.此时,半径为|AP|=√(2-1)2+(-1-0)2=√2.故所求圆的标准方程为(x-1)2+y 2=2.(方法二)设圆的半径为r,根据直线与圆相切的关系得r=√2=√m 2+2m+1m 2+1=√1+2mm 2+1,当m<0时,1+2m m 2+1<1,故1+2mm 2+1无最大值; 当m=0时,r=1;当m>0时,m 2+1≥2m(当且仅当m=1时取等号). 所以r≤√1+1=√2,即r max =√2, 故半径最大的圆的方程为(x-1)2+y 2=2. 13.(2015·全国1·理T14)一个圆经过椭圆x 216+y 24=1的三个顶点,且圆心在x 轴的正半轴上,则该圆的标准方程为___________. 【答案】(x -32)2+y 2=254【解析】由条件知圆经过椭圆的三个顶点分别为(4,0),(0,2),(0,-2),设圆心为(a,0)(a>0),所以√(a -0)2+(0-2)2=4-a,解得a=32,故圆心为(32,0),此时半径r=4-32=52,因此该圆的标准方程是(x -3)2+y 2=25.14.(2014·重庆·理T13)已知直线ax+y-2=0与圆心为C 的圆(x-1)2+(y-a)2=4相交于A,B 两点,且△ABC 为等边三角形,则实数a= .【答案】4±√15【解析】由△ABC 为等边三角形可得,C 到AB 的距离为√3,即(1,a)到直线ax+y-2=0的距离d=2=√3,即a 2-8a+1=0,可求得a=4±√15.15.(2014·陕西·理T12)若圆C 的半径为1,其圆心与点(1,0)关于直线y=x 对称,则圆C 的标准方程为 .【答案】x 2+(y-1)2=1【解析】因为(1,0)关于y=x 的对称点为(0,1),所以圆C 是以(0,1)为圆心,以1为半径的圆,其方程为x 2+(y-1)2=1.16.(2011·浙江·文T12)若直线x-2y+5=0与直线2x+my-6=0互相垂直,则实数m= .【答案】1【解析】由题意知1×2+(-2)·m=0,即m=1.17.(2010·全国·理T15)过点A(4,1)的圆C 与直线x-y-1=0相切于点B(2,1),则圆C 的方程为 .【答案】(x-3)2+y 2=2【解析】由题意知A,B 两点在圆C 上,∴线段AB 的垂直平分线x=3过圆心C.又圆C 与直线y=x-1相切于点B(2,1),∴k BC =-1.∴直线BC 的方程为y-1=-(x-2),即y=-x+3.y=-x+3与x=3联立得圆心C 的坐标为(3,0),∴r=|BC|=√(3-2)2+(0-1)2=√2. ∴圆C 的方程为(x-3)2+y 2=2. 18.(2010·全国·文T13)圆心在原点且与直线x+y-2=0相切的圆的方程为 .【答案】x 2+y 2=2【解析】圆心(0,0)到直线x+y-2=0的距离R=√1+1=√2.∴圆的方程为x 2+y 2=2.三、计算题1.(2015·全国1·文T20)已知过点A(0,1)且斜率为k 的直线l 与圆C:(x-2)2+(y-3)2=1交于M,N 两点.(1)求k 的取值范围;(2)若OM⃗⃗⃗⃗⃗⃗ ·ON ⃗⃗⃗⃗⃗⃗ =12,其中O 为坐标原点,求|MN|. 【解析】(1)由题设,可知直线l 的方程为y=kx+1.因为l 与C 交于两点, 所以√1+k <1.解得4-√73<k<4+√73. 所以k 的取值范围为(4-√73,4+√73). (2)设M(x 1,y 1),N(x 2,y 2).将y=kx+1代入方程(x-2)2+(y-3)2=1,整理得(1+k 2)x 2-4(1+k)x+7=0.所以x 1+x 2=4(1+k )1+k 2,x 1x 2=71+k 2.OM⃗⃗⃗⃗⃗⃗ ·ON ⃗⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2 =(1+k 2)x 1x 2+k(x 1+x 2)+1=4k (1+k )1+k 2+8. 由题设可得4k (1+k )1+k 2+8=12,解得k=1,所以l 的方程为y=x+1.故圆心C 在l 上,所以|MN|=2.2.(2015·广东·理T20)已知过原点的动直线l 与圆C 1:x 2+y 2-6x+5=0相交于不同的两点A,B.(1)求圆C 1的圆心坐标;(2)求线段AB 的中点M 的轨迹C 的方程;(3)是否存在实数k,使得直线L:y=k(x-4)与曲线C 只有一个交点?若存在,求出k 的取值范围;若不存在,说明理由.【解析】(1)由x 2+y 2-6x+5=0,得(x-3)2+y 2=4,从而可知圆C 1的圆心坐标为(3,0).(2)设线段AB 的中点M(x,y),由弦的性质可知C 1M ⊥AB,即C 1M ⊥OM.故点M 的轨迹是以OC 1为直径的圆,该圆的圆心为C (32,0),半径r=12|OC 1|=12×3=32,其方程为(x -32)2+y 2=(32)2,即x 2+y 2-3x=0.又因为点M 为线段AB 的中点,所以点M 在圆C 1内,所以√(x -3)2+y 2<2.又x 2+y 2-3x=0,所以可得x>53.易知x≤3,所以53<x≤3. 所以线段AB 的中点M 的轨迹C 的方程为x 2+y 2-3x=0(53<x ≤3).(3)存在实数k 满足题意. 由(2)知点M 的轨迹是以C (32,0)为圆心,32为半径的圆弧EF ⏜(如图所示,不包括两个端点),且E (53,2√53),F (53,-2√53). 又直线L:y=k(x-4)过定点D(4,0),当直线L 与圆C 相切时,由|k (32-4)-0|√k +1=32,得k=±34. 又k DE =-k DF =-0-(-2√53)4-53=2√5,结合上图可知当k ∈{-3,3}∪[-2√5,2√5]时,直线L:y=k(x-4)与曲线C 只有一个交点.3.(2014·全国1·文T20)已知点P(2,2),圆C:x 2+y 2-8y=0,过点P 的动直线l 与圆C 交于A,B 两点,线段AB 的中点为M,O 为坐标原点.(1)求M 的轨迹方程;(2)当|OP|=|OM|时,求l 的方程及△POM 的面积.【解析】设M(x,y),则CM ⃗⃗⃗⃗⃗⃗ =(x,y-4),MP⃗⃗⃗⃗⃗⃗ =(2-x,2-y). 由题设知CM⃗⃗⃗⃗⃗⃗ ·MP ⃗⃗⃗⃗⃗⃗ =0, 故x(2-x)+(y-4)(2-y)=0,即(x-1)2+(y-3)2=2.由于点P 在圆C 的内部,所以M 的轨迹方程是(x-1)2+(y-3)2=2.(2)由(1)可知M 的轨迹是以点N(1,3)为圆心,√2为半径的圆.由于|OP|=|OM|,故O 在线段PM 的垂直平分线上,又P 在圆N 上,从而ON ⊥PM. 因为ON 的斜率为3,所以l 的斜率为-13,故l 的方程为y=-13x+83.又|OM|=|OP|=2√2,O 到l 的距离为4√105,|PM|=4√105,所以△POM 的面积为165.4.(2013·江苏·T17)如图,在平面直角坐标系xOy 中,点A(0,3),直线l:y=2x-4.设圆C 的半径为1,圆心在l上.(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.【解析】(1)由题设,圆心C是直线y=2x-4和y=x-1的交点,解得点C(3,2),于是切线的斜率必存在. 设过A(0,3)的圆C的切线方程为y=kx+3,由题意,√k+1=1,解得k=0或k=-34,故所求切线方程为y=3或3x+4y-12=0.(2)因为圆心在直线y=2x-4上,所以圆C的方程为(x-a)2+[y-2(a-2)]2=1. 设点M(x,y),因为MA=2MO,所以√x2+(y-3)2=2√x2+y2,化简得x2+y2+2y-3=0,即x2+(y+1)2=4,所以点M在以D(0,-1)为圆心,2为半径的圆上.由题意,点M(x,y)在圆C上,所以圆C与圆D有公共点,则|2-1|≤CD≤2+1, 即1≤√a2+(2a-3)2≤3.由5a2-12a+8≥0,得a∈R;由5a2-12a≤0,得0≤a≤125.所以点C的横坐标a的取值范围为[0,125].。
高三数学-2018年高考直线与圆试题集锦 精品
2001~2018年高考直线试题集锦§1.直线的方程、两条直线的位置关系1.(18北京春招文)直线(a 为实常数)的倾斜角的大小是_________.30︒ 2.(18浙江文)直线2=y 与直线02=-+y x 的夹角是( A )A .4π B .3π C .2π D .43π3.(18安徽春招)在x 轴和y 轴上的截距分别是2-、3的直线方程是( C )A .2360x y --=B .3260x y --=C .3260x y -+=D .2360x y -+=4.(01天津卷)设A 、B 是x 轴上的两点,点P 的横坐标为2且||||PA PB =.若直线PA 的方程为10x y -+=,则直线PB 的方程是( A )A .50x y +-= B .210x y --= C .240y x --= D .270x y +-= 5.(18全国理4)过点(1,3)-且垂直于直线032=+-y x 的直线方程为( A )A .012=-+y xB .052=-+y xC .052=-+y xD .072=+-y x 6.(18全国文3)已知点(1,2)A 、(3,1)B ,则线段AB 的垂直平分线的方程是( B )A .524=+y xB .524=-y xC .52=+y xD .52=-y x7.(01上海理)3a =是直线230ax y a ++=和直线3(1)7x a y a +-=-平行且不重合的( C )A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分也非必要条件8.(18江苏)设1k >,()(1)f x k x =-(x R ∈).在平面直角坐标系xOy 中,函数()y f x =的图象与x 轴交于A 点,它的反函数1()y fx -=的图象与y 轴交于B 点,并且这两个函数的图象交于P 点.已知四边形OAPB 的面积是3,则k 等于( B ) A .3 B .32 C .43D .65x y O x y O x y O xyO9.(18北京文)若直线l:y kx =2360x y +-=的交点位于第一象限,则直线l 的倾斜角的取值范围是( B ) A .[,)63ππB .(,)62ππC .(,)32ππ D .[,]62ππ10.(18辽宁文)在同一直角坐标系中,表示直线y ax =与y x a =+正确的是( C )A .B .C .D .11.(18全国文)已知点(,2)a (0a >)到直线l :30x y -+=的距离为1,则a =( C )AB.C1D112.(18上海文)已知定点(0,1)A ,点B 在直线0x y +=上运动,当线段AB 最短时,点B 的坐标是__________.11(,)22-13.(18全国文)直线2y x =关于x 轴对称的直线方程为( C ) A .12y x =-B .12y x =C .2y x =-D .2y x =14.(18安徽春招)已知直线l :10x y --=,1l :220x y --=.若直线2l 与1l 关于l 对称,则2l 的方程是(B )A .210x y -+=B .210x y --=C .10x y +-=D .210x y +-=15.(18全国卷)已知长方形四个顶点(0,0)A ,(2,0)B ,(2,1)C 和(0,1)D .一质点从AB的中点0P 沿与AB 夹角为θ的方向射到BC 上的点1P 后,依次反射到CD 、DA 和AB 上的点2P 、3P 和4P (入射角等于反射角).设4P 的坐标为4(,0)x .若412x <<,则t a n θ的取值范围是( C ) A .1(,1)3B .12(,)33C .21(,)52D .22(,)5316.(18全国文4)已知函数14log y x =与y kx =的图象有公共点A ,且点A 的横坐标为2,则k 等于( A )A .41-B .41 C .21-D .21 17.(18全国理3)已知平面上直线l 的方向向量43(,),55e =-点(0,0)O 和(1,2)A -在l 上的射影分别是O '和A ',则O A e λ''=,其中λ=( D )A .511 B .511-C .2D .2-§2.简单的线性规划1.(18湖南理)设集合{(,)|,}U x y x R y R =∈∈,{(,)|20}A x y x y m =-+>,{(,)|0}B x y x y n =+-≤,那么点(2,3)U P A B ∈ð的充要条件是( A )A .5,1<->n mB .5,1<-<n mC .5,1>->n mD .5,1>-<n m2.(18全国理3)设y x ,满足约束条件:⎪⎩⎪⎨⎧≤-≥≥,12,,0y x y x x 则y x z 23+=的最大值是 .53.(18全国理4)设y x ,满足约束条件:⎪⎩⎪⎨⎧≥≤≤+,0,,1y x y y x ,则y x z +=2的最大值是 .24.(18上海文)当x 、y 满足不等式组2438x y x y ≤≤⎧⎪≥⎨⎪+≤⎩时,目标函数32k x y =-的最大值为________.65.(18浙江理)z x y =-,式中变量x 和y 满足条件3020x y x y +-≥⎧⎨-≥⎩,则z 的最小值为( A )A .1B .1-C .3D .3-6.(18广东理)变量x 、y 满足下列条件: 212,2936,2324,0,0.x y x y x y x y +≥⎧⎪+≥⎪⎨+=⎪⎪≥≥⎩ 则使32z x y =+的值最小的(,)x y 是( )A .(4.5,3)B .(3,6)C .(9,2)D .(6,4)7.(00上海文)图中阴影部分的点满足不等式组5260,0x y x y x y +≤⎧⎪+≤⎨⎪≥≥⎩,在这些点中,使目标函数68K x y =+取得最大值的点的坐标是______.(0,5)8.(18北京春招理)在直角坐标系xOy 中,已知AOB ∆三边所在直线的方程分别为0x =,0y =,23300x y ++=,则AOB ∆内部和边上整点(即横、纵坐标均为整数的点)的总数是( B )A .95B .91C .88D .75§3.圆的方程1.(18上海理)圆心在直线270x y --=上的圆C 与y 轴交于两点(0,4)A -,(0,2)B -,则圆C 的方程为 .22(2)(3)5x y -++=2.(18上海文)圆心在直线2x =上的圆C 与y 轴交于两点(0,4)A -,(0,2)B -,则圆C 的方程为 .22(2)(3)5x y -++=3.(18上海春招)过抛物线24y x =的焦点F 作垂直于x 于x 轴的直线,交抛物线于A 、B 两点,则以F 为圆心、AB 为直径的圆方程是________________.22(1)4x y -+=4.(18全国理3)已知圆C 与圆1)1(22=+-y x 关于直线x y -=对称,则圆C 的方程为( C ) A .22(1)1x y ++=B .221x y +=C .1)1(22=++y x D .1)1(22=-+y x5.(01全国)过点(1,1)A -、(1,1)B -且圆心在直线20x y +-=上的圆的方程是( C )A .22(3)(1)4x y -++=B . 22(3)(1)4x y ++-=C . 22(1)(1)4x y -+-=D . 22(1)(1)4x y +++=6.(18全国文4)已知圆C 的半径为2,圆心在x 轴的正半轴上,直线0443=++y x 与圆C 相切,则圆C 的方程为( D ) A .03222=--+x y xB .0422=++x y xC .03222=-++x y xD .0422=-+x y x7.(18北京文)圆的圆心坐标是________,(0,1)-如果直线与该圆有公共点,那么实数a 的取值范围是_____________.11a ≤≤8.(18北京春招)圆22221x y +=与直线sin 10x y θ+-=(,,2R k k Z πθθπ∈≠+∈)的位置关系是( C )A .相交B .相切C .相离D .不确定的9.(18广东理)如右下图,定圆半径为(,)b c ,则直线0ax by c ++=与直线10x y -+=的交点在( )A .第四象限B . 第三象限C .第二象限D . 第一象限10.(18全国理1)圆0422=-+x y x 在点)3,1(P 处的切线方程为( D ) A .023=-+y x B .043=-+y xC .043=+-y xD .023=+-y x11.(18全国文)直线(1)10a x y +++=与圆2220x y x +-=相切,则a 的值为( D )A .1,1-B . 2,2-C . 1D . 1-12.(18江苏)以点(1,2)为圆心,与直线43350x y +-=相切的圆的方程是______________.22(1)(2)25x y -+-=13.(18辽宁)若经过点(1,0)P -的直线与圆032422=+-++y x y x 相切,则此直线在y 轴上的截距是 .114.(18上海理)已知圆22(1)1x y ++=和圆外一点(0,2)P ,过点P 作圆的切线,则两条切线夹角的正切值是__________.4315.(18上海文)已知圆22(1)1x y +-=和圆外一点(2,0)P -,过点P 作圆的切线,则两条切线夹角的正切值是__________.4316.(18北京理)已知P 是直线3480x y ++=上的动点,PA 、PB 是圆222210x y x y +--+=的两条切线,A 、B 是切点,C 是圆心,那么四边形PACB 面积的最小值是__________.17.(18全国理2)由动点P 向圆122=+y x 引两条切线PA 、PB ,切点分别为A 、B ,60=∠APB ,则动点P 的轨迹方程为 .224x y +=18.(18北京春招)已知直线0ax by c ++=(0abc ≠)与圆221x y +=相切,则三条边长分别为||a 、||b 、||c 的三角形( B )A .是锐角三角形B .是直角三角形C .是钝角三角形D . 不存在19.(18全国理)圆22(1)1x y -+=的圆心到直线3y x =的距离是( A )A .12 B . 2C .1D 20.(18重庆理)圆222430x y x y +-++=的圆心到直线1x y -=的距离为( D )A .2B .2C .1D 21.(18全国理)已知圆C :22()(2)4x a y -+-=(0a >)及直线l :30x y -+=.当直线l 被C 截得的弦长为a =( C )A B .2- C 1 D 122.(18福建理)直线20x y +=被曲线2262150x y x y +---=所截得的弦长等 .423.(18天津理)若)1,2(-P 为圆25)1(22=+-y x 的弦AB 的中点,则直线AB 的方程是( A ) A . 03=--y x B . 032=-+y xC . 01=-+y xD . 052=--y x24.(18天津文)若过定点(1,0)M -且斜率为k 的直线与圆22450x x y ++-=在第一象限内的部分有交点,则k 的取值范围是( A )A .0k <<B .0k <<C .0k <<D .05k <<25.(18全国文1)设P 为圆122=+y x 上的动点,则点P 到直线01043=--y x 的距离的最小值为 .126.(18北京文)圆222210x y x y +--+=上的动点Q 到直线3480x y ++=距离的最小值为___________.2 27.(18北京理)曲线C :(为参数)的普通方程是_______,22(1)1x y ++=如果曲线C 与直线有公共点,那么实数a 的取值范围是_____.11a ≤28.(18北京)在平面直角坐标系中,已知两点(cos80,sin80)A ,(cos20,sin 20)B ,则||AB 的值是( D )A .12B C D .1 29.(18浙江理)点P 从(1,0)出发,沿单位圆221x y +=逆时针方向运动23π弧长到达Q 点,则Q 点的坐标为( A )A .1(2-B .1()2-C .1(,2-D .1()230.(18湖北文)两个圆221:2220C x y x y +++-=与222:4210C x y x y +--+=的公切线有且仅有( B )A .1条B .2条C .3条D .4条31.(18全国理3)在坐标平面内,与点(1,2)A 距离为1,且与点(3,1)B 距离为2的直线共有( B ) A .1条B .2条C .3条D .4条32.(18全国文4)已知直线1l 为曲线22-+=x x y 在点(1,0)处的切线,2l 为该曲线的另一条切线,且12l l ⊥. (Ⅰ)求直线2l 的方程;(Ⅱ)求由直线1l 、2l 和x 轴所围成的三角形的面积. 解:(Ⅰ)21y x '=+. 直线1l 的方程为33y x =-.设直线2l 过曲线22y x x =+-上的点2(,2)B b bb +-,则2l 的方程为2(21)2y b x b =+--.因为l 1⊥l 2,则有2b+1=.32,31-=-b 所以直线l 2的方程为.92231--=x y (II )解方程组⎪⎩⎪⎨⎧--=-=92231,33x y x y 得⎪⎪⎩⎪⎪⎨⎧-==.25,61y x 所以直线l 1和l 2的交点的坐标为15(,)62-. l 1、l 2与x 轴交点的坐标分别为(1,0)、)0,322(-. 所以所求三角形的面积 1255125||23212S =⨯⨯-=.。
高考数学二轮复习专题四解析几何第10讲直线与圆课件
第10讲 直线与圆
l1=3x-y+1=0,直线l2过点(1,0),且l1的倾斜角是l2的倾斜角的2倍,则直线l2
的方程为
.
答案 3x+4y-3=0
解析 设直线l1的倾斜角是α,则tan α=3,直线l2的倾斜角是2α,斜率k=tan 2α=
2 tan α 1 tan2α
围为
.
答案
,
3 4
解析 设直线m的斜率为k,则m:kx-y-3k=0.设C(x,y),则由A,B,C三点到直线m的
有向距离之和为0,得 4k + 2k + kx y 3k =0,化简得,kx-y-9k=0.又圆x2+(y
k2 1 k2 1
k2 1
-18)2=81上存在一点C,则直线kx-y-9k=0与圆有公共点.所以| 18 9k | ≤9.解得
3-1 在平面直角坐标系xOy中,已知圆C:(x+1)2+y2=2,点A(2,0).若圆C上存在点
M,满足|MA|2+|MO|2≤10,则点M的纵坐标的取值范围是
.
答案
7, 2
7
2
解析 设M(x,y),则|MA|2+|MO|2=(x-2)2+y2+x2+y2≤10,化简得(x-1)2+y2≤4,则点M
形,符合题意的面积最大的圆是该三角形的内切圆,则圆心为(1,0),半径r=
3 6
×
4 3=2.故该圆的标准方程是(x-1)2+y2=4.
【方法归纳】 (1)求直线方程主要有以下两种方法:①直接法:根据已知条 件,选择适当的直线方程形式,直接求出直线方程;②待定系数法:先设出直线 方程,再根据已知条件求出待定系数,最后代入,求出直线方程. (2)求圆的方程一般有以下两种方法:①几何法:通过研究圆的性质、直线与 圆的位置关系、圆与圆的位置关系,从而求得圆的基本量和方程;②代数法: 先设出圆的方程,再由已知条件求出待定系数,从而求得圆的方程.另外,圆心 到切线的距离等于半径,该结论在解题过程中会经常用到,需牢记. (3)边长为a的正三角形的内切圆的圆心与外接圆的圆心重合,都是正三角形
2010-2019“十年高考”数学真题分类汇总 直线与圆 (可下载)
2010-2019“十年高考”数学真题分类汇总解析几何——直线与圆(附详细答案解析)1.(2019北京文8)如图,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,APB ∠是锐角,大小为β。
图中阴影区域的面积的最大值为(A )4β+4cos β(B )4β+4sin β(C )2β+2cos β(D )2β+2sin β【答案】(B).【解析】由题意和题图可知,当P 为优弧 AB 的中点时,阴影部分的面积取最大值,设圆心为O ,2AOB β∠=,()1222BOP AOP ββ∠=∠=π-=π-.此时阴影部分面积BOP AOP AOB S S S S ∆∆++=扇形()⎥⎦⎤⎢⎣⎡-⨯⨯⨯⨯+⨯⨯=βπβsin 2221222212ββsin 44+=.故选B.2.(2019北京文11)设抛物线y 2=4x 的焦点为F ,准线为l .则以F 为圆心,且与l 相切的圆的方程为__________.【答案】()2214x y -+=.【解析】24y x =的焦点为()1,0,准线为1x =-,故符合条件的圆为()2214x y -+=.3.(2019江苏18)如图,一个湖的边界是圆心为O 的圆,湖的一侧有一条直线型公路l ,湖上有桥AB (AB 是圆O 的直径).规划在公路l 上选两个点P 、Q ,并修建两段直线型道路PB 、QA .规划要求:线段PB 、QA 上的所有点到点O 的距离均不小于圆....O 的半径.已知点A 、B 到直线l 的距离分别为AC 和BD (C 、D 为垂足),测得AB =10,AC =6,BD =12(单位:百米).(1)若道路PB 与桥AB 垂直,求道路PB 的长;(2)在规划要求下,P 和Q 中能否有一个点选在D 处?并说明理由;(3)在规划要求下,若道路PB 和QA 的长度均为d (单位:百米).求当d 最小时,P 、Q 两点间的距离.【解析】解法一:(1)过A 作AE BD ⊥,垂足为E .由已知条件得,四边形ACDE 为矩形,6, 8DE BE AC AE CD =====.'因为PB ⊥AB ,所以84cos sin 105PBD ABE ∠=∠==.所以12154cos 5BD PB PBD ===∠.因此道路PB的长为15(百米).(2)①若P 在D 处,由(1)可得E 在圆上,则线段BE 上的点(除B ,E )到点O 的距离均小于圆O 的半径,所以P 选在D 处不满足规划要求.②若Q 在D 处,联结AD,由(1)知10AD ==,从而2227cos 0225AD AB BD BAD AD AB +-∠==>⋅,所以∠BAD 为锐角.所以线段AD 上存在点到点O 的距离小于圆O 的半径.因此,Q 选在D 处也不满足规划要求.综上,P 和Q 均不能选在D 处.(3)先讨论点P 的位置.当︒<∠90OBP 时,线段PB 上存在点到点O 的距离小于圆O 的半径,点P 不符合规划要求;当︒≥∠90OBP 时,对线段PB 上任意一点F ,OB OF ≥,即线段PB 上所有点到点O 的距离均不小于圆O 的半径,点P符合规划要求.设1P 为l 上一点,且1PB AB ⊥,由(1)知,1P B =15,此时11113sin cos 1595PD PB PBD PB EBA =∠=∠=⨯=;当∠OBP >90°时,在1PPB △中,115PB PB >=.由上可知,d ≥15.再讨论点Q 的位置.由(2)知,要使得QA ≥15,点Q 只有位于点C 的右侧,才能符合规划要求.当QA =15时,CQ ==此时,线段QA 上所有点到点O 的距离均不小于圆O 的半径.综上,当PB ⊥AB ,点Q 位于点C 右侧,且CQ =时,d 最小,此时P ,Q 两点间的距离PQ =PD +CD +CQ =17+因此,d 最小时,P ,Q 两点间的距离为17+解法二:(1)如图,过O 作OH ⊥l ,垂足为H.以O 为坐标原点,直线OH 为y 轴,建立平面直角坐标系.因为BD =12,AC =6,所以OH =9,直线l 的方程为y =9,点A ,B 的纵坐标分别为3,−3.因为AB 为圆O 的直径,AB =10,所以圆O 的方程为x 2+y 2=25.从而A (4,3),B (−4,−3),直线AB 的斜率为34.因为PB ⊥AB ,所以直线PB 的斜率为43-,∴直线PB 的方程为42533y x =--.所以P (−13,9),15PB ==.因此道路PB 的长为15(百米).(2)①若P 在D 处,取线段BD 上一点E (−4,0),则EO =4<5,所以P 选在D 处不满足规划要求.②若Q 在D 处,联结AD ,由(1)知D (−4,9),又A (4,3),所以线段AD :36(44)4y x x =-+- .在线段AD 上取点M (3,154),因为5OM =,所以线段AD 上存在点到点O 的距离小于圆O 的半径.因此Q 选在D 处也不满足规划要求.综上,P 和Q 均不能选在D 处.(3)先讨论点P 的位置.当∠OBP <90°时,线段PB 上存在点到点O 的距离小于圆O 的半径,点P 不符合规划要求;当∠OBP ≥90°时,对线段PB 上任意一点F ,OF ≥OB ,即线段PB 上所有点到点O 的距离均不小于圆O 的半径,点P 符合规划要求.设1P 为l 上一点,且1PB AB ⊥,由(1)知,1P B =15,此时1P (−13,9);当∠OBP >90°时,在1PPB △中,115PB PB >=.由上可知,d ≥15.再讨论点Q 的位置.由(2)知,要使得QA≥15,点Q 只有位于点C 的右侧,才能符合规划要求.当QA =15时,设Q (a ,9),由15(4)AQ a ==>,得a =4+Q (4+此时,线段QA 上所有点到点O 的距离均不小于圆O 的半径.综上,当P (−13,9),Q (4+9)时,d 最小,此时P ,Q 两点间的距离4(13)17PQ =+-=+因此,d 最小时,P ,Q 两点间的距离为17+4.(2019浙江12)已知圆C 的圆心坐标是(0,)m ,半径长是r 。
2009年高考题分类解析——直线和圆、圆锥曲线
C( 5 4) ,
如 图 1 当 z = 4 Y= , ,
一
一
0 1 ( 2 ' 4 ) 1
一
可得丝 一 2 从 可 拿,选B a 而 得 一C 故 .
,
.
2时 , 5= Y— z 一 一 2— 4
一
\
x Y2 0 + -=
6 最 小值 . 为
( )方 程 问 题 2
点 B, 若蔚 一 3 , J 商 则
( A)√ ( B)2
I ( 一
( C)√
) .
( D)3
解 析 过点 B作 B _ 于 M , M lz I 并设右准线 z 与
B2 有・z{一屯 (Y则 z z =x xz ≠ , 4, ,, l
两 式相减 , 得 一 一 4 x 一z ) 故 l - ; ( z , X -
1 基 础 知 识 的 考查
1 即 b 一 3 故 b一 . , , C 选 .
例 5 ( 西6 江 )过 椭 圆 + 2 2
—
() 性 规 划 问题 1线 例 1 (北 京 理 l ) 若 实 数 X Y 满 足 O ,
r + Y一 2≥ 0 ,
1( 口> 6> o )
程是
.
— —
解 双 线 一2 1焦 (o 渐 析 曲 等 = 的 点4) 近 2 ,到
线 Y一
A.
解 析 将 直 线 z+ y一 6化 为 z+ y一 6— 0, 圆 的半 径 r= 2— 1— 6 l
一
的距离为 —L
一2 选
,
5
i _ 一 ’
所 以 圆 的方 程 为 ( z一 2 。 ( ) + + 1 。一 5 ) 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【考情概览】
【应试策略】
1.已知点A (-3,-1),B (1,5),直线l 过线段AB 的中点,且在x 轴上的截距是它在y 轴上的截距的2倍.求直线l 的方程. 【答案】230x y +-=
【应试策略】
求直线方程的常用方法有
1.直接法:根据已知条件灵活选用直线方程的形式,写出方程.
2.待定系数法:先根据已知条件设出直线方程,再根据已知条件构造关于待定系数的方程(组)求系数,最后代入求出直线方程.
3. 直线在x (y )轴上的截距是直线与x (y )轴交点的横(纵)坐标,所以截距是一个实数,可正、可负,也可为0,而不是距离.
2.圆x 2
+y 2
-4x-4y-10=0上的点到直线x+y-8=0的最大距离与最小距离的差是( )
A. 18
B. 6【答案】C
【应试策略】
1.确定圆的方程常用待定系数法,其步骤为:一根据题意选择标准方程或一般方程;二是根据题设条件列出方程组;三是由方程组求出待定的系数,代入所设的圆的方程;
2.在求圆的方程时,常用到圆的以下几个性质:一是圆心在过切点且与切线垂直的直线上;二是圆心在任一弦的中垂线上;
3.解方程组时,把所求的值代入检验一下是否正确.
3.直线l 经过点(5,5)P ,且与圆22:25C x y +=相交,截得弦长为l 的方程. 【答案】250x y --=或250x y -+=
=
解得2k =或1
2
k =.代入所设l 的方程化简为:250x y --=或250x y -+=. 【应试策略】
1. 如下图所示,涉及直线与圆相交及弦长的题,都在Rt AOB ∆中,利用勾股定理,得半径弦长及弦心距之间的关系式.
2.弦长的计算:方法一、设圆的半径为R ,圆心到直线的距离为d ,则弦长l =方法二、设直线的斜率为k ,直线与圆的交点坐标为1122(,),(,)P x y Q x y ,则弦长
11PQ x x y y =-=-【真题展示】
1.【2012年.浙江卷.理3】设a ∈R ,则“a =1”是“直线l 1:ax +2y -1=0与直线l 2:x +(a +1)y +4=0平行”的( )
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既不充分也不必要条件 【答案】A
【解析】l 1与l 2平行的充要条件为a (a +1)=2×1且a ×4≠1×(-1),可解得a =1或a =-2,故a =1是
l 1∥l 2的充分不必要条件.
2.【2014年.浙江卷.文5】已知圆0222
2=+-++a y x y x 截直线02=++y x 所得弦的长度为4,则实
数a 的值为( )
A.2-
B. 4-
C. 6-
D.8- 【答案】B
3.【2009年.浙江卷.文9】已知三角形的三边长分别为3,4,5,则它的边与半径为1的圆的公共点个数最多为( )
A .3
B .4
C .5
D .6 【答案】C
【解析】对于半径为1的圆有一个位置是正好是三角形的内切圆,此时只有三个交点,对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能实现. 二、填空题
4.【2012年.浙江卷.理16】定义:曲线C 上的点到直线l 的距离的最小值称为曲线C 到直线l 的距离.已知曲线C 1:y =x 2
+a 到直线l :y =x 的距离等于曲线C 2:x 2
+(y +4)2
=2到直线l :y =x 的距离,则实数a =__________. 【答案】
94
5.【2013年.浙江卷.文13】直线y =2x +3被圆x 2
+y 2
-6x -8y =0所截得的弦长等于__________.
【答案】
【解析】圆的圆心为(3,4),半径是5,圆心到直线的距离
d ==
可知弦长l ==.
6.【2011年.浙江卷.文12】若直线与直线250x y -+=与直线260x my +-=互相垂直,则实数
m =_______
【答案】1 【解析】:121212,,12k k k k m =
=-∴⋅=- 直线互相垂直,,即12
()1,12m m
⋅-=-∴= 7.【2016高考浙江文数】已知a ∈R ,方程222(2)4850a x a y x y a +++++=表示圆,则圆心坐标是_____,半径是______. 【答案】(2,4)--,5 【解析】
试题分析:由题意,知22a a =+,12a =-或,当1a =-时,方程为224850x y x y +++-=,即
22(2)(4)25x y +++=,圆心为(2,4)--,半径为5,当2a =时,方程为224448100x y x y ++++=,
2215
()(1)24
x y +++=-不表示圆.
【易错点睛】由方程222(2)4850a x a y x y a +++++=表示圆可得a 的方程,解得a 的值,一定要注意检验a 的值是否符合题意,否则很容易出现错误.
【对症下药】
1、两圆公共弦长的求解方法
点拨:当两圆相交求其公共弦所在的直线方程或公共弦长时,把两圆方程相减消去二次项,所得方程就是公共弦所在的直线方程,再根据其中一个圆的方程和这条直线方程就可以求出公共弦长. 2、圆的中点弦问题的解法
说明:解法1利用根与系数的关系求解,是一种通法,但运算量很大;解法2用的是点差法,利用弦端点坐标满足曲线方程得到两个关系式,把两个等式相减直接得出弦的中点坐标和斜率的关系,也是一种常用的方法;解法3充分运用圆这种特殊曲线的几何性质解题,从而使解题过程大大简化,在解答解析几何问题中,如能恰当运用几何图形的几何性质,常常可以简化解题过程. 3、与圆有关的最值问题的解题策略
点拨:与圆上点(),x y 有关的最值问题的常见类型及解法: (1)形如y b
t x a
-=
-的最值转化为过点(),a b 和(),x y 的直线的斜率的最值. (2)形如t ax by =+的最值,转化为动直线截距的最值.
(3)形如()()22
t x a y b =-+-的最值,转化为点(),x y 与(),a b 的距离的平方的最值.
【考题预测】
1.设直线y=x +2a 与圆C :x 2
+y 2
-2ay -2=0相交于A ,B 两点,若,则圆C 的面积为 .
【答案】4π
2.已知圆M :2220(0)x y ay a +-=>截直线0x y +=所得线段的长度是M 与圆N :
2
2(1)1x y +-=(-1)的位置关系是( )
(A )内切(B )相交(C )外切(D )相离 【答案】B 【解析】 试题分析:
3.已知直线()():21440l m x m y m ++-+-=上总存在点M ,使得过M 点作的圆C :
222430x y x y ++-+=的两条切线互相垂直,则实数m 的取值范围是( )
A. 1m ≤或2m ≥
B. 28m ≤≤
C. 210m -≤≤
D. 2m ≤-或8m ≥ 【答案】C
【解析】
4.过点()2,1作圆()()2
2
124x y -+-=的弦,其中最短的弦长为 .
【答案】
【解析】如下图所示,圆的圆心坐标为()1,2A ,点()2,1P ,过点P 作圆的弦BC ,过点A 作AD BC ⊥,
垂足为点D
,则BC ==AD AP ≤,当点D 与点P 重合时,AD 取最大
值,此时BC 取最小值,且
max AD AP ==
=
min BC ==
【综合点评】
数形结合思想的应用,是解析几何的重要特征,解题过程中要通过分析题目的条件和结论,灵活的加以转化.
5.在平面直角坐标系xOy 中,已知()2
2
1125x y -+=, 22240x y -+=,则()()2
2
1212x x y y -+-的最
小值为( ) A.
515
C. 1215
D. 5
【答案】B。
