第三章单元测试题(1)
人教版八年级物理第三章《物态变化》单元测试卷一
人教版八年级物理第三章《物态变化》单元测试卷一一．选择题（共25小题）1．下列估测结果正确的是（）A．一般洗澡水的温度大约是60℃B．中学生百米赛跑的速度大约是10m/sC．人心脏跳动一次的时间大约是3sD．乒乓球的直径大约是40mm2．在恒温环境下将温度计放入一杯冰水混合物中，从温度计放入开始计时，放入时间足够长，下列哪幅图可表示温度计内液体的体积随时间变化的情况（）A．A B．B C．C D．D3．自制温度计：如图所示，在小瓶里装满带颜色的水。
给小瓶配一个橡皮塞，橡皮塞上插进一根细玻璃管，使橡皮塞塞住瓶口。
将小瓶分别放入热水、冷水中。
关于下列说法中错误的是（）A．小瓶放热水中，细管中的水柱上升B．小瓶放冷水中，细管中的水柱上升C．温度计是根据液体的热胀冷缩的规律制成的D．利用细玻璃管是将水的体积变化更便于观察4．用实验室常用温度计测量烧杯中热水的温度时，下列说法正确的是（）A．温度计的感温泡可以碰到容器壁B．将感温泡浸入热水马上读出温度C．读数时温度计可以离开被测热水D．读数时如图所示，测量数据偏大5．关于生活中常用的体温计与实验室常用的温度计，下列说法正确的是（）A．两者的测量范围相同B．体温计不能离开人体后读数C．使用前应该用沸水给体温计消毒D．两者都是利用测温液体热胀冷缩的性质制成的6．抗击疫情期间，某同学用一支已有示数为37.8℃的水银体温计去测体温，若没有将水银甩下去，结果测得自己的体温为37.8℃，则他的实际体温（）A．一定为37.8℃B．一定高于37.8℃C．一定低于37.8℃D．一定不高于37.8℃7．夏天在饮料中加上几个冰块，会使饮料的温度下降.这样做一方面是因为冰块的温度比饮料低，另一方面是因为冰块（）A．液化放热B．凝华放热C．汽化吸热D．熔化吸热8．如图，民间艺人在制作“糖画”，只见他先将白糖熬成糖浆，再用勺子舀起来，接着手起勺落，用糖浆在光滑的大理石板上绘出图案。
不一会，便凝结成了图中的“自行车”。
(苏教版)最新七年级生物上册：第三单元 细胞是生命活动的基本的单位 单元测试卷(一)含答案与解析
（苏教版）七年级生物上册第三章单元测试卷（一）细胞是生命活动的基本的单位班级___________ 姓名___________ 学号____________ 分数____________（考试时间：30分钟试卷满分：50分）一、判断题：请判断下列叙述是否正确，正确的写“√”，错误的打“×”，本题共10小题，每小题1分，共10分。
1.在细胞中，与呼吸作用有关，为生命活动提供能量的结构是线粒体。
2.洋葱鳞片叶内表皮细胞含有叶绿体。
3.在细胞分裂过程中，一般会出现染色体等结构。
4.植物细胞中具有保护细胞内部结构和维持形态作用的结构是细胞膜。
5.由形态相似、结构和功能不同的细胞等组成的细胞群叫组织。
二、单项选择题：本题共15小题，每小题1分，共分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
6.草履虫和仙人掌的细胞结构最主要区别是有无A．细胞质 B．细胞核 C．细胞膜 D．细胞壁7.食用没有成熟的青苹果时，常感到酸，这种酸性物质主要存在于细胞的A．细胞质中 B．细胞膜中 C．液泡中 D．叶绿体中8.蝾螈受精卵横缢实验结果发现，有核部分能正常分裂和发育，无核部分不能分裂和发育。
这说明控制生物体形态结构和生理特性的遗传物质存在于细胞的A．细胞膜 B．细胞核 C．细胞质 D．细胞壁9.下图为植物细胞分裂过程中不同时期的图像，其排列顺序正确的是A．a→c→d→b B．a→b→c→d C．c→d→a→b D．a→d→b→c 10.各种细胞的形态、结构和功能出现很大差异的原因是A．细胞生长 B．细胞分化 C．细胞分裂 D．器官形成11.下图为洋葱鳞片叶表皮细胞和人的神经细胞，形态上差异很大，但它们都具有的基本结构是A．细胞壁、细胞膜、细胞核 B．细胞壁、细胞质、细胞核C．染色体、叶绿体、线粒体 D．细胞核、细胞膜、细胞质12.细胞分裂时，变化最明显的结构是A．细胞膜 B．染色体 C．细胞质 D．细胞壁13.下列有关细胞分裂的叙述中，正确的是A．是一个亲代细胞形成一个子代的细胞 B．遗传物质在细胞分裂前没有加倍C．染色体在细胞分裂过程中没有移动细胞 D．子代细胞中的染色体与亲代细胞一样14.下列细胞结构中，属于动植物细胞共有的结构是①细胞壁②细胞膜③细胞质④细胞核⑤叶绿体⑥大液泡A. ①②③B. ②③④C.③④⑤D. ④⑤⑥15.下列组织中，属于植物组织的是A.上皮组织B.结缔组织C.神经组织D.保护组织16.构成植物的主要组织有A．保护组织、营养组织、分生组织、输导组织、机械组织B．上皮组织、结缔组织、营养组织、分生组织、保护组织C．上皮组织、结缔组织、肌肉组织、神经组织、输导组织D．保护组织、结缔组织、肌肉组织、神经组织、机械组织17.下列关于人体的四种基本组织中，具有营养、连接、支持和保护功能的组织是A．上皮组织 B．结缔组织 C．肌肉组织 D．神经组织18.下面四幅示意图中不属于组织的是19.下列关于植物细胞的形态、结构与功能的叙述中，正确的是A.植物细胞是植物体生命活动的基本单位B.植物细胞都具有叶绿体、线粒体和细胞壁C.植物细胞的形态多种多样，结构互不相同D.不是所有的植物细胞都具有中央大液泡20. 洋葱根尖的一个细胞经过一次分裂，结果是A．形成两个细胞，遗传物质减少一半 B．形成两个细胞，遗传物质不变C．形成一个细胞，遗传物质减少一半 D．形成一个细胞，遗传物质不变三、双项选择题：下列各题的四个选项中，有两项符合题意，选对一项得1分，选对2项得2分，有错选不得分。
第三章《物质在水溶液中行为》单元测试题
第三章《物质在水溶液中行为》单元测试题姓名 学号一、选择题（每小题有1-2个选项，每题4分，共60分）１、向10mL 0.1mol ·L −1NH 4Al(SO 4)2溶液中，滴加等浓度Ba(OH)2溶液x mL ，下列叙述正确的是A ．x=10时，溶液中有NH 4＋、Al 3＋、SO 42－，且c(NH 4＋)>c(Al 3＋)B ．x=10时，溶液中有NH 4＋、AlO 2－、SO 42－，且c(NH 4＋)>c(SO 42－)C ．x=30时，溶液中有Ba 2＋、AlO 2－、OH －，且c(OH －)<c(AlO 2－)D ．x=30时，溶液中有Ba 2＋、Al 3＋、OH －，且c(OH －) = c(Ba 2＋)２、（２０１２四川）常温下，下列溶液中的微粒浓度关系正确的是A ．新制氯水中加入固体NaOH ：c （Na +）= c （Cl –）+ c （ClO –）+ c （OH –）B ．pH=8.3的NaHCO 3溶液：c （Na +）＞ c （HCO 3–）＞ c （CO 32–）＞ c （H 2CO 3）C ．pH=11的氨水与pH=3的盐酸等体积混合：c （Cl –）= c （NH 4+）＞ c （OH –）=c （H +）D ．0.2mol/L 的CH 3COOH 溶液与0.1mol/L 的NaOH 溶液等体积混合：2c （H +）– 2c （OH –）= c （CH 3COO –）– c （CH 3COOH ）３、（２０１２浙江）下列说法正确的是A ．常温下，将pH ＝3的醋酸溶液稀释到原体积的10倍后，溶液的pH ＝4B ．为确定某酸H 2A 是强酸还是弱酸，可测NaHA 溶液的pH 。
若pH ＞7，则H 2A 是弱酸；若pH ＜7，则H 2A 是强酸C ．用0.2000 mol/L NaOH 标准溶液滴定HCl 与CH 3COOH 的混合溶液（混合液中两种酸的浓度均约为0.1 mol/L ）,至中性时，溶液中的酸未被完全中和D ．相同温度下，将足量氯化银固体分别放入相同体积的①蒸馏水、②0.1mol/L 盐酸、③0.1 mol/L氯化镁溶液、④0.1mol/L 硝酸银溶液中，Ag ＋浓度：①＞④＝②＞③４、(2012新课标) 已知温度T 时水的离子积常数为K W 。
人教版高中数学必修二第三章单元测试(一)及参考答案
2018-2019学年必修二第三章训练卷直线与方程(一)注意事项：1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答：每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,直线l 1、l 2、l 3的斜率分别为k 1、k 2、k 3,则必有( )A.k 1<k 3<k 2B.k 3<k 1<k 2C.k 1<k 2<k 3D.k 3<k 2<k 12.直线x ＋2y －5＝0与2x ＋4y ＋a ＝0之间的距离为5,则a 等于( ) A.0B.－20C.0或－20D.0或－103.若直线l 1：ax ＋3y ＋1＝0与l 2：2x ＋(a ＋1)y ＋1＝0互相平行,则a 的值是( ) A.－3B.2C.－3或2D.3或－24.下列说法正确的是( )A.经过定点P 0(x 0,y 0)的直线都可以用方程y －y 0＝k (x －x 0)表示B.经过定点A (0,b )的直线都可以用方程y ＝kx ＋b 表示C.不经过原点的直线都可以用方程x a ＋yb＝1表示 D.经过任意两个不同的点P 1(x 1,y 1)、P 2(x 2,y 2)的直线都可以用方程(y －y 1)(x 2－x 1)＝(x －x 1)(y 2－y 1)表示5.点M (4,m )关于点N (n ,－3)的对称点为P (6,－9),则( ) A.m ＝－3,n ＝10 B.m ＝3,n ＝10 C.m ＝－3,n ＝5D.m ＝3,n ＝56.以A (1,3),B (－5,1)为端点的线段的垂直平分线方程是( ) A.3x －y －8＝0 B.3x ＋y ＋4＝0 C.3x －y ＋6＝0D.3x ＋y ＋2＝07.过点M (2,1)的直线与x 轴,y 轴分别交于P ,Q 两点,且|MP |＝|MQ |,则l 的方程是( ) A.x －2y ＋3＝0 B.2x －y －3＝0 C.2x ＋y －5＝0D.x ＋2y －4＝08.直线mx －y ＋2m ＋1＝0经过一定点,则该点的坐标是( ) A.(－2,1)B.(2,1)C.(1,－2)D.(1,2)9.如果AC <0且BC <0,那么直线Ax ＋By ＋C ＝0不通过( ) A.第一象限B.第二象限C.第三象限D.第四象限10.直线2x ＋3y －6＝0关于点(1,－1)对称的直线方程是( ) A.3x －2y ＋2＝0 B.2x ＋3y ＋7＝0 C.3x －2y －12＝0D.2x ＋3y ＋8＝011.已知点P (a ,b )和Q (b －1,a ＋1)是关于直线l 对称的两点,则直线l 的方程是( ) A.x ＋y ＝0 B.x －y ＝0C.x ＋y －1＝0D.x －y ＋1＝012.设x ＋2y ＝1,x ≥0,y ≥0,则x 2＋y 2的最小值和最大值分别为( ) A.15,1 B.0,1C.0,15D.15,2二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.不论a 为何实数,直线(a ＋3)x ＋(2a －1)y ＋7＝0恒过第________象限. 14.原点O 在直线l 上的射影为点H (－2,1),则直线l 的方程为______________. 15.经过点(－5,2)且横、纵截距相等的直线方程是____________________. 16.与直线3x ＋4y ＋1＝0平行且在两坐标轴上截距之和为73的直线l 的方程为______________. 三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)此卷只装订不密封班级 姓名 准考证号 考场号 座位号17.(10分)已知直线2x＋(t－2)y＋3－2t＝0,分别根据下列条件,求t的值：(1)过点(1,1)；(2)直线在y轴上的截距为－3.19.(12分)光线从A(－3,4)点出发,到x轴上的点B后,被x轴反射到y轴上的C点, 18.(12分)直线l过点(1,4),且在两坐标轴上的截距的积是18,求此直线的方程.又被y轴反射,这时反射光线恰好过D(－1,6)点,求直线BC的方程.20.(12分)如图所示,某县相邻两镇在一平面直角坐标系下的坐标为A(1,2),B(4,0),一条河所在的直线方程为l：x＋2y－10＝0,若在河边l上建一座供水站P,使之到A,B两镇的管道最省,那么供水站P应建在什么地方？21.(12分)已知△ABC的顶点A为(3,－1),AB边上的中线所在直线方程为6x＋10y－59＝0,∠B的平分线所在直线方程为x－4y＋10＝0,求BC边所在直线的方程.22.(12分)已知直线l过点P(3,1),且被两平行直线l1：x＋y＋1＝0和l2：x＋y＋6＝0截得的线段长度为5,求直线l的方程.2018-2019学年必修二第三章训练卷直线与方程(一)答 案一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.【答案】A【解析】由于直线1l 向左倾斜,故10k <,直线2l 与直线3l 均向右倾斜,且2l 更接近y 轴,所以：1320k k k <<<,故选A. 2.【答案】C 3.【答案】A 4.【答案】D【解析】斜率有可能不存在,截距也有可能不存在.故选D. 5.【答案】D【解析】由对称关系462n =+,239m -=-,可得m ＝3,n ＝5.故选D. 6.【答案】B【解析】所求直线过线段AB 的中点(－2,2),且斜率k ＝－3, 可得直线方程为3x ＋y ＋4＝0.故选B. 7.【答案】D【解析】由题意可知M 为线段PQ 的中点,Q (0,2),P (4,0), 可求得直线l 的方程x ＋2y －4＝0.故选D. 8.【答案】A【解析】将原直线化为点斜式方程为y －1＝m (x ＋2), 可知不论m 取何值直线必过定点(－2,1).故选A. 9.【答案】C【解析】将原直线方程化为斜截式为A Cy x B B=--,由AC <0且BC <0,可知AB >0,直线斜率为负,截距为正,故不过第三象限.故选C. 10.【答案】D【解析】所求直线与已知直线平行,且和点(1,－1)等距,不难求得直线为2x ＋3y ＋8＝0.故选D. 11.【答案】D 【解析】∵k PQ ＝11a bb a+---＝－1,∴k l ＝1.显然x －y ＝0错误,故选D.12.【答案】A【解析】x 2＋y 2为线段AB 上的点与原点的距离的平方,由数形结合知, O 到线段AB 的距离的平方为最小值,即d 2＝15,|OB |2＝1为最大值.故选A.二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.【答案】二【解析】直线方程可变形为：(3x －y ＋7)＋a (x ＋2y )＝0.由⎩⎪⎨⎪⎧ 3x －y ＋7＝0x ＋2y ＝0得,⎩⎪⎨⎪⎧x ＝－2y ＝1. ∴直线过定点(－2,1).因此直线必定过第二象限. 14.【答案】2x －y ＋5＝0【解析】所求直线应过点(－2,1)且斜率为2,故可求直线为2x －y ＋5＝0. 15.【答案】y ＝－25x 或x ＋y ＋3＝0【解析】不能忽略直线过原点的情况. 16.【答案】3x ＋4y －4＝0【解析】所求直线可设为3x ＋4y ＋m ＝0,再由－3m －4m ＝73,可得m ＝－4.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)17.【答案】(1)3；(2)95.【解析】(1)代入点(1,1), 得2＋(t －2)＋3－2t ＝0,则t ＝3.(2)令x ＝0,得y ＝232t t --＝－3,解得t ＝95.18.【答案】2x ＋y －6＝0或8x ＋y －12＝0. 【解析】设直线l 的方程为x a ＋yb ＝1,则18141ab a b=⎧⎪⎨+=⎪⎩,解得36a b =⎧⎨=⎩或3212a b ⎧=⎪⎨⎪=⎩ 则直线l 的方程2x ＋y －6＝0或8x ＋y －12＝0. 19.【答案】5x －2y ＋7＝0. 【解析】如图所示,由题设,点B 在原点O 的左侧,根据物理学知识,直线BC 一定过(－1,6)关于y 轴的对称点(1,6),直线AB 一定过(1,6)关于x 轴的对称点(1,－6)且k AB ＝k CD , ∴k AB ＝k CD ＝4631+--＝－52.∴AB 方程为y －4＝－52(x ＋3). 令y ＝0,得x ＝－75,∴B 7,05⎛⎫- ⎪⎝⎭.CD 方程为y －6＝－52(x ＋1). 令x ＝0,得y ＝72,∴C 70,2⎛⎫ ⎪⎝⎭. ∴BC 的方程为75x -＋72y＝1,即5x －2y ＋7＝0.20.【答案】见解析. 【解析】如图所示,过A 作直线l 的对称点A ′,连接A ′B 交l 于P , 若P ′(异于P )在直线上,则|AP ′|＋|BP ′|＝|A ′P ′|＋|BP ′|>|A ′B |. 因此,供水站只有在P 点处,才能取得最小值,设A ′(a ,b ), 则AA ′的中点在l 上,且AA ′⊥l ,即1221002221112a b a a ++⎧+⨯-=⎪⎪⎨-⎛⎫⎪⋅-=- ⎪⎪-⎝⎭⎩解得36a b =⎧⎨=⎩即A ′(3,6).所以直线A ′B 的方程为6x ＋y －24＝0,解方程组⎩⎪⎨⎪⎧6x ＋y －24＝0，x ＋2y －10＝0，得38113611x y ⎧=⎪⎪⎨⎪=⎪⎩所以P 点的坐标为⎝⎛⎭⎫3811，3611.故供水站应建在点P ⎝⎛⎭⎫3811，3611处. 21.【答案】2x ＋9y －65＝0. 【解析】设B (4y 1－10,y 1),由AB 中点在6x ＋10y －59＝0上,可得：114716+1059=22y y --⋅⋅-0,y 1＝5, 所以B (10,5).设A 点关于x －4y ＋10＝0的对称点为A ′(x ′,y ′), 则有3141002211134x y y x ''''⎧+--⋅+=⎪⎪⎨+⎪⋅=-⎪-⎩⇒A ′(1,7),∵点A ′(1,7),B (10,5)在直线BC 上,∴51075110y x --=--,故BC ：2x ＋9y －65＝0. 22.【答案】x ＝3或y ＝1.【解析】若直线l 的斜率不存在,则直线l 的方程为x ＝3,此时与直线l 1,l 2的交点分别为A (3,－4),B (3,－9).截得的线段AB 的长为|AB |＝|－4＋9|＝5,符合题意. 若直线l 的斜率存在,则设直线l 的方程为y ＝k (x －3)＋1.解方程组()311y k x x y ⎧=-+⎪⎨++=0⎪⎩得321411k x k k y k -⎧=⎪⎪+⎨-⎪=-⎪+⎩所以点A 的坐标为3241,11k k k k --⎛⎫- ⎪++⎝⎭.解方程组()316y k x x y ⎧=-+⎪⎨++=0⎪⎩得371911k x k k y k -⎧=⎪⎪+⎨-⎪=-⎪+⎩,所以点B 的坐标为3791,11k k k k --⎛⎫- ⎪++⎝⎭.因为|AB |＝5,所以2232374191=251111k k k k k k k k --⎡--⎤⎛⎫⎛⎫⎛⎫-+--- ⎪ ⎪ ⎪⎢⎥++++⎝⎭⎝⎭⎝⎭⎣⎦. 解得k ＝0,即所求直线为y ＝1.综上所述,所求直线方程为x ＝3或y ＝1.。
《第三章 物态变化》单元测试卷及答案(三套)
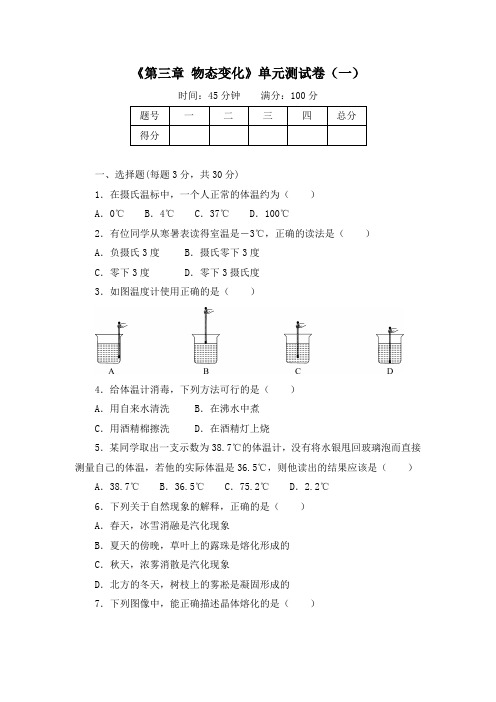
《第三章物态变化》单元测试卷（一）时间：45分钟满分：100分题号一二三四总分得分一、选择题(每题3分，共30分)1．在摄氏温标中，一个人正常的体温约为（）A．0℃ B．4℃ C．37℃ D．100℃2．有位同学从寒暑表读得室温是－3℃，正确的读法是（）A．负摄氏3度 B．摄氏零下3度C．零下3度 D．零下3摄氏度3．如图温度计使用正确的是（）4．给体温计消毒，下列方法可行的是（）A．用自来水清洗 B．在沸水中煮C．用酒精棉擦洗 D．在酒精灯上烧5．某同学取出一支示数为38.7℃的体温计，没有将水银甩回玻璃泡而直接测量自己的体温，若他的实际体温是36.5℃，则他读出的结果应该是（）A．38.7℃ B．36.5℃ C．75.2℃ D．2.2℃6．下列关于自然现象的解释，正确的是（）A．春天，冰雪消融是汽化现象B．夏天的傍晚，草叶上的露珠是熔化形成的C．秋天，浓雾消散是汽化现象D．北方的冬天，树枝上的雾凇是凝固形成的7．下列图像中，能正确描述晶体熔化的是（）8．下列实例中，为了加快蒸发的是（）A．用地膜覆盖农田B．给盛有饮料的瓶子加盖C．把湿衣服晾晒在通风向阳的地方D．农业灌溉中用管道输水代替沟渠输水9．下列各种现象，需要放出热量的是（）A．北方冬天户外冰冻的衣服变干B．春天冰雪消融C．用电吹风将湿头发吹干D．深秋，清晨草地上出现霜10．随着科技的进步和生活水平的日益提高，人们主动利用科技知识改善生活环境的意识逐渐增强。
如图所示的四幅图片场景，是人们应用物理知识改善生活环境的几种做法，其中主要是用来降温的是（）二、填空题(每空2分，共26分)11．甲流肆虐全球，严重威胁人们健康。
如图是在预防甲流中我们常常使用的汞体温计。
它是利用液体的性质来工作的。
12．温泉的开发是人们利用地热的一种形式。
冬天，温泉水面的上方笼罩着一层白雾，这是水蒸气遇冷形成的小水滴；雪花飘落到池水中立刻不见踪影，这是雪花成水融入温泉水中。
第三章单元测试卷_1
第三章单元测试卷一、单项选择题(本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中只有一个是符合题目要求的) 1．函数f(x)＝的定义域为( )A．(1，＋∞) B．[1，＋∞)C．[1,2) D．[1,2)∪(2，＋∞)2．德国数学家狄利克雷在数学上做出了名垂史册的重大贡献，函数D(x)＝是以他名字命名的函数，则D(D(π))＝( ) A．1 B．0C．π D．－13．已知f(x)是偶函数，g(x)是奇函数，且f(x)＋g(x)＝2x2－2x ＋1，则f(－1)＝( )A．3 B．－3C．2 D．－24．若函数y＝f(x)的定义域是[0,2]，则函数g(x)＝的定义域是( )A．[－4,0] B．[－4,0)C．[－4，－1)∪(－1,0] D．(－4,0)5．若幂函数y＝(m2－3m＋3)xm－2的图象不过原点，则m的取值范围为( )A．1≤m≤2 B．m＝1或m＝2C．m＝2 D．m＝16．已知函数f(x)是定义在R上的偶函数，x≥0时，f(x)＝x2－2x，则函数f(x)在R上的解析式是( )A．f(x)＝－x(x－2) B．f(x)＝x(|x|－2)C．f(x)＝|x|(x－2) D．f(x)＝|x|(|x|－2)7．已知函数f(x)＝若f(x－4)>f(2x－3)，则实数x的取值范围是( )A．(－1，＋∞) B．(－∞，－1)C．(－1,4) D．(－∞，1)8．甲、乙二人从A地沿同一方向去B地，途中都使用两种不同的速度v1与v2(v1<v2)，甲前一半的路程使用速度v1，后一半的路程使用速度v2；乙前一半的时间使用速度v1，后一半的时间使用速度v2，关于甲、乙二人从A地到达B地的路程与时间的函数图象及关系，有如图所示的四个不同的图示分析(其中横轴t表示时间，纵轴s表示路程，C是AB的中点)，则其中可能正确的图示分析为( )二、多项选择题(本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分)9．关于函数f(x)＝的结论正确的是( )A．定义域、值域分别是[－1,3]，[0，＋∞) B．单调增区间是(－∞，1]C．定义域、值域分别是[－1,3]，[0,2] D．单调增区间是[－1,1]10．已知f(2x－1)＝4x2，则下列结论正确的是( )A．f(3)＝9 B．f(－3)＝4C．f(x)＝x2 D．f(x)＝(x＋1)211．关于定义在R上的函数f(x)，下列命题正确的是( ) A．若f(x)满足f(2 018)>f(2 017)，则f(x)在R上不是减函数B．若f(x)满足f(－2)＝f(2)，则函数f(x)不是奇函数C．若f(x)在区间(－∞，0)上是减函数，在区间[0，＋∞)也是减函数，则f(x)在R上是减函数D．若f(x)满足f(－2 018)≠f(2 018)，则函数f(x)不是偶函数12．定义在R上的函数f(x)满足f(x＋y)＝f(x)＋f(y)，当x<0时，f(x)>0，则函数f(x)满足( )A．f(0)＝0 B．y＝f(x)是奇函数C．f(x)在[m，n]上有最大值f(n) D．f(x－1)>0的解集为(－∞，1)三、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．已知函数f(x)＝若f(a)＋f(1)＝0，则实数a的值等于________．14．长为4，宽为3的矩形，当长增加x，宽减少时，面积达到最大，此时x的值为________．15．定义在R上的奇函数f(x)满足：当x≥0，f(x)＝x2－2x＋a，则a＝________，f(－3)＝________.(本题第一空2分，第二空3分)16．已知f(x)＝是R上的单调递增函数，则实数a的取值范围为________．四、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．(本小题满分10分)已知函数f(x)＝，x∈[3,5]．(1)判断f(x)在区间[3,5]上的单调性并证明；(2)求f(x)的最大值和最小值．18．(本小题满分12分)已知函数f(x)＝(1)求f(f(－2))的值；(2)若f(a)＝，求a.19．(本小题满分12分)已知幂函数f(x)＝x－2m2－m＋3，其中m∈{x|－2<x<2，x∈Z}满足：(1)在区间(0，＋∞)上是增函数；(2)对任意的x∈R，都有f(－x)＋f(x)＝0.求同时满足条件(1)(2)的幂函数f(x)的解析式，并求当x∈[0,3]时，f(x)的值域．20．(本小题满分12分)设f(x)为定义在R上的偶函数，当x≥0时，f(x)＝－(x－2)2＋2.(1)求函数f(x)在R上的解析式；(2)在直角坐标系中画出函数f(x)的图象；(3)若方程f(x)－k＝0有四个解，求实数k的取值范围．21．(本小题满分12分)如图所示，A、B两城相距100 km，某天然气公司计划在两地之间建一天然气站D给A、B两城供气．已知D地距A城x km，为保证城市安全，天然气站距两城市的距离均不得少于10 km.已知建设费用y(万元)与A、B 两地的供气距离(km)的平方和成正比，当天然气站D距A城的距离为40 km时，建设费用为1300万元．(供气距离指天然气站到城市的距离)(1)把建设费用y(万元)表示成供气距离x(km)的函数，并求定义域；(2)天然气供气站建在距A城多远，才能使建设费用最小，最小费用是多少？22．(本小题满分12分)已知f(x)的定义域为(0，＋∞)，且满足f(2)＝1，f(xy)＝f(x)＋f(y)，又当x2>x1>0时，f(x2)>f(x1)．(1)求f(1)，f(4)，f(8)的值；(2)若有f(x)＋f(x－2)≤3成立，求x的取值范围．第三章单元测试卷1．解析：根据题意有解得x≥1且x≠2.答案：D2．解析：∵函数D(x)＝，∴D(π)＝0，D(D(π))＝D(0)＝1.故选A.答案：A3．解析：令x＝1，得f(1)＋g(1)＝1，令x＝－1，得f(－1)＋g(－1)＝5，两式相加得：f(1)＋f(－1)＋g(1)＋g(－1)＝6.又∵f(x)是偶函数，g(x)是奇函数，∴f(－1)＝f(1)，g(－1)＝－g(1)．∴2f(－1)＝6，∴f(－1)＝3，故选A.答案：A4．解析：∵y＝f(x)的定义域是[0,2]，∴要使g(x)＝有意义，需∴－4≤x≤0且x≠－1.∴g(x)＝的定义域为[－4，－1)∪(－1,0]．答案：C5．解析：由题意得解得∴m＝1或m＝2.答案：B6．解析：设x<0，则－x>0，f(x)＝f(－x)＝x2－2(－x)＝x2＋2x.故f(x)＝|x|(|x|－2)．答案：D7.解析：f(x)的图象如图．由图知，若f(x－4)>f(2x－3)，则解得－1<x<4.故实数x的取值范围是(－1,4)．答案：C8．解析：由题意可知，开始时，甲、乙速度均为v1，所以图象是重合的线段，由此排除C，D.再根据v1<v2可知两人的运动情况均是先慢后快，图象是折线且前“缓”后“陡”，故图示A 分析正确．答案：A9．解析：f(x)＝则定义域满足：－x2＋2x＋3≥0解得：－1≤x≤3即定义域为[－1,3]考虑函数y＝－x2＋2x＋3＝－(x－1)2＋4在－1≤x≤3上有最大值4，最小值0.在[－1,1]上单调递增，在(1,3]上单调递减．故f(x)＝的定义域为[－1,3]，值域为[0,2]，在[－1,1]上单调递增，在(1,3]上单调递减．故选CD.答案：CD10．解析：f(2x－1)＝(2x－1)2＋2(2x－1)＋1，故f(x)＝x2＋2x＋1，故选项C错误，选项D正确；f(3)＝16，f(－3)＝4，故选项A错误，选项B正确．故选BD.答案：BD11．解析：由题意，对于A中，由2 018>2 017，而f(2 018)>f(2 017)，由减函数定义可知，f(x)在R 上一定不是减函数，所以A正确；对于B中，若f(x)＝0，定义域关于原点对称，则f(－2)＝f(2)＝－f(2)，则函数f(x)可以是奇函数，所以B错误；对于C中，由分段函数的单调性的判定方法，可得选项C不正确；对于D中，若f(x)是偶函数，必有f(－2 018)＝f( 2018)，所以D正确．故选AD.答案：AD12．解析：令x＝y＝0，则f(0)＝f(0)＋f(0)，所以f(0)＝0，故A正确；再令y＝－x，代入原式得f(0)＝f(x)＋f(－x)＝0，所以f(－x)＝－f(x)，故该函数为奇函数，故B正确；由f(x＋y)＝f(x)＋f(y)得f(x＋y)－f(x)＝f(y)，令x1<x2，再令x1＝x＋y，x2＝x，则y＝x1－x2<0，结合x<0时，f(x)>0，所以f(x1)－f(x2)＝f(x1－x2)>0，所以f(x1)>f(x2)，所以原函数在定义域内是减函数，所以函数f(x)在[m，n]上递减，故f(n)是最小值，f(m)是最大值，故C错误；又f(x－1)>0，即f(x－1)>f(0)，结合原函数在定义域内是减函数可得，x－1<0，解得x<1，故D正确．故选ABD.答案：ABD13．解析：若a>0，则2a＋2＝0，得a＝－1，与a>0矛盾，舍去；若a≤0，则a＋1＋2＝0，得a＝－3，所以实数a的值等于－3.答案：－314．解析：由题意，S＝(4＋x)，即S＝－x2＋x＋12，∴当x＝1时，S最大．答案：115．解析：由定义在R上的奇函数f(x)满足：当x≥0，f(x)＝x2－2x＋a，可得f(0)＝a＝0，当x≥0，f(x)＝x2－2x，则f(－3)＝－f(3)＝－(32－2×3)＝－3.答案：0 －316．解析：f(x)＝显然函数f(x)在(1，＋∞)上单调递增．故由已知可得解得1≤a<.答案：17．解析：(1)函数f(x)在[3,5]上为增函数，证明如下：设x1，x2是[3,5]上的任意两个实数，且x1<x2，则f(x1)－f(x2)＝－＝.∵3≤x1≤x2≤5，∴x1－x2<0，x1＋1>0，x2＋1>0，∴f(x1)－f(x2)<0，即f(x1)<f(x2)，∴函数f(x)在[3,5]上为增函数．(2)由(1)知函数f(x)在[3,5]单调递增，所以函数f(x)的最小值为f(x)min＝f(3)＝＝，函数f(x)的最大值为f(x)max＝f(5)＝＝.18．解析：(1)因为－2<－1，所以f(－2)＝2×(－2)＋3＝－1，所以f(f(－2))＝f(－1)＝2.(2)当a>1时，f(a)＝1＋＝，所以a＝2>1；当－1≤a≤1时，f(a)＝a2＋1＝，所以a＝±∈[－1,1]；当a<－1时，f(a)＝2a＋3＝，所以a＝－>－1(舍去)．综上，a＝2或a＝±.19．解析：因为m∈{x|－2<x<2，x∈Z}，所以m＝－1,0,1.因为对任意的x∈R，都有f(－x)＋f(x)＝0，即f(－x)＝－f(x)，所以f(x)是奇函数．当m＝－1时，f(x)＝x2只满足条件(1)而不满足条件(2)；当m＝1时，f(x)＝x0，条件(1)(2)都不满足；当m＝0时，f(x)＝x3，条件(1)(2)都满足．因此m＝0，且f(x)＝x3在区间[0,3]上是增函数，所以0≤f(x)≤27，故f(x)的值域为[0,27]．20．解析：(1)若x<0，则－x>0，f(x)＝f(－x)＝－(－x－2)2＋2＝－(x＋2)2＋2，则f(x)＝(2)图象如图所示，(3)由于方程f(x)－k＝0的解就是函数y＝f(x)的图象与直线y＝k的交点的横坐标，观察函数y＝f(x)图象与直线y＝k的交点情况可知，当－2<k<2时，函数y＝f(x)图象与直线y＝k有四个交点，即方程f(x)－k＝0有四个解．21．解析：(1)由题意知D地距B城(100－x)km，则∴10≤x≤90.设比例系数为k，则y＝k[x2＋(100－x)2](10≤x≤90)．又x＝40时，y＝1 300，所以1 300＝k(402＋602)，即k＝，所以y＝[x2＋(100－x)2]＝(x2－100x＋5 000)(10≤x≤90)．(2)由于y＝(x2－100x＋5 000)＝(x－50)2＋1 250，所以当x＝50时，y有最小值为1 250万元．所以当供气站建在距A城50 km时，能使建设费用最小，最小费用是1 250万元．22．解析：(1)f(1)＝f(1)＋f(1)，所以f(1)＝0，f(4)＝f(2)＋f(2)＝1＋1＝2，f(8)＝f(2)＋f(4)＝1＋2＝3.(2)因为f(x)＋f(x－2)≤3，所以f[x(x－2)]≤f(8)，又因为对于函数f(x)，当x2>x1>0时，f(x2)>f(x1)，所以f(x)在(0，＋∞)上为增函数，所以解得2<x≤4.故x的取值范围为(2,4]．第三章单元测试卷一、单项选择题(本大题共8个小题，每小题5分，共40分，在每小题给出的四个选项中只有一个是符合题目要求的)1．函数f(x)＝的定义域为( )A．(1，＋∞) B．[1，＋∞)C．[1,2) D．[1,2)∪(2，＋∞)2．德国数学家狄利克雷在数学上做出了名垂史册的重大贡献，函数D(x)＝是以他名字命名的函数，则D(D(π))＝( )A．1 B．0C．π D．－13．已知f(x)是偶函数，g(x)是奇函数，且f(x)＋g(x)＝2x2－2x＋1，则f(－1)＝( )A．3 B．－3C．2 D．－24．若函数y＝f(x)的定义域是[0,2]，则函数g(x)＝的定义域是( )A．[－4,0] B．[－4,0)C．[－4，－1)∪(－1,0] D．(－4,0)5．若幂函数y＝(m2－3m＋3)xm－2的图象不过原点，则m的取值范围为( )A．1≤m≤2 B．m＝1或m＝2C．m＝2 D．m＝16．已知函数f(x)是定义在R上的偶函数，x≥0时，f(x)＝x2－2x，则函数f(x)在R上的解析式是( )A．f(x)＝－x(x－2) B．f(x)＝x(|x|－2)C．f(x)＝|x|(x－2) D．f(x)＝|x|(|x|－2)7．已知函数f(x)＝若f(x－4)>f(2x－3)，则实数x的取值范围是( )A．(－1，＋∞) B．(－∞，－1)C．(－1,4) D．(－∞，1)8．甲、乙二人从A地沿同一方向去B地，途中都使用两种不同的速度v1与v2(v1<v2)，甲前一半的路程使用速度v1，后一半的路程使用速度v2；乙前一半的时间使用速度v1，后一半的时间使用速度v2，关于甲、乙二人从A地到达B 地的路程与时间的函数图象及关系，有如图所示的四个不同的图示分析(其中横轴t表示时间，纵轴s表示路程，C是AB的中点)，则其中可能正确的图示分析为( )二、多项选择题(本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得3分，有选错的得0分)9．关于函数f(x)＝的结论正确的是( )A．定义域、值域分别是[－1,3]，[0，＋∞) B．单调增区间是(－∞，1]C．定义域、值域分别是[－1,3]，[0,2] D．单调增区间是[－1,1]10．已知f(2x－1)＝4x2，则下列结论正确的是( )A．f(3)＝9 B．f(－3)＝4C．f(x)＝x2 D．f(x)＝(x＋1)211．关于定义在R上的函数f(x)，下列命题正确的是( )A．若f(x)满足f(2 018)>f(2 017)，则f(x)在R上不是减函数B．若f(x)满足f(－2)＝f(2)，则函数f(x)不是奇函数C．若f(x)在区间(－∞，0)上是减函数，在区间[0，＋∞)也是减函数，则f(x)在R上是减函数D．若f(x)满足f(－2 018)≠f(2 018)，则函数f(x)不是偶函数12．定义在R上的函数f(x)满足f(x＋y)＝f(x)＋f(y)，当x<0时，f(x)>0，则函数f(x)满足( ) A．f(0)＝0 B．y＝f(x)是奇函数C．f(x)在[m，n]上有最大值f(n) D．f(x－1)>0的解集为(－∞，1)三、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．已知函数f(x)＝若f(a)＋f(1)＝0，则实数a的值等于________．14．长为4，宽为3的矩形，当长增加x，宽减少时，面积达到最大，此时x的值为________．15．定义在R上的奇函数f(x)满足：当x≥0，f(x)＝x2－2x＋a，则a＝________，f(－3)＝________.(本题第一空2分，第二空3分)16．已知f(x)＝是R上的单调递增函数，则实数a的取值范围为________．四、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤) 17．(本小题满分10分)已知函数f(x)＝，x∈[3,5]．(1)判断f(x)在区间[3,5]上的单调性并证明；(2)求f(x)的最大值和最小值．18．(本小题满分12分)已知函数f(x)＝(1)求f(f(－2))的值；(2)若f(a)＝，求a.19．(本小题满分12分)已知幂函数f(x)＝x－2m2－m＋3，其中m∈{x|－2<x<2，x∈Z}满足：(1)在区间(0，＋∞)上是增函数；(2)对任意的x∈R，都有f(－x)＋f(x)＝0.求同时满足条件(1)(2)的幂函数f(x)的解析式，并求当x∈[0,3]时，f(x)的值域．20．(本小题满分12分)设f(x)为定义在R上的偶函数，当x≥0时，f(x)＝－(x－2)2＋2.(1)求函数f(x)在R上的解析式；(2)在直角坐标系中画出函数f(x)的图象；(3)若方程f(x)－k＝0有四个解，求实数k的取值范围．21．(本小题满分12分)如图所示，A、B两城相距100 km，某天然气公司计划在两地之间建一天然气站D给A、B两城供气．已知D地距A城x km，为保证城市安全，天然气站距两城市的距离均不得少于10 km.已知建设费用y(万元)与A、B两地的供气距离(km)的平方和成正比，当天然气站D距A城的距离为40 km时，建设费用为1300万元．(供气距离指天然气站到城市的距离)(1)把建设费用y(万元)表示成供气距离x(km)的函数，并求定义域；(2)天然气供气站建在距A城多远，才能使建设费用最小，最小费用是多少？22．(本小题满分12分)已知f(x)的定义域为(0，＋∞)，且满足f(2)＝1，f(xy)＝f(x)＋f(y)，又当x2>x1>0时，f(x2)>f(x1)．(1)求f(1)，f(4)，f(8)的值；(2)若有f(x)＋f(x－2)≤3成立，求x的取值范围．第三章单元测试卷1．解析：根据题意有解得x≥1且x≠2.答案：D2．解析：∵函数D(x)＝，∴D(π)＝0，D(D(π))＝D(0)＝1.故选A.答案：A3．解析：令x＝1，得f(1)＋g(1)＝1，令x＝－1，得f(－1)＋g(－1)＝5，两式相加得：f(1)＋f(－1)＋g(1)＋g(－1)＝6.又∵f(x)是偶函数，g(x)是奇函数，∴f(－1)＝f(1)，g(－1)＝－g(1)．∴2f(－1)＝6，∴f(－1)＝3，故选A.答案：A4．解析：∵y＝f(x)的定义域是[0,2]，∴要使g(x)＝有意义，需∴－4≤x≤0且x≠－1.∴g(x)＝的定义域为[－4，－1)∪(－1,0]．答案：C5．解析：由题意得解得∴m＝1或m＝2.答案：B6．解析：设x<0，则－x>0，f(x)＝f(－x)＝x2－2(－x)＝x2＋2x.故f(x)＝|x|(|x|－2)．答案：D7.解析：f(x)的图象如图．由图知，若f(x－4)>f(2x－3)，则解得－1<x<4.故实数x的取值范围是(－1,4)．答案：C8．解析：由题意可知，开始时，甲、乙速度均为v1，所以图象是重合的线段，由此排除C，D.再根据v1<v2可知两人的运动情况均是先慢后快，图象是折线且前“缓”后“陡”，故图示A分析正确．答案：A9．解析：f(x)＝则定义域满足：－x2＋2x＋3≥0解得：－1≤x≤3即定义域为[－1,3]考虑函数y＝－x2＋2x＋3＝－(x－1)2＋4在－1≤x≤3上有最大值4，最小值0.在[－1,1]上单调递增，在(1,3]上单调递减．故f(x)＝的定义域为[－1,3]，值域为[0,2]，在[－1,1]上单调递增，在(1,3]上单调递减．故选CD.答案：CD10．解析：f(2x－1)＝(2x－1)2＋2(2x－1)＋1，故f(x)＝x2＋2x＋1，故选项C错误，选项D 正确；f(3)＝16，f(－3)＝4，故选项A错误，选项B正确．故选BD.答案：BD11．解析：由题意，对于A中，由2 018>2 017，而f(2 018)>f(2 017)，由减函数定义可知，f(x)在R 上一定不是减函数，所以A正确；对于B中，若f(x)＝0，定义域关于原点对称，则f(－2)＝f(2)＝－f(2)，则函数f(x)可以是奇函数，所以B错误；对于C中，由分段函数的单调性的判定方法，可得选项C不正确；对于D中，若f(x)是偶函数，必有f(－2 018)＝f( 2018)，所以D正确．故选AD.答案：AD12．解析：令x＝y＝0，则f(0)＝f(0)＋f(0)，所以f(0)＝0，故A正确；再令y＝－x，代入原式得f(0)＝f(x)＋f(－x)＝0，所以f(－x)＝－f(x)，故该函数为奇函数，故B正确；由f(x＋y)＝f(x)＋f(y)得f(x＋y)－f(x)＝f(y)，令x1<x2，再令x1＝x＋y，x2＝x，则y＝x1－x2<0，结合x<0时，f(x)>0，所以f(x1)－f(x2)＝f(x1－x2)>0，所以f(x1)>f(x2)，所以原函数在定义域内是减函数，所以函数f(x)在[m，n]上递减，故f(n)是最小值，f(m)是最大值，故C错误；又f(x－1)>0，即f(x－1)>f(0)，结合原函数在定义域内是减函数可得，x－1<0，解得x<1，故D正确．故选ABD.答案：ABD13．解析：若a>0，则2a＋2＝0，得a＝－1，与a>0矛盾，舍去；若a≤0，则a＋1＋2＝0，得a＝－3，所以实数a的值等于－3.答案：－314．解析：由题意，S＝(4＋x)，即S＝－x2＋x＋12，∴当x＝1时，S最大．答案：115．解析：由定义在R上的奇函数f(x)满足：当x≥0，f(x)＝x2－2x＋a，可得f(0)＝a＝0，当x≥0，f(x)＝x2－2x，则f(－3)＝－f(3)＝－(32－2×3)＝－3.答案：0 －316．解析：f(x)＝显然函数f(x)在(1，＋∞)上单调递增．故由已知可得解得1≤a<.答案：17．解析：(1)函数f(x)在[3,5]上为增函数，证明如下：设x1，x2是[3,5]上的任意两个实数，且x1<x2，则f(x1)－f(x2)＝－＝.∵3≤x1≤x2≤5，∴x1－x2<0，x1＋1>0，x2＋1>0，∴f(x1)－f(x2)<0，即f(x1)<f(x2)，∴函数f(x)在[3,5]上为增函数．(2)由(1)知函数f(x)在[3,5]单调递增，所以函数f(x)的最小值为f(x)min＝f(3)＝＝，函数f(x)的最大值为f(x)max＝f(5)＝＝.18．解析：(1)因为－2<－1，所以f(－2)＝2×(－2)＋3＝－1，所以f(f(－2))＝f(－1)＝2.(2)当a>1时，f(a)＝1＋＝，所以a＝2>1；当－1≤a≤1时，f(a)＝a2＋1＝，所以a＝±∈[－1,1]；当a<－1时，f(a)＝2a＋3＝，所以a＝－>－1(舍去)．综上，a＝2或a＝±.19．解析：因为m∈{x|－2<x<2，x∈Z}，所以m＝－1,0,1.因为对任意的x∈R，都有f(－x)＋f(x)＝0，即f(－x)＝－f(x)，所以f(x)是奇函数．当m＝－1时，f(x)＝x2只满足条件(1)而不满足条件(2)；当m＝1时，f(x)＝x0，条件(1)(2)都不满足；当m＝0时，f(x)＝x3，条件(1)(2)都满足．因此m＝0，且f(x)＝x3在区间[0,3]上是增函数，所以0≤f(x)≤27，故f(x)的值域为[0,27]．20．解析：(1)若x<0，则－x>0，f(x)＝f(－x)＝－(－x－2)2＋2＝－(x＋2)2＋2，则f(x)＝(2)图象如图所示，(3)由于方程f(x)－k＝0的解就是函数y＝f(x)的图象与直线y＝k的交点的横坐标，观察函数y ＝f(x)图象与直线y＝k的交点情况可知，当－2<k<2时，函数y＝f(x)图象与直线y＝k有四个交点，即方程f(x)－k＝0有四个解．21．解析：(1)由题意知D地距B城(100－x)km，则∴10≤x≤90.设比例系数为k，则y＝k[x2＋(100－x)2](10≤x≤90)．又x＝40时，y＝1 300，所以1 300＝k(402＋602)，即k＝，所以y＝[x2＋(100－x)2]＝(x2－100x＋5 000)(10≤x≤90)．(2)由于y＝(x2－100x＋5 000)＝(x－50)2＋1 250，所以当x＝50时，y有最小值为1 250万元．所以当供气站建在距A城50 km时，能使建设费用最小，最小费用是1 250万元．22．解析：(1)f(1)＝f(1)＋f(1)，所以f(1)＝0，f(4)＝f(2)＋f(2)＝1＋1＝2，f(8)＝f(2)＋f(4)＝1＋2＝3.(2)因为f(x)＋f(x－2)≤3，所以f[x(x－2)]≤f(8)，又因为对于函数f(x)，当x2>x1>0时，f(x2)>f(x1)，所以f(x)在(0，＋∞)上为增函数，所以解得2<x≤4.故x的取值范围为(2,4]．。
小学数学苏教版(2014秋)二年级下册第三章 认识方向单元复习-章节测试习题(1)
章节测试题1.【答题】邮局在银行的南面，报社在银行的北面，报社在邮局的（）面.A.南B.北C.东北【答案】B【分析】此题考查的是描述物体所在的方向.【解答】根据题意，画出示意图，如果以邮局为观测点，那么报社在邮局的北面.选B.2.【答题】如果小玲家在小云家的西北方，那么小云家在小玲家的（）方.A.东北B.东南C.西北【答案】B【分析】此题考查的是描述物体所在的方向.【解答】根据题意，画出示意图，如果以小玲家为观测点，那么小云家在小玲家的东南方.选B.3.【答题】看图判断对错.（1）教室在操场的西面. （）（2）食堂在校门的东北面. （）（3）操场在食堂的北面. （）（4）校门在操场的南面. （）（5）教室在食堂的西南面. （）（6）操场在校门的东面. （）【答案】× × ✓× × ✓【分析】此题考查的是描述物体所在的方向.【解答】看图可知，以操场为观测点，教室在操场的东面；以校门为观测点，食堂在校门的东南面；以食堂为观测点，操场在食堂的北面；以操场为观测点，校门在操场的西面；以食堂为观测点，教室在食堂的东北面；以校门为观测点，操场在校门的东面.故此题的答案是×、×、✓、×、×、✓.4.【综合题文】看图辨认方向后回答问题.【答题】面对学校平面图，上方是____面，下方是____面，左边是____面，右边是____面.【答案】北南西东【分析】此题考查的是给定一个方向，辨认其他方向.【解答】看图可知，图上的上方是北面，则下面是南面，左边是西面，右边是东面.故此题的答案是北、南、西、东.【答题】实验楼在国旗台的____面，办公楼在国旗台的____面，教学楼在国旗台的____面，大门在国旗台的____面.【答案】西北东南【分析】此题考查的是描绘物体所在的方向.【解答】看图可知，以国旗台为观测点，实验楼在国旗台的西面，办公楼在国旗台的北面，教学楼在国旗台的东面，大门在国旗台的南面.故此题的答案是西、北、东、南.【答题】运动场在实验楼的____面，在办公楼的____面，实践园地在大门的____面，在教学楼的____面，食堂在办公楼的____面，在教学楼的____面.【答案】北西东南东北【分析】此题考查的是描绘物体所在的方向.【解答】看图可知，以实验楼为观测点，运动场在实验楼的北面，以办公楼为观测点，运动场在办公楼的西面；以大门为观测点，实践园地在大门的东面，以教学楼为观测点，实践园地在教学楼的南面；以办公楼为观测点，食堂在办公楼的东面，以教学楼为观测点，食堂在教学楼的北面.故此题的答案是北、西、东、南、东、北.【答题】说一说，运动场、食堂、实践园地、厕所分别在国旗台的什么方向？【答案】运动场在国旗台的西北方向；食堂在国旗台的东北方向；实践园地在国旗台的东南方向，厕所在国旗台的西南方向.【分析】此题考查的是描述物体所在的方向.【解答】看图可知，以国旗台为观测点，运动场在国旗台的西北方向；食堂在国旗台的东北方向；实践园地在国旗台的东南方向，厕所在国旗台的西南方向.5.【答题】仔细辨，定方位.（将动物的名字写在方框里）熊猫住在学校的东南面；山羊住在学校的北面；小猴住在学校的东北面；小兔住在学校的西南面；小狗住在学校的西北面.【答案】小狗山羊小猴小兔熊猫【分析】此题考查的是认识方向.【解答】6.【答题】当你面向北时，你的右边是东面.（）【答案】✓【分析】此题考查的是给定一个方向，辨认其他方向.【解答】当你面向北时，你的后面是南面，左边是西面，右边是东面.故此题是正确的.7.【答题】小兰的影子在小兰的西面，太阳应在小兰的东面.（）【答案】✓【分析】此题考查的是方向的相对性.【解答】小兰的影子在小兰的西面，则太阳应该是从东面照射过来的，即太阳应在小兰的东面.故此题是正确的.8.【答题】红旗向北飘扬时，风从南边吹来.（）【答案】✓【分析】此题考查的是方向的相对性.【解答】红旗向北飘扬时，则风是从南面吹向北边的，即风从南边吹来.故此题是正确的.9.【答题】小冬面向西站立，当他向后转之后，他的左面是东、右面是西.（）【答案】×【分析】此题考查的是给定一个方向，辨认其他方向.【解答】小冬面向西站立，他的后面是东，所以当他向后转之后，是面向东，这是他的左面是北，右面是南.故此题是错误的.10.【答题】三（1）班教室的黑板在教室的西面，那么王亮在黑板上做题时面向东面.（）【答案】×【分析】此题考查的是给定一个方向，辨认其他方向.【解答】三（1）班教室的黑板在教室的西面，那么王亮在黑板上做题时面向的是黑板，即面向西面.故此题的答案是错误的.11.【答题】丁丁家在学校的西北方向，学校在丁丁家的（）方向.A. 东南B. 东北C. 西南【答案】A【分析】此题考查的是方向的相对性.【解答】与西北相对的方向是东南，所以丁丁家在学校的西北方向，学校在丁丁家的东南方向.选A.12.【答题】超市的东北面是银行，那么超市在银行的（）方向.A. 东北B. 东南C. 西南【答案】C【分析】此题考查的是方向的相对性.【解答】与东北相对的方向是西南，所以超市的东北面是银行，那么超市在银行的西南方向.选C.13.【答题】小明家在学校的北面，小芳家在学校的南面，小明家在小芳家的（）面.A. 南B. 西C. 北【答案】C【分析】此题考查的是描述物体所在的方向.【解答】如图，小明家在学校的北面，小芳家在学校的南面，小明家在小芳家的北面.选C.14.【答题】东南风是从东南面向（）面吹的.A. 东北B. 西南C. 西北【答案】C【分析】此题考查的是方向的相对性.【解答】与东南相对的方向是西北，所以东南风是从东南面向西北面吹的.选C.15.【答题】图书馆在学校的东北面，学校在图书馆的（）面.A. 东南B. 西南C. 西北【答案】B【分析】此题考查的是方向的相对性.【解答】与东北相对的方向是西南，所以图书馆在学校的东北面，学校在图书馆的西南面.选B.16.【答题】小松鼠在蚂蚁的____面，小青蛙在蚂蚁的____面，小鹿在蚂蚁的____面，小猴在蚂蚁的____面.【答案】南西东北【分析】此题考查的是描述物体所在的方向.【解答】看图可知，以蚂蚁为观测点，小松鼠在蚂蚁的南面，小青蛙在蚂蚁的西面，小鹿在蚂蚁的东面，小猴在蚂蚁的北面.故此题的答案是南、西、东、北.。
冀教版七年级上册第三章《代数式》单元测试卷内含知识点解析及答案(含分值)
第三章《代数式》单元测试卷第Ⅰ卷选择题一、选择题（本大题共16 个小题，1～6 小题，每小题2 分；7～16 小题，每小题3 分，共42 分）1.在下列表述中，不能表示代数式“4a”的意义的是【】A.4 的a倍B.a的4倍C.4 个a相加D.4 个a相乘2.下列各式中：-x+1，π+3,9>2，x yx y-+，S=πR2，代数式有【】A.5 个B.4 个C.3 个D.2 个3.下列式子中，符合代数式的书写格式的是【】A.22x yB.423abC.（a+b）÷5D.mn×24.对于代数式2()a b-，下列叙述正确的是【】A.a与b 的差的绝对值B.a与b 的平方差的绝对值C.a与b 的差的绝对值的平方D.a与b 的差的平方的绝对值5.有一个两位数，十位数字是x，个位数字是1，如果把它们的位置颠倒一下，则得到新的两位数是【】A.x+1 B.10x+1C.x+10D.10x+106.一台电视机成本价为a元，销售价比成本价增加25%，因库存积压，所以按销售价的70%出售，那么每台电视机实际售价为【】A.（1+25%）（1+70%）a元B.70%（1+25%）a元C.（1+25%）（1-70%）a元D.（1+25%+70%）a元7.已知x=1，y=2，则62x yy-的值为【】A.1B.2C.32D.238.当a=13，b=9 时，下列代数式的值是24 的是【】A.（3a+2）（b -1）B.（2a+1）（b +10）C.（2a+3）（b -1）D.（a+2）（b+1）9.根据《国家中长期教育改革和发展规划纲要》，教育经费投入应占当年GDP的4%，若设2013 年GDP 的总值为n 亿元，则2013 年教育经费投入可表示为【】A.4%n 亿元B.（1+4%n）亿元C.（1-4%）n 亿元D.（4%+n）亿元10.如图所示，这个图形的面积是【】A. 112xyB. 132xyC.6xyD.3xy11.有一大捆粗细均匀的钢筋，现要确定其长度，先称出这捆钢筋的总质量为m kg，再从中截取5 m长的钢筋，称出它的质量为n kg，那么这捆钢筋的总长度为【】A.mnm B.5mnmC. 5mnm D.（5mn-5）m12.找规律：①8+0.3；②16+0.6；③24+0.9，…，则第8 个式子为【】A.24+1.2B.32+1.6C.32+1.2D.64+2.413.在下列2×2的方格中（如图所示）找出规律，你认为x应为【】A.10B.-2C.2D.214.当x=3 时，代数式ax4+x2的值为2 013，则当x=-3 时，代数式ax4+x2+1的值为【】A.2 013B.-2 013C.2 014D.2 01215.用如图所示的程序计算代数式的值，若输入n的值为5，则输出y的结果为【】A.16B.2.5C.18.5D.13.516.已知整数a1，a2，a3，a4，…满足下列条件：a1=0，a2=-11a-+，a3=-22a-+，a 4=- 33a-+，…，依次类推，则a2 014的值是【】A.-1 006B.-1 007C.-1 008D.-2 014第Ⅱ卷选择题二、填空题（本大题共4 个小题，每小题3 分，共12 分）17.王红步行t h 所走的路程是s km，如果她骑自行车的速度是步行速度的5 倍，那么她骑自行车的速度是km/h.18.长方形的长为a cm，宽为b cm，四角各割去一个相同的边长为x cm的小正方形，折起来做成一个无盖的长方体，这个长方体的长是 cm，宽是cm，高是 cm.19.“青山常在，碧水长流”，经研究发现1 hm2有林地比1 hm2无林地可多蓄水300 t，等于一座地下水库.如果1 hm2无林地蓄水a t，那么1 hm2有林地蓄水可达 t.20.下列图案是由边长相等的小正方形按一定的规律拼接而成.依此规律，第5个图案中小正方形的个数为.第1个第2个第3个三、解答题（本大题共6 个小题，共66 分）21.（9 分）用代数式表示：（1）比x 的3 倍大6 的数；（2）比x 小6 的数的三分之一；（3）a，b 两数的和与a，b 两数的差的积.22.（10 分）3月5 日某校组织305 位同学参加“学雷锋”活动，在活动中有25的同学每人做好事a件，其余同学每人做好事（a+1）件. （1）你能用代数式表示他们共做好事的件数吗？（2）如果a=5，那么他们共做好事多少件？（3）如果a=8，那么他们共做好事又是多少件？23.（10 分）已知a=5，b=-2，那么代数式a3-b3与代数式（a-b）（a2 +ab+b2）的值分别是多少？它们的值相等吗？24.（11 分）（1）在下列两个条件下，分别求代数式a2-2ab+b2和（a-b）2的值.①a=5，b=3；②a=12，b=13.（2）观察这两个代数式，你发现了什么？（3）利用你的发现，求125.52-2×125.5×25.5+25.52的值.25.（12分）如图所示，有一块长方形的土地，长为20 m，宽为15 m，在四周留出宽度都是x m 的小路，中间余下的长方形部分（阴影部分）作为菜地.（1）用含x 的代数式表示菜地的长a和宽b；（2）用含x 的代数式表示菜地的面积S；（3）当x 的值分别取0.5 m、1 m、2 m时，菜地的面积S 分别是多少平方米？26.（14分）整体思想与转化思想是初中数学学习中的两大重要思想，试使用这两种思想求当a ba b+-=-4 时，下列代数式的值.（1）2288a ba b+-；（2）3()4()a b a ba b a b+---+.答案第三章《代数式》单元测试卷一、1.D 提示：4 个a相乘可表示为a·a·a·a或a4.2.C 提示：代数式有-x+1，π+3，x yx y-+共3 个.3.A 提示：B 应写为143ab；C 应写为5a b+；D 应写为2mn.4.D 提示：该式子是先求差，再求平方，再求绝对值.5.C 提示：由题意可得，新两位数的十位数字是1，个位数字是x，所以这个两位数是10+x，故选C.6.B 提示：根据题意可得，每台电视机的实际售价为70%（1+25%）a元.7.A 提示：62612212x yy-⨯-⨯==.8.A 提示：将a=13，b=9 依次代入各选项中即可.9.A 提示：n 亿元的4%表示为4%n 亿元.10.A 提示：阴影部分面积=2y （3x-0.5x ）+0.5xy=112xy. 11.C 提示：由题意可得，每米钢筋的质量为5nkg ，所以这捆钢筋的总长度为m ÷5n = 5m nm. 12.D 提示：第n 个式子为8n+0.3n. 13.B 提示：x=3+7-12=-2.14.C 提示：原式=2 013+1=2 014.15.A 提示：因为5 是奇数，按y=3n+1 计算，得y=3×5+1=16.16.B 提示：计算可得a 1=0，a 2=-1，a 3=-1，a 4=-2，a 5=-2，a 6=-3，a 7=-3，…，除a 1 外，每两个数的值相等.又因为（2 014-1）÷2=1 006……1，所以a 2 014=-1 006-1=-1 007. 二、17. 5s t 提示：王红步行的速度为s t .18.（a-2x ）；（b-2x ）；x 提示：画出草图即可快速得到.19.（a+300） 提示：根据题意可得，1 hm 2有林地蓄水可达（300+a ）t. 20.41 提示：第n 个图案中小正方形的个数为2n （n-1）+1. 三、 21.解：（1）3x+6.（2）13（x-6）.（3）（a+b ）（a-b ）.22.解：（1）他们共做好事：25×305a+35×305（a+1）=［122a+183（a+1）］（件）.（2）当a=5 时，［122a+183（a+1）］=[122×5+183×（5+1）]=1 708（件），即他们共做好事1 708 件. （3）当a=8 时，［122a+183（a+1）］=[122×8+183×（8+1）]=2 623（件），即他们共做好事2 623 件.23.解：当a=5，b=-2 时，a 3-b 3=133，（a-b ）（a 2 +ab+b 2）=133，它们的值相等.24.解：（1）①当a=5，b=3 时，两式的值都为4；②当a=12，b=13时，两式的值都为136.（2）发现了：a 2-2ab+b 2=（a-b ）2.（3）125.52-2×125.5×25.5+25.52=（125.5-25.5）2=10 000. 25.解：（1）长：（20-2x ）m ，宽：（15-2x ）m ； （2）S=（20-2x ）（15-2x ）； （3）当x=0.5 m 时，S=266（m 2），当x=1 m 时，S=234（m 2），当x=2 m 时，S=176（m 2）.26.解：（1）原式=14×a ba b+-=14×（-4）=-1.（2）原式=3×（-4）-14×（-4）=-111516.。
人教版数学七年级上册 第3章 一元一次方程单元测试试题(一)
一元一次方程单元测试试题（一）一．选择题1．方程4x＝﹣2的解是（）A．x＝﹣2B．x＝2C．x＝﹣D．x＝2．2020年初新冠疫情肆虐，社会经济受到严重影响．地摊经济是就业岗位的重要来源．小李把一件标价60元的T恤衫，按照8折销售仍可获利10元，设这件T恤的成本为x元，根据题意，下面所列的方程正确的是（）A．60×0.8﹣x＝10B．60×8﹣x＝10C．60×0.8＝x﹣10D．60×8＝x﹣103．下列变形中正确的是（）A．方程3x﹣2＝2x+1，移项，得3x﹣2x＝﹣1+2B．方程3﹣x＝2﹣5（x﹣1），去括号，得3﹣x＝2﹣5x﹣5C．方程t＝，未知数系数化为1，得t＝1D．方程＝x化为＝x4．某车间有22名工人，每人每天可以生产1200个螺钉或2000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母正好配套，设有x名工人生产螺钉，其他工人生产螺母，则根据题意可列方程为（）A．2000x＝1200（22﹣x）B．2×1200x＝2000（22﹣x）C．2×2000x＝1200（22﹣x）D．1200x＝2000（22﹣x）5．某书店把一本新书按标价的八折出售，仍可获利10%，若该书的进价为24元，则标价为（）A．30元B．31元C．32元D．33元6．如图，正方形ABCD的边长是2个单位，一只乌龟从A点出发以2个单位/秒的速度顺时针绕正方形运动，另有一只兔子也从A点出发以6个单位/秒的速度逆时针绕正方形运动，则第2020次相遇在（）A．点A B．点B C．点C D．点D7．下列方程：①y＝x﹣7；②2x2﹣x＝6；③m﹣5＝m；④＝1；⑤＝1，⑥6x ＝0，其中是一元一次方程的有（）A．2个B．3个C．4个D．5个8．下列等式变形正确的是（）A．若﹣2x＝5，则x＝B．若3（x+1）﹣2x＝1，则3x+1﹣2x＝1C．若5x﹣6＝﹣2x﹣8，则5x+2x＝8+6D．若，则2x+3（x﹣1）＝69．疫情无情人有情，爱心捐款传真情．某校三个年级为疫情重灾区捐款，经统计，七年级捐款数占全校三个年级捐款总数的，八年级捐款数是全校三个年级捐款数的平均数，已知九年级捐款1964元，求其他两个年级的捐款数．若设七年级捐款数为x元，则可列方程为（）A．x+x+1964＝x B．x+x+1964＝xC．x+x+1964＝x D．x+x+1964＝3x10．把1～9这9个数填入3×3方格中，使其任意一行，任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”．它源于我国古代的“洛書”（图①），是世界上最早的“幻方”．图②是仅可以看到部分数值的“九宫格”，则其中x的值为（）A．1B．3C．4D．6二．填空题11．已知关于x的一元一次方程mx＝5x﹣2的解为x＝2，则m值为．12．某商贩卖出两双皮鞋，相比进价，一双盈利30%，另一双亏本10%，两双共卖出200元．商贩在这次销售中要有盈利，则亏本的那双皮鞋的进价必须低于元．13．解方程5（x﹣2）＝6（﹣）．有以下四个步骤，其中第①步的依据是．解：①去括号，得5x﹣10＝3x﹣2．②移项，得5x﹣3x＝10﹣2．③合并同类项，得2x＝8．④系数化为1，得x＝4．14．防控新冠肺炎疫情期间．某药店在市场抗病毒药品紧缺的情况下，将某药品提价后，使价格翻一番（即为原价的2倍），物价部门查处后，其价格降到比原价高10%．则该药品降的百分比是．15．新定义：对非负数x“四舍五入”到个位的值记为（x）．即当n为非负整数时，若n﹣≤x＜n+则（x）＝n．如（0.46）＝0，（3.67）＝4．给出下列关于（x）的结论：①（1.493）＝1；②（2x）＝2（x）；③若（x﹣1）＝4，则x的取值范围是9≤x＜11；④当x≥0，m为非负整数时，有（m+2020x）＝m+（2020x）；其中正确的结论有（填写所有正确的序号）．三．解答题16．解方程：3（2x﹣1）﹣2（1﹣x）＝0．17．如图，数轴上点A对应的有理数为12，点P以每秒1个单位长度的速度从点A出发，点Q以每秒2个单位长度的速度从原点O出发，且P、Q两点同时向数轴正方向运动．设运动时间为t秒．（1）填空：当t＝2时，P，Q两点对应的有理数分別为，，PQ＝．（2）当PQ＝8时，求t的值．18．王莉骑自行车从A地到B地，陈平骑自行车从B地到A地，两人都沿同一公路匀速前进，已知两人在上午8时同时出发，到上午10时，两人还相距24km，到中午12时，两人又相距24km．求A、B两地间的路程．某车间有24名工人，每人每天平均生产螺栓12个或螺母18个，两个螺栓配三个螺母．为了使每天的产品刚好配套，应该分配多少名工人生产螺栓，多少名工人生产螺母？（2）某校举行元旦汇演，七（01）、七（02）班各需购买贺卡70张，已知贺卡的价格如下：50张以上购买贺卡数不超过30张30张以上不超过50张每张价格3元 2.5元2元（ⅰ）若七（01）班分两次购买，第一次购买24张，第二次购买46张，七（02）班一次性购买贺卡70张，则七（01）班、七（02）班购买贺卡费用各是多少元？哪个班费用更节省？省多少元？（ⅱ）若七（01）班分两次购买贺卡共70张（第二次多于第一次），共付费150元，则第一次、第二次分别购买贺卡多少张？参考答案与试题解析一．选择题1．【解答】解：方程4x＝﹣2，解得：x＝﹣．故选：C．2．【解答】解：设这件T恤的成本为x元，根据题意，可得：60×0.8﹣x＝10．故选：A．3．【解答】解：方程3x﹣2＝2x+1，移项，得3x﹣2x＝1+2，故选项A变形错误；方程3﹣x＝2﹣5（x﹣1），去括号，得3﹣x＝2﹣5x+5，故选项B变形错误；方程t＝，未知数系数化为1，得t＝，故选项C变形错误；方程＝x化为＝x，利用了分数的基本性质，故选项D正确．故选：D．4．【解答】解：∵有x名工人生产螺钉，∴有（22﹣x）名工人生产螺母．∵每天生产螺母的总数是生产螺钉总数的2倍，∴2×1200x＝2000（22﹣x）．故选：B．5．【解答】解：设这本新书的标价为x元，依题意得：0.8x﹣24＝24×10%，解得：x＝33．故选：D．6．【解答】解：设运动x秒后，乌龟和兔子第2020次相遇，依题意，得：2x+6x＝2×4×2020，解得：x＝2020，∴2x＝4040．又∵4040÷（2×4）＝505，505为整数，∴乌龟和兔子第2020次相遇在点A．故选：A．7．【解答】解：一元一次方程有m﹣5＝m，＝1，6x＝0，共3个，故选：B．8．【解答】解：A、若﹣2x＝5，则x＝﹣，错误，故本选项不符合题意；B、若3（x+1）﹣2x＝1，则3x+3﹣2x＝1，错误，故本选项不符合题意；C、若5x﹣6＝﹣2x﹣8，则5x+2x＝﹣8+6，错误，故本选项不符合题意；D、若+＝1，则2x+3（x﹣1）＝6，正确，故本选项符合题意；故选：D．9．【解答】解：由题意可得，七年级捐款数为x元，则三个年级的总的捐款数为：x÷＝x，故八年级的捐款为：，则x++1964＝x，故选：A．10．【解答】解：由题意，可得8+x＝2+7，解得x＝1．故选：A．二．填空题11．【解答】解：∵关于x的一元一次方程mx＝5x﹣2的解为x＝2，∴2m＝10﹣2，解得：m＝4．故答案为：4．12．【解答】解：设亏本的那双皮鞋的进价为x元，则亏本的那双皮鞋的售价为（1﹣10%）x元，盈利的那双皮鞋的售价为[200﹣（1﹣10%）x]元，盈利的那双皮鞋的进价为元，依题意，得：（1﹣10%）x﹣x+[200﹣（1﹣10%）x]﹣＞0，解得：x＜150．故答案为：150．13．【解答】解：第①步去括号的依据是：乘法分配律．故答案是：乘法分配律．14．【解答】解：设该药品的原价为a元，降价的百分比为x，依题意，得：2a（1﹣x）＝（1+10%）a，解得：x＝0.45＝45%．故答案为：45%．15．【解答】解：①（1.493）＝1，故①符合题意；②（2x）≠2（x），例如当x＝0.3时，（2x）＝1，2（x）＝0，故②不符合题意；③若（x﹣1）＝4，则4﹣x﹣1＜4+，解得：9≤x＜11，故③符合题意；④m为非负整数，故（m+2020x）＝m+（2020x），故④符合题意；综上可得①③④正确．故答案为：①③④．三．解答题16．【解答】解：去括号，得6x﹣3﹣2+2x＝0，移项，得6x+2x＝3+2，合并同类项，得8x＝5，系数化为1，得x＝．17．【解答】解：（1）∵2×2＝4，12+2×1＝14，∴当t＝2时，P，Q两点对应的有理数分别是4，14，∴PQ＝14﹣4＝10．故答案为：4；14；10．（2）当运动t秒时，P、Q两点对应的有理数分别为12+t，2t．①当点P在点Q右侧时：∵PQ＝8，∴（12+t）﹣2t＝8，解得t＝4．②当点P在点Q的左侧时：∵PQ＝8，∴2t﹣（12+t）＝8，解得t＝20．综上所述，当PQ＝8时，t的值为4或20．18．【解答】解：设A、B两地间的路程为xkm，依题意，得：＝，解得：x＝72．答：A、B两地间的路程为72km．19．【解答】解：（1）设分配x名工人生产螺栓，则分配（24﹣x）名工人生产螺母，依题意，得：＝，解得：x＝12，∴24﹣x＝12．答：应该分配12名工人生产螺栓，12名工人生产螺母．（2）（i）七（01）班购买贺卡费用为3×24+2.5×46＝187（元），七（02）班购买贺卡费用为2×70＝140（元）．187＞140，187﹣140＝47（元）。
八年级数学下册《第三章图形的平移与旋转》单元测试题含答案
第三章图形的平移与旋转第Ⅰ卷(选择题共30分)一、选择题(每小题3分，共30分)1．下列英文字母既是中心对称图形又是轴对称图形的是( )图12．如图2所示的各组图形中，由图形甲变成图形乙，既能用平移，又能用旋转的是( )图23．如图3，如果将△ABC的顶点A先向下平移3格，再向左平移1格到达A′点，连接A′B，那么线段A′B与线段AC的关系是( )图3A．互相垂直 B．相等C．互相平分 D．互相垂直且平分4．如图4，将△PQR先向右平移2个单位长度，再向下平移3个单位长度，则顶点P 平移后的坐标是( )图4A．(－2，－4) B．(－2，4) C．(2，－3) D．(－1，－3)5．已知A(－1，3)，B(2，－3)两点，现将线段AB平移至A1B1，如果A1(a，1)，B1(5，－b)，那么a b的值是( )A ．16B ．25C ．32D ．496．如图5所示，将边长为2的正方形ABCD 沿对角线AC 向右平移，使点A 移至线段AC 的中点A ′处，得到新正方形A ′B ′C ′D ′，则新正方形与原正方形重叠部分(图中阴影部分)的面积是( )图5A. 2B.12 C ．1 D.147．如图6所示，在△ABC 中，AB ＝4，BC ＝6，∠B ＝60°，将△ABC 沿射线BC 的方向平移，得到△A ′B ′C ′，再将△A ′B ′C ′绕点A ′逆时针旋转一定角度后，点B ′恰好与点C 重合，则平移的距离和旋转角的度数分别为( )图6A ．4，30°B ．2，60°C ．1，30°D ．3，60°8．如图7，在△ABC 中，∠CAB ＝75°，在同一平面内，将△ABC 绕点A 旋转到△AB ′C ′的位置，使得CC ′∥AB ，则∠BAB ′的度数为( )图7A ．30°B ．35°C ．40°D ．50°9．如图8，将△ABC 绕点C (0，1)旋转180°得到△A ′B ′C ，若点A 的坐标为(a ，b )，则点A ′的坐标是( )图8A ．(－a ，－b )B ．(－a ，－b －1)C ．(－a ，－b ＋1)D ．(－a ，－b ＋2) 10．如图9所示，在Rt △ABC 中，∠ACB ＝90°，∠B ＝30°，AC ＝1，且AC 在直线l 上，将△ABC 绕点A 顺时针旋转到位置①，可得到点P 1，此时AP 1＝2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2＝2＋3；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3＝3＋3……按此规律继续旋转，直到得到点P为止，则AP等于( )图9A．＋673 3 B．＋672 3 C．＋672 3 D．＋673 3第Ⅱ卷(非选择题共70分)二、填空题(每小题3分，共18分)11．有下列运动：①物体随传送带的移动；②踢足球时，足球的移动；③轻轨列车在笔直轨道上行驶；④从书的某一页翻到下一页时，这一页上的某个图形的移动．其中属于平移现象的有________．(将所有正确的序号都填上)12．如图10，把△ABC绕点C按顺时针方向旋转35°，得到△A′B′C，A′B′交AC 于点D.若∠A′DC＝90°，则∠A＝________°.图1013.如图11，在平面直角坐标系中，点A的坐标为(－1，2)，点C的坐标为(－3，0)，先将点C绕点A逆时针旋转90°，再向下平移3个单位长度，此时点C的对应点的坐标为________．图1114．如图12，在等边三角形ABC中，AB＝10，D是BC的中点，将△ABD绕点A旋转后得到△ACE，则线段DE的长为________．图1215．如图13，在△ABC中，∠C＝90°，AC＝BC＝2，将△ABC绕点A顺时针旋转60°到△AB′C′的位置，连接C′B，则C′B的长为________．图1316．有两张完全重合的长方形纸片，小亮同学将其中一张绕点A顺时针旋转90°后得到长方形AMEF(如图14①)，连接BD，MF，此时他测得∠ADB＝30°.小红同学用剪刀将△BCD 与△MEF剪去，与小亮同学探究．他们将△ABD绕点A顺时针旋转得到△AB1D1，AD1交MF于点K(如图②)，设旋转角为β(0°＜β＜90°)，当△AFK为等腰三角形时，旋转角β的度数为________．图14三、解答题(共52分)17．(6分)青花瓷是我国民族艺术瑰宝之一，它以洁白细腻的胎体、晶莹透明的釉色、幽靓浓艳的纹饰、华美丰富的造型而闻名于世，它的清新雅丽、质朴率真最能代表中华民族含蓄而豪迈的民族风格，因而素有“国瓷”之誉．请欣赏下面这幅青花瓷图案，试用两种方法分析图案的形成过程．图1518．(6分)如图16，在△ABC和△ADE中，点E在BC边上，∠BAC＝∠DAE，∠B＝∠D，AB＝AD.(1)求证：△ABC≌△ADE；(2)如果∠AEC＝75°，将△ADE绕着点A逆时针旋转一定角度(小于90°)后与△ABC重合，求这个旋转角的大小．图1619．(6分)如图17，桌面内，直线l上摆放着两个大小相同的三角板，它们中较大锐角的度数为60°.将△ECD沿直线l向左平移到△E′C′D′的位置，使点E′落在AB上，P 为AC与E′D′的交点，试解决下列问题：(1)求∠CPD′的度数；(2)求证：AB⊥E′D′.图1720．(6分)如图18，△ABC是边长为3的等边三角形，将△ABC沿直线BC向右平移BC 的长度，得到△DCE，连接BD，交AC于点F.(1)猜想AC与BD的位置关系，并证明你的结论；(2)求线段BD的长．图1821．(6分)如图19，用等腰直角三角板画∠DOB＝45°，并将三角板沿OB方向平移到如图所示的△AMB处后，再将三角板绕点M逆时针旋转22°得到△EMC，EM与OD交于点D，求此时三角板的斜边与射线OD的夹角∠ODM的度数．图1922．(6分)如图20所示，在平面直角坐标系中，有一直角三角形ABC，且A(0，5)，B(－5，2)，C(0，2)，△AA1C1是由△ABC经过旋转变换得到的．图20(1)由△ABC旋转得到△AA1C1的旋转角的度数是多少？并写出旋转中心的坐标；(2)请你画出仍以(1)中的旋转中心为旋转中心，将△AA1C1按顺时针，△ABC按逆时针各旋转90°后得到的两个三角形，并写出△AA1C1按顺时针旋转90°后点A1的对应点A2的坐标；(3)利用变换前后所形成的图案证明勾股定理(设△ABC的两直角边长分别为a，b，斜边长为c)．23．(8分)如图21所示，△ABC，△ECD都是等边三角形．(1)试确定AE，BD之间的大小关系；(2)如果把△CDE绕点C按逆时针方向旋转到如图②所示的位置，那么(1)中的结论还成立吗？请说明理由．图2124．(8分)如图22，在正方形ABCD中，E为BC上任意一点，将△ABE旋转后得到△CBF.(1)指出旋转中心和旋转角的度数；(2)判断AE与CF的位置关系；(3)如果正方形的面积为18 cm2，△BCF的面积为4 cm2，那么四边形AECD的面积是多少？图221．D 2.C 3.D 4.A 5.C 6.B7．B 8．A 9．D 10.D11.①③12.55 13.(1，－3) 14.5 3 15.3－1 16.60°或15°17．解：(答案不唯一)方案一：以一个花瓣为基本图案，依次旋转45°，90°，135°，180°，225°，270°，315°可得到整个图案；方案二：以相邻两个花瓣为基本图案，依次旋转90°，180°，270°可得到整个图案．18．解：(1)证明：在△ABC和△ADE中，∵∠BAC＝∠DAE，AB＝AD，∠B＝∠D，∴△ABC≌△ADE.(2)∵△ABC≌△ADE，∴AC与AE是一组对应边，∴∠CAE为旋转角．∵AE＝AC，∠AEC＝75°，∴∠ACE＝∠AEC＝75°，∴∠CAE＝180°－75°－75°＝30°.即旋转角为30°.19．解：(1)由平移的性质知DE∥D′E′，∴∠CPD′＝∠CED＝60°.(2)证明：由平移的性质知CE∥C′E′，∠CED＝∠C′E′D′＝60°，∴∠BE′C′＝∠BAC＝30°，∴∠BE′D′＝90°，∴AB⊥E′D′.20．解：(1)AC⊥BD.证明如下：∵△DCE是由△ABC平移而得到的，∴△DCE≌△ABC，AC∥DE.又∵△ABC是等边三角形，∴BC＝CD＝CE＝DE，∠DCE＝∠CDE＝60°，∴∠DBC＝∠BDC＝30°，∴∠BDE＝90°，∴DE⊥BD.∵AC∥DE，∴AC⊥BD.(2)在Rt△BED中，∵BE＝6，DE＝3，∴BD＝BE2－DE2＝62－32＝3 3.21．解：∵三角板绕点M逆时针旋转了22°，∴∠BMC＝22°.∵∠DMC＝45°，∴∠OMD＝180°－45°－22°＝113°.又∵∠DOB＝45°，∴∠ODM＝180°－113°－45°＝22°，即此时三角板的斜边与射线OD的夹角∠ODM的度数是22°.22．解：(1)旋转角为90°，旋转中心的坐标为(－1，1)．(2)如图所示，点A1的对应点A2的坐标为(－2，－3)．(3)证明：设AC＝a，BC＝b，则正方形AA1A2B的面积为c2，正方形C1C2C3C的面积为(b －a)2，由图可得c2－(b－a)2＝4×12 ab，即c2－b2＋2ab－a2＝2ab，∴c2＝a2＋b2. 23．解：(1)在△ACE和△BCD中，∵AC＝BC，∠ACE＝∠BCD＝60°，CE＝CD，∴△ACE≌△BCD，∴AE＝BD.(2)成立．理由如下：∵∠ACB＝∠ECD＝60°，∴∠ACE＝∠BCD.在△ACE和△BCD中，∵AC＝BC，∠ACE＝∠BCD，CE＝CD，∴△ACE≌△BCD，∴AE＝BD.24．解：(1)旋转中心是点B，旋转角是90°.(2)如图，延长AE交CF于点M.∵△CBF是由△ABE旋转得到的，∴△CBF≌△ABE，∴∠FCB＝∠EAB.∵∠AEB＝∠CEM，∴∠BAE＋∠AEB＝∠FCB＋∠CEM.∵四边形ABCD是正方形，∴∠ABE＝90°，∴∠BAE＋∠AEB＝90°，∴∠FCB＋∠CEM＝90°，∴∠CME＝90°，∴AE⊥CF.(3)∵△CBF≌△ABE，△CBF的面积为4 cm2，∴△ABE的面积为4 cm2.∵正方形的面积为18 cm2，∴四边形AECD的面积为14 cm2.11/ 11。
八年级数学上《第三章位置与坐标》单元测试题(含答案)
第三章位置与坐标第Ⅰ卷(选择题共30分)一、选择题(每题3分，共30分)1．下列关于确定一个点的位置的说法中，能具体确定点的位置的是()A．东北方向B．东经35°10′，北纬12°C．距点A100米D．偏南40°，8000米2．若点M(x，y)满足(x＋y)2＝x2＋y2－2，则点M所在的象限是()A．第一象限或第三象限B．第二象限或第四象限C．第一象限或第二象限D．不能确定3．如图1，△ABC与△DFE关于y轴对称，若点A的坐标为(－4，6)，则点D的坐标为()图1A．(－4，6) B．(4，6)C．(－2，1) D．(6，2)4．若A(a，b)，B(a，d)表示两个不同的点，且a≠0，则这两个点在()A．平行于x轴的直线上B．第一、三象限的角平分线上C．平行于y轴的直线上D．第二、四象限的角平分线上5．甲、乙两名同学用围棋子做游戏，如图2所示，现轮到黑棋下子，黑棋下一子后白棋下一子，使黑棋的5个棋子组成轴对称图形，白棋的5个棋子也组成轴对称图形，则下列下子方法不正确的是[说明：棋子的位置用数对表示，如点A在(6，3)]()图2A．黑(3，7)，白(5，3) B．黑(4，7)，白(6，2)C．黑(2，7)，白(5，3) D．黑(3，7)，白(2，6)6．以下是甲、乙、丙三人看地图时对四个地标的描述： 甲：从学校向北直走500米，再向东直走100米可到图书馆； 乙：从学校向西直走300米，再向北直走200米可到博物馆； 丙：博物馆在体育馆正西方向200米处．根据三人的描述，若从图书馆出发，其终点是体育馆，则下列描述正确的是( ) A ．向南直走300米，再向西直走200米 B ．向南直走300米，再向西直走600米 C ．向南直走700米，再向西直走200米 D ．向南直走700米，再向西直走600米7．若点P(－m ，3)与点Q(－5，n)关于y 轴对称，则m ，n 的值分别为( ) A ．－5，3 B ．5，3 C ．5，－3 D ．－3，58．有甲、乙、丙三个人，他们所处的位置不同，甲说：“以我为坐标原点，乙的位置是(2，3)．”丙说：“以我为坐标原点，乙的位置是(－3，－2)．”则以乙为坐标原点，甲、丙的坐标分别是(已知三人所建立的直角坐标系中x 轴、y 轴的方向相同，且单位长度一致)( )A ．(－3，－2)，(2，－3)B ．(－3，2)，(2，3)C ．(－2，－3)，(3，2)D ．(－2，－3)，(－2，－3)9．已知点A(1，0)，B(0，2)，点P 在x 轴上，且△PAB 的面积为5，则点P 的坐标为( )图3A ．(－4，0)B ．(6，0)C ．(－4，0)或(6，0)D ．无法确定10．如图3所示，在平面直角坐标系中，半径均为1个单位长度的半圆O 1，O 2，O 3，…组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒π2个单位长度，则第2019秒时，点P 的坐标是( )A ．(2019，0)B ．(2019，－1)C ．(2019，1)D ．(2018，0) 请将选择题答案填入下表：二、填空题(每题3分，共18分)11．若m＞0，n＜0，则点P(m，n)关于x轴的对称点在第________象限．12．已知A(2x－1，3x＋2)是第一、三象限角平分线上的点，则点A的坐标是________．13．在同一直角坐标系中，一同学误将点A的横、纵坐标的次序颠倒，写成A(a，b)；另一同学误将点B的坐标写成关于y轴对称的点的坐标，写成B(－b，－a)，则A，B两点原来的位置关系是__________．14．在平面直角坐标系中，已知点A(－3，0)，B(3，0)，点C在坐标轴上，且AC＋BC＝10，写出满足条件的所有点C的坐标：________．15．已知等边三角形ABC的两个顶点的坐标分别为A(－4，0)，B(2，0)，则点C的坐标为____________，△ABC的面积为________．16．如图4是某同学在课下设计的一款软件，蓝精灵从点O第一跳落到A1(1，0)，第二跳落到A2(1，2)，第三跳落到A3(4，2)，第四跳落到A4(4，6)，第五跳落到A5________，到达A2n后，要向________方向跳________个单位长度落到A2n＋1.图4三、解答题(共52分)17．(6分)如图5，△ABC中，AB＝AC＝13，BC＝24，请你建立适当的平面直角坐标系，并直接写出A，B，C三点的坐标．图518．(6分)(1)若点M(5＋a，a－3)在第二、四象限角平分线上，求a的值；(2)已知点N的坐标为(2－a，3a＋6)，且点N到两坐标轴的距离相等，求点N的坐标．19．(6分)在平面直角坐标系中，将坐标是(－5，0)，(－4，－2)，(－3，0)，(－2，－2)，(－1，0)的点用线段依次连接起来形成一个图案Ⅰ.(1)作出该图案关于y轴对称的图案Ⅱ；(2)将所得到的图案Ⅱ沿x轴向上翻折180°后得到一个新图案Ⅲ，试写出它的各顶点的坐标；(3)观察图案Ⅰ与图案Ⅲ，比较各顶点的坐标和图案位置，你能得到什么结论？20．(6分)已知在平面直角坐标系中有A(－2，1)，B(3，1)，C(2，3)三点．请回答下列问题：(1)在坐标系内描出点A，B，C的位置．(2)求出以A，B，C三点为顶点的三角形的面积．(3)在y轴上是否存在点P，使以A，B，P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．图621．(6分)已知点P(2m＋4，m－1)．根据下列条件，求出点P的坐标．(1)点P在y轴上；(2)点P在x轴上；(3)点P的纵坐标比横坐标大3；(4)点P在过点A(2，－3)且与x轴平行的直线上．22.(6分)如图7，四边形OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA＝10，OC＝8，在OC边上取一点D，若将纸片沿AD 翻折，使点O落在BC边上的点E处，求D，E两点的坐标．图723．(8分)如图8，正方形ABFG和正方形CDEF的顶点在边长为1的正方形网格的格点上．(1)建立平面直角坐标系，使点B，C的坐标分别为(0，0)和(5，0)，并写出点A，D，E，F，G的坐标；(2)连接BE和CG相交于点H，BE和CG相等吗？并计算∠BHC的度数．图824.(8分)如图9，在平面直角坐标系中，直线l过点M(3，0)且平行于y轴．(1)如果△ABC三个顶点的坐标分别是A(－2，0)，B(－1，0)，C(－1，2)，△ABC关于y轴的对称图形是△A1B1C1，△A1B1C1关于直线l的对称图形是△A2B2C2，写出△A2B2C2的三个顶点的坐标；(2)如果点P的坐标是(－a，0)，其中a＞0，点P关于y轴的对称点是P1，点P1关于直线l的对称点是P2，求PP2的长．图91．B 2．B3．B 4．C 5．C6．A7．A8.C 9．C10．B11.一12.(－7，－7)13．关于x轴对称14．(－5，0)，(5，0)，(0，4)，(0，－4)15．(－1，3 3)或(－1，－3 3)9 3[解析] 当点C 在第二象限时，作CH ⊥AB 于点H .因为A (－4，0)，B (2，0)，所以AB ＝6.因为△ABC 是等边三角形，所以AH ＝BH ＝3.由勾股定理得CH ＝3 3，所以C (－1，3 3)；同理，当点C在第三象限时，C (－1，－3 3)．所以△ABC 的面积为12×6×3 3＝9 3.16．(9，6) 正东 (2n ＋1) [解析] 因为蓝精灵从点O 第一跳落到A 1(1，0)，第二跳落到A 2(1，2)，第三跳落到A 3(4，2)，第四跳落到A 4(4，6)，所以蓝精灵先向正东跳动，再向正北跳动，每次跳动的距离为前一次的距离加1，即可求出．第五跳落到A 5(9，6)．到达A 2n 后，要向正东方向跳(2n ＋1)个单位长度落到A 2n ＋1.17．解：答案不唯一，如以BC 所在直线为x 轴，过点B 作BC 的垂线为y 轴建立平面直角坐标系，由图可知，点A (12，5)，B (0，0)，C (24，0)． 18．解：(1)由题意可得5＋a ＋a －3＝0，解得a ＝－1.(2)由题意可得|2－a |＝|3a ＋6|，即2－a ＝3a ＋6或2－a ＝－(3a ＋6)，解得a ＝－1或a ＝－4，所以点N 的坐标为(3，3)或(6，－6)．19．解：图案Ⅰ如图． (1)作出图案Ⅱ如图．(2)作出图案Ⅲ如图．图案Ⅲ各个顶点的坐标分别为(5，0)，(4，2)，(3，0)，(2，2)，(1，0)． (3)观察图案Ⅰ与图案Ⅲ，不难发现：①从各顶点坐标看，横、纵坐标均互为相反数；②从图案的位置上看，图案Ⅰ在第三象限，图案Ⅲ在第一象限，二者关于坐标原点对称．20．解：(1)描点如图．(2)如图，依题意，得AB ∥x 轴，且AB ＝3－(－2)＝5， 所以S △ABC ＝12×5×2＝5.(3)存在．因为AB ＝5，S △ABP ＝10，所以点P 到AB 的距离为4.又因为点P 在y 轴上，所以点P 的坐标为(0，5)或(0，－3)．21．解：(1)由题意，得2m ＋4＝0，解得m ＝－2，则m －1＝－3，所以点P 的坐标为(0，－3)． (2)由题意，得m －1＝0，解得m ＝1，则2m ＋4＝6，所以点P 的坐标为(6，0)．(3)由题意，得m －1＝(2m ＋4)＋3，解得m ＝－8，则2m ＋4＝－12，m －1＝－9, 所以点P 的坐标为(－12，－9)．(4)由题意，得m －1＝－3，解得m ＝－2，则2m ＋4＝0，所以点P 的坐标为(0，－3)． 22．解：由题意，可知折痕AD 所在的直线是四边形OAED 的对称轴．在Rt △ABE 中，AE ＝OA ＝10，AB ＝8，所以BE ＝AE 2－AB 2＝102－82＝6， 所以CE ＝4，所以E (4，8)． 在Rt △DCE 中，DC 2＋CE 2＝DE 2， 又DE ＝OD ，所以(8－OD )2＋42＝OD 2， 所以OD ＝5，所以D (0，5)．23．解：(1)按已知条件建立平面直角坐标系(如图)，A (－3，4)，D (8，1)，E (7，4)，F (4，3)，G (1，7)．(2)连接BE 和CG 相交于点H ，由题意，得BE ＝72＋42＝65，CG ＝72＋42＝65，所以BE ＝CG . 借助全等及三角形内角和等性质可得∠BHC 的度数：∠BHC ＝90°.24．解：(1)△A 2B 2C 2的三个顶点的坐标分别是A 2(4，0)，B 2(5，0)，C 2(5，2)．(2)①如图①，当0＜a ≤3时，因为点P 与点P 1关于y 轴对称，P (－a ，0)，所以P 1(a ，0)．因为点P 1与点P 2关于直线x ＝3对称，设P 2(x ，0)，可得x ＋a2＝3，即x ＝6－a ，所以P 2(6－a ，0)，则PP 2＝6－a －(－a )＝6－a ＋a ＝6.②如图②，当a ＞3时，因为点P 与点P 1关于y 轴对称，P (－a ，0)，所以P 1(a ，0)．因为点P 1与点P 2关于直线x ＝3对称，设P 2(x ，0)，可得x ＋a2＝3，即x ＝6－a ，所以P 2(6－a ，0)，则PP 2＝6－a －(－a )＝6－a ＋a ＝6.综上所述，PP 2的长为6.。
高一数学必修1《第三章 函数的应用》单元测试题(含答案)
高一数学必修1《第三章 函数的应用》单元测试题（满分150分 时间 120分钟）班级：__________ 姓名：__________ 成绩：__________第Ⅰ卷（选择题，共50分）一、选择题 （每题5分，共50分） 1. 函数223y x x =--的零点是（ ）A ．1,3-B ．3,1-C ．1,2D ．不存在2. 方程1lg x x -=必有一个根的区间是（ ）A ．(0.1,0.2)B ．(0.2,0.3)C ．(0.3,0.4)D ．(0.4,0.5)3．下列函数中增长速度最快的是（ ）Ａ．1100xy e =B ．y=100ln xC ．y=100xD ．y=1002x ⋅4．已知函数2212341,2,21,2,x y y x y x y x==--=-=其中能用二分法求出零点的函数个数是（ ）A ．1B ．2C ．3D ．45. 若函数()f x 唯一的零点一定在三个区间(2,16)2824、（，）、（，）内，那么下列命题中正确的是（ ）A ．函数()f x 在区间(2,3)内有零点B ．函数()f x 在区间(2,3(3,4)）或内有零点C ．函数()f x 在区间(3,16)内有零点D ．函数()f x 在区间(4,16)内无零点6. 如图表示人的体重与年龄的关系，则（ ）A ．体重随年龄的增长而增加B ．25岁之后体重不变C ．体重增加最快的是15~25岁D ．体重增加最快的是15岁之前7. 世界人口已超过60亿，若按千分之一的年增长率计算，则两年增长的人口约为（ ）A ．120万B ．1100万C ．1200万D ．12000万8. 已知函数()24f x mx =+，若在[]2,1-上存在0x 使0()0f x =，则实数m 的取值范围是（ ）A ．5,42⎡⎤-⎢⎥⎣⎦B.(][),21,-∞-+∞C. []1,2-D. []2,1-9. 若商品进价每件40元，当售价为50元/件时，一个月能卖出500件，通过市场调查发现，若每件商品的单价每提高1元，则商品一个月的销售量会减少10件。
第三章《概率的进一步认识》单元测试题(含答案)
第三章 概率的进一步认识第Ⅰ卷 (选择题 共30分)一、选择题(每小题3分，共30分)1．三张外观相同的卡片上分别标有数字1，2，3，从中随机一次性抽出两张，这两张卡片上的数字恰好都小于3的概率是( )A.13B.23C.16D.192．某学校在八年级开设了数学史、诗词赏析、陶艺三门课程，若小波和小睿两名同学每人随机选择其中一门课程，则小波和小睿选到同一门课程的概率是( )A.12B.13C.16D.193．布袋中有红、黄、蓝三种颜色的球各一个，从中摸出一个球之后不放回布袋，再摸第二个球，这时得到的两个球的颜色中有“一红一黄”的概率是( )A.16B.29C.13D.234．有3个整式x ，x ＋1，2，先随机取一个整式作为分子，再从余下的整式中随机取一个作为分母，恰能组成分式的概率是( )A.13B.12C.23D.565．在物理课上，某实验的电路图如图1所示，其中S 1，S 2，S 3表示电路的开关，L 表示小灯泡，R 为保护电阻．若闭合开关S 1，S 2，S 3中的任意两个，则小灯泡L 发光的概率为( )图1A.16B.13C.12D.236．如图2，两个转盘分别自由转动一次，当它们都停止转动时，两个转盘的指针都指向2的概率为( )图2A.12B.14C.18D.1167．在一个不透明的口袋里装了只有颜色不同的黄球、白球若干只．某小组做摸球试验：将球搅匀后从中随机摸出一个，记下颜色，再放回袋中，不断重复这一过程．下表是活动中的一组数据，则摸到黄球的概率约是( )A.0.4 B ．0.5 C ．0.6 D ．0.78．某学习小组做“用频率估计概率”的试验时，统计了某一结果出现的频率，绘制了如下表格，则符合这一结果的试验最有可能的是( )A.一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃 B ．在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” C ．抛一个质地均匀的正六面体骰子，向上的面点数是5 D ．抛一枚硬币，出现反面的概率9．为了估计不透明的袋子里装有多少个球，先从袋中摸出10个球都做上标记，然后放回袋中去，充分摇匀后再摸出10个球，发现其中有一个球有标记，那么你估计袋中大约有球( )A ．10个B ．20个C ．100个D ．121个10．有A ，B 两粒质地均匀的正方体骰子(骰子每个面上的点数分别为1，2，3，4，5，6)，小王掷骰子A ，朝上的数字记作x ；小张掷骰子B ，朝上的数字记作y .在平面直角坐标系中有一矩形，四个点的坐标分别为(0，0)，(6，0)，(6，4)和(0，4)，小王、小张各掷一次所确定的点P (x ，y )落在矩形内(不含矩形的边)的概率是( )A.23B.512C.12D.712请将选择题答案填入下表：第Ⅱ卷 (非选择题 共90分)二、填空题(每小题3分，共18分)11．一个不透明的袋子中装有2个红球，1个绿球，这些球除颜色不同外其余都相同，从袋子中随机摸出一个小球记下颜色后放回，再随机摸出一个小球，则一次摸到红球一次摸到绿球的概率为________．12．从－1，0，1，2这四个数中，任取两个不同的数作为点的坐标，则该点在第一象限的概率为________．13．小明和小亮做游戏，先是各自背着对方在纸上写一个自然数，然后同时呈现出来．他们约定：若两人所写的数都是奇数或都是偶数，则小明获胜；否则，小亮获胜．这个游戏对双方________．(填“公平”或“不公平”)．14．点P 的坐标是(a ，b)，从－2，－1，0，1，2这五个数中任取一个数作为a 的值，再从余下的四个数中任取一个数作为b 的值，则点P(a ，b)在平面直角坐标系中第二象限内的概率是________．15．在围棋盒中有x 颗白色棋子和y 颗黑色棋子，从盒中随机取出一颗棋子，取到白色棋子的概率是25.若再往盒中放进3颗黑色棋子，则取到白色棋子的概率变为14，原来围棋盒中有白色棋子______颗．16．如果任意选择一对有序整数(m ，n)，其中|m|≤1，|n|≤3，每一对这样的有序整数被选择的可能性是相等的，那么关于x 的方程x 2＋nx ＋m ＝0有两个相等实数根的概率是________．三、解答题(共72分)17．(6分)不透明的文具袋中装有规格相同的红、黑两种颜色的通用中性笔芯，其中红色的有3支，黑色的有2支．(1)从文具袋中随机抽取1支笔芯，求恰好抽到的是红色笔芯的概率；(2)从文具袋中随机抽取2支笔芯，求恰好抽到的都是黑色笔芯的概率．(请用画树状图法或列表法求解)18．(6分)研究问题：一个不透明的盒中装有若干个只有颜色不一样的红球和黄球．怎样估算不同颜色球的数量？操作方法：先从盒中摸出8个球，画上记号放回盒中，再进行摸球试验．摸球试验的要求：先搅拌均匀，每次摸出1个球，放回盒中再继续．活动结果：摸球试验活动一共做了50次，统计结果如下表：由上述摸球试验可推算：(1)盒中红球、黄球占总球数的百分比分别是多少？(2)盒中有红球多少个？19．(8分)甲、乙、丙三名同学站成一排进行毕业合影留念，请用列表或画树状图的方法列出所有可能的情形，并求出甲、乙两人相邻的概率是多少．20．(8分)九年级某班组织全班活动，班委会准备买一些奖品．班长王倩拿15元钱去商店全部用来购买圆珠笔和铅笔两种奖品，已知圆珠笔的价格为2元/支，铅笔的价格为1元/支，且每种笔至少买一支．(1)有多少种购买方案？请列举所有可能的结果；(2)从上述方案中任选一种方案购买，求买到的圆珠笔与铅笔数量相等的概率．21．(10分)小明参加某个智力竞答节目，答对最后两道单选题就顺利通关．第一道单选题有3个选项，第二道单选题有4个选项，这两道题小明都不会，不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项)．(1)如果小明第一题不使用“求助”，那么小明答对第一道题的概率是________；(2)如果小明将“求助”留在第二题使用，请用画树状图或者列表的方法来分析小明顺利通关的概率；(3)从概率的角度分析，你建议小明在第几题使用“求助”？22．(10分)小明、小芳做一个“配色”的游戏．如图3是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色．同时转动两个转盘，如果转盘A 转出了红色，转盘B转出了蓝色，或者转盘A转出了蓝色，转盘B转出了红色，则红色和蓝色在一起配成紫色，这种情况下小芳获胜；同样，蓝色和黄色在一起配成绿色，这种情况下小明获胜；在其他情况下不分胜负．(1)利用列表或画树状图的方法表示此游戏所有可能出现的结果；(2)此游戏规则对小明、小芳公平吗？试说明理由．图323．(12分)一个暗箱中有大小相同的1个黑球和n个白球(记为白1、白2、…、白n)，每次从中取出一个球，取到白球得1分，取到黑球得2分，甲从暗箱中有放回地依次取出2个球，而乙从暗箱中一次性取出2个球．(1)若n＝2，分别求甲取得3分的概率和乙取得3分的概率；(请用“画树状图”或“列表”等方式给出分析过程)(2)若乙取得3分的概率小于120，则白球至少有多少个？(请直接写出结果)24．(12分)五一假期，某公司组织部分员工分别到A，B，C，D四地旅游，公司按定额购买了前往各地的车票．图4是未制作完的车票种类和数量的条形统计图，根据统计图回答下列问题：(1)若去D地的车票占全部车票的10%，求去D地车票的数量，并补全条形统计图；(2)若公司采用随机抽取的方式分发车票，每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀)，则员工小胡抽到去A地的车票的概率是多少？(3)若有一张车票，小王、小李都想要，最后决定采取抛掷一枚各面分别标有数字1，2，3，4的正四面体骰子的方法来确定，具体规则是：“每人各抛掷一次，若小王掷得着地一面的数字比小李掷得着地一面的数字小，车票给小王，否则给小李”．试用列表或画树状图的方法分析这个规则对双方是否公平．图4详解详析1．A [解析] 列表如下：3的情况有2种，∴P(两张卡片上的数字都小于3)＝26＝13.解题突破从m(m ＞2)张卡片中一次性抽出两张卡片，可以理解为先抽出一张，再从剩下的里面抽出一张，即属于“抽出不放回”试验问题，可见为两步试验问题，可用列表法求解．2．B [解析] 列表如下：共有9所以其概率为39＝13.故选B . 3．C [解析] 画树状图如下：一共有6种情况，“一红一黄”的情况有2种，∴P(一红一黄)＝26＝13.故选C .4．C [解析] 画树状图如下：共有6种等可能的结果，其中恰能组成分式的结果数为4种， 所以恰能组成分式的概率为46＝23.5．B [解析] 列表如下：共有613L 发光的概率是26＝13.故选B .6．D [解析] 列表如下：∵共有指针都指向2的概率为116.故选D .7．B [解析] 观察表格得：通过多次摸球试验后发现摸到黄球的频率稳定在0.5左右，则P(摸到黄球)＝0.5.8．B [解析] A ．一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃的概率为14，不符合题意；B .在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”的概率是13，符合题意；C .抛一个质地均匀的正六面体骰子，向上的面点数是5的概率为16，不符合题意；D .抛一枚硬币，出现反面的概率为12，不符合题意．故选B .9．C10．B [解析] 画树状图如下：∵共有36种等可能的结果，小王、小张各掷一次所确定的点P(x ，y)落在矩形内(不含矩形的边)的有15种情况，∴小王、小张各掷一次所确定的点P(x ，y)落在矩形内(不含矩形的边)的概率是1536＝512.故选B .11.49[解析] 画树状图如下：∵共有9种等可能的结果，一次摸到红球一次摸到绿球的有4种情况，∴一次摸到红球一次摸到绿球的概率是49.12.16[解析] 画树状图如下：∵共有12种等可能的结果，点落在第一象限的可能是(1，2)，(2，1)两种情形， ∴该点在第一象限的概率为212＝16. 13．公平 [解析] 两人写的数共有奇偶、偶奇、偶偶、奇奇四种情况，因此同为奇数或同为偶数的概率为24＝12，一奇一偶的概率也为24＝12，所以这个游戏对双方公平．14.15[解析] 画树状图如下：共有20种等可能的结果，其中点P(a ，b)在平面直角坐标系中第二象限内的结果数为4，所以点P(a ，b)在平面直角坐标系中第二象限内的概率＝420＝15.15．216.17 [解析] 依题意知m ＝0，±1，n ＝0，±1，±2，±3，∴有序整数(m ，n)共有3×7＝21(种)．∵方程x 2＋nx ＋m ＝0有两个相等的实数根，∴Δ＝n 2－4m ＝0，有(0，0)，(1，2)，(1，－2)三种可能，∴关于x 的方程x 2＋nx ＋m ＝0有两个相等实数根的概率是321＝17.17．[解析] (1)由不透明的文具袋中装有规格相同的红、黑两种颜色的通用中性笔芯，其中红色的有3支，黑色的有2支，直接利用概率公式求解即可求得答案；(2)首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好抽到的都是黑色笔芯的情况，再利用概率公式即可求得答案．解：(1)∵不透明的文具袋中装有规格相同的红、黑两种颜色的通用中性笔芯，其中红色的有3支，黑色的有2支，∴恰好抽到的是红色笔芯的概率为33＋2＝35.(2)画树状图如下：∵共有20种等可能的结果，恰好抽到的都是黑色笔芯的只有2种情况， ∴恰好抽到的都是黑色笔芯的概率为220＝110.18．解：(1)由题意可知，50次摸球试验活动中，出现红球20次，黄球30次， 所以红球所占百分比为20÷50×100%＝40%，黄球所占百分比为30÷50×100%＝60%. 答：盒中红球占总球数的40%，黄球占总球数的60%.(2)由题意可知，50次摸球试验活动中，出现有记号的球4次，所以总球数为8÷450＝100，所以红球有40%×100＝40(个)．答：盒中有红球40个． 19．解：用树状图分析如下：∵一共有6种等可能的情况，甲、乙两人相邻的有4种情况， ∴甲、乙两人相邻的概率是46＝23.20．解：(1)设买圆珠笔x 支，铅笔y 支， 则2x ＋y ＝15，所以y ＝15－2x. 当x ＝1时，y ＝13； 当x ＝2时，y ＝11； 当x ＝3时，y ＝9； 当x ＝4时，y ＝7； 当x ＝5时，y ＝5； 当x ＝6时，y ＝3； 当x ＝7时，y ＝1. 所以共有7种购买方案．(2)在这7种方案中，买到的圆珠笔与铅笔数量相等的只有1种，所以P(买到的圆珠笔与铅笔数量相等)＝17.21．解：(1)∵第一道单选题有3个选项，∴如果小明第一题不使用“求助”，那么小明答对第一道题的概率是13.故答案为：13.(2)分别用A ，B ，C 表示第一道单选题的3个选项，a ，b ，c 表示第二道单选题剩下的3个选项．画树状图如下：∵共有9种等可能的结果，小明顺利通关的只有1种情况， ∴小明顺利通关的概率为19.(3)∵如果在第一题使用“求助”，小明顺利通关的概率为18，如果在第二题使用“求助”，小明顺利通关的概率为19，∴建议小明在第一题使用“求助”． 解题突破(1)直接利用概率公式求解；(2)此问属于两次试验概率问题，注意第二次试验时只有三种可能；(3)比较第一题使用“求助”小明顺利通关的概率与第二题使用“求助”小明顺利通关的概率的大小，把“求助”用在通关概率大的那一次上．22．解：(1)用列表法将所有可能出现的结果表示如下：(2)不公平．理由：上面等可能出现的12种结果中，有3种情况能配成紫色，故配成紫色的概率是312，即小芳获胜的概率是14；但只有2种情况能配成绿色，故配成绿色的概率是212，即小明获胜的概率是16.而14＞16，故小芳获胜的可能性大，这个“配色”游戏规则对双方是不公平的．23．解：(1)得3分，即为取到黑球、白球各1个． 甲从暗箱中有放回地依次取出2个球，画树状图如下：∴甲取得3分的概率为49；乙从暗箱中一次性取出2个球，画树状图如下：∴乙取得3分的概率＝46＝23.(2)若乙取得3分的概率小于120，则2n ＋1＜120，∴n ＞39，∴白球至少有40个． 24．解：(1)设去D 地的车票有x 张，则x ＝(x ＋20＋40＋30)×10%，解得x ＝10. 答：去D 地的车票有10张． 补全条形统计图如图所示．(2)小胡抽到去A 地的车票的概率为2020＋40＋30＋10＝15.答：员工小胡抽到去A 地的车票的概率是15.(3)列表如下：小的有6种：(1，2)，(1，3)，(1，4)，(2，3)，(2，4)，(3，4)，∴小王掷得着地一面的数字比小李掷得的着地一面数字小的概率为616＝38.则小王掷得着地一面的数字不小于小李掷得的着地一面数字的概率为1－38＝58.∵58≠38，∴这个规则对双方不公平．。
第三章 单元测试卷
第三章 指数运算与指数函数第三章 单元测试卷第Ⅰ部分 选择题(共60分)一、单选题(本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.☉%#682@1@￥%☉(2020·枣庄高一月考)√4-2√3+√(1-√3)33+√(1-√3)44=( )。
A.√3-1 B.1-√3 C.3-3√3 D.3√3-3 答案：A解析：由于√4-2√3=√(√3-1)2=|√3-1|=√3-1,√(1-√3)33=1-√3,√(1-√3)44=|1-√3|=√3-1,故原式=(√3-1)+(1-√3)+(√3-1)=√3-1。
故选A 。
2.☉%@00##4#3%☉(2020·郑州高一质量检测)已知3a =5b=15,则a ,b 不可能满足的关系是( )。
A.a +b >4 B.ab >4C.(a -1)2+(b -1)2>2 D.a 2+b 2<8 答案：D解析：由3a=5b=15,可得(3a )b=15b,(5b )a =15a,∴3ab=15b,5ab=15a,∴3ab·5ab=15a·15b=15a +b,即15ab=15a +b,∴a +b =ab ,又a ,b 为不相等的正数,∴a +b >2√ab ,∴ab >2√ab ,即ab >4,故A ,B 正确;∵(a -1)2+(b -1)2>2等价于a 2+b 2>2(a +b ),又a 2+b 2>2ab ,且a +b =ab ,故C 正确;a 2+b 2>2ab ,ab >4,∴a 2+b 2>8,故D 错误。
故选D 。
3.☉%@0#538#*%☉(2020·济宁二中月考)下列函数:①y =4x 2;②y =6x ;③y =32x ;④y =3·2x ;⑤y =2x+1(以上各函数定义域为x ∈N *)。
【名校习题】人教版七年级上册数学单元知识检测题：第三章一元一次方程(含答案).doc
人教版七年级上册第三章一元一次方程单元测试卷(1)一、选择题1.下列方程是一元一次方程的是( )A.x2+x=2B.5x+2=5x+3C.x-9=3D.=2答案 C2.方程x-2=2-x的解是( )A.x=1B.x=-1C.x=2D.x=0答案 C3.如果5(x-2)与x-3互为相反数,那么x的值是( )A.7B.C.D.答案 B4.下列运用等式的性质,变形不正确的是( )A.若x=y,则x+5=y+5B.若a=b,则ac=bcC.若=,则a=bD.若x=y,则=答案 D5.如图所示,两个天平都平衡,则3个“球体”的重量等于个正方体的重量.( )A.3B.4C.5D.6答案 C6.下列变形正确的是( )A.由7x=4x-3移项,得7x-4x=3B.由-=1+-去分母,得2(2x-1)=1+3(x-3)C.由2(2x-1)-3(x-3)=1去括号,得4x-2-3x-9=1D.由2(x+1)=x+7去括号、移项、合并同类项,得x=5答案 D7.某品牌自行车1月份销售量为100辆,每辆车售价相同.2月份的销售量比1月份增加10%,每辆车的售价比1月份降低了80元,2月份与1月份的销售总额相同,则1月份的售价为( )A.880元B.800元C.720元D.1080元答案 A8.解方程4(x-1)-x=2,步骤如下:①去括号,得4x-4-x=2x+1.②移项,得4x+x-2x=1+4.③合并同类项,得3x=5.④系数化为1,得x=.经检验知,x=不是原方程的解,说明解题的四个步骤中有错误,其中做错的一步是( ) A.① B.② C.③ D.④答案 B9.服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利60元,则这款服装每件的标价比进价多( )A.60元B.80元C.120元D.180元答案 C10.陈老师打算购买气球装扮学校“六一儿童节”活动会场,气球的种类有笑脸和爱心两种.两种气球的价格不同,但同一种气球的价格相同.由于会场布置的需要,购买时应以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )A.19元B.18元C.16元D.15元答案 C11.一件夹克衫先按成本提高50%标价，再以8折（标价的80%）出售，结果获利28元，若设这件夹克衫的成本是x元，根据题意，可得到的方程是A．（1+50%）x×80%=x–28 B．（1+50%）x×80%=x+28C．（1+50%x）×80%=x–28 D．（1+50%x）×80%=x+28答案B12.七年级一班的马虎同学在解关于x的方程3a–x=13时，误将–x看成+x，得方程的解x=–2，则原方程正确的解为 A ．–2B ．2C ．–D ．答案B二、填空题13.一个数x 的2倍减去7,得36,列方程为 . 答案 2x-7=36 14.如果方程x 2m-1-3=0是关于x 的一元一次方程,那么方程的解为 .答案 x=315.如果方程6x+3a=22与方程3x+5=11的解相同,那么a= . 答案16.写出一个解为x=2的一元一次方程(只写一个即可) . 答案 x-2=0(答案不唯一)17.某市为提倡节约用水,采取分段收费.若每户每月用水不超过20 m 3,每立方米收费2元;若用水超过20 m 3,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水 m 3. 答案 2818.相邻的5个自然数的和为45,则这5个自然数分别为 . 答案 7、8、9、10、1119.用一根长18米的铁丝围成一个长是宽的2倍的长方形框架,其面积为 平方米. 答案 18 20.小明解方程-=-3,在去分母时,方程右边的-3忘记乘6,因而求出的解为x=2,则原方程正确的解为 . 答案 x=-13三、解答题21.解方程. (1)3x+1=9-x;1212(2)-=1-.答案(1)x=2.(2)x=.22.某种商品因换季准备打折出售,如果按标价的7.5折出售将赔25元,而按标价的9折出售将赚20元,问这种商品的标价是多少元?答案设该商品的标价为x元.根据题意得75%x+25=90%x-20,解得x=300.答:这种商品的标价为300元.23.小亮和他哥哥在离家2千米的同一所学校上学,小亮的哥哥以4千米/小时的速度步行去学校,小亮因找不到数学课本耽误了15分钟,然后骑自行车以12千米/小时的速度去追他哥哥.请问到校前小亮能追上他哥哥吗?若能,则小亮追上他哥哥时,他们距学校多远?若不能,请说明理由.答案 能追上.理由如下:设小亮走了x 个小时才追上他哥哥, 根据题意得4×+4x=12x,解得x=,即小亮走了个小时才追上他哥哥. 小亮追上他哥哥时走了12×=1.5(千米), 又因为1.5<2,所以到校前小亮能追上他哥哥. 此时他们距学校2-1.5=0.5(千米).24.贡江新区位于贡江南岸,由长征出发地体验区、文教体育综合区、贡江新城三大板块组成,与贡江北岸老城区相呼应,构建成“一江两岸”的城市新格局.为建设市民河堤漫步休闲通道,贡江新区现有一段长为180米的河堤整治任务由A 、B 两个工程队先后接力完成,A 工程队每天整治12米,B 工程队每天整治8米,共用时20天.(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程如下: 甲:12x+8(20-x)=180;乙: + -=20. 根据甲、乙人教版七年级数学上册第三章一元一次方程单元测试（含答案）一、单选题1．下列方程是一元一次方程的是（ ） A.4x+2y=3 B.y+5=0 C.x 2=2x ﹣l D.1y+y=2 2．在下列方程中①221x x +=，②139x x -=，③102x =，④123233-=，⑤2133y y -=+是一元一次方程的有（ ）个．A ．1B ．2C ．3D ．43．下列解方程过程中，变形正确的是（ ） A.由5x ﹣1=3，得5x=3﹣1 B.由，得C.由，得D.由，得2x ﹣3x=14．下列选项中，移项正确的是( ) A ．方程8x 6-=变形为x 68-=+ B ．方程5x 4x 8=+变形为5x 4x 8-= C ．方程3x 2x 5=+变形为3x 2x 5-=- D ．方程32x x 7-=+变形为x 2x 73-=+ 5．方程23x +=的解是（ ） A ．1x =；B ．1x =-；C ．3x =；D ．3x =-.6．若代数式32x +与代数式510x -的值互为相反数，则x 的值为（ ） A.1B.0C.-1D.27．如果关于 的方程 － 无解，那么 满足（ ）. A. B.C. D.任意实数8．方程去分母后正确的结果是( )A. B. C.D.9．若 是方程 的解，则代数式 的值为（ ） A.-5B.-1C.1D.510．有一道数学的题目如图所示，两个天平都平衡，则三个球体的重量等于几个正方体的重量？（ ）A.2B.3C.4D.511．一艘船在静水中的速度为25千米/时，水流速度为5千米/时，这艘船从甲码头到乙码头顺流航行，再返回到甲码头共用了6个小时，求甲、乙两个码头的距离，可设甲、乙两个码头的距离是x 千米，则列方程正确的是（ ） A.()()254254x x +=- B.2556x x += C.6255x x += D.6255255x x+=+- 12．甲、乙两人去买东西，他们所带钱数的和为120元，甲花去30元，乙花去20元，两人余下的钱数之比为3：2，则甲、乙两人所带的钱数分别是 （ ） A ．70,49 B ．65,48C ．72,48D ．73,47二、填空题13．一个长方形周长是44cm ，长比宽的3倍少10cm ，则这个长方形的面积是______． 14．方程320x -+=的解为________．15．已知a 、b 、c 、d 为有理数，现规定一种新运算a b ad bc c d=-，如131(5)321125=⨯--⨯=--，那么当2422(1)7x =+时，则x 的值为_____.16．今有浓度分别为 3%、8%、11%的甲、乙、丙三种盐水 50 千克、70 千克、60 千克，现要用甲、乙、丙这三种盐水配制浓度为 7%的盐水 100 千克，则丙种盐水最多可用_________千克 三、解答题17.解方程：（1）8x-2=0；(2)2x-5=4x+3 18．解方程：（1）51312423-+--=x x x ；（2）30.4110.50.3---=x x 19．已知A ＝2x 2+mx ﹣m ，B ＝3x 2﹣mx +m ． （1）求A ﹣B ；（2）如果3A ﹣2B +C ＝0，那么C 的表达式是什么？（3）在（2）的条件下，若x ＝4是方程C ＝20x +5m 的解，求m 的值．20．如图，在数轴上点O 为原点，A 点表示数a ，B 点表示数b ，且a 、b 满足|a+2|+|b-4|=0；(1)点A 表示的数为 ；点B 表示的数为 ；(2)如果M 、N 为数轴上两个动点.点M 从点A 出发，速度为每秒1个单位长度；点N 从点B出发，速度为点A的3倍，它们同时向左运动.①当运动2秒时，点M、N对应的数分别是、.②当运动t秒时，点M、N对应的数分别是、.(用含t的式子表示)③运动多少秒时，点M、N、O中恰有一个点为另外两个点所连线段的中点？(可以直接写出答案)21．某公司要生产若干件新产品，需要加工后才能投放市场．现有红星和巨星两个工厂都想加工这批产品，已知红星厂单独加工这批产品比巨星厂单独加工多用20天，红星厂每天可以加工16个，巨星厂每天可以加工24个．公司需付红星厂每天加工费80元，巨星厂每天加工费120元．(1)这家公司要生产多少件新产品？(2)公司制定产品加工方案如下：可由每个厂家单独完成，也可由两个厂共同合作完成．在加工过程中，公司需派一名工程师每天到厂家进行技术指导，并负担每天的补助费5元．请你帮公司选择一种既省钱又省时的加工方案人教版七年级上册数学第三章一元一次方程单元测试题(含答案）一、选择题1.在方程，，中一元一次方程的个数为（）A. 1个B. 2个C. 3个D. 4个2.方程3x﹣7=5的解是（）A. x=2B. x=3C. x=4D. x=53.如果a+1与互为相反数，那么a=( )A. B. 10 C. － D. －104.若x=1是关于x的方程ax+1=2的解，则a是（）A. 1B. 2C. -1D. -25.设P=2y-2，Q=2y+3，有2P-Q=1，则y的值是（）A. 0.4B. 4C. -0.4D. -2.56.某车间有技术工85人，平均每天每人可加工甲种部件16个或乙种部件10个，2个甲种部件和3个乙种部件配一套，问加工甲、乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套？设安排x名工人加工甲部件，可列出方程为（）A. 3×16x=2×10（85－x）B. 2×16x=3×10（85－x）C. 8×16x=5×10（85－x）D. 5×16x=8×10（85－x）7.下列方程中，解为x=2的方程是（）A. 3x-2=3B. -x+6=2xC. 4-2(x-1)=1D.8.解方程时，去分母、去括号后，正确结果是（）A. 4x+1﹣10x+1=1B. 4x+2﹣10x﹣1=1C. 4x+2﹣10x﹣1=6D. 4x+2﹣10x+1=69.下列说法正确的有（）（1）若ac=bc，则a=b；（2）若，则a=﹣b；（3）若x2=y2，则﹣4ax2=﹣4by2；（4）若方程2x+5a=11﹣x与6x+3a=22的解相同，则a的值为0．A. 4B. 3C. 2D. 110.某书店把一本新书按标价的九折出售，仍可获利20%.若该书的进价为21元，则标价为( )A. 26元B. 27元C. 28元D. 29元二、填空题11.若（a﹣1）x|a|+3=6是关于x的一元一次方程，则a=________．12.写出一个以为解的一元一次方程________．13.已知x=3是方程ax﹣6=a+10的解，则a=________.14.在数轴上与表示-2的点相距5个单位长度的点所表示的数是________．15.若“★”是新规定的某种运算符号，设a★b=ab+a﹣b，则2★n=﹣8，则n=________．16.若关于x的方程3x﹣7=2x+a的解与方程4x+3=7的解相同，则a的值为 ________17.代数式的值是1,则k = ________.18.小明在做作业时，不小心把方程中的一个常数污染了看不清楚，被污染的方程为：■，怎么办？小明想了想，便翻看了书后的答案，此方程的解为，于是，他很快知道了这个常数，他补出的这个常数是________．19.某服装厂专门安排160名工人手工缝制衬衣，每件衬衣由2个衣袖、1个衣身组成，如果每人每天能够缝制衣袖10个或衣身15个，那么应安排________名工人缝制衣袖，才能使每天缝制出的衣袖、衣身正好配套。
2020届人教版高中地理选修1单元测试题：第三章 地球的演化和地表形态的变化(一)-含答案
第三章地球的演化和地表形态的变化同步练习(一)一、选择题。
（60分，每小题2分）1. 地壳垂直运动的结果是（）A. 常形成巨大的褶皱山系B. 地势的高低起伏和海陆变迁C. 发生地震、火山喷发D. 岩层发生上下运动和弯曲变形2. 我国华山的地质成因是（）A. 向斜成山B. 背斜成山C. 断层形成的块状山地D. 褶皱形成的高地3．地貌的形成与流水侵蚀作用有关的是（）A．长江三峡 B．戈壁和裸岩荒漠 C．河口三角洲 D. 沙丘、沙垄2003年7月21日，我国云南省楚雄彝族自治州大姚县发生6.2级地震，地震发生后，大姚县又发生降雨，造成多处山体滑坡和泥石流，给地震救援带来困难。
据此回答4—6题4. 对云南省地震的正确描述是（）A. 大姚县地震是20世纪初全球破坏性最大的地震灾害之一B. 6．2级地震释放的能量约是5级地震释放能量的60倍C. 大姚县地震的发生与云南的地质构造密切有关D. 由于地震发生在地球内部，人类是无法做出预报的5. 地震引发的滑坡是（）A. 山区爆发的特殊洪流，破坏力极强B. 斜坡上的岩体或土体，在重力作用下沿一定的滑动面整体下滑的现象C. 人类对植被的破坏，是滑坡日趋频繁的原因D. 大规模的工程活动是造成滑坡现象的主要原因6. 我国的地震、滑坡和泥石流等地质灾害发生频繁，其中楚雄地区处于（）A. 东部沿海地区B. 东北地区C. 西北地区D. 川、滇、黔地区7．以外力作用为主形成的地形是（）A．吐鲁番盆地 B．黄土高原C．喜马拉雅山脉 D．青藏高原8. 关于板块构造学说的说法正确的有（）A．地球的岩石圈不是整体一块，而是分割成两个单元，即海洋板块和大陆板块B．板块漂浮在地幔之上，处在不断运动中C．在板块相撞挤压的地区形成海沟和山脉D．板块内部比较活跃，边缘比较稳定9．属于世界上两大地震带的是（）A．印度洋大洋中脊 B．环大西洋地震带C．地中海—喜马拉雅地震带 D．地中海—东非裂谷地震带10．地壳水平运动的结果是（）A．常形成巨大的褶皱山系 B．地势的高低起伏和海陆变迁C．发生地震、山崩和火山 D．岩层发生上下运动和弯曲变形11．喜马拉雅山是（）A．非洲板块与亚欧板块碰撞形成 B．亚欧板块与印度洋板块碰撞形成C．非洲板块与印度洋板块碰撞形成 D．太平洋板块与亚欧板块碰撞形成12．日本多地质灾害的根本原因是（）A．位于西北太平洋上的岛国B．位于亚洲的东部C．位于板块的生长边界 D．位于板块碰撞带上13．我国西北部城镇分散的主要原因是（）A．平原面积小 B．水源供给不足C．交通便利 D．山地面积广大14. 冲积扇常常形成于：（）A. 河源地带B. 滨海地带C. 山麓地带D. 河流中下游15．关于板块构造学说的叙述，正确的是（）Ａ．板块的生长边界是海岭和海沟Ｂ．板块的消亡边界是造山带和裂谷Ｃ．冰岛和红海均处于生长边界上Ｄ．智利多地震是因为它处在板块内部16．板块构造学说认为，大西洋的形成是由于（）Ａ．板块挤压Ｂ．板块俯冲Ｃ．板块张裂Ｄ．板块碰撞17．板块构造学说、大陆漂移学说、海底扩张学说都认为（）Ａ．板块作水平运动Ｂ．大洋地壳、大陆地壳都作垂直运动Ｃ．可解释火山、地震的形成Ｄ．海底岩石年龄很轻，不超过2亿年18．图示褶曲中，岩层的新老关系为（）A．自西向东由老到新B．自东向西由老到新C．自中心向两侧由老到新D．自中心向两侧由新到老19．图示山岭是（）A．沿顶部裂隙侵蚀而成的背斜山B．因槽部坚实抗侵蚀而成的向斜山C．因顶部坚实抗侵蚀而成的背斜山D．沿槽部裂隙侵蚀而成的向斜山读图回答20—23题。
八年级数学上《第三章位置与坐标》单元测试题(含答案)
第三章位置与坐标第Ⅰ卷(选择题共30分)一、选择题(每题3分，共30分)1．下列关于确定一个点的位置的说法中，能具体确定点的位置的是( )A．东北方向B．东经35°10′，北纬12°C．距点A100米D．偏南40°，8000米2．若点M(x，y)满足(x＋y)2＝x2＋y2－2，则点M所在的象限是( )A．第一象限或第三象限B．第二象限或第四象限C．第一象限或第二象限D．不能确定3．如图1，△ABC与△DFE关于y轴对称，若点A的坐标为(－4，6)，则点D的坐标为( )图1A．(－4，6) B．(4，6)C．(－2，1) D．(6，2)4．若A(a，b)，B(a，d)表示两个不同的点，且a≠0，则这两个点在( )A．平行于x轴的直线上B．第一、三象限的角平分线上C．平行于y轴的直线上D．第二、四象限的角平分线上5．甲、乙两名同学用围棋子做游戏，如图2所示，现轮到黑棋下子，黑棋下一子后白棋下一子，使黑棋的5个棋子组成轴对称图形，白棋的5个棋子也组成轴对称图形，则下列下子方法不正确的是[说明：棋子的位置用数对表示，如点A在(6，3)]( )图2A．黑(3，7)，白(5，3) B．黑(4，7)，白(6，2)C．黑(2，7)，白(5，3) D．黑(3，7)，白(2，6)甲：从学校向北直走500米，再向东直走100米可到图书馆； 乙：从学校向西直走300米，再向北直走200米可到博物馆； 丙：博物馆在体育馆正西方向200米处．根据三人的描述，若从图书馆出发，其终点是体育馆，则下列描述正确的是( )A ．向南直走300米，再向西直走200米B ．向南直走300米，再向西直走600米C ．向南直走700米，再向西直走200米D ．向南直走700米，再向西直走600米7．若点P(－m ，3)与点Q(－5，n)关于y 轴对称，则m ，n 的值分别为( )A ．－5，3B ．5，3C ．5，－3D ．－3，58．有甲、乙、丙三个人，他们所处的位置不同，甲说：“以我为坐标原点，乙的位置是(2，3)．”丙说：“以我为坐标原点，乙的位置是(－3，－2)．”则以乙为坐标原点，甲、丙的坐标分别是(已知三人所建立的直角坐标系中x 轴、y 轴的方向相同，且单位长度一致)( )A ．(－3，－2)，(2，－3)B ．(－3，2)，(2，3)C ．(－2，－3)，(3，2)D ．(－2，－3)，(－2，－3)9．已知点A(1，0)，B(0，2)，点P 在x 轴上，且△PAB 的面积为5，则点P 的坐标为( )图3A ．(－4，0)B ．(6，0)C ．(－4，0)或(6，0)D ．无法确定10．如图3所示，在平面直角坐标系中，半径均为1个单位长度的半圆O 1，O 2，O 3，…组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒π2个单位长度，则第2019秒时，点P 的坐标是( )A ．(2019，0)B ．(2019，－1)C ．(2019，1)D ．(2018，0)请将选择题答案填入下表：二、填空题(每题3分，共18分)11．若m＞0，n＜0，则点P(m，n)关于x轴的对称点在第________象限．12．已知A(2x－1，3x＋2)是第一、三象限角平分线上的点，则点A的坐标是________．13．在同一直角坐标系中，一同学误将点A的横、纵坐标的次序颠倒，写成A(a，b)；另一同学误将点B的坐标写成关于y轴对称的点的坐标，写成B(－b，－a)，则A，B两点原来的位置关系是__________．14．在平面直角坐标系中，已知点A(－3，0)，B(3，0)，点C在坐标轴上，且AC＋BC＝10，写出满足条件的所有点C的坐标：________．15．已知等边三角形ABC的两个顶点的坐标分别为A(－4，0)，B(2，0)，则点C的坐标为____________，△ABC的面积为________．16．如图4是某同学在课下设计的一款软件，蓝精灵从点O第一跳落到A1(1，0)，第二跳落到A2(1，2)，第三跳落到A3(4，2)，第四跳落到A4(4，6)，第五跳落到A5________，到达A2n后，要向________方向跳________个单位长度落到A2n＋1.图4三、解答题(共52分)17．(6分)如图5，△ABC中，AB＝AC＝13，BC＝24，请你建立适当的平面直角坐标系，并直接写出A，B，C三点的坐标．图518．(6分)(1)若点M(5＋a，a－3)在第二、四象限角平分线上，求a的值；(2)已知点N的坐标为(2－a，3a＋6)，且点N到两坐标轴的距离相等，求点N的坐标．19．(6分)在平面直角坐标系中，将坐标是(－5，0)，(－4，－2)，(－3，0)，(－2，－2)，(－1，0)的点用线段依次连接起来形成一个图案Ⅰ.(1)作出该图案关于y轴对称的图案Ⅱ；(2)将所得到的图案Ⅱ沿x轴向上翻折180°后得到一个新图案Ⅲ，试写出它的各顶点的坐标；(3)观察图案Ⅰ与图案Ⅲ，比较各顶点的坐标和图案位置，你能得到什么结论？20．(6分)已知在平面直角坐标系中有A(－2，1)，B(3，1)，C(2，3)三点．请回答下列问题：(1)在坐标系内描出点A，B，C的位置．(2)求出以A，B，C三点为顶点的三角形的面积．(3)在y轴上是否存在点P，使以A，B，P三点为顶点的三角形的面积为10？若存在，请直接写出点P 的坐标；若不存在，请说明理由．图621．(6分)已知点P(2m＋4，m－1)．根据下列条件，求出点P的坐标．(1)点P在y轴上；(2)点P在x轴上；(3)点P的纵坐标比横坐标大3；(4)点P在过点A(2，－3)且与x轴平行的直线上．22.(6分)如图7，四边形OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA＝10，OC＝8，在OC边上取一点D，若将纸片沿AD翻折，使点O落在BC边上的点E处，求D，E两点的坐标．图723．(8分)如图8，正方形ABFG和正方形CDEF的顶点在边长为1的正方形网格的格点上．(1)建立平面直角坐标系，使点B，C的坐标分别为(0，0)和(5，0)，并写出点A，D，E，F，G的坐标；(2)连接BE和CG相交于点H，BE和CG相等吗？并计算∠BHC的度数．图824.(8分)如图9，在平面直角坐标系中，直线l 过点M(3，0)且平行于y 轴．(1)如果△ABC 三个顶点的坐标分别是A(－2，0)，B(－1，0)，C(－1，2)，△ABC 关于y 轴的对称图形是△A 1B 1C 1，△A 1B 1C 1关于直线l 的对称图形是△A 2B 2C 2，写出△A 2B 2C 2的三个顶点的坐标；(2)如果点P 的坐标是(－a ，0)，其中a ＞0，点P 关于y 轴的对称点是P 1，点P 1关于直线l 的对称点是P 2，求PP 2的长．图91．B 2．B 3．B 4．C 5．C 6．A 7．A 8.C 9．C 10．B 11.一 12.(－7，－7) 13．关于x 轴对称14．(－5，0)，(5，0)，(0，4)，(0，－4) 15．(－1，3 3)或(－1，－3 3) 9 3[解析] 当点C 在第二象限时，作CH ⊥AB 于点H .因为A (－4，0)，B (2，0)，所以AB ＝6.因为△ABC 是等边三角形，所以AH ＝BH ＝3.由勾股定理得CH ＝3 3，所以C (－1，3 3)；同理，当点C 在第三象限时，C (－1，－3 3)．所以△ABC 的面积为12×6×3 3＝9 3.第三跳落到A3(4，2)，第四跳落到A4(4，6)，所以蓝精灵先向正东跳动，再向正北跳动，每次跳动的距离为前一次的距离加1，即可求出．第五跳落到A5(9，6)．到达A2n后，要向正东方向跳(2n＋1)个单位长度落到A2n＋1.17．解：答案不唯一，如以BC所在直线为x轴，过点B作BC的垂线为y轴建立平面直角坐标系，由图可知，点A(12，5)，B(0，0)，C(24，0)．18．解：(1)由题意可得5＋a＋a－3＝0，解得a＝－1.(2)由题意可得|2－a|＝|3a＋6|，即2－a＝3a＋6或2－a＝－(3a＋6)，解得a＝－1或a＝－4，所以点N的坐标为(3，3)或(6，－6)．19．解：图案Ⅰ如图．(1)作出图案Ⅱ如图．(2)作出图案Ⅲ如图．图案Ⅲ各个顶点的坐标分别为(5，0)，(4，2)，(3，0)，(2，2)，(1，0)．(3)观察图案Ⅰ与图案Ⅲ，不难发现：①从各顶点坐标看，横、纵坐标均互为相反数；②从图案的位置上看，图案Ⅰ在第三象限，图案Ⅲ在第一象限，二者关于坐标原点对称．20．解：(1)描点如图．(2)如图，依题意，得AB∥x轴，且AB＝3－(－2)＝5，1(3)存在．因为AB＝5，S△ABP＝10，所以点P到AB的距离为4.又因为点P在y轴上，所以点P的坐标为(0，5)或(0，－3)．21．解：(1)由题意，得2m＋4＝0，解得m＝－2，则m－1＝－3，所以点P的坐标为(0，－3)．(2)由题意，得m－1＝0，解得m＝1，则2m＋4＝6，所以点P的坐标为(6，0)．(3)由题意，得m－1＝(2m＋4)＋3，解得m＝－8，则2m＋4＝－12，m－1＝－9, 所以点P的坐标为(－12，－9)．(4)由题意，得m－1＝－3，解得m＝－2，则2m＋4＝0，所以点P的坐标为(0，－3)．22．解：由题意，可知折痕AD所在的直线是四边形OAED的对称轴．在Rt△ABE中，AE＝OA＝10，AB ＝8，所以BE＝AE2－AB2＝102－82＝6，所以CE＝4，所以E(4，8)．在Rt△DCE中，DC2＋CE2＝DE2，又DE＝OD，所以(8－OD)2＋42＝OD2，所以OD＝5，所以D(0，5)．23．解：(1)按已知条件建立平面直角坐标系(如图)，A(－3，4)，D(8，1)，E(7，4)，F(4，3)，G(1，7)．(2)连接BE和CG相交于点H，由题意，得BE＝72＋42＝65，CG＝72＋42＝65，所以BE＝CG.借助全等及三角形内角和等性质可得∠BHC的度数：∠BHC＝90°.24．解：(1)△A2B2C2的三个顶点的坐标分别是A2(4，0)，B2(5，0)，C2(5，2)．(2)①如图①，当0＜a≤3时，因为点P与点P1关于y轴对称，P(－a，0)，所以P1(a，0)．因为点P 1与点P 2关于直线x ＝3对称，设P 2(x ，0)，可得x ＋a2＝3，即x ＝6－a ，所以P 2(6－a ，0)，则PP 2＝6－a －(－a )＝6－a ＋a ＝6.②如图②，当a ＞3时，因为点P 与点P 1关于y 轴对称，P (－a ，0)，所以P 1(a ，0)．因为点P 1与点P 2关于直线x ＝3对称，设P 2(x ，0)，可得x ＋a2＝3，即x ＝6－a ，所以P 2(6－a ，0)，则PP 2＝6－a －(－a )＝6－a ＋a ＝6.综上所述，PP 2的长为6.。
选修2-1空间向量单元测试题(一)
第三章 单元质量评估(一)时限：120分钟满分：150分第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的)1．在空间四边形ABCD 中，连接AC 、BD ，若△BCD 是正三角形，且E 为其中心，则AB →＋12BC →－32DE →－AD →的化简结果为( )A.AB → B ．2BD → C ．0D ．2DE→ 解析：如图，F 是BC 的中点，E 是DF 的三等分点，∴32DE →＝DF →.∵12BC →＝BF →，则AB →＋12BC →－32DE →－AD →＝AB →＋BF →－DF →－AD →＝AF →＋FD→－AD →＝AD →－AD →＝0. 答案：C2．在以下命题中，不．正确的个数为( ) ①|a |－|b |＝|a ＋b |是a ，b 共线的充要条件；②若a ∥b ，则存在唯一的实数λ，使a ＝λb ；③对空间任意一点O 和不共线的三点A ，B ，C ，若OP →＝ 2OA→－2OB →－OC →，则P ，A ，B ，C 四点共面； ④若{a ，b ，c }为空间的一个基底，则{a ＋b ，b ＋c ，c ＋a }构成空间的另一个基底；⑤|(a ·b )·c |＝|a |·|b |·|c |. A ．2 B ．3 C ．4D ．5解析：①|a |－|b |＝|a ＋b |⇒a 与b 的夹角为π，故是充分不必要条件，故不正确；②b 需为非零向量，故不正确；③因为2－2－1≠1，由共面向量定理知，不正确；④由基底的定义知正确；⑤由向量的数量积的性质知，不正确．答案：C3．已知A 、B 、C 、D 为四个不同点，且AB →＋BC →＋CD →＋DA →＝0，则( )A ．A 、B 、C 、D 四点必共面B ．A 、B 、C 、D 四点构成一个空间四边形 C ．A 、B 、C 、D 四点必共线D ．A 、B 、C 、D 四点的位置无法确定解析：共线、共面和构成一个空间四边形三种情况都可能出现，故选D.答案：D4．如图，在四面体ABCD 中，已知AB→＝b ，AD →＝a ，AC →＝c ，BE →＝12EC →，则DE→＝( )A ．－a ＋23b ＋13cB ．a ＋23b ＋13c C ．a －23b ＋13c D.23a －b ＋13c解析：DE →＝DA →＋AB →＋BE →＝DA →＋AB →＋13(AC →－AB →)＝－a ＋23b ＋13c ，故选A.答案：A5．已知向量a ＝(1，x,1)，b ＝(2,1，－1)，a ·b >0，则函数y ＝x 2＋4x －1的值域是( )A ．(－∞，3)B ．(－∞，－3)C ．(－4，＋∞)D ．(－∞，－4)解析：由a ·b >0，得2＋x －1>0，解得x >－1.而函数y ＝x 2＋4x －1在(－1，＋∞)上是增函数，∴y >(－1)2＋4×(－1)－1，即y >－4.答案：C6．已知a ＝(－1，－5，－2)，b ＝(x,2，x ＋2)，若a ⊥b ，则x 的值为( )A ．0B ．－143C ．－6D ．±6解析：∵a ⊥b ，∴a ·b ＝(－1，－5，－2)·(x,2，x ＋2)＝－x －10－2x －4＝－3x －14＝0，∴x ＝－143，故选B.答案：B7．已知点A (－3,4,3)，O 为坐标原点，则OA 与坐标平面yOz 所成角的正切值为( )A.34B.35C.53D ．1解析：A 点在面yOz 上射影为B (0,4,3)且|OB |＝5，所以OA 与平面yOz 所成角θ满足tan θ＝|AB ||OB |＝35.答案：B8．已知a ＝(cos α，1，sin α)，b ＝(sin α，1，cos α)，则向量a ＋b 与a －b 的夹角是( )A ．90°B ．60°C ．30°D ．0°解析：(a ＋b )·(a －b )＝a 2－b 2＝(cos 2α＋sin 2α＋1)－(sin 2α＋1＋cos 2α)＝0，∴(a ＋b )⊥(a －b )． 答案：A9．如图所示，直三棱柱ABC —A 1B 1C 1中，AA 1＝AB ＝AC ，AB ⊥AC ，M 是CC 1的中点，Q 是BC 的中点，P 是A 1B 1的中点，则直线PQ 与AM 所成的角为( )A.π6B.π4C.π3D.π2解析：以A 为坐标原点，AB 、AC 、AA 1所在直线为x 、y 、z 轴建立如图所示的空间直角坐标系，设AA 1＝AB ＝AC ＝2，则AM →＝(0,2,1)，Q (1,1,0)，P (1,0,2)，QP →＝(0，－1,2)，所以QP →·AM →＝0，所以QP 与AM 所成角为π2.答案：D10．已知A (1,1,1)，B (2,2,2)，C (3,2,4)，则△ABC 的面积为( ) A. 3 B ．2 3 C. 6D.62解析：∵A (1,1,1)，B (2,2,2)，C (3,2,4)， ∴AB→＝(1,1,1)，AC →＝(2,1,3)， ∴cos 〈AB →，AC →〉＝AB →·AC →|AB →|·|AC →|＝2＋1＋33·14＝427，∴sin 〈AB →，AC →〉＝77， ∴S △ABC ＝12|AB →|·|AC →|·sin 〈AB →，AC →〉 ＝12×3×14×77＝62，故选D. 答案：D11．如图，在棱长为1的正方体ABCD —A 1B 1C 1D 1中，E 、F 分别为棱AA 1、BB 1的中点，G 为棱A 1B 1上的一点，且A 1G ＝λ(0≤λ≤1)，则点G 到平面D 1EF 的距离为( )A. 3B.22 C.23D.55解析：∵A 1B 1∥EF ，点G 在A 1B 1上，∴点G 到平面D 1EF 的距离即为点A 1到平面D 1EF 的距离，即是点A 1到D 1E 的距离．∵D 1E ＝52，由三角形面积可得所求距离为1×1252＝55，故选D.答案：D12．如图，已知点P 为菱形ABCD 外一点，且P A ⊥平面ABCD ，P A ＝AD ＝AC ，点F 为PC 中点，则二面角C —BF —D 的正切值为( )A.36 B.34 C.33D.23 3解析：如图，连接BD ，AC ∩BD ＝O ，连接OF ，以O 为原点，OB 、OC 、OF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系，设P A ＝AD ＝AC ＝1，则BD ＝3，∴B ⎝ ⎛⎭⎪⎫32，0，0，F ⎝ ⎛⎭⎪⎫0，0，12， C ⎝ ⎛⎭⎪⎫0，12，0，D ⎝ ⎛⎭⎪⎫－32，0，0.结合图形可知，OC →＝⎝⎛⎭⎪⎫0，12，0，且OC →为平面BDF 的一个法向量，由BC →＝⎝ ⎛⎭⎪⎫－32，12，0，FB →＝⎝ ⎛⎭⎪⎫32，0，－12，可求得平面BCF 的一个法向量n ＝(1，3，3)． ∴cos 〈n ·OC →〉＝217，sin 〈n ，OC →〉＝277， ∴tan 〈n ，OC →〉＝233. 答案：D第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题，每小题5分，共20分，请把答案填写在题中横线上)13．若a ＝(1,1,0)，b ＝(－1,0,2)，则与a ＋b 同方向的单位向量是________．解析：∵a ＋b ＝(0,1,2)，∴|a ＋b |＝5，∴与a ＋b 同方向的单位向量是⎝ ⎛⎭⎪⎫0，15，25，即⎝ ⎛⎭⎪⎫0，55，255. 答案：⎝ ⎛⎭⎪⎫0，55，255 14．在长方体ABCD —A 1B 1C 1D 1中，若E 为矩形ABCD 的中心，设A 1E →＝A 1A →＋xA 1B 1→＋yA 1D 1→，则x ＝________，y ＝________.解析：∵A 1E →＝A 1A →＋AE →＝A 1A →＋12AC → ＝A 1A →＋12A 1B 1→＋12A 1D 1→，∴x ＝y ＝12. 答案：12 1215．已知a ＝(3,1,5)，b ＝(1,2，－3)，向量c 与z 轴垂直，且满足a ·c ＝9，b ·c ＝－4，则c ＝________.解析：设c ＝(x ，y ，z )，则⎩⎪⎨⎪⎧(0，0，1)·(x ，y ，z )＝z ＝0，(3，1，5)·(x ，y ，z )＝3x ＋y ＋5z ＝9，(1，2，－3)·(x ，y ，z )＝x ＋2y －3z ＝－4.解得⎩⎪⎨⎪⎧x ＝225，y ＝－215，z ＝0，所以c ＝(225，－215，0)．答案：(225，－215，0)16．如图所示，已知正四面体A —BCD 中，AE ＝14AB ，CF ＝14CD ，则直线DE 和BF 所成的角的余弦值为________．解析：ED →＝EA →＋AD →＝14BA →＋AD →， BF →＝BC →＋CF →＝BC →＋14CD →， cos 〈ED →，BF →〉＝ED →·BF →|ED →|·|BF →|＝(14BA →＋AD →)·(BC →＋14CD →)(14BA →＋AD →)2·(BC →＋14CD →)2＝413.答案：413三、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．)17．(10分)如图，在正方体ABCD —A 1B 1C 1D 1中，E 、F 分别在DB 、D 1C 上，且DE ＝D 1F ＝23a ，其中a 为正方体棱长．求证：EF ∥平面BB 1C 1C .证明：如图，建立空间直角坐标系， 则E ⎝ ⎛⎭⎪⎫a 3，a 3，0，F ⎝ ⎛⎭⎪⎫0，a 3，2a 3，故EF →＝⎝⎛⎭⎪⎫－a 3，0，2a 3.又AB →＝(0，a,0)显然为平面BB 1C 1C 的一个法向量，而AB →·EF→ ＝(0，a,0)·⎝ ⎛⎭⎪⎫－a3，0，2a 3＝0， ∴AB→⊥EF →. 又∵E ∉平面BB 1C 1C ，∴EF ∥平面BB 1C 1C .18．(12分)如图，已知点P 在正方体ABCD —A 1B 1C 1D 1的对角线BD 1上，∠PDA ＝60°.(1)求DP 与CC 1所成角的大小； (2)求DP 与平面AA 1D 1D 所成角的大小．解：如图，以D 为原点，DA 为单位长建立空间直角坐标系Dxyz .则DA →＝(1,0,0)，CC 1→＝(0,0,1)．连接BD ，B 1D 1. 在平面BB 1D 1D 中，延长DP 交B 1D 1于H . 设DH→＝(m ，m,1)(m >0)， 由已知〈DH →，DA →〉＝60°，由DH →·DA →＝|DA →||DH →|cos 〈DA →，DH →〉， 可得2m ＝2m 2＋1.解得m ＝22，所以DH →＝(22，22，1)． (1)因为cos 〈DH →，CC 1→〉＝22×0＋22×0＋1×11×2＝22， 所以〈DH →，CC 1→〉＝45°. 即DP 与CC 1所成的角为45°.(2)平面AA 1D 1D 的一个法向量是DC→＝(0,1,0)． 因为cos 〈DH →，DC →〉＝22×0＋22×1＋1×01×2＝12，所以〈DH →，DC →〉＝60°，可得DP 与平面AA 1D 1D 所成的角为30°.19．(课标全国卷Ⅰ)如图，三棱柱ABC —A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60°.(1)证明：AB⊥A1C；(2)若平面ABC⊥平面AA1B1B，AB＝CB，求直线A1C与平面BB1C1C所成角的正弦值．解：(1)取AB的中点O，连接OC，OA1，A1B.因为CA＝CB，所以OC⊥AB.由于AB＝AA1，∠BAA1＝60°，故△AA1B为等边三角形，所以OA1⊥AB.因为OC∩OA1＝O，所以AB⊥平面OA1C.又A1C⊂平面OA1C，故AB⊥A1C.(2)由(1)可知OC⊥AB，OA1⊥AB.又平面ABC ⊥平面AA 1B 1B ，交线为AB ，所以OC ⊥平面AA 1B 1B ，故OA ，OA 1，OC 两两相互垂直．以O 为坐标原点，OA→的方向为x 轴的正方向，|OA →|为单位长，建立如图所示的空间直角坐标系O －xyz .由题设知A (1,0,0)，A 1(0，3，0)，C (0,0，3)，B (－1,0,0)． 则BC →＝(1,0，3)，BB 1→＝AA 1→＝(－1，3，0)，A 1C →＝(0，－3，3)．设n ＝(x ，y ，z )是平面BB 1C 1C 的法向量， 则⎩⎨⎧n ·BC →＝0，n ·BB 1→＝0.即⎩⎨⎧x ＋3z ＝0，－x ＋3y ＝0.可取n ＝(3，1，－1)．故cos 〈n ，A 1C →〉＝n ·A 1C →|n ||A 1C →|＝－105. 所以A 1C 与平面BB 1C 1C 所成角的正弦值为105.20．(12分)如图所示，在正方体ABCD —A 1B 1C 1D 1中，E 是棱DD 1的中点．(1)求直线BE 和平面ABB 1A 1所成的角的正弦值；(2)在棱C 1D 1上是否存在一点F ，使B 1F ∥平面A 1BE ？证明你的结论．解：设正方体ABCD —A 1B 1C 1D 1的棱长为1.如图所示，以AB →，AD →，AA 1→为单位正交基底建立空间直角坐标系． (1)依题意，得B (1,0,0)，E (0,1，12)，A (0,0,0)，D (0,1,0)，所以BE →＝(－1,1，12)，AD →＝(0,1,0)．在正方体ABCD —A 1B 1C 1D 1中，因为AD ⊥平面ABB 1A 1，所以AD →是平面ABB 1A 1的一个法向量，设直线BE 与平面ABB 1A 1所成的角为θ，则sin θ＝|BE →·AD →||BE →|·|AD →|＝132×1＝23.即直线BE 和平面ABB 1A 1所成的角的正弦值为23. (2)依题意，得A 1(0,0,1)， BA 1→＝(－1,0,1)，BE →＝(－1,1，12)．设n ＝(x ，y ，z )是平面A 1BE 的一个法向量， 则由n ·BA 1→＝0，n ·BE →＝0， 得⎩⎪⎨⎪⎧－x ＋z ＝0，－x ＋y ＋12z ＝0.所以x ＝z ，y ＝12z .取z ＝2，得n ＝(2,1,2)．设F 是棱C 1D 1上的点，则F (t,1,1)(0≤t ≤1)， 又B 1(1,0,1)，所以B 1F →＝(t －1,1,0)． 而B 1F ⊄平面A 1BE ，于是B 1F ∥平面A 1BE ⇔B 1F →·n ＝0⇔(t －1,1,0)·(2,1,2)＝0⇔2(t －1)＋1＝0⇔t ＝12⇔F 为C 1D 1的中点．这说明在棱C 1D 1上存在点F (C 1D 1的中点)，使B 1F ∥平面A 1BE . 21．(12分)如图，在四棱锥P —ABCD 中，P A ⊥平面ABCD ，底面ABCD是菱形，AB＝2，∠BAD＝60°.(1)求证：BD⊥平面P AC；(2)若P A＝AB，求PB与AC所成角的余弦值；(3)当平面PBC与平面PDC垂直时，求P A的长．解：(1)证明：∵四边形ABCD是菱形，∴AC⊥BD.又∵P A⊥平面ABCD，∴P A⊥BD，∴BD⊥平面P AC.(2)设AC∩BD＝O，∵∠BAD＝60°，P A＝AB＝2，∴BO＝1，AO＝CO＝ 3.如图，以O 为坐标原点，建立空间直角坐标，则P (0，－3，2)，A (0，－3，0)，B (1,0,0)，C (0，3，0)，∴PB→＝(1，3，－2)，AC →＝(0,23，0)． 设PB 与AC 所成角为θ，则cos θ＝⎪⎪⎪⎪⎪⎪⎪⎪PB →·AC →|PB →||AC →|＝622×23＝64.(3)由(2)，知BC→＝(－1，3，0)． 设P (0，－3，t )(t >0)， 则BP→＝(－1，－3，t )． 设平面PBC 的法向量m ＝(x ，y ，z )， 则⎩⎨⎧BC →·m ＝0，BP→·m ＝0，∴⎩⎨⎧－x ＋3y ＝0，－x －3y ＋tz ＝0.令y ＝3，则x ＝3，z ＝6t .∴平面PBC 的法向量为m ＝⎝ ⎛⎭⎪⎫3，3，6t .同理，平面PDC 的法向量为n ＝⎝ ⎛⎭⎪⎫－3，3，6t .∵平面PBC ⊥平面PDC ， ∴m ·n ＝0，即－6＋36t 2＝0， 解得t ＝6，∴P A ＝ 6. 故P A 的长为 6.22．(12分)如图，在正四棱柱ABCD —A 1B 1C 1D 1中，AA 1＝2，AB ＝1，点N 是BC 的中点，点M 在CC 1上，设二面角A 1—DN —M 的大小为θ.(1)当θ＝90°时，求AM 的长； (2)当cos θ＝66时，求CM 的长．。
第3章 一元一次不等式单元测试卷（含解析）
绝密★启用前第三章一元一次不等式单元测试卷题号一二三总分得分注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第Ⅰ卷（选择题）请点击修改第I卷的文字说明评卷人得分一．选择题（共10小题，每小题3分，共30分）1．有下列数学表达式：①3＞0；②4x+5＞0；③x=3；④x2+x；⑤x≠﹣4；⑥x+2＜x+1．其中是不等式的有（）A．2个B．3个C．4个D．5个2．若a＜b，则下列不等式正确的是（）A．B．ac2＜bc2 C．﹣b＜﹣a D．b﹣a＜03．不等式的解集在数轴上表示为（）A．B．C．D．4．下列哪个选项中的不等式与不等式5x＞8+2x组成的不等式组的解集为＜x＜5（）A．x+5＜0 B．2x＞10 C．3x﹣15＜0 D．﹣x﹣5＞05．关于x的不等式组的解集为x＞1，则a的取值范围是（）A．a≥1 B．a＞1 C．a≤1 D．a＜16．不等式组的解集是x＞2，则m的取值范围是（）A．m≤2 B．m≥2 C．m≤1 D．m＞17．已知关于x的不等式3x﹣m+1＞0的最小整数解为2，则实数m的取值范围是（）A．4≤m＜7 B．4＜m＜7 C．4≤m≤7 D．4＜m≤78．已知不等式≤＜，其解集在数轴上表示正确的是（）A．B．C．D．9．一宾馆有二人间，三人间，四人间三种客房供游客租住，某旅行团20人准备同时租用这三种客房共7间，如果每个房间都住满，租房方案有（）A．4种B．3种C．2种D．1种10．已知关于x的不等式组仅有三个整数解，则a的取值范围是（）A．≤a＜1 B．≤a≤1 C．＜a≤1 D．a＜1第Ⅱ卷（非选择题）请点击修改第Ⅱ卷的文字说明评卷人得分二．填空题（共8小题，每小题3分，共24分）11．用适当的不等式表示下列关系：（1）a是非负数；（2）x与2差不足15．12．若x＞y，且（a﹣3）x＜（a﹣3）y，则a的取值范围为．13．写出一个解集为x＞1的一元一次不等式组：．14．不等式组的非负整数解有个．15．小菲受《乌鸦喝水》故事的启发，利用量筒和体积相同的小球进行了如下操作，请根据图中给出的信息，量筒中至少放入小球时有水溢出．16．若无解，则a的取值范围是．17．若不等式|x+1|+|x﹣2|＞a对任意实数x恒成立，则a的取值范围是．18．为迎接G20杭州峰会的召开，某校八年级（1）（2）班准备集体购买一种T恤衫参加一项社会活动．了解到某商店正好有这种T恤衫的促销，当购买10件时每件140元，购买数量每增加1件单价减少1元；当购买数量为60件（含60件）以上时，一律每件80元．如果八（1）（2）班共购买了100件T恤衫，由于某种原因需分两批购买，且第一批购买数量多于30件且少于60件．已知购买两批T恤衫一共花了9200元，则第一批T恤衫的购买件．评卷人得分三．解答题（共6小题，共46分）19．（6分）解下列不等式，并把它的解集在数轴上表示出来．（1）2（x+1）﹣3（x+2）＜0（2）＜﹣2．20．（6分）解不等式组，并求不等式组的所有整数解．21．（8分）若关于x的不等式组的正整数解只有2个，求a的取值范围．22．（8分）三月份学校开展了“朗读月”系列活动，活动结束后，为了表彰优秀，学校准备购买一些钢笔和笔记本作为奖品进行奖励，如果购买3支钢笔和4本笔记本需要93元；如果买2支钢笔和5本笔记本需要90元．（1）试求出每支钢笔和每本笔记本的价格是多少元？（2）学校计划用不超过500元购买两种奖品共40份，问：最多可以买几支钢笔？23．（8分）某车间加工A型和B型两种零件，平均一个工人每小时能加工7个A型零件和3个B型零件，而且3个A型与2个B型配套，就可以包装进库房，剩余不能配套的只能暂时存放起来，如果B型零件单独存放，对环境的要求远高于A型零件，已知该车间原有工人69名．（1）怎样分配工人进行工作才能保证生产出的产品及时包装运进库房；（2）后来因为工作调动，有4名工人调离了该车间，那么你认为现在应该怎样分配工人工作最合适呢？请通过计算说明你的依据．24．（10分）宁波某企业新增了一个化工项目，为了节约资源，保护环境，该企业决定购买A、B两种型号的污水处理设备共10台，具体情况如下表：A型B型价格（万元/台）1512月污水处理能力（吨/月）250200经预算，企业最多支出136万元购买设备，且要求月处理污水能力不低于2150吨．（1）该企业有哪几种购买方案？（2）哪种方案更省钱？并说明理由．参考答案与试题解析1．解：根据不等式的定义，只要有不等符号的式子就是不等式，⑥x+2＜x+1应该是x+2＞＞x+1，所以不是不等式，所以①3＞0；②4x+5＞0；⑤x≠﹣4共有3个．故选：B．2．解：A、当b＜0时，由a＜b得出＞1，故本选项错误；B、当c=0时，ac2=bc2，故本选项错误；C、∵a＜b，∴两边都乘以﹣1得：﹣a＞﹣b，故本选项正确；D、∵a＜b，∴b﹣a＞0，故本选项错误；故选：C．3．解：不等式两边同乘12得：8x﹣3（x﹣5）＞10，去括号，移项，合并同类项得：5x＞﹣5，x系数化为1，得：x＞﹣1故选：C．4．解：5x＞8+2x，解得：x＞，根据大小小大中间找可得另一个不等式的解集一定是x＜5，故选：C．5．解：∵关于x的不等式组的解集为x＞1，∴a的取值范围是：a≤1．故选：C．6．解：∵不等式组的解集是x＞2，解不等式①得x＞2，解不等式②得x＞m+1，不等式组的解集是x＞2，∴不等式，①解集是不等式组的解集，∴m+1≤2，m≤1，故选：C．7．解：解不等式3x﹣m+1＞0，得：x＞，∵不等式有最小整数解2，∴1≤＜2，解得：4≤m＜7，故选：A．8．解：根据题意得：，由①得：x≥2，由②得：x＜5，∴2≤x＜5，表示在数轴上，如图所示，故选：A．9．解：设租二人间x间，租三人间y间，则四人间客房7﹣x﹣y．依题意得：，解得：x＞1．∵2x+y=8，y＞0，7﹣x﹣y＞0，∴x=2，y=4，7﹣x﹣y=1；x=3，y=2，7﹣x﹣y=2．故有2种租房方案．故选：C．10．解：由x＞2a﹣3，由2x＞3（x﹣2）+5，解得：2a﹣3＜x≤1，由关于x的不等式组仅有三个整数：解得﹣2≤2a﹣3＜﹣1，解得≤a＜1，故选：A．11．解：（1）a是非负数则：a≥0；（2）x与2差不足15：x﹣2＜15．故答案为：x﹣2＜15．12．解：由不等号的方向改变，得a﹣3＜0，解得a＜3，故答案为：a＜3．13．解：2x﹣2＞0的解集为x＞1，x+1＞0的解集为x＞﹣1．所以解集为x＞1的不等式组可为．故答案为．14．解：解不等式2x+7＞3（x+1），得：x＜4，解不等式x﹣≤，得：x≤8，则不等式组的解集为x＜4，所以该不等式组的非负整数解为0、1、2、3这4个，故答案为：4．15．解：设放入球后量桶中水面的高度y（cm）与小球个数x（个）之间的一次函数关系式为y=kx+b，由题意，得：，解得：，即y=2x+30；由2x+30＞49，得x＞9.5，即至少放入10个小球时有水溢出．方法2：由题意可得每添加一个球，水面上升2cm，设至少放入x个小球时有水溢出，则2x+30＞49，解得x＞9.5，即至少放入10个小球时有水溢出．16．解：上面表示﹣1≤x≤2，不等式无解，即x＜a与上面的不等式没有公共部分，因而a≤﹣1a的取值范围是a≤﹣1．故答案为：a≤﹣1．17．解：∵|x+1|+|x﹣2|表示数轴上的x对应点到﹣1、2对应点的距离之和，∴它的最小值为3，∵不等式|x+1|+|x﹣2|＞a对任意的实数x恒成立，∴a＜3，故答案为：a＜3．18．解：设第一批购买x件，则第二批购买（100﹣x）件．①，解得x1=30（舍去），x2=40；②无实数解；所以：第一批购买数量为40件．故答案是：40．19．解：（1）去括号得2x+2﹣3x﹣6＜0，移项得2x﹣3x＜6﹣2，合并得﹣x＜4，系数化为1得x＞﹣4；如图，（2）去分母得4（x﹣1）＜3（x+1）﹣24，去括号得4x﹣4＜3x+3﹣24，移项得4x﹣3x＜3﹣24+4，合并得x＜﹣17．如图，20．解：原不等式组为，解不等式①，得x＞﹣2，解不等式②，得x≤1，∴原不等式组的解集为﹣2＜x≤1，所以不等式组的所有整数解为﹣1，0，1．21．解：解不等式（1）得：x＜21，解不等式（2）得：x＜﹣3a﹣2，∵不等式组只有两个正整数解，∴2＜﹣3a﹣2≤3．解得：﹣≤a＜﹣．22．解：（1）设一支钢笔需x元，一本笔记本需y元，由题意得：，解得：，答：一支钢笔需15元，一本笔记本需12元．（2）设购买钢笔的数量为x，则笔记本的数量为（40﹣x）本，由题意得：15x+12（40﹣x）≤500，解得：x≤6，答：学校最多可以购买6支钢笔．23．解：（1）设分配加工A型零件工人为x人，加工B型零件工人为（69﹣x）人，由题意得x=，解得：x=27．答：分配加工A型零件工人为27人，加工B型零件工人为42人．（2）若调走4名工人，设分配生产A型零件工人为x人，则生产B型为（65﹣x）人，由题意得x≥，解得：x≥25，∵x为整数，∴x=26，65﹣x=39．答：分配加工A型零件工人为26人，加工B型零件工人为39人．24．解：（1）设购买A型号的污水处理设备x台，则购买B型号的污水处理设备（10﹣x）台，根据题意得：，解得：3≤x≤．∵x是整数，∴x=3或4或5．当x=3时，10﹣x=7；当x=4时，10﹣x=6；当x=5时，10﹣x=5．答：有3种购买方案：第一种是购买3台A型污水处理设备，7台B型污水处理设备；第二种是购买4台A型污水处理设备，6台B型污水处理设备；第三种是购买5台A型污水处理设备，5台B型污水处理设备．（2）当x=3时，购买资金为15×3+12×7=129（万元），当x=4时，购买资金为15×4+12×6=132（万元），当x=5时，购买资金为15×5+12×5=135（万元）．∵135＞132＞129，∴为了节约资金，应购污水处理设备A型号3台，B型号7台．答：购买3台A型污水处理设备，7台B型污水处理设备更省钱．21世纪教育网–中小学教育资源及组卷应用平台21世纪教育网。
高中历史必修3第三章《古代中国的科学技术与文学艺术》单元测试(一)
203601.(浙江省嘉兴市七校2018-2019 学年期中)以下关于中国古代四大发明的描述，正确的是A.汉代蔡伦发明了中国古代最早的纸B.最初的指南仪大约出现在夏商时期C.火药的发明与古人炼丹制药的长期实践有关D. 明代王祯成功创制了木活字和铜活字2.(浙江省余姚中学2018-2019 学年期中)《武经总要》是中国第一部官修综合性军事著作。
曾公亮和丁度历五年时间编成后，由宋仁宗写序言后下令刻本发行，颁给各高级将领。
下列有关此书的说法正确的是A.介绍多种武器并记载三种火药配方B.记录了早期自动爆炸的地雷、水雷C.记载了磁石摩擦钢针制作指南针技术D.提到“风雨冥晦时，惟凭针盘而行”3.(江西省鹰潭市2018-2019 学年期末)下表为不同文献对某一事物的历史叙述。
据此能够被认定的事实是A.指南针在航海中普及较快B.指南针最早出现于宋代C.宋代中国航海业高度发达.D.宋代指南针应用于海航4.(江苏省盐城中学2019 年质检)下图生动反映了我国古代一项技术发明的工艺流程。
该技术发明A.唐朝末年开始应用于军事B.为远洋航行提供技术支持C.最终成熟归功于北宋毕升D. 曾促进西欧文化事业发展5.(河北省邢台市六校2018—2019 学年联考)司南发明之初，必须有地盘(刻有干支)配合才能使用。
而南宋罗盘不但有子午正针，还有子午丙壬间缝针，两者之间有一夹角，即磁偏角。
上述材料反映了A.传统科技催生近代科学B. 自然科学逐渐取代封建迷信C.传统科技的自我完善D. 中国古代海域不断扩大6.(江苏省南通市海安高级中学2018-2019 学年期中)史书明确记录了公元前186 年吕后当政时发生了一次日食，但现代天文学研究表明，所记日食绝不可能发生。
日食记录居然因政治上的原因而有所增减：统治者残暴，记载的日食现象就多；统治者开明，日食便很少发生。
这说明A.天象变化体现天人感应思想B.天象记录与历法制定密切相关C.天象变化体现君权神授思想D.天象记录与现实政治密切相关7.(山东省潍坊市2018-2019 学年期中)中国的印刷术用于传播古老的观念，而不是新思想；火药加固了皇帝的统治，而不是正在出现的诸民族君主的地位；指南针除郑和用于著名的远航外，并不像西方人那样用于世界范围的探险、贸易和帝国的建立。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 字母表示数 测试题
七年 班 姓名： 学号：
二、选择题（每题3分，共30分）
1、下列各式符合代数式书写规范的是（ ）。
A 、a
b
B 、a ×3
C 、1÷3x
D 、2
21n
2、下列各式中，是代数式的有（ ）个
32).6(1
15).5(1
2)4(0).3().2()1(34).1(2
=-+--<--+y x x x x a x
A 、2
B 、3
C 、4
D 、5
3、乙数为a ，甲数比乙数的3倍少2，则甲数为（ ）；
A 、3a-2
B 、3a+2
C 、
32+a D 、32-a
4、下列各式中，（ ）中的两项是同类项；
A 、2233
1xy y x -和 B 、
b a b
c a 2222-和 C 、44-和 D 、222和x
5、某品牌平板彩电降价30%以后，每台售价a 元，则该品牌彩电的标价为（ ）元
A 、3
.0a
B 、
7.0a C 、0.3a D 、0.7a
6、与
y x 2
2
1不仅所含字母相同，而且相同字母的指数也相同的是（ ）
A.z x 221
B. xy 2
1 C.2yx - D. x 2y 7、
)]([n m ---去括号得 （ ）
A 、n
m -- B 、n
m +- C 、
n m + D 、n m -
8、下列各等式中，成立的是（ ）
A 、
)(b a b a +-=+- B 、)8(383+=+x x C 、 x
x 8412=- D 、)
25(52--=-x x
9、小明编制了一个计算程序。
当输入任一有理数，显示屏显示输出的结果是一个有理数，若输入1-，并将所显示的结果再次输入，这时显示的结果应当是（ ）
A －21
B －23
C －24
D －25
10、若
y
x n
2
1
与
m
y
x3是同类项，则m＋n的值是（）。
A、5
B、4
C、3
D、2
一、填空题（每空2分，共18分）
11、教室里有x人，走了y人，此时教室里有人。
12、代数式
ab
-的系数是_________，
5
22
xy
-
的系数是_______；
13、观察下面的一列数，按某种规律在横线上填上适当的数：
1，－3 ， 5，－7，________ , ________ ，－13。
14、去括号：
()=
-
+b
a；()=
+
-b
a。
15、当m = 3，n = －2时，代数式
2
22n
m-的值是。
16、用语言叙述代数式2x+3y表示的实际意义可以是_______________ ____________________；
三、合并同类项（本题共4小题，每题4分，共16分）
17、
x
x
x10
4
15-
+
18、
x
y
yx
xy
y
x2
2
2
22
3-
+
-
19、
)3
(4
)4
(-
-
+
-
-b
b 20、)
5(
)
3
(22
2a
ab
a
ab-
+
-
-
四、（本题共2小题，每题6分，共12分）
21、
x
x
x
x4
5
22
2+
+
-
，其中
3-
=
x。
22、先化简再求值：１４（－4x 2
+ 2x - 8y ）－ (１２x －2y),其中x = １２,y = 2010 ；
23、某市出租车收费标准是：起步价10元，可乘3千米,超过3千米，每千米价2.4元。
（1）、若某人乘坐了x(x ＞3)千米的路程，则他应支付的费用是多少？（2分）
（2）、小李乘坐的路程是13千米，他应支付的费用是多少？（2分）
24、计算并填表：（本题8分）
（2）、当x 非常大时，x
x 21-的值接近于什么数？
25、（本题8分）用棋子摆出下列一组图形：
（1）填写下表：
（2）照这样的方式摆下去，写出摆第n 个图形棋子的枚数 ； （3）如果某一图形共有99枚棋子，你知道它是第几个图形吗？
26、（本题4分）某商场将进价a 元的货物提价40%后销售，后因积压又按售价的60%出售，用代数式表示实际的售价，问这次是亏了还是赚了？
（1）
（2）（3）
图形中棋子的 6
5 4 3 2 1 图形编号。