哈工大离散数学试卷(计算机网络学院)
哈工大离散数学zst

一、解答下列问题,要求只给出答案(总分10 分,每小题1分)1.设},,2,1{n A =,{}1,2B =,试求从A 到B 的满射的个数。
( )2.设{}1,2,,10A = ,试求A 上自反二元关系的个数。
( )3.X ={1,2,…,n},X 上有多少个对称的二元关系? ( )4.设X 为集合且}5,4,3,2,1{=X ,计算X 上有多少个二元运算。
( )5.设A ={1,2,3},则A 上有多少个划分? ( )6.设},,2,1{n V =,计算以V 为顶点集的无向图的个数。
( )7.设},,2,1{n V =,计算以V 为顶点集的有向图的个数。
( )8.二元树T 有0n 个叶子,2n 个出度为2的顶点,则0n 和2n 满足什么样的关系式?( )9.正整数m 和n 为什么值时,Km n 为欧拉图? ( ) 10.),(P P 连通图中有多少个圈? ( )二、以下各题要求只给出答案(总分20 分,每小题2分)1.下列集合表达式哪一个等于A\(B C )? ( ) (a)(A\B )∩(A\C ); (b)(A\B ) (A\C );(c)(A B )\(A C ); (d) 都不对2.:,f X Y B Y →⊆,则 ( )(a)1(())f f B B -⊇;(b)1(())f f B B -=;(c)1(())f f B B -⊆;(d)都不对。
3. 画出偏序集),2(}3,2,1{⊇的哈斯图。
4.是否存在一个同时不满足自反性,对称性,反对称性,传递性和反自反性的二元关系?若有请举一例,设X={1,2,3,4}。
( )5.X ={1,2,…,n },X 上有多少个反自反且对称的二元关系? ( )6.设r ≥2,G 是r-正则图且1)(=G χ,则 ( )(a)x(G)=r ;(b)x(G)<r ;(c)x(G)≤〔2r 〕;(d)x(G)=〔2r 〕。
(a) m<n ; (b) m>n ; (c) m =n ; (d) m =n 或m =n+1。
大学试卷《离散数学》及答案.docx

离散数学一、填空题(本大题共48分,共16小题,每小题3分)1.--公式为之充分必要条件是其合取范式之每一合取项中均必同时包含一命题变元及其否定2.无向图G具有是生成树,当且仅当的,若G为(n,m)连通图,要确定G的一棵生成树必删掉G的条边。
3.一个无向图的欧拉回路要求经过图中一次且仅一次,汉密顿图要求经过图中一次且仅一次。
4.设P:我生病,Q:我去学校(1)命题“我虽然生病但我仍去学校”符号化为o (2)命题“只有生病的时候,我才不去学校”符号化为o (3)命题"如果我生病,那么我不去学校”符号化为o5.设有33盏灯,拟公用一个电源,则至少需要5个插头的接线板数6.若HlAH2A-AHn是 ,则称Hl, H2, -Hn是相容的,若HlAH2A-AHn是 ,则称H1.H2, -Hn是不相容的7.设f,g,h 是N 到N上的函数(N 为自然数集合),f(n)=n+l;g(n)=2n;h(n)=0;贝lj(fdg)oh=8.K5的点连通度为 ,边连通度为o9.A={1, 2, 3, 4, 5, 6, 8, 10, 24, 36}, R 是A 上的整除关系。
子B={1, 2, 3, 4},那么B的上界是; B的下界是;:6的上确界是; B的下确界为10.命题公式P-*QAR的对偶式为11.设入={1, {2}, <t>},则A的幕集有元素个。
12.设A={0, 1,2, 3}, B={4,6, 7}, C={8, 9, 12, 14}, R1 是由A 到B 的关系,R2 是由B到C原关系,分别定义为Rl={<2, 6>, <3, 4>, <0, 7>} ;R2={<4, 8>, <4, 12>, <6, 12>,〈7, 14〉},则复合关系RloR2 为:13.设A= {<i)}, B={<t>, (<!>}},贝i]P(A) nP(B)= 。
《离散数学》考试试卷(试卷库20卷)及答案

《离散数学》考试试卷(试卷库20卷)及答案第 1 页/共 4 页《离散数学》考试试卷(试卷库20卷)试题总分: 100 分考试时限:120 分钟、选择题(每题2分,共20分)1. 设论域为全总个体域,M(x):x 是人,Mortal(x):x 是要死的,则“人总是要死的”谓词公式表示为( )(A ))()(x Mortal x M → (B ))()(x Mortal x M ∧(C )))()((x Mortal x M x →?(D )))()((x Mortal x M x ∧?2. 判断下列命题哪个正确?( )(A )若A∪B=A∪C,则B =C (B ){a,b}={b,a}(C )P(A∩B)≠P(A)∩P (B)(P(S)表示S 的幂集)(D )若A 为非空集,则A ≠A∪A 成立3. 集合},2{N n x x A n∈==对( )运算封闭(A )乘法(B )减法(C )加法(D )y x -4. 设≤><,N 是偏序格,其中N 是自然数集合,“≤”是普通的数间“小于等于”关系,则N b a ∈?,有=∨b a ( )(A )a(B )b(C )min(a ,b)(D ) max(a ,b)5. 有向图D=,则41v v 到长度为2的通路有( )条(A )0 (B )1 (C )2 (D )36. 设无向图G 有18条边且每个顶点的度数都是3,则图G 有( )个顶点(A )10 (B )4 (C )8 (D )127. 下面哪一种图不一定是树?()(A )无回路的连通图(B )有n 个结点n-1条边的连通图(C )每对结点间都有通路的图(D )连通但删去一条边则不连通的图 8. 设P :我将去镇上,Q :我有时间。
命题“我将去镇上,仅当我有时间”符号化为()(A )P →Q (B )Q →P (C )P Q (D )Q P ?∨? 9. 下列代数系统中,其中*是加法运算,()不是群。
离散数学试题(2006)_C(答案)
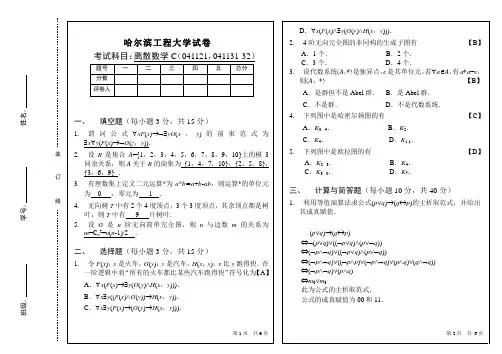
第2页 共 2页D .∀x (F (x )∧∃y (G (y )∧H (x ,y ))).2. 4阶无向完全图的非同构的生成子图有 【B 】 A .1个. B .2个.C .3个.D .4个. 3. 设代数系统〈A ,*〉是独异点,e 是其单位元,若∀a ∈A ,有a *a =e ,则〈A ,*〉 【B 】A .是群但不是Abel 群.B .是Abel 群.C .不是群.D .不是代数系统.4. 下列图中是哈密尔顿图的有 【C 】A .K 3,4.B .K 2.C .K 4.D .K 1,1.5. 下列图中是欧拉图的有 【D 】A .K 2,3.B .K 4.C .K 3,3.D .K 7.三、 计算与简答题(每小题10分,共40分)1. 利用等值演算法求公式(p ∨q )→(q ↔p )的主析取范式,并给出其成真赋值.(p ∨q )→(q ↔p )⇔⌝(p ∨q )∨((⌝p ∨q )∧(p ∨⌝q )) ⇔(⌝p ∧⌝q )∨((⌝p ∨q )∧(p ∨⌝q ))⇔(⌝p ∧⌝q )∨((⌝p ∧p )∨(⌝p ∧⌝q )∨(p ∧q )∨(q ∧⌝q )) ⇔(⌝p ∧⌝q )∨(p ∧q ) ⇔m 0∨m 3此为公式的主析取范式. 公式的成真赋值为00和11.第4页 共 4页4. 设集合A={a ,b ,c ,d }上的二元关系R={〈a ,b 〉,〈b ,a 〉,〈b ,c 〉,〈c ,b 〉},利用关系矩阵求R 的传递闭包t (R ).解 关系R 的关系矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0000001001010010R M , ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00000101001001012R M ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00000010010100103R M ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0000010100100114R M , 因此⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=000011101110111)(R t M ,从而R 的传递闭包 t (R )={〈a ,a 〉,〈a ,b 〉,〈a ,c 〉,〈b ,a 〉,〈b ,b 〉,〈b ,c 〉,〈c ,a 〉,〈c ,b 〉,〈c ,c 〉,〈d ,d 〉}.四、 证明题(共20分)1. 在一阶逻辑中构造下面推理的证明:前提:∀x (F (x )→G (x )),∃x (F (x )∧H (x )). 结论:∃x (G (x )∧H (x )).证明 (1)∃x (F (x )∧H (x )) 前提引入 (2)F (a )∧H (a )) EI 规则 (3)F (a ) (2)化简 (4)H (a ) (2)化简 (5)∀x (F (x )→G (x )) 前提引入 (6)F (a )→G (a ), UI 规则 (7)G (a ) 假言推理 (8)G (a ) ∧H (a ) (7)(4)合取第5页 共6页(9)∃x (G (x )∧H (x )). EG 规则2. 设〈B ,∧,∨,',1,0〉为一布尔代数,证明:∀a ,b ∈B ,有(a ∨b )' = a'∧b'.证明(a ∨b )∧(a'∧b')=(a ∧a'∧b')∨(b ∧a'∧b') =((a ∧a')∧b')∨(a'∧(b ∧b')) =0∨0=0(a ∨b )∨(a'∧b')=(a ∨b ∨a')∧(a ∨b ∨b') =((a ∨a')∨b )∧(a ∨(b ∨b')) =1∧1=1因此,(a ∨b )' = a'∧b'.3. 证明:设e 为无向连通图G 的桥,则e 在G 的每棵生成树中. 证明 假设存在G 的一棵生成树T ,其中不含G 的桥e .这样,在G 中去掉桥e 后仍可得该生成树T .另一方面,由于e 为图G 的桥,在G 中去掉桥e 后,所得图G ′一定不连通,它没有生成树,矛盾.因此,e 在G 的每棵生成树中.。
哈工大离散数学期末

《集合论与图论》计算机学院03年秋季(本试题满分90分)一、(10分,每小题1分)计算:1.设X 和Y 是集合且X m =,Y n =。
计算从X 到Y 的映射的个数。
(答案: )2.设X 和Y 是集合且X m =,Y n =。
若m ≤n,计算从X 到Y 的单射的个数。
(答案: )3.设X 为集合且X n =。
计算X 到X 的双射的个数。
(答案: )4.设X 为集合且X n =。
计算X 上有多少个不同的自反的二元关系。
(答案: )5.设X 为集合且X n =。
计算X 上有多少个二元运算。
(答案: )6.设V={}12,p u u u L 。
计算以V 为顶点集无向图的个数。
(答案: ) 7.设V={}12,p u u u L 。
计算以V 为顶点集的有向图的个数。
(答案: )8.设V={}12,p u u u L 。
计算以V 为顶点集的比赛图的个数。
(答案: )9.(P,P)连通图中有多少个圈?(答案: )10. n 个叶子的正则二元树中有多少条有向弧?(答案: )二、(10分,每小题1分)以下每小题中给出了四个答案,其中仅有一个是正确的。
请找出正确的答案并将其号码添在括号中。
11. Km,n 是哈密顿图当且仅当。
( )(a)m≤n (b)m≥n (c)m=n(d)(m<n 或m>n) 12. 下面哪个条件是Km,n 有哈密顿路的充要条件?( )(a)m<n (b)m>n (c)m=n(d)m=n 或m=n+1 13. 设r≥2,G 是r-正则图且1)(=G χ,则( )14. 把平面分为α个区域,使任两个区域相邻,则α的最大值为( ) (a)x(G)=r (b)x(G)<r (c)x(G)≤〔2r 〕 (d)x(G)=〔2r 〕 (a)5 (b)3 (c)2 (d)415. 4个顶点的二元树(顶点无标号)共有( )(a)3个 (b)4 (c)7 (d)816. 设f:,X Y A X →⊆,则( )(a)1(())f f A A −⊆ (c)-1f A A f ⊇))(((b)1(())f f A A −= (d)(a)或(b)17. :,f X Y B Y →⊆,则( )(a)1(())f fB B −⊇ (c)1(())f f B B −⊆ (b)1(())f f B B −= (d)(b)或(c)18.设,R X X X ⊆×为集合。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项不是离散数学的研究对象?A. 图论B. 组合数学C. 微积分D. 逻辑学答案:C2. 在逻辑学中,下列哪个命题是真命题?A. 如果今天是周一,那么明天是周二。
B. 如果今天是周一,那么明天是周三。
C. 如果今天是周一,那么明天是周四。
D. 如果今天是周一,那么明天是周五。
答案:A3. 在集合论中,下列哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 在图论中,下列哪个术语描述的是图中的顶点集合?A. 边B. 路径C. 子图D. 顶点答案:D二、填空题(每题5分,共20分)1. 如果一个集合A包含5个元素,那么它的子集个数是______。
答案:322. 在逻辑学中,如果命题P和命题Q都是真命题,那么复合命题“P且Q”的真值是______。
答案:真3. 在图论中,如果一个图的顶点数为n,那么它的最大边数是______。
答案:n(n-1)/24. 如果一个二叉树的深度为3,那么它最多包含______个节点。
答案:7三、简答题(每题10分,共30分)1. 请简述什么是图的连通性,并给出一个例子。
答案:图的连通性是指在图中任意两个顶点之间都存在一条路径。
例如,在一个完全图K3中,任意两个顶点之间都可以通过一条边直接连接,因此它是连通的。
2. 解释什么是逻辑蕴含,并给出一个例子。
答案:逻辑蕴含是指如果一个命题P为真,则另一个命题Q也必须为真。
例如,命题P:“如果今天是周一”,命题Q:“明天是周二”。
如果今天是周一,那么根据逻辑蕴含,明天必须是周二。
3. 请描述什么是二叉搜索树,并给出它的一个性质。
答案:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
它的一个性质是中序遍历可以得到一个有序序列。
四、计算题(每题15分,共30分)1. 给定一个集合A={1, 2, 3, 4, 5},请计算它的幂集,并列出所有元素。
哈工大离散数学it
应用计算机数学试题A (软件学院DIT )(本考卷满分70分,每题5分)1.设{}1234S =,,,,并设A S S =⨯,在A 上定义关系R 为:()(,)(,)a b c d R a b c d ∈⇔+=+,, 证明:(1)R 是等价关系;(2)计算等价类。
证: (1) (),a b A ∀∈,a+b=a+b 显示成立,故((a,b)(a,b))∈R ,即R 自反;(2) ()(),,,a b c d A ∀∈,若((a,b),(c,d)) ∈R ⇔a b c d c d a b +=+⇔+=+ ()()(),,,c d a b R ⇔∈,即R 对称的。
(3) ()()(),,,,,a b c d e f A ∀∈,若((a,b),(c,d)) ∈R 且()()(),,,c d e f R a b c d ∈⇔+=+且()()(),,,c d e f a b e f a b e f R +=+⇔+=+⇔∈,即R 是传递的。
由(1)、(2)、(3)可知,R 是A 上的传递关系。
2.设{1,2,3}A =,R 是A 的幂集{}2,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}Aφ=上的二元关系且R={(a ,b)︱a ∩b ≠¢},则R 不满足下列哪些性质?为什么?(1)自反性;(2)反自反性;(3)对称性;(4)反对称性;(5)传递性。
答:R 不满足:自反性,反自反性,反对称性,传递性。
R 满足:对称性3.设f Y C D Y →⊆:X ,,, 证明:111f C D f C f D ---∆=∆()()() 证:()()()()()1111[\\]\\f C D f C D D C f C D f D C ----∆=⋃=⋃=()()()()1111\\f C f D f D f C ----⎡⎤⎡⎤⋃⎣⎦⎣⎦=()()11f C f D --∆4.设f Y g →→:X ,:Y Z ,证明:(1)若f 与g 都是可逆的,则g f 也是可逆的; (2)求g f 的逆。
离散数学试题及答案解析
离散数学试题及答案解析一、选择题1. 在集合{1,2,3,4}中,含有3个元素的子集有多少个?A. 4B. 8C. 16D. 32答案:B解析:含有3个元素的子集可以通过组合数公式C(n, k) = n! / [k!(n-k)!]来计算,其中n为集合的元素个数,k为子集中的元素个数。
在本题中,n=4,k=3,所以C(4, 3) = 4! / [3!(4-3)!] = 4。
2. 下列哪个命题是真命题?A. 所有偶数都是整数。
B. 所有整数都是偶数。
C. 所有整数都是奇数。
D. 所有奇数都是整数。
答案:A解析:偶数是指能被2整除的整数,因此所有偶数都是整数,选项A是真命题。
选项B、C和D都是错误的,因为并非所有整数都是偶数或奇数。
二、填空题1. 逻辑运算符“非”(NOT)的真值表是:当输入为真时,输出为______;当输入为假时,输出为真。
答案:假解析:逻辑运算符“非”(NOT)是一元运算符,它将输入的真值取反。
如果输入为真,则输出为假;如果输入为假,则输出为真。
2. 命题逻辑中,合取词“与”(AND)的真值表是:当两个命题都为真时,输出为真;否则输出为______。
答案:假解析:合取词“与”(AND)是二元运算符,只有当两个命题都为真时,输出才为真;如果其中一个或两个命题为假,则输出为假。
三、简答题1. 解释什么是等价关系,并给出一个例子。
答案:等价关系是定义在集合上的一个二元关系,它满足自反性、对称性和传递性。
例如,考虑整数集合上的“同余”关系。
对于任意整数a,b,如果a和b除以同一个正整数n后余数相同,则称a和b模n同余。
这个关系是自反的(a同余a),对称的(如果a同余b,则b同余a),并且是传递的(如果a同余b且b同余c,则a同余c)。
2. 什么是图的连通性?一个图是连通的需要满足什么条件?答案:图的连通性是指在无向图中,任意两个顶点之间都存在一条路径。
一个图是连通的需要满足以下条件:图中的任意两个顶点v和w,都可以通过图中的边相互到达。
离散数学考试试题(A、B卷及答案)
离散数学考试试题(A 卷及答案)一、证明题(10分) 1) (P ∧Q ∧AC )∧(A P ∨Q ∨C ) (A ∧(P Q ))C 。
P<->Q=(p->Q)合取(Q->p )证明: (P ∧Q ∧A C )∧(A P ∨Q ∨C ) (P ∨Q ∨A ∨C )∧(A ∨P ∨Q ∨C )((P ∨Q ∨A )∧(A ∨P ∨Q ))∨C 反用分配律 ((P ∧Q ∧A )∨(A ∧P ∧Q ))∨C( A ∧((P ∧Q )∨(P ∧Q )))∨C 再反用分配律( A ∧(PQ ))∨C(A ∧(P Q ))C 2) (PQ)PQ 。
证明:(P Q)((P ∧Q))(P ∨Q))PQ 。
二、分别用真值表法和公式法求(P (Q ∨R ))∧(P ∨(Q R ))的主析取范式与主合取范式,并写出其相应的成真赋值和成假赋值(15分)。
主析取范式与析取范式的区别:主析取范式里每个括号里都必须有全部的变元。
主析取范式可由 析取范式经等值演算法算得。
证明:公式法:因为(P (Q ∨R ))∧(P ∨(Q R ))(P ∨Q ∨R )∧(P ∨(Q ∧R )∨(Q ∧R ))(P ∨Q ∨R )∧(((P ∨Q )∧(P ∨R ))∨(Q ∧R ))分配律 (P ∨Q ∨R )∧(P ∨Q ∨Q )∧(P ∨Q ∨R )∧(P ∨R ∨Q )∧(P ∨R ∨R )(P ∨Q ∨R )∧(P ∨Q ∨R )∧(P ∨Q ∨R )4M ∧5M ∧6M 使(非P 析取Q 析取R )为0所赋真值,即100,二进制为4 0m ∨1m ∨2m ∨3m ∨7m所以,公式(P (Q ∨R ))∧(P ∨(Q R ))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。
真值表法:P Q RQRP(Q∨R)P∨(Q R)(P(Q∨R))∧(P∨(Q R ))0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1 1111111111111111111111为000、001、010、011、111:成假赋值为:100、101、110。
离散数学试题(2006)_A(答案)
一、填空题(每小题3分,共15分)1.设F(x):x是苹果,H(x,y):x与y完全相同,L(x,y):x=y,则命题“没有完全相同的苹果”的符号化(利用全称量词)为∀x∀y(F(x)∧F(y)∧⌝L(x,y)→⌝H(x,y)).2.命题“设L是有补格,在L中求补元运算‘′’是L中的一元运算”的真值是0.3.设G={e,a,b,c}是Klein四元群,H=〈a〉是G的子群,则商群G/H={〈a〉,{b,c}}={{e,a},{b,c}}.4.设群G=〈P({a,b,c}),⊕〉,其中⊕为集合的对称差运算,则由集合{a,b}生成的子群〈{a,b}〉 ={∅,{a,b}}.5.已知n阶无向简单图G有m条边,则G的补图有n(n-1)/2-m条边.二、选择题(每小题3分,共15分)1.命题“只要别人有困难(p),小王就会帮助他(q),除非困难已经解决了(r)”的符号化为【B】A.⌝(p∧r)→q.B.(⌝r∧p)→q.C.⌝r→(p∧q).D.⌝r→(q→ p).2.设N为自然数集合,“≤”为通常意义上的小于等于关系,则偏序集〈N,≤〉是【C】A.有界格.B.有补格.C.分配格.D.布尔代数.3.设n (n≥3) 阶无向图G=〈V,E〉是哈密尔顿图,则下列结论中不成立的是【D】A.∀V1⊂V,p(G-V1)≤|V1|.B.|E|≥n.C.无1度顶点.D.δ(G)≥n/2.4.设A={a,b,c},在A上可以定义个二元运算,其中有个是可交换的,有个是幂等的.【A】A.39,36,36.B.39,36,33.C.36,36,33.D.39,36,39.5.下列图中是欧拉图的有【C】A.K4,3.B.K6.C.K5.D.K3,3.三、计算与简答题(每小题8分,共40分)1.利用等值演算方法求命题公式(p∨q) → (q→p)的主合取范式;利用该主合取范式求公式的主析取范式,并指出该公式的成真赋值和成假赋值.(p∨q) → (q→p)⇔⌝(p∨q)∨(⌝q∨p)⇔(⌝p∧⌝q)∨(⌝q∨p)⇔(⌝p∨⌝q∨p)∧(⌝q∨⌝q∨p)⇔⌝q∨p⇔p∨⌝q⇔M1此为公式的主合取范式.该公式的主析取范式是m0∨m2∨m3.公式的成真赋值为00,10,11.公式的成假赋值为01.哈尔滨工程大学试卷考试科目:离散数学(041121,041131-32)考试时间:14:00-16:3012. 求群〈Z 18,⊕18〉的所有生成元和子群,画出〈Z 18,⊕18〉的子群格,指出该子群格的全下界、全上界和有补元,并求其补元. 与18互质的数有1,5,7,11,13,17,因此,1,5,7,11,13,17是群〈Z 18,⊕18〉的生成元.18的因数有1,2,3,6,9,18,因此,群〈Z 18,⊕18〉的子群有 〈1〉=〈Z 18,⊕18〉,〈2〉=〈{0,2,4,6,8,10,12,14,16},⊕18〉, 〈3〉=〈{0,3,6,9,12,15},⊕18〉,〈6〉=〈{0,6,12},⊕18〉, 〈9〉=〈{0,9},⊕18〉,〈18〉=〈{0},⊕18〉. 〈Z 18,⊕18〉的子群格为〈{〈18〉,〈9〉,〈6〉,〈3〉,〈2〉,〈1〉},⊆〉,其哈斯图为 全下界为〈18〉,全上界为〈1〉, 〈18〉’=〈1〉,〈1〉’=〈18〉,〈2〉’=〈9〉,〈9〉’=〈2〉,〈3〉和〈6〉没有补元. 3. 若R 1,R 2均是非空集合A 上的等价关系,那么R 1,R 2的交R 1∩R 2、并R 1∪R 2和复合R 1○ R 2也是A 上的等价关系吗?若是,证明你的结论.R 1∩R 2是A 上的等价关系.事实上, (1) 因R 1,R 2是A 上的自反关系,有I A ⊆R 1,I A ⊆R 2,因此,I A ⊆R 1∩R 2,即R 1∩R 2是A 上的自反关系.(2) 因R 1,R 2是A 上的对称关系,有R 1=R 1-1,R 2=R 2-1,而(R 1∩R 2)-1=R 1-1∩R 2-1=R 1∩R 2,因此,R 1∩R 2是A 上的对称关系.(3) 因R 1,R 2是A 上的传递关系,有R 12⊆R 1,R 22⊆R 2,而(R 1∩R 2)2=(R 1∩R 2)ο(R 1∩R 2)=R 12∩R 22∩R 1οR 2∩R 2οR 1⊆R 12∩R 22⊆R 1∩R 2,因此,R 1∩R 2是A 上的传递关系.4. 设无向连通图G 如下图,求其最小生成树T 及T 的权W (T ),写出G 的对应于T 的基本回路系统和基本割集系统.G 的最小生成树T 如图(以实线表示),权W (T )=11. G 的对应于T 的基本回路系统为{C bd ,C cd ,C de },其中 C bd =bdab ,C cd =cdabc , C de =dead .G 的对应于T 的基本割集系统为{S ab ,S ad ,S ae ,S bc },其中 S ab ={ab ,bd ,cd },S ad ={ad ,bd ,cd ,de }, S ae ={ae ,de },S bc ={bc ,cd }.5. 设〈B,∧,∨,′,0,1〉是布尔代数,a ,b ,c ∈B ,化简公式 (a ∧b )∨(a ∧(b ∧c )’ )∨c .(a ∧b )∨(a ∧(b ∧c )’ )∨c =(a ∧b )∨(a ∧(b’∨c’ ))∨c =(a ∧b )∨((a ∧(b’∨c’ ))∨c ) =(a ∧b )∨((a ∨c )∧(b’ ∨c’ ∨c )) =(a ∧b )∨(a ∨c ) =(a ∨(a ∨c ))∧(b ∨a ∨c ) =(a ∨c )∧(a ∨c ∨b ) =a ∨c〈3〉3四、 证明题(共20分)1. 在自然推理系统中,构造推理证明: 前提:∀x (F (x )∨G (x )) 结论:⌝∀xF (x )→ ∃xG (x )证明:(1) ⌝∀xF (x ) 附加前提引入 (2) ∃x ⌝F (x ) (1)置换 (3) ⌝F (c ) (2)EI 规则 (4) ∀x (F (x )∨G (x )) 前提引入 (5) F (c )∨G (c ) (4)UI 规则(6) G (c )) (3)(5)析取三段论 (7) ∃xG (x ) (6)EG 规则2. 设代数系统〈A ,*〉是独异点,e 是其单位元.若∀a ∈A ,有a *a =e ,证明:〈A ,*〉是Abel 群.证明:由于对∀a ∈A ,有a *a =e ,因此,A 中任意元素a 都有逆元,且a=a -1.又〈A ,*〉是有单位元的独异点,从而〈A ,*〉是群. ∀a ,b ∈A ,有a *b ∈A ,且a=a -1,b=b -1,(a *b )-1=a *b .又(a *b )-1=b -1*a -1=b *a ,因此 a *b =b *a ,即〈A ,*〉是Abel 群.3. 证明:若无向图G 为欧拉图,则G 无桥.证明:(1)假设G 中有桥,不妨设e =(u ,v ) 为其一座桥.这样,从中删去边e =(u ,v )后,所得图G ’一定不连通(G ’至少含有两个连通分支).由于G 为欧拉图,因此它是连通图,且有经过每条边一次且仅一次的回路,这条回路必经过G 的所有顶点.从而存在顶点v 1,v 2,…,v s ,使得uv 1v 2…v s vu 是G 的一条回路.从G 中删去边e =(u ,v )后,所得图G ’仍有从u 到v 的通路uv 1v 2…v s v ,这样G ’仍是连通图.矛盾.因此,G 中一定无桥.(2)由于G 为欧拉图,其每个顶点的度数均为偶数.假设G 中有桥,不妨设e =(u ,v ) 为其一座桥.这样,从中删去边e =(u ,v )后,所得图G ’至少有两个连通分支.而且,顶点u ,v 的度数都是奇数,这与每个连通分支为图矛盾(与握手定理矛盾),因此,G 中一定无桥.五、 应用题(10分)今有a ,b ,c ,d ,e ,f 和g 七人,已知a 会讲英语;b 会讲英语和汉语;c 会讲英语、意大利语和俄语;d 会讲汉语和日语;e 会讲德语和意大利语;f 会讲法语、日语和俄语;g 会讲法语和德语,试问:如何将这七个人安排围坐在一张圆桌上,使得每个人都可和他身边的人交谈.以a ,b ,c ,d ,e ,f 和g 七人为顶点,如果两人有共同语言,连接这两个顶点,以此为边做一个图,如右图.在图中如果能找到一条哈密尔顿回路,则将这七个人安排围坐在一张圆桌上,每个人都可和他身边的人交谈.该回路为abdfgeca .。
