教育统计学与SPSS课后作业答案祥解题目
《统计分析与SPSS的应用(第五版)》课后练习答案(第2章)
《统计分析与SPSS的应用（第五版）》（薛薇）课后练习答案第2章SPSS数据文件的建立和管理1、SPSS中有哪两种基本的数据组织形式？各自的特点和应用场合是什么？SPSS中两个基本的数据组织方式：原始数据的组织方式和计数数据的组织方式。
●原始数据的组织方式：待分析的数据是一些原始的调查问卷数据，或是一些基本的统计指标。
●计数数据的组织方式：所采集的数据不是原始的调查问卷数据，而是经过分组汇总后的数据。
2、什么是SPSS的个案？什么SPSS的变量？个案：在原始数据的组织方式中，数据编辑器窗口中的一行称为一个个案或观测。
变量：数据编辑器窗口中的一列。
3、在定义SPSS数据结构时，默认的变量名和变量类型是什么？如果希望增强SPSS统计分析结果的易读性，还需要对数据结构的哪些方面进行必要说明？默认的变量名：VAR------；默认的变量类型：数值型。
变量名标签和变量值标签可增强统计分析结果的可读性。
4、收集到以下关于两种减肥产品试用情况的调查数据，请问在SPSS中应如何组织该份资料？产品类型体重变化情况明显减轻无明显变化第一种产品27 19第二种产品20 33问：在SPSS中应如何组织该数据？数据文件如图所示：5、什么是SPSS的用户缺失值？为什么要对用户缺失值进行定义？如何在SPSS中指定用户缺失值？缺失值分为用户缺失值（User Missing Value）和系统缺失值（System MissingValue）。
用户缺失值指在问卷调查中，将无回答的一些数据以及明显失真的数据当作缺失值来处理。
用户缺失值的编码一般用研究者自己能够识别的数字来表示，如“0”、“9”、“99”等。
系统缺失值主要指计算机默认的缺失方式，如果在输入数据时空缺了某些数据或输入了非法的字符，计算机就把其界定为缺失值，这时的数据标记为一个圆点“•”。
在变量视图中定义。
6、从计量尺度角度看，变量包括哪三种主要类型？请各举出一个相应的实际数据。
《统计分析和SPSS的应用（第五版）》课后练习答案解析（第6章）
《统计分析和SPSS的应用（第五版）》课后练习答案解析（第6章）《统计分析与SPSS的应用（第五版）》（薛薇）课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异，设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人，并随机地将他们分为五个组，每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额，如下表所示：第一组20.0 16.8 17.9 21.2 23.9 26.8 22.4第二组24.9 21.3 22.6 30.2 29.9 22.5 20.7第三组16.0 20.1 17.3 20.9 22.0 26.8 20.8第四组17.5 18.2 20.2 17.7 19.1 18.4 16.5第五组25.2 26.2 26.9 29.3 30.4 29.7 28.21）请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2）绘制各组的均值对比图，并利用LSD方法进行多重比较检验。
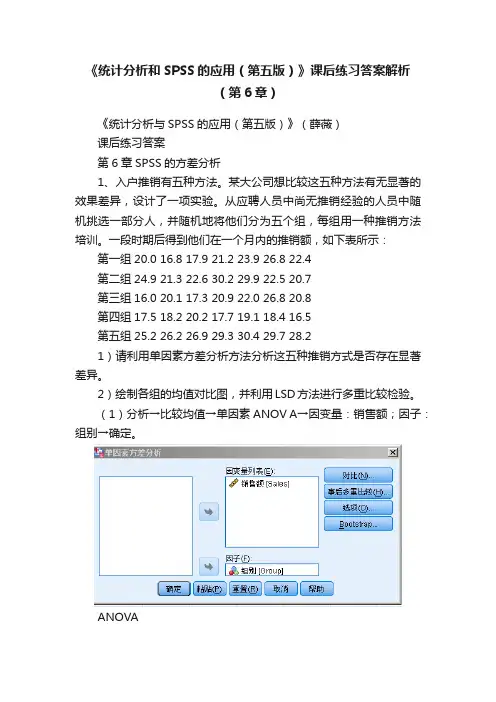
（1）分析→比较均值→单因素ANOV A→因变量：销售额；因子：组别→确定。
ANOVA销售额平方和df 均方 F 显著性组之间405.534 4 101.384 11.276 .000组内269.737 30 8.991总计675.271 34概率P-值接近于0，应拒绝原假设，认为5种推销方法有显著差异。
（2）均值图：在上面步骤基础上，点选项→均值图；事后多重比较→LSD多重比较因变量: 销售额 LSD(L)(I) 组别 (J) 组别平均差(I-J) 标准错误显著性95% 置信区间下限值上限第一组第二组 -3.30000*1.60279 .048 -6.5733 -.0267 第三组 .72857 1.60279 .653 -2.5448 4.0019 第四组3.05714 1.60279 .066 -.2162 6.3305 第五组-6.70000* 1.60279 .000 -9.9733 -3.4267 第二组第一组 3.30000* 1.60279 .048 .0267 6.5733 第三组 4.02857* 1.60279 .018 .7552 7.3019 第四组 6.35714* 1.60279 .000 3.0838 9.6305 第五组-3.40000* 1.60279 .042 -6.6733 -.1267 第三组第一组 -.72857 1.60279 .653 -4.0019 2.5448 第二组 -4.02857* 1.60279 .018 -7.3019 -.7552 第四组 2.32857 1.60279 .157 -.9448 5.6019 第五组-7.42857* 1.60279 .000 -10.7019 -4.1552 第四组第一组-3.057141.60279.066-6.3305.2162第二组-6.35714* 1.60279 .000 -9.6305 -3.0838第三组-2.32857 1.60279 .157 -5.6019 .9448第五组-9.75714* 1.60279 .000 -13.0305 -6.4838第五组第一组6.70000* 1.60279 .000 3.4267 9.9733 第二组3.40000* 1.60279 .042 .1267 6.6733第三组7.42857* 1.60279 .000 4.1552 10.7019第四组9.75714* 1.60279 .000 6.4838 13.0305*. 均值差的显著性水平为 0.05。
统计学spss课后题答案解析
实操训练答案目录第一章 (1)第二章 (2)第三章 (3)第四章 (4)第五章 (7)第六章 (10)第七章 (17)第八章 (21)第九章 (26)第十章 (31)第一章（一）思考题略（二）练习题1.（1）定类变量（2）定类变量（3）定序变量（4）数值型变量（5）数值型变量2. A3. B4. A B C D5. D A6. A B（三）操作题略1第二章（一）思考题略（二）练习题1. BD AC2. C3. D4. D5. A（三）操作题1. 见SPSS文件2.1.sav。
2. 略。
3. 略。
4. 略。
第三章1. 2011年人均国内生产总值（agdp2011），排在前五位的是天津、上海、北京、江苏、浙江；排在后五位的是广西、西藏、甘肃、云南、贵州。
. 2011年国内生产总值（gdp2011），在东部各省市里，排在第1位的是广东，排在最后1位的分别是海南；在中部各省市里，排在第1位的是河南，排在最后1位的分别是吉林；在西部各省市里，排在第1位的是四川，排在最后1位的分别是西藏。
2. 见SPSS文件3.2.sav。
3. 见SPSS文件3.3.sav。
4. A老师提供的管理学成绩见SPSS文件3.4-1.sav，B老师提供的经济学成绩见SPSS文件3.4-2.sav，合并后的文件见SPSS文件3.4.sav。
5. 见SPSS文件3.5.sav。
6. 见SPSS文件3.6.sav。
7. 见SPSS文件3.7.sav。
8. 见SPSS文件3.8.sav。
9. 两门课程都在80分以上的共4人，见SPSS文件3.5.sav。
10. 管理学成绩在80-89，经济学成绩在90分以上的只有1人，见SPSS文件3.6.sav。
第四章1. 由于变量品牌（brand）是定类变量，所以分别用众数和异众比来描述其集中趋势和离散趋势。
由分析结果可知，众数是B，异众比是（800-279）/800=65.1%。
统计量品牌N 有效800缺失0众数 2品牌频率百分比有效百分比累积百分比有效 A 164 20.5 20.5 20.5B 279 34.9 34.9 55.4C 110 13.8 13.8 69.1D 55 6.9 6.9 76.0E 192 24.0 24.0 100.0合计800 100.0 100.02．由于变量《统计学》这门课程难吗（v2.4）是定序变量，所以用众数，中位数，四分位数来描述其集中趋势，用四分位差来描述其离散趋势。
《统计分析与SPSS的应用(第五版)》课后练习答案(第2章)
《统计分析与SPSS的应用（第五版）》（薛薇）课后练习答案第2章SPSS数据文件的建立和管理1、SPSS中有哪两种基本的数据组织形式？各自的特点和应用场合是什么？SPSS中两个基本的数据组织方式：原始数据的组织方式和计数数据的组织方式。
●原始数据的组织方式：待分析的数据是一些原始的调查问卷数据，或是一些基本的统计指标。
●计数数据的组织方式：所采集的数据不是原始的调查问卷数据，而是经过分组汇总后的数据。
2、什么是SPSS的个案？什么SPSS的变量？个案：在原始数据的组织方式中，数据编辑器窗口中的一行称为一个个案或观测。
变量：数据编辑器窗口中的一列。
3、在定义SPSS数据结构时，默认的变量名和变量类型是什么？如果希望增强SPSS统计分析结果的易读性，还需要对数据结构的哪些方面进行必要说明？默认的变量名：VAR------；默认的变量类型：数值型。
变量名标签和变量值标签可增强统计分析结果的可读性。
4、收集到以下关于两种减肥产品试用情况的调查数据，请问在SPSS中应如何组织该份资料？产品类型体重变化情况明显减轻无明显变化第一种产品27 19第二种产品20 33问：在SPSS中应如何组织该数据？数据文件如图所示：5、什么是SPSS的用户缺失值？为什么要对用户缺失值进行定义？如何在SPSS中指定用户缺失值？缺失值分为用户缺失值（User Missing Value）和系统缺失值（System MissingValue）。
用户缺失值指在问卷调查中，将无回答的一些数据以及明显失真的数据当作缺失值来处理。
用户缺失值的编码一般用研究者自己能够识别的数字来表示，如“0”、“9”、“99”等。
系统缺失值主要指计算机默认的缺失方式，如果在输入数据时空缺了某些数据或输入了非法的字符，计算机就把其界定为缺失值，这时的数据标记为一个圆点“•”。
在变量视图中定义。
6、从计量尺度角度看，变量包括哪三种主要类型？请各举出一个相应的实际数据。
《统计分析与SPSS的应用》课后练习答案(第2章)
《统计分析与SPSS的应用（第五版）》课后练习答案第2章SPSS数据文件的建立和管理1、S PSS中有哪两种基本的数据组织形式？各自的特点和应用场合是什么？SPSS中两个基本的数据组织方式：原始数据的组织方式和计数数据的组织方式。
原始数据的组织方式：待分析的数据是一些原始的调查问卷数据，或是一些基本的统计指标。
计数数据的组织方式：所采集的数据不是原始的调查问卷数据，而是经过分组汇总后的数据。
2、什么是SPSS的个案？什么SPSS的变量？个案：在原始数据的组织方式中，数据编辑器窗口中的一行称为一个个案或观测。
变量：数据编辑器窗口中的一列。
3、在定义SPSS数据结构时，默认的变量名和变量类型是什么？如果希望增强SPSS统计分析结果的易读性，还需要对数据结构的哪些方面进行必要说明？默认的变量名：VAR------;默认的变量类型：数值型。
变量名标签和变量值标签可增强统计分析结果的可读性。
4、收集到以下关于两种减肥产品试用情况的调查数据，请问在SPSS中应如何组织该份资料？问：在S P S S中应如何组织该数据?数据文件如图所示：5、什么是SPSS的用户缺失值？为什么要对用户缺失值进行定义？如何在SPSS中指定用户缺失值？缺失值分为用户缺失值（User Miss ing Value ）和系统缺失值（System Miss ingValue ）。
用户缺失值指在问卷调查中，将无回答的一些数据以及明显失真的数据当作缺失值来处理。
用户缺失值的编码一般用研究者自己能够识别的数字来表示，如“0” “9”、“99”等。
系统缺失值主要指计算机默认的缺失方式，如果在输入数据时空缺了某些数据或输入了非法的字符，计算机就把其界定为缺失值，这时的数据标记为一个圆点“？”。
在变量视图中定义。
6、从计量尺度角度看，变量包括哪三种主要类型？请各举出一个相应的实际数据。
如何在SPSS 中指定变量的计算尺度？变量类型包括：数值型（身高）、定序型（受教育程度）以及定类型（性别）。
《统计分析和SPSS的应用（第五版）》课后练习的答案解析（第4章）
《统计分析和SPSS的应⽤（第五版）》课后练习的答案解析（第4章）《统计分析与SPSS的应⽤（第五版）》（薛薇）课后练习答案第4章SPSS基本统计分析1、利⽤第2章第7题数据采⽤SPSS频数分析，分析被调查者的常住地、职业和年龄分布特征，并绘制条形图。
分析——描述统计——频率，选择“常住地”，“职业”和“年龄”到变量中，然后，图表——条形图——图表值（频率）——继续，勾选显⽰频率表格，点击确定。
Statistics户⼝所在地职业年龄N Valid 282 282 282Missing 0 0 0户⼝所在地Frequency Percent ValidPercentCumulativePercentValid 中⼼城市200 70.9 70.9 70.9 边远郊区82 29.1 29.1 100.0 Total 282 100.0 100.0职业Frequency Percent ValidPercentCumulativePercentValid 国家机关24 8.5 8.5 8.5 商业服务业54 19.1 19.1 27.7 ⽂教卫⽣18 6.4 6.4 34.0 公交建筑业15 5.3 5.3 39.4 经营性公司18 6.4 6.4 45.7 学校15 5.3 5.3 51.1 ⼀般农户35 12.4 12.4 63.5 种粮棉专业户4 1.4 1.4 64.9种果菜专业户10 3.5 3.5 68.4 ⼯商运专业户34 12.1 12.1 80.5 退役⼈员17 6.0 6.0 86.5 ⾦融机构35 12.4 12.4 98.9 现役军⼈ 3 1.1 1.1 100.0 Total 282 100.0 100.0年龄Frequency Percent ValidPercent Cumulative PercentValid 20岁以下 4 1.4 1.4 1.4 20~35岁146 51.8 51.8 53.2 35~50岁91 32.3 32.3 85.5 50岁以上41 14.5 14.5 100.0 Total 282 100.0 100.0分析：本次调查的有效样本为282份。
《统计分析与SPSS的应用(第五版)》课后练习答案
《统计分析与SPSS的应用(第五版)》课后练习答案第一章练习题答案1、SPSS的中文全名是：社会科学统计软件包（后改名为：统计产品与服务解决方案）英文全名是：StatiticalPackagefortheSocialScience.(StatiticalProductandServic eSolution)2、SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
●数据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据；●结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、SPSS的数据集：●SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合（简称数据集）。
●活动数据集：其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS的三种基本运行方式：●完全窗口菜单方式、程序运行方式、混合运行方式。
●完全窗口菜单方式：是指在使用SPSS的过程中，所有的分析操作都通过菜单、按钮、输入对话框等方式来完成，是一种最常见和最普遍的使用方式，最大优点是简洁和直观。
●程序运行方式：是指在使用SPSS的过程中，统计分析人员根据自己的需要，手工编写SPSS命令程序，然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
●混合运行方式：是前两者的综合。
5、.av是数据编辑器窗口中的SPSS数据文件的扩展名.pv是结果查看器窗口中的SPSS分析结果文件的扩展名.p是语法窗口中的SPSS程序6、SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中；统计分析和绘图功能主要集中在分析、图形等菜单中。
7、概率抽样(probabilityampling)：也称随机抽样，是指按一定的概率以随机原则抽取样本，抽取样本时每个单位都有一定的机会被抽中，每个单位被抽中的概率是已知的，或是可以计算出来的。
统计分析与SPSS课后习题课后习题答案汇总(第五版)
第一章练习题答案1、SPSS的中文全名是：社会科学统计软件包（后改名为：统计产品与服务解决方案）英文全名是：Statistical Package for the Social Science.(Statistical Product and Service Solutions)2、SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
数据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据；结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、SPSS的数据集：SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合（简称数据集）。
活动数据集：其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS的三种基本运行方式：完全窗口菜单方式、程序运行方式、混合运行方式。
完全窗口菜单方式：是指在使用SPSS的过程中，所有的分析操作都通过菜单、按钮、输入对话框等方式来完成，是一种最常见和最普遍的使用方式，最大优点是简洁和直观。
程序运行方式：是指在使用SPSS的过程中，统计分析人员根据自己的需要，手工编写SPSS命令程序，然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
混合运行方式：是前两者的综合。
5、.sav是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPSS分析结果文件的扩展名.sps是语法窗口中的SPSS程序6、SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中；统计分析和绘图功能主要集中在分析、图形等菜单中。
7、概率抽样(probability sampling)：也称随机抽样，是指按一定的概率以随机原则抽取样本，抽取样本时每个单位都有一定的机会被抽中，每个单位被抽中的概率是已知的，或是可以计算出来的。
概率抽样包括简单随机抽样、系统抽样（等距抽样）、分层抽样（类型抽样）、整群抽样、多阶段抽样等。
统计分析与SPSS课后习题课后习题汇总(第五版)
《统计分析与SPSS的应用（第五版）》课后练习答案第一章练习题答案1、SPSS的中文全名是：社会科学统计软件包（后改名为：统计产品与服务解决方案）英文全名是：Statistical Package for the Social Science.(Statistical Product and Service Solutions)2、SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
●数据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据；●结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、SPSS的数据集：●SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合（简称数据集）。
●活动数据集：其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS的三种基本运行方式：●完全窗口菜单方式、程序运行方式、混合运行方式。
●完全窗口菜单方式：是指在使用SPSS的过程中，所有的分析操作都通过菜单、按钮、输入对话框等方式来完成，是一种最常见和最普遍的使用方式，最大优点是简洁和直观。
●程序运行方式：是指在使用SPSS的过程中，统计分析人员根据自己的需要，手工编写SPSS命令程序，然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
●混合运行方式：是前两者的综合。
5、.sav是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPSS分析结果文件的扩展名.sps是语法窗口中的SPSS程序6、SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中；统计分析和绘图功能主要集中在分析、图形等菜单中。
7、概率抽样(probability sampling)：也称随机抽样，是指按一定的概率以随机原则抽取样本，抽取样本时每个单位都有一定的机会被抽中，每个单位被抽中的概率是已知的，或是可以计算出来的。
《统计分析与SPSS的应用(第五版)》课后练习答案(第2章)
《统计分析与SPSS的应用（第五版）》（薛薇）课后练习答案第2章SPSS数据文件的建立和管理1、SPSS中有哪两种基本的数据组织形式？各自的特点和应用场合是什么？SPSS中两个基本的数据组织方式：原始数据的组织方式和计数数据的组织方式。
●原始数据的组织方式：待分析的数据是一些原始的调查问卷数据，或是一些基本的统计指标。
●计数数据的组织方式：所采集的数据不是原始的调查问卷数据，而是经过分组汇总后的数据。
2、什么是SPSS的个案？什么SPSS的变量？个案：在原始数据的组织方式中，数据编辑器窗口中的一行称为一个个案或观测。
变量：数据编辑器窗口中的一列。
3、在定义SPSS数据结构时，默认的变量名和变量类型是什么？如果希望增强SPSS统计分析结果的易读性，还需要对数据结构的哪些方面进行必要说明？默认的变量名：VAR------；默认的变量类型：数值型。
变量名标签和变量值标签可增强统计分析结果的可读性。
4、收集到以下关于两种减肥产品试用情况的调查数据，请问在SPSS中应如何组织该份资料？产品类型体重变化情况明显减轻无明显变化第一种产品27 19第二种产品20 33问：在SPSS中应如何组织该数据？数据文件如图所示：5、什么是SPSS的用户缺失值？为什么要对用户缺失值进行定义？如何在SPSS中指定用户缺失值？缺失值分为用户缺失值（User Missing Value）和系统缺失值（System MissingValue）。
用户缺失值指在问卷调查中，将无回答的一些数据以及明显失真的数据当作缺失值来处理。
用户缺失值的编码一般用研究者自己能够识别的数字来表示，如“0”、“9”、“99”等。
系统缺失值主要指计算机默认的缺失方式，如果在输入数据时空缺了某些数据或输入了非法的字符，计算机就把其界定为缺失值，这时的数据标记为一个圆点“•”。
在变量视图中定义。
6、从计量尺度角度看，变量包括哪三种主要类型？请各举出一个相应的实际数据。
教育统计与SPSS应用智慧树知到课后章节答案2023年下潍坊学院
教育统计与SPSS应用智慧树知到课后章节答案2023年下潍坊学院潍坊学院第一章测试1.教育统计学、数理统计学和应用统计学具有怎样的关系？答案:null2.统计量和参数有何区别，请举出几个常见统计量和参数的表示符号。
答案:null3.SPSS中常用的变量包括定距型变量、定类型变量和定序型变量，请分别举例说明。
答案:null4.为研究山东省地方本科院校大学生的就业情况，某研究团队从山东省地方本科院校已经毕业五年的毕业生中，抽取了1500名毕业生进行调查研究，请你说出本研究的总体、个体和样本，并说明应如何科学地抽样这一样本？答案:null5.教育统计学的主要内容包括描述统计、推断统计和研究设计。
答案:对第二章测试1.调查研究的基本过程包括哪几个环节？调查研究中，研究题目、研究目的和研究内容具有怎样的关系？答案:null2.如何设计调查问卷。
答案:null3.选择你感兴趣的主题，进行调查，写出调查的策划书并设计问卷。
答案:null4.获得调查问卷的数据后，如何将其输入到SPSS软件中？答案:null5.SPSS中，“编码”和“计算变量”等功能会根据设置的要求修改原来的数据。
答案:对第三章测试1.用自己的话解释以下概念：加权平均数、众数、中位数、方差、标准差。
答案:null2.什么是3σ原则？答案:null3.在一堂统计课上，教师进行了三项测试。
每位学生的成绩都在原始成绩上有权重。
测试一、测试二和测试三的权重分别是1、2和2。
下面是一位学生的测试分数，求这个学生分数的总体平均数。
测试 1 2 3分数83 97 92答案:null4.标准差与原始分数的量纲相同，因此，在表示数据的离散程度方向，标准差比方差更好理解。
答案:对5.在期末通考中，八年级一班英语平均成绩是85分，方差是36，张萌计算后得到的标准分数是-2分，求她得的原始分是多少？答案:716.集中量数和差异量数各表示数据的什么特征？答案:null第四章测试1.什么是抽样分布？它与样本分布和总体分布有什么区别？答案:null2.中心极限定理的内容是什么？举例说明。
《统计分析与SPSS的应用(第五版)》课后练习答案(第9章)
《统计分析与SPSS的应用（第五版）》（薛薇）课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据，任意选择两门课程成绩作为解释变量和被解释变量，利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图，并在图上绘制三条回归直线，其中，第一条针对全体样本，第二和第三条分别针对男生样本和女生样本，并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤：图形今旧对话框今散点图今简单散点图今定义分将fore导入Y轴，将phy导入X轴，将sex导入设置标记今确定。
sexO femaleOrnateOU.UU-60.00-40.00-20.00-40.0050.0060.0070.0080.0090.00100.00phy接下来在SPSS输出查看器中，双击上图，打开图表编辑今点击子组拟合线今选择线性3应用。
分析：如上图所示，通过散点图，被解释变量y（即：fore）与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的？相关分析是回归分析的基础和前提，回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式，而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时，进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前，就进行回归分析，很容易造成“虚假回归”。
与此同时，相关分析只研究变量之间相关的方向和程度，不能推断变量之间相互关系的具体形式，也无法从一个变量的变化来推测另一个变量的变化情况，因此，在具体应用过程中，只有把相关分析和回归分析结合起来，才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种，研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
统计分析与SPSS的应用第五版课后练习答案doc1
《统计分析与SPSS的应用（第五版）》课后练习答案第一章练习题答案1、SPSS的中文全名是：社会科学统计软件包（后改名为：统计产品与服务解决方案）英文全名是：Statistical Package for the Social Science.（Statistical Product and Service Solutions）2、SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
数据编辑器窗口的主要功能是定义SPSSa据的结构、录入编辑和管理待分析的数据；结果查看器窗口的主要功能是现实管理SPS必计分析结果、报表及图形。
3、SPSS的数据集：SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合（简称数据集）。
活动数据集：其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS的三种基本运行方式：完全窗口菜单方式、程序运行方式、混合运行方式。
完全窗口菜单方式：是指在使用SPSS的过程中，所有的分析操作都通过菜单、按钮、输入对话框等方式来完成，是一种最常见和最普遍的使用方式，最大优点是简洁和直观。
程序运行方式：是指在使用SPSS的过程中，统计分析人员根据自己的需要，手工编写SPS%令程序，然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
混合运行方式：是前两者的综合。
5、.sav是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPS的析结果文件的扩展名.sps 是语法窗口中的SPS钠序6、SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中；统计分析和绘图功能主要集中在分析、图形等菜单中。
7、概率抽样（probability sampling）:也称随机抽样，是指按一定的概率以随机原则抽取样本，抽取样本时每个单位都有一定的机会被抽中，每个单位被抽中的概率是已知的，或是可以计算出来的。
《统计分析与SPSS的应用(第五版)》课后练习答案(第2章)
《统计分析与SPSS的应用（第五版）》（薛薇）课后练习答案第2章SPSS数据文件的建立和管理1、SPSS中有哪两种基本的数据组织形式？各自的特点和应用场合是什么？SPSS中两个基本的数据组织方式：原始数据的组织方式和计数数据的组织方式。
●原始数据的组织方式：待分析的数据是一些原始的调查问卷数据，或是一些基本的统计指标。
●计数数据的组织方式：所采集的数据不是原始的调查问卷数据，而是经过分组汇总后的数据。
2、什么是SPSS的个案？什么SPSS的变量？个案：在原始数据的组织方式中，数据编辑器窗口中的一行称为一个个案或观测。
变量：数据编辑器窗口中的一列。
3、在定义SPSS数据结构时，默认的变量名和变量类型是什么？如果希望增强SPSS统计分析结果的易读性，还需要对数据结构的哪些方面进行必要说明？默认的变量名：VAR------；默认的变量类型：数值型。
变量名标签和变量值标签可增强统计分析结果的可读性。
4、收集到以下关于两种减肥产品试用情况的调查数据，请问在SPSS中应如何组织该份资料？产品类型体重变化情况明显减轻无明显变化第一种产品27 19第二种产品20 33问：在SPSS中应如何组织该数据？数据文件如图所示：5、什么是SPSS的用户缺失值？为什么要对用户缺失值进行定义？如何在SPSS中指定用户缺失值？缺失值分为用户缺失值（User Missing Value）和系统缺失值（System MissingValue）。
用户缺失值指在问卷调查中，将无回答的一些数据以及明显失真的数据当作缺失值来处理。
用户缺失值的编码一般用研究者自己能够识别的数字来表示，如“0”、“9”、“99”等。
系统缺失值主要指计算机默认的缺失方式，如果在输入数据时空缺了某些数据或输入了非法的字符，计算机就把其界定为缺失值，这时的数据标记为一个圆点“•”。
在变量视图中定义。
6、从计量尺度角度看，变量包括哪三种主要类型？请各举出一个相应的实际数据。
《统计分析与SPSS的应用(第五版)》课后练习答案(第2章)
《统计分析与SPSS的应用（第五版）》（薛薇）课后练习答案第2章SPSS数据文件的建立和管理1、SPSS中有哪两种基本的数据组织形式？各自的特点和应用场合是什么？SPSS中两个基本的数据组织方式：原始数据的组织方式和计数数据的组织方式。
●原始数据的组织方式：待分析的数据是一些原始的调查问卷数据，或是一些基本的统计指标。
●计数数据的组织方式：所采集的数据不是原始的调查问卷数据，而是经过分组汇总后的数据。
2、什么是SPSS的个案？什么SPSS的变量？个案：在原始数据的组织方式中，数据编辑器窗口中的一行称为一个个案或观测。
变量：数据编辑器窗口中的一列。
3、在定义SPSS数据结构时，默认的变量名和变量类型是什么？如果希望增强SPSS统计分析结果的易读性，还需要对数据结构的哪些方面进行必要说明？默认的变量名：VAR------；默认的变量类型：数值型。
变量名标签和变量值标签可增强统计分析结果的可读性。
4、收集到以下关于两种减肥产品试用情况的调查数据，请问在SPSS中应如何组织该份资料？产品类型体重变化情况明显减轻无明显变化第一种产品27 19第二种产品20 33问：在SPSS中应如何组织该数据？数据文件如图所示：5、什么是SPSS的用户缺失值？为什么要对用户缺失值进行定义？如何在SPSS中指定用户缺失值？缺失值分为用户缺失值（User Missing Value）和系统缺失值（System MissingValue）。
用户缺失值指在问卷调查中，将无回答的一些数据以及明显失真的数据当作缺失值来处理。
用户缺失值的编码一般用研究者自己能够识别的数字来表示，如“0”、“9”、“99”等。
系统缺失值主要指计算机默认的缺失方式，如果在输入数据时空缺了某些数据或输入了非法的字符，计算机就把其界定为缺失值，这时的数据标记为一个圆点“•”。
在变量视图中定义。
6、从计量尺度角度看，变量包括哪三种主要类型？请各举出一个相应的实际数据。
《统计分析与SPSS的应用》课后练习答案(第6章)
《统计分析与SP SS的应用(第五版)》课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异，设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人，并随机地将他们分为五个组，每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额，如下表所示：第一组20.0 16. 8 17. 9 21. 2 23.9 26.8 22.4第二组24.9 21. 3 22.6 30.2 29.9 22.5 20.7第三组16.0 20. 1 17.3 20.9 22.0 26.8 20.8第四组17.5 18.2 20.2 17.7 19. 1 18.4 16. 5第五组25.2 26.2 26.9 29.3 (30.4 29.7 28.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图，并利用LSD方法进行多重比较检验。
(1)分析比较均值单因素ANOVA因变量：销售额；因子：组别确定。
［勰ib融巴］卫£也r「匪抽I普型ANOVA 销售额平方和df 均方 F 显著性组之间405. 534 4 101. 384 11.276 .000组内269. 737 30 8. 991总计675. 271 34概率P-值接近于0,应拒绝原假设，认为5种推销方法有显著差异。
(2)均值图：在上面步骤基础上，点选项均值图；事后多重比较LSDV LSDs-ffj-k"alii^Du^carii1 gqnfWTn- i二口呛achsk:IL 鉴 F*b .Dumrt1 5=11 卅 Djncan:节.Thll ： ! Ise-屮1 R'E G AF_ Hochhsras GT2七赴 --------------- 1 R-E-iS-A q0 lb riel潑哎I 叫口辱■带1—lHiihar^/ !T2□ ISjFtt®」（fllTWWIWiiEI 1曲匡I 町K 柱竝圭WI Brctwn~*orEylheI 昌业hDynrisittTi=创 nwsH* ■询 IDjJrruKtC就夕值創玦1研JTI*附探曲□朗闽耶H ■■宅IL” ［两II 药耐丨Aj ni M(D 组别J)组别平均差(I-J) 标准错误显著性95%置信区间下限值上限第一组第二组 -3. 30000 *1. 60279 .048 -6.5733 0267第三组.72857 1. 60279 .653 -2.54484.0019第四组3.05714 1. 60279 .066 2162 6. 3305第五组-6.70000 * 1. 60279 .000 -9.9733-3. 4267 第二组第一组 3. 30000 * 1. 60279 .048 .0267 6. 5733第三组4. 02857* 1. 60279 .018 .7552 7. 3019第四组6. 35714* 1. 60279 .000 3. 0838 9.6305第五组-3. 40000 *1. 60279 .042 -6.6733 1267 第三组第一组 72857 1. 60279 .653 -4.0019 2.5448第二组-4.02857 * 1. 60279 .018 -7. 30197552第四组2. 32857 1. 60279 .157 9448 5. 6019第五组-7. 42857 ♦ 1. 60279 .000 -10. 7019 -4.1552笫四组第一组-3. 057141. 60279.066-6. 3305.2162多重比较LSD (L)0.05可知，1和纟.1和5、2和3, 2和4, 2和5, 3和5, 4和5有显著差异。
教育统计学与SPSS课后作业答案祥解题目
教育统计学课后作业一、P118 1题目：10位大一学生平均每周所花的学习时间与他们的期末考试成绩见表6-17.试问：（1） 学习时间与考试成绩之间是否相关？ （2） 比较两组数据谁的差异程度大一些？ （3） 比较学生2与学生9的期末考试测验成绩。
表6-17 学习时间与期末考试成绩1 2 3 4 5 6 7 8 9 10 学习时间 考试成绩 40 5843 7318 5610 4725 5833 5427 4517 3230 6847 69解题步骤：（1）第一步：定义变量：“xuexishijian ”、“xuexichengji ”后，输入数据.如下图： 第二步：单击选择“分析(Analyze)”中的“相关(Correlate)”中的“双变量(Bivariate Correlations)”，将上图中的“xuexishijian ”和“xuexichengji ”添加到右边变量框中，如下图： 第三步：点击“确定“后，输出结果如下图： 第四步：分析结果由上图可知：学习时间与学习成绩之间的pearson 相关系数为0.714，p （双侧）为0.20。
自由度 df=10-2=8时，查“皮尔逊积差相关系数显著临界值表”知：r 0.05= 0.623 ； r 0.01=0.765。
因为0.765 > 0.714 >0.623，所以在0.05水平上学习时间和学习成绩是相关显著的。
（2）SPSS 软件分析结果如下图：由上图可知：学习时间标准差和平均值为：S 1=12.037 ⎺X 1= 29.00 ；学习时间标准差和平均值为：S 2=12.437 ⎺X 2=56.00 根据差异系数公式可知： 学习时间差异系数为：%100⨯=XSCV S =12.037/29.00×100%=41.51%学习成绩差异系数为：%100⨯=XSCV S =12.437/56.00×100%= 22.27% 有上述结果可知学习时间差异程度大于学习成绩差异程度。
统计分析与SPSS课后习题课后习题答案汇总
《统计分析与SPSS的应用（第五版）》课后练习答案第一章练习题答案1、SPSS的中文全名是：社会科学统计软件包（后改名为：统计产品与服务解决方案）英文全名是：Statistical Package for the Social Science.(Statistical Product and Service Solutions)2、SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
数据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据；结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、SPSS的数据集：SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合（简称数据集）。
活动数据集：其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS的三种基本运行方式：完全窗口菜单方式、程序运行方式、混合运行方式。
完全窗口菜单方式：是指在使用SPSS的过程中，所有的分析操作都通过菜单、按钮、输入对话框等方式来完成，是一种最常见和最普遍的使用方式，最大优点是简洁和直观。
程序运行方式：是指在使用SPSS的过程中，统计分析人员根据自己的需要，手工编写SPSS命令程序，然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
混合运行方式：是前两者的综合。
5、.sav是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPSS分析结果文件的扩展名.sps是语法窗口中的SPSS程序6、SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中；统计分析和绘图功能主要集中在分析、图形等菜单中。
7、概率抽样(probability sampling)：也称随机抽样，是指按一定的概率以随机原则抽取样本，抽取样本时每个单位都有一定的机会被抽中，每个单位被抽中的概率是已知的，或是可以计算出来的。
统计分析与SPSS课后习题课后习题答案汇总(第五版)
《统计分析与SPSS的应用（第五版）》课后练习答案第一章练习题答案1、SPSS的中文全名是：社会科学统计软件包（后改名为：统计产品与服务解决方案）英文全名是：Statistical Package for the Social Science.(Statistical Product and Service Solutions)2、SPSS的两个主要窗口是数据编辑器窗口和结果查看器窗口。
●数据编辑器窗口的主要功能是定义SPSS数据的结构、录入编辑和管理待分析的数据；●结果查看器窗口的主要功能是现实管理SPSS统计分析结果、报表及图形。
3、SPSS的数据集：●SPSS运行时可同时打开多个数据编辑器窗口。
每个数据编辑器窗口分别显示不同的数据集合（简称数据集）。
●活动数据集：其中只有一个数据集为当前数据集。
SPSS只对某时刻的当前数据集中的数据进行分析。
4、SPSS的三种基本运行方式：●完全窗口菜单方式、程序运行方式、混合运行方式。
●完全窗口菜单方式：是指在使用SPSS的过程中，所有的分析操作都通过菜单、按钮、输入对话框等方式来完成，是一种最常见和最普遍的使用方式，最大优点是简洁和直观。
●程序运行方式：是指在使用SPSS的过程中，统计分析人员根据自己的需要，手工编写SPSS命令程序，然后将编写好的程序一次性提交给计算机执行。
该方式适用于大规模的统计分析工作。
●混合运行方式：是前两者的综合。
5、.sav是数据编辑器窗口中的SPSS数据文件的扩展名.spv是结果查看器窗口中的SPSS分析结果文件的扩展名.sps是语法窗口中的SPSS程序6、SPSS的数据加工和管理功能主要集中在编辑、数据等菜单中；统计分析和绘图功能主要集中在分析、图形等菜单中。
7、概率抽样(probability sampling)：也称随机抽样，是指按一定的概率以随机原则抽取样本，抽取样本时每个单位都有一定的机会被抽中，每个单位被抽中的概率是已知的，或是可以计算出来的。
《统计分析和SPSS的应用(第五版)》课后练习答案与解析(第5章)
《统计分析与SPSS的应用（第五版）》（薛薇）课后练习答案第5 章SPSS的参数检验1、某公司经理宣称他的雇员英语水平很高，如果按照英语六级考试的话，一般平均得分为75分。
现从雇员中随机选出11人参加考试，得分如下：80, 81, 72, 60, 78, 65, 56, 79,77,87, 76 请问该经理的宣称是否可信。
原假设：样本均值等于总体均值即u=u0=75步骤：生成spss 数据→分析→比较均值→单样本t 检验→相关设置→输出结果（Analyze->compare means->one-samples T test ；）采用单样本T 检验（原假设H0:u=u0=75, 总体均值与检验值之间不存在显著差异）；单个样本统计量N 均值标准差均值的标准误成绩11 73.73 9.551 2.880单个样本检验检验值= 75差分的95% 置信区间t df Sig.( 双侧) 均值差值下限上限成绩-.442 10 .668 -1.273 -7.69 5.14分析：指定检验值:在test 后的框中输入检验值（填75），最后ok!分析：N=11 人的平均值（mean）为73.7，标准差（std.deviation）为9.55,均值标准误差(std error mean) 为2.87.t 统计量观测值为-4.22，t 统计量观测值的双尾概率p-值（sig.(2-tailed)）为0.668，六七列是总体均值与原假设值差的95%的置信区间,为(-7.68,5.14), 由此采用双尾检验比较 a 和p。
T 统计量观测值的双尾概率p-值（sig.(2-tailed) ）为0.668＞a=0.05 所以不能拒绝原假设；且总体均值的95% 的置信区间为(67.31,80.14), 所以均值在67.31~80.14 内,75 包括在置信区间内,所以经理的话是可信的。
2、在某年级随机抽取35 名大学生，调查他们每周的上网时间情况，得到的数据如下（单位：小时）：（1）请利用SPSS 对上表数据进行描述统计，并绘制相关的图形。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
教育统计学课后作业一、P118 1题目：10位大一学生平均每周所花的学习时间与他们的期末考试成绩见表6-17.试问：（1）学习时间与考试成绩之间是否相关？（2）比较两组数据谁的差异程度大一些？（3）比较学生2与学生9的期末考试测验成绩。
表6-17 学习时间与期末考试成绩1 2 3 4 5 6 7 8 9 10学习时间考试成绩4058437318561047255833542745173230684769解题步骤：（1）第一步：定义变量：“xuexishijian”、“xuexichengji”后，输入数据.如下图：1第二步：单击选择“分析(Analyze)”中的“相关(Correlate)”中的“双变量(Bivariate Correlations)”，将上图中的“xuexishijian”和“xuexichengji”添加到右边变量框中，如下图：第三步：点击“确定“后，输出结果如下图：第四步：分析结果3由上图可知：学习时间与学习成绩之间的pearson 相关系数为0.714，p （双侧）为0.20。
自由度 df=10-2=8时，查“皮尔逊积差相关系数显著临界值表”知：r 0.05= 0.623 ； r 0.01=0.765。
因为0.765 > 0.714 >0.623，所以在0.05水平上学习时间和学习成绩是相关显著的。
（2）SPSS 软件分析结果如下图：由上图可知：学习时间标准差和平均值为：S 1=12.037 ⎺X 1= 29.00 ；学习时间标准差和平均值为：S 2=12.437⎺X 2=56.00 根据差异系数公式可知： 学习时间差异系数为：%100⨯=XSCV S =12.037/29.00×100%=41.51% 学习成绩差异系数为：%100⨯=XSCV S =12.437/56.00×100%=22.27% 有上述结果可知学习时间差异程度大于学习成绩差异程度。
（4） 把学生2和学生9的期末考试成绩转化成标准分数：Z 2=(X -⎺X) /S= (73—56)/12.437=1.367 Z 9=(X-⎺X)/S=(68—56)/12.437=0.965 由上计算可知：学生2期末考试测验成绩优于学生9的期末考试测验成绩。
二、P119 2题目：某班数学的平均成绩为90，标准差10；化学的平均分为85，标准差为8；物理的平均分为79，标准差为15.某生这三科成绩分别为95,80,80.试问 （1） 该生在哪一学科上突出一些？（2） 该班三科成绩的差异度如何？有无学习分化现象？ （3） 该生的学期分数是多少？ （4） 三科的总平均和总标准差是多少？ 解题步骤：（1） 将该生地三科成绩转化为标准分数： Z 数=(X - ⎺X) /S= (95—90)/ 10=0.500 Z 化=(X -⎺X) /S= (80—85)/8=-0.625 Z 物=(X -⎺X) /S= (80—79)/15=0.067由以上计算可以看出该生在数学上突出一些。
（2） 根据差异系数系数公式%100⨯=XSCV S 可知：该班三科成绩的差异系数分别为数学差异系数：%100⨯=XSCV S = 10/90×100%=11.11% 化学差异系数：%100⨯=XSCV S = 8/85×100%=9.41% 物理差异系数：%100⨯=XSCV S = 15/79×100%=18.99% 由上述计算可以看出三门学科的差异系数9%~20%，所以这三门学科均存在分化苗头。
（3） 由（1）可知三门学科的标准分数，所以标准分数的加权平均数为： 标准分数的加权平均分⎺0.5(0.625)0.0670.0193fZ Z f+-+===-∑∑ 计算结果表明：该生的学期分数在班平均分数以下0.019个标准差的位置上，与平均水平非常接近。
（4） 总平均分：100%10/71100%14.08%S SXCV =⨯=⨯= 离差tdX X =-d 数= 90-85=5 d 化=85-85=0 d 物=79-85= -6总标准差：5ts==三、P119 5题目：三位教师对6位青年在大学的学习成绩进行评定（在0到20内），结果见表6-18.试问三位教师的评定是否一致？ 表6-18 学习成绩评定结果 教师 1 2 3 4 5 6 A 15 12 18 4 8 17 B 8 13 16 5 2 10 C 10 9 15 4 5 12 R 33 34 49 13 15 39 R 21089 1156 2401 169 225 1521 R ∑183 2R∑6561解题步骤：因为评定对象为6，所以用W 系数检验法进行判断： 由上图可知：R ∑= 334892R ∑=6561SS=22/()N R R -∑∑=6561-33489/6=979.5查肯德尔W 系数临界值表9，当N=6，k=3时，SS 0.05=103.9 SS 0.01=122.8 因为SS=979.5>SS 0.01=122.8,所以一致性极显著，三位教师的评定一致。
四、P120 12题目：六年级的周宾在一次期末考试时语文96分，数学84分，父母批评他的数学学的不好，这种说法对吗？为什么？已知他所在班语文平均成绩为92，标准差为9.54，数学平均分为73，标准差为7.12. 解题步骤：父母的这种说法是不科学的，语文、数学两个基准不一样的学科不能单单从表面上进行比较，要转化成标准分数才能判断优劣：9692=0.4199.54Z -=语文8473 1.5457.12Z -==数学由上述计算可知，周宾的数学成绩明显优于语文成绩，其父母的判断是错误的。
五、P196 1题目：假设对4000名大学新生的英语进行分班考试，结果考试成绩是正态分布。
若将学生分为四个等级进行分班教学，则各个等级应当分布多少学生？ 解题步骤：（1） 确定各组在正态分布上的位置正态分布区间以6个标准差为全距，因能力分组是等距的，则每一个等级的区间在横轴上的距离为6σ/4=1.5σ。
则四个组的能力区间范围是：A 组1.5σ以上，B 组为0σ~1.5σ，C 组为0σ~-1.5σ，D 组为-1.5σ以下。
（2） 查表，有Z 求p 。
A 组：P A =0.5-0.4331=0.0669 B 组：P B =0.4331 C 组：P C =0.4331D 组：P D =0.5-0.4331=0.0669 (3) 求各组人数A=D=4000⨯0.0669=267.6 B=C=4000⨯0.4331=1732.4六、P196 3题目：为了对某门课的教学方法进行改革，某校对情况相似的两个班进行了教改7实验。
甲班45人，采用教师面授的方法；乙班36人，采用教师讲授要点，学生讨论的方法。
一年后，用同一试卷对两个班进行测验。
结果，甲班平均分为69.5，标准差为8.35；乙班平均分为78，标准差为16.5（假设方差齐性）。
试问： （1） 两种教学方法的效果有无显著差异？ （2） 哪种教学方法的差异程度大些？ （3） 两种教法的总体均数是多少？ 解题步骤： (1)1、条件分析根据题意，可知总体为正态分布，总体方差未知，样本为独立，样本容量大于30，为双侧检验，可选择t 检验或Z ’检验。
2、检验过程 ① 建立假设：H o ：两种教学方法的效果无明显差异 H a ：两种教学方法的效果有明显差异② 检验值计算：均数之差的标准误：2.86D XSE===检验值：127869.5t 2.972.86D XX X SE--===③比较决策：当df=n 1+n 2-2=79时，t (79)0.01/2=2.650。
因为t=2.97> t (79)0.01/2=2.650，p<0.01即t=2.97处于-2.650~2.65之外。
所以差异极其显著，拒绝虚无假设，接受研究假设，说明两种教学方法存在明显的差异。
(2)根据差异系数公式：%100⨯=XSCV S可知甲班、乙班的差异系数为：CV甲=8.35/69.5×100%=12.01%CV乙=16.5/78×100%=21.15%上述计算结果表明，乙班的教学方法差异程度大于甲班。
（3）两种教法的总体均数=（69.5×45+78×36）/（45+36）=73.28七、P274 1题目：用三种不同的教学方法分别对三个随机抽取的实验组进行教学实验，试实验后同一测验成绩如下，试问三中教学方法的效果是否存在显著差异（假设实验结果呈正态分布）教法A：76 , 78 , 60 , 62 , 74教法B：83 , 70 , 82 , 76 , 69教法C：92 , 86 , 83 , 85 , 79解题步骤：(1)定义变量“jiaofa”和“chengji”，输入数据并保存。
(2)点击“分析”→“比较均值”→“单因素ANOVA”(3)选择“shuju”到“自变量”,选择“jiaofa”到“因子”。
(4)点击“选项”，选择“描述”、“方差同质性检验”,点击“继续”返回。
(5)点击“两两比较…”，选择“Tukey”，点击“继续”返回。
(6)点击“确定”，结果如下。
上述结果表示样本方差齐性，可以选用“Tukey”法计算。
上述结果表明，三组学习成绩间存在显著性差异，即不同的教法对学生的学习产生了极显著影响。
上述结果表明在0.05水平上教法A明显优于教法C八、P275 4题目：某地区在甲、乙两所中学随机抽取40名学生进行了语文统一测验，结果：甲校平均成绩为74分，标准差为5分；乙校平均成绩为71分，标准差为10分。
试问：（1）甲、乙两所学校的数学成绩有无显著差异？（2）甲、乙两所学校数学成绩谁的差异程度大一些？（3）在甲、乙两所学校同得80分得学生，其位置一样吗？为什么？（4）根据甲、乙两所学校的情况，试估计该地区数学测验成绩的真实情况。
解题步骤：9（1）该题为非正态，总体方差未知，样本独立。
样本容量大于30，，为双侧检验，选择Z ’检验。
建立假设：H o ：μ1=μ2 H a ：μ1≠μ2均数之差标准误：1.94DXSE====()127471/1,941.55DXZ X X SE-'==-=因为Z ’=1.55<Z0.05/2=1.96,即Z ’=1，55处于-1.96~1.96之内，差异不显著，接受虚无假设。
拒绝研究假设，两所学校的数学成绩无明显差异。
（2）甲校差异系数为：100%5/74100% 6.76%S SXCV =⨯=⨯= 乙校差异系数为：100%10/71100%14.08%S SXCV =⨯=⨯= 结果表明，乙校的数学成绩差异程度大于甲校。