教育统计学课后练习参考答案
王孝玲《教育统计学》第六章课后练习题超详细解答步骤
15 答： 错误：拒绝了属于真实的零假设，犯这类错误的可能性的大小为α值的大小。通过选择 适当的显著性水平加以控制，加大保留区范围。 错误：保留了属于不真实的零假设，犯这类错误的可能性的大小为β值的大小。（1）利
用已知的实际总体参数值有假设参数之间的大小关系，合理安排拒绝区的位置，尽量减小 β值；（2）将样本容量增大，这样的话，形态高狭，两侧面积小，β值小。 16 答： 采用右侧检验，控制β 错误的发生。 H0：µ ≤ ，H1：µ > 3
7䁤 − 7 䁤 − 䁤 = =− 䁤 8 䁤4 䁤 4 − 朴− 根据假设，采用双侧检验 显著性水平临界值为 t(14)0.05=2.145, t(14)0.01=2.977
由于|t|= 䁤 8 < 2.145= t(14)0.05 ， P>0.05，因此保留 H0 假设，拒绝 H1 假设，即该校测验成绩与全 区之间没有显著差异。 20. 答： 由于总体标准差未知，且样本容量小 n<30，因此可按 t 分布计算 ≥ 朴 䁤8，H1： 提出假设 H0： 计算统计量 t = 49䁤朴， = 7䁤8，n= 28，μ = 朴 䁤8 < 朴 䁤8
由于总体标准差未知，且样本量小 n<30, 因此置信区间可按 t 分布计算
=(92+94+96+66+84+71+45+98+94+67)/10= 807/10=80.7
P 8 䁤7 −
P
−
t 䁤 朴
9 䁤 朴
7䁤
<μ<
< μ < 8 䁤7 + 4
+
t 䁤 朴 9 䁤 朴
7䁤
统计学课后习题答案(全)
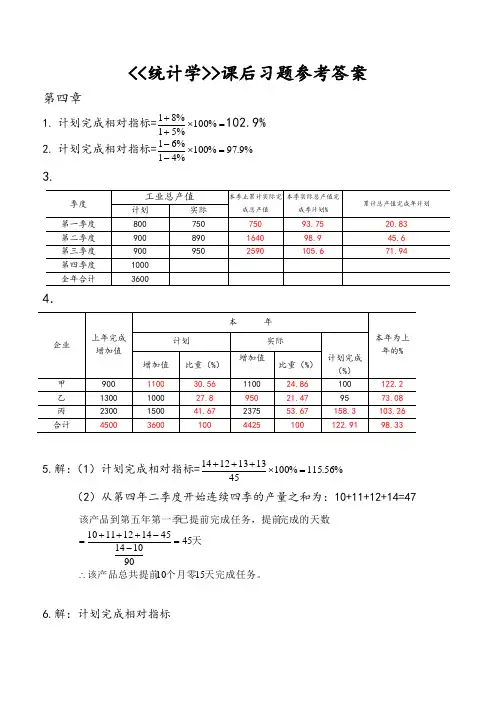
<<统计学>>课后习题参考答案第四章1. 计划完成相对指标==⨯++%100%51%81102.9% 2. 计划完成相对指标=%9.97%100%41%61=⨯-- 3.4．5.解：（1）计划完成相对指标=%56.115%1004513131214=⨯+++（2）从第四年二季度开始连续四季的产量之和为：10+11+12+14=47天完成任务。
个月零该产品总共提前天完成的天数已提前完成任务，提前该产品到第五年第一季1510459010144514121110∴=--+++=6.解：计划完成相对指标=%75.126%100%1.0102005354703252795402301564=⨯⨯⨯++++++（2）156+230+540+279+325+470=2000（万吨） 所以正好提前半年完成计划。
7．8．略第五章 平均指标与标志变异指标1．甲X =.309343332313029282726=++++++++乙X =44.319403836343230282520=++++++++ AD 甲=}22.29303430333032303130303029302830273026=-+-+-+-+-+-+-+-+-AD 乙=}06.594044.313844.313644.313444.313244.313044.312844.312544.3120=-+-+-+-+-+-+-+-+-R 甲=34-26=8 R 乙=40-20=20σ甲 =9)3334()3033()3032()3031()3030()3029()3028()3027()3026(222222222-+-+-+-+-+-+-+-+-=2.58 σ乙=9)44.3140()44.3138()44.3136()44.3134()44.3132()44.3130()44.3128()44.3125()44.3120(222222222-+-+-+-+-+-+-+-+-=6.06V 甲=1003058.2⨯%=8.6% V 乙=%3.19%10044.3106.6=⨯ 所以甲组的平均产量代表性大一些. 2.解：计算过程如下表：甲X =.)(5.101780元= 乙X =（元）9708077600= 3.解：计算过程如下表：甲X =.4.11980=（件） 乙X =8.120809660=（件） σ甲＝06.98075.6568=（件） σ乙=81.10809355=（件） V 甲=1004.11906.9⨯%=7.58% V 乙=%94.8%1008.12081.10=⨯ 所以甲厂工人的平均产量的代表性要高些.4. 解:()()94.761018102457047.7610121871871870775121873595128518757653550=⨯-+==⨯-+--+==++++⨯+⨯+⨯+⨯+⨯=e M M X 5.解:(1)上期的平均计划完成程度为:()()第六章元解解度为下期的平均计划完成程tH V P X P P P P /3.2884102950943.5062900255.3212800604.43210943.506255.321604.432:.7%1.32%1009067.0291.0291.0%67.901%67.90%67.90%67.90%10030028300:.6%37.103%1031400%1011200%107810%110961400120081096:)2(%67.99%1001500100070080%951500%1001000%108700%1108044=⨯⎪⎭⎫ ⎝⎛++⨯++==⨯==-⨯====⨯-==++++++=⨯+++⨯+⨯+⨯+⨯σ1.()())(7.788%67.41500:2000%67.41500600:.6)(6.62126907106557306806702650600269071061527106556552655730620273068060026806706402670650:2)(7.62327107006907206806202680610271070062527006906452690720640272068062026806206002620680:)1(:.5%63.79%10026206005802580257646245002435:.4%85.105%100%113385%102350%97463%120485%105412%112410%98368%106350%105310%110324%102306%101303385350463485412410368350310324306303::.3872232122221030980329809002290010201210208402284067022670600.2104万吨年该县粮食产量为平均增长速度解元工人的月平均工资为乙工区上半年建筑安装元工人的月平均工资为甲工区上半年建筑安装解解度为全年月平均计划完成程解=+⨯=-==++++++⨯++⨯++⨯++⨯++⨯++⨯+=++++++⨯++⨯++⨯++⨯++⨯++⨯+=⨯++++++==⨯++++++++++++++++++++++=+++++⨯++⨯++⨯++⨯++⨯++⨯+=C a 7解:计算过程如下表:)(94.6653.444.45:1994:3.46025844.4594092万元年的地方财政支出额为则直线趋势方程为=⨯++=======∑∑∑bta y t tyb ny a二次曲线方程为:y = 0.0108x 2 + 4.1918x + 24.143(过程略) 指数曲线方程为:y = 26.996e 0.0978x8.解:计算过程如下表:9.解：(1)同季平均法求季节比率的过程如下表:(2)趋势剔除法测定的季节变动如下表:第七章 统计指数()()()()01001011111175000124000081138.44%5000012350008750002540000182138.03%500002535000181075000940000390.98%127500084000022750002540000425qqzpk q z q zq p q p q z kq z p q k p q⨯+⨯===⨯+⨯⨯+⨯===⨯+⨯⨯+⨯===⨯+⨯⨯+⨯==∑∑∑∑∑∑∑∑111111110102.12%75000184000015602.108.8%1200360110%105%pp q p q k p q p q p p=⨯+⨯====+∑∑∑∑11111560.135.65%1150135.65%124.68%108.8%.120%1800115%90096%6003.114.27%330042003300111.38%114.27%.pqpq qpqpq p qp q k p qk k k q q p q p q k q p q pkk k======⨯+⨯+⨯=======∑∑∑∑∑∑ 110101001013200005.100%128%250000128%123.1%14%320000307692.3104%307692.325000057692.3320000307692.312307.pq pqq PpK K K p qp q K p q p qq p q =⨯====+===-=-=-=-=∑∑∑∑∑∑1解：K 零售量变动对零售额变动影响的绝对值为：（万元）零售物价变动对零售总额变动影响的绝对值为：p 1110010000107350000120%120%180000110%110%116%116%17.6%107.6%350000291666.67120%180000163636.36.110%1pq pq q q pq pq q q K q K q p q Kq p q K p q p q ==+===+==+==+========⨯=∑∑∑∑∑∑∑∑城1城农城农1农1城城城1农农农城城城（万元）6.解：已知p ，，p ，，K ，K p 则p K 0010111101001116%291666.67338333.33107.6%163636.36176072.72350000180000103.03%338333.33176072.723%q pp q p q p q q q k p q p q p q ⨯==⨯=⨯=++====++∴∑∑∑∑∑∑∑∑农农农11城农城农K p p 该地区城乡价格上涨了。
心理与教育统计学课后题答案
张厚粲现代心理与教育统计学第一章答案1名词概念（1）随机变量答：在统计学上把取值之前，不能准确预料取到什么值的变量，称为随机变量。
（2）总体答：总体（population）又称为母全体或全域，是具有某种特征的一类事物的总体，是研究对象的全体。
（3）样本答：样本是从总体中抽取的一部分个体。
（4）个体答：构成总体的每个基本单元。
（5）次数是指某一事件在某一类别中出现的数目，又称作频数，用f表示。
（6）频率答：又称相对次数，即某一事件发生的次数除以总的事件数目，通常用比例或百分数来表示。
（7）概率答：概率(probability),概率论术语，指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值，称为事件A的概率，记为P（A）。
（8）统计量答：样本的特征值叫做统计量，又称作特征值。
（9）参数答：又称总体参数，是描述一个总体情况的统计指标。
（10）观测值答：随机变量的取值，一个随机变量可以有多个观测值。
2何谓心理与教育统计学？学习它有何意义？答：（1）心理与教育统计学是专门研究如何运用统计学原理和方法，搜集、整理、分析心理与教育科学研究中获得的随机性数据资料，并根据这些数据资料传递的信息，进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲，就是在心理与教育研究中，通过调查、实验、测量等手段有意地获取一些数据，并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理，最后得出结论的一种研究方法。
（2）学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中。
它的主要任务是对客观事实进行预测和分类，从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力，就必须运用科学的方法。
统计学正是提供了这样一种科学方法。
统计方法是从事科学研究的一种必不可少的工具。
《教育统计学》(教育学)作业参考答案
《教育统计学》作业参考答案（教育学专业）一、名词解释1. 分层抽样：按与研究内容有关的因素或指标先将总体划分成几个部分，然后从各部分（即各层）中进行单纯随机抽样或机械抽样，这种抽样方法称为分层抽样。
2. 描述统计：对已获得的数据进行整理、概括，显现其分布特征的统计方法称为描述统计。
3. 集中量：集中量是代表一组数据典型水平或集中趋势的量。
它能反映频数分布中大量数据向某一点集中的情况。
4. 统计表：统计表是用来表达统计指标与被说明的事物之间数量关系的表格。
5. 总体：总体是我们所研究的具有某种共同特性的个体的总和。
样本是从总体中抽出的作为观察对象的一部分个体。
6. 二列相关：当两个变量都是正态连续变量，其中一个变量被人为的划分为二分变量，表示这两个变量之间的相关，称为二列相关。
7. 参数：总体上的各种数字特征是参数。
业绩反映总体上各种特征的数量是参数。
8. 小概率事件：样本统计量（随机事件）在其抽样分布上出现的概率小于或等于事先规定的水平，则该事件为小概率事件。
9. 中位数：在一组安大小顺序排列的数据中，位于中央位置上的那个数称为中为数。
10. 统计量和参数：样本上的数字特征量是统计量。
总体上的各种数字特征量是参数。
11. 回归分析：把存在相关的两个变量，一个作为自变量，另一个作为因变量，并建立方程式，由自变量的值估计、预测因变量的值，这一过程称为回归分析。
12. 相关关系：两个变量间的不精确、不稳定的变化关系称为相关关系。
二、填空题1. 从变化方向上看，两个变量之间的相关类型有正相关、负相关、零相关。
2. 教育统计资料的来源有两个方面：经常性资料、专题性资料。
3. 表示间断变量的统计图有直条图和圆形图。
4. 假设检验一般有两个相互对立的假设，即零假设和备择假设。
5. 统计图的结构一般包括标题、图号、标目、图形、图注等。
6. 差异系数是标准差与平均数的百分比。
7. 统计数据按来源方式可分为点计数据和测量数据。
王孝玲《教育统计学》第十一章课后练习题超详细解答步骤
(3) 检验形式 双侧检验 (4) 决断 由于 Z0.05=1.96， Z0.01=2.98
因此，Z=11.295 > 2.98= Z0.01，因此在 0.01 的显著性水平上拒绝 H0，保留 H1，即这个样本不是来 自于ρ=0 的总体。
3. 答： 该题属于ρ=ρ0，n< 50 条件下，相关系数的显著性检验。 (1) 假设 H0: ρ=0.54, H1: ρ≠0.54 (2) 统计量 等距转换之后 Zr=0.365， Zρ=0.604 2
9. 答： 该题为二列相关问题。 首先, 计算 150 个人的二列相关系数 rb：
测验分数
10
20
30
40
50
60
70
80
90
人数总 人数比 和 率
测验平均数
标准差
6
组中值 X 对某提 合格 回答的 情况 不合格
15
25
35 4
45 11 12
55 28 19
65 20 8
75 18 5
85 9 1
教育统计学（第四版），王孝玲著，华东师范大学出版社 课后题参考答案
第十一章. 练习题参考答案
1. 答： X 89 75 77 73 68 78 81 90 70 74 79 总和 854 Y 92 82 76 78 70 84 83 85 75 80 77 882 XY 8188 6150 5852 5694 4760 6552 6723 7650 5250 5920 6083 68822 X 平方 7921 5625 5929 5329 4624 6084 6561 8100 4900 5476 6241 66790 Y 平方 8464 6724 5776 6084 4900 7056 6889 7225 5625 6400 5929 71072
教育统计学王孝玲课后答案
教育统计学王孝玲课后真题及答案王孝玲教育统计学课后真题及答案
一、单选题
1．定義變量的取值由（）决定。
A、樣本
B、規格範圍
C、研究方法
D、計量方法
答案：B
2．家政電器市場形勢把根據一定的分析方法預測將來家政電器市場的發展情況稱為（）。
A、抽樣
B、比較
C、預測
D、評價
答案：C
3．蒐集教育統計資料有以下（）等方法。
A、追蹤调查法
B、定点调查法
C、聯屬模式
D、抽樣調查法
答案：A、B、C、D
二、多选题
1．教育統計學的核心內容有（）。
A、定義教育統計
B、數理基礎
C、研究技術
D、教育統計學研究
答案：A、B、C、D
2．教育統計資料的分類有以下（）等。
A、樣本資料
B、非樣本資料
C、統計資料
D、記錄資料
答案：A、B、C、D
三、填空题
1．教育统计学是统计学在教育研究领域应用的学科，主要研究（）。
A、教育資料的標準化原則
B、教育研究的抽樣方法
C、教育研究的統計研究方法
D、教育研究的數據統計分析答案：A、B、C、D。
XXX18秋[0282]《教育统计学》作业答案
![XXX18秋[0282]《教育统计学》作业答案](https://img.taocdn.com/s3/m/05b04fab50e79b89680203d8ce2f0066f53364a9.png)
XXX18秋[0282]《教育统计学》作业答案1.√2.√3.√4.√5.√6.√7.√8.×（几何平均数是同一变量不同时间或不同空间的比率的平均数）9.√10.√11.√12.×（样本容量指样本中个体的数量）13.√14.√15.√16.×（中位数是80）17.×（标准差越小，说明数据分布的范围越小，分布越整齐）18.×（两个变量之间的变化方向相反时，它们之间的关系称为负相关）19.√20.√21.√22.√23.×（统计表的标题要写在表的上方）24.√25、√ 差异系数是一种用于比较不同数据集变异程度的指标，它是方差与算术平均数的百分比。
26、√ 总体的各种数字特征称为参数，它们可以通过样本统计量的计算来估计。
27、×相关系数的值介于-1和1之间，它可以反映两个变量之间的相关关系强度和方向。
28、√ 双向表χ检验适用于按照两种标准分类的点计数据资料，可以用于判断两个分类变量之间是否存在关联。
29、√ 两个变量之间的相关系数为正数，说明它们存在正相关关系，即随着一个变量的增加，另一个变量也会增加。
30、√ 任何随机事件的概率都是介于0和1之间的正数，且所有可能事件的概率之和为1.31、√ 标准差是一种用于衡量数据集中数据离散程度的指标，可以用来比较两组单位不同的数据资料的差异程度。
32、×一组数据中有极端数值时，算术平均数可能会受到影响，因此可以使用中位数等其他集中趋势指标来描述数据的典型水平。
33、√ 直条图是一种用面积表示频数分布的图形，可以用于展示数据的分布情况。
34、× χ2分布呈现出右偏态或左偏态的情况，而不是正偏态。
35、√ 相关系数可以描述两个变量之间的变化方向和密切程度，通常用于研究变量之间的关系。
36、×有5个学生的体育成绩分别为：88、73、88、78、98分，这组成绩的众数是88分，而不是98分。
第四章 教育统计学课后练习题参考答案
2
X X
3.12
MD
M
d
X
n
2 .8
4. 答：
分数 组中值 频数
10 15 1
20 25 0
30 35 0
40 45 3
50 55 4
60 65 5
70 75 4
80 85 2
90 95 1
总和 20
由于已知 Md=64 因此，平均差为
2
MD
n 1 15 64 0 0 3 45 64 4 55 64 5 65 64 4 75 64 2 85 64 1 95 64 20
教育统计学（第四版），王孝玲著，华东师范大学出版社 课后题参考答案
第四章. 练习题参考答案
1.
答：
1 全距 R=Xmax-Xmin=36-20=16
四分位距 20，23，25，27，29，31，33，36 由于，Q1=24，Q3=32
2
QD
2.
Q3 Q1 32 24 4 2 2
答：
f
X Md
13.2
5. 答：
1
定义公式
由于平均数为 X
41 39 37 35 38 38 5
因此， 方差为
2 x
X X 41 - 38 39 - 38 37 - 38 35 - 38 38 - 38
2 2 2 2 2
男生 CV 因此，离散程度女生比男生大 9. 答：
平均数小于中位数，因此分布呈负偏态
偏态量 SK
3( X M d )
X
《教育统计学》答案
《教育统计学》答案一、简答题1．举例说明什么是分层抽样。
分层抽样是先按与研究内容有关的因素将总体各单位(或个体)分为不同的等级或类型，然后按比例或不按比例从每一层中再用简单随机抽样或机械抽样的方法抽取一定数量的个体构成样本。
它可抽到总体内各种类型或水平层次的个体，样本对总体的代表性强，其原则是各层内个体差越小越好，而层间的差异越大越好。
2．检验的适用资料是什么？它有哪些用途？检验是检验计数资料或次数资料实际观察次数分布与理论次数分布之间差异是否显著的方法，是检验计数资料最常用的方法。
主要用途有两个：一是用于按一个分类标志分类的资料，检验各类实际观察次数与理论次数是否相符合，即吻合性检验；二是用于按两个分类标志分类的资料，检验这两个分类标志（或因素）之间是否独立，即独立性检验。
3．参数假设检验与非参数假设检验有什么区别？ 参数检验法主要有检验、检验、检验等，是在假设总体正态分布的前提下，用样本统计量推断总体相应参数的特征，它受样本容量与总体分布形态限制。
在总体分布非正态或分布形态不清时，通过样本信息去推断总体时，不能直接对总体参数进行检验，而是通过检验其分布情况实现的，这时采用的是非参数检验法。
它与参数检验最大的区别是对样本信息利用不全面。
4．简述解释和运用相关系数时应注意的问题。
第一，两变量间存在相关，仅意味着变量间有关联，并不一定是因果关系。
第二，相关系数不是等距的测量单位，不能做加、减、乘、除运算。
第三，相关系数r 受变量取值区间大小及观测值个数的影响较大。
第四，一定的相关系数在一定情况下使用才具有意义；在另一种情况下运用便失去了意义。
第五，通过实际观测值计算的相关系数，须经过显著性检验确定其是否有意义。
二、计算题1. 某市去年对中学生进行健康检查，八年级学生的近视率为38％，今年在一些中学随机抽取了八年级学生有1200人进行视力检查，患近视的有520人。
该市教育局长认为今年八年级学生的视力比去年有了明显的减退。
2020年智慧树知道网课《教育统计学》课后习题章节测试满分答案
第一章测试1【单选题】(2分)最早使用统计学这一学术用语的是（）A.政治算术学派B.国势学派C.社会统计学派D.数理统计学派2【单选题】(2分)数理统计学的奠基人是（）A.阿亨瓦尔B.威廉·配第C.凯特勒D.恩格尔3【单选题】(2分)学校实验室的设备台数、设备价格是（）A.前者是离散变量B.前者是连续变量C.离散变量D.连续变量4【单选题】(2分)对某地区学校教师情况进行研究，统计总体是（）A.该地区全部学校B.该地区全部学校的全部教师C.每个学校的全部教师D.每个学校5【单选题】(2分)统计的总体性特征表现在（）A.它是从总体入手，达到对个体的认识B.它只对总体现象的量进行认识，抛开了对总体现象质的认识C.它排除了认识个体现象的必要性D.它是从个体入手，达到对总体的认识6【单选题】(2分)在学生调查中，学生的“身高”是（）A.连续变量值B.随机变量值C.离散变量D.连续变量7【单选题】(2分)构成统计总体的必要条件是（）A.差异性B.综合性C.同质性D.社会性8【单选题】(2分)你询问了你们班的8位同学在去年的教育统计学成绩，这些成绩的平均数是65分。
基于这种信息，你认为全班在去年的教育统计学平均成绩不超过70分。
这个例子属于统计学的（）A.参数统计B.推论统计C.理论统计D.描述统计。
王孝玲《教育统计学》第五章课后练习题超详细解答步骤
考试科 目 物理 化学 数学 总和
标准分数 甲生 -3 0.67 0.92 -1.41 乙生 2 -0.67 -0.08 1.25
在团体中的位置（在改分数之下的人数比例） 甲生 0.00135 0.74857 0.82121 乙生 0.97725 0.25143 0.46812
5
总平均
-0.47
0.416667
18（人）
226（人）
11 （人）
18（人）
6
13. 答： 首先，通过人数比例计算每个等级的所占面积；其次，寻找每个面积对应的中位数来代表等 级的数量化分数 教师甲（人 等级 优 良 中 差 极差 总和 数） 10 20 5 5 0 40 甲比率（人数比 例） 0.25 0.5 0.125 0.125 0 本组 1/2 至 Z=0 的 面积 0.375 0 0.3125 0.4375 中位数 1.15 0 -0.89 -1.53 -
7. 答： (1) 直接查表 (2) P(2.8)-P(0.5)= 0.49744 – 0.19146=0.30598 (3) 直接查绝对值 (4) P(-1.5)+P(1.8)=0.43319+0.46407=0.89726 (5) P(-1.8)-P(-0.5)= 0.46407-0.19146=0.27261 (6) P(-2.5)+P(0.8)=0.49379+0.28814=0.78193 8. 答： (1) 直接查绝对值 (2) 直接查表 (3) P(Z)=0.5-0.2=0.3 ~ 0.29955 Y=0.28034 (4) P(Z)=0.8/2=0.4 ~ 0.39973 Y=0.17585
本组 1/2 至 Z=0 的
中位数
教育统计学答案
（0282）《教育统计学》复习思考题答案一、填空题1. 统计学是研究统计原理和方法的科学。
2．我们所研究的具有某种共同特性的个体总和称为总体。
3．一般情况下，大样本是指样本容量超过30 的样本。
4．表示总体的数字特征的特征量称为参数。
5．要了解一组数据的集中趋势，需计算该组数据的集中量。
6. “65、69、72、87、89”这组数据的算术平均数是76.4 。
7. “78、69、53、77、54”这组数据的中位数是69 。
8. 6位学生的身高分别为：145、135、128、145、140、130厘米，他们的众数是145厘米。
9. 要了解一组数据的差异程度，需计算该组数据的差异量。
10．有7个学生的语文成绩分别为：80、65、95、70、55、87、69分，他们的全距是40分。
11.若某班学生数学成绩的标准差是5分，平均分是85分，其差异系数是5.88% 。
12．比较某班学生在身高和体重两方面的差异程度，要把学生身高和体重的标准差转化为差异系数。
13.两个变量之间不精确、不稳定的变化关系称为相关关系。
14．要描述两个变量之间变化方向及密切程度，需要计算相关系数。
15. 若两个变量之间存在正相关，则它们的相关系数是正数。
16．若两个变量之间的相关系数是负数，则它们之间存在负相关。
17．质与量的相关分析的方法主要包括二列相关、点二列相关和多系列相关。
18．品质相关的分析方法包括四分相关、Φ相关和列联相关。
20. 某班50个学生中有30个女生，若随机抽取一个同学，抽到男生的概率是2/5。
21．某一种统计量的概率分布称为抽样分布。
22．平均数差异显著性检验中需要判断两个样本是相关样本还是独立样本。
23. 单纯随机抽样能保证抽样的随机性和独立性。
24. χ2检验的数据资料是点计数据。
25. 单向表是把实测的点计数据按一种分类标准编制而得的表。
26. 单向表χ2检验是对单向表的数据进行χ2检验，即单因素的χ2检验。
《教育统计》(数学)作业参考答案
《教育统计》作业参考答案（数学专业）一．填空1．简单随机抽样；分层机样；等距抽样2．分散程度；极差；四分位差；平均差；标准差3．1=ρ4．,E A S S S +=∑ E S ， A S5．线性；正态6．d M M x ,,07．Q U Syy +=8．信度；效度；难度；区分度9．差异程度，R Q ， D A ⋅ ，S10．0=ρ11．E A S S S +=∑12．回归系数，回归方程13．集中趋势，d M M x ,,0 14．极差系数 四分位差系数 C ，V 15．Q u Q u S yy ,,+= 二．计算题1. 9973.0199865.021)3(2)33()3)3(=-⨯=-Φ=<≤-=+<≤-Z P X P σμσμ2．μ的95%的区间估计为 ]30496.12.81[±3．64:0=μH 96.1125.3366.96469||>=-=u故否定0H ，即有显著差异。
4．11.3665.07=⨯-=-=x b y a 65.0==Sxx Sxy b5．6826.018413.021)1(2)11()8575(=-⨯=-Φ=<≤-=<≤Z P X P人数：120⨯00.6826=82（人）6．]1109.36262.23.82[-±7．82:0=μH 96.137.21048285||>=-=u 否定0H ，有显著差异8．516.017580.021)7.0(2)7.07.0()8872(=-⨯=-Φ=<≤-=≤Z P X P人数：45×0.516=23(人)9．]1104.11262.23.82[-±10．80:0=μH 96.15.1948082||<=-=u ，接受0H 无显著差异。
11．16.0)1(1)1(1)48(1)48(=Φ-=<-=<-=>Z P X P X P12．]108.496.174[±13．80:0=μH 96.1506.5805.82||>-=u 故否定0H ，有显著差异。
教育统计学与SPSS课后作业答案祥解题目
教育统计学课后作业一、P118 1题目：10位大一学生平均每周所花的学习时间与他们的期末考试成绩见表6-17.试问：（1） 学习时间与考试成绩之间是否相关？ （2） 比较两组数据谁的差异程度大一些？ （3） 比较学生2与学生9的期末考试测验成绩。
表6-17 学习时间与期末考试成绩1 2 3 4 5 6 7 8 9 10 学习时间 考试成绩 40 5843 7318 5610 4725 5833 5427 4517 3230 6847 69解题步骤：（1）第一步：定义变量：“xuexishijian ”、“xuexichengji ”后，输入数据.如下图： 第二步：单击选择“分析(Analyze)”中的“相关(Correlate)”中的“双变量(Bivariate Correlations)”，将上图中的“xuexishijian ”和“xuexichengji ”添加到右边变量框中，如下图： 第三步：点击“确定“后，输出结果如下图： 第四步：分析结果由上图可知：学习时间与学习成绩之间的pearson 相关系数为0.714，p （双侧）为0.20。
自由度 df=10-2=8时，查“皮尔逊积差相关系数显著临界值表”知：r 0.05= 0.623 ； r 0.01=0.765。
因为0.765 > 0.714 >0.623，所以在0.05水平上学习时间和学习成绩是相关显著的。
（2）SPSS 软件分析结果如下图：由上图可知：学习时间标准差和平均值为：S 1=12.037 ⎺X 1= 29.00 ；学习时间标准差和平均值为：S 2=12.437 ⎺X 2=56.00 根据差异系数公式可知： 学习时间差异系数为：%100⨯=XSCV S =12.037/29.00×100%=41.51%学习成绩差异系数为：%100⨯=XSCV S =12.437/56.00×100%= 22.27% 有上述结果可知学习时间差异程度大于学习成绩差异程度。
教育统计学课后练习参考答案
教育统计学课后练习参考答案第一章1、教育统计学，就是应用数理统计学的一般原理和方法，对教育调查和教育实验等途径所获得的数据资料进行整理、分析，并以此为依据，进行科学推断，从而揭示蕴含在教育现象中的客观规律的一门科学。
教育统计学既是统计科学中的一个分支学科，又是教育科学中的一个分支学科，是两种科学相互结合、相互渗透而形成的一门交叉学科。
从学科体系来看，教育统计学属于教育科学体系的一个方法论分支；从学科性质来看，教育统计学又属于统计学的一个应用分支。
2、描述统计主要是通过对数据资料进行整理，计算出简单明白的统计量数来描述庞大的资料，以显示其分布特征的统计方法。
推断统计又叫分析统计，它根据统计学的原理和方法，从我们所研究的全体对象（即总体）中，按照等可能性原则采取随机抽样的方法，抽出总体中具有代表性的部分个体组成样本，在样本所提供的数据的基础上，运用概率理论进行分析、论证，在一定可靠程度上对总体的情况进行科学推断的一种统计方法。
3、在自然界或教育研究中，一种事物常存在几种可能出现的情况或获得几种可能的结果，这类现象称为随机现象。
随机现象具的特点：（1）一次条件完全相同的实验有多种可能的结果（这样的实验称为随机实验）；（2）在实验之前不能确切知道哪种结果会发生；（3）在相同的条件下可以重复进行这样的实验。
4、总体，也叫做母体或全域，是指具有某种共同特征的个体的总和。
当所研究的总体数量非常大时，可以从总体中抽取其中一部分个体来观测，由此来推断总体的信息，从总体中抽出的这部分个体就称为样本，它是用以表征总体的个体的集合。
通常将样本中样本个数大于或等于30个的样本称为大样本，小于30个的称为小样本。
5、复置抽样指每次抽出的个体经观测后，仍放回原总体，然后再从总体中抽取下一个个体。
6、反映总体特征的量数叫做总体参数，简称参数。
反映样本特征的量数叫做样本统计量，简称统计量。
参数是总体的真正数值，是固定的常量，理论上应该通过计算总体中全部个体的数值而获得，但由于总体中个体的数量通常很大，总体参数往往很难获得，在统计分析中一般通过样本的数值来估计。
教育统计参考答案
教育统计参考答案教育统计参考答案教育统计是一种重要的数据分析方法，通过对教育领域的各种数据进行收集、整理和分析，可以为决策者提供有力的参考依据。
在这个信息爆炸的时代，教育统计的重要性愈发凸显。
本文将从教育统计的意义、数据收集方法以及数据分析的应用等方面进行探讨。
一、教育统计的意义教育统计作为一种数据分析方法，具有重要的意义。
首先，教育统计可以帮助我们了解教育领域的现状和趋势。
通过统计教育资源的分布情况、学生的学习成绩、教师的教学水平等数据，我们可以全面了解到教育的发展状况，为制定相关政策提供科学依据。
其次，教育统计可以帮助我们发现问题并及时采取措施。
通过对教育数据的分析，我们可以发现教育资源的不均衡分布、学生学习成绩的差异等问题，从而及时采取针对性的措施，促进教育公平和提高教育质量。
最后，教育统计可以帮助我们评估教育政策的效果。
通过对教育数据的长期跟踪和比较分析，我们可以评估各种教育政策的效果，为政府和学校的决策提供科学依据，进一步改善教育质量。
二、数据收集方法在进行教育统计时，数据的收集是至关重要的一环。
常用的数据收集方法包括问卷调查、实地观察和数据挖掘等。
问卷调查是一种常见的数据收集方法，通过发放问卷并收集回馈，可以获取大量的定量和定性数据。
问卷调查可以针对学生、教师、家长等不同群体进行，以了解他们对教育的需求、态度和满意度等。
实地观察是另一种常用的数据收集方法，通过实地考察学校、教室和课堂等教育场所，可以直接观察到教育资源的配置情况、教学过程的质量等。
实地观察可以提供真实、客观的数据，对于了解教育现状非常有帮助。
数据挖掘是一种利用计算机技术从大量数据中挖掘出有用信息的方法。
通过对教育数据的挖掘，我们可以发现隐藏在数据背后的规律和趋势，为教育决策提供科学依据。
三、数据分析的应用教育数据的分析是教育统计的核心环节，它可以帮助我们从海量的数据中提取出有价值的信息。
常用的数据分析方法包括描述统计分析、回归分析和聚类分析等。
温忠麟心理与教育统计学课后题答案
温忠麟心理与教育统计学课后题答案1、如果平面a和平面β有公共点A，则这两个平面就相交（）[单选题] *A、经过点A的一个平面B、经过点A的一个平面(正确答案)C、点AD、无法确定2、4、已知直角三角形的直角边边长分别是方程x2-14x+48=0的两个根，则此三角形的第三边是（）[单选题] *A、6B、10(正确答案)C、8D、23、14、在等腰中，如果的长是的2倍，且三角形周长为40，那么的长是（）[单选题] * A．10B．16 (正确答案)C．10D．16或204、下列说法错误的是[单选题] *A.+（-3）的相反数是3B.-（+3）的相反数是3C.-（-8）的相反数是-8(正确答案)C.-（+八分之一）的相反数是85、39．若（x﹣3）（2x+1）＝2x2+ax﹣3，则a的值为（）[单选题] * A．﹣7B．﹣5(正确答案)C．5D．76、49．若（x+2）（x﹣3）＝7，（x+2）2+（x﹣3）2的值为（）[单选题] * A．11B．15C．39(正确答案)D．537、2、在轴上的点的纵坐标是（）[单选题] *A．正数B．负数C．零(正确答案)D．实数8、方程（x+3）(x-2)=0的根是（）[单选题] *A．x=-3B．x=2C．x1=3，x2=-2D．x1=-3x2=2(正确答案)9、抛物线y2=-8x的焦点坐标为（）[单选题] *A、（-2，0）(正确答案)B、（-2，1）C、（0，-2）D、（0，2）10、39、在平面直角坐标系中，将点A（m，m+9）向右平移4个单位长度，再向下平移2个单位长度，得到点B，若点B在第二象限，则m的取值范围是（）[单选题] *A．﹣11＜m＜﹣4B．﹣7＜m＜﹣4(正确答案)C．m＜﹣7D．m＞﹣411、37．若x2+2（m﹣1）x+16是完全平方式，则m的值为（）[单选题] * A．±8(正确答案)B．﹣3或5C．﹣3D．512、19．如图，共有线段（）[单选题] *A．3条B．4条C．5条D．6条(正确答案)13、下列函数是奇函数的是（）[单选题] *A、f（x）=3x(正确答案)B、f（x）=4xC、f（x）= +2x-1D、f（x）=14、已知10?＝5，则100?的值为( ) [单选题] *A. 25(正确答案)B. 50C. 250D. 50015、10. 已知方程组的解为，则、对应的值分别为（）[单选题] *A、1，2B、1，5C、5，1(正确答案)D、2，416、?方程x2?+2X-3=0的根是（? ? ? ??）[单选题] *A、X1=-3, X2=1(正确答案)B、X1=3 ,X2=-1C、X1=3, X2=1D. X1=-3, X2=-117、由数字1、2、3、4、5可以组成多少个不允许有重复数字的三位数?（）[单选题]*A、125B、126C、60(正确答案)D、12018、42．已知m、n均为正整数，且2m+3n＝5，则4m?8n＝（）[单选题] * A．16B．25C．32(正确答案)D．6419、在0°~360°范围中，与645°终边相同的角是（）[单选题] *285°(正确答案)-75°295°75°20、函数式?的化简结果是（）[单选题] *A.sinα-cosαB.±（sinα-cosα）(正确答案)C.sinα·cosαD.cosα-sinα21、37、已知A（3，﹣2），B（1，0），把线段AB平移至线段CD，其中点A、B分别对应点C、D，若C（5，x），D（y，0），则x+y的值是（）[单选题] *A．﹣1B．0C．1(正确答案)D．222、下列各式中能用平方差公式的是（）[单选题] *A. (x＋y)(y＋x)B. （x＋y)(y－x)(正确答案)C. (x＋y)(－y－x)D. (－x＋y)(y－x)23、花粉的质量很小，一粒某种植物花粉的质量约为000037毫克，已知1克=1000毫克，那么000037毫克可用科学记数法表示为[单选题] *A. 7×10??克B. 7×10??克C. 37×10??克D. 7×10??克(正确答案)24、48、如图，△ABC≌△AED，连接BE．若∠ABC＝15°，∠D＝135°，∠EAC＝24°，则∠BEA的度数为（）[单选题] *A．54°B．63°(正确答案)C．64°D．68°25、15．一次社会调查中，某小组了解到某种品牌的薯片包装上注明净含量为，则下列同类产品中净含量不符合标准的是（）[单选题] *A 56gB .60gC．64gD.68g(正确答案)26、14．将△ABC的三个顶点坐标的横坐标都乘以-1，并保持纵坐标不变，则所得图形与原图形的关系是（）[单选题] *A．关于x轴对称B．关于y轴对称(正确答案)C．关于原点对称D．将原图形沿x轴的负方向平移了1个单位27、? 转化成角度为（）[单选题] *A. 150°B. 120°(正确答案)C. 270°D. 90°28、已知二次函数f（x）=2x2-x+2，那么f（-2）的值为（）。
教育统计学课后试题及答案汤舒俊
教育统计学课后试题及答案汤舒俊1. 一位研究者随机调查了50 名城市居民为孩子购买课外读物的花费，另外还搜集了老师对这些孩子的总体评价，得到积差相关系数为0.53，下列推断中，正确的是* [单选题] *A．如果另外再随机调查50 名乡镇居民，他们为孩子购买课外读物的花费与老师对其孩子总体评价之间的相关系数会非常接近0.53B．用城市居民为孩子购买课外读物的花费预测老师对其孩子总体评价的准确率为53％C．城市居民为孩子购买课外读物的花费决定老师对其子女的总体评价D．城市居民为孩子购买课外读物的花费与老师对其孩子的总体评价之间存在中等程度的相关(正确答案)2. 已知r1= − 0.7，r2 = 0.7 下列表述正确的是 * [单选题] *A．r1和r2代表的意义相同B．r2代表的相关程度高于r1C．r1和r2代表的相关程度相同(正确答案)D．r1和r2的散点图相同3. 当积差相关系数r=0 时，对两个变量之间关系的最佳解释是 * [单选题] *A．相关程度很低B．不存在任何相关C．不存在线性相关关系(正确答案)D．存在非线性相关关系4. 有300 名考生，期中和期末成绩的相关系数为0.62，两次考试成绩平均分数均为80 分，如给所有考生的期中成绩各加8 分，加分后两次成绩的相关系数是 * [单选题] *A.0.52B.0.62(正确答案)C.0.70D.0.725. 在标准正态曲线下，正、负三个标准差范围内的面积占总面积的比例是 * [单选题] *A. 99.73%(正确答案)B. 99.00%B. 95.46%D. 95.00%6. 下列关于样本量的描述，正确的是 * [单选题] *A．样本量需要等于或大于总体的30%B．样本量大小不是产生误差的原因C．总体差异越大，所需样本量就越小D．已知置信区间和置信水平可以计算出样本量(正确答案)7. 当总体中的个体具有周期性规律时，不适用抽样方法是 * [单选题] *A．简单随机抽样B．分层抽样C．等距抽样(正确答案)D．方便抽样8. 在假设检验中，通常用来表示统计检验力(power of test)的是 * [单选题] *A．1–αB．1–β(正确答案)C．α+βD．α–β9. 在假设检验中，统计检验的显著性水平α的值是 * [单选题] *A．犯I 型错误的概率(正确答案)B．犯II 型错误的概率C．犯I 型与犯II 型错误的概率之和D．犯I 型与犯II 型错误的概率之差10. 某心理学实验有相互独立的一个实验组和一个控制组，为了考察两组连续型数据平均值之间的差异是否具有统计学意义，最恰当的统计方法是 * [单选题] * A．回归分析B．相关分析C．t 检验(正确答案)D．χ2检验11. 要检验20 对分开抚养的同卵双生子在15 岁时智力测验分数的差异，最恰当的检验方是 * [单选题] *A．两相关样本的t 检验(正确答案)B．两独立样本的t 检验C．样本与总体均数的t 检验D．χ2检验12. 心理学研究中，协方差分析能够 * [单选题] *A．控制无关变异(正确答案)B．使实验变异最大化C．减少个体误差D．减少随机误差13. 一组数据中每个数的值都是5 ，那么这组数据的标准差和方差分别是 * [单选题] *A. 0, 0(正确答案)B. 5, 25C. 0, 5D. 0, 2514. 有一组数据：2，3，4，5，6，7，8 该组数据的平均数和标准差分别是5 和2 如果给这组数据的每个数都加上3，再乘以2，那么可以得到一组新数据其平均数和标准差分别是 * [单选题] *A．8，2B．8，5C．16，4(正确答案)D．16，1015. 能够用来比较不同样本或不同心理特质测试数据之间相对离散程度的统计量是* [单选题] *A.决定系数B.变异系数(正确答案)C.相关系数D.回归系数16. 某考生在一项测验中得分60，经换算百分等级为70，这表明在所有考生中，得分低于该考生的人数占总人数的 * [单选题] *A．30％B．40％C．60％D．70％(正确答案)17. 当样本容量一定时，置信区间的宽度 * [单选题] *A．随着显著性水平α的增大而增大B．随着显著性水平α的增大而减小(正确答案)C．与显著性水平α的大小无关D．与显著性水平α的平方根成正比18. 假设正常人情绪稳定性近似服从正态分布，某研究者拟根据 3000 正常人的情绪稳定性数据制定 95%正常值范围，但计算时用了求 99%置信区间的公式，产生的结果是 * [单选题] *A.提高了精确度B.降低了精确度C.该指标异常者容易被判为正常(正确答案)D.该指标正常者容易被判为异常19. 某年高考正态分布，其中u=500, σ=100，考虑到招生指标，只有5%的考生可以升入重点中学，请问重点中学的最低分数线应该为( ) [单选题] *696758664685(正确答案)20. 随机抽取一个容量为100的样本，其均值X ̅=80，标准差S=10,则总体均值的95%的置信区间为( ) [单选题] *80±2.5880±2.3580±1.96(正确答案)80±2.9821. 某班有30名同学的平均成绩为75分，其中10名女生的平均成绩为85分，则该班男生的平均分为() [单选题] *6570(正确答案)756822. 当我们按性别差异，将男性指定用数字“1”来代表，女性指定用数字“2”来代表，这里所得到的数据是( ) [单选题] *称名数据(正确答案)顺序数据比率数据23. 中数的优点是() [单选题] *不受极端值影响(正确答案)灵敏适于代数运算全部数据都参与运算24. 一班32名学生的平均分为72．6，二班40人的平均分为80．2，三班36人的平均分为75，则三个班级总平均分为( ) [单选题] *75.9376.21(正确答案)80.27325. 若将我们班每个人的统计学考试分数都加上10分，那么与原来相比其平均数和标准差的变化是( ) [单选题] *平均数减少，标准差不变平均数增加，标准差增加平均数增加，标准差不变(正确答案)平均数增加，标准差减少26. 如果相互关联的两变量的变化方向一致(同时增大或同时减小)，这表明两变量之间有() [单选题] *负相关正相关(正确答案)零相关27. 研究性别男、女与购房区域城区、郊区选择之间的关系，应该使用( ) [单选题] *积差相关等级相关点二列相关φ相关(正确答案)28. 两个变量分布都是真正的二分变量，要计算两者之间的关系系数，最恰当的方法是() [单选题] *四分相关φ相关(正确答案)积差相关点二列相关29. 要检验20 对分开抚养的同卵双生子在15 岁时智力测验分数的差异，最恰当的检验方是() [单选题] *两相关样本的t 检验(正确答案)两独立样本的t 检验样本与总体均数的t 检验χ2检验30. 为描述身高和体重之间的关系，最适合的图形是() [单选题] *直方图(正确答案)饼图散点图线形图31. 描述定性数据两种常用的图示法是() [单选题] *条形图和饼图(正确答案)散点图和饼图散点图和条形图条形图和茎叶图32. 以下论述中，那个不是计算皮尔逊积差相关时对需要符合条件的假定() [单选题] *两列变量时等距或等比的测量数据两列变量来自的总体必须符合正态或者近似正态的单峰分布两列变量之间必须具备一一对应的关系一个变量的数值增大，另一个变量的数值也应增大(正确答案)33. 若P90等于83，则表明在该次数分布中有()的个案低于83，其中百分位数是指( ) [单选题] *10%, P9090%, P90(正确答案)10%, 9090%, 9034. 在重复测量的方差分析中，如果各组均值不变，被试间差异增大，那么() [单选题] *F 值会变小F 值保持不变组间方差会变小误差方差会变小(正确答案)35. 在方差分析中，反映样本数据与其组平均的差异的是()，自变量不同水平引起的差异是( ) [单选题] *总离差，误差组间差异区组效应误差，组间差异组内差异，组间差异(正确答案)36. 两列变量是等距或等比变量，且服从正态分布，计算它们的相关系数最恰当的方法是() [单选题] *积差相关(正确答案)等级相关点二列相关φ相关37. 一个测验由0、1计分的100道单选题构成，根据原始得分计算题目区分度的恰当方法是() [单选题] *φ相关等级相关积差相关点二列相关(正确答案)38. 关于 t 分布与标准正态分布两者之间的关系，正确的表述是() [单选题] * t 分布的均值大于标准正态分布的均值标准正态分布的标准差大于t 分布的标准差两者的标准差、均值都相同随着自由度增大， t 分布接近于标准正态分布(正确答案)39. 能够反映估计量精确性的统计量是() [单选题] *标准误(正确答案)标准差方差四分位差40. 对于相关系数r=0,下列表述正确的是() [单选题] *相关程度较低不存在任何相关关系不存在线性相关关系(正确答案)存在非线性相关关系41. 下列关于χ2分布的特点描述，正确的有： * *A．χ2取值均为正值(正确答案)B．χ2分布是正偏态分布(正确答案)C．χ2分布为非连续性分布D．χ2分布的标准差与自由度相同42. 方差分析需要满足的前提条件有 * *A．总体正态分布(正确答案)B．各处理方差齐性(正确答案)C．总体方差已知D．各组样本容量相同43. 以下检验方法中，属于非参数检验的是 *X2检验(正确答案)T检验F检验符号检验(正确答案)44. 为了了解教学方法对学生成绩的影响，共有3种教学方法，选择高一年级六个平行班。
现代心理与教育统计学课后题答案第八章
现代心理与教育统计学课后题答案第八章1.对某河流污染状况进行统计调查，需采用( ) [单选题] *A.重点调查(正确答案)B.普查C.典型调查D.抽样调查3.下列指标属于强度相对指标是( ) [单选题] *A.产品质量等级(正确答案)B.人口平均寿命C.手机普及率D.产品合格率2.下列指标中必须以整数形式进行统计的是( ) [单选题] *A.工资总额(正确答案)B.股价指数C.恩格尔系数D.设备台数5.某一特定类别或组中的数据个数称为( )。
[单选题] *A.频数(正确答案)B.累积频数D.累积频率7．下列指标中属于时点指标的是( )。
[单选题] *A. 股票购买量(正确答案)B. 商品销售额C. 股票收盘价格D. 股票成交金额8．下列属于连续变量的是( )。
[单选题] *A、职工人数(正确答案)B、设备台数C、职工工资总额D、生猪存栏头数9．若某组数据呈现出右偏分布，则该组数据的众数、中位数、均值的大小关系是( )。
[单选题] *A.众数＞中位数＞均值(正确答案)B.均值＞中位数＞众数C.中位数＞众数＞均值D.中位数＞均值＞众数4.某银行5年期间利率(复利)变动情况为：第1年—第3年7%；第4年—第5年8.2%。
则该银行5年期间平均年利率为( ) [单选题] *A.108%(正确答案)C.107.5%D.7.5%6一般情况下，计算数量指标综合指数时，采用( )方法。
[单选题] *A.拉式数量指数(正确答案)B.拉式质量指数C.帕式数量指数D.帕式质量指数10.增长一个百分点对应增加的绝对量称为( )。
[单选题] *A.平均增长率(正确答案)B.环比增长率C.增长1%的绝对值D.定基增长率12某公司12月份与11月份相比产品销售价格平均下降6%，产品销售量平均增长6%，则12月份与11月份相比产品零售额( )。
[单选题] *A.保持不变(正确答案)B.平均下降0.36%C.平均下降36%D.平均下降0.9964%13.各变量值与其算数平均数离差平方的算术平均数的平方根称为( )。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
教育统计学课后练习参考答案第一章1、教育统计学，就是应用数理统计学的一般原理和方法，对教育调查和教育实验等途径所获得的数据资料进行整理、分析，并以此为依据，进行科学推断，从而揭示蕴含在教育现象中的客观规律的一门科学。
教育统计学既是统计科学中的一个分支学科，又是教育科学中的一个分支学科，是两种科学相互结合、相互渗透而形成的一门交叉学科。
从学科体系来看，教育统计学属于教育科学体系的一个方法论分支；从学科性质来看，教育统计学又属于统计学的一个应用分支。
2、描述统计主要是通过对数据资料进行整理，计算出简单明白的统计量数来描述庞大的资料，以显示其分布特征的统计方法。
推断统计又叫分析统计，它根据统计学的原理和方法，从我们所研究的全体对象（即总体）中，按照等可能性原则采取随机抽样的方法，抽出总体中具有代表性的部分个体组成样本，在样本所提供的数据的基础上，运用概率理论进行分析、论证，在一定可靠程度上对总体的情况进行科学推断的一种统计方法。
3、在自然界或教育研究中，一种事物常存在几种可能出现的情况或获得几种可能的结果，这类现象称为随机现象。
随机现象具的特点：（1）一次条件完全相同的实验有多种可能的结果（这样的实验称为随机实验）；（2）在实验之前不能确切知道哪种结果会发生；（3）在相同的条件下可以重复进行这样的实验。
4、总体，也叫做母体或全域，是指具有某种共同特征的个体的总和。
当所研究的总体数量非常大时，可以从总体中抽取其中一部分个体来观测，由此来推断总体的信息，从总体中抽出的这部分个体就称为样本，它是用以表征总体的个体的集合。
通常将样本中样本个数大于或等于30个的样本称为大样本，小于30个的称为小样本。
5、复置抽样指每次抽出的个体经观测后，仍放回原总体，然后再从总体中抽取下一个个体。
6、反映总体特征的量数叫做总体参数，简称参数。
反映样本特征的量数叫做样本统计量，简称统计量。
参数是总体的真正数值，是固定的常量，理论上应该通过计算总体中全部个体的数值而获得，但由于总体中个体的数量通常很大，总体参数往往很难获得，在统计分析中一般通过样本的数值来估计。
在进行推断统计时，就是根据样本统计量来推断总体相应的参数。
第二章1、按照数据的来源，可分为计数数据和度量数据；按照数据的取值情况，可分为间断性数据和连续性数据；按照数据的测量水平，可分为称名数据、顺序数据、等距数据和比率数据。
2、数据整理的基本方法包括对数据进行排序、统计分组、绘制统计图表等。
3、表的结构要简洁明了；表的层次要清晰；主谓分明。
4、连续性数据：（2），（3）；间断性数据：（1），（4）。
5、略6、（1）50；（2）75；（3）34；（4）5；（5）457、（1）表2-1 某幼儿园40名教师成绩次数分布表水平，不及格的有3人，及格以上的有37人。
8、（1）表2-2 某学校120名12岁男生身高次数分布表（3）19.17%9、略第三章1、集中量数是代表一组数据典型水平或集中趋势的统计量。
常用的集中量数有算术平均数、加权算术平均数、几何平均数、中位数、众数等。
2、算术平均数，是指一组数据中各个分数的和再除以这组数据的总次数所得的商。
平均数与总次数的乘积等于各观测值的总和；各观测值与其平均数的差（离差）的代数和等于零；如果一组观测值由两部分（或几部分）组成，这组观测值的平均数可以由其各组成部分的平均数求得。
3、484、Mo=3Ｍd-2Ｍ=3×65.3-2×68.6=195.9-137.2=58.75、97.5%（Z =1.96，P=0.475）6、Mo=15.81；X=15.87；Ｍd=16W7、73.5第四章1、百分等级分数是指按一定顺序排列的数据中，某个数据以下的数据次数占总次数的百分比；标准分数又称Z分数，是原始分数与其平均数的差除以标准差所得的商数。
2、对平均数的离散程度越大，标准差越大；如果各观测值相等，则标准差为零；各观测值同时加减一个常数，其标准差不变；各观测值同时乘以一个常数Ｃ，标准差是原标准差的Ｃ倍。
3、6.44 4、Z =0.7 5、826、)(身高CV =0.045；)(体重CV =0.3237、第五章1、变量之间确实存在而关系数值又不固定的相互依存关系，称为相关关系。
种类有单相关和复相关，直线相关和曲线相关，正相关、负相关、零相关，高度相关、中度相关和低相关。
2、相关系数是用来描述两个变量相互之间变化方向及密切程度的数字特征量。
相关系数的取值一般介于1~1+-之间，即-1≤r ≤+1；相关系数的正负号表示变量的相关方向；相关系数的数值大小表示相关程度的强弱；相关系数不能直接进行加、减、乘、除的数学运算；相关系数只能描述两个变量之间的变化方向及密切程度，并不能揭示两者之间的内在本质联系。
3、两个变量的变动方向相同，即一个变量变动时，另一个变量也发生或大或小的方向相同的变动，这两个变量之间的关系叫做正相关；当两个变量都是正态连续变量，而且两者之间关系用图像表示接近于一条直线，表示这两个变量之间的相关称为积差相关；以等级次序排列或以等级次序表示的变量，变量所在的总体不一定呈正态分布，样本容量也不一定大于30的变量间的相关关系，称为等级相关。
4、当两列变量都是正态连续变量，其中一列变量被人为地划分为二分变量，表示这两列变量之间的相关称为二列相关。
5、当两个变量中一个是正态连续变量，另一个是固有的二分分类变量表示这两个变量之间的相关叫做点二列相关。
6、r =0.8617、R r =-0.18、R r =0.4第六章一、略二、1、（1）661611()264P C ==(2)224261115()()2264P C ==2、88299101010101013131()()()()()44444P C C C =++ 0.000416= 3、 (1)0.38493 (2)0.41924 (3)0.30598 (4)0.27261 (5)0.781934、 (1)0.11092 (2)0.28969 (3)0.28034 (4)概率为1/2×P 时的Y 值.5、100856P =0.117= 0.5－0.117=0.383,Z=1.1992 1.1921116.99X X Z σ=+=+⨯=(分)6、160650.2520Z -==- 280650.7520Z -== 10.09817P = 0.5－0.09817=0.40183,0.40183×300=120(人),即60分以下的人数为120.2P =0.273370.5-0.27337=0.22663,0.22663×300=67(人),即80分以上共有67人.7、Z =(88-83)/6.5=0.7691P =0.27935P =0.5-0.27935=0.22065235×0.22065=52(人)。
第七章1、（1）157.05；8.35 （2）44.28；7.24。
2、总体呈正态分布，总体方差2210σ=，故用正态分布理论进行估计。
2.583X SE === 0.95的置信区间为：74 1.96 2.5874 1.96 2.58μ-⨯<<+⨯ 即 68.9479.06μ<<3、60,72,11.5n n X S ===，因为样本容量大于30，样本平均数的抽样分布近似正态分布。
1.485X SE === 0.99的置信区间为：72 2.58 1.48572 1.485 2.58μ-⨯<<+⨯ 即：68.1775.83μ<<。
4、77.6,1030,12.21n X n S ==<=4.07X SE ===。
19,0.05df n α=-==。
查t 值表，得0.05/2 2.262t = 0.95的置信区间为：77.6 2.26 4.0777.6 2.26 4.07μ-⨯<<+⨯ 即 68.486.8μ<<。
5、0.05/215,2,0.05, 1.96Z σα=∆===22/2 1.9615()()216.092Z n ασ⋅⨯===∆ 即至少应抽取216人。
6、0.05/25.5, 2.5,0.05, 1.96Z σα=∆===22/2 1.96 5.5()()18.592.5Z n ασ⋅⨯===∆ 即 n=19（人）。
第八章1、t =1.35 ，P ＞0.05，26名学生成绩与全县一致。
2、t =0.97 ，P ＞0.05，两校测验成绩间没有显著差异。
3、t =3.77，P ＜0.01，差异非常显著。
4、Z =0.64，P ＞0.05，差异不显著。
5、Z =0.75，P ＞0.106、t =2.22，P ＜0.05，有显著差异。
7、Z =4.95，P ＜0.01，差异非常显著。
8、r 大于临界值，P ＜0.05，与零相关有显著差异。
9、X SE =4.66 10、（略）第九章1、略。
2、略。
3、略。
4、略。
5、F =1.38，P ＞0.056、F =73.88，P ＜0.017、F =11.81，P ＜0.01第十章1、χ2检验是对样本的频数分布所来自的总体分布是否服从某种理论分布或某种假设分布所作的假设检验，即根据样本的频数分布来推断总体的分布，它对总体分布情况没有作严格的要求，所处理的数据的类型为点计而来的间断变量，所以χ2检验是一种非参数检验的方法。
2、拟合优度检验、独立性检验和同质性检验。
3、根据正态分布理论计算理论次数，然后把实际分组次数和理论次数代入χ2检验基本公式，求出χ2值，查表确定差异是否显著。
如果差异显著，则说明实际次数分布与正态分布不吻合；如果差异不显著，则说明实际次数分布与正态分布吻合。
4、220.01(4)33.1315.09df χχ==>=5、220.01(1)9.74 6.63df χχ==>=，0.44φγ=6、220.01(2)18.609.21df χχ==>= 7.、220.01(2)18.609.21df χχ==>=第十一章1、回归分析与相关分析既有联系又有区别。
联系表现为（1）二者均是分析两个或两个以上变量间关系的方法且均不能推断因果关系，所以有些学者认为相关分析包括回归分析，（2）相关分析是回归分析的基础，如果变量间不存在显著相关，就没有必要进一步作回归分析；二者的区别表现为相关分析是检验变量关系的密切程度，而回归分析则用精确的数学方程式表达变量间的数量关系，进而根据一个或几个变量值去预测另一个变量的取值。
2、 确定回归方程或回归直线的一种方法。
其基本思想是使散点图中各数据点到回归线的纵向距离平方和µ()2Y Y-∑最小，即令误差平方和最小。