3.4 实际问题与一元一次方程-等积变形问题
七年级数学上第三章一元一次方程单元教学计划

第三章《一元一次方程》
一、单元教学内容及教材分析
1.本章的主要内容:
列方程,一元一次方程的概念及解法,列一元一次方程解应用题。
2.本章的地位及作用:
一元一次方程是数学中的主要内容之一,它不仅是学习其它方程的基础,而且是一种重要的数学思想——方程思想,利用方程思想可以使许多实际问题变得直接易懂,体会方程是刻画现实世界的一个有效的数学模型。
更深刻地体会数学的应用价值。
3.本章涉及到的主要数学思想及方法:
a.转化思想:主要体现在利用方程的同解原理,将复杂的方程转化为简单的方程,直至求出它的解。
b.整体思想:例如:解方程3/2(3x+1)—1/2(3x+1)=5运用整体思想可以使解题步骤简捷,思路清晰。
c.数学建模思想:它是在对问题深入地思考、分析、抽象的基础上,用数学方法去解决实际问题,建立数学模型。
方程是刻画现实世界的一个有效的数学模型。
本章中的列方程解应用题就是培养学生的数学建模思想。
注重几种基本题型的应用题:商品利润问题,储蓄问题,行程问题,行船问题,工程问题,调配问题,比例分配问题,数字问题,等积变形问题。
这是一些经典题型。
同时注意一些图表型应用题,阅读理解型等新颖的应用题。
d.数形结合思想:这主要体现在列方程解应用题时,尤其是对行程问题的分析解决中。
二、单元教学重点、难点:
重点:列方程,一元一次方程的解法,
难点:解有分母的一元一次方程和应用一元一次方程解决实际问题。
三、单元教学目标:。
一元一次方程实际应用题之等积变形问题
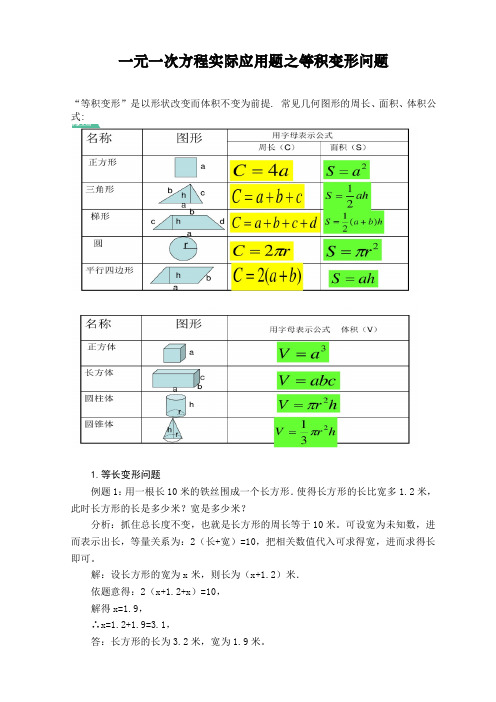
一元一次方程实际应用题之等积变形问题“等积变形”是以形状改变而体积不变为前提. 常见几何图形的周长、面积、体积公式:1.等长变形问题例题1:用一根长10米的铁丝围成一个长方形.使得长方形的长比宽多1.2米,此时长方形的长是多少米?宽是多少米?分析:抓住总长度不变,也就是长方形的周长等于10米。
可设宽为未知数,进而表示出长,等量关系为:2(长+宽)=10,把相关数值代入可求得宽,进而求得长即可。
解:设长方形的宽为x米,则长为(x+1.2)米.依题意得:2(x+1.2+x)=10,解得x=1.9,∴x=1.2+1.9=3.1,答:长方形的长为3.2米,宽为1.9米。
2.等体积变形问题例题2:要锻造直径为60mm,高为30mm的圆柱形毛坯,需截取直径为40mm的圆钢长是多少毫米?分析:抓住锻造前后的体积不变,此题的等量关系为:锻造前的体积=锻造后的体积.据此列方程求解。
要注意的是,题目中已知直径,需要转化为半径。
解:设需截取直径为40mm的圆钢长xmm,60÷2=30(mm)、40÷2=20(mm);依题意得:π×30^2×30=π×20^2×x解得:x=67.5例题3:有一段钢材可作一个底面直径 8 厘米,高 9 厘米的圆柱形零件。
如果把它改制成高是 12 厘米的圆锥形零件,零件的底面积是多少平方厘米?分析:根据“底面直径8厘米,高9厘米的圆柱形零件”,利用圆柱体积公式,可以求出圆柱的体积,又因为把圆柱形的零件改制成圆锥形零件时,此段钢的体积不变,根据体积不变列出方程求解。
解:零件的底面积是x平方厘米。
8÷2=4(厘米)依题意得:3×π×4^2×9=x×12解得:x=36π答:零件的底面积是36π平方厘米。
3.等面积变形问题例题4:如图,某小学将一块梯形空地改成宽为30m的长方形运动场地,要求面积不变.若在改造后的运动场地,小王、小李两人同时从点A出发,小李沿着长方形边顺时针跑,小王则是逆时针跑,并且小王每秒比小李多跑2m,经过10秒钟他们相遇.(1)求长方形的长;(2)求小王、小李两人的速度分析:(1)求得原梯形的面积,利用面积不变和长方形的面积求得长方形的长即可;(2)设小李的速度是xm/s,则小王的速度是(x+2)m/s,利用10秒钟他们相遇所走的路程为长方形的周长列出方程解决问题。
(最新整理)列一元一次方程解实际问题的一般方法

2021/7/26
31
知1-讲
(1)审题:审清题意,找出已知量和未知量; (2)设未知数:设该年级的男生有x人,那么女生有
__(_1_7_0_-__x_)_人; (3)列方程:根据相等关系,列方程为__3_x_=__7_(_1_7_0_-__x_)_; (4)解方程,得x=___1_1_9___,则女生有___5_1__人; (5)检验:将解得的未知数的值放入实际问题中进行验证; (6)作答:答:该年级有男生__1_1_9__人,女生__5_1___人.
当x=3时,130-30 x =2, 20
运费为3×500+2×400=2 300(元)<2 500(元).
故安排3辆甲种货车和2辆乙种货车,运费最省,
需2 300元.
2021/7/26
12
例6 某景点的门票价格如下表:
购票人数/人 1~50 51~100 100以上
每人门票价/元 12
10
8
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班 人数少于50人,(2)班人数多于50人且少于100人,如果 两班都以班为单位单独购票,则一共支付1 118元;如果 两班联合起来作为一个团体购票,则只需花费816元. (1)两个班各有多少名学生? (2)团体购票与单独购票相比较,两个班各节约了多少钱?
(1)这两次各购进电风扇多少台?
(2)商场以250元/台的售价卖完这两批电
风扇,商场获利多少元?
2021/7/26
9
解:(1)设第一次购进电风扇x台, 则第二次购进电风扇(x-10)台. 由题意可得150x=180(x-10),解得x=60. 则x-10=60-10=50. 所以第一次购进电风扇60台,第二次购进电 风扇50台.
§_3.4实际问题与一元一次方程(练习答案)

§ 3.4实际问题与一元一次方程(知识要点)一、销售问题在生活中,人们购买商品和销售商品时,经常会遇到进价、原价(标价)、售价、打折等概念,在了解这些概念后,还必须熟悉销售问题中的两个基本关系式:① 利润=售价-进价; ② 利润率=进价利润×100%. 在①式中若等式左边的“利润”为正,就是盈利;若为负,就是亏损;由①和②式可以得到:利润=售价-进价=利润率×进价。
【例1】 某商店将某种服装按进价提高30%作为标价,又以九折优惠卖出,结果仍可获利17元,则这种服装每件进价是多少元?分析:此题要用的等量关系是:利润=售价-进价,如果把进价设为x 元,则标价为(1+30%)x ,打九折后售价为0.9×(1+30%)x ,再减去进价x 元得到的就是利润17元。
解:设这种服装每件的进价为x 元,依题意列方程为:0.9×(1+30%)x -x =17解得x =100答:这种服装的进价是100元。
练习:某商店对一种商品进行调价,按原价的八折出售,打折后利润率是20%,已知商品的原价是63元,求该商品的进价?二、行程问题1、相遇问题:主要是指两车(戓人)从两地同时相向而行。
其基本等量关系为两车(戓人)所行的路程这和恰好等于两地的距离;两车(或人)人开始行驶到相遇所用的时间相等。
2、追赶问题:主要是指甲、乙同向而行,快者追慢者称为追赶问题。
① 基本公式:速度差×追赶时间=被追赶的路程;② 对于同向同地不同时出发的问题有相等关系:追赶者行进路程=被追赶者行进路程; ③ 对于同时同向不同地出发的问题有等量关系:追赶者的行驶时间=被追赶者的行驶时间。
3、航行问题:基本公式:顺水速度=静水速度+水速,逆水速度=静水速度-水速 顺风速度=无风速度+风速,逆风速度=无风速度-风速 符号公式:v 顺水=v 静水+v 水 v 顺风=v 无风+v 风v 逆水=v 静水-v 水 v 逆风=v 无风-v 风 4、行程问题一般都能通过画线段示意图来分析,通过线段示意图,等量关系就能直观地显示出来,进而用方程表示出来。
人教版七年级数学导学案3.4实际问题与一元一次方程——数字与等积含课后配套作业及答案

实际问题与一元一次方程(数字与等积) 【教学目标】1.了解数与数位上的数之间的关系,利用这种关系解决数位问题;2.了解常见物体的体积、常见图形的体积和面积公式,利用公式解决有关等积问题.【复习引入】 1.填空:(1)一个两位数的十位数字是4,个位数字是5,则这个两位数是 45 .(2)一个两位数的十位数字是x ,个位数字是5,则这个两位数是可表示为 10x+5 .(3)一个两位数的十位数字是5,个位数字是y ,则这个两位数是可表示为 50+y .(4)一个两位数的十位数字是a ,个位数字是b ,则这个两位数是可表示为 10a+b . 2.根据条件填空:(1)一个三角形一边长为a ,这边上的高是h ,三角形的面积为S =ah 21. (2)一个圆的半径为r ,则这个圆的面积 S=2r π.(3)长方体的长、宽、高分别为a 、b 、h ,则这个长方体的体积S =abh .(4)一个圆柱体的直径、高分别是d 、h ,那么这个圆柱体的体积V =h d 2)2(π.【要点梳理】1.数字问题(1)多位数的表示法:abcd 是一个多位数, 则d c b a abcd +⨯+⨯+⨯=10101023其中b 、c 、d 均表示为大于或等于零而小于10的整数且a 是大于零而小于10的整数. (2)寻找等量关系的方法是:①抓住数字间或新数、原数之间的关系寻找相等关系②常需要设间接未知数.例 1 一个两位数,十位上的数字比个位上的数字小1,十位与个位上数字之和是这个两位数的51.求这个两位数. 分析:设十位上的数为x ,则个位上的数为 x+1 ,它们的和 2x+1 ,这个两位数用x 可以表示为 10x+x+1 . 根据问题中的数量关系:十位与个位上数字之和是这个两位数的51 .列方程得:)110(5112++=+x x x . 解:x=4 练习1.一个三位数满足以下条件: (1)三个数位上的数字之和为8;(2)百位上的数字比十位上的数字大4; (3)个位上的数字是十位上的数字的2倍. 如果设十位上的数字为x ,则可的方程是824=+++x x x .2.一个两位数,十位上的数字比个位上的数字小4,如果把十位上的数与个位上的数对调后,那么所得的两位数比原来的两位数的2倍小12,求原来的两位数. 答案:解:设原来十位上的数字为x ,则个位上的数为x+4.依题意得:10(x+4)+x=2(10x+x+4)-12 解方程得:x=4则,原来的两位数是48. 2.等积变形问题:(1)基本数量关系是常见图形的体积公式. (2)寻找相等关系的方法是:①形变积不变;②形变积也变,但重量不变. 例2 已知圆柱(2)的体积是圆柱(1)的体积的3倍, 圆柱(1)的直径为40毫米, 圆柱(2)的直径和高都是60毫米,求圆柱(1)的高.分析:设圆柱(1)的高为x 毫米,则它的体积可以表示为x π220.根据问题中的数量关系:圆柱(2)的体积是圆柱(1)的体积的3倍, . 列方程得: 3×x π220=60302⨯π. 解:45=x 毫米 练习1.甲、乙两水池分别盛水1003m 和883m .从两池中共放出503m 水后,两水池剩余的水的体积相等,则从甲池中放出了 3m 水. 解:设从甲池中放出了x 3m 水则100-x=88-(50-x) 解得:x=31答:从甲池中放出了313m 水。
3.4_实际问题与一元一次方程-等积变形问题

_ _x厘米 30厘米 15厘米 可列方程:π×32x-π22(18-15)=π×22×15
3厘米
等量关系2:水的体积+水中金属柱的体积=水加柱的体积
可列方程:π×32×15+π×22×18=π×32(15+x)
解:设容器内放入金属圆柱后水面升高x厘米
(1)容器内的水面升高后没有淹没金属圆柱,那么由题
一元一次方程的应用
等积变形问题
要想求出某个同学的体积是多少?你怎么测量呢?
升高的水的 体积恰好等 于人的体积。
R h
你还能举出相类似的事例吗? (古代:曹冲称象)
例题7
2厘米
设水面升高了x厘米
18厘米
2厘米
3厘米
3厘米 x 厘 米
厘 米 30厘米 15厘米
x
18厘米 15厘米
金属柱没有被淹没的情况:
(或:π×32×15+π×22×18=π×32(15+x)) 解得:x=8 经检验x=8符合题意 所以,容器内水面升高8厘米
练习
一个盛有水的圆柱形容器里的内半径为 10cm,容器内水的高度为12cm, 把一根半径为2cm,高2厘米的玻璃柱放 入水中,问容器内水将升高多少厘米 。
意得
π×32x+π22(18-15)=π×22×15
(或π×32×15+π×22×(15+x)=π×32(15+x))
解得:x=12
因为12+15=27>18,所以此时容器内的水面已经淹没了金属柱, 不符合假定,应舍去 (2)如果容器内的水面升高后淹没放入的金属圆柱,那么由题意得
π×32x+π22(18-15)=π×22×15
一元一次方程的应用—等积变形和行程问题

解决行程问题的基本步骤:
问题的已 知条件
画出线 段图
找出等 量关系
列方程 并求解
作答
同向追及问题
同地不同时:甲路程=乙路程 同时不同地:甲路程+路程差=乙路程;
相向相遇问题 甲的路程+乙的路程=总路程
根据等量关系列出方程,得: 等积变形就是无论物体
π
200 2
2
x
300
300
90.
怎么变化都存在一个等 量关系,即物体变化前 后面积或体积不变
解方程,得: x 258.
答:应截取258mm长的圆柱体钢.
归纳总结
列方程解应用题的一般步骤: 1:弄清题意和题中数量关系,用字母(如 x,y)表示问题中的未知数;
A.12.5千米/时 B.15千米/时 C.17.5千米/时 D.20千米/时
3.一个底面直径为16厘米的圆柱形木桶内装满水,
水中淹没着一个底面直径为8厘米、高为15厘米的 铁质小圆柱体.当铁质小圆柱体取出后,木桶内
水面下降了多少?
[解析] 木桶内水面下降的圆柱体体积=铁质
小圆柱体体积.
解:设木桶内水面下降xcm.由题意得:
导入新课
情景引入
一支牙膏出口处直径为5mm,小明每次刷牙都挤 出1cm长的牙膏,这样一支牙膏可以用36次。该品牌 牙膏现推出新包装,只是将出口直径改为6mm,小明 还是按习惯每次挤出1cm长的牙膏,这样,这只牙膏 能用多少次?
直径为5mm
1cm长的牙膏 直径为6mm
讲授新课
一 等积变形问题
例1:如图,用直径为200mm的圆柱体钢,锻造一个长、 宽、高分别为300mm、300mm和90mm的长方体毛坯底板, 应截取圆钢多少(圆柱的体积公式:体积 = 底面积 高线长.计算时取3.14.要求结果误差不超过1mm)?
一元一次方程应用题归类汇集超详细解题过程含答案(特级教师整理版)

一元一次方程应用题归类汇集含详细答案整理版本一、列方程解应用题的一般步骤(解题思路)(1)审—审题:认真审题,弄清题意,找出能够表示本题含义的相等关系(找出等量关系).(2)设—设出未知数:根据提问,巧设未知数.(3)列-列出方程:设出未知数后,表示出有关的含字母的式子,然后利用已找出的等量关系列出方程.(4)解——解方程:解所列的方程,求出未知数的值.(5)答—检验,写答案:检验所求出的未知数的值是否是方程的解,是否符合实际,检验后写出答案.(注意带上单位)二、各类题型解法分析一元一次方程应用题归类汇集:行程问题,工程问题,和差倍分问题(生产、做工等各类问题),等积变形问题,调配问题,分配问题,配套问题,增长率问题,数字问题,方案设计与成本分析 ,古典数学,浓度问题等.第一类、行程问题基本的数量关系:(1)路程=速度×时间 ⑵ 速度=路程÷时间 ⑶ 时间=路程÷速度要特别注意:路程、速度、时间的对应关系(即在某段路程上所对应的速度和时间各是多少)常用的等量关系:1、甲、乙二人相向相遇问题⑴甲走的路程+乙走的路程=总路程 ⑵二人所用的时间相等或有提前量2、甲、乙二人中,慢者所行路程或时间有提前量的同向追击问题⑴甲走的路程-乙走的路程=提前量 ⑵二人所用的时间相等或有提前量3、单人往返⑴ 各段路程和=总路程 ⑵ 各段时间和=总时间 ⑶ 匀速行驶时速度不变4、行船问题与飞机飞行问题⑴ 顺水速度=静水速度+水流速度 ⑵ 逆水速度=静水速度-水流速度5、考虑车长的过桥或通过山洞隧道问题将每辆车的车头或车尾看作一个人的行驶问题去分析,一切就一目了然。
6、时钟问题:⑴ 将时钟的时针、分针、秒针的尖端看作一个点来研究⑵ 通常将时钟问题看作以整时整分为起点的同向追击问题来分析.常用数据:① 时针的速度是0。
5°/分 ② 分针的速度是6°/分 ③ 秒针的速度是6°/秒一、一般行程问题(相遇与追击问题)1、从甲地到乙地,某人步行比乘公交车多用3.6小时,已知步行速度为每小时8千米,公交车的速度为每小时40千米,设甲、乙两地相距x 千米,则列方程为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级上册
人民教育出版社出版
王斌制作
精讲
例题
200
例 如图,用直径为200
毫米的圆钢,锻造一个
x 长、宽、高分别为300 毫米、300毫米和80毫
米的长方体毛坯底板,
应截取圆钢多少(圆柱 的体积公式:体积 = 底面积 高线长.计算 时取3.14.要求结果误 差不超过1毫米)?
精讲
例题
例 如图,用直径为200
毫米的圆钢,锻造一个
长、宽、高分别为300 毫米、300毫米和80毫 应截取圆钢多少(圆柱 的体积公式:体积 = 底面积 高线长.计算 时取3.14.要求结果误 差不超过1毫米)? 解:设应截取的圆钢长为x 毫米, 根据题意得:
米的长方体毛坯底板, •(200/2)2 • x = 300 × 300 × 80
80
300 300
三、根据等量关系列 出方程;
精讲
例题
200
分
析
思考4:如何解这个方程? x
•(200/2)2 • x = 300×300×80
化简的3.14x=720,故x≈230。
80
四、解方程,求出未 知数的值;
300 300
精讲
例题
200
分
析
答:略。 x
80
300 300
五、检验求得的值 是否正确和符合实 际情形,并写出答 案.
出答案.
练
习
1.将一个底面直径为10厘米,高为36厘米的“瘦
长”形圆柱锻压成底面直径是20厘米的“矮胖”
形圆柱,高变成了多少?
锻压
等量关系:变形前的体积=变形后的体积
练
习
2.已知一圆柱形容器底面半径为0.5m,高线长为1.5m,里面盛 有1m深的水,将底面半径为0.3m,高线长为0.5m的圆柱形铁 块沉入水中,问容器内水面将升高多少?
精讲
例题
200
分
析
思考2:如何用字母(未知 数x)表示圆钢的体积? x
圆钢的体积 =(200/2)2 x 立方毫米.
80
300 300
二、用含未知数x的 一次式表示有关的量;
精讲
例题
200
分
析
思考3:如何根据等量关系 “圆钢体积=长方体毛胚的体积” 列出方程? 根据等量关系列出方程,得:
x
•(200/2)2 • x = 300×300×80
精讲
例题
一、分析题意,找出等量关系 :
圆钢体积 = 长方体毛坯体积, 设应截取圆钢长为x毫米
例 如图,用直径为200
毫米的圆钢,锻造一个
长、宽、高分别为300 毫米、300毫米和80毫
二、用字母的一次式表示有关的量:是 指圆钢的体积是 (200/2)2 x立方毫 米 . 三、根据等量关系列出方程,得:
0.52 x = 0.32 ×0.5 方程为:___________________ x =0.18 解这个方程:__________
容器内水面将升高0.18m。 答:______________________
小结:说说列方程解应用题的一半步骤:
列一元一次方程解应用题的一般步骤:
1、分析题意,找出等量关系,分析题中数量及其 关系,用字母(例如x),表示问题里的未知数. 2、用字母的一次式表示有关的量. 3、根据等量关系列出方程. 4、解方程,求出未知数的值. 5、检验求得的值是否正确和符合实际情形,并写 出答案.
3.14 x=720 x 230 答:应截取圆钢的长为230毫米 .
归
纳
列一元一次方程解应用题的一般步骤: 1、分析题意,找出等量关系,分析题中数量及其 关系,用字母(例如x),表示问题里的未知数. 2、用字母的一次式表示有关的量. 3、根据等量关系列出方程.
4符合实际情形,并写
80 300
300
精讲
例题
200
分
析
思考1:题目中有哪些已知 量和未知量?它们之间有什么关
系?如何设未知数?
x 已知:圆钢直径(200mm)、 长方体毛胚的长宽高(300mm、
80
300 300
300mm、80mm) 一、分析题意,找出 未知:圆钢的高 等量关系,分析题中 相等关系: 数量及其关系,用字 圆钢体积=长方体毛胚的体积 母(例如x),表示问 设未知数: 设应截取圆钢x毫米。 题里的未知数;
5dm 1. 5m
3dm
0. 5m
分析: 根据以上演示我们知道了它们的等量关系: 水位上升部分的体积=小圆柱形铁块的体积 圆柱形体积公式是_______, 水升高后的体积 小铁块的体积 (__________)
0.52 x 0.32 ×0.5 (_________) r2h
解:设水面将升高x米, 根据题意得
米的长方体毛坯底板,
应截取圆钢多少(圆柱 的体积公式:体积 = 底面积 高线长.计算 时取3.14.要求结果误 差不超过1毫米)?
•(200/2)2 • x = 300×300×80
四、解方程求出未知数的值,即解这个 方程得: 3.14 x =720 x 230
五、检验求得的值是否正确和符合实际 情形,并写出答案:应截取圆钢的长为 230毫米.
