新课标 重庆市中考数学专项训练 动点函数图像
2020年重庆中考复习数学函数图象专题训练三(含答案)

2020年重庆中考复习数学函数图象专题训练三(含答案)1、(八中定时练习五2018秋•通州区期末)如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB=30°,D是直径AB上一动点,连接CD并过点D作CD的垂线,与⊙O的其中一个交点记为点E(点E位于直线CD上方或左侧),连接EC.已知AB=6cm,设A、D两点间的距离为xcm,C、D两点间的距离为y1cm,E、C两点间的距离为y2cm.小雪根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小雪的探究过程:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值,请将表格补充完整;x/cm0123456y1/cm 5.20 4.36 3.60 2.65 2.65y2/cm 5.20 4.56 4.22 4.24 4.77 5.60 6.00(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1的图象;(3)结合函数图象,解决问题:当∠ECD=60°时,AD的长度约为cm.2、(八中定时练习6)3、(2019秋•门头沟区期末)如图,是直径AB所对的半圆弧,点C在上,且∠CAB=30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.小明根据学习函数的经验,对线段AE,AD长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:(1)对于点D在AB上的不同位置,画图、测量,得到线段AE,AD长度的几组值,如下表:位置1位置2位置3位置4位置5位置6位置7位置8位置9AE/cm0.000.410.77 1.00 1.15 1.000.00 1.00 4.04…AD/cm0.000.50 1.00 1.41 2.00 2.45 3.00 3.21 3.50…在AE,AD的长度这两个量中,确定的长度是自变量,的长度是这个自变量的函数;(2)在下面的平面直角坐标系xOy中,画出(1)中所确定的函数的图象;(3)结合画出的函数图象,解决问题:当AE=AD时,AD的长度约为cm(结果精确到0.1).4、(2019•海淀区校级模拟)如图,∠MAN=30°,在射线AN上取一点B,使AB=4 cm,过点B作BC⊥AM于点C,点D为边AB上的动点(点D不与点A,点B重合),连接CD,过点D作ED⊥CD交直线AC于点E.在点D由点A到点B运动过程中,设AD=xcm,AE=ycm.(1)取指定点作图,根据下面表格预填结果,先通过作图确定AD=2 cm时,点E的位置,测量AE 的长度.①根据题意,在答题卡上补全图形;②把表格补充完整:通过取点、画图、测量,得到了x与y的几组对应值,如表:x/cm…123…ycm…0.40.8 1.0m 1.00 4.0…则m=(结果保留一位小数).(2)在下面的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当AE=AD时,AD的长度约为cm.5、(2019秋•东城区校级期中)如图1,Rt△ABC中,∠ACB=90°,点D为AB边上的动点(点D不与点A,点B重合),过点D作ED⊥CD交直线AC于点E,已知∠A=30°,AB=4cm,在点D由点A 到点B运动的过程中,设AD=xcm,AE=ycm.(1)通过取点、画图、测量,得到了x与y的几组值,如表:x/cm…1 2 3…y/cm…0.40.8 1.0 1.00 4.0…小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(说明:补全表格时相关数值,保留一位小数)(2)在如图2的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当AE=AD时,AD的长度约为cm.2020年重庆中考复习数学函数图象专题训练三答案1、(八中定时练习五2018秋•通州区期末)如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB=30°,D是直径AB上一动点,连接CD并过点D作CD的垂线,与⊙O的其中一个交点记为点E(点E位于直线CD上方或左侧),连接EC.已知AB=6cm,设A、D两点间的距离为xcm,C、D两点间的距离为y1cm,E、C两点间的距离为y2cm.小雪根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小雪的探究过程:(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值,请将表格补充完整;x/cm0123456y1/cm 5.20 4.36 3.603 2.65 2.653y2/cm 5.20 4.56 4.22 4.24 4.77 5.60 6.00(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1的图象;(3)结合函数图象,解决问题:当∠ECD=60°时,AD的长度约为 4.5或6cm.解:(1)当x=3时,∵AB=6,AD=3,∴点D与点O重合,此时△DCE是等腰直角三角形,∴CD=DE=3,∴y1=3,当x=6时,点D与B重合,∴CD=BC,∵∠CAB=30°,∴CD=BC=AB=3,故答案为3,3.(2)函数图象如图所示:(3)当∠ECD=60°时,在Rt△ECD中,∵∠EDC=90°,∴∠CED=30°,∴EC=2CD,∴y2=2y1,关系图象可知,满足条件的x的值为4.5cm或6cm.2、(八中定时练习五)解:(1)2k = , 1b =- ;(2)如图,性质:y 随x 的增大而增大 (3) 1533x << .3、(2019秋•门头沟区期末)如图,是直径AB所对的半圆弧,点C在上,且∠CAB=30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.小明根据学习函数的经验,对线段AE,AD长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:(1)对于点D在AB上的不同位置,画图、测量,得到线段AE,AD长度的几组值,如下表:位置1位置2位置3位置4位置5位置6位置7位置8位置9AE/cm0.000.410.77 1.00 1.15 1.000.00 1.00 4.04…AD/cm0.000.50 1.00 1.41 2.00 2.45 3.00 3.21 3.50…在AE,AD的长度这两个量中,确定AD的长度是自变量,AE的长度是这个自变量的函数;(2)在下面的平面直角坐标系xOy中,画出(1)中所确定的函数的图象;(3)结合画出的函数图象,解决问题:当AE=AD时,AD的长度约为 2.2或3.3cm(结果精确到0.1).解:(1)根据题意,D为AB边上的动点,∴AD的长度是自变量,AE的长度是这个自变量的函数;∴故答案为:AD,AE.(2)根据已知数据,作图得:(3)当AE=AD时,y=x,在(2)中图象作图,并测量两个函数图象交点得:AD=2.2或3.3 4、(2019•海淀区校级模拟)如图,∠MAN=30°,在射线AN上取一点B,使AB=4 cm,过点B作BC⊥AM于点C,点D为边AB上的动点(点D不与点A,点B重合),连接CD,过点D作ED⊥CD交直线AC于点E.在点D由点A到点B运动过程中,设AD=xcm,AE=ycm.(1)取指定点作图,根据下面表格预填结果,先通过作图确定AD=2 cm时,点E的位置,测量AE 的长度.①根据题意,在答题卡上补全图形;②把表格补充完整:通过取点、画图、测量,得到了x与y的几组对应值,如表:x/cm…123…ycm…0.40.8 1.0m 1.00 4.0…则m= 1.2(结果保留一位小数).(2)在下面的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当AE=AD时,AD的长度约为 2.4或3.3cm.解:(1)根据题意,测量得m=1.2,∴故答案为:1.2(2)根据已知数据,作图得:(3)当AE=AD时,y=x,在(2)中图象作图,并测量两个函数图象交点得:AD=2.4或3.35、(2019秋•东城区校级期中)如图1,Rt△ABC中,∠ACB=90°,点D为AB边上的动点(点D不与点A,点B重合),过点D作ED⊥CD交直线AC于点E,已知∠A=30°,AB=4cm,在点D由点A 到点B运动的过程中,设AD=xcm,AE=ycm.(1)通过取点、画图、测量,得到了x与y的几组值,如表:x/cm…1 2 3…y/cm…0.40.8 1.0 1.2 1.00 4.0…小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(说明:补全表格时相关数值,保留一位小数)(2)在如图2的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;(3)结合画出的函数图象,解决问题:当AE=AD时,AD的长度约为 2.4或3.3cm.解:(1)根据题意,测量得1.2(2)根据已知数据,作图得:(3)当AE=AD时,y=x,在(2)中图象作图,并测量两个函数图象交点得:AD=2.4或3.3.。
2021年重庆中考数学第22题新函数图像题专题训练
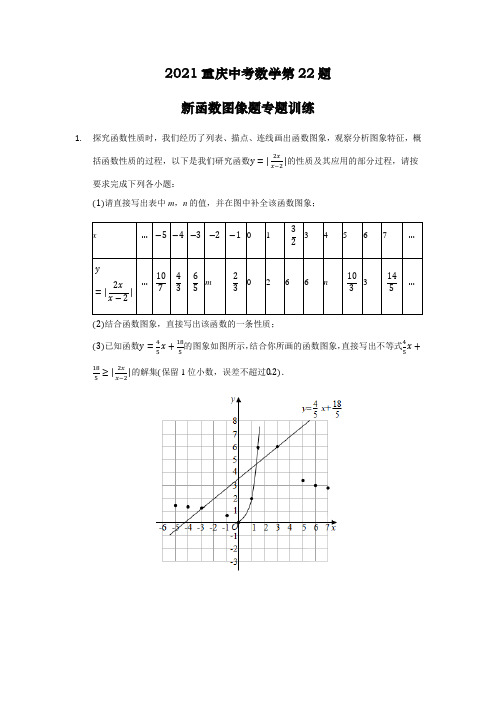
2021重庆中考数学第22题新函数图像题专题训练1.探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程,以下是我们研究函数y=|2xx−2|的性质及其应用的部分过程,请按要求完成下列各小题:(1)请直接写出表中m,n的值,并在图中补全该函数图象;x…−5−4−3−2−1013234567…y=|2xx−2|…1074365m230266n1033145…(2)结合函数图象,直接写出该函数的一条性质;(3)已知函数y=45x+185的图象如图所示,结合你所画的函数图象,直接写出不等式45x+18 5≥|2xx−2|的解集(保留1位小数,误差不超过0.2).2.在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数y=−6x−6x2−2x+2性质及其应用的部分过程,请按要求完成下列各小题.(1)请把下表补充完整,并在图中补全该函数图象:x…−5−4−3−2−1012345…y=−6x−6x2−2x+2…363715132417______12530−3______ −952417…(2)观察函数图象,写出该函数的一条性质:______ ;(3)已知函数y=−75x+1的图象如图所示,结合你所画的函数图象,直接写出不等式−6x−6x2−2x+2≥−75x+1的解集(保留1位小数,误差不超过0.2).x3−2x的图象与性质进行探究.3.根据我们学习函数的过程和方法,对函数y=14(1)如表是y与x的几组对应值:则m的值为______ ,n的值为______ .(2)描点、连线,在所给的平面直角坐标系中画出该函数的图象,写出该函数的一条性质:______ .x3−2x≥x,结合图象,直接写出x的取值范围______ .(3)若144.在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数y=|5xx2+4|性质及其应用的部分过程,请按要求完成下列各小题.(1)补全表:(2)在平面直角坐标系中,补全函数图象,根据函数图象,写出这个函数的一条性质:______ ;(3)已知函数y=52x−1的图象如图所示,结合你所画的函数图象,直接写出关于x的方程|5xx2+4|=52x−1的近似解(保留1位小数,误差不超过0.2).5.探究函数性质时,我们经历了列表,描点,连线画出函数图象,观察分析图象特征,概括函数性质的过程,结合已有的学习经验,请结合表中的数据,画图并探究该函数y=−ax2+2的性质.x…−4−3−2−101234…y…−23−1211−2−4−6−4−2−b−23…(1)根据表中数据可得:a=______ ,b=______ .(2)描点、连线,在所给的平面直角坐标系中画出该函数的图象;(3)观察该函数图象,写出该函数图象的一条性质:______ ;(4)已知函数y=−23x−103的图象如图所示,结合你所画的函数图象,直接写出不等式−ax2+2≤−23x−103的解集______ .6.某“数学兴趣小组”根据学习函数的经验,对函数y=−4x+6(x−2)2的图象和性质进行了探究,探究过程如下,请补充完整:x…−3−2−10323456…y (18)2574109m0−6−52n−98…(1)m=______ ,n=______ ;(2)同学们先找到y与x的几组对应值,然后在下图的平面直角坐标系xOy中,描出各对应值为坐标的点.请你根据描出的点,画出该函数的图象;(3)根据函数图象,写出该函数的一条性质:______ .(4)结合你所画的函数图象,直接写出不等式−x+2≤−4x+6的解集为______ .(x−2)27.在函数的学习中,我们经历“确定函数表达式--画函数图象--利用函数图象研究函数性质--利用图象解决问题”的学习过程,画函数图象时,我们常通过描点或平移或翻折的方法画函数图象,请根据你学到的函数知识探究函数y 1={2−|x|(x <2)x−2x−1(x ≥2)的图象与性质并利用图象解决如下问题: 列出y 1与x 的几组对应的值如表: x…−3−2−1 01234 5 …y … m 0 1 2 1 0 n 2334…(1)根据表格中x 、y 的对应关系可得m = ______ ,n = ______ ;(2)用你喜欢的方式画出该函数图象:根据函数图象,写出该函数的一条性质:______ ; (3)直接写出当函数y 1的图象与直线y 2=kx +1有三个交点时,k 的取值范围是______ .8.小明结合自己的学习经验,对新函数y=bkx2+1的解析式、图象、性质及应用进行探究:已知当x=0时,y=2;当x=1时,y=1.(1)函数解析式探究:根据给定的条件,可以确定由该函数的解析式为:______ .(2)函数图象探究:①根据解析式,补全如表,则m=______ ,n=______ .②根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象.x…−4−3−2−1−121212n4…y (2)171525m8528512515217…(3)函数性质探究:请你结合函数的解析式及所画图象,写出该函数的一条性质:______ .(4)综合应用:已知函数y=|715x−815|的图象如图所示,结合你所画的函数图象,直接写出不等式|7 15x−815|≤bkx2+1.9.根据我们学习函数的过程与方法,对函数y=x2+bx+2−c|x−1|的图象和性质进行探究,已知该函数图象经过(−1,−2)与(2,1)两点,(1)该函数的解析式为______ ,补全下表:(2)描点、连线,在所给的平面直角坐标系中画出该函数的图象,写出这个函数的一条性质:______ .(3)结合你所画的图象与函数y=x的图象,直接写出x2+bx+2−c|x−1|≤x的解集______ .x|ax+b|(a>0)的图象与性质进行探10.小帆根据学习函数的过程与方法,对函数y=14究.已知该函数图象经过点(2,1),且与x轴的一个交点为(4,0).(1)求函数的解析式;(2)在给定的平面直角坐标系中:①补全该函数的图象;②当2≤x≤4时,y随x的增大而______(在横线上填增大或减小);x|ax+b|的最大值是______;③当x<4时,y=14x|ax+b|有两个交点,则k=______.①直线y=k与函数y=1411.已知函数y=a−b|x−1|(a、b为常数),当x=1时,y=1;当x=2时,y=0;请对该函数及其图象进行如下探究:(1)求函数的解析式;(2)请在给出的平面直角坐标系中画出该函数的图象,并结合图象写出该函数的一条性质:______;根据函数图象解决下列问题:①若A(m,c),B(n,c)为该函数图象上不同的两点,则m+n=______;x+k有两个不相等的实数解x1,x2,且x1⋅x2>0,则k的取②若方程a−b|x−1|=12值范围是______.12.函数图象在探索函数的性质中有非常重要的作用,现在就一类特殊的函数展开探索:y=x+a,探索函数图象和性质过程如下:x(1)上表是该函数y与自变量x的几组对应值,则a=______ ,m=______ ,n=______ ;(2)如图,在平面直角坐标系中,已经描出了表中部分点,请根据描出的点画出该函数图象;(3)由函数图象,写出该函数的一条性质:______ ;(4)请在同一个平面直角坐标系中画出函数y=2x的图象,并直接写出不等式x+ax≤2x 的解集:______ .13.若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数,下面我们参照学习函数的过程与方法,探究分段函数y={|x+1|(x≤1)2x(x>1)的图象与性质,探究过程如下,请补充完整.(1)列表:x…−4−3−2−101234…y…3m10121n 12…其中,m=______,n=______.(2)描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象.(3)研究函数并结合图象与表格,回答下列问题:①点A(72,y1),B(5,y2),C(x1,52),D(x2,6)在函数图象上,则y1______y2,x1______x2;(填“>”,“=”或“<”)②当函数值y=1时,求自变量x的值;(4)若直线y=−x+b与函数图象有且只有一个交点,请直接写出b的取值范围.14.学习函数时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,下面我们对函数y ={−2x (x <0)x 3−3x 2+2(x ≥0)的图象和性质进行探究,请将以下探究过程补充完整:(1)选取适当的值补全表格;描点、连线,在所给的平面直角坐标系中画出函数的图象:(2)结合图象,写出该函数的一条性质:______ ; (3)结合这个函数的图象与性质,解决下列问题:①若点A(x 1,y 1),B(x 2,y 2),C(x 3,y 3)在这个函数的图象上,且0<x 3<3,−1<x 1<x 2<0,请写出y 1,y 2,y 3的大小关系:______ (用“<”连接).②若直线y =2a +1(a 是常数)与该函数图象有且只有三个交点,则a 的取值范围为______ .15. 在初中阶段的函数学习中,我们经历了“确定函数的表达式--利用函数图象研究其性质--运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义|a|={a(a ≥0)−a(a <0).小东结合上面的学习过程,对函数y =|32x −3|+12x −5的图象与性质进行了探究.(1)化简函数的表达式:当x ≥2时,y = ______ ,当x <2时,y = ______ ; (2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质:______ ;(3)已知函数y =2x (x >0)的图象如图所示,结合你所画函数图象,直按写出|32x −3|+12x −5=2x 的近似解______ .(精确到0.1)16.已知函数y=a|x−2|+x+b(a,b为常数).当x=3时,y=0,当x=0时,y=−1,请对该函数及其图象进行探究:(1)a=______ ,b=______ ;(2)请在给出的平面直角坐标系中画出该函数图象,并结合所画图象,写出该函数的一条性质.(3)已知函数y=−x2+4x+5的图象如图所示,结合图象,直接写出不等式a|x−2|+x+b≥−x2+4x+5的解集.17.在画函数图象时,我们常常通过描点或平移或翻折的方法画函数图象.小明根据学到的函数知识探究函数y1=|ax+4|−b的图象与性质并利用图象解决问题.小明列出了如表y1与x的几组对应的值:(1)根据表格,直接写出a=______ ,b=______ ;(2)在平面直角坐标系中,画出该函数图象,并根据函数图象,写出该函数的一条性质______ ;(3)当函数y1的图象与直线y2=mx−1有两个交点时,直接写出m的取值范围.18.已知y=a|2x+4|+bx(a,b为常数).当x=1时,y=5;当x=−1时,y=3.(1)a=______ ,b=______ ;(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数图象;并写出函数的一条性质:______ ;(3)已知函数y=25的图象如图所示,结合你所画的函数图象,直接写出方程a|2x+ |2x−2|4|+bx=25的近似解(精确到0.1).|2x−2|。
2020年重庆中考复习数学函数图象专题训练一(含答案)

(2)①∵b=8,∴y=|﹣x2+8x﹣7|﹣4,当 x=﹣ 时,y= ;当 x=4 时,y=5;
∴m= ,n=5;②如图所示:
(3)函数关于 x=4 对称;
第 17 页(共 34 页)
(4)当 ,|﹣x2+8x﹣7|=m+4 有四个根,
解(1)当 x=0 时,y=﹣2+2+3=3,即 m=3, 当 x=3 时,y=﹣0.5+1+3=3.5,即 n=3.5 (2)图象如图所示:
(3)图象关于直线 x=2 对称
第 16 页(共 34 页)
(4)∵﹣ (x﹣2)2+|x﹣2|+3=k 有 3 个不相等的实数根,即函数 y=﹣ (x﹣2)2+|x﹣2|+3 图象与
y=k 图象有三个交点,由图象得,k=3. 2、(2019 秋•北碚区校级月考)已知关于 x 函数 y=|﹣x2+bx﹣7|﹣4,点(4,5)在函数上,且 b 为整数,
根据我们已有的研究函数的经验,请对该函数及其图象进行如下探究,并完成以下问题:
(1)求 b= 8 ; (2)函数图象探究:
①下表是 y 与 x 的几组对应值,请直接写出 m 与 n 的值:m=
;
(2)在给出的平面直角坐标系中,画出这个函数的图象并写出这个函数的一条性质
;
(3)进一步探究函数图象并解决问题:
①直线 y=k 与函数 y=a|x2+bx|+c 有三个交点,则 k= ;
②已知函数 y=x﹣3 的图象如图所示,结合你所画的函数图象,写出不等式 a|x2+bx|+c≤x﹣3 的解
集:
图1
(3)请结合所画函数图象,写出函数图象的一条性质; (4)解决问题:若函数y1 与y2 2a 2 至少有2 个交点,求a 的取值范围.
2020年重庆中考复习数学函数图象专题训练四(含答案)

2020年重庆中考复习数学函数图象专题训练四(含答案)1.九年级8班的王源同学根据学习经验,决定从问题的简单、特殊情形入手进行探究函数y=的图象和性质,下面是他的探究过程,请你一起来完成.(1)下表是y与x的几组对应值:x…﹣4﹣3﹣2﹣101234…y…97m3163n…经计算,m的值为,n的值为;(2)如图,在平面直角坐标系xOy中描出上列各点,请画出该函数图象;(3)根据函数图象,写出该函数的一条性质:.2.小明研究一函数的性质,下表是该函数的几组对应值:x…﹣4﹣3﹣2﹣101234…y…830﹣1030﹣3﹣6…(1)在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图象(2)根据所画函数图象,写出该函数的一条性质:;(3)根据图象直接写出该函数的解析式及自变量的取值范围:;(4)若一次函数y=x+n与该函数图象有三个交点,则n的范围是.3.已知函数y1=的部分图象如图所示,(1)请在图中补全y的函数图象;(2)已知函数y2的图象与函数y1的图象关于y轴对称,请在图中画出函数y2的图象;(3)若直线y3=x+a与函数y1、y2的图象有且只有一个交点,则a的取值范围是.4.八年级(1)班张山同学利用所学函数知识,对函数y=|x+2|﹣x﹣1进行了如下研究:列表如下:x…﹣5﹣4﹣3﹣2﹣10123…Y…753m1n111…描点并连线(如下图)(1)自变量x的取值范围是;(2)表格中:m=;n=;(3)在给出的坐标系中画出函数y=|x+2|﹣x﹣1的图象;(4)一次函数y=﹣x+3的图象与函数y=|x+2|﹣x﹣1的图象交点的坐标为.5.有这样一个问题探究函数(b、c为常数)的图象和性质.元元根据学习函数的经验,对该函数的图象和性质进行了以下探究:下面是元元的探究过程,请你补充完整x……﹣10123456……y……0 2.54m4 2.501……(1)根据上表信息,其中b=,c=,m=.(2)如图,在下面平面直角坐标系中,描出以补全后的表中各对应值为坐标的点,并画出该函数的另一部分图象;(3)观察函数图象,请写出该函数的一条性质:.(4)解决问题:若直线y=3n+2(n为常数)与该函数图象有3个交点时,求n的范围.6.已知函数y1=ax+2﹣,其自变量的取值范围是x>﹣2.当x=2时,y1=﹣2;当x=6时,y1=﹣5.(1)根据给定的条件,求出a、b的值和y1的函数解析式;(2)根据你所求的函数解析式,选取适当的自变量x完成如表,并在下面的平面直角坐标系中描点并画出函数的大致图象:x…6…y…﹣5…(3)请画出y2=x﹣4的图象,并结合图象直接写出:当y1>y2时,x的取值范围是.7.初三某班“挑战极限”学习小组根据学习函数的经验,通过研究一个未学过的函数的图象,从而探究其各方面的性质.下表是函数y与自变量x的几组对应值:x…﹣6﹣5﹣4﹣3﹣2﹣1012…y…2 2.434630﹣3﹣6…(1)在如图所示的平面直角坐标系xOy中,每个小方格的边长为一个单位长度,请根据上表中各组对应值为坐标描出点,并画出该函数的图象;(2)请根据画出的函数图象,直接写出该函数的关系式y=,(要求写出自变量的取值范围),并写出该函数的一条性质;(3)当直线y=x+b与该函数图象有3个交点时,求b的取值范围.2020年重庆中考复习数学函数图象专题训练四答案解析1.九年级8班的王源同学根据学习经验,决定从问题的简单、特殊情形入手进行探究函数y=的图象和性质,下面是他的探究过程,请你一起来完成.(1)下表是y与x的几组对应值:x…﹣4﹣3﹣2﹣101234…y…97m3163n…经计算,m的值为5,n的值为2;(2)如图,在平面直角坐标系xOy中描出上列各点,请画出该函数图象;(3)根据函数图象,写出该函数的一条性质:当x<0时,y随x的增大而减小;当x>0时,y随x 的增大而减小.解:(1)当x=﹣2时,m=﹣2×(﹣2)+1=5,当x=3时,y==2,(2)如图(3)当x<0时,y随x的增大而减小;当x>0时,y随x的增大而减小.故答案为5,2;当x<0时,y随x的增大而减小;当x>0时,y随x的增大而减小.2.小明研究一函数的性质,下表是该函数的几组对应值:x…﹣4﹣3﹣2﹣101234…y…830﹣1030﹣3﹣6…(1)在平面直角坐标系中,描出以上表格中的各点,根据描出的点,画出该函数图象(2)根据所画函数图象,写出该函数的一条性质:x<﹣1时,y随x的增大而减小;(3)根据图象直接写出该函数的解析式及自变量的取值范围:;(4)若一次函数y=x+n与该函数图象有三个交点,则n的范围是.解:(1)根据表格的点所画的图象如图所示:(2)观察图象可得其中的一条性质为:x<﹣1时,y随x的增大而减小(3)当x<1时,函数经过点点(﹣3,3)(﹣2,0)(0,0)故设函数的解析式为y=a(x+2)(x﹣0),将点(﹣4,6)代入解得3=a(﹣3+2)×(﹣3),解得a=1,∴x<1时,函数解析式为:y=x2+2x,(x<1)当x≥1时,函数经过点(1,3)(2,0)故设函数解析式为:y=kx+b,解得∴x≥1时,函数解析式为:y=﹣3x+6故答案为:,(4)由图象可知,一次函数y=x+n与函数y=﹣3x+6交点在(1,3)时有3=+n得,n=一次函数y=x+n与y=x2+2x有且仅有一个交点时,有⇒∴△=,解得n=故一次函数y=x+n与该函数图象有三个交点时,n的范围是故答案为:3.已知函数y1=的部分图象如图所示,(1)请在图中补全y的函数图象;(2)已知函数y2的图象与函数y1的图象关于y轴对称,请在图中画出函数y2的图象;(3)若直线y3=x+a与函数y1、y2的图象有且只有一个交点,则a的取值范围是a>1或﹣1<a<1.解:(1)函数y1的图象如图所示,(2)函数y2的图象如图所示;(3)∵直线y3=x+a与函数y1、y2的图象有且只有一个交点,∴a的取值范围为:a>1或﹣1<a<1.4.八年级(1)班张山同学利用所学函数知识,对函数y=|x+2|﹣x﹣1进行了如下研究:列表如下:x…﹣5﹣4﹣3﹣2﹣10123…Y…753m1n111…描点并连线(如下图)(1)自变量x的取值范围是全体实数;(2)表格中:m=1;n=1;(3)在给出的坐标系中画出函数y=|x+2|﹣x﹣1的图象;(4)一次函数y=﹣x+3的图象与函数y=|x+2|﹣x﹣1的图象交点的坐标为(﹣6,9)和(2,1).解:(1)∵函数y=|x+2|﹣x﹣1,∴自变量x的取值范围为全体实数(2)当x=﹣2时,m=|﹣2+2|+2﹣1=1,当x=0时,n=|0+2|﹣0﹣1=1,(3)如下图:(4)在(3)中坐标系中作出直线y=﹣x+3,如下:由图象得:一次函数y=﹣x+3的图象与函数y=|x+2|﹣x﹣1的图象交点的坐标为(﹣6,9)和(2,1)5.有这样一个问题探究函数(b、c为常数)的图象和性质.元元根据学习函数的经验,对该函数的图象和性质进行了以下探究:下面是元元的探究过程,请你补充完整x……﹣10123456……y……0 2.54m4 2.501……(1)根据上表信息,其中b=2,c= 2.5,m= 4.5.(2)如图,在下面平面直角坐标系中,描出以补全后的表中各对应值为坐标的点,并画出该函数的另一部分图象;(3)观察函数图象,请写出该函数的一条性质:当x<2时,y随x的增大而增大.(4)解决问题:若直线y=3n+2(n为常数)与该函数图象有3个交点时,求n的范围.解:(1)由表格数据得:当x=﹣1时,y=0;当x=5时,y=0;当x=0时,y=2.5;∴﹣b==2,c=2.5,∴y=∴当x=2时,y=4.5,即m=4.5,故答案为:2,2.5,4.5;(2)图象如下:(3)观察图象可知:当x<2时,y随x的增大而增大(4)∵当x=2时,y=4.5;∴由图象可知直线y=4.5与该函数图象有2个交点,直线y=0与该函数图象有2个交点,∴直线y=3n+2(n为常数)与该函数图象有3个交点时,0<3n+2<4.5,∴﹣<n<.6.已知函数y1=ax+2﹣,其自变量的取值范围是x>﹣2.当x=2时,y1=﹣2;当x=6时,y1=﹣5.(1)根据给定的条件,求出a、b的值和y1的函数解析式;(2)根据你所求的函数解析式,选取适当的自变量x完成如表,并在下面的平面直角坐标系中描点并画出函数的大致图象:x…6…y…﹣5…(3)请画出y2=x﹣4的图象,并结合图象直接写出:当y1>y2时,x的取值范围是﹣1<x<2.解:(1)∵y1=ax+2﹣,把x=2,y1=﹣2;x=6,y1=﹣5代入,得,解得,∴y1的函数解析式为y1=﹣x+2﹣;(2)填表如下:x…﹣10123456…y…﹣5﹣2﹣﹣2﹣﹣﹣﹣5…图象如图所示:(3)函数y2=x﹣4的图象如图所示.由图可知,当y1>y2时,x的取值范围是﹣1<x<2.7.初三某班“挑战极限”学习小组根据学习函数的经验,通过研究一个未学过的函数的图象,从而探究其各方面的性质.下表是函数y与自变量x的几组对应值:x…﹣6﹣5﹣4﹣3﹣2﹣1012…y…2 2.434630﹣3﹣6…(1)在如图所示的平面直角坐标系xOy中,每个小方格的边长为一个单位长度,请根据上表中各组对应值为坐标描出点,并画出该函数的图象;(2)请根据画出的函数图象,直接写出该函数的关系式y=,(要求写出自变量的取值范围),并写出该函数的一条性质;(3)当直线y=x+b与该函数图象有3个交点时,求b的取值范围.解:(1)如图,即为该函数的图象:(2)当x<﹣2时,y随x的增大而增大;x>2时.y随增大而减小;故答案为:;(3)依题意可得:,整理得:x2+3bx+36=0当△=0,即b=4时直线与反比例函数有一个交点,当直线经过点(﹣2,6)时,即当时,直线与该函数有三个交点.。
中考数学专题 动态几何与函数10题-含答案

动态几何与函数10题(1)请直接写出1y ,2y 与t 之间的函数关系式以及对应的t 的取值范围;
(2)请在平面直角坐标系中画出1y ,2y 的图象,并写出1y 的一条性质;
(3)求当12y y >时,t 的取值范围.
(1)求出12,y y与x的函数关系式,并注明
(2)先补全表格中1y的值,再画出
x123456
y12632
1
(3)在直角坐标系内直接画出2y的函数图像,结合1y和2y的函数图像,x的取值范围.(结果取精确值)
(1)请求出1y 和2y 关于x 的函数解析式,并说明x 的取值范围;
(2)在图2中画出1y 关于x 的函数图象,并写出一条这一函数的性质:(3)若12103
y y -≥,请结合函数图像直接写出x 的取值范围(近似值保留一位小数,误差不超过0.2)
4.
(2023春·重庆江津·九年级校联考期中)如图,在矩形ABCD 中,3AB =,4BC =,点P 从点A 出发,以每秒2个单位的速度沿折线A B C D →→→运动,当它到达D 点时停止运动;同时,点Q 从点A 出发,以每秒1个单位的速度沿射线AD 运动,过Q 点做直线l 平行于AB ,点M 为直线l 上的一点,满足AMQ △的面积为2,设点P 点Q 的运动时间为t (0t >),ADP △的面积为1y ,QM 的长度为2y .
(1)分别求出1y ,2y 与t 的函数关系,并注明t 的取值范围;
(2)在坐标系中画出1y ,2y 的函数图象;
(3)结合函数图象,请直接写出当12y y <时t 的取值范围.。
2021重庆年中考17题一次函数图形行程问题专题训练(3)
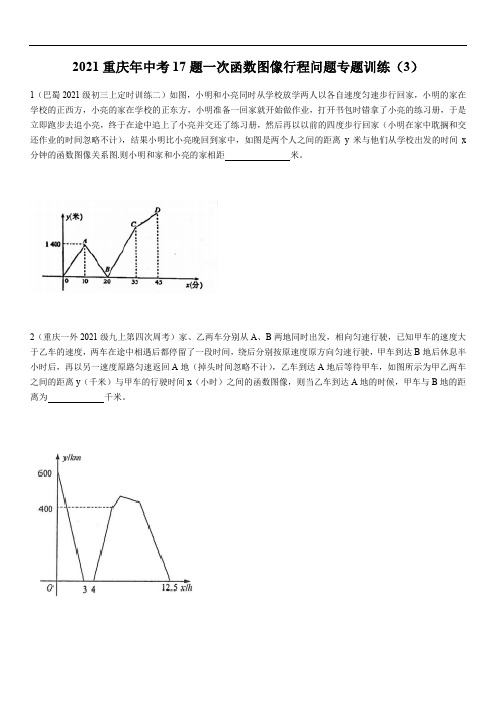
2021重庆年中考17题一次函数图像行程问题专题训练(3)1(巴蜀2021级初三上定时训练二)如图,小明和小亮同时从学校放学两人以各自速度匀速步行回家,小明的家在学校的正西方,小亮的家在学校的正东方,小明准备一回家就开始做作业,打开书包时错拿了小亮的练习册,于是立即跑步去追小亮,终于在途中追上了小亮并交还了练习册,然后再以以前的四度步行回家(小明在家中耽搁和交还作业的时间忽略不计),结果小明比小亮晚回到家中,如图是两个人之间的距离y米与他们从学校出发的时间x 分钟的函数图像关系图.则小明和家和小亮的家相距米。
2(重庆一外2021级九上第四次周考)家、乙两车分别从A、B两地同时出发,相向匀速行驶,已知甲车的速度大于乙车的速度,两车在途中相遇后都停留了一段时间,绕后分别按原速度原方向匀速行驶,甲车到达B地后休息半小时后,再以另一速度原路匀速返回A地(掉头时间忽略不计),乙车到达A地后等待甲车,如图所示为甲乙两车之间的距离y(千米)与甲车的行驶时间x(小时)之间的函数图像,则当乙车到达A地的时候,甲车与B地的距离为千米。
3(重庆八中2021级九上第一次月考模拟)一艘轮船额一艘快艇分别从甲、乙两个港口出发(水流速度不计)相向而行,快艇匀速航行到达甲港后,立即原速返回乙港(掉头时间忽略不计)在返回途中追上轮船刚好到达一个景点,轮船靠岸一小时供游客观赏游玩,绕后继续以原速航行到乙港,两船到达乙港均停止航行,轮船和快艇之间的距离y(千米)与轮船出发时间x(小时)之间的函数图像如图所示,当快艇返回到乙港时,轮船距乙港还有千米4(重庆育才2021级九上第一次月考复习)一条笔直的公路上顺次有A、B、C三地,小明驾车从B地出发匀速行驶前往A地,到达A地后停止,在小明出发的同时,小李驾车从B地匀速出发行驶前往A地,到达A地停留2小时后,调头按原速向C行驶,若AB两地之间相距200千米,在行驶的过程中,两人之间的距离y(千米)与小李驾车时间x(小时)之间的函数图像如图所示,则在他们出发后经过小时相遇。
中考数学复习----《动点问题的函数图像》压轴真题练习(含答案解析)

中考数学复习----《动点问题的函数图像》压轴真题练习(含答案解析)1.(2021•益阳)如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是()A.B.C.D.【答案】B【解答】解:∵▱ABCD的面积为4,x+y是平行四边形面积的一半,∴x+y=2,∴y=2﹣x,∴y是x的一次函数,且当x=0时,y=2;x=2时,y=0;故只有选项B符合题意.2.(2021•河南)如图1,矩形ABCD中,点E为BC的中点,点P沿BC从点B运动到点C,设B,P两点间的距离为x,PA﹣PE=y,图2是点P运动时y随x变化的关系图象,则BC的长为()A.4B.5C.6D.7【答案】C【解答】解:由函数图象知:当x=0,即P在B点时,BA﹣BE=1.利用三角形两边之差小于第三边,得到PA﹣PE≤AE.∴y的最大值为AE,∴AE=5.在Rt△ABE中,由勾股定理得:BA2+BE2=AE2=25,设BE的长度为t,则BA=t+1,∴(t+1)2+t2=25,即:t2+t﹣12=0,∴(t+4)(t﹣3)=0,由于t>0,∴t+4>0,∴t﹣3=0,∴BC=2BE=2t=2×3=6.故选:C.3.(2022•鞍山)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4cm,CD⊥AB,垂足为点D,动点M从点A出发沿AB方向以cm/s的速度匀速运动到点B,同时动点N从点C出发沿射线DC方向以1cm/s的速度匀速运动.当点M停止运动时,点N也随之停止,连接MN.设运动时间为ts,△MND的面积为Scm2,则下列图象能大致反映S与t之间函数关系的是()A.B.C.D.【答案】B【解答】解:∵∠ACB=90°,∠A=30°,AB=4,∴∠B=60°,BC=AB=2,AC=BC=6,∵CD⊥AB,∴CD=AC=3,AD=CD=3,BD=BC=,∴当M在AD上时,0≤t≤3,MD=AD﹣AM=3﹣t,DN=DC+CN=3+t,∴S=MD•DN=(3﹣t)(3+t)=﹣t2+,当M在BD上时,3<t≤4,MD=AM﹣AD=t﹣3,∴S=MD•DN=(t﹣3)(3+t)=t2﹣,故选:B.4.(2022•菏泽)如图,等腰Rt△ABC与矩形DEFG在同一水平线上,AB=DE =2,DG=3,现将等腰Rt△ABC沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰Rt△ABC与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为()A.B.C.D.【答案】B【解答】解:如图,作CH⊥AB于点H,∵AB=2,△ABC是等腰直角三角形,∴CH=1,当0≤x≤1时,y=×2x•x=x2,当1<x≤3时,y==1,当3<x≤4时,y=1﹣=﹣(x﹣3)2+1,故选:B.5.(2022•鄂尔多斯)如图①,在正方形ABCD中,点M是AB的中点,点N 是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为()A.B.2C.D.【答案】 A【解答】解:如图,连接AC交BD于点O,连接NC,连接MC交BD于点N′.∵四边形ABCD是正方形,∴O是BD的中点,∵点M是AB的中点,∴N′是△ABC的重心,∴N′O=BO,∴N′D=BD,∵A、C关于BD对称,∴NA=NC,∴AN+MN=NC+MN,∵当M、N、C共线时,y的值最小,∴y的值最小就是MC的长,∴MC=2,设正方形的边长为m,则BM=m,在Rt△BCM中,由勾股定理得:MC2=BC2+MB2,∴20=m2+(m)2,∴m=4,∴BD=4,∴a=N′D=BD=×4=,故选:A.6.(2021•鞍山)如图,△ABC是等边三角形,AB=6cm,点M从点C出发沿CB方向以1cm/s的速度匀速运动到点B,同时点N从点C出发沿射线CA 方向以2cm/s的速度匀速运动,当点M停止运动时,点N也随之停止.过点M作MP∥CA交AB于点P,连接MN,NP,作△MNP关于直线MP对称的△MN′P,设运动时间为ts,△MN′P与△BMP重叠部分的面积为Scm2,则能表示S与t之间函数关系的大致图象为()A.B.C.D.【答案】A【解答】解:如图1中,当点N′落在AB上时,取CN的中点T,连接MT.∵CM=t(cm),CN=2t(cm),CT=TN,∴CT=TN=t(cm),∵△ABC是等边三角形,∴∠C=∠A=60°,∴△MCT是等边三角形,∴TM=TC=TN,∴∠CMN=90°,∵MP∥AC,∴∠BPM=∠A=∠MPN=60°,∠BMP=∠C=60°,∠C+∠CMP=180°,∴∠CMP=120°,△BMP是等边三角形,∴BM=MP,∵∠CMP+∠MPN=180°,∴CM∥PN,∵MP∥CN,∴四边形CMPN是平行四边形,∴PM=CN=BM=2t,∴3t=6,∴t=2,如图2中,当0<t≤2时,过点M作MK⊥AC于K,则MK=CM•sin60°=t,∴S=•(6﹣t)•t=﹣t2+t.如图3中,当2<t≤6时,S=•MQ•PQ=×(6﹣t)×(6﹣t)=×(6﹣t)2,观察图象可知,选项A符合题意,故选:A.7.(2021•威海)如图,在菱形ABCD中,AB=2cm,∠D=60°,点P,Q同时从点A出发,点P以1cm/s的速度沿A﹣C﹣D的方向运动,点Q以2cm/s 的速度沿A﹣B﹣C﹣D的方向运动,当其中一点到达D点时,两点停止运动.设运动时间为x(s),△APQ的面积为y(cm2),则下列图象中能大致反映y与x之间函数关系的是()A.B.C.D.【答案】A【解答】解:∵四边形ABCD为菱形,∴AB=BC=CD=DA=2cm,∠B=∠D=60°.∴△ABC、△ACD都是等边三角形,∴∠CAB=∠ACB=∠ACD=60°.如图1所示,当0≤x≤1时,AQ=2xcm,AP=xcm,作PE⊥AB于E,∴PE=sin∠PAE×AP=(cm),∴y=AQ•PE=×2x×=,故D选项不正确;如图2,当1<x≤2时,AP=xcm,CQ=(4﹣2x)cm,作QF⊥AC于点F,∴QF=sin∠ACB•CQ=(cm),∴y===,故B选项不正确;如图3,当2<x≤3时,CQ=(2x﹣4)cm,CP=(x﹣2)cm,∴PQ=CQ﹣CP=2x﹣4﹣x+2=(x﹣2)cm,作AG⊥DC于点G,∴AG=sin∠ACD•AC=×2=(cm),∴y===.故C选项不正确,故选:A.8.(2021•日照)如图,平面图形ABD由直角边长为1的等腰直角△AOD和扇形BOD组成,点P在线段AB上,PQ⊥AB,且PQ交AD或交于点Q.设AP=x(0<x<2),图中阴影部分表示的平面图形APQ(或APQD)的面积为y,则函数y关于x的大致图象是()A.B.C.D.【答案】D【解答】解:当Q在AD上时,即点P在AO上时,有0<x≤1,此时阴影部分为等腰直角三角形,∴y=,该函数是二次函数,且开口向上,排除B,C选项;当点Q在弧BD上时,补全图形如图所示,阴影部分的面积等于等腰直角△AOD的面积加上扇形BOD的面积,再减去平面图形PBQ的面积即减去弓形QBF的面积,设∠QOB=θ,则∠QOF=2θ,∴,S弓形QBF=﹣S△QOF,当θ=45°时,AP=x=1+≈1.7,S弓形QBF=﹣=﹣,y=+﹣(﹣)=≈1.14,当θ=30°时,AP=x≈1.87,S弓形QBF=﹣=﹣,y=+﹣(﹣)=≈1.24,当θ=60°时,AP=x≈1.5,y≈0.98,在A,D选项中分别找到这两个特殊值,对比发现,选项D符合题意.故选:D.法二、当1<x<2时,即P在OB之间时,设∠QOD=θ,则θ∈(0,),则PQ=cosθ,OP=sinθ,则弧QD的长为θπ,此时S阴影=+θπ+sinθcosθ=+θ+sin2θ,∴y随x的增大而增大,而且增加的速度越来越慢,分析四个选项中的图象,只有选项D符合.故选:D.9.(2021•辽宁)如图,在矩形ABCD中,AB=6,AD=4,E是CD的中点,射线AE与BC的延长线相交于点F,点M从A出发,沿A→B→F的路线匀速运动到点F停止.过点M作MN⊥AF于点N.设AN的长为x,△AMN 的面积为S,则能大致反映S与x之间函数关系的图象是()A.B.C.D.【答案】B【解答】解:如图,∵E是CD的中点,∴CE=DE,∵四边形ABCD是矩形,∴∠D=∠DCF=90°,AD=BC=4,在△ADE与△FCE中,,∴△ADE≌△FCE(SAS),∴CF=AD=4,∴BF=CF+BC=8,∴AF=,当点M在AB上时,在Rt△AMN和Rt△AFB中,tan∠NAM=,∴NM=x=x,∴△AMN的面积S=×x×x=x2,∴当点M在AB上时,函数图象是开口向上、经过原点的抛物线的一部分;当点M在BF上时,如图,AN=x,NF=10﹣x,在Rt△FMN和Rt△FBA中,tan∠F=,∴=﹣,∴△AMN的面积S==﹣,∴当点M在BF上时,函数图象是开口向下的抛物线的一部分;故选:B.10.(2021•苏州)如图,线段AB=10,点C、D在AB上,AC=BD=1.已知点P从点C出发,以每秒1个单位长度的速度沿着AB向点D移动,到达点D后停止移动.在点P移动过程中作如下操作:先以点P为圆心,PA、PB的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面,设点P的移动时间为t(秒),两个圆锥的底面面积之和为S,则S关于t的函数图象大致是()A.B.C.D.【答案】D【解答】解:∵AB=10,AC=BD=1,∴CD=10﹣1﹣1=8,∵PC=t,∴AP=t+1,PB=8﹣t+1=9﹣t,设围成的两个圆锥底面圆半径分别为r和R则:2πr=;.解得:r=,R=,∴两个圆锥的底面面积之和为S===,根据函数关系式可以发现该函数图象是一个开口向上的二次函数.故选:D.11.(2021•甘肃)如图1,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从A点出发,沿折线AB→BC方向运动,运动到点C停止.设点M的运动路程为x,△AMD的面积为y,y与x的函数图象如图2,则AC的长为()A.3B.6C.8D.9【答案】B【解答】解:由图2知,AB+BC=2,∵AB=BC,∴AB=,∵AB=BC,BD⊥AC,∴AC=2AD,∠ADB=90°,在Rt△ABD中,AD²+BD²=AB²=13①,设点M到AC的距离为h,∴S△ADM=AD•h,∵动点M从A点出发,沿折线AB→BC方向运动,∴当点M运动到点B时,△ADM的面积最大,即h=BD,由图2知,△ADM的面积最大为3,∴AD•BD=3,∴AD•BD=6②,①+2×②得,AD²+BD²+2AD•BD=13+2×6=25,∴(AD+BD)²=25,∴AD+BD=5(负值舍去),∴BD=5﹣AD③,将③代入②得,AD(5﹣AD)=6,∴AD=3或AD=2,∵AD>BD,∴AD=3,∴AC=2AD=6,故选:B.12.(2021•百色)如图,矩形ABCD各边中点分别是E、F、G、H,AB=2,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是()A.B.C.D.【答案】D【解答】解:①当M点运动在AE段,此时S=S△HAE+S△GHD﹣S△EOM﹣S△GPS,∵四边形ABCD是矩形,直线l⊥AB,H、E、F、G为AD、AB、BC、CD的中点,∴AH=AD==1,AE=AB=,S△HAE=S△GHD,S△EOM=S△GPS,∴S=2S△HAE﹣2S△EOM,∴S△HAE=AE•AH=;∵直线l⊥AB,∴∠OME=∠A=90°,∠HEA=∠OEM,∴△HAE∽△OME,∴,∴OM=,又∵ME=AE﹣AM=﹣x,∴OM=ME=,∴S△EOM=,∴S=2S△HAE﹣2S△EOM=,此时,对应抛物线开口向下;②当M点运动到在BE段,此时,S=S△HAE+S△GHD+S△EO1M1+S△GP1S1,即S=2S△HAE+2S△EO1M1,与①同理,O1M1=,又∵M1E=AM1﹣AE=x﹣,∴O1M1=M1E=,∴S△EO1M1=,∴S=2S△HAE+2S△EO1M1=,此时,对应抛物线开口向上,故选:D.13.(2021•鄂尔多斯)如图①,在矩形ABCD中,H为CD边上的一点,点M 从点A出发沿折线AH﹣HC﹣CB运动到点B停止,点N从点A出发沿AB 运动到点B停止,它们的运动速度都是1cm/s,若点M、N同时开始运动,设运动时间为t(s),△AMN的面积为S(cm2),已知S与t之间函数图象如图②所示,则下列结论正确的是()①当0<t≤6时,△AMN是等边三角形.②在运动过程中,使得△ADM为等腰三角形的点M一共有3个.③当0<t≤6时,S=.④当t=9+时,△ADH∽△ABM.⑤当9<t<9+3时,S=﹣3t+9+3.A.①③④B.①③⑤C.①②④D.③④⑤【答案】A【解答】解:由图②可知:点M、N两点经过6秒时,S最大,此时点M在点H处,点N在点B处并停止不动,如图,①∵点M、N两点的运动速度为1cm/s,∴AH=AB=6cm,∵四边形ABCD是矩形,∴CD=AB=6 cm.∵当t=6s时,S=9cm2,∴×AB×BC=9.∴BC=3cm.∵当6≤t≤9时,S=且保持不变,∴点N在B处不动,点M在线段HC上运动,运动时间为(9﹣6)秒,∴HC=3 cm,即点H为CD的中点.∴BH=cm.∴AB=AH=BH=6cm,∴△ABM为等边三角形.∴∠HAB=60°.∵点M、N同时开始运动,速度均为1cm/s,∴AM=AN,∴当0<t≤6时,△AMN为等边三角形.故①正确;②如图,当点M在AD的垂直平分线上时,△ADM为等腰三角形:此时有两个符合条件的点;当AD=AM时,△ADM为等腰三角形,如图:当DA=DM时,△ADM为等腰三角形,如图:综上所述,在运动过程中,使得△ADM为等腰三角形的点M一共有4个.∴②不正确;③过点M作ME⊥AB于点E,如图,由题意:AM=AN=t,由①知:∠HAB=60°.在Rt△AME中,∵sin∠MAE=,∴ME=AM•sin60°=tcm,∴S=AN×ME=cm2.∴③正确;④当t=9+时,CM=cm,如图,由①知:BC=3cm,∴MB=BC﹣CM=2cm.∵AB=6cm,∴tan∠MAB=,∴∠MAB=30°.∵∠HAB=60°,∴∠DAH=90°﹣60°=30°.∴∠DAH=∠BAM.∵∠D=∠B=90°,∴△ADH∽△ABM.∴④正确;⑤当9<t<9+3时,此时点M在边BC上,如图,此时MB=9+3﹣t,∴S=×AB×MB=×6×(9+3﹣t)=27+9﹣3t.∴⑤不正确;综上,结论正确的有:①③④.故选:A.14.(2021•通辽)如图,在矩形ABCD中,AB=4,BC=3,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接PQ.设点P的运动路程为x,PQ2为y,则y关于x的函数图象大致是()A.B.C.D.【答案】C【解答】解:当0≤x≤3时,在Rt△APQ中,∠QAP=90°,AP=AQ=x,∴PQ2=2x2.∴y=PQ2=2x2;当3≤x≤4时,DQ=x﹣3,AP=x,∴y=PQ2=32+32=18;当4≤x≤7时,CP=7﹣x,CQ=7﹣x,∴y=PQ2=CP2+CQ2=2x2﹣28x+98.故选:C.15.(2021•湖北)如图,AC为矩形ABCD的对角线,已知AD=3,CD=4,点P沿折线C﹣A﹣D以每秒1个单位长度的速度运动(运动到D点停止),过点P作PE⊥BC于点E,则△CPE的面积y与点P运动的路程x间的函数图象大致是()A.B.C.D.【答案】D【解答】解:∵BC∥AD,∴∠ACB=∠DAC,∵∠PEC=∠D=90°,∴△PCE∽△CAD,∴==,∵AD=3,CD=4,∴AC==5,∴当P在CA上时,即当0<x≤5时,PE==x,CE==x,∴y=PE•CE==x2,当P在AD上运动时,即当5<x≤8时,PE=CD=4,CE=8﹣x,∴y=PE•CE=×4×(8﹣x)=16﹣2x,综上,当0<x≤5时,函数图象为二次函数图象,且y随x增大而增大,当5<x≤8时,函数图象为一次函数图象,且y随x增大而减小,故选:D.16.(2021•衡阳)如图1,菱形ABCD的对角线AC与BD相交于点O,P、Q 两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P 的运动路线为O﹣A﹣D﹣O,点Q的运动路线为O﹣C﹣B﹣O.设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在A﹣D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为厘米.【答案】(2+3)【解答】解:由图分析易知:当点P从O→A运动时,点Q从O→C运动时,y不断增大,当点P运动到A点,点Q运动到C点时,由图象知此时y=PQ=2cm,∴AC=2cm,∵四边形ABCD为菱形,∴AC⊥BD,OA=OC==cm,当点P运动到D点,Q运动到B点,结合图象,易知此时,y=BD=2cm,∴OD=OB=BD=1cm,在Rt△ADO中,AD===2(cm),∴AD=AB=BC=DC=2cm,如图,当点P在A﹣D段上运动,点P运动到点E处,点Q在C﹣B段上运动,点Q运动到点F处时,P、Q两点的距离最短,此时,OE=OF==,AE=CF===,∴当点P在A﹣D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为:(cm),故答案为:(2+3).17.(2021•武汉)如图(1),在△ABC中,AB=AC,∠BAC=90°,边AB上的点D从顶点A出发,向顶点B运动,同时,边BC上的点E从顶点B出发,向顶点C运动,D,E两点运动速度的大小相等,设x=AD,y=AE+CD,y 关于x的函数图象如图(2),图象过点(0,2),则图象最低点的横坐标是.【答案】﹣1【解答】解:∵图象过点(0,2),即当x=AD=BE=0时,点D与A重合,点E与B重合,此时y=AE+CD=AB+AC=2,∵△ABC为等腰直角三角形,∴AB=AC=1,过点A作AF⊥BC于点F,过点B作NB⊥BC,并使得BN=AC,如图所示:∵AD=BE,∠NBE=∠CAD,∴△NBE≌△CAD(SAS),∴NE=CD,又∵y=AE+CD,∴y=AE+CD=AE+NE,当A、E、N三点共线时,y取得最小值,如图所示,此时:AD=BE=x,AC=BN=1,∴AF=AC•sin45°=,\又∵∠BEN=∠FEA,∠=∠AFE∴△NBE∽△AFE∴,即,解得:x=,∴图象最低点的横坐标为:﹣1.故答案为:.18.(2022•营口)如图1,在四边形ABCD中,BC∥AD,∠D=90°,∠A=45°,动点P,Q同时从点A出发,点P以cm/s的速度沿AB向点B运动(运动到B点即停止),点Q以2cm/s的速度沿折线AD→DC向终点C运动,设点Q的运动时间为x(s),△APQ的面积为y(cm2),若y与x之间的函数关系的图象如图2所示,当x=(s)时,则y=cm2.【答案】【解答】解:过点D作DE⊥AB,垂足为E,在Rt△ADE中,∵∠AED=90°,∠EAD=45°,∴,∵点P的速度为cm/s,点Q的速度为2cm/s,∴AP=x,AQ=2x,∴,在△APQ和△AED中,=,∠A=45°,∴△AED∽△APQ,∴点Q在AD上运动时,△APQ为等腰直角三角形,∴AP=PQ=x,∴当点Q在AD上运动时,y=AP•AQ=×x×x=x2,由图像可知,当y=9此时面积最大,x=3或﹣3(负值舍去),∴AD=2x=6cm,当3<x≤4时,过点P作PF⊥AD于点F,如图:此时S△APQ=S△APF+S四边形PQDF﹣S△ADQ,在Rt△APF中,AP=x,∠PAF=45°,∴AF=PF=x,FD=6﹣x,QD=2x﹣6,∴S△APQ=x2+(x+2x﹣6)•(6﹣x)﹣×6×(2x﹣6),即y=﹣x2+6x,当x=时,y=﹣()2+6×=,故答案为:.。
重庆中考数学二次函数和动点问题1

中考数学压轴题——二次函数和动点问题试题集1、如图,在梯形ABCD 中,AD ∥BC ,∠B =90°,BC =6,AD =3,∠DCB =30°.点E 、F 同时从B 点出发,沿射线BC 向右匀速移动.已知F 点移动速度是E 点移动速度的2倍,以EF 为一边在CB 的上方作等边△EFG .设E 点移动距离为x (x >0).⑴△EFG 的边长是____(用含有x 的代数式表示),当x =2时,点G 的位置在_______; ⑵若△EFG 与梯形ABCD 重叠部分面积是y ,求 ①当0<x ≤2时,y 与x 之间的函数关系式; ②当2<x ≤6时,y 与x 之间的函数关系式;⑶探求⑵中得到的函数y 在x 取含何值时,存在最大值,并求出最大值.2.如图,在△ABC 中,∠C =45°,BC =10,高AD =8,矩形EFPQ 的一边QP 在BC 边上,E 、F 两点分别在AB 、AC 上,AD 交EF 于点H . (1)求证:AH AD =EFBC;(2)设EF =x ,当x 为何值时,矩形EFPQ 的面积最大?并求其最大值;(3)当矩形EFPQ 的面积最大时,该矩形EFPQ 以每秒1个单位的速度沿射线QC 匀速运动(当点Q 与点C 重合时停止运动),设运动时间为t 秒,矩形EFFQ 与△ABC 重叠部分的面积为S ,求S 与t 的函数关系式.(第2题)A DG3.如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC=AC与直线x=4交于点E.(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.4、如图,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3) .(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;(2)记该抛物线的对称轴为直线l,设抛物线上的点P(m,n)在第四象限,点P关于直线l的对称点为E,点E关于y轴的对称点为F,若四边形OAPF的面积为20,求m、n的值.5、抛物线y=ax2+bx+c(a>0)的图象经过点B(12,0)和C(0,-6),对称轴为x=2.(1)求该抛物线的解析式;(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点Q以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PQ 被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点Q的运动速度;若不存在,请说明理由;(3)在(2)的结论下,直线x=1上是否存在点M使,△MPQ为等腰三角形?若存在,请求出所有点M的坐标,若不存在,请说明理由..6.将直角边长为6的等腰Rt△AOC放在平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(–3,0).(1)求该抛物线的解析式;(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;(3)在第一象限内的该抛物线上是否存在点G,使△AGC的面积与(2)中△APE的最大面积相等?若存在,请求出点G的坐标;若不存在,请说明理由.1. 【答案】解:⑴ x ,D 点⑵ ①当0<x ≤2时,△EFG 在梯形ABCD 内部,所以y =43x 2; ②分两种情况:Ⅰ.当2<x <3时,如图1,点E 、点F 在线段BC 上, △EFG 与梯形ABCD 重叠部分为四边形EFNM ,∵∠FNC =∠FCN =30°,∴FN =FC =6-2x.∴GN =3x -6. 由于在Rt △NMG 中,∠G =60°, 所以,此时 y =43x 2-83(3x -6)2=2392398372-+-x x . Ⅱ.当3≤x ≤6时,如图2,点E 在线段BC 上,点F 在射线CH 上, △EFG 与梯形ABCD 重叠部分为△ECP , ∵EC =6-x, ∴y =83(6-x )2=239233832+-x x . ⑶当0<x ≤2时,∵y =43x 2在x >0时,y 随x 增大而增大, ∴x =2时,y 最大=3; 当2<x <3时,∵y =2392398372-+-x x 在x =718时,y 最大=739; 当3≤x ≤6时,∵y =239233832+-x x 在x <6时,y 随x 增大而减小, ∴x =3时,y 最大=839. 综上所述:当x =718时,y 最大=739.2.【答案】解:(1)∵ 四边形EFPQ 是矩形,∴ EF ∥QP . ∴ △AEF ∽△ABC .又∵ AD ⊥BC , ∴ AH ⊥EF .B E FC 图1 图2∴ AH AD =EFBC(2)由(1)得AH 8=x 10.AH =45x .∴ EQ =HD =AD -AH =8-45x ,∴ S 矩形EFPQ =EF ·EQ =x (8-45x ) =-45x 2+8 x =-45(x -5)2+20.∵ -45<0, ∴ 当x =5时,S 矩形EFPQ 有最大值,最大值为20.(3)如图1,由(2)得EF =5,EQ =4.∴ ∠C =45°, ∴ △FPC 是等腰直角三角形. ∴ PC =FP =EQ =4,QC =QP +PC =9.分三种情况讨论:① 如图2.当0≤t <4时,设EF 、PF 分别交AC 于点M 、N ,则△MFN 是等腰直角三角形.∴ FN =MF =t .∴S =S 矩形EFPQ -S Rt △MF N =20-12t 2=-12t 2+20;②如图3,当4≤t <5时,则ME =5-t ,QC =9-t . ∴ S =S 梯形EMCQ =12[(5-t )+(9-t )]×4=-4t +28;③如图4,当5≤t ≤9时,设EQ 交AC 于点K ,则KQ =QC =9-t . ∴ S =S △K QC =12 (9-t )2=12( t -9)2.图2 图3 图4 综上所述:S 与t 的函数关系式为:图1S =221204)24285)1(9)9)2t t t t t t ⎧-+<⎪⎪--<⎨⎪⎪-<⎩ (0, (4, (5.≤≤≤ 3.【答案】解:(1)点C的坐标.设抛物线的函数关系式为2(4)y a x m =-+,则1604a m a m +=+=⎧⎨⎩63a m =-=∴所求抛物线的函数关系式为24)63y x =--+…………①设直线AC 的函数关系式为,y kx b =+则402k b k b -+=+=⎧⎨⎩33k b ==.∴直线AC的函数关系式为33y x =+,∴点E的坐标为 把x =4代入①式,得2(44)633y =--+=,∴此抛物线过E 点. (2)(1)中抛物线与x 轴的另一个交点为N (8,0),设M (x ,y ),过M 作MG ⊥x 轴于G ,则S△CMN=S △MNG +S 梯形MGBC —S △CBN=111(8)(2)(82)222x y y x -++--⨯-⨯g=2233()632y x x x -=-++-=-+-=25)22x -+∴当x =5时,S △CMN24.【答案】解:(1) 抛物线y =-x 2+bx +c 过点 A(4,0)B(1,3).∴16404,,130b c b b c c -++==⎧⎧⎨⎨-++==⎩⎩∴24y x x =-+,2(2)4y x =--+,对称轴为直线2x =,顶点坐标为(2,4)(2)∵直线EP ∥OA,E 与P 两点关于直线2x =对称,∴OE=AP,∴梯形OEPA 为等腰梯形,∴∠OEP=∠APE,∵OE=OF, ∴∠OEP=∠AFE,∴∠OFP=∠APE,∴OF ∥AP,∴四边形OAPF 为平行四边形,∵四边形OAPF 的面积为20,∴24(4)20m m -=,∴121(5m m =-=舍),∴5n =-.5.【答案】解:(1)方法一:∵抛物线过点C (0,-6) ∴c =-6,即y =ax 2 +bx -6由2,21441260ba ab ⎧-=⎪⎨⎪+-=⎩解得:116a =,14b =-∴该抛物线的解析式为2116164y x x =-- 方法二:∵A 、B 关于x =2对称∴A (-8,0) 设(8)(12)y a x x =+- C 在抛物线上,∴-6=a ×8×(12)-,即a =116∴该抛物线解析式为:2116164y x x =-- (2)存在,设直线CD 垂直平分PQ , 在Rt △AOC 中,AC=10=AD ∴点D 在抛物线的对称轴上,连结DQ ,如图:显然∠PDC =∠QDC , 由已知∠PDC =∠ACD∴∠QDC =∠ACD ,∴DQ ∥AC DB =AB -AD =20-10=10 ∴DQ 为△ABC 的中位线∴DQ =12AC =5 AP =AD -PD =AD -DQ =10-5=5 ∴t =5÷1=5(秒)∴存在t =5(秒)时,线段PQ 被直线CD 垂直平分 在Rt △BOC 中,BC∴CQ=∴点Q(3)存在.如图,过点Q 作QH ⊥x轴于H ,则QH =3,PH =9 在Rt △PQH 中,PQ①当MP =MQ ,即M 为顶点,设直线CD 的直线方程为y =kx +b (k ≠0),则: 602b k b -=⎧⎨=+⎩,解得:36k b =⎧⎨=-⎩ ∴y =3x -6当x =1时,y =-3 ∴M 1(1,-3)②当PQ 为等腰△MPQ 的腰时,且P 为顶点, 设直线x =1上存在点M (1,y ),由勾股定理得: 42+y 2=90,即y ∴M 2(1;M 3(1③当PQ 为等腰△MPQ 的腰时,且Q 为顶点.过点Q 作QE ⊥y 轴于E ,交直线x =1于F ,则F (1,-3)设直线x =1存在点M (1,y )由勾股定理得: 22(3)590y ++=,即y =-3∴M 4(1,-3;M 5(1,-3综上所述,存在这样的五个点:M 1(1,-3);M 2(1;M 3(1;M 4(1,-3;M 5(1,-3.6.【答案】解:(1)由题意知:A (0,6),C (6,0),设经过点A 、B 、C 的抛物线解析式为y=ax 2+bx+c则:⎪⎩⎪⎨⎧++=+-==c b a c b a c 63603906解得:⎪⎪⎩⎪⎪⎨⎧==-=6131c b a∴该抛物线的解析式为6312++-=x x y (2)如图:设点P (x ,0),∵PE ∥AB ,∴△CPE ∽△ABC , ∴2ABC CPE )BCCP S (△△=S又∵S △ABC =21B C ×OA=27 ∴2CPE )9x -627(△=S ∴S △CPE =3)6(2x -=124312+-x xS △ABP =21B P ×OA=3x+9 设△APE 的面积为S 则S= S △ABC —S △ABP —S △CPE =427)23(3163122+--=++-x x x 当x=23时,S 最大值为427∴点P 的坐标为(23,0)(3)假设存在点G (x ,y ),使△AGC 的面积与(2)中△APE 的最大面积相等.在(2)中,△APE 的最大面积为427,过点G 做GF 垂直y 轴与点F . ①当y >6时,S △AGC =S 梯形GFOC —S △GFA —S △AOC =21(x+6)y —21x (y-6)—21×6×6=3x+3y-18 即3x+3y-18=427, 又∵点G 在抛物线上,6312++-=x x y , ∴3x+3)631(2++-x x -18=427解得:23,2921==x x ,当x=29时,y=415,当x=23时,y=427.又∵y >6,∴点G 的坐标为(23,427)②当y <6时,如图:S △AGC =S △GAF +S 梯形GFOC —S △AOC =21x (6—y )+)6(21+x y -18=3x+3y-18 即3x+3y-18=427, 又∵点G 在抛物线上,6312++-=x x y , ∴3x+3)631(2++-x x -18=427解得:23,2921==x x ,当x=29时,y=415,当x=23时,y=427.又因为y <6,所以点G 的坐标为(29,415). 综和①②所述,点G 的坐标为(23,427)和(29,415).(3)解法2:可以向x轴作垂线,构成了如此下图的图形: 则阴影部分的面积等于S△AGC=S△GCF+S梯形AGFO—S△AOC下面的求解过程略.这样作可以避免了分类讨论.11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆市中考数学专项训练 动点函数图像专练(第9小题)
1.如图,点P 按M C B A →→→的顺序在边长为1的正方形边上运动,M 是CD 边上的中点,设点P 经过的路程x 为自变量,△APM 的面积为y ,则函数y 的大致图象为( )
2. 如图所示,在平行四边形ABCD 中,3cm, 6cm, 60,AB AD D ==∠=o
点P 以lcm/s 的速度沿AD 从点A 向终点D 运动,同时点Q 以2cm/s 的速度沿折线AB BC CD --从点
A 向终点D 运动,设运动时间为x 秒,APQ ∆的面积为y cm 2,则能反映y 与x 之间的函数
图象是
( )
3. 如图,ABC ∆和DEF ∆是两个形状大小完全相同的等腰直角三角形,
90B DEF ∠=∠=o ,点B C E F 、、、在同一直线上.现从点C E 、重合的位置出发,让
ABC ∆在直线EF 上向右作匀速 运动,而DEF ∆的位置不动.设两个三角形重合部分的面
积为y ,运动的距离为x .下面表示y 与x 函数关系的图象大致是( )
A
B
C
M
D
P (第1题图)
y
x 0
1 2 A
y x
1 2 B
y x 0
1 2 C
y x
1 2 D
4.
如图
,
在
直
角
梯
形ABCD 中
,
AD
90A ∠=o
1cm3cm
45D ∠=o
2cm
1cm
x ∆y y x
图,
在梯形ABCD 中,AB=BC=10cm,CD=6cm,∠C=∠D=ο
90,动点 P 、Q 同时以每秒1cm 的速度从点B 出发,点P 沿BA 、AD 、DC 运动,点 Q 沿BC 、CD 运动,P 点与Q 点相遇时停止,设P 、Q 同时从点B 出发t 秒时,P 、Q 经过的路径与线段PQ 围成的图形的面积为y (
)2
cm ,则y
与t 之间的函数关系的大致图象为( )
6. 如图,M 是边长为4的正方形AD 边的中点,动点P 自A 点起,由A →B →C →D 匀速运动,直线MP 扫过正方形所形 成的面积为y ,点P 运动的路程为x ,则表示y 与x 的函数关 系的图象为( ).
x
y
10 12 14 30 36 O
x
y
10 12 14 30 36 O
x y 10 12 14 30
36 O
x
y
10 12 14 30
36 O
A
B
C
D
A
B
C
P
Q
(第5题图)
y
x
4
12
416
y x
04812
4
1216y x
081212
16
16124
12
840
x
y 6题图
P
M D
C
B
A
A .
B .
C .
D .
7. 如图,两个等腰Rt ABC Rt DEF ∆∆、的斜边都为42cm ,
D M 、分别是AB AC 、边上的中点,又D
E 与AC (或BC )
交于点P ,当点P 从M 出发以lcm /s 的速度沿MC 运动 至C 后又立即沿CB 运动至B 结束.
若运动时间为t (单位:s ), Rt ABC ∆与Rt DEF ∆重叠部分的面积为y (单位:cm 2).则y 的图像大致是( )
8. 如图,已知菱形ABCD 的边长为2㎝,︒=∠60A ,点M 从点A 出发,以1㎝/s 的速度向点B 运动,点N 从点 A 同时出发,以2㎝/s 的速度经过点D 向点C 运动, 当其中一个动点到达端点时,另一个动点也随之停止运 动. 则△AMN 的面积y (㎝2
) 与点M 运动的时间t (s)的 函数的图像大致是( )
9. 如图,M 是边长为4的正方形AD 边的中点,动点P 自A 点起,由A B C D
→→→(9题图)
y
x
O
1 2 3
y
x
O
2 3 y
x
O
1 2 3
A
B
C
D
y
x
O
1
2 3
M
N · A
B
D ·
匀速运动,直线MP扫过正方形所形成面积为,y点P运动的路程为,x则表示y与x的函数关系的图象为( )
10. 如图,矩形ABCD中,1
AB=cm,2
AD=cm,M是BC的中点,点P在矩形的边长
沿A D C M
→→→运动,速度为2cm/s,点Q在矩形的边上沿A B M
→→运动,速
度为1cm/s,若P Q
、两点同时出发,则APQ
∆的面积y(cm2)与运动时间t(s)之间的函
数关系用图象表示大致是下图中的( )
11. 如图,三个大小相同的正方形拼成六边形ABCDEF,一动点P从点A出发沿着
A B C
→→→D E
→方向匀速运动,最后到达点.E运动过程中PEF
∆的面积S 随时间t变化的图象大致是( )
O 4 12
16
4
A.
.
B.
.
C.
.
D.
.
9题图
O 8 12
16
12
O 8
16
4
12
4 O 8
16
4
12
4 B
A
C
D
P
M
12
12
s
t
O
s
t
O
s
t
O
s
t
O
A B C D
A B
C
P
(9题图)
12.如图,一艘旅游船从码头A 驶向景点,C 途经景点.B D 、它先从码头
A 沿以D 为圆心的弧A
B 行驶到景点,B 然后从B 沿直径B
C 行驶到
D e 上的景点.C 假如旅游船在整个行驶过程中保持匀速,则下面各图
中能反映旅游船与景点D 的距离随时间变化的图象大致是( )
13. 如图,梯形ABCD 中,//,,
AB CD AB BC ⊥M 为AD 中点,
2cm,2cm,0.5AB BC CD ===cm,点P 在梯形的边上沿B C D M →→→运动,速度
为1cm/s ,则BPM ∆的面积2
cm y 与点P 经过的路程x cm 之间的函数关系用图象表示大致是下图中的( )
A C
B D
9题图
B
P。
