2017暑-06-数学-(培优班)-6-课后作业
人教版三年级数学下册培优作业

人教版三年级数学下册培优作业
第1次
(1)刺猬在小狗的()面;(2)梅花鹿在小狗的()面;
(3)小猫在小狗的()面;(4)小猴在小狗的()面;
(5)小狗在小猴的()面;(6)小猴在梅花鹿的()面。
小华从家向()面走,又向()方向走,能到便民超市。
第2次
1、同学们到果园里去采摘,女同学有36人,男同学有54人。
如果3个同学分成一组,一共可以分成多少个小组?
2、三年级的同学们做了78件玩具,分给二年级18件,剩下的平均分给一年级的两个班,一年级每班分得多少件玩具?
3、三(1)班同学春游,要到小河的对岸去,现在岸边只有一条小船,船上最多只能坐4人,31名同学最少用多少次可以全部到对岸去?(小船每过一次河算一次,同学们可以自己划船。
)
第3次
1、369÷5,被除数百位上的3比除数5(),不够商1个(),就要看它的前两位,36个()除以5,商()个(),所以商()应写在()位上。
先判断商是几位数,再计算。
(1)532÷4=
532÷7=
(2)465÷3=
465÷5=
(3)846÷6=
846÷9=
2、三位数除以一位数,商可能是()位数,也可能是()位数。
第4次
1、王老师带了400元,买了3个足球之后还剩85元。
每个足球多少钱?
2、工厂里的叔叔在装油,每5kg装一桶,158kg油大约需要多少个桶?
下面是某超市一、二月份销售某品牌酸奶情况统计表。
根据上表,将下面的表格填写完整,再回答问题。
(1)一月份()味酸奶卖的最多,二月份()味酸奶卖的最少。
著名机构讲义暑假06-七年级培优版-整式的乘法-课后作业-教师版

【作业1】计算(1)= ; (2)= .(3)= ; (4) = .(5)= .(6)= ; (7)= . 【答案】(1)(2)(3)(4)(5)(6)(7)【作业2】长方体的长是毫米,宽是毫米,高是200毫米,用科学记数法表示它的体积是 立方毫米. 【答案】【作业3】请你以为底数,1、2、3为指数,写出一个算式,使它的运算结果是(指数可以重复使用): .【答案】【作业4】解答题(1) (2)(23)(2)m n m n +-66(0.1)10⋅323(2)(3)x x y ⋅-321()()2m mt t -⋅23(32)(32)(23)x y x y y x -⋅-⋅-2(1)(1)x x x -++2011201250.2⋅2226m mn n --15324x y -512m t -()632x y --3x x -0.238.210⨯21.510⨯82.4610⨯a 10a 11233a a a a a ⋅⋅⋅⋅232223(2)(8)()()x y x x y -+⋅-⋅-6233()0.1[()]4m n m n ---+-+整式的乘法(3) (4) 【答案】(1)(2)(3)(4)【作业5】解方程与不等式:(1)(2)(3) 【答案】(1)(2)(3)【作业6】先化简在求值:,其中x =2002,y = 【答案】【作业7】先化简,再求值:,其中,. 【答案】【作业8】先化简,再求值:,其中,.(4)()6(2)(3)m n m n m n m n +--+-12(0.75)(0.5)33m n m n +-6372x y -()61720m n -+225329m n mn -++2211116722m mn n --2(3)(3)(21)(7)x x x x x +-=-+-2(2)(4)6x x x ++=+2(3)2(4)(5)x x x x x -≥-+-213x =-13x =-5x ≤-()()()y x x y x x y x x y x 322322522-+---+-61112-231(0.5)( 3.5)7y xy x y -⋅--⋅0.2x =2y =-65-1(912)3(34)n n n n y y y yy ++---3y =-2n =【答案】【作业9】长方形的长为厘米,宽比长小3厘米,在该长方形的中间挖去一个面积为1平方厘米的圆.(1)用含的多项式表示剩余部分的面积; (2)当时,计算剩余部分的面积.【答案】(1)(2)【作业10】我们规定一种运算:※=.如3※2=.请你计算: (1)4※; (2)※.【答案】(1)(2)【作业11】若,求的值.【答案】【作业12】如果的展开式中不含和项,求的值.【答案】81x x 4x =231x x --3a b ab a b --32321⨯--=3a (1)x +(21)x -94a -2221x x --210m m +-=3222008m m ++200922(3)(3)y ay y y b ++-+2y 3y ,a b 36a b =⎧⎨=⎩。
七年级数学培优班试题及答案

七年级数学培优班选拔试题填空题(共25题,满分100)1、有一只手表每小时比准确时间慢3分钟,若在清晨4:30与准确时间对准,则当天上午手表指示的时间是10:50,准确时间应该是。
2、将正方形纸片由下往上对折,再由左向右对折,称为完成一次操作(见下图).按上边规则完成五次操作以后,剪去所得小正方形的左下角. 问:当展开这张正方形纸片后,一共有个小孔3、已知关于x的整系数的二次三项式ax2+bx+c,当x分别取1,3,6,8时,某同学算得这个二次三项式的值分别为1,5,25,50,经过验算,只有一个结果是错误的,这个错误的结果是。
4、下表记录了某次钓鱼比赛中,钓到n条鱼的选手数:n 0 1 2 3 …13 14 15 钓到n条鱼的人数9 5 7 23 … 5 2 1已知:(1)冠军钓到了15条鱼; (2)钓到3条或更多条鱼的所有选手平均钓到6条鱼; (3)钓到12条或更少鱼的所有选手平均钓到5条鱼;则参加钓鱼比赛的所有选手共钓到条鱼。
5、如图,在一个正方体的两个面上画了两条对角线AB,AC,那么这两条对角线的夹角等于度。
6、一个木制的立方体,棱长为n(n是大于2的整数),表面涂上黑色,用刀片平行于立方体的各面,将它切成3n个棱长为1的小立方体,若恰有一个面涂黑色的小立方体的个数等于没有一个面涂黑色的小立方体的个数,则n= .7、把8张不同的扑克牌交替的分发成左右两叠:左一张,右一张,左一张,右一张,……;然后把左边一叠放在右边一叠上面,称为一次操作。
重复进行这个过程,为了使扑克牌恢复到最初的次序,至少要进行操作的次数是。
8、一台大型计算机中排列着500个外形相同的同一种元件,其中有一只元件已损坏,为了找出这一元件,检验员将这些元件按1-500的顺序编号,第一次先从中取出单数序号的元件,发现其中没有坏元件,他将剩下的元件在原来的位置上又按1-250编号。
(原来的2号变成1号,原来的4号变成2号…)又从中取出单数序号的元件进行检查,仍没有发现…如此下去,检查到最后一个元件,才是坏元件。
最新六年级数学培优作业含详细答案

最新六年级数学培优作业含详细答案一、培优题易错题1.在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所.已知青少年宫在学校东300m处. 商场在学校西200m处,医院在学校东500m处.若将马路近似地看做一条直线,以学校为原点,向东方向为正方向,用1个单位长度表示100m.(1)在数轴上表示出四家公共场所的位置.(2)列式计算青少年宫与商场之间的距离.【答案】(1)解:如图所示:(2)解:由题意可得:300-(-200)=500或︱-200-300︱=500.答:青少年宫与商场之间的距离是500 m【解析】【分析】(1)根据题意画出学校为原点的数轴,在数轴上表示出四家公共场所的位置;(2)根据题意青少年宫与商场之间的距离是300-(-200),再根据减去一个数等于加上这个数的相反数,求出青少年宫与商场之间的距离.2.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是神秘数.(1)28和2012这两个数是神秘数吗?为什么?(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?【答案】(1)解:找规律:4=4×1=22-02, 12=4×3=42-22, 20=4×5=62-42, 28=4×7=82-62,…,2012=4×503=5042-5022,所以28和2012都是神秘数(2)解:(2k+2) 2-(2 k) 2=4(2k +1),因此由这两个连续偶数构造的神秘数是4的倍数(3)解:由(2)知,神秘数可以表示成4(2k+1),因为2 k +1是奇数,因此神秘数是4的倍数,但一定不是8的倍数.另一方面,设两个连续奇数为2 n +1和2 n -1,则(2 n +1) 2-(2n-1)2=8n,即两个连续奇数的平方差是8的倍数.因此,两个连续奇数的平方差不是神秘数.【解析】【分析】(1)根据规律得到28=4×7=82-62, 2012=4×503=5042-5022,得到28和2012这两个数是神秘数;(2)由(2k+2)2-(2k)2=(2k+2+2k)(2k+2-2k)=4(2k +1),因此由这两个连续偶数构造的神秘数是4的倍数;(3)神秘数可以表示成4(2k+1),因为2k +1是奇数,因此神秘数是4的倍数,但一定不是8的倍数;两个连续奇数的平方差是8的倍数,因此这两个连续奇数的平方差不是神秘数.3.如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是________数(填“无理”或“有理”),这个数是________;(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是________;(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?【答案】(1)无理;﹣2π(2)4π或﹣4π(3)解:①∵圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3,∴第4次滚动后,A点距离原点最近;第3次滚动后,A点距离原点最远;②∵|+2|+|﹣1|+|+3|+|﹣4|+|﹣3|=13,∴13×2π×1=26π,∴A点运动的路程共有26π;∵(+2)+(﹣1)+(+3)+(﹣4)+(﹣3)=﹣3,(﹣3)×2π=﹣6π,∴此时点A所表示的数是:﹣6π【解析】【解答】解:(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是无理数,这个数是﹣2π;故答案为:无理,﹣2π;(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是4π或﹣4π;故答案为:4π或﹣4π;【分析】(1)利用圆的半径以及滚动周数即可得出滚动距离;(2)利用圆的半径以及滚动周数即可得出滚动距离;(3)①利用滚动的方向以及滚动的周数即可得出A点移动距离变化;②利用绝对值的性质以及有理数的加减运算得出移动距离和A表示的数即可.4.数轴上有、、三点,分别表示有理数、、,动点从出发,以每秒个单位的速度向右移动,当点运动到点时运动停止,设点移动时间为秒.(1)用含的代数式表示点对应的数:________;(2)当点运动到点时,点从点出发,以每秒个单位的速度向点运动,点到达点后,再立即以同样的速度返回点.①用含的代数式表示点在由到过程中对应的数:________ ;②当 t=________ 时,动点 P、 Q到达同一位置(即相遇);③当PQ=3 时,求 t的值.________【答案】(1)(2)2t-58;当时,t=32 ;当时,t=;t=3,29,35,,【解析】(1)点所对应的数为:( 2 )①② 点从运动到点所花的时间为秒,点从运动到点所花的时间为秒当时,:,:,解之得当时,:,:,解之得【分析】(1)向右移动,左边的数加上移动的距离就得移动后的数;(2)需分类讨论,16≤t≤39 和39 ≤ t ≤ 46两类分别计算.5.操作探究:已知在纸面上有一数轴(如图所示),(1)操作一:折叠纸面,使数字1表示的点与﹣1表示的点重合,则﹣3表示的点与________表示的点重合;(2)操作二:折叠纸面,使﹣1表示的点与5表示的点重合,回答以下问题:①10表示的点与数________表示的点重合;(3)②若数轴上A、B两点之间距离为15,(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?【答案】(1)3(2)﹣6(3)解:由题意可得,A、B两点距离中心点的距离为15÷2=7.5,∵中心点是表示2的点,∴A、B两点表示的数分别是﹣5.5,9.5.【解析】【解答】解:(1)因为折叠纸面,使数字1表示的点与﹣1表示的点重合,可确定中心点是表示0的点,所以﹣3表示的点与3表示的点重合,故答案为:3;(2)①因为折叠纸面,使﹣1表示的点与5表示的点重合,可确定中心点是表示2的点,所以10表示的点与数﹣6表示的点重合,故答案为:﹣6;【分析】(1)先求出中心点,再求出对应的数即可;(2)①求出中心点是表示2的点,再根据对称求出即可;②求出中心点是表示2的点,求出A、B到表示2的点的距离是7.5,即可求出答案.6.在甲、乙、丙三缸酒精溶液中,纯酒精的含量分别占、和,已知三缸酒精溶液总量是千克,其中甲缸酒精溶液的量等于乙、丙两缸酒精溶液的总量.三缸溶液混合后,所含纯酒精的百分数将达.那么,丙缸中纯酒精的量是多少千克?【答案】解:设丙缸酒精溶液的重量为千克,则乙缸为千克。
高中数学培优班专题资料(包含答案)
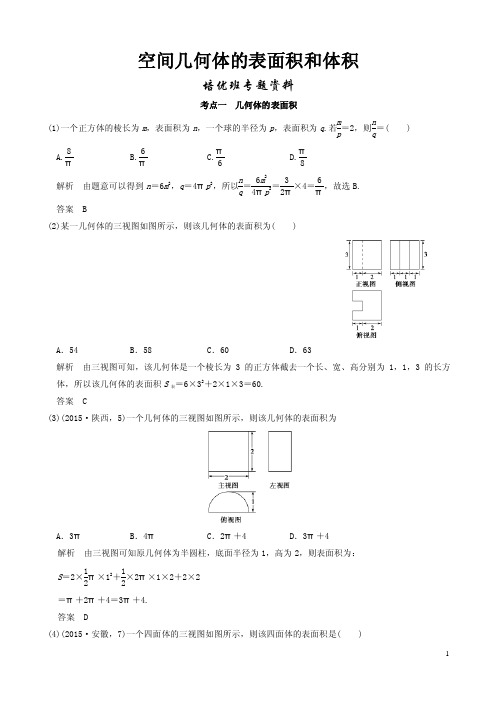
空间几何体的表面积和体积培优班专题资料考点一 几何体的表面积(1)一个正方体的棱长为m ,表面积为n ,一个球的半径为p ,表面积为q .若m p =2,则n q=( ) A.8πB.6πC.π6D.π8解析 由题意可以得到n =6m 2,q =4πp 2,所以n q =6m 24πp 2=32π×4=6πB. 答案 B(2)某一几何体的三视图如图所示,则该几何体的表面积为( )A .54B .58C .60D .63解析 由三视图可知,该几何体是一个棱长为3的正方体截去一个长、宽、高分别为1,1,3的长方体,所以该几何体的表面积S 表=6×32+2×1×3=60. 答案 C(3)(2015·陕西,5)一个几何体的三视图如图所示,则该几何体的表面积为A .3πB .4πC .2π+4D .3π+4解析 由三视图可知原几何体为半圆柱,底面半径为1,高为2,则表面积为:S =2×12π×12+12×2π×1×2+2×2=π+2π+4=3π+4. 答案 D(4)(2015·安徽,7)一个四面体的三视图如图所示,则该四面体的表面积是( )A .1+ 3B .2+ 3C .1+2 2D .2 2解析 由空间几何体的三视图可得该空间几何体的直观图,如图,∴该四面体的表面积为S 表=2×12×2×1+2×34×(2)2=2+3,故选B. 答案 B(5)(2015·新课标全国Ⅱ,9)已知A ,B 是球O 的球面上两点,∠AOB =90°,C 为该球面上的动点,若三棱锥O -ABC 体积的最大值为36,则球O 的表面积为( ) A .36πB .64πC .144πD .256π解析 如图,要使三棱锥O -ABC 即C -OAB 的体积最大,当且仅当点C 到平面OAB 的距离,即三棱锥C -OAB 底面OAB 上的高最大,其最大值为球O 的半径R ,则V O -ABC 最大=V C -OAB 最大=13×12S △OAB ×R =13×12×R 2×R =16R 3=36,所以R =6,得S 球O =4πR 2=4π×62=144π,选C. 答案 C(6)(2014·重庆,7)某几何体的三视图如图所示,则该几何体的表面积为( )A .54B .60C .66D .72解析 该几何体的直观图如图所示,易知该几何体的表面是由两个直角三角形,两个直角梯形和一个矩形组成的,则其表面积S =12×3×4+12×3×5+2+52×5+2+52×4+3×5=60.选B.答案 B(7)(2014·浙江,3)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )A .90 cm 2B .129 cm 2C .132 cm 2D .138 cm 2解析 由三视图可知该几何体由一个直三棱柱与一个长方体组合而成(如图),其表面积为S =3×5+2×12×4×3+4×3+3×3+2×4×3+2×4×6+3×6=138(cm 2).答案 D(8)(2014·大纲全国,8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( ) A.81π4B .16πC .9πD.27π4解析 设球的半径为R ,由题意可得(4-R )2+(2)2=R 2,解得R =94,所以该球的表面积为4πR 2=81π4.故选A.(9)(2014·安徽,7)一个多面体的三视图如图所示,则该多面体的表面积为( )A .21+ 3B .18+3C .21D .18解析 根据题意作出直观图如图,该多面体是由正方体切去两个角而得到的,根据三视图可知其表面积为6(22-12×1×1)+2×34×(2)2=6×72+3=21+ 3.故选A.答案 A(10)(2012·安徽,12)某几何体的三视图如图所示,该几何体的表面积是________.解析 由三视图可知,该几何体为底面是直角梯形且侧棱垂直于底面的棱柱,故该几何体的表面积为S=2×12×(2+5)×4+[2+5+4+42+(5-2)2]×4=92.答案 92考点二 几何体的体积(1)某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x 的值是( )A .2 B.92 C.32D .3解析 根据三视图判断几何体为四棱锥,其直观图是:V =13×1+22×2x =3⇒x =3. 故选D. 答案 D(2)(2015·山东,7)在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.2π3B.4π3C.5π3D .2π解析 如图,由题意,得BC =2,AD =AB =1.绕AD 所在直线旋转一周后所得几何体为一个圆柱挖去一个圆锥的组合体.所求体积V =π×12×2-13π×12×1=53π.答案 C(3)(2015·重庆,5)某几何体的三视图如图所示,则该几何体的体积为( )A.13+π B.23+π C.13+2π D.23+2π解析 这是一个三棱锥与半个圆柱的组合体,V =12π×12×2+13⎝⎛⎭⎫12×1×2×1=π+13,选A.答案 A (4)(2015·新课标全国Ⅱ,6)一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为()A.18B.17C.16D.15解析 如图,由题意知,该几何体是正方体ABCD -A 1B 1C 1D 1被过三点A 、B 1、D 1的平面所截剩余部分,截去的部分为三棱锥A -A 1B 1D 1,设正方体的棱长为1,则截去部分体积与剩余部分体积的比值为111111A A B D B C D ABCDV V --=1111111111A AB D A BCD ABCD A A B D V V V ----=13×12×12×113-13×12×12×1=15,选D.答案 D(5)某几何体的三视图如图所示,它的体积为()A .72πB .48πC .30πD .24π解析 由三视图可知,该几何体是半个球体和一个倒立圆锥体的组合体,球的半径为3,圆锥的底面半径为3,高为4,则根据体积公式可得几何体的体积为30π,故选C.答案 C(6)(2014·陕西,5)已知底面边长为1,侧棱长为2的正四棱柱的各顶点均在同一个球面上,则该球的体积为( ) A.32π3B .4πC .2πD.4π3解析 如图为正四棱柱AC 1.根据题意得AC =2,∴对角面ACC 1A 1为正方形,∴外接球直径2R =A 1C =2,∴R =1,∴V 球=4π3,故选D.答案 D(7)(2014·湖北,8)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式V ≈136L 2h .它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V ≈275L 2h 相当于将圆锥体积公式中的π近似取为( ) A.227B.258C.15750D.355113解析 圆锥的体积V =13πr 2h =13π⎝⎛⎭⎫L 2π2h =L 2h 12π,由题意得12π≈752,π近似取为258,故选B.答案 B(8)(2014·新课标全国Ⅱ,6)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm ,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解析 由三视图知该零件是两个圆柱的组合体.一个圆柱的底面半径为2 cm ,高为4 cm ;另一个圆柱的底面半径为3 cm ,高为2 cm.则零件的体积V 1=π×22×4+π×32×2=34π(cm 3).而毛坯的体积V =π×32×6=54π(cm 3),因此切削掉部分的体积V 2=V -V 1=54π-34π=20π(cm 3),所以V 2V =20π54π=1027.故选C.答案 C (9)(2012·新课标全国,11)已知三棱锥S ABC 的所有顶点都在球O 的球面上, △ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( ) A.26B.36C.23D.22解析 如图,H 为△ABC 的外接圆圆心,则∠BHC =120°,设△ABC 的外接圆半径为r ,则1=BC 2=HC 2+HB 2-2HC ·HB ·cos 120°=3r 2, ∴r =33. 连接OH ,根据球的截面性质知,OH ⊥平面ABC ,∴OH =OC 2-CH 2=1-13=63∵O 为SC 的中点,∴S 到平面ABC 的距离为2OH =263,∴V S ABC =13S △ABC ×263=13×34×263=26.答案 A(10)(2015·江苏,9)现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为________.解析 设新的底面半径为r ,由题意得13πr 2·4+πr 2·8=13π×52×4+π×22×8,解得r =7.答案7(11)(2014·江苏,8)设甲、乙两个圆柱的底面积分别为S 1,S 2,体积分别为V 1,V 2,若它们的侧面积相等,且S 1S 2=94,则V 1V 2的值是________.解析 设圆柱甲的底面半径为r 1,高为h 1,圆柱乙的底面半径为r 2,高为h 2.由题意得S 1S 2=πr 21πr 22=94,∴r 1r 2=32. 又∵S 甲侧=S 乙侧,即2πr 1h 1=2πr 2h 2,∴h 1h 2=r 2r 1=23, 故V 1V 2=S 1h 1S 2h 2=S 1S 2·h 1h 2=94×23=32答案 32(12)(2013·江苏,8)如图,在三棱柱A 1B 1C 1ABC 中,D ,E ,F 分别是AB ,AC ,AA 1的中点,设三棱锥F ADE 的体积为V 1,三棱柱A 1B 1C 1ABC 的体积为V 2,则V 1∶V 2=________.解析 由题意可知点F 到面ABC 的距离与点A 1到面ABC 的距离之比为1∶2,S △ADE ∶S △ABC =1∶4. 因此V 1∶V 2=13AF ·S △AED 2AF ·S △ABC=1∶24.答案 1∶24。
高中数学暑期培优讲义数列部分答案

负数.∴ 2 ,22,…,29中,25最大,故选 B.
12
9
5
例 4 [思路点拨] (1)根据题意,可得数列{an}的通项公式,这是一个类似于分段函数的通项公式,结合分段函数的单调性,建立不 等式组即可求解;(2)首先根据数列的通项公式求得 Sn,通过配方结合二次函数的图像确定出对称轴,由此可求得结果.
an=
3( 2(
= 1), ≥ 2).
【课堂考点探究】
例 1 [思路点拨] (1)把数列化为22,-34,48,-156,…,根据各项的特点写出它的一个通项公式;(2)观察可知,相邻项符号相反,分子为 1,
分母为 n(n+1),从而得数列的通项公式.
(1)A
(2)(-1)n
(
1 +1)
[解析] (1)数列 1,-34,12,-156,…可以化为22,-34,48,-156,…,
4.-1 [解析] 因为 a1=2,an+1= -1=1- 1 ,所以 a2=1-12=12,a3=1-2=-1,a4=1+1=2,…,所以数列{an}是周期数列,周期为 3,所以
a2019=a673×3=a3=-1.
5.6 [解析] 由 2+8=232,得 n=6 或 n=43(舍),故232是该数列的第 6 项.
≥ 2,故选 D.
(2)由
Sn=2n2-3n+1,得
Sn-1=2(n-1)2-3(n-1)+1(n≥2),两式相减,得
an=Sn-Sn-1=4n-5,当 n=1 时,a1=0,不满足上式,∴an=
0, 4
= -5,
1, ≥
2.
例3
[思路点拨] (1)将数列{an}的通项公式分离参数,结合单调性即可得出;(2)利用一般方法可求得数列
暑假培优参考答案

暑假培优参考答案暑假培优参考答案暑假是学生们放松心情、享受自由的时光,然而对于一些追求卓越的学生来说,暑假是一个提升自己学业能力的绝佳时机。
因此,很多学生会选择参加暑假培优班来强化自己的学习能力。
在这篇文章中,我将分享一些暑假培优参考答案,希望能对广大学生有所帮助。
首先,数学是许多学生感到困惑的科目之一。
在暑假培优班中,数学的参考答案是学生们最关心的。
数学题目往往需要灵活的思维和准确的计算能力。
针对初中数学,一道常见的题目是如何求解一元一次方程。
考虑到这个问题,我们可以给出以下参考答案:假设一元一次方程为ax + b = 0,其中a和b为已知数。
首先,将方程转化为标准形式,即将常数项移到等号右边。
得到方程ax = -b。
接下来,将方程两边都除以a,得到x = -b/a。
这就是一元一次方程的解。
除了数学,英语也是学生们需要提高的重要科目。
在英语学习中,阅读理解是一个常见的难题。
为了帮助学生更好地理解阅读材料,我们可以提供以下参考答案:首先,仔细阅读文章,理解文章的主题和大意。
其次,注意文章中的关键词和词组,它们有助于理解文章的细节。
然后,根据问题的要求,找到文章中对应的信息。
最后,将问题和文章中的信息进行对比,选择正确的答案。
除了数学和英语,科学也是学生们需要加强的科目之一。
在科学学习中,实验设计和数据分析是关键的技能。
以下是一个关于实验设计和数据分析的参考答案:首先,明确实验的目的和假设。
然后,设计实验的步骤和所需材料。
在实验过程中,记录实验数据并保持准确性。
完成实验后,对数据进行分析,包括计算平均值、标准差和相关性等。
最后,根据实验结果得出结论,并与假设进行比较。
除了学科知识,培养学生的学习方法和思维能力也是暑假培优的重要目标。
以下是一些建议和参考答案:首先,制定学习计划,合理安排学习时间和任务。
其次,培养良好的学习习惯,如定期复习、做笔记和解题技巧等。
此外,培养批判性思维和问题解决能力,通过思考和讨论来加深对知识的理解。
培优作业参考答案

培优作业参考答案培优作业参考答案在当今的教育体制中,培优班作业成为了许多学生和家长关注的焦点。
培优班作业的要求通常更高,内容更加深入,对学生的能力和才华有着更高的要求。
然而,对于许多学生来说,培优班作业常常成为了一道难以逾越的坎。
如何正确完成培优作业成为了学生和家长们的一大挑战。
本文将探讨一些培优作业的参考答案,以帮助学生更好地完成这些作业。
首先,对于数学作业来说,一些常见的题型如代数、几何和概率统计等,往往是学生们最头疼的部分。
对于代数题,学生可以通过列方程、运用代数运算规则以及解方程等方法来解决。
例如,对于一个典型的代数方程题目“若3x + 5 = 20,则x的值是多少?”,学生可以运用代数运算规则,将方程变形为3x = 20- 5,再进一步计算得出x = 5的答案。
对于几何题,学生需要熟悉各种几何定理和公式,如勾股定理、相似三角形的性质等。
例如,对于一个典型的几何题目“已知直角三角形的直角边长分别为3和4,求斜边的长”,学生可以运用勾股定理,计算得出斜边的长为5。
对于概率统计题,学生需要掌握概率计算和统计分析的方法。
例如,对于一个典型的概率统计题目“从一副扑克牌中抽取一张牌,求抽到红心的概率”,学生可以通过计算红心牌的数量与总牌数的比值,得出概率为1/4的答案。
其次,语文作业也是培优作业中的重要一环。
对于阅读理解题,学生需要仔细阅读文章,理解文章的主旨和细节,并根据问题选择正确的答案。
例如,对于一个典型的阅读理解题目“根据文章内容,作者最有可能是哪个年龄段的人?”,学生需要通过理解文章的语气、观点等细节信息,结合自己的常识和推理能力,选择最合适的答案。
对于作文题,学生需要注意文章的结构和逻辑,合理组织语言,表达自己的观点和思考。
例如,对于一个典型的作文题目“如何保护环境?”,学生可以从多个方面展开思考,如节约能源、减少污染、推广可持续发展等,通过论述这些观点,并给出具体的建议和措施,来完成作文。
