【35套试卷合集】东北育才中学2019-2020学年数学高一上期末模拟试卷含答案
2019-2020学年高一上册数学期末模拟试卷附答案

2019-2020学年第一学期期末试卷高一数学一、填空题(本大题共14小題.每小题4分.共计56分.不需要写出解答过程,请将答案填写在答題K 相应的位置上・)1.已知集合A={1, 2},集合B={G 1・,}・若AriB={2},则实数a 的值为 ___________________2・若戶5則点W ,si 讪位于第—象限.5. 函数/(x) = log 2(sin 2.r + l)的值域为 __________ •6. 若堀形的弧长为3”.圆心角为芋.则该扇形的而积为 _____________ •47. 若函数/(x) = 2x +x-2的零点在区何(匕£+l )awZ)中,则斤的值为 ______________ . 8. 已知慕函数y = x a 的图象经过点(2, V2),则cos (-彳”)的值为 ____________ ・9. 已知向=(sincos&)・ h =(2> •!)•若a //h .则 tan 20 = _____________________ . 10. 若2sina-3cos0 = -£, 2cosa-3sin0 = -£,则sin(a + 〃)= ____________________ . 11. 已知函数/(x)+ " xvl,若/⑴是定义在R 上的减函数,则实数aiog a x n 1的取值范围是3.若点P 是线段AB 上靠近A 的三等分点,则丽= AB.4. x 2-h x>0/(.r +> 则 /(-2)=12. 已知/(X)是定义在R上的偶曲数.且在(-00, 0]上单调递减.若/(1) = 0,则不等式/(In x) < 0的解集为 _______ .13. 在ZXABC中,已知B=y, |AB-AC|=2, HJ I JABAC的取值范用是 ______________ ・14. 已知肖疋(0, 1)时,函数y = (nvc^\)2的图^*j.v = .v + m的图象仃且只冇一个交点・则实数加的取值范国是_______ •二、解答题(本大題共6小題.共计64分.请在答题纸指定区域内作答,解答应写出文字说明.证明过程或演算步骤15. (本題满分10分)已知向fia =(3・・4), h =(4, 3)・⑴求0-耳的值:(2)若(2a + b)丄(方+M),求实数*的值.16. (本題满分10分)已知函数/(x) = ln(g~ Y)(o e R)的定义域为集合A.函数g(x) = 2x + l的值域为集合B.X(1)当a=3时,求AUB:(2)若AC|B=0・求实数a的取值范围.17. (本題满分10分)已斶(0)弓且沙第哒限角,求下列各式的值.(1) tan(a -------- );2 sin2 a +sin 2acos 2a418.(本題满分10分)设曲数f(x) = s\n((ox-- )+ COS(/T-QX)•其中0ve<3・ /(—) = 0.6 6(1)求函数/(x)的虽小正周期及单调増区何:(2)将换数/(x)的图彖上符点的横坐标变为原来的2倍(纵坐标不变〉,再将得到的图彖向左平移兰个肌位,得到函数g(x)的图彖,求g(x)在辺)上的值域.4 4 419. (本题满分12分)如图.某校生物兴趣小组计划利用学校角落处一块空地隅出一个周长为10米的直角三角形ABC作为试验地.设ZABC=0, AABC的面枳为S.(1)求S关于0的函数关系式:(2)当刃为何值时.试验地的面枳虽大?求出该而积的虽大值.20. (本題满分12分)2已知me R 9函数/(x) = lg(/w + —).x(I)若函数g(x) = /(x) + lgx2有且仅有一个零点,求实数加的值:(2)设m>0.任取兀,x2e[t. f+2],若不等式|/(x,)-/(x2)|< 1 对任意0*1]恒成立,求加的取值范围.一、填空題:本大題共14小題.每小题4分,共计56分. 1. 2 2・二3.4. 35. [0,1]6.7. 0沁29.10.兰 2511. 3 27 12. 13・卜») 4 14. (0・l)U(3,z)6rt (「c) 二、解答題:本大題共6小Jffi,共计64分.2 ■*> 34亍 解苔时应頁出文字说明、证明过程或演算步棵.15.(木小题满分10分〉解:<1) A | o - 61» 7(- D 2 + (-7)2 = 5^2. (2) 11]题意.2a + 6 = (】0.-5)・ a +肋=(3 +4 匕・4$3&) • V(2a + A) l(a + M)9 ••• (2么")(° + 肪)=10(3 + 4灯-5(-4 + 3切-0・解得* = -2・10分16.(本小题满分10分) :〉;。
辽宁省沈阳市东北育才学校2024-2025学年高三上学期第一次模拟考试暨假期质量测试数学试卷

辽宁省沈阳市东北育才学校2024-2025学年高三上学期第一次模拟考试暨假期质量测试数学试卷学校:___________姓名:___________班级:___________考号:___________三、填空题(2)当3n =时,求3号盒子里的红球的个数x 的分布列;(3)记n 号盒子中红球的个数为n X ,求n X 的期望()nE X .的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a 的范围【详解】由函数()()g x f x b =-有两个零点可得()f x b =有两个零点,即()y f x =与y b =的图象有两个交点,结合函数图象有以下几种情况,y x =与2y x =的图象如图1所示,则()y f x =在定义域内不能是单调函数,对于a 的值进行分类讨论,则:当a<0时,如图2所示;当0a =时,如图3所示;当01a <<时,如图4所示;当1a =时,如图5所示;当1a >时,如图6所示;对于图2,有可能有两个交点,因为存在y b =使得与二次函数有两个交点;对于图3,因为图象是单调的,故不可能有两个交点;对于图4,可能有两个交点,因为存在R b Î使得y b =与分段函数有两个交点;对于图5,不可能有两个交点;对于图6,不可能有两个交点;综上所述:当1a <且0a ¹成立;故选:B.ACD【分析】根据正态分布的对称性、线性相关性的性质,结合独立事件的定义、残差的公式逐一判断即可.【详解】因为()2~2,X N s ,且(6)0.4P X >=,所以有因此1(22)(2)0.12P X P X -<<=-<-=,所以选项根据线性相关有正相关和负相关,因此两个具有线性相关关系的变量的相关性越强,则线性相关系数r 的绝对值越接近于1,所以选项由()512()()()623P A B P A P B P AB È=+-Þ=+-。
2019-2020学年辽宁省实验中学、大连二十四中、鞍山一中、东北育才学校高一上学期期末考试数学试题

2019-2020高一上学期期末辽宁省五校联考数学试卷一. 选择题1.已知集合{}124A =,,,集合{}2log (1)1B x x =+>,则A B =( )A .{}14,B .{}24,C .{}12,D .{}42.用反证法证明命题“若220a b +=,则a ,b 全为0(a ,b R ∈)”,其假设正确的是( )A .a ,b 至少有一个不为0B .a ,b 至少有一个为0C .a ,b 全不为0D .a ,b 中只有一个为03.已知函数2()log (39)x f x =- )A .(23),B .(34],C .(24],D .(23)(34],,4.已知2log 3.4a =, 1.22.1b =,0.3log3.8c =,则a 、b 、c 的大小关系为( ) A .a b c << B .c a b << C .b c a << D .c b a <<5.设0a >且1a ≠,则“函数3()(2)g x a x =-在R 上是增函数”是“函数()xf x a =在R 上是减函数”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件6.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( ) 注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.A .互联网行业从业人员中90后占一半以上B .互联网行业中从事技术岗位的人数超过总人数的20%C .互联网行业中从事运营岗位的人数90后比80前多D .互联网行业中从事技术岗位的人数90后比80后多7. 点O 在ABC ∆内部,520AO AB AC --=,则AOB ∆与ABC ∆的面积比为( ) A. 51 B. 52 C. 53 D. 548. 若函数)(x f 是定义在R 上的奇函数,且)(x f 在)0,(-∞上是减函数,0)2(=f ,则不等式0)(≥x f 的解集为( )A. ),2[]2,(+∞⋃--∞B. ]2,0[]2,(⋃--∞C. ]2,0(]2,(⋃--∞D. ]2,2[- 9. 函数()()222x f x x x e =+的图象大致是( )A. B. C. D.10. 甲、乙、丙、丁、戊5名同学参加“庆国庆70周年,爱国主义知识大赛”活动,决出第1名到第5名的名次,甲乙两名同学去询问成绩,回答者对甲说“虽然你的成绩比乙好,但是你俩都没得到第一名”;对乙说“你当然不会是最差的”.从以上回答分析,丙是第一名的概率是( )A.31 B. 41 C. 51 D. 6111. 已知函数x x x f 2)(2+=,m x g x +=)21()(,若对任意]2,1[1∈x ,存在]1,1[2-∈x ,使得)()(21x g x f ≥,则实数m 的取值范围是( )A.]2,(-∞B. ]25,(-∞C. ),2[+∞D. ),25[+∞12. 已知函数)0(1)(11<-=++x ee xf x x 与xx ae e x g -=2)(的图像上存在关于y 轴对称的点,则实数a 的取值范围是( )A.)11,(e +-∞B. ),1(+∞-eC. )11,(e --∞D. ),12(+∞-e二. 填空题13. 求2,3,5,6,8,10,12,13,15,16,18,19的25%的分位数_________.14. 已知平面向量(2,-1),(1,1),-2,1a b c ===(),如果//a kb c +(),则实数k 的值为____...15. 若2个正实数x ,y 满足211x y+=,且222x y m m +>+恒成立,则实数m 的取值范围是____.16. 已知函数()()1022-10xx f x f x x ⎧⎛⎫≤⎪ ⎪=⎝⎭⎨⎪>⎩,,,(1)()2f =_____;(2)若方程f (x )=32x +a有且仅有一个实根,则实数a 的取值范围_______.三. 解答题17.已知命题p :{}2230A x x x x R =--≤∈,, 命题q :{}22240B x x mx m x R m R =-+-≤∈∈,, (1)若[13]AB =,,求实数m 的值;(2)若p 是q ⌝的充分条件,求实数m 的取值范围.18. 已知幂函数)()(322Z m x x f m m∈=++-是奇函数,且)2()1(f f <.(1)求m 的值,并确定)(x f 的解析式;(2)求函数()()22212log log f x f x y ⎡⎤⎣⎦⎡⎤=+⎣⎦,]2,21[∈x 的值域.19. 港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件,从某企业生产的桥梁构件中抽取100件,测量这些桥梁构件的质量指标值,有测量结果得到如果所示的频率分布直方图,质量指标落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1(1)求这些桥梁构件质量指标值的平均值;(2)用分层抽样的方法在区间[45,75)内抽取一个容量为6的样本,将该样本看成一个总体,从中抽取2件桥梁构件,求这2件桥梁构件都在区间[45,65)内的概率.20. 已知ABC ∆中,AB mAM =,AC nAN =,(0m >,0n >),若MN 与BC 交于点O ,且点O 为BC 的中点.(1)如果ABC ∆内一点D 满足420DA BD BC -+=,求DODA的值; (2)求12m n+的最小值.21. 已知函数()22f x x mx =--. (1)当1m =时,13212223x xx n f -⎛⎫≤--⎪⎝⎭在[]1,1x ∈-上恒成立,求n 的取值范围. (2)若函数()22f x x mx =--的两个零点分别为12,x x ,若对[]1,1m ∀∈-,[]1,1a ∀∈-,不等式22123x x t at -≤-+恒成立,求实数t 的取值范围.22. 已知函数()f x 的定义域为D ,对于给定的()*k k N ∈,若存在[],a b D ⊆,使得函数()f x 满足:①函数()f x 在[],a b 上是单调函数;②函数()f x 在[],a b 上的值域是[],ka kb ,则称[],a b 是函数()f x 的k 级“理想区间”.(1)判断函数3y x =是否存在1级“理想区间”,若存在,请写出它们所有的“理想区间”(只需要直接写出结果);(2)证明:函数()xf x e =存在3级“理想区间”;( 2.71828e ≈);(3)设函数()241xg x x =+,[]0,1x ∈,若函数()g x 存在k 级“理想区间”,求k 的值.。
2024届辽宁省沈阳市东北育才学校高一数学第一学期期末达标检测模拟试题含解析

2024届辽宁省沈阳市东北育才学校高一数学第一学期期末达标检测模拟试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的 1.若a b c >>,则()A.“x b >”是“x a >”的充分不必要条件B.“x a >”是“x c >”的充要条件C.“x c >”是“x a >”的必要不充分条件D.“x b >”是“x c >”的既不充分也不必要条件2.国家质量监督检验检疫局发布的相关规定指出,饮酒驾车是指车辆驾驶人员血液中的酒精含量大于或者等于20mg/100ml ,小于80mg/100ml 的驾驶行为;醉酒驾车是指车辆驾驶人员血液中的酒精含量大于或者等于80mg/100ml 的驾驶行为.一般的,成年人喝一瓶啤酒后,酒精含量在血液中的变化规律的“散点图”如图所示,且图中的函数模型为: ()0.5π40sin 13,02390e 14,2x x x f x x -⎧⎛⎫+≤<⎪ ⎪=⎝⎭⎨⎪+≥⎩,假设某成年人喝一瓶啤酒后至少经过*(N )n n ∈小时才可以驾车,则n 的值为( )(参考数据:ln15 2.71≈,ln30 3.40≈)A.5B.6C.7D.83.已知点P (1,a )在角α的终边上,tan ()4a π+=-1,3则实数a 的值是()A.2B.12 C.-2 D.-124.集合的真子集的个数是( ) A.16B.8C.7D.45.已知幂函数()f x x α=的图象过点()93,,若()2f t =,则实数t 的值为() A.2 B.2± C.4±D.46.下列说法正确的是( )A.向量a 与b 共线,b 与c 共线,则a 与c 也共线B.任意两个相等的非零向量的始点与终点是一个平行四边形的四个顶点C.向量a 与b 不共线,则a 与b 都是非零向量D.有相同起点的两个非零向量不平行7.定义域为R 的偶函数()f x 满足对任意的x ∈R ,有()2f x +=()()1,f x f +且当[]2,3x ∈时,()f x =221218x x -+-,若函数y =()()log 1a f x x -+在(0,+)∞上恰有六个零点,则实数a 的取值范围是A.30,3⎛⎫⎪ ⎪⎝⎭ B.5,1?5⎛⎫⎪ ⎪⎝⎭C.53,? 53⎛⎫ ⎪ ⎪⎝⎭D.3,13⎛⎫⎪ ⎪⎝⎭8.函数2()log cos f x x x =+的大致图象是() A.B.C. D.9.已知函数()log ,04(3)1022,4a x x f x a x a x <<⎧=⎨-+-≥⎩是(0,)+∞上的增函数(其中0a >且1a ≠),则实数a 的取值范围为() A.()1,2 B.2,22⎡⎣ C.()1,3D.[)2,310.下列区间中,函数()7sin 6f x x π⎛⎫=-⎪⎝⎭单调递增的区间是()A.0,2π⎛⎫⎪⎝⎭ B.,2ππ⎛⎫⎪⎝⎭C.3,2ππ⎛⎫ ⎪⎝⎭D.3,22ππ⎛⎫ ⎪⎝⎭二、填空题:本大题共6小题,每小题5分,共30分。
【40套试卷合集】东北育才中学2019-2020学年化学高一上期末模拟试卷含答案

2019-2020学年高一上化学期末模拟试卷含答案可能用到相对原子量:Al:27 Na:23 H:1 O:16 Mg:24 Cl:35.5C:12 N:14一、选择题:(每题只有一个选项,每题6分,共42分)1、我国重点城市近年来已发布“空气质量日报”。
下列物质中不列入首要污染物的是( )。
A、二氧化硫B、二氧化氮C、二氧化碳 D.可吸入颗粒物2、下列离子方程式中,正确的是( )。
A、稀硫酸滴在铁片上:2Fe+6H+=2Fe3++3H2↑B、碳酸氢钠溶液与稀盐酸混合:HC O3—+H+=H20+C02↑C、硫酸铜溶液与氢氧化钠溶液混合:CuS04+20H—=Cu(OH)2↓+SO42-D、硝酸银溶液与氯化钠溶液混合:AgN03+C1—=AgCl↓+NO3—3、下列说法或操作:①做实验时可用手直接拿取金属钠②用托盘天平称量50.56gCl③用酒精可以从饱和碘水中萃取碘④让一束光通过胶体,从垂直于光线的方向可以看到一条光亮的“通路”⑤检验某溶液里是否含有Fe2+时,可先滴加新制氯水,再滴加SCN溶液。
其中正确的是 ( )A.①②③④⑤ B、②④⑤ C、②③④ D、④4、设阿伏加德罗常数的数值为N A,则下列说法正确的是A、常温下,2.7g铝与足量的氢氧化钠溶液反应失去的电子数为0.1N AB.0.1mol/L的Na2S04溶液中含SO42—的个数为0.1N AC.1.7g NH3中含有的原子数为0.4N AD.11.2L C02与8.5g NH3所含分子数都是0.5 N A5、某溶液中含有较大量的C1-、CO32—、OH—等3种阴离子,如果只取一次该溶液就能够分别将3种阴离子依次检验出来,下列实验操作顺序正确的是 ( )①滴加Mg(N03)2溶液;②过滤;③滴加AgNO3溶液;④滴加Ba(NO3)2溶液A、①②④②③ B.④②①②③ C、①②③②④ D、④②③②①6、通过对实验现象的观察、分析、推理得出正确的结论是化学学习的方法之一,下列对各实验事实的解释正确的是 ( )7、下列说法正确的是 ( )A.经测定一瓶气体中只含两种元素,则这瓶气体不可能是一种单质和一种化合物的混合物B.水泥、普通玻璃和陶瓷都是应用广泛的硅酸盐产品C、一般情况下,合金的熔点和硬度都比各成分金属的高D、光导纤维以硅为主要原料制成二、填空题:8、(16分)在氮的单质和常见化合物中:(1)常用作保护气(如填充灯泡、焊接保护等)的物质是___________,原因是____________________________________________________________。
东北育才学校2019年高三一模数学(理)试题及答案
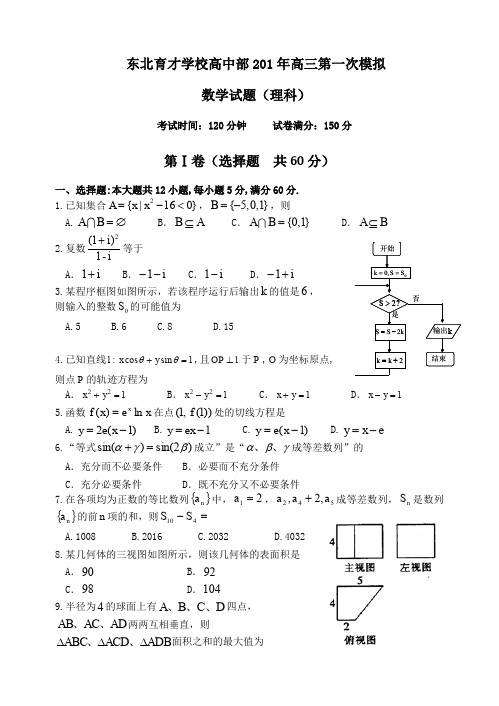
开始结束输出是否,0S S k ==?2>S kS S 2-=2+=k k k东北育才学校高中部201年高三第一次模拟数学试题(理科)考试时间:120分钟 试卷满分:150分第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,满分60分. 1.已知集合2{|160}A x x =-<,{5,0,1}B =-,则 A.AB =∅ B .B A ⊆C .{0,1}A B =D .A B ⊆2.复数ii -1)1(2+等于A .i +1B .i --1C .i -1D .i +-1 3.某程序框图如图所示,若该程序运行后输出k 的值是6, 则输入的整数0S 的可能值为A.5B.6C.8D.154.已知直线1sin cos :=+θθy x l ,且l OP ⊥于P ,O 为坐标原点, 则点P 的轨迹方程为A .122=+y xB .122=-y xC .1=+y xD .1=-y x5.函数x e x f xln )(=在点))1(,1(f 处的切线方程是A.)1(2-=x e yB.1-=ex yC.)1(-=x e yD.e x y -= 6.“等式)2sin()sin(βγα=+成立”是“γβα、、成等差数列”的 A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分又不必要条件7.在各项均为正数的等比数列{}n a中,21=a ,542,2,a a a +成等差数列,n S 是数列{}n a 的前n 项的和,则=-410S SA.1008B.2016C.2032D.4032 8.某几何体的三视图如图所示,则该几何体的表面积是 A .90 B .92 C .98 D .104 9.半径为4的球面上有D C B A 、、、四点,AD AC AB 、、两两互相垂直,则ADB ACD ABC ∆∆∆、、面积之和的最大值为A .8B .16C .32 D.6410.设等差数列{}n a 的前n 项和为n S ,若0,0109<>S S ,则993322122,2,2aa a a ,中最大的是A .12a B .552aC .662aD .992a11.已知函数)()(()(321x x x x x x x f ---=)(其中321x x x <<),)12s i n (3)(++=x x x g ,且函数)(x f 的两个极值点为)(,βαβα<.设2,23221xx x x +=+=μλ,则A .)()()()(μβλαg g g g <<<B .)()()()(μβαλg g g g <<<C .)()()()(βμαλg g g g <<<D .)()()()(βμλαg g g g <<<12.设双曲线)0,0(12222>>=-b a by a x 的右焦点为F ,过点F 作x 轴的垂线交两渐近线于点B A ,两点,且与双曲线在第一象限的交点为P ,设O 为坐标原点,若)R OB OA OP ∈+=μλμλ,(,8522=+μλ,则双曲线的离心率为( )A .332B .553C .223D .89第Ⅱ卷(非选择题共90分)二.填空题:本大题共4小题,每小题5分.13.若n S 是数列{}n a 的前n 项的和,且762++-=n n S n ,则数列{}n a 的最大项的值为___________.14.设221(32)=⎰-a x x dx ,则二项式261()-ax x展开式中的第4项为___________.15. 已知正方形ABCD 的边长为2,点E 为AB 的中点.以A 为圆心,AE 为半径,作弧交AD 于点F ,若P 为劣弧EF 上的动点,则PC PD 的最小值为___________.16.已知函数xx a x f 22)(1+=+在]3,21[-上单调递增,则实数a 的取值范围_________.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本题满分12分)已知函数))(12(sin 2)62sin(3)(2R x x x x f ∈-+-=ππ(I )求函数)(x f 的最小正周期;(Ⅱ)求使函数)(x f 取得最大值的x 的集合.18.(本小题满分12分)如图,在四棱锥ABCD P -中,底面ABCD 是菱形,︒=∠60DAB ,,1,==⊥AD PD ABCD PD 平面 点,E F 分别为AB 和PD 中点.(Ⅰ)求证:直线PEC AF 平面//; (Ⅱ)求PC 与平面PAB 所成角的正弦值.19.(本小题满分12分)某网站用“10分制”调查一社区人们的治安满意度.现从调查人群中随机抽取16名,以下茎叶图记录了他们的治安满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶).(I )若治安满意度不低于9.5分,则称该人的治安满意度为“极安全”,求从这16人中随机选取3人,至多有1人是“极安全”的概率; (II )以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记X 表示抽到“极安全”的人数,求X 的分布列及数学期望.20.(本小题满分12分)如图,已知直线1:+=my x l 过椭圆1:2222=+by a x C 的右焦点F ,抛物线:y x 342=的焦点为椭圆C 的上顶点,且直线l 交椭圆C 于B A 、两点,点BF A 、、在直线4=x g :上的射影依次为点E K D 、、.FE BDCAP(Ⅰ)求椭圆C 的方程;(Ⅱ)若直线l 交y 轴于点M ,且BF MB AF MA 21λλ==,,当m 变化时,探求21λλ+的值是否为定值?若是,求出21λλ+的值,否则,说明理由.21.(本小题满分12分)设x m =和x n =是函数21()ln (2)2f x x x a x =+-+的两个极值点,其中 m n <,a R ∈.(Ⅰ) 求()()f m f n +的取值范围; (Ⅱ) 若12a e e≥+-,求()()f n f m -的最大值.22.(本小题满分10分)选修4-1:几何证明选讲 如图所示,已知⊙O 的半径长为4,两条弦BD AC ,相交于点E ,若34=BD ,DE BE >,E为AC 的中点,AE AB 2=.(Ⅰ) 求证:AC 平分BCD ∠; (Ⅱ)求ADB ∠的度数.23.(本小题满分10分)选修4-4:坐标系与参数方程已知曲线1C 的参数方程为⎩⎨⎧==θθsin 3cos 2y x (其中θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为01sin cos =+-θρθρ.(Ⅰ) 分别写出曲线1C 与曲线2C 的普通方程;(Ⅱ)若曲线1C 与曲线2C 交于B A ,两点,求线段AB 的长.24.(本小题满分10分) 选修4-5:不等式选讲 已知函数|12|)(-=x x f . (Ⅰ)求不等式2)(<x f 的解集;(Ⅱ)若函数)1()()(-+=x f x f x g 的最小值为a ,且)0,0(>>=+n m a n m ,求nn m m 1222+++的最小值. .ABCDEO东北育才高中部第三次模拟数学(理科)答案一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项符合题目要求.1.C2.D3.C4.A5.C6.B7.B8.D9.C 10.B 11.D 12.A 二.填空题:本大题共4小题,每小题5分.13.12 14.31280-x 15.525- 16.[﹣1,1]三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(Ⅰ) f(x)=3sin(2x -π6)+1-cos2(x -π12)= 2[32sin2(x -π12)-12 cos2(x -π12)]+1 =2sin[2(x -π12)-π6]+1= 2sin(2x -π3) +1∴ T=2π2=π(Ⅱ)当f(x)取最大值时, sin(2x -π3)=1,有 2x -π3 =2k π+π2即x=k π+ 5π12(k ∈Z)∴所求x 的集合为{x ∈R|x= k π+ 5π12 , (k ∈Z)}.18.解:(Ⅰ)证明:作FM ∥CD 交PC 于M . ∵点F 为PD 中点,∴CD FM 21=. …………2分 ∵21=k ,∴FM AB AE ==21, ∴AEMF 为平行四边形,∴AF ∥EM , ……4分 ∵AF PEC EM PEC ⊄⊂平面,平面, ∴直线AF //平面PEC . ……………6分MFEBACDP(Ⅱ)60DAB ∠=,DE DC ∴⊥.如图所示,建立坐标系,则P (0,0,1),C (0,1,0),E (32,0,0),A (32,12-,0),31(,,0)22B , ∴31,,122AP ⎛⎫=-⎪ ⎪⎝⎭,()0,1,0AB =. …8分 设平面PAB 的一个法向量为(),,n x y z =.∵0n AB ⋅=,0n AP ⋅=,∴⎪⎩⎪⎨⎧==++-02123y z y x ,取1x =,则32z =, ∴平面PAB 的一个法向量为3(1,0,)2n =. …………………………10分 设向量n PC θ与所成角为,∵(0,1,1)PC =-,∴3422cos 14724n PC n PCθ-⋅===-⨯, ∴P C 平面PAB 所成角的正弦值为4214..…………………………12分19.FE BACDyz xP20.解:(Ⅰ)易知椭圆右焦点F(1,0),∴c=1,抛物线的焦点坐标,∴∴b2=3 ∴a2=b2+c2=4∴椭圆C的方程(Ⅱ)易知m≠0,且l与y轴交于,设直线l交椭圆于A(x1,y1),B(x2,y2)由∴△=(6m)2+36(3m2+4)=144(m2+1)>0∴又由∴同理∴∵∴所以,当m变化时,λ1+λ2的值为定值;(Ⅲ)证明:由(Ⅱ)知A(x1,y1),B(x2,y2),∴D(4,y1),E(4,y2)方法1)∵当时,==∴点在直线l AE上,同理可证,点也在直线l BD上;∴当m变化时,AE与BD相交于定点方法2)∵=∴k EN =k AN ∴A 、N 、E 三点共线, 同理可得B 、N 、D 也三点共线; ∴当m 变化时,AE 与BD 相交于定点.解:函数()f x 的定义域为(0,)+∞,21(2)1()(2)x a x f x x a x x-++'=+-+=.依题意,方程2(2)10x a x -++=有两个不等的正根m ,n (其中m n <).故2(2)40020a a a ⎧+->⇒>⎨+>⎩, 并且 2,1m n a mn +=+=.所以,221()()ln ()(2)()2f m f n mn m n a m n +=++-++2211[()2](2)()(2)1322m n mn a m n a =+--++=-+-<- 故()()f m f n +的取值范围是(,3)-∞-(Ⅱ)解:当12a e e≥+-时,21(2)2a e e +≥++.若设(1)nt t m =>,则222()11(2)()22m n a m n t e mn t e ++=+==++≥++.于是有 111()(1)0t e t e t e t e te +≥+⇒--≥⇒≥222211()()ln ()(2)()ln ()()()22n n f n f m n m a n m n m n m n m m m -=+--+-=+--+-2222111ln ()ln ()ln ()22211ln ()2n n n m n n m n m m m mn m m n t t t-=--=-=--=-- 构造函数11()ln ()2g t t t t =--(其中t e ≥),则222111(1)()(1)022t g t t t t-'=-+=-<. 所以()g t 在[,)e +∞上单调递减,1()()122e g t g e e≤=-+.故()()f n f m -的最大值是1122e e-+22.(本小题满分10分)解:(1)由E 为AC 的中点,AE AB 2=得AB ACAE AB ==2 又CAB BAE ∠=∠ ABE ∆∴∽ACB ∆ ACB ABE ∠=∠∴ 又ABE ACD ∠=∠ ACB ACD ∠=∠∴故AC 平分BCD ∠………………5分(2)连接OA ,由点A 是弧BAD 的中点,则BD OA ⊥,设垂足为点F ,则点F 为弦BD 的中点,32=BF 连接OB ,则2)32(42222=-=-=BF OB OF ,224=-=-=OF OA AF ,60,2142cos =∠===∠∴AOB OB OF AOB 3021=∠=∠∴AOB ADB ………………10分.AB CDE OF23.(本小题满分10分)解:(1)曲线1C 134:22=+y x ,………………2分 曲线2C :01=+-y x ………………4分(2)联立⎪⎩⎪⎨⎧=+=+-1340122y x y x ,得08872=-+x x , 设),(),,(2211y x B y x A ,则78,782121-=-=+x x x x 于是7244)(2112122121=-+⋅=-+=x x x x x x AB . 故线段AB 的长为724.………………10分 24.(本小题满分10分) 解:(1)由2)(<x f 知2|12|<-x ,于是2122<-<-x ,解得2321<<-x ,故不等式2)(<x f 的解集为⎪⎭⎫ ⎝⎛-23,21;……………………3分 (2)由条件得2|)32(12||32||12|)(=---≥-+-=x x x x x g ,当且仅当⎥⎦⎤⎢⎣⎡∈23,21x 时,其最小值2=a ,即2=+n m …………………6分又()()223212*********+≥⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛++=+n m m n n m n m n m ,…………8分 所以n n m m 1222+++()22321212++≥+++=n m n m 2227+=, 故nn m m 1222+++的最小值为2227+,此时222,224-=-=n m .……10分 12分。
辽宁省东北育才学校2024-2025学年高三上学期高中学段联合考试数学试卷

辽宁省东北育才学校2024-2025学年高三上学期高中学段联合考试数学试卷一、单选题1.已知集合{}820A x x =∈-N ,{}2|B y y x ==,则A B =I ( )A .[]0,2B .[)0,4C .{}0,1D .{}0,1,2,32.复数12z z 、满足1212,z z z z +=若11i z =+,则2z =( )A B .1C .2 2D . 23.已知命题p :x ∀∈R ,210ax ax -+>;q :x ∃∈R ,20x x a -+≤.均为真命题,则a 的取值范围是( ) A .(),4-∞B .[)0,4C .10,4⎛⎤ ⎥⎝⎦D .10,4⎡⎤⎢⎥⎣⎦4.将函数()8sin f x x =图象向右平移π8后,再将所得图象上各点横坐标扩大为原来的4倍,得到()g x 的图象,若方程()4g x =在[0,8π]内有两不等实根,αβ,则πco s ()6αβ++=( )A .BC .1-D .12-5.如图,在四边形ABCD 中,4,2,60AC AD CAD ==∠=o u u u r u u u r ,E 为线段AC 中点,2DE EB =u u u r u u u r ,则DB DC ⋅=u u u r u u u r( )A B .15 C .18 D .96.已知函数()20252025x xf x -=-,若0a >,0b >,且()()20f a f b -+=,则3111a b +++的最小值为( )A B .1C .1D .7.定义在R 上的函数()f x 满足()00f =,()()11f x f x +-=,()152x f f x ⎛⎫= ⎪⎝⎭,且当1201x x ≤<≤时,()()12f x f x ≤,则12025f ⎛⎫= ⎪⎝⎭( )A .1256B .1128C .164D .1328.若关于x 不等式()ln ax x b ≤+恒成立,则当1e ea ≤≤时,1e lnb a +-的最小值为( )A .11e+B .e 1-C .1D .e二、多选题9.下列四个命题为真命题的是( ).A .在ABC V 中,角,,ABC 所对的边分别为,,a b c,若a =2b =,A θ=,要使满足条件的三角形有且只有两个,则π0,6θ⎛⎫∈ ⎪⎝⎭B .若向量()5,0a =r,()2,1b =r ,则a r 在b r 上的投影向量为()4,2C .已知向量()cos ,sin a αα=r ,()2,1b =r ,则a b -rr1D .在ABC V 中,若sin sin AB AC AO AB B AC C λ⎛⎫ ⎪=+ ⎪⎝⎭u u u r u u u r u u u r u u u r u u u r (λ∈R ),则动点O 的轨迹一定通过ABC ∆的重心10.若0a >,0b >,且22a b +=,则下列结论正确的是( )A .224a b +的最小值为2B .24a b +的最小值为4C .()sin 123a b ++>D .若实数1c >,则22321(2)1a abc ab c ++-⋅+-的最小值为8 11.已知函数()sin cos e e x xf x =-,其中e 是自然对数的底数,下列说法中正确的是( )A .()f x 在π0,2⎛⎫⎪⎝⎭上是增函数B .()f x 的图象关于点π,04⎛⎫⎪⎝⎭中心对称C .()f x 在 0,π 上有两个极值点D .若0x 为()f x 的一个极小值点,且()0cos 0e tan xa f x x -<+恒成立,则1a <-三、填空题12.已知方程2340z z ++=的两个复数根分别为1z ,2z ,则12z z -=.13.如图,在ABC V 中,已知1AB =,2AC =,60BAC ∠=︒,BC ,AC 边上的两条中线AM ,BN 相交于点P ,则MPN ∠的余弦值为.14.若()2216ln 8ln 122x x f x x ⎛⎫=+-+ ⎪⎝⎭,则()f x 的最小值为.四、解答题15.在ABC V 中,角A ,B ,C 所对的边分别为a ,b ,c ,且()1c o s c o s c o s 02B cB bC a ++=.(1)求角B 的大小:(2)若8a c +=,7b =,a c <,求()sin 2A C +的值;(3)设D 是边AC 上一点,BD 为角平分线且2AD DC =,求cos A 的值.16.已知函数()()2e 2e x xf x a ax =+--.(1)当2a =时,求曲线()y f x =在点()()1,1f 处的切线方程; (2)讨论()f x 的单调区间.17.在复数集中有这样一类复数:i z a b =+与i z a b =-(),R a b ∈,我们把它们互称为共轭复数,0b ≠时它们在复平面内的对应点关于实轴对称,这是共轭复数的特点.它们还有如下性质:(1)设i z ≠,1z =,求证:21+zz 是实数; (2)已知13z =,25z =,127z z -=,求12z z 的值;(3)设i z x y =+,其中x ,y 是实数,当1z =时,求21z z -+的最大值和最小值.18.已知函数()()()5cos sin 5sin 3tan 4sin 5sin f x x x x θθθθ=⋅--+--(π02θ<<)的图象关于y 轴对称. (1)求tan θ;(2)设()()π2h x f x f x ⎛⎫=⋅+ ⎪⎝⎭,求()h x 的最大值和此时的x 的集合;(3)设函数()()π2g x f x f x λωω⎛⎫=-+ ⎪⎝⎭(0λ>,0ω>).已知()y g x =在π6x =处取最小值并且点2π,443λ⎛⎫- ⎪⎝⎭是其图象的一个对称中心,试求λω+的最小值.19.请阅读下列2段材料:材料1:若函数()y f x =的导数()f x 仍是可导函数,则()'f x 的导数()f'x '⎡⎤⎣⎦称为()f x 的二阶导数,记为()''f x :若()''f x 仍是可导函数,则()''f x 的数()'f''x ⎡⎤⎣⎦称为()f x 的三阶导数,记为()'''f x ;以此类推,我们可以定义n 阶导数:设函数()y f x =的1n -阶导数()1n f x -(2n ≥,n +∈N )仍是可导函数,则()1n f x -的导数()1n f x '-⎡⎤⎣⎦称为()f x 的n 阶导数,记为()nf x ,即()()1n n f x f x '-⎡⎤=⎣⎦.材料2:帕德逼近是法国数学家亨利·帕德发现的对任意函数的一种用有理函数逼近的方法.帕德逼近有阶的概念,如果分子是m 次多项式,分母是n 次多项式,那么帕德逼近就是mn阶的帕德逼近.一般地,函数()f x 在0x =处的[],m n 阶帕德逼近函数定义为:()0111mm nn a a x a x R x b x b x +++=+++L L 且满足()()00f R =,()()00f'R'=,()()00f''R''=,…,()()()()00m n m n fR ++=(其中e 2.71878=…为自然对数的底数). 请根据以上材料回答下列问题:(1)求函数()()ln 1f x x =+在0x =处的[]1,1阶帕德逼近函数()R x ,并比较()f x 与()R x 的大小;(2)求证:当()0,x ∈+∞时,23x x >恒成立. (3)在(1)条件下,若()()()()12f x h x m f x R x ⎛⎫=-- ⎪⎝⎭在()0,∞+上存在极值,求m 的取值范围。
东北育才学校2019届高三上学期第一次模拟考试数学(理)试卷(含答案)

2018—2019学年度上学期高三第一次模拟考试理科数学试卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数2= A.1-B.1C.i -D.i2.已知全集2{|8120}U x Z x x =∈-+≤,{}3,4,5A =,{}C 5,6U B =,则A B =A.{}5,6B.{}3,4C.{}2,3D.{}2,3,4,53.甲乙两名同学6次考试的成绩统计如下图,甲乙两组数 据的平均数分别为甲x 、乙x ,标准差分别为,甲乙σσ,则 A.甲乙x x <,甲乙σσ< B.甲乙x x <,甲乙σσ> C.甲乙x x >,甲乙σσ< D.甲乙x x >,甲乙σσ>4.一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则截去..的几何体是 A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱5.下列命题中真命题的是A.若p q ∧为假命题,则p ,q 均为假命题;B.“22bm am<”是“b a <”的充要条件;C.命题:若12=x ,则1=x 或1-=x 的逆否命题为:若1≠x 或1-≠x ,则12≠x ;D.对于实数,x y ,:8p x y +≠,:2q x ≠或6y ≠,则p 是q 的充分不必要条件. 6.已知1cos 25πα⎛⎫-= ⎪⎝⎭,则cos 2α A .725 B .725- C .2325 D .2325-7.若实数,x y 满足210220x x y x y ≤-+≥+-≥⎧⎪⎨⎪⎩,则2=-z x y 的最小值为A.4B.1 C .1- D .4- 8.已知函数lg(y x =是定义在R 上的奇函数,且函数2()+=x ag x x在()0,+∞上单调递增,则实数a 的值为 A .1-B .2-C .1D .29.某次文艺汇演,要将A 、B 、C 、D 、E 、F 这六个不同节目编排成节目单,如下表:A .192种B .144种C .96种D .72种10.函数()sin()f x A x ωϕ=+(其中A >0,ϕ<π2)的图象如图所示,为了得到 ()sin3g x x =的图象,只需将()f x的图象A.向右平移π4个单位长度 B.向左平移π4个单位长度 C.向右平移π12个单位长度 D.向左平移π12个单位长度 11.设点1F 为双曲线2222:1(0,0)x y C a b a b-=>>的左焦点,点P 为C 右支上一点,点O 为坐标原点,若1OPF ∆是底角为030的等腰三角形,则C 的离心率为 A 1 B 1 C .12 D .1212.已知函数()f x 的导函数为()'f x ,且对任意的实数x 都有'5()(2)()2-=+-x f x e x f x (e 是自然对数的底数),且()01f =,若关于x 的不等式()0f x m -<的解集中恰唯一一个整数,则实数m 的取值范围是 A.e (,0)2- B. e (,0]2- C .3e (,0]4- D .3e 9(,]42e -第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知()1nmx +的展开式中,二项式系数和为32,各项系数和为243,则m = .14.已知抛物线24y x =的焦点为F ,点A 在y 轴上,线段AF 的中点B 在抛物线上,则AF = .15.在正四面体P ABC -中,其侧面积与底面积之差为为 .16.如图,设ABC ∆的内角,,A B C 所对的边分别为,,a b c ,cos cos sin a C c A b B +=,且6CA B π∠=.若点D 是ABC ∆外一点,2,3DC DA ==,则当四边形A B C D 面积最大值时,sin D = .三、解答题:解答应写出文字说明、证明过程或演算步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020学年高一上数学期末模拟试卷含答案一.选择题:(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、设集合{}012345U =,,,,,,集合{}035M =,,,{}145N =,,,则()U M C N ⋂等于( )A .{}0,1,3,4,5B .{}0,2,3,5C .{}0,3D .{}5 2、函数2()log f x x =的定义域为( ) A .(0,2]B .(0,2)C .(0,1)(1,2)⋃D . (0,1)(1,2]⋃3、用二分法研究函数13)(3-+=x x x f 的零点时,第一次经计算0)5.0(0)0(><f f ,,可得其中 一个零点∈0x ,第二次应计算 .以上横线上应填的内容为( )A .(0.5,1),)75.0(fB .(0,0.5),)125.0(fC .(0,0.5),)25.0(fD .(0,1),)25.0(f 4、已知向量(1,1),(1,1),(1,2)a b c ==-=--,则c = ( ) A.1322a b -- B.1322a b -+ C.3122a b - D.3122a b -+5、sin570°的值是 ( ) A .21 B .-21C . 23D . -236、若角α的终边落在直线x -y =0上,则ααααcos cos 1sin 1sin 22-+-的值等于( ) A 2 B 2- C 2-或2 D 07、一质点受到平面上的三个力123,,F F F (单位:牛顿)的作用而处于平衡状态.已知12,F F 成120 角,且12,F F 的大小分别为1和2,则有 ( )A .13,F F 成90角B .13,F F 成150角C .23,F F 成90角D .23,F F 成60角8、设函数 ,则满足 的x 的取值范围是 ( )A .[-1,2]B .[0,+ )C .[1,+ )D .[0,2]9、函数b x A x f +ϕ+ω=)sin()(图象如右图,则)(x f 的解析式与++=)1()0(f f S )(f )(f 20122+⋯+的值分别为( )⎩⎨⎧>-≤=-1,log 11,2)(21x x x x f x 2)(≤x f ∞∞A . 12sin 21)(+π=x x f , 2013=SB . 12sin 21)(+π=x x f ,212013=SC .12sin 21)(+π=x x f , 2012=S D .12sin 21)(+π=x x f , 212012=S10、在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y =f (x ),一种是平均价格曲线y =g (x )(如f (2)=3表示开始交易后第2小时的即时价格为3元;g (2)=4表示开始交易后两个小时内所有成交股票的平均价格为4元).下面所给出的四个图象中,实线表示y =f (x ),虚线表示y =g (x ),其中可能正确的是( ).A .B .C .D二.填空题:(本大题共7小题,每小题4分,共28分.)11、设)x (f 是定义在R 上的奇函数,当0≤x 时,x x )x (f -=22,则)(f 1= .12、函数x tan y =在),(π20内的零点是 .13、函数3x x y +=的值域是 .14、△ABC 中,5,4,3===CA BC AB ,则CB CA ⋅= .15、若 , 则a,b,c 的大小关系是 .16、下面有五个命题:①终边在y 轴上的角的集合是{β|β=Z k ,k ∈+22ππ}.②设一扇形的弧长为4cm ,面积为4cm 2,则这个扇形的圆心角的弧度数是2. ③函数x cos x sin y 44-=的最小正周期是2π. ④的图象为了得到x sin y 23=,只需把函数.)x sin(y 6323ππ的图象向右平移+=⑤函数上,在⎪⎭⎫⎢⎣⎡----=2πππ)x tan(y 是增函数. 所有正确命题的序号是 . (把你认为正确命题的序号都填上),sin log a 72π=,log b 311π=312=c17、 定义在R 上的奇函数)(x f 满足:对于任意).x (f )x (f ,R x -=∈2有若,tan 21=α )cos sin (f αα10-则的值为 .三.解答题(本大题共5小题,满分52分.解题应写出文字说明,证明过程或演算步骤)且AB 注:答案超出边框部分无效19、(本小题满分10分)(1)求值: (2)化简:20、(本小题满分10分) 已知函数)x sin()x (f 6221πω++=(其中01ω<<), 若直线3x π=是函数)x (f 图象的一条对称轴.(1)求ω及最小正周期; (2)求函数()f x ,[]ππ,x -∈的单调减区间.3tan()cos(2)sin()2.cos()sin()ππαπαααππα---+----3556331103252718lg )log (log log log ++⋅++-21、(本小题满分10分)已知向量3(sin ,),(cos ,1).2a xb x ==- (1)当//a b 时,求 x cos x sin x cos 222- 的值;(2)求函数)b a ()b a (x sin )x (f -⋅++=2在,02π⎡⎤-⎢⎥⎣⎦上的最小值,及取得最小值时x 的值.22、(本小题满分12分)已知函数212(),03()11,02x x f x x x x ⎧-≤⎪⎪=⎨⎪-+>⎪⎩ .(1)写出该函数的单调区间;(2)若函数()()g x f x m =-恰有3个不同零点,求实数m 的取值范围;(3) 若12)(2+-≤bn n x f 对所有[1,1],[1,1]x b ∈-∈-恒成立,求实数n 的取值范围.答案一、选择题11、3- ; 12、π; 13、[)+∞,0 ; 14、 16 ; 15、c b a <<; 16 、②④; 17、0.三、解答题(本大题共5小题,满分52分。
解答应写出文字说明、证明过程或演算步骤) 18.解:(1)易得),(B 2321-……… 2分 则=∠COA sin 23,=∠COA cos 21-,=∠COA tan 3-. ……… 5分 (2) ),(B 2321-,),(C 01 ∴ 3= …… 8分四边形OBAC 是菱形,∴BC OA ⋅=0 …… 10分19. 解:(1)原式36log 5log 3log )2(5633313+⋅++=-- ……… 2分31321++-=……… 6分 (2)原式=αααααs i n c o s )c o s (c o s t a n ⋅--⋅⋅- ……… 9分 = -1 ……… 10分20. (1)解:由题可知)z k (k ∈+=+⋅2632ππππω故有k 2321+=ω 又2110=∴<<ωω (3)分ππ2621=++=∴T )x sin()x (f 周期 ……… 5分(2)23=X sin y ,x X ⎤⎡+=+=πππ3216的单调减区间为则设≤+≤+622πππx k ππk 223+ ∴≤≤+x k ππ23ππk 234+ ……… 7分 ⎥⎦⎤⎢⎣⎡++=ππππk ,k A 23423设,[]ππ,B -=⎥⎦⎤⎢⎣⎡⋃⎥⎦⎤⎢⎣⎡--=⋂ππππ,,B A 332则 ……… 9分 ⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--ππππ,,)x (f 332和的单调减区间为故 .……… 10分 21.(1)解: ||a b ,∴3cos sin 02x x +=,∴ 3tan 2x =- ……… 2分.1320tan 1tan 22cos sin cos sin 2cos 22sin cos 222222=+-=+-=-x x x x x x x x x.……… 4分(2) .……… 6分41222++=∴x sin x sin )x (f =412122-+)x (sin . ……… 8分 []0121,-∈-.)x (f ,x ,x sin min 41621-=-=-=∴π即时当 ……… 10分22.(1)解:(1)函数()f x 的图象如右图;函数()f x 的单调递减区间是(0,1) 单调增区间是(,0)-∞及(1,)+∞ …………3分(2)作出直线y m =,函数()()g x f x m =-恰有3个不同零点等价于函数y m = 与函数)(x f 的图象恰有三个不同公共点。
由函数212(),03()11,02x x f x x x x ⎧-≤⎪⎪=⎨⎪-+>⎪⎩ 又f(0)=1 f(1)= 1241222222++=-+=x sin x sin x sin )x (f 0102≤≤-∴≤≤-x sin x π∴1(,1)2m ∈ …………6分(2)解:∵f(x)是增函数,且f (x)≤n 2-2bn+1对所有x ∈[-1,1]恒成立∴[f(x)]max ≤n 2-2bn+1 [f(x)]max =f(1)=1 ∴n 2-2bn+1≥1即n 2-2bn ≥0在b ∈[-1,1]恒成立∴y= -2nb+n 2在b ∈[-1,1]恒大于等于0 ……………9分∴⎪⎩⎪⎨⎧≥+⨯-≥+-⨯-0120)1(222n n n n ,∴⎩⎨⎧≥≤-≤≥2020n n n n 或或∴n 的取值范围是)2[}0{]2-(∞+-∞,, ……12分2019-2020学年高一上数学期末模拟试卷含答案本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至4页。
全卷共150分。
注意事项:1.答题前,考生务必将自己的姓名、座位号、考号填写在答题卡上,并将条形码贴在答题卡上对应的虚线框内。
2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
第Ⅱ卷用0.5 mm 黑色墨水签字笔在答题卡上书写作答,在试题卷上作答,答案无效。
3.考试结束,监考人只将答题卡收回。
第Ⅰ卷 (选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.集合{12}A =,,{123}B =,,,则下列关系正确的是 (A) A B = (B) A B =∅ (C) A B ⊆(D) A B ⊇2.已知3sin 5α=,则sin()απ+= (A) 45-(B) 35-(C)35(D)453.下列函数中与函数y x =相等的是(A) y =(B) y =(C) 2y =(D) 2x y x=[]4.在ABC ∆中,已知1cos 2A =,则sin A =(A)12(B) (C) (D)5.函数()f x =(A) (02), (B) [2)+∞, (C) (0)+∞,(D) (2)-∞,6.函数11(01)x y a a a -=+>≠,过定点(A) (01), (B) (02), (C) (11),(D) (12),7.已知角α的顶点与平面直角坐标系的原点重合,始边与x 轴非负半轴重合,终边经过点(1,P ,则cos α=(A)(B) 12-(C)12(D)8.若将函数sin()3y x π=-图象上各点的横坐标变为原来的2倍,纵坐标不变,则所得图象对应的函数解析式为(A) 1sin()23y x π=-(B) 1sin()26y x π=-(C) sin(2)3y x π=-(D) sin(2)3y x 2π=-9.已知2log 0()(10)0x x f x f x x >⎧=⎨+⎩,,,,≤则(2016)f -的值为(A) 1 (B) 2(C) 3(D)4gkstkCom 10.点P 从点O 出发,按逆时针方向沿周长为l 的图形运动一周,O ,P 两点连线的距离y 与点P 走过的路程x 的函数关系如右图所示,那么点P 所走的图形可能是11.函数2()2x f x x =-的零点个数为(A) 0个(B) 1个(C) 2个(D) 3个12.设函数31()411x x f x x x ⎧>=⎨-⎩,,,,≤则满足()(())3f a f f a =的实数a 的取值范围是(A) 1[)2+∞,(B) 2[)3+∞,(C) (1)+∞,(D) [1)+∞,第Ⅱ卷(非选择题 共90分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目指示的答题区域内作答。
