2019年高考数学一轮复习学案+训练+课件(北师大版文科): 单元评估检测2 函数、导数及其应用 文 北师大版
2019年高考数学一轮复习学案+训练+课件(北师大版文科): 坐标系与参数方程 第2节 参数方程学案 文

第二节 参数方程[考纲传真] 1.了解参数方程,了解参数的意义.2.能选择适当的参数写出直线、圆和椭圆曲线的参数方程.(对应学生用书第161页)[基础知识填充]1.曲线的参数方程一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x ,y 都是某个变数t 的函数Error!并且对于t 的每一个允许值,由这个方程组所确定的点M (x ,y )都在这条曲线上,那么这个方程组就叫做这条曲线的参数方程,联系变数x ,y 的变数t 叫做参变数,简称参数.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式.一般地,可以通过消去参数从参数方程得到普通方程.(2)如果知道变数x ,y 中的一个与参数t 的关系,例如x =f (t ),把它代入普通方程,求出另一个变数与参数的关系y =g (t ),那么Error!就是曲线的参数方程.3.常见曲线的参数方程和普通方程点的轨迹普通方程参数方程直线y -y 0=tan α(x -x 0)Error!(t 为参数)圆x 2+y 2=r 2Error!(θ为参数)椭圆+=1(a >b >0)x 2a 2y 2b 2Error!(φ为参数)温馨提示:在直线的参数方程中,参数t 的系数的平方和为1时,t 才有几何意义且几何意义为:|t |是直线上任一点M (x ,y )到M 0(x 0,y 0)的距离.[基本能力自测]1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)参数方程Error!中的x ,y 都是参数t 的函数.( )(2)过M 0(x 0,y 0),倾斜角为α的直线l 的参数方程为Error!(t 为参数).参数t 的几何意义表示:直线l 上以定点M 0为起点,任一点M (x ,y )为终点的有向线段的数M 0M→量.( )(3)方程Error!表示以点(0,1)为圆心,以2为半径的圆.( )(4)已知椭圆的参数方程Error!(t 为参数),点M 在椭圆上,对应参数t =,点O 为原π3点,则直线OM .( )3[答案] (1)√ (2)√ (3)√ (4)×2.(教材改编)曲线Error!(θ为参数)的对称中心( )A .在直线y =2x 上B .在直线y =-2x 上C .在直线y =x -1上D .在直线y =x +1上B [由Error!得Error!所以(x +1)2+(y -2)2=1.曲线是以(-1,2)为圆心,1为半径的圆,所以对称中心为(-1,2),在直线y =-2x 上.]3.(教材改编)在平面直角坐标系中,曲线C :Error!(t 为参数)的普通方程为________.x -y -1=0 [由x =2+t ,且y =1+t ,2222消去t ,得x -y =1,即x -y -1=0.]4.在平面直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.曲线C 1的极坐标方程为ρ(cos θ+sin θ)=-2,曲线C 2的参数方程为Error!(t 为参数),则C 1与C 2交点的直角坐标为________.(2,-4) [由ρ(cos θ+sin θ)=-2,得x +y =-2.①由Error!消去t 得y 2=8x .②联立①②得Error!即交点坐标为(2,-4).]5.(2016·江苏高考)在平面直角坐标系xOy 中,已知直线l 的参数方程为Error!(t 为参数),椭圆C 的参数方程为Error!(θ为参数).设直线l 与椭圆C 相交于A ,B 两点,求线段AB 的长. 【导学号:00090372】[解] 椭圆C 的普通方程为x 2+=1.2分y 24将直线l 的参数方程Error!代入x 2+=1,得2+=1,即7t 2+16t =0,y 24(1+12t)(32t )24解得t 1=0,t 2=-,所以AB =|t 1-t 2|=.10分167167(对应学生用书第162页)参数方程与普通方程的互化 已知直线l 的参数方程为Error!(t 为参数),圆C 的参数方程为Error!(θ为参数).(1)求直线l 和圆C 的普通方程;(2)若直线l 与圆C 有公共点,求实数a 的取值范围.[解] (1)直线l 的普通方程为2x -y -2a =0,2分圆C 的普通方程为x 2+y 2=16.4分(2)因为直线l 与圆C 有公共点,故圆C 的圆心到直线l 的距离d =≤4,8分|-2a |5解得-2≤a ≤2.10分55[规律方法] 1.将参数方程化为普通方程,消参数常用代入法、加减消元法、三角恒等变换消去参数.2.把参数方程化为普通方程时,要注意哪一个量是参数,并且要注意参数的取值对普通方程中x 及y 的取值范围的影响,要保持同解变形.[变式训练1] 在平面直角坐标系xOy 中,若直线l :Error!(t 为参数)过椭圆C :Error!(φ为参数)的右顶点,求常数a 的值.[解] 直线l 的普通方程为x -y -a =0,椭圆C 的普通方程为+=1,4分x 29y 24所以椭圆C 的右顶点坐标为(3,0),若直线l 过椭圆的右顶点(3,0),则3-0-a =0,所以a =3.10分参数方程的应用 (2018·合肥模拟)已知曲线C :+=1,直线l :Error!(t 为参数).x 24y 29(1)写出曲线C 的参数方程,直线l 的普通方程;(2)过曲线C 上任意一点P 作与l 夹角为30°的直线,交l 于点A ,求|PA |的最大值与最小值.[解] (1)曲线C 的参数方程为Error!(θ为参数).直线l 的普通方程为2x +y -6=0.4分(2)曲线C 上任意一点P (2cosθ,3sin θ)到l 的距离为d =|4cos θ+3sin55θ-6|,则|PA |==|5sin(θ+α)-6|,其中α为锐角,且tan α=.8分d sin 30°25543当sin(θ+α)=-1时,|PA |取得最大值,最大值为.2255当sin(θ+α)=1时,|PA |取得最小值,最小值为.10分255[规律方法] 1.解决直线与圆的参数方程的应用问题时,一般是先化为普通方程,再根据直线与圆的位置关系来解决问题.2.对于形如Error!(t 为参数),当a 2+b 2≠1时,应先化为标准形式后才能利用t 的几何意义解题.[变式训练2] (2017·石家庄质检)在平面直角坐标系xOy 中,圆C 的参数方程为Error!(θ为参数),直线l 经过点P (1,2),倾斜角α=.π6(1)写出圆C 的普通方程和直线l 的参数方程;(2)设直线l 与圆C 相交于A ,B 两点,求|PA |·|PB |的值. 【导学号:00090373】[解] (1)由Error!消去θ,得圆C 的普通方程为x 2+y 2=16.2分又直线l 过点P (1,2)且倾斜角α=,π6所以l 的参数方程为Error!即Error!(t 为参数).4分(2)把直线l 的参数方程Error!代入x 2+y 2=16,得2+2=16,t 2+(+2)t -11=0,(1+32t)(2+12t )3所以t 1t 2=-11,8分由参数方程的几何意义,|PA |·|PB |=|t 1t 2|=11.10分参数方程与极坐标方程的综合应用 (2017·全国卷Ⅲ)在直角坐标系xOy 中,直线l 1的参数方程为Error!(t 为参数),直线l 2的参数方程为Error!(m 为参数).设l 1与l 2的交点为P ,当k 变化时,P 的轨迹为曲线C .(1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l 3:ρ(cos θ+sin θ)-=0,M 为l 3与C 的交点,求M 的极径.2[解] (1)消去参数t 得l 1的普通方程l 1:y =k (x -2);1分消去参数m 得l 2的普通方程l 2:y =(x +2).2分1k 设P (x ,y ),由题设得Error!消去k 得x 2-y 2=4(y ≠0).所以C 的普通方程为x 2-y 2=4(y ≠0).4分(2)C 的极坐标方程为ρ2(cos 2θ-sin 2θ)=4(0<θ<2π,θ≠π).5分联立Error!得cos θ-sin θ=2(cos θ+sin θ).6分故tan θ=-,从而cos 2θ=,sin 2θ=.8分13910110代入ρ2(cos 2θ-sin 2θ)=4得ρ2=5,所以交点M 的极径为.10分5[规律方法] 1.参数方程和极坐标方程的综合题,求解的一般方法是分别化为普通方程和直角坐标方程后求解.当然,还要结合题目本身特点,确定选择何种方程.2.数形结合的应用,即充分利用参数方程中参数的几何意义,或者利用ρ和θ的几何意义,直接求解,可化繁为简.[变式训练3] (2016·全国卷Ⅲ)在直角坐标系xOy 中,曲线C 1的参数方程为Error!(α为参数).以坐标原点为极点,以x 轴的正半轴为极轴,建立极坐标系,曲线C 2的极坐标方程为ρsin=2.(θ+π4)2(1)写出C 1的普通方程和C 2的直角坐标方程;(2)设点P 在C 1上,点Q 在C 2上,求|PQ |的最小值及此时P 的直角坐标.[解] (1)C 1的普通方程为+y 2=1,2分x 23由于曲线C 2的方程为ρsin=2,(θ+π4)2所以ρsin θ+ρcos θ=4,因此曲线C 2的直角坐标方程为x +y -4=0.4分(2)由题意,可设点P 的直角坐标为(cos α,sin α).3因为C 2是直线,所以|PQ |的最小值即为P 到C 2的距离d (α)的最小值,8分又d (α)==,|3cos α+sin α-4|22|s in (α+π3)-2|当且仅当α=2k π+(k ∈Z )时,d (α)取得最小值,最小值为,此时P 的直角坐标π62为.10分(32,12)。
【小初高学习】2019年高考数学一轮复习学案+训练+课件(北师大版文科): 第2章 函数、导数及其应

第三节函数的奇偶性与周期性[考纲传真] 1.了解函数奇偶性的含义.2.会运用基本初等函数的图像分析函数的奇偶性.3.了解函数周期性、最小正周期的含义,会判断、应用简单函数的周期性.(对应学生用书第11页)[基础知识填充]1.奇函数、偶函数的概念图像关于原点对称的函数叫作奇函数.图像关于y轴对称的函数叫作偶函数.2.判断函数的奇偶性判断函数的奇偶性,一般都按照定义严格进行,一般步骤是(1)考察定义域是否关于原点对称.(2)考察表达式f(-x)是否等于f(x)或-f(x):若f(-x)=-f(x),则f(x)为奇函数;若f(-x)=f(x),则f(x)为偶函数;若f(-x)=-f(x)且f(-x)=f(x),则f(x)既是奇函数又是偶函数;若f(-x)≠-f(x)且f(-x)≠f(x),则f(x)既不是奇函数又不是偶函数,既非奇非偶函数.3.函数的周期性(1)周期函数:对于函数f(x),如果存在非零实数T,对定义域内的任意一个x,都有f(x+T)=f(x),就把f(x)称为周期函数,T称为这个函数的周期.(2)最小正周期:如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期.[知识拓展]1.函数奇偶性常用结论(1)如果函数f(x)是偶函数,那么f(x)=f(|x|).(2)奇函数在两个对称的区间上具有相同的单调性;偶函数在两个对称的区间上具有相反的单调性.(3)在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.2.函数周期性常用结论对f(x)定义域内任一自变量的值x:(1)若f(x+a)=-f(x),则T=2a(a>0).(2)若f (x +a )=1f x,则T =2a (a >0). (3)若f (x +a )=-1f x,则T =2a (a >0).[基本能力自测]1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)偶函数图像不一定过原点,奇函数的图像一定过原点.( )(2)若函数y =f (x +a )是偶函数,则函数y =f (x )关于直线x =a 对称.( ) (3)若函数y =f (x +b )是奇函数,则函数y =f (x )关于点(b,0)中心对称.( ) (4)函数f (x )在定义域上满足f (x +a )=-f (x ),则f (x )是周期为2a (a >0)的周期函数.( )[答案] (1)× (2)√ (3)√ (4)√2.已知f (x )=ax 2+bx 是定义在[a -1,2a ]上的偶函数,那么a +b 的值是( ) A .-13B .13C .12D .-12B [依题意b =0,且2a =-(a -1), ∴b =0且a =13,则a +b =13.]3.(2015·广东高考)下列函数中,既不是奇函数,也不是偶函数的是( ) A .y =x +sin 2x B .y =x 2-cos x C .y =2x+12D .y =x 2+sin xD [A 项,定义域为R ,f (-x )=-x -sin 2x =-f (x ),为奇函数,故不符合题意; B 项,定义域为R ,f (-x )=x 2-cos x =f (x ),为偶函数,故不符合题意; C 项,定义域为R ,f (-x )=2-x +12-x =2x+12x =f (x ),为偶函数,故不符合题意;D 项,定义域为R ,f (-x )=x 2-sin x ,-f (x )=-x 2-sin x ,因为f (-x )≠-f (x ),且f (-x )≠f (x ),故为非奇非偶函数.]4.(2017·全国卷Ⅱ)已知函数f (x )是定义在R 上的奇函数,当x ∈(-∞,0)时,f (x )=2x 3+x 2,则f (2)=________. 12 [法一:令x >0,则-x <0. ∴f (-x )=-2x 3+x 2.∵函数f (x )是定义在R 上的奇函数, ∴f (-x )=-f (x ).∴f (x )=2x 3-x 2(x >0). ∴f (2)=2×23-22=12. 法二:f (2)=-f (-2)=-[2×(-2)3+(-2)2]=12.]5.(教材改编)已知函数f (x )是奇函数,在(0,+∞)上是减函数,且在区间[a ,b ](a <b <0)上的值域为[-3,4],则在区间[-b ,-a ]上( ) A .有最大值4 B .有最小值-4 C .有最大值-3D .有最小值-3B [法一:根据题意作出y =f (x )的简图,由图知,选B .法二:当x ∈[-b ,-a ]时,-x ∈[a ,b ], 由题意得f (b )≤f (-x )≤f (a ), 即-3≤-f (x )≤4, ∴-4≤f (x )≤3,即在区间[-b ,-a ]上f (x )min =-4,f (x )max =3,故选B .](对应学生用书第12页)(1)f (x )=(x +1)1-x1+x; (2)f (x )=lg(1+4x 2-2x ); (3)f (x )=3-x 2+x 2-3;(4)f (x )=⎩⎪⎨⎪⎧x 2+x ,x >0,x 2-x ,x <0.【导学号:00090021】[解] (1)由1-x1+x ≥0可得函数的定义域为(-1,1].∵函数定义域不关于原点对称, ∴函数为非奇非偶函数.(2)函数的定义域为R ,且f (-x )=lg(1+4x 2+2x )=lg ⎝ ⎛⎭⎪⎫11+4x 2-2x =-lg(1+4x 2-2x )=-f (x ). 故原函数为奇函数.(3)由⎩⎪⎨⎪⎧3-x 2≥0,x 2-3≥0,得x 2=3,∴x =±3,即函数f (x )的定义域为{-3,3}, 从而f (x )=3-x 2+x 2-3=0. 因此f (-x )=-f (x )且f (-x )=f (x ), ∴函数f (x )既是奇函数又是偶函数.(4)易知函数的定义域为(-∞,0)∪(0,+∞),关于原点对称,又当x >0时,f (x )=x 2+x ,则当x <0时,-x >0, 故f (-x )=x 2-x =f (x );当x <0时,f (x )=x 2-x ,则当x >0时,-x <0, 故f (-x )=x 2+x =f (x ),故原函数是偶函数. [规律方法] 1.利用定义判断函数奇偶性的步骤:2.判断分段函数的奇偶性应分段分别证明f (-x )与f (x )的关系,只有对各段上的x 都满足相同的关系时,才能判断其奇偶性;也可以利用函数的图像进行判断. [变式训练1] (1)(2018·商丘模拟)已知函数f (x )=ln(e +x )+ln(e -x ),则f (x )是( )A .奇函数,且在(0,e)上是增加的B .奇函数,且在(0,e)上是减少的C .偶函数,且在(0,e)上是增加的D .偶函数,且在(0,e)上是减少的(2)(2014·全国卷Ⅰ)设函数f (x ),g (x )的定义域都为R ,且f (x )是奇函数,g (x )是偶函数,则下列结论中正确的是( ) 【导学号:00090022】 A .f (x )g (x )是偶函数B .|f (x )|g (x )是奇函数C .f (x )|g (x )|是奇函数D .|f (x )g (x )|是奇函数(1)D (2)C [(1)f (x )的定义域为(-e ,e),关于原点对称.f (-x )=ln(e -x )+ln(e +x )=f (x ),∴函数f (x )是偶函数.又f (x )=ln(e 2-x 2),所以f (x )在(0,e)上是减少的.(2)A :令h (x )=f (x )·g (x ),则h (-x )=f (-x )·g (-x )=-f (x )·g (x )=-h (x ), ∴h (x )是奇函数,A 错.B :令h (x )=|f (x )|g (x ),则h (-x )=|f (-x )|g (-x )=|-f (x )|·g (x )=|f (x )|g (x )=h (x ),∴h (x )是偶函数,B 错.C :令h (x )=f (x )|g (x )|,则h (-x )=f (-x )|g (-x )|=-f (x )|·g (x )|=-h (x ),∴h (x )是奇函数,C 正确.D :令h (x )=|f (x )·g (x )|,则h (-x )=|f (-x )·g (-x )|=|-f (x )·g (x )|=|f (x )·g (x )|=h (x ), ∴h (x )是偶函数,D 错.]a =________. (2)已知f (x )是定义在R 上的奇函数,当x >0时,f (x )=x 2-4x ,则f (x )=________.(1)1 (2)⎩⎪⎨⎪⎧x 2-4x ,x >0,0,x =0,-x 2-4x ,x <0[(1)∵f (x )为偶函数,∴f (-x )-f (x )=0恒成立,∴-x ln(-x +a +x 2)-x ln(x +a +x 2)=0恒成立, ∴x ln a =0恒成立,∴ln a =0,即a =1. (2)∵f (x )是定义在R 上的奇函数,∴f (0)=0.又当x <0时,-x >0,∴f (-x )=x 2+4x .又f (x )为奇函数, ∴f (-x )=-f (x ), 即f (x )=-x 2-4x (x <0),∴f (x )=⎩⎪⎨⎪⎧x 2-4x ,x >0,0,x =0,-x 2-4x ,x <0.][规律方法] 1.已知函数的奇偶性求参数,一般采用待定系数法求解,根据f (x )±f (x )=0得到关于待求参数的恒等式,由系数的对等性得参数的值或方程(组),进而得出参数的值.2.已知函数的奇偶性求函数值或解析式,将待求区间上的自变量转化到已知区间上,再利用奇偶性求出,或充分利用奇偶性得出关于f (x )的方程(组),从而可得f (x )的值或解析式.[变式训练2] (1)设f (x )为定义在R 上的奇函数.当x ≥0时,f (x )=2x+2x +b (b 为常数),则f (-1)=( ) A .-3 B .-1 C .1D .3(2)(2018·青岛模拟)若f (x )=ln(e 3x+1)+ax 是偶函数,则a =________.(1)A (2)-32 [(1)因为f (x )为定义在R 上的奇函数,所以有f (0)=20+2×0+b =0,解得b =-1,所以当x ≥0时,f (x )=2x +2x -1,所以f (-1)=-f (1)=-(21+2×1-1)=-3. (2)f (-x )=ln(e-3x+1)-ax =ln 1+e 3xe3x -ax =ln(1+e 3x)-3x -ax ,依题意得,对任意x∈R ,都有f (-x )=f (x ),即ln(1+e 3x)-3x -ax =ln(1+e 3x)+ax , 化简得2ax +3x =0(x ∈R ),因此2a +3=0,解得a =-32.](1)(201=f (x -2).若当x ∈[-3,0]时,f (x )=6-x ,则f (919)=________.(2)设定义在R 上的函数f (x )满足f (x +2)=f (x ),且当x ∈[0,2)时,f (x )=2x -x 2,则f (0)+f (1)+f (2)+…+f (2 017)=________.(1)6 (2)1 009 [(1)∵f (x +4)=f (x -2), ∴f ((x +2)+4)=f ((x +2)-2),即f (x +6)=f (x ), ∴f (x )是周期为6的周期函数, ∴f (919)=f (153×6+1)=f (1). 又f (x )是定义在R 上的偶函数, ∴f (1)=f (-1)=6,即f (919)=6.(2)∵f (x +2)=f (x ),∴函数f (x )的周期T =2.又当x ∈[0,2)时,f (x )=2x -x 2,∴f (0)=0,f (1)=1,f (0)+f (1)=1. ∴f (0)+f (1)=f (2)+f (3)=f (4)+f (5)=…=f (2 016)+f (2 017)=1, ∴f (0)+f (1)+f (2)+…+f (2 017)=1 009.][母题探究1] 若将本例(2)中“f (x +2)=f (x )”改为“f (x +1)=-f (x )”,则结论如何?[解] ∵f (x +1)=-f (x ),∴f (x +2)=f [(x +1)+1]=-f (x +1)=f (x ). 故函数f (x )的周期为2.由本例可知,f (0)+f (1)+f (2)+…+f (2 017)=1 009. [母题探究2] 若将本例(2)中“f (x +2)=f (x )”改为“f (x +1)=1f x”,则结论如何?[解] ∵f (x +1)=1f x,∴f (x +2)=f [(x +1)+1]=1fx +=f (x ).故函数f (x )的周期为2.由本例可知,f (0)+f (1)+f (2)+…+f (2 017)=1 009.[规律方法] 1.判断函数的周期只需证明f (x +T )=f (x )(T ≠0)便可证明函数是周期函数,且周期为T ,根据函数的周期性,可以由函数局部的性质得到函数的整体性质. 2.在解决具体问题时,要注意“若T 是函数的周期,则kT (k ∈Z 且k ≠0)也是函数的周期”的应用.[变式训练3] (2017·长沙模拟(一))已知定义在R 上的函数f (x )满足f (x +1)=-f (x ),且f (x )=⎩⎪⎨⎪⎧1,-1<x ≤0,-1,0<x ≤1,则下列函数值为1的是( )A .f (2.5)B .f (f (2.5))C .f (f (1.5))D .f (2)D [由f (x +1)=-f (x )知f (x +2)=-f (x +1)=f (x ),于是f (x )是以2为周期的周期函数,从而f (2.5)=f (0.5)=-1,f (f (2.5))=f (-1)=f (1)=-1,f (f (1.5))=f (f (-0.5))=f (1)=-1,f (2)=f (0)=1,故选D .]。
2019年高考数学一轮复习学案 训练 课件(北师大版文科) 第2章 函数、导数及其应用 第2节 函数的单调性与最
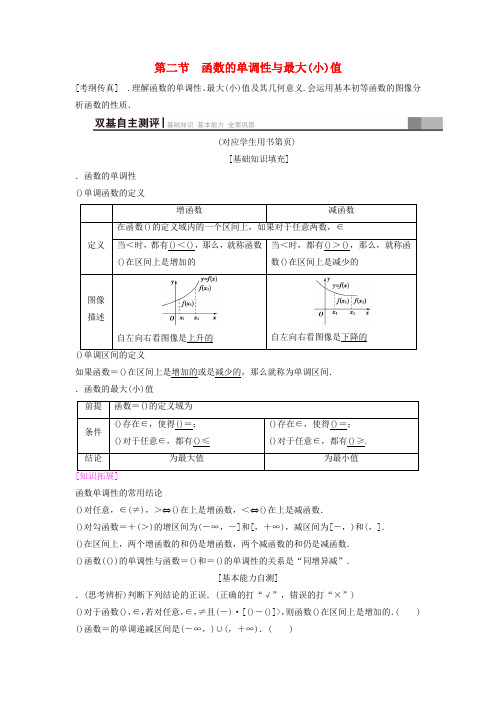
第二节 函数的单调性与最大(小)值[考纲传真] .理解函数的单调性、最大(小)值及其几何意义.会运用基本初等函数的图像分析函数的性质.(对应学生用书第页)[基础知识填充].函数的单调性()单调函数的定义如果函数=()在区间上是增加的或是减少的,那么就称为单调区间..函数的最大(小)值函数单调性的常用结论()对任意,∈(≠),>⇔()在上是增函数,<⇔()在上是减函数.()对勾函数=+(>)的增区间为(-∞,-]和[,+∞),减区间为[-,)和(,].()在区间上,两个增函数的和仍是增函数,两个减函数的和仍是减函数.()函数(())的单调性与函数=()和=()的单调性的关系是“同增异减”.[基本能力自测].(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)()对于函数(),∈,若对任意,∈,≠且(-)·[()-()]>,则函数()在区间上是增加的.( )()函数=的单调递减区间是(-∞,)∪(,+∞).( )()函数=在上是增加的.( )()函数=-在区间[,+∞)上是增加的,则函数=-的单调递增区间为[,+∞).( ) [答案]()√()×()×()×.(·深圳二次调研)下列四个函数中,在定义域上不是单调函数的是( ).=.=.=.=[选项,中函数在定义域内均为单调递增函数,选项为在定义域内为单调递减函数,选项中,设<(,≠),则-=-=,因为-<,当,同号时>,-<,当,异号时<,->,所以函数=在定义域上不是单调函数,故选.].(教材改编)已知函数()=,∈[],则()的最大值为,最小值为.[可判断函数()=在[]上为减函数,所以()=()=,()=()=.].函数=(+)+在上是减函数,则的取值范围是.[由题意知+<,得<-.].()=-,∈[-]的单调增区间为,()=.[][()=(-)-,故()的单调增区间为[],()=(-)=.](对应学生用书第页).(-∞,-) .(-∞,).(,+∞).(,+∞)()试讨论函数()=+(>)的单调性.【导学号:】() [由-->,得>或<-.设=--,则=在∈(,+∞)上为增函数.欲求函数()的单调递增区间,即求函数=--的单调递增区间.∵函数=--的单调递增区间为(,+∞),∴函数()的单调递增区间为(,+∞).故选.]()法一:由解析式可知,函数的定义域是(-∞,)∪(,+∞).在(,+∞)内任取,,令<<,那么()-()=-=(-)+=(-)·.因为<<,所以->,>.故当,∈(,+∞)时,()<(),即函数在(,+∞)上是增加的.。
2019年高考数学一轮复习学案+训练+课件(北师大版文科):重点强化训练2平面向量文北师大版_36

重点强化训练(二) 平面向量A组 基础达标(建议用时:30分钟)一、选择题1.(2017·石家庄模拟)已知a,b是两个非零向量,且|a+b|=|a|+|b|,则下列说法正确的是 ( )A.a+b=0B.a=bC.a与b共线反向D.存在正实数λ,使a=λbD [因为a,b是两个非零向量,且|a+b|=|a|+|b|.则a与b共线同向,故D正确.]2.若a,b,c均为单位向量,且a·b=0,(a-c)·(b-c)≤0,则|a+b-c|的最大值为( ) 【导学号:00090149】2A.-1 B.1 2C. D.2B [因为|a|=|b|=|c|=1,a·b=0,所以|a+b|2=a2+b2+2a·b=2,故|a+b|=2.展开(a-c)·(b-c)≤0,得a·b-(a+b)·c+c2≤0,即0-(a+b)·c+1≤0,整理,得(a+b)·c≥1.而|a+b-c|2=(a+b)2-2(a+b)·c+c2=3-2(a+b)·c,所以3-2(a+b)·c≤3-2×1=1.所以|a+b-c|2≤1,即|a+b-c|≤1.]3.(2016·北京高考)设a,b是向量,则“|a|=|b|”是“|a+b|=|a-b|”的( ) A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件D [若|a|=|b|成立,则以a,b为邻边的平行四边形为菱形.a+b,a-b表示的是该菱形的对角线,而菱形的两条对角线长度不一定相等,所以|a+b|=|a-b|不一定成立,从而不是充分条件;反之,若|a+b|=|a-b|成立,则以a,b为邻边的平行四边形为矩形,而矩形的邻边长度不一定相等,所以|a|=|b|不一定成立,从而不是必要条件.故“|a|=|b|”是“|a+b|=|a-b|”的既不充分也不必要条件.]4.在平面直角坐标系中,已知O是坐标原点,A(3,0),B(0,3),C(cos α,sin α),若|+|=,α∈(0,π),则与的夹角为( )OA → OC → 13OB → OC → A . B . π6π3C .πD .π2356A [由题意,得+=(3+cos α,sin α),OA → OC→ 所以|+|=OA → OC→ 3+cos α 2+sin2α==,10+6cos α13即cos α=,12因为α∈(0,π),所以α=,C .π3(12,32)设与的夹角为θ,OB → OC→ 则cos θ===.OB → ·OC → |OB →|·|OC →|3233×132因为θ∈[0,π],所以θ=.]π65.已知直线ax +by +c =0与圆O :x 2+y 2=1相交于A ,B 两点,且AB =,则·的3OA → OB→ 值是 ( )A .- B .1212C .-D .034A [取AB 的中点C ,连接OC ,AB =,3则AC =,又因为OA =1,32所以sin =sin∠AOC ==,(12∠AOB)AC OA 32所以∠AOB =120°,则·=1×1×cos 120°=-.]OA → OB→12二、填空题6.设O 是坐标原点,已知=(k,12),=(10,k ),=(4,5),若A ,B ,C 三点共线,OA → OB → OC→ 则实数k 的值为________.11或-2 [由题意得=-=(k -4,7),CA → OA → OC→ =-=(6,k -5),CB → OB → OC → 所以(k -4)(k -5)=6×7,k -4=7或k -4=-6,即k =11或k =-2.]7.(2018·黄冈模拟)已知两个平面向量a ,b 满足|a |=1,|a -2b |=,且a 与b 的夹21角为120°,则|b |=________. 【导学号:00090150】2 [由|a -2b |=得a 2-4a·b +4b 2=21.21即1+2|b |+4|b |2=21,解得|b |=2或|b |=-(舍).]528.已知点A ,B ,C 满足||=3,||=4,||=5,AB → BC → CA→ 则·+·+·=________.AB → BC → BC → CA → CA → AB→ -25 [由||2+||2=||2得∠B =90°,cos C =,cos A =,·=0,·AB → BC → CA → 4535AB → BC → BC →=4×5×=-16,·=5×3×=-9,所CA → (-45)CA → AB → (-35)以·+·+·=-25.]AB → BC → BC → CA → CA → AB→三、解答题9.在直角坐标系xOy 中,已知点A (1,1),B (2,3),C (3,2),点P (x ,y )在△ABC 三边围成的区域(含边界)上,且=m +n (m ,n ∈R ).OP → AB → AC→ (1)若m =n =,求||;23OP→(2)用x ,y 表示m -n ,并求m -n 的最大值.[解] (1)∵m =n =,=(1,2),=(2,1),23AB → AC→ ∴=(1,2)+(2,1)=(2,2),3分OP→ 2323∴||==2.5分OP→ 22+222(2)∵=m (1,2)+n (2,1)=(m +2n,2m +n ),OP→ ∴Error!8分两式相减,得m -n =y -x .令y -x =t ,由图知,当直线y =x +t 过点B (2,3)时,t 取得最大值1,故m -n 的最大值为1.12分10.设向量a =(sin x ,sin x ),b =(cos x ,sin x ),x ∈.3[0,π2](1)若|a |=|b |,求x 的值;(2)设函数f (x )=a ·b ,求f (x )的最大值.【导学号:00090151】[解] (1)由|a |2=(sin x )2+(sin x )2=4sin 2x ,3|b |2=(cos x )2+(sin x )2=1,及|a |=|b |,得4sin 2x =1.3分又x ∈,从而sin x =,所以x =.5分[0,π2]12π6(2)f (x )=a ·b =sin x ·cos x +sin 2x 3=sin 2x -cos 2x +=sin+,8分321212(2x -π6)12当x =∈时,sin 取最大值1.π3[0,π2](2x -π6)所以f (x )的最大值为.12分32B 组 能力提升(建议用时:15分钟)1.(2018·兰州模拟)已知向量a ,b 的夹角为60°,且|a |=2,|b |=3,设=a ,=b ,=m a -2b ,若△ABC 是以BC 为斜边的直角三角形,则m =( )OA → OB → OC → 【导学号:00090152】A .-4B .3C .-11D .10C [a ·b =2×3×cos 60°=3,=-=b -a ,=-OA =(m -1)a -2B .AB → OB → OA → AC → OC → ∵AB ⊥AC ,∴·=0,AB → AC→即(b -a )·[(m -1)a -2b ]=0,∴(1-m )a 2-2b 2+(m -1)a ·b +2a ·b =0,即4(1-m )-18+3(m -1)+6=0,解得m =-11.故选C .]2.如图2,菱形ABCD 的边长为2,∠BAD =60°,M 为DC 的中点,若N 为菱形内任意一点(含边界),则·的最大值为________.AM → AN→图29 [由平面向量的数量积的几何意义知,·等于与在方向上的投影AM → AN → AM → AN → AM→ 之积,所以(·)max =·=·(+)=2+2+·=9.]AM → AN → AM → AC→ (12AB → +AD → )AB → AD → 12AB → AD → 32AB → AD → 3.已知函数f (x )=a ·b ,其中a =(2cos x ,-sin 2x ),b =(cos x,1),x ∈R .3(1)求函数y =f (x )的单调递减区间;(2)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,f (A )=-1,a =,且向量7m =(3,sin B )与n =(2,sin C )共线,求边长b 和c 的值.[解] (1)f (x )=a ·b =2cos 2x -sin 2x =1+cos2x -sin332x =1+2cos,2分(2x +π3)令2k π≤2x +≤2k π+π(k ∈Z ),π3解得k π-≤x ≤k π+(k ∈Z ),π6π3∴f (x )的单调递减区间为(k ∈Z ).5分[k π-π6,k π+π3](2)∵f (A )=1+2cos =-1,(2A +π3)∴cos=-1.7分(2A +π3)又<2A +<,∴2A +=π,即A =.9分π3π37π3π3π37∵a=,由余弦定理得a2=b2+c2-2bc cos A=(b+c)2-3bc=7.①∵向量m=(3,sin B)与n=(2,sin C)共线,∴2sin B=3sin C.由正弦定理得2b=3c,②由①②可得b=3,c=2.12分。
【K12教育学习资料】2019年高考数学一轮复习学案+训练+课件(北师大版文科): 第2章 函数、导

第十二节导数与函数的极值、最值[考纲传真] 1.了解函数在某点取得极值的必要条件和充分条件.2.会用导数求函数的极大值、极小值(其中多项式函数不超过三次).3.会求闭区间上函数的最大值、最小值(其中多项式函数不超过三次).(对应学生用书第34页)[基础知识填充]1.函数的极值与导数(1)极值点与极值设函数f(x)在点x0及附近有定义,且在x0两侧的单调性相反或导数值异号,则x0为函数f(x)的极值点,f(x0)为函数的极值.(2)极大值点与极小值点①若先增后减(导数值先正后负),则x0为极大值点;②若先减后增(导数值先负后正),则x0为极小值点.(3)求可导函数极值的步骤:①求f′(x);②求方程f′(x)=0的根;③检查f′(x)在方程f′(x)=0的根的左右两侧的符号.如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值.2.函数的最值与导数的关系(1)函数f(x)在[a,b]上有最值的条件如果在区间[a,b]上函数y=f(x)的图像是一条连续不断的曲线,那么它必有最大值和最小值.(2)求y=f(x)在[a,b]上的最大(小)值的步骤①求函数y=f(x)在(a,b)内的极值;②将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.[知识拓展]1.对于可导函数f′(x),f′(x)=0是函数f(x)在x=x0处有极值的必要不充分条件.2.求函数在无穷区间(或开区间)上的最值,不仅要研究其极值情况,还要研究其单调性,并通过单调性和极值情况,画出函数的大致图像,然后借助图像观察得到函数的最值.[基本能力自测]1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)函数的极大值一定比极小值大.( )(2)对可导函数f(x),f′(x0)=0是x0为极值点的充要条件.( )(3)函数的最大值不一定是极大值,函数的最小值也不一定是极小值.( )(4)若实际问题中函数定义域是开区间,则不存在最优解.( )[答案](1)×(2)×(3)√(4)×2.(教材改编)函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图像如图2121所示,则函数f(x)在开区间(a,b)内极小值点的个数为( )图2121A.1 B.2C.3 D.4A[导函数f′(x)的图像与x轴的交点中,左侧图像在x轴下方,右侧图像在x轴上方的只有一个,所以f(x)在区间(a,b)内有一个极小值点.]3.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-1x3+81x-234,则使该生产厂家获取最大年利润的年产量为( )3A.13万件B.11万件C.9万件D.7万件C[y′=-x2+81,令y′=0得x=9或x=-9(舍去).当x∈(0,9)时,y′>0,当x∈(9,+∞)时,y′<0,则当x=9时,y有最大值.即使该生产厂家获取最大年利润的年产量为9万件.]4.(2016·四川高考)已知a为函数f(x)=x3-12x的极小值点,则a=( ) A.-4 B.-2C.4 D.2D[由题意得f′(x)=3x2-12,令f′(x)=0得x=±2,∴当x<-2或x>2时,f′(x)>0;当-2<x<2时,f′(x)<0,∴f(x)在(-∞,-2)上是增加的,在(-2,2)上为减函数,在(2,+∞)上是增加的.∴f(x)在x=2处取得极小值,∴a=2.]5.函数y=2x3-2x2在区间[-1,2]上的最大值是________. 【导学号:00090069】8[y′=6x2-4x,令y′=0,得x =0或x =23.∵f (-1)=-4,f (0)=0,f ⎝ ⎛⎭⎪⎫23=-827, f (2)=8,∴最大值为8.](对应学生用书第35页)角度1 设函数f (x )在R 上可导,其导函数为f ′(x ),且函数y =(1-x )f ′(x )的图像如图2122所示,则下列结论中一定成立的是( )图2122A .函数f (x )有极大值f (2)和极小值f (1)B .函数f (x )有极大值f (-2)和极小值f (1)C .函数f (x )有极大值f (2)和极小值f (-2)D .函数f (x )有极大值f (-2)和极小值f (2)D [由题图可知,当x <-2时,f ′(x )>0;当-2<x <1时,f ′(x )<0;当1<x <2时,f ′(x )<0;当x >2时,f ′(x )>0.由此可以得到函数f (x )在x =-2处取得极大值,在x =2处取得极小值.] 角度2 求函数的极值求函数f (x )=x -a ln x (a ∈R )的极值.【导学号:00090070】[解] 由f ′(x )=1-a x =x -ax,x >0知:(1)当a ≤0时,f ′(x )>0,函数f (x )为(0,+∞)上的增函数,函数f (x )无极值;5分(2)当a >0时,由f ′(x )=0,解得x =A .又当x ∈(0,a )时,f ′(x )<0;当x ∈(a ,+∞)时,f ′(x )>0,9分从而函数f (x )在x =a 处取得极小值,且极小值为f (a )=a -a ln a ,无极大值. 综上,当a ≤0时,函数f (x )无极值;当a >0时,函数f (x )在x =a 处取得极小值a -a lna ,无极大值. 12分角度3 已知极值求参数(1)(2018·青岛模拟)若函数f (x )=x (x -c )2在x =2处有极大值,则常数c 的值为( ) A .2 B .6 C .2或6D .-2或-6(2)(2018·广州一模)若函数f (x )=x (x -a )2在x =2处取得极小值,则a =________. (1)B (2)2 [(1)∵函数f (x )=x (x -c )2=x 3-2cx 2+c 2x ,它的导数为f ′(x )=3x 2-4cx +c 2,由题意知,在x =2处的导数值为12-8c +c 2=0,∴c =6,或c =2,又函数f (x )=x (x -c )2在x =2处有极大值,故导数值在x =2处左侧为正数,右侧为负数.当c =2时,f ′(x )=3x 2-8x +4=3⎝ ⎛⎭⎪⎫x -23(x -2),不满足导数值在x =2处左侧为正数,右侧为负数.当c =6时,f ′(x )=3x 2-24x +36=3(x 2-8x +12)=3(x -2)(x -6),满足导数值在x =2处左侧为正数,右侧为负数,故c =6.故选B . (2)求导函数可得f ′(x )=3x 2-4ax +a 2, ∴f ′(2)=12-8a +a 2=0,解得a =2,或a =6,当a =2时,f ′(x )=3x 2-8x +4=(x -2)(3x -2),函数在x =2处取得极小值,符合题意;当a =6时,f ′(x )=3x 2-24x +36=3(x -2)(x -6),函数在x =2处取得极大值,不符合题意,∴a =2.][规律方法] 利用导数研究函数极值的一般流程(1)求f (x )的单调区间;(2)求f (x )在区间[0,1]上的最小值.[解] (1)由f (x )=(x -k )e x ,得f ′(x )=(x -k +1)e x, 令f ′(x )=0,得x =k -1.2分f (x )与f ′(x )的变化情况如下:单调递减单调递增(2)当k -1≤0,即k ≤1时,函数f (x )在[0,1]上是增加的, 所以f (x )在区间[0,1]上的最小值为f (0)=-k , 7分当0<k -1<1,即1<k <2时,由(1)知f (x )在[0,k -1)上是减少的,在(k -1,1]上是增加的, 所以f (x )在区间[0,1]上的最小值为f (k -1)=-ek -1.当k -1≥1,即k ≥2时,函数f (x )在[0,1]上是减少的, 所以f (x )在区间[0,1]上的最小值为f (1)=(1-k )e. 10分综上可知,当k ≤1时,f (x )min =-k ; 当1<k <2时,f (x )min =-ek -1;当k ≥2时,f (x )min =(1-k )e.12分[规律方法] 求函数f (x )在[a ,b ]上的最大值、最小值的步骤: (1)求函数在(a ,b )内的极值;(2)求函数在区间端点的函数值f (a ),f (b );(3)将函数f (x )的极值与f (a ),f (b )比较,其中最大的为最大值,最小的为最小值. [变式训练1] (2018·南昌模拟)函数y =x e -x,x ∈[0,4]的最小值为( ) A .0 B .1e C .4e4D .2e2 A [f ′(x )=1-xe x ,当x ∈[0,1)时,f ′(x )>0,f (x )单调递增,当x ∈(1,4]时,f ′(x )<0,f (x )单调递减,∵f (0)=0,f (4)=4e 4>0,∴当x =0时,f (x )有最小值,且f (0)=0.]与销售价格x (单位:元/千克)满足关系式y =a x -3+10(x -6)2,其中3<x <6,a 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克. (1)求a 的值;(2)若该商品的成本为3元/千克,试确定销售价格x 的值,使商场每日销售该商品所获得的利润最大.【导学号:00090071】[解] (1)因为x =5时,y =11,所以a2+10=11,a =2.5分(2)由(1)可知,该商品每日的销售量为y =2x -3+10(x -6)2, 所以商场每日销售该商品所获得的利润为f (x )=(x -3)⎣⎢⎡⎦⎥⎤2x -3+x -2=2+10(x -3)(x -6)2,3<x <6.7分从而,f ′(x )=10[(x -6)2+2(x -3)(x -6)]=30(x -4)(x -6), 于是,当x 变化时,f ′(x ),f (x )的变化情况如下表:所以,当x =4时,函数f (x )取得最大值,且最大值等于42.即当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.12分 [规律方法] 利用导数解决生活中优化问题的一般步骤(1)设自变量、因变量,建立函数关系式y =f (x ),并确定其定义域; (2)求函数的导数f ′(x ),解方程f ′(x )=0;(3)比较函数在区间端点和f ′(x )=0的点的函数值的大小,最大(小)者为最大(小)值; (4)回归实际问题作答.[变式训练2] 某品牌电动汽车的耗电量y 与速度x 之间有关系y =13x 3-392x 2-40x (x >0),为使耗电量最小,则速度应定为________. 40 [由y ′=x 2-39x -40=0, 得x =-1或x =40, 由于0<x <40时,y ′<0;x >40时,y ′>0.所以当x =40时,y 有最小值.]。
2019高考数学一轮复习学案+训练+课件(北师大版文科): 第2章 函数、导数及其应用 第7节 函数的图像课件

[规律方法] 函数图像的识辨可从以下方面入手: (1)从函数的定义域,判断图像的左右位置;从函数的值域,判断图像的上下 位置; (2)从函数的单调性,判断图像的变化趋势; (3)从函数的奇偶性,判断图像的对称性; (4)从函数的周期性,判断图像的循环往复; (5)从函数的特征点,排除不合要求的图像.
)
【导学号:00090038】
C
[令
f(x)=1-sinco2sx
, x
∵f(1)=1-sinco2s 1>0,f(π)=1-sinco2sππ=0,
∴排除选项 A,D.
由 1-cos x≠0 得 x≠2kπ(k∈Z),
故函数 f(x)的定义域关于原点对称.
又∵f(-x)=1-sinco-s2-xx=-1-sinco2sx x=-f(x),
[变式训练 1] 分别画出下列函数的图像: (1)y=|lg x|;(2)y=sin|x|. [解] (1)∵y=|lg x|=l-g lxg,xx,≥01<,x<1. ∴函数 y=|lg x|的图像,如图①.
(2)当 x≥0 时,y=sin|x|与 y=sin x 的图像完全相同,又 y=sin|x|为偶函数,图 像关于 y 轴对称,其图像如图②.
①
A.甲是图①,乙是图② C.甲是图③,乙是图②
②
③
④
图 2-7-1
B.甲是图①,乙是图④
D.甲是图③,乙是图④
B [设甲骑车速度为 V 甲骑,甲跑步速度为 V 甲跑,乙骑车速度为 V 乙骑,乙跑 步速度为 V 乙跑,依题意 V 甲骑>V 乙骑>V 乙跑>V 甲跑,故选 B.]
3.函数 f(x)的图像向右平移 1 个单位长度,所得图像与曲线 y=ex 关于 y 轴对称,
[知识拓展] 1.一个函数图像的对称关系
2019年高考数学一轮复习学案 训练 课件(北师大版文科)重点强化训练2平面向量文北师大版_36

重点强化训练(二) 平面向量组基础达标(建议用时:分钟)一、选择题.(·石家庄模拟)已知,是两个非零向量,且+=+,则下列说法正确的是 ( ) .+=.=.与共线反向.存在正实数λ,使=λ[因为,是两个非零向量,且+=+.则与共线同向,故正确.].若,,均为单位向量,且·=,(-)·(-)≤,则+-的最大值为( ) 【导学号:】.-...[因为===,·=,所以+=++·=,故+=.展开(-)·(-)≤,得·-(+)·+≤,即-(+)·+≤,整理,得(+)·≥.而+-=(+)-(+)·+=-(+)·,所以-(+)·≤-×=.所以+-≤,即+-≤.].(·北京高考)设,是向量,则“=”是“+=-”的( ).充分而不必要条件.必要而不充分条件.充分必要条件.既不充分也不必要条件[若=成立,则以,为邻边的平行四边形为菱形.+,-表示的是该菱形的对角线,而菱形的两条对角线长度不一定相等,所以+=-不一定成立,从而不是充分条件;反之,若+=-成立,则以,为邻边的平行四边形为矩形,而矩形的邻边长度不一定相等,所以=不一定成立,从而不是必要条件.故“=”是“+=-”的既不充分也不必要条件.].在平面直角坐标系中,已知是坐标原点,(),(),( α,α),若+=,α∈(,π),则与的夹角为( )...π.π[由题意,得+=(+α,α),所以+=α+α)=α)=,即α=,因为α∈(,π),所以α=,.设与的夹角为θ,则θ===.因为θ∈[,π],所以θ=.].已知直线++=与圆:+=相交于,两点,且=,则·的值是 ( ) .-..-.[取的中点,连接,=,则=,又因为=,所以=∠==,所以∠=°,则·=×× °=-.]二、填空题.设是坐标原点,已知=(),=(,),=(),若,,三点共线,则实数的值为.或-[由题意得=-=(-),=-=(,-),所以(-)(-)=×,-=或-=-,即=或=-.].(·黄冈模拟)已知两个平面向量,满足=,-=,且与的夹角为°,则=. 【导学号:】[由-=得-·+=.即++=,解得=或=-(舍).].已知点,,满足=,=,=,则·+·+·=.-[由+=得∠=°,=,=,·=,·=××=-,·=××=-,所以·+·+·=-.]三、解答题。
2019高考数学一轮复习学案+训练+课件(北师大版文科): 第2章 函数、导数及其应用 第8节 函数与方程课件

[变式训练 2] (1)(2015·湖北高考)函数 f(x)=2sin xsinx+π2-x2 的零点个数为
________.
(2)若定义在 R 上的偶函数 f(x)满足 f(x+2)=f(x),且当 x∈[0,1]时,f(x)=x,
则方程 f(x)=log3|x|的解的个数是( )
A.0
B.2
C.4
D.6
(1)2 (2)C [(1)f(x)=2sin xsinx+π2-x2=2sin xcos x-x2=sin 2x-x2,由 f(x) =0,得 sin 2x=x2. 设 y1=sin 2x,y2=x2,在同一平面直角坐标系中画出二者的图像,如图所示.
由图像知,两个函数图像有 2 个交点,故函数 f(x)有两个零点.
loga10>2,
解得 6<a< 10.
故 a 的取值范围是( 6, 10).
[规律方法] 已知函数有零点求参数取值范围常用的方法 (1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定 参数范围; (2)分离参数法:先将参数分离,转化成求函数值域问题加以解决; (3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图 像,然后数形结合求解.
[解] 由 f(x-4)=f(x)知,函数的周期为 4,又函数为偶函数, 所以 f(x-4)=f(x)=f(4-x), 所以函数图像关于 x=2 对称,且 f(2)=f(6)=f(10)=2,要使方程 f(x)=logax 有三个不同的根,
则满足af>6<1,2, f10>2,
a>1, 如图,即loga6<2,
A.y=cos x
B.y=sin x
C.y=ln x
D.y=x2+1
A [由于 y=sin x 是奇函数;y=ln x 是非奇非偶函数,y=x2+1 是偶函数但
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单元评估检测(二)函数、导数及其应用(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设函数f (x )=1-3x+1log 12x +,则函数的定义域为()A .⎝ ⎛⎭⎪⎫-12,0 B .⎝ ⎛⎭⎪⎫-12,+∞C .⎝ ⎛⎭⎪⎫-12,0∪(0,+∞) D .⎝ ⎛⎭⎪⎫-12,2 A2.已知函数f (x )=⎩⎪⎨⎪⎧log 12x ,x >0,3x ,x ≤0,则f (f (4))的值为()A .-19B .-9C .19D .9C3.设a =log 37,b =21.1,c =0.83.1,则() A .b <a <c B .a <c <b C .c <b <a D .c <a <bD4.下列函数中,在(-1,1)内有零点且单调递增的是() A .y =log 2x B .y =2x-1 C .y =x 2-2 D .y =-x 3B5.函数y =a -a x(a >0,a ≠1)的定义域和值域都是[0,1],则log a 56+log a 485=()A .1B .2C .3D .4C6.设函数f (x )是定义在R 上的奇函数,且f (x )=⎩⎪⎨⎪⎧log 2x +,x ≥0,g x ,x <0,则g (f (-7))=()A .3B .-3C .2D .-2D7.某商场销售A 型商品,已知该商品的进价是每件3元,且销售单价与日均销售量的关系如表所示:/件)应为() A .4 B .5.5 C .8.5 D .10C8.函数y =1ln|e x -e -x |的部分图象大致为()D9.过点(-1,0)作抛物线y =x 2+x +1的切线,则其中一条切线为() A .2x +y +2=0 B .3x -y +3=0 C .x +y +1=0 D .x -y +1=0D10.已知a 是常数,函数f (x )=13x 3+12(1-a )x 2-ax +2的导函数y =f ′(x )的图象如图1所示,则函数g (x )=|a x-2|的图象可能是()图1D11.若函数f (x )=1+2x +12x +1+sin x 在区间[-k ,k ](k >0)上的值域为[m ,n ],则m +n =()A .0B .1C .2D .4D12.设定义在R 上的函数f (x )是最小正周期为2π的偶函数,f ′(x )是f (x )的导函数.当x ∈[0,π]时,0<f (x )<1;当x ∈(0,π)且x ≠π2时,⎝⎛⎭⎪⎫x -π2f ′(x )>0,则函数y=f (x )-sin x 在[-3π,3π]上的零点个数为() A .4 B .5 C .6 D .8C二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上) 13.已知幂函数f (x )=(m 2-3m +3)·x m +1为奇函数,则不等式f (2x -3)+f (x )>0的解集为________. (1,+∞)14.已知函数f (x )=|x 2+3x |,x ∈R ,若方程f (x )-a =0恰有4个互异的实数根x 1,x 2,x 3,x 4,则x 1+x 2+x 3+x 4=________.-615.已知函数f (x )=a x(a >0且a ≠1)在区间[-1,2]上的最大值为8,最小值为m ,若函数g (x )=(3-10m )x 是单调增函数,则a =________.1816.某同学在研究函数f (x )=x 2+1+x 2-6x +10的性质时,受到两点间距离公式的启发,将f (x )变形为f (x )=x -2+-2+x -2++2,则f (x )表示|PA |+|PB |(如图2),下列关于函数f (x )的描述正确的是________(填上所有正确结论的序号)图2①f (x )的图象是中心对称图形; ②f (x )的图象是轴对称图形; ③函数f (x )的值域为[13,+∞); ④方程f (f (x ))=1+10有两个解. ②③三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.,F (x )=⎩⎪⎨⎪⎧f x,x >0,-fx ,x <0.若f (-1)=0,且对任意实数x 均有f (x )≥0恒成立.(1)求F (x )的表达式.(2)当x ∈[-2,2]时,g (x )=f (x )-kx 是单调函数,求k 的取值范围.(1)F (x )=⎩⎪⎨⎪⎧x 2+2x +1,x >0,-x 2-2x -1,x <0.(2)(-∞,-2]∪[6,+∞) 18.(12分)已知实数x 满足32x -4-103·3x -1+9≤0且f (x )=log 2x 2·log 2x2. (1)求实数x 的取值范围.(2)求f (x )的最大值和最小值,并求此时x 的值. [解](1)由32x -4-103·3x -1+9≤0, 得32x -4-10·3x -2+9≤0,即(3x -2-1)(3x -2-9)≤0,所以1≤3x -2≤9,2≤x ≤4.(2)因为f (x )=log 2x 2·log 2x2=(log 2x -1)(log 2x -2)=(log 2x )2-3log 2x +2=⎝⎛⎭⎪⎫log 2x -322-14,当log 2x =32,即x =22时,f (x )min =-14.当log 2x =1或log 2x =2,即x =2或x =4时,f (x )max =0.19.(12分)设函数f (x )=(ax +b )e x,g (x )=-x 2+cx +d ,若函数f (x )和g (x )的图象都过点P (0,1),且在点P 处有相同的切线y =2x +1. (1)求a ,b ,c ,d 的值.(2)当x ∈[0,+∞)时,判断函数h (x )=f (x )-g (x )的单调性.[解](1)f ′(x )=(ax +a +b )e x, 所以⎩⎪⎨⎪⎧f =b =1,f=a +b =2,所以a =b =1, g ′(x )=-2x +c ,所以⎩⎪⎨⎪⎧g =d =1,g=c =2,所以c =2,d =1.(2)由(1)可知h (x )=f (x )-g (x )=(x +1)e x -(-x 2+2x +1)=(x +1)e x +x 2-2x -1, 所以h ′(x )=(x +2)e x +2x -2=(x +2)e x +2x +4-6=(x +2)(e x+2)-6≥2×3-6=0,所以h (x )在[0,+∞)上为增函数.20.(12分)设函数f (x )=a x -(k -1)a -x(a >0且a ≠1)是定义域为R 的奇函数.(1)求k 的值.(2)若f (1)<0,试判断函数的单调性,并求使不等式f (x 2+tx )+f (4-x )<0恒成立的t 的取值范围.(3)若f (1)=32,且g (x )=a 2x +a -2x-2mf (x )在[1,+∞)上的最小值为-2,求m 的值.[解](1)因为f (x )是定义域为R 的奇函数,所以f (0)=a 0-(k -1)a 0=1-(k -1)=0,所以k =2.(2)由(1)知f (x )=a x-a -x(a >0且a ≠1). 因为f (1)<0,所以a -1a<0,又a >0且a ≠1,所以0<a <1,所以y =a x 在R 上单调递减,y =a -x在R 上单调递增, 故f (x )=a x -a -x在R 上单调递减.不等式f (x 2+tx )+f (4-x )<0可化为f (x 2+tx )<f (x -4),所以x 2+tx >x -4, 所以x 2+(t -1)x +4>0恒成立,所以Δ=(t -1)2-16<0,解得-3<t <5. (3)因为f (1)=32,所以a -1a =32,即2a 2-3a -2=0,所以a =2或a =-12(舍去).所以g (x )=22x+2-2x-2m (2x -2-x )=(2x -2-x )2-2m (2x -2-x)+2.令n =f (x )=2x -2-x,因为f (x )=2x-2-x为增函数,x ≥1,所以n ≥k (1)=32.令h (n )=n 2-2mn +2=(n -m )2+2-m 2⎝ ⎛⎭⎪⎫n ≥32. 若m ≥32时,则当n =m 时,h (n )min =2-m 2=-2,所以m =2.若m <32,则当n =32时,h (n )min =174-3m =-2,所以m =2512>32(舍去).综上可知,m =2.21.(12分)已知函数f (x )=x -(a +1)ln x -a x (a ∈R ),g (x )=12x 2+e x -x e x.(1)当x ∈[1,e]时,求f (x )的最小值.(2)当a <1时,若存在x 1∈[e ,e 2],使得对任意的x 2∈[-2,0],f (x 1)<g (x 2)恒成立,求a 的取值范围.[解](1)f (x )的定义域为(0,+∞),f ′(x )=x -x -ax2.①当a ≤1时,x ∈[1,e]时,f ′(x )≥0,f (x )为增函数,f (x )min =f (1)=1-A .②当1<a <e 时,x ∈[1,a ]时,f ′(x )≤0,f (x )为减函数; x ∈(a ,e]时,f ′(x )>0,f (x )为增函数.所以x ∈[1,e]时,f (x )min =f (a )=a -(a +1)·ln a -1. ③当a ≥e 时,x ∈[1,e]时,f ′(x )≤0,f (x )在[1,e]上为减函数. f (x )min =f (e)=e -(a +1)-ae.综上,在x ∈[1,e]上,当a ≤1时,f (x )min =1-a ; 当1<a <e 时,f (x )min =a -(a +1)ln a -1; 当a ≥e 时,f (x )min =e -(a +1)-ae.(2)由题意知,当a <1时,f (x )(x ∈[e ,e 2])的最小值小于g (x )(x ∈[-2,0])的最小值.由(1)可知,当a <1时,f (x )在[e ,e 2]上单调递增, 则f (x )min =f (e)=e -(a +1)-ae ,又g ′(x )=(1-e x)x ,当x ∈[-2,0]时,g ′(x )≤0,g (x )为减函数,g (x )min =g (0)=1,所以e -(a +1)-ae <1,即a >e 2-2ee +1,所以a 的取值范围为⎝ ⎛⎭⎪⎫e 2-2e e +1,1.22.(a 为常数).(1)若函数y =f (x )在区间[1,+∞)上是单调递增函数,求实数a 的取值范围.(2)若函数y =f (x )有两个极值点x 1,x 2,且x 1<x 2,求证:0<f x 2x 1<-12+ln2. [解](1)根据题意知:f ′(x )=2x 2+2x +ax +1≥0在[1,+∞)上恒成立.即a ≥-2x 2-2x 在区间[1,+∞)上恒成立.令g (x )=-2x 2-2x , 因为g (x )=-2x 2-2x 在区间[1,+∞)上的最大值为-4,所以a ≥-4. 经检验:当a =-4时,f ′(x )=2x 2+2x -4x +1=x +2x -x +1≥0,x ∈[1,+∞).所以a 的取值范围是[-4,+∞).(2)f ′(x )=2x 2+2x +ax +1=0在区间(-1,+∞)上有两个不相等的实数根,即方程2x 2+2x +a =0在区间(-1,+∞)上有两个不相等的实数根. 记g (x )=2x 2+2x +a ,则有⎩⎪⎨⎪⎧-12>-1,g ⎝ ⎛⎭⎪⎫-12<0,g ->0,解得0<a <12.所以x 1+x 2=-1,2x 22+2x 2+a =0,x 2=-12+1-2a 2,-12<x 2<0. 所以f x 2x 1=x 22-x 22+2x 2x 2+-1-x 2.令k (x )=x 2-x 2+2xx +-1-x,x ∈⎝ ⎛⎭⎪⎫-12,0.k ′(x )=x 2+x2+2ln(x +1), 记p (x )=x 2+x2+2ln(x +1).所以p ′(x )=2x 2+6x +2+x3,p ′⎝ ⎛⎭⎪⎫-12=-4,p ′(0)=2.所以存在x 0∈⎝ ⎛⎭⎪⎫-12,0使得p ′(x 0)=0. 当x ∈⎝ ⎛⎭⎪⎫-12,x 0时,p ′(x )<0; 当x ∈(x 0,0)时,p ′(x )>0.所以k ′(x )在⎝ ⎛⎭⎪⎫-12,x 0上单调递减,在(x 0,0)上单调递增,因为k ′⎝ ⎛⎭⎪⎫-12=1-2ln2<0,k ′(0)=0. 所以当x ∈⎝ ⎛⎭⎪⎫-12,0时,k ′(x )<0, 所以k (x )在⎝ ⎛⎭⎪⎫-12,0上单调递减, 即0<f x 2x 1<-12+ln2.。
