离散时间BAM神经网络周期解的存在性
【国家自然科学基金】_bam神经网络_基金支持热词逐年推荐_【万方软件创新助手】_20140801
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 bam神经网络 神经网络 时滞 故障诊断 故障树分析 指数稳定性 拓扑度 微分不等式 平衡点 全局指数稳定性 lyapunov泛函
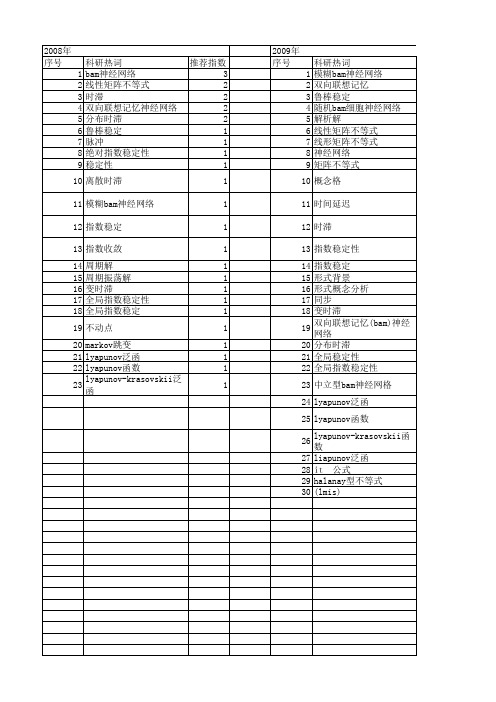
2009年 序号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 halanay型不等式 30 (lmis)
科研热词 模糊bam神经网络 双向联想记忆 鲁棒稳定 随机bam细胞神经网络 解析解 线性矩阵不等式 线形矩阵不等式 神经网络 矩阵不等式 概念 时间延迟 时滞 指数稳定性 指数稳定 形式背景 形式概念分析 同步 变时滞 双向联想记忆(bam)神经网络 分布时滞 全局稳定性 全局指数稳定性 中立型bam神经网格 lyapunov泛函 lyapunov函数 lyapunov-krasovskii函数 liapunov泛函
推荐指数 2 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2011年 科研热词 推荐指数 时滞 3 双向联想记忆神经网络 3 脉冲 1 稳定性 1 概周期解 1 振动性 1 平衡点 1 存在性 1 周期解 1 双向联想记忆神经网络:m-矩阵 1 分布时滞 1 全局渐近稳定性 1 全局指数稳定性 1 不稳定性 1 n个神经元bam神经网络 1 mawhin连续定理 1
2014年 序号 1 2 3 4
2014年 科研热词 随机 指数同步 s-分布时滞 bam神经网络 推荐指数 1 1 1 1
具有变化时滞和变化系数的Cohen-Grossberg神经网络周期解的存在性

成它 的特殊情 况 , 近年来 , 许多学 者对 它进行 了广泛 的研究 . 由于时滞 不可避 免 , 具有 时滞 的 C h n—G oseg神经 网络被 提 出_ . oe rsb r 8 现在 , J 具有 时滞 的 C hn— oe
Goseg 经网络 理论 已经广泛 应用 于优化 计算 、 工智 能 、 式识别 等领域 . rsbr 神 人 模
神经 网络 周期解 的存在 性 已经 被一 些学者 研 究
. 文献 [ ] 通 过 建立 合适 的 Lauo 在 3 中, yp nv函数 ,
应 用分 析方法 , 作者给 出 了判定 细胞 神经 网络周期 解 的存在 性 和 唯一性 的几 个充 分 条件 . 文 献 [ ] 在 6 中, 作者研 究 了一类广 义时滞 细胞神 经 网络周期 解 的存 在性 . 在文 献 [4 中, 2 ] 作者 研 究 了具 有变 化 时 滞 的 Chn—Gose oe rsbr g神经 网络 , 在放 大 函数 的有界 性条件 下获 得 了模 型周期 解存 在性 的判据 . 笔 者继续这 方 面的工作 , 究具 有变 化时滞 的 C hn—Goseg神经 网络周 期 解 的存 在性 . 们 研 oe rsbr 我
在 神经 网络 的应用 中 , 系统 的稳定性 是实 际应用 者最为 关心 的问题 . 近年 来 , 具有 时滞 的 C hn— oe Goseg rsbr 神经 网络 的稳定性 得到 了广泛 研究 . 在文献 [ ] , . n 9 中 L Wag和 X F Z u分 析 了时滞 对 ..o C hn—G oseg神经网络 稳定性 的有 害影 响 ; oe rsbr 在文 献 [ 0— 0 中 , 1 2 ] 一些 作者 给 出了具 有 常数 时滞 和
扰动的离散神经网络多重周期解的存在性和稳定性

c{ : : . c{ 二; 二 I H ; _ H ; : _ 茎 , : , , 。 : , 。
对 系统 ( ) 文献 [ 3 获 得 了存 在 ,k周 期 轨 。文 献 [ 确定 了存 在 周 期 轨 的数 目。文献 [ ] 虑 1, 2— ] 2 4] 5考
维普资讯
第1 8卷
第 2期
长
春
大
学
学
报
Vo . 8 N . 11 o 2 Ap .2 0 r 08
20 0 8年 4月
J OURN HANGCHUN UNI AL OF C VER r Y Sr
文章编号 :0 9— 97 2 0 ) 2— 0 3— 4 10 3 0 (0 8 0 0 1 0
2 周期解的存在性
令 : = ; …方2化 凡 = 凡 ( = 1 = 程 可 + F _ 三) 1 ) 。 为
r f1 ,#2 ; ∞ + √≠ j k
() 3
其中 (1 2 ∞)FR —R : () { + ∞+ +1 一 ) = ; = ∞, , ,:2 }弛 ∞ = ) u( 1, ∞ …, 1 凡 _ ,
了块状 结构 的神 经 网格模 型 。本 文考 虑具 有 扰 动 的神经 网络模 型
f( )= 凡一1 q ,凡一k )+u( x凡 犀( )+ ) ( ) 凡一1 ; )
【( ) ( 1 + ( — ) + : n 1 。 ) n = n一 ) q , n k ) u( 一 )
定理 1 假设( ) (I) H。 ,I 成立 , O卢∈( ,) : > , 0 1 , 0 /(, ) /(, ) > ,。/ ,7 一1 ,:/ / 7 , 一1 使得 r 口 < ’ R, < ’ b < 那么对
【国家自然科学基金】_周期解的存在性_基金支持热词逐年推荐_【万方软件创新助手】_20140730

科研热词 推荐指数 周期解 39 正周期解 11 概周期解 10 存在性 9 重合度 7 时滞 7 无穷时滞 6 泛函微分方程 5 差分方程 5 脉冲 4 渐近概周期解 4 全局吸引性 4 逐段常变量 3 稳定性 3 渐近概周期序列 3 扩散 3 偏差变元 3 临界点 3 中立型微分方程 3 不动点定理 3 liapunov函数 3 高阶liénard型方程 2 非线性 2 锥不动点定理 2 重合度理论 2 脉冲效应 2 脉冲微分方程 2 神经网络 2 环绕定理 2 持续生存 2 抛物型方程 2 微分方程 2 延拓定理 2 叠合度 2 变时滞 2 反问题 2 反周期解 2 全局渐近稳定 2 中立型 2 不动点 2 rayleigh方程 2 lyapunov函数 2 lotka-volterra系统 2 leray-schauder不动点定理 2 高阶差分方程 1 高阶中立型泛函微分方程 1 食物-种群系统 1 非自治捕食-被捕食系统 1 重合度拓展理论 1 重合度. 1 遥远概周期函数 1 退化时滞微分方程 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
科研热词 周期解 重合度 时滞 正周期解 稳定性 存在性 微分方程 脉冲 概周期解 时滞微分方程 拓扑度 周期边值问题 反馈控制 不动点定理 hopf分支 重合度理论 时间周期解 差分方程 多解性 临界点 lyapunov函数 duffing方程 零航速 阶段结构捕食系统 逐段常变量 神经网络 特征方程 特征值 渐近概周期解 正解 无扭周期解 收获率 捕食者-食饵系统 捕食与被捕食 扩散 平衡点 局部渐近稳定 吕卡提方程 反周期解 分歧 分布时滞 全局指数稳定性 先验估计 中立型微分方程 中立型 不动点理论 不动点 lotka-volterra系统 logistic模型 kdv方程 hopf分岔 aubry-mather集
时滞BAM神经网络周期振荡解的存在性和指数收敛性

时 滞 的 BA 神经 网络 周 期 振荡 解 的存在 性 与 指数 收敛 性 ,导 出 了周 期 振荡 解 存 在 和指 数 收敛 的充 M 分 判 据 ,对 激 励 函数 的 限制 较 少 ,得 到 的充 分 判 据 具 有 较 小 的保 守 性 , 因而 有 助 于 周 期 振荡 时 滞
维普资讯
第2 2卷
2 0 年 08
第 1 期
2 月
五邑大学学报 (自然科学版 )
J U A O WUY U V ST ( a rl c ne dt n O RN L F I NIER IY N t a u Si c E io ) e i
V_ .2 NO. 0 2 I 1
n t rs e wo k wih e a s s t d l y i di c s e b u i g fx d p i t h o e s u s d y s n i e - o n t e r m, c n t u t n u t b e y p n v o s r c i g s i l L a u o a f n to s nd s me a a y i e hn q e .S me s fi i n o ii n r e i e i h a e o r a u c i n ,a o n l s s t c i u s o u fc e t c nd to s a e d rv d wh c r f g e t s g ii a e i he d s g n pp i a i n f BAM t e a s h o d to s a e e s o c e k i i n fc nc n t e i n a d a lc to s o wi d l y .T e c n ii n r a y t h c n h p a tc y s mp e a g b a c me h d .Fi a l ,a x mp e i i e o il s r t h fe t v n s f r c ie b i l le r i t o s n ly n e a l s g v n t lu ta e t e e f c i e e s o o rr s l. u e u t
一类二元离散细胞神经网络的收敛性与周期解的存在性

E A b r n a dD. Al sn r t和 P E C v l r a dM. let i n D’ e a do9 i s 1 ial i n e
GiiO l[l 的工作使 得我们 对二元细 胞神经 网络模型解 l1等人
的 稳 定 性 有 了 较 深 入 地 理 解 .袁 朝 晖 t1 论 了具 饱 和 非 “讨
熊佩 英 ,李雪梅 , -
4 34 ; .湖南 师范大学 数学与计算机科学学 院 , 10 9 2 长沙 408 ) 10 1
(1 湖南城市学院 数学 与计算科学系 , . 湖南 益阳 摘
要 :主要研 究 了一 类反馈矩 阵为对称 矩阵的二元 离散 细胞神 经 网络 模型的收敛 性和周期 解的存在
维普资讯
第 1卷 第3 5 期
湖
J Our nal
报
(自然科 学版 )
Vo.1 NO3 1 5 .
2 0年9 0 6 Y]
(Na u a Sce c ) trl in e
S p .2 0 e t 0 6
一
类二元离散细胞神经网络的收敛性与周期解的存在性
入 地 研 究 t 1 对 于 系统 的稳 定 性 ,已有 相 当 丰 富 的结 果 , . 一
{ 一f 2,(【q2,(【+“ 3 I +l【】+a2)f .( 詈 ( )1)) 妻 ,) 1(1a(1 2 ) () ,f'2 ,+ -,,】 一一)r+a f ) 【) f
其 中 ( , () f y t 表示神经元 的内部活动状 态 ,【 表示取整 ) . 】
符 , :a 1为 数 阵 称 反 矩 , 号 A IaJ 常 矩 , 为 馈 阵 【以2l 2 l - 以l 2 2
时滞忆阻Cohen-Grossberg神经网络周期解的存在性

时滞忆阻Cohen-Grossberg神经网络周期解的存在性王有刚;武怀勤【摘要】研究了一类具有时变时滞的忆阻Cohen-Grossberg神经网络的周期动力行为.借助M-矩阵理论,微分包含理论和Mawhin-like收敛定理,证明了网络系统周期解的存在性.最后,用一个数值算例验证了本文结论的正确性和可行性,并通过图形模拟直观地描述了周期解和平衡点的存在性.%The objective of this paper is to investigate the periodic dynamical behaviors for a class of Memristive Cohen-Grossberg neural networks with time-varying delays. By employing M-matrix theory, differential inclusions theory and the Mawhin-like coin-cidence theorem in set-valued analysis, the existence of the periodic solution for the network system was proved. Finally, an illustra-tive example was given to demonstrate the validity of the theoretical results and the existence of periodic solution and equilibrium point was described visually by graphical simulation.【期刊名称】《西华大学学报(自然科学版)》【年(卷),期】2017(036)005【总页数】10页(P22-30,35)【关键词】忆阻;Cohen-Grossberg神经网络;周期解;时变时滞【作者】王有刚;武怀勤【作者单位】吕梁学院数学系,山西吕梁 033001;燕山大学理学院,河北秦皇岛066004【正文语种】中文【中图分类】TP1831971年, 华裔科学家蔡少棠(Leon O. Chua)从理论推断在电阻、电容和电感器之外,应该还有一种组件,代表着电荷与磁通量之间的关系。
带有周期系数和时滞的细胞神经网络模型的周期解的存在性和全局指数稳定性

一
I ma << l @ 一 ( i << 0 { ) t o m x x a )
收稿 日期: 0 6 20 . 作者简介 :刘艳青(9 4 1 2 0 — —7 0 1 7 年1 月生) ,女,博士,讲师. 究方向:神经网络动力系统 ,微 研
分与差分方程.
基 金项 目:国家 自然科学基金(O 7 O 9 . 74 14)
维普资讯
周期的,为 了方便起见 ,我们引入下面的符号。
口 al 『 石 /口t, 6 a『 l 去 ≤口 , nl) 去 6 , m r x jd m ( x
-
b( , i t j
=
d( t { ,
=蹬
l j
五: (, 1 Id / it 0 t )
文章编号: 0—052 0)609—2 1 538(070—951 0
带有周期 系数和 时滞 的细胞神 经 网络模 型 的周 期解 的存在性和 全局指数稳 定性 木
刘艳青 , 唐万生 , 一
(一 1 天津大学系统工程研究所 ,天津 3 0 7 ; 2 0 02 一天津 大学 数学 系,天津 3 0 7 ) 0 0 2 摘 要:本文运用非奇异 M 矩 阵的性质 ,不等式分析法和建立在重合度基础上 的连 续性 定理,得到了带 有周期系数和周期时滞的细胞 神经网络的周期解 的存在性以及 全局指数稳定性的新判据。并且给 出 了 指 数 收 敛 率 的估 计 。
维普资讯
第2卷 第6 4 期
2 0 年 1 月 07 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
— s p∈ I ( <+ ∞ ( u 才 )I 愚一 1 2 … , ( ) , , 愚) 本 文 中采用 如下 符号 :
其 中 EZ , l 0< a ( < 1 口 ( )> 0 + 垃 ) (垃
定义 差分算 子
As n ( )一 s n+ 1 ( )一 s ) (
则本 文所讨 论 的系统 ( ) 成 : 2变
( 一 A () ( +∑ W3 () 一 ∑ g (z (一z + ( 一 z ) ) ( ( 3 ()z ( ) () 3 3 ) 3 ) )
维普资讯
6 Leabharlann 青 岛 大 学 学 报 (自然 科 学 版 )
( ): ^ ( H2 I )I ≤ ( 一 1 ;i 1 2 ,2 一 , ,… , ( ) , p 是 ) z∈ R,
第2 0卷
( 3: z≥0 ∑ 鼬( < H ) g( ) , z +∞(一1 2i , , ( ; ∈ ) ) 愚 , ; 一1 2 …, 愚 l , )
Vo . O No 2 12 .
J r 20 07 uL
文章 编 号 :0 6—1 3 (0 70 —0 0 0 10 0 7 20 ) 2 0 5— 5
离散时 间 B AM 神 经 网络 周 期 解 的 存在 性
潘 瑞 芬 ,张 微 微 ,冯 国涛 ,张安 彩
( 中南 大 学 数 学 学院 ,长 沙 4 0 8 ) 1 0 3 摘 要 :利用迭 合度 连续 定 理研究 了具有周 期 系数 的离 散 时 间 B AM 神 经 网络周 期 解 的存 在性 , 到 了 比原有 结果 更优 化 的结论 。 得 关键 词 : AM 神 经 网络 ;周期 解 ; 散时 问模 拟 B 离
中图分 类号 : 7 O1 5 文献 标识 码 : A
双 向联想 记忆 神经 网络 由 Kot[ 于 18 so 9 8年提 出 , 主要应 用 于 图像 处理 、 型识 别 、 模 自动 控制 等 领 。 域 。因模 型储 存 与周期解 的稳定 性有 关 , 以有必 要研 究 B 所 AM 神经 网络 周期解 的存 在性 。文献 [] 具 有 6对
维普资讯
‘
第 2卷 第 2 o 期 2007年 6月
青 岛 大 学 学 报 (自 然 科 学 版 )
J U NA F Q N A NI E ST ( au a S i c dt n O R L O I GD O U V R I Y N tr l ce eE io ) n i
其 中
A ( )一 1一 a ) (
本 文 中有如 下基 本假设 :
( ): H1 0< a ( ) 1 Wk( 和 ( ( < , j ) ) 一 1 2 一 1 2 … , ( ) N 一 周 期序 列 ( E z- , , ;i , , ) 是 ; o )
( 1 )
其 中各 符 号意义 参见 文献 I - -1 7。
本 文 主要讨论 系统 ()的离 散时 间模 型 , 用文 献 E]的方 法 可得 : 1 利 7
z(+ ) a( z( +∑ 胁 ( ( - ( 1一 ) ) 叫 3j 3 ) k ∑苫g (z (一 )+ ( ) ()z ( z ( 2 3 )3 ) ) )
一
∑ 。( , ( 是 N N 其中 一 ) - - 1 ) 一周 列; 期序
王( 一 A( ( +∑ W ( ∑苫g )z () —)+In )一 ) ) ( 卜( ) ( J)Hj z a ) (z ( ) (
令 X, y是 B n c a a h空 间 , X 中定 义 抽象方 程 : . — a 在 / x Hx 其 中 L : o X — y是线 性算 子 , : — y是 连续 算子 , ∈ ( ,1 是 参数 同时 定 义两个 投影 D mL H X O ) 算子 P : o X n D mL— KeL, : — X/mL。 r Q X I 引 理[-令 Q是 B n c 间 X 中的一个 有界 开集 , s: a ah空 L是 一个 零指标 的 F e h l 子 ,H : 一 X 在 rd om算 上是 L一 紧 的 , 若有 :
用 迭合 度 连续定 理 给 出其周 期解 的存 在 性 。
1 周 期解 的存 在 性
首 先考 虑具 有周 期 系数 和连续 分 布时滞 的连续 时 间 B AM 神经 网络 系统 。
z ( )一 一 a £z £ £ ( ) ( )+
( 3 p
-
一
一
1
W £3 Igks(j一) + £ ( ( ( (jXk£s ) ( 3 ) 。 3( 3( 一 _ - )- ) ) )
周期 系数 和 连续分 布 时滞 的连续 时 间 B AM 神 经 网络 进行 了讨论 , 得 到 了其 周 期解 的存 在 性 与全 局 指 数 并 稳 定性 。此 外 , 们发 现大 部分 作者 只是 对连 续 时 间 B 我 AM 神 经 网络进 行 研究 , 对 离散 时 间 B 而 AM 神 经 网 络_ 周期 解 的存在 性 问题研 究 的还 比较少 。基 于此 , 文将 进一 步讨论 离 散 时 间 B 7 ] 本 AM 神经 网络模 型 , 利 并
收 稿 日期 : 0 7—0 —2 20 2 5 基 金 项 目 :湖南 省 自然 科 学 基 金 (6j0 3 。 0 j 1 ) 5 作者 简 介 :潘 瑞 芬 ( 9 2 )女 , 1 8 一 , 山东 潍 坊 人 , 士 研 究 生 , 要 从 事 微 分 方 程 、 硕 主 神经 网 络与 离 散 动 力 系 统 方 面 的 研 究 。
