第1章学案4
2014年《步步高》高中物理配套Word版文档(人教选修3-1)第一章 学案4

学案4 电场线[学习目标定位] 1.理解电场强度的概念及公式,并会进行有关的计算.2.会用电场线表示电场,并熟记几种常见电场的电场线分布特征.3.理解点电荷的电场强度及场强叠加原理.一、电场法拉第认为在电荷的周围存在着由它产生的 ,处在电场中的其他电荷受到的 就是这个电场给予的.近代物理学认为电场以及磁场是一种客观存在,并且是互相联系的,统称为 , 与 是物质存在的两种不同形式. 二、电场强度试探电荷在电场中某个位置 与它的 的比值叫电场强度,用公式E =Fq 表示;单位是 ,符号为 ;电场强度是矢量,方向与 的受力方向相同. 三、电场线电场线是画在电场中的一条条有方向的曲线,曲线上每点的切线方向表示该点的电场强度方向.在同一幅图中,电场强度较大的地方电场线较密,电场强度较小的地方电场线较疏,电场线不是实际存在的线,而是为了形象地描述电场而假想的线.三、电场线 匀强电场 [问题设计]1.电场线是如何表示电场方向和强弱的?2.电场线是真实存在的吗?能不能相交?[要点提炼]1.电场线的特点有:(1)起始于无限远或正电荷,终止于负电荷或无限远.(2)任意两条电场线不相交.(3)在同一幅图中,电场线的疏密表示场强的大小,电场线某点的切线方向表示该点电场强度的方向.2.匀强电场中各点的电场强度大小相等,方向相同;电场线是间距相等的平行线.[延伸思考]1.点电荷、等量同号点电荷、等量异号点电荷电场的电场线有何特点?答案点电荷的电场:正电荷的电场线从正电荷出发延伸到无限远处,负电荷的电场线由无限远处延伸到负电荷,如图所示,其特点有:(1)点电荷形成的电场中,不存在场强相同的点.(2)若以点电荷为球心作一个球面,电场线处处与球面垂直.在此球面上场强大小处处相等,方向各不相同.等量同号点电荷的电场:电场线分布如图所示(以等量正点电荷为例),其特点有:(1)两点电荷连线上,中点O处场强为零,向两侧场强逐渐增大,方向指向中点.(2)两点电荷连线中点O沿中垂面(中垂线)到无限远,电场线先变密后变疏,即场强先变大后变小,方向背离中点.等量异号点电荷的电场:电场分布如图所示,其特点有:(1)两点电荷连线上的各点场强方向从正电荷指向负电荷,沿电场线方向场强先变小再变大,中点处场强最小.(2)两点电荷连线的中垂面(中垂线)上,电场线的方向均相同,即电场强度方向都相同,总与中垂面(或中垂线)垂直且指向负点电荷一侧.沿中垂面(中垂线)从中点到无限远处,场强大小一直减小,中点处场强最大.2.电场线和带电粒子在电场中的运动轨迹相同吗?答案不一定相同.电场线是为了形象地描述电场而引入的假想曲线,规定电场线上每点的切线方向为该点的场强方向,也是正电荷在该点的受力方向(与负电荷受力方向相反).运动轨迹是带电粒子在电场中实际通过的径迹,径迹上每点的切线方向为粒子在该点的速度方向.在力学的学习中我们就已经知道,物体运动速度的方向和它的加速度的方向是两回事,不一定相同,因此,电场线与运动轨迹不能混为一谈,不能认为电场线就是带电粒子在电场中运动的轨迹.只有当电场线是直线,且带电粒子只受静电力作用(或受其他力,但方向沿电场线所在直线),同时带电粒子的初速度为零或初速度方向沿电场线所在直线时,运动轨迹才和电场线重合,这只是一种特殊情况.一、电场线的理解和应用例1某电场的电场线分布如图5所示,下列说法正确的是()图5A.c点的电场强度大于b点的电场强度B.若将一试探电荷+q由a点静止释放,它将沿电场线运动到b点C.b点的电场强度大于d点的电场强度D.a点和b点的电场强度的方向相同例2关于电场线的特征,下列说法中正确的是()A.如果某空间中的电场线是曲线,那么在同一条电场线上各处的场强不相同B.如果某空间中的电场线是直线,那么在同一条电场线上各处的场强相同C.如果空间中只存在一个孤立的点电荷,那么这个空间中的任意两条电场线相交;如果空间中存在两个以上的点电荷,那么这个空间中有许多电场线相交D.电场中任意两条电场线都不相交例3下列各电场中,A、B两点电场强度相同的是()例4如图所示是某静电场的一部分电场线分布情况,下列说法中正确的是()A.这个电场可能是负点电荷的电场B.点电荷q在A点处受到的电场力比在B点处受到的电场力大C.负电荷在B点处受到的电场力的方向沿电场线的切线方向D.点电荷q在A点处的瞬时加速度比在B点处的瞬时加速度小(不计重力)例5如图所示,有一水平方向的匀强电场,场强大小为900 N/C,在电场内一水平面上作半径为10 cm的圆心为O的圆,圆上取A、B两点,AO沿电场方向,BO⊥OA,另在圆心处放一电荷量为10-9C的正点电荷,则A处场强大小E A=________ N/C,B处场强大小E B=________ N/C.1.如图6所示,带箭头的直线是某一电场中的一条电场线,在这条线上有A、B两点,用E A、E B表示A、B两处的场强,则()图6A.A、B两处的场强方向相同B.因为A、B在一条电场线上,且电场线是直线,所以E A=E BC.电场线从A指向B,所以E A>E BD.不知A、B附近电场线的分布情况,E A、E B的大小不能确定2.如图2所示是点电荷Q周围的电场线,图中A到Q的距离小于B到Q的距离.以下判断正确的是()图2A.Q是正电荷,A点的电场强度大于B点的电场强度B.Q是正电荷,A点的电场强度小于B点的电场强度C.Q是负电荷,A点的电场强度大于B点的电场强度D.Q是负电荷,A点的电场强度小于B点的电场强度3.如图5所示,实线是一簇未标明方向的由点电荷Q产生的电场线,若带电粒子q(|Q|≫|q|)由a运动到b,静电力做正功.已知在a、b两点粒子所受静电力分别为F a、F b,则下列判断正确的是()图5A.若Q为正电荷,则q带正电,F a>F bB.若Q为正电荷,则q带正电,F a<F bC.若Q为负电荷,则q带正电,F a>F bD.若Q为负电荷,则q带正电,F a<F b。
2020高中数学 第一章 三角函数 阶段复习课 第1课 任意角的三角函数及诱导公式学案 4

第一课 任意角的三角函数及诱导公式[核心速填]1.与角α终边相同的角的集合为S ={β|β=α+k ·360°,k ∈Z }.2.角度制与弧度制的换算3.弧度制下扇形的弧长和面积公式 (1)弧长公式:l =|α|r . (2)面积公式:S =12lr =12|α|r 2.4.任意角的三角函数(1)定义1:设任意角α的终边与单位圆交于点P (x ,y ),则sin α=y ,cos α=x ,tan α=y x(x ≠0). (2)定义2:设任意角α的终边上任意一点P 的坐标为(x ,y ),r =|OP |=x 2+y 2,则sin α=y r,cos α=x r ,tan α=y x(x ≠0).5.同角三角函数基本关系式sin 2α+cos 2α=1;sin αcos α=tan α.6.诱导公式记忆口诀 奇变偶不变,符号看象限.[体系构建][题型探究]象限角及终边相同的角已知α(1)把α改写成β+2k π(k ∈Z,0≤β<2π)的形式,并指出α是第几象限角;(2)求γ,使γ与α的终边相同,且γ∈⎝ ⎛⎭⎪⎫-π2,π2. [解] (1)∵-800°=-3×360°+280°,280°=149π,∴α=-800°=14π9+(-3)×2π.∵α与角14π9终边相同,∴α是第四象限角.(2)∵与α终边相同的角可写为2k π+14π9,k ∈Z 的形式,而γ与α的终边相同,∴γ=2k π+14π9,k ∈Z .又γ∈⎝ ⎛⎭⎪⎫-π2,π2,∴-π2<2k π+14π9<π2,k ∈Z ,解得k =-1,∴γ=-2π+14π9=-4π9.[规律方法] 1.灵活应用角度制或弧度制表示角 (1)注意同一表达式中角度与弧度不能混用. (2)角度制与弧度制的换算设一个角的弧度数为α,角度数为n ,则αrad =⎝⎛⎭⎪⎫α·180π°,n °=⎝ ⎛⎭⎪⎫n ·π180rad. 2.象限角的判定方法(1)根据图象判定.利用图象实际操作时,依据是终边相同的角的概念,因为0°~360°之间的角与坐标系中的射线可建立一一对应的关系.(2)将角转化到0°~360°范围内.在直角坐标平面内,0°~360°范围内没有两个角终边是相同的. [跟踪训练]1.若α角与8π5角终边相同,则在[0,2π]内终边与α4角终边相同的角是________.【导学号:84352139】2π5,9π10,7π5,19π10 [由题意,得α=8π5+2k π(k ∈Z ),α4=2π5+k π2(k ∈Z ). 又α4∈[0,2π],所以k =0,1,2,3,α4=2π5,9π10,7π5,19π10.]弧度制下扇形弧长及面积公式的计算(1)如图11,△ABC 是正三角形,曲线CDEF 叫做正三角形的渐开线,其中弧、弧、弧的圆心依次是A 、B 、C ,如果AB =1,那么曲线CDEF 的长是________.图11(2)一扇形的圆心角为2弧度,记此扇形的周长为c ,面积为S ,则c -1S的最大值为________. (1)4π (2)4 [(1)弧的长是120π×1180=2π3,弧的长是:120π×2180=4π3,弧的长是:120π×3180=2π,则曲线CDEF 的长是:2π3+4π3+2π=4π.(2)设扇形的弧长为l ,半径为r ,圆心角大小为2弧度, 则l =2r ,可求:c =l +2r =2r +2r =4r , 扇形的面积为S =12lr =12r 2×2=r 2,所以c -1S =4r -1r 2=-⎝ ⎛⎭⎪⎫1r 2+4r=-⎝ ⎛⎭⎪⎫1r-22+4≤4.r =12时等号成立,所以c -1S的最大值为4.] [规律方法] 弧度制下有关弧长、扇形面积问题的解题策略1明确弧度制下弧长公式l =|α|r ,扇形的面积公式是S =12lr =12|α|r 2其中l 是扇形的弧长,α是扇形的圆心角;2涉及扇形的周长、弧长、圆心角、面积等的计算,关键是先分析题目已知哪些量、求哪些量,然后灵活运用弧长公式、扇形面积公式直接求解或列方程组求解.[跟踪训练]2.如图12,已知扇形AOB 的圆心角为120°,半径长为6,求弓形ACB 的面积.【导学号:84352140】图12[解] ∵120°=120180π=23π,∴l =6×23π=4π,∴的长为4π.∵S 扇形OAB =12lr =12×4π×6=12π,如图所示,作OD ⊥AB ,有S △OAB =12×AB ×OD =12×2×6cos 30°×3=9 3.∴S 弓形ACB =S 扇形OAB -S △OAB =12π-9 3. ∴弓形ACB 的面积为12π-9 3.任意角三角函数的定义(1)若一个角的终边上有一点P (-4,a ),且sin α·cos α=3,则a 的值为( ) A .4 3 B .±4 3 C .-43或-433D. 3(2)已知角α的终边经过点P (12m ,-5m )(m ≠0),求sin α,cos α,tan α的值.【导学号:84352141】(1)C [(1)因为α角的终边上有一点P (-4,a ),所以tan α=-a4,所以sin αcos α=sin αcos αsin 2α+cos 2α=tan αtan 2α+1=-a4⎝ ⎛⎭⎪⎫-a 42+1=34, 整理得3a 2+16a +163=0,(a +43)(3a +4)=0,所以a =-43或-433.](2)r =12m2+-5m2=13|m |,若m >0,则r =13m ,α为第四象限角, sin α=y r =-5m 13m =-513,cos α=x r =12m 13m =1213,tan α=y x =-5m 12m =-512.若m <0,则r =-13m ,α为第二象限角, sin α=y r =-5m -13m =513,cos α=x r =12m -13m =-1213,tan α=y x =-5m 12m =-512.[规律方法] 利用定义求三角函数值的两种方法1先由直线与单位圆相交求出交点坐标,再利用正弦、余弦、正切函数的定义,求出相应的三角函数值. 2取角α的终边上任意一点P a ,b 原点除外,则对应的角α的正弦值sin α=b a 2+b 2,余弦值cos α=aa 2+b2,正切值tan α=ba.当角α的终边上点的坐标以参数形式给出时,要根据问题的实际情况对参数进行分类讨论.[跟踪训练]3.如果点P (sin θ·cos θ,2cos θ)位于第三象限,试判断角θ所在的象限.【导学号:84352142】[解] 因为点P (sin θ·cos θ,2cos θ)位于第三象限, 所以sin θ·cos θ<0,2cos θ<0,即⎩⎪⎨⎪⎧sin θ>0,cos θ<0,所以角θ在第二象限.同角三角函数基本关系和诱导公式的应用(1)已知sin(-π+θ)+2cos(3π-θ)=0,则sin θ+cos θsin θ-cos θ=________.(2)已知f (α)=sin2π-α·cos 2π-α·tan -π+αsin -π+α·tan -α+3π.①化简f (α);②若f (α)=18,且π4<α<π2,求cos α-sin α的值;③若α=-47π4,求f (α)的值. 【导学号:84352143】[思路探究] 先用诱导公式化简,再用同角三角函数基本关系求值. (1)13 [(1)由已知得-sin θ-2cos θ=0,故tan θ=-2, 则sin θ+cos θsin θ-cos θ=tan θ+1tan θ-1=-2+1-2-1=13.] (2)①f (α)=sin 2α·cos α·tan α-sin α-tan α=sin α·cos α.②由f (α)=sin α·cos α=18可知,(cos α-sin α)2=cos 2α-2sin α·cos α+sin 2α =1-2sin α·cos α=1-2×18=34,又∵π4<α<π2,∴cos α<sin α,即cos α-sin α<0, ∴cos α-sin α=-32. ③∵α=-474π=-6×2π+π4,∴f ⎝ ⎛⎭⎪⎫-474π=cos ⎝ ⎛⎭⎪⎫-474π·sin ⎝ ⎛⎭⎪⎫-474π=cos ⎝ ⎛⎭⎪⎫-6×2π+π4·sin ⎝ ⎛⎭⎪⎫-6×2π+π4=cos π4·sin π4=22×22=12.母题探究:1.将本例(2)中“18”改为“-8”“π4<α<π2”改为“-π4<α<0”求cos α+sin α.[解] 因为-π4<α<0,所以cos α>0,sin α<0且|cos α|>|sin α|,所以cos α+sin α>0,又(cos α+sin α)2=1+2sin αcos α=1+2×⎝ ⎛⎭⎪⎫-18=34,所以cos α+sin α=32. 2.将本例(2)中的用tan α表示1fα+cos 2α.[解]1f α+cos 2α=1sin αcos α+cos 2α=sin 2α+cos 2αsin αcos α+cos 2α=tan 2α+1tan α+1. [规律方法] 1.牢记两个基本关系式sin 2α+cos 2α=1及sin αcos α=tan α,并能应用两个关系式进行三角函数的求值、化简、证明.在应用中,要注意掌握解题的技巧.比如:已知sin α±cos α的值,可求cos αsinα.注意应用(cos α±sin α)2=1±2sin αcos α.2.诱导公式可概括为k ·π2±α(k ∈Z )的各三角函数值的化简公式.记忆规律是:奇变偶不变,符号看象限.。
人教版-数学-4上-分类讲学案-第1章-大数的认识-04专项练习-近似数的改写-答案
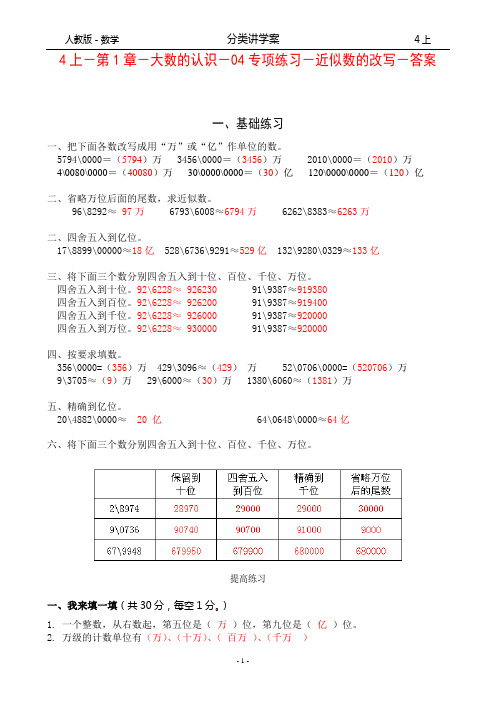
4上-第1章-大数的认识-04专项练习-近似数的改写-答案一、基础练习一、把下面各数改写成用“万”或“亿”作单位的数。
5794\0000=(5794)万3456\0000=(3456)万 2010\0000=(2010)万4\0080\0000=(40080)万30\0000\0000=(30)亿120\0000\0000=(120)亿二、省略万位后面的尾数,求近似数。
96\8292≈97万6793\6008≈6794万6262\8383≈6263万二、四舍五入到亿位。
17\8899\00000≈18亿 528\6736\9291≈529亿132\9280\0329≈133亿三、将下面三个数分别四舍五入到十位、百位、千位、万位。
四舍五入到十位。
92\6228≈ 926230 91\9387≈919380四舍五入到百位。
92\6228≈ 926200 91\9387≈919400四舍五入到千位。
92\6228≈ 926000 91\9387≈920000四舍五入到万位。
92\6228≈ 93000091\9387≈920000四、按要求填数。
356\0000=(356)万 429\3096≈(429)万 52\0706\0000=(520706)万9\3705≈(9)万 29\6000≈(30)万1380\6060≈(1381)万五、精确到亿位。
20\4882\0000≈20 亿 64\0648\0000≈64亿六、将下面三个数分别四舍五入到十位、百位、千位、万位。
提高练习一、我来填一填(共30分,每空1分。
)1. 一个整数,从右数起,第五位是(万)位,第九位是(亿)位。
2. 万级的计数单位有(万)、(十万)、(百万)、(千万)万级的数位有(万位)、(十万位)、(百万位)、(千万位)3. 70050000是(8)位数,最高位是(千万)位,7表示(7个千万),5表示(5个万)。
4. 比最大的八位数多1的数是(100000000),比最小的九位数少1的数是(99999999)。
2021新高考化学鲁科版一轮复习学案:第1章第4讲 物质的量浓度及溶液的配制 Word版含解析

祝学长学业有成,取得好成绩Evaluation Only. Created with Aspose.Words. Copyright 2003-2016 Aspose Pty Ltd.第4讲物质的量浓度及溶液的配制【2021·备考】最新考纲素养落地1。
了解溶液浓度的表示方法。
理解溶液中溶质的质量分数和物质的量浓度的概念,并能进行有关计算.2。
掌握配制一定溶质质量分数溶液和物质的量浓度溶液的方法.由宏观数据——溶液的体积、物质的量浓度与溶质微粒数目的关系多视角层次地认识溶液;从实验实际出发,设计配制一定物质的量浓度溶液的方案,分析实验过程中存在的误差问题,发展学生的实验探究意识与批判意识。
错误!『知识梳理』1.溶液组成的两种表示方法(1)物质的量浓度错误!(1)物质的量浓度中的体积是指溶液的体积,不能用水的体积代替,如溶液混合,也不是两份溶液体积和。
(2)对于某浓度的溶液,取出任意体积的溶液,其浓度、密度、质量分数不变,但所含溶质的物质的量、质量则因体积不同而改变。
(2)质量分数①概念:用溶质的质量与溶液质量的比值来表示溶液组成的物理量,一般用百分数表示。
②表达式:饱和溶液(溶质的溶解度用S表示)w=错误!×100%2.有关物质的量浓度的计算(1)标准状况下气体溶质溶于水所得溶液浓度的计算错误!c=错误!(注意溶液体积的单位)(2)溶质的质量分数与物质的量浓度的换算计算公式:c=1 000ρwM(c为溶质的物质的量浓度,单位:mol·L-1,ρ为溶液密度,单位g·cm-3,w 为溶质的质量分数,M为溶质的摩尔质量,单位g·mol-1)。
错误!正确判断溶液的溶质(1)与水反应生成新物质如Na、Na2O、Na2O2错误!NaOHSO3错误!H2SO4NO2错误!HNO3(2)特殊物质如NH3溶于水后溶质为NH3·H2O,但计算浓度时仍以NH3作为溶质(3)含结晶水的物质CuSO4·5H2O―→CuSO4Na2CO3·10H2O―→Na2CO3[链接新教材]①(新教材LK第一册P305习题精选练)4 ℃时,100 mL水中溶解了22。
七年级上册地理第一章学案

第一章地球和地图第一节地球和地球仪第1课时地球的形状和大小地球的模型——地球仪班级姓名小组学习目标1.感知人类对地球形状的认识过程,感受前人不畏艰难的探索精神。
2.学会用相关数据说明地球的大小。
3.观察地球仪,说出它的基本构造,并尝试自制简易地球仪。
学习过程【基础链接】晴朗的白天,我们能够看到太阳像一个火红的圆球;十五的夜晚,我们可以看到月亮像明亮的圆盘。
站在地球表面,我们无法看到她的全貌;正如苏轼的一句诗“不识庐山真面目,只缘身在此山中”。
让我们寻着古人的足迹,经历认识地球形状和大小的全过程……【新课学习】学习主题一:地球的形状和大小一、阅读课本P2-3,感知人类认识地球形状的过程。
1.古代人凭直觉认识世界,对地球形状的认识是怎样的?2.最早证实地球是球体的事件是什么?3.人类如何确证地球是一个球体的?4.从这个认识过程中,你感悟到了什么?二、填出下面用来说明地球大小的数据:地球表面积;地球平均半径;最大周长。
学习主题二:地球的模型——地球仪三、阅读课本P4-5,认识地球仪。
1.地球仪的定义:人们地球的形状,并且按一定的把它缩小,制做了地球的模型——地球仪。
2.地球仪的作用:可以方便我们认识地球的,了解地球表面各种地理事物的。
【我的问题】请写出你自主学习后发现的问题:【拓展深化】你有自已的地球仪吗?观察它的结构和表面内容,写下你的发现。
达标检测一、选择题1.下列关于人类对地球形状的认识的叙述中,正确的是()A.自古以来,人们就认为地球是一个球体B.直到卫星照片成功拍摄,人们才认识到地球是一个球体C.人类对地球形状的认识,经历了一个漫长的过程D.麦哲伦环球航行的成功,足以证明地球是一个球体了2.有关地球形状的说法正确的是()A.天圆地方 B.是个球体 C.是个圆 D.以上说法都对3.下列关于地球大小的数据,描述正确的是()A.地球的极半径约6337千米B.地球的平均半径约是6371千米C.地球的体积约12830亿立方千米D.赤道的长度约是8万千米图1-14.下列有关地球仪的说法正确的是 ( ) A .地球仪就是地球本身B .地球仪是人们仿照地球的形状,并且按一定比例缩小而成的C .地轴是地球内的一根轴,离开它地球无法转动D .以上说法都不对 5.人们把地球仪做成标准球体,是因为 ( ) A .为了美观 B .为了便于地球仪转动C .地球赤道半径与极半径是相等的D .地球缩小到地球仪大小时,极半径与赤道半径的差别可以忽略不计二、综合题6.图1-1是“麦哲伦环球航行路线图”,读图并结合课本阅读材料,回答下列问题。
九年级化学上册第1章 精品学案(含答案WORD)

绪言化学使世界变得更加绚丽多彩知识点1 化学研究的内容化学是在分子、原子层次上研究物质性质、组成、结构与变化规律的科学。
知识点2 化学发展史(1)道尔顿和阿伏加德罗创立了原子论和分子学说,奠定了近代化学的基础,该理论认为:物质是由原子和分子构成的,分子中原子的重新组合是化学变化的基础。
(2)1869年,俄国化学家门捷列夫发现了元素周期律并编制出元素周期表,使化学学习和研究变得有规律可循。
知识点3 化学与人类的关系化学与我们的工农业生产、生活、国防密不可分,人类的衣、食、住、行、医疗、环保及新材料的研发都离不开化学。
1.(知识点1)下列关于物质的说法错误的是(D)A.看不见、摸不着的空气属于物质B.化学物质都是由微小的粒子构成的C.你的身体、课桌都属于物质D.化学物质都是有污染的2.(知识点2)下列关于化学史的认识错误的是(D)A.化学的发展离不开人们的生产实践B.原子论和分子学说的创立,奠定了近代化学的基础C.绿色化学使化学生产向着环境友好的方向发展D.火的发现和利用奠定了近代化学的基础3.(知识点2)根据化学发展的实际情况,下列顺序排列正确的是(C)①原子论和分子学说的创立②绿色化学的提出③门捷列夫发现了元素周期律并编制出元素周期表④火的利用和发现⑤利用先进仪器进行微观探测A.①②③④⑤B.②①④③⑤C.④①③⑤②D.④①⑤③②4.(知识点3)化学与生产、生活关系密切,以下说法你认为不正确的是(C)A.利用化学生产化肥和农药,可以增加粮食的产量B.利用化学合成药物,可以治疗疾病,保障人体健康C.塑料、合成纤维、合成橡胶的使用,对人类“有百利而无一害”D.开发利用氢能源,可减少化石燃料的使用,减缓空气的污染5.(知识点3)化学在使人类生活得更美好方面发挥了巨大的作用,请将下列化学研究内容与人类面临的问题用短线连接起来:合成药物环境问题生产化肥和农药健康问题发展绿色化学能源问题开发清洁能源粮食问题略6.(综合题)化学是以自然界的物质为研究对象,它研究物质性质、组成、结构与变化规律等。
初中语文第1章教案

初中语文第1章教案一、教学目标:1. 知识与技能:(1)能够正确地朗读课文,理解课文的大意。
(2)学习生字词,并能灵活运用到实际情景中。
(3)分析课文中的人物形象,理解作者通过人物描写所表现的主题思想。
2. 过程与方法:(1)通过自主学习、合作学习的方式,提高学生的语文素养。
(2)运用多媒体教学手段,直观地展示课文中所描述的场景,帮助学生更好地理解课文。
(3)开展课堂讨论,培养学生的思辨能力和口头表达能力。
3. 情感态度与价值观:(1)培养学生热爱大自然、珍惜友谊的美好情感。
(2)教育学生学会关爱他人,树立团结合作的意识。
二、教学重点:1. 正确朗读课文,理解课文大意。
2. 学习生字词,提高语文素养。
3. 分析人物形象,理解主题思想。
三、教学难点:1. 课文中一些生僻字词的理解和运用。
2. 人物形象的分析,主题思想的挖掘。
四、教学过程:1. 导入新课:(1)利用多媒体展示草原的图片,引导学生欣赏草原的美景。
(2)邀请学生分享他们对草原的了解和印象。
2. 自主学习:(1)让学生自主朗读课文,感受课文中所描绘的草原风光。
(2)学生自学生字词,组内交流学习心得。
3. 课堂讲解:(1)讲解生字词,帮助学生正确理解课文。
(2)分析课文结构,概括课文大意。
(3)详细讲解课文中所描述的人物形象,阐述作者通过人物描写所表现的主题思想。
4. 课堂讨论:(1)分组讨论,让学生发表自己对课文的理解和感悟。
(2)邀请学生代表分享讨论成果,教师点评并总结。
5. 课后作业:(1)要求学生熟读课文,巩固生字词。
(2)结合课文内容,写一篇关于草原的作文。
五、教学反思:本节课通过自主学习、课堂讲解和课堂讨论等多种教学手段,使学生对课文内容有了较为深入的理解。
在教学过程中,注意调动学生的积极性,激发他们的学习兴趣。
同时,通过课堂讨论,培养了学生的团队合作意识和口头表达能力。
但在教学过程中,也要注意对学生的学习情况进行全面了解,针对不同学生的需求进行针对性辅导,以提高教学效果。
新教材鲁科版必修第一册 第1章 第4节 加速度 学案

第4节加速度课标解读课标要求素养要求1.理解加速度的概念,知道速度、速度变化量和加速度三者之间的区别与联系。
2理解加速度的矢量性。
3.掌握比值定义法在形成加速度公式上的思维模式,学会运用公式来推导物理量单位的物理思维方式。
1.物理观念:通过对加速度的学习,促进学生运动的物理观念的形成。
2.科学思维:用类比的方法探究推理,培养学生运用类比的学习方法。
3.科学探究:通过对速度、速度的变化量、速度的变化率三者的比拟分析,提高学生的比拟、分析问题以及解决问题的能力。
4.科学态度与责任:通过具体问题分析,增强学生的交通平安意识。
要点加速度、速度的变化量在物理学中,物体运动速度的变化跟发生这一变化所用时间之比,称为物体运动的加速度❶,用字母a表示。
如果用v0表示物体运动的初速度,v t表示末速度,那么在时间t内物体运动速度的变化❷为v t-v0,加速度a可用定义式a=v t-v0t表示。
加速度的单位由速度和时间的单位确定。
加速度的单位是米/秒2。
加速度是矢量,其方向与速度变化的方向相同。
❶有同学认为,速度变化所用时间越短,加速度一定越大。
这种观点正确吗?提示这种观点是错误的。
由加速度的定义式可知,加速度由速度的变化量和所用时间两个因素共同定义的。
速度变化量越大,假设速度变化所用时间未知,故不能确定加速度一定越大;速度变化所用时间越短,假设速度变化量的大小未确定,故也不能确定加速度一定越大。
❷A、B、C、D四个物体均以恒定加速度运动,经过一段时间后的速度情况如下: 物体A运动的初速度为2m/s,末速度为5m/s;物体B运动的初速度为5m/s,末速度为3m/s;物体C运动的初速度为3m/s,末速度为-5m/s;物体D运动的初速度为-5m/s,末速度为-3m/s;那么物体A、B、C、D速度的变化量分别为多少?哪一个的速度变化量大,为什么?提示根据定义Δv=v t-v0,可知Δv A=3m/s,Δv B=-2m/s,Δv C=-8m/s,Δv D=2m/s,物体C的速度变化量最大,因为速度变化量是矢量,其“+〞“-〞表示速度变化的方向与规定的正方向相同或相反,绝对值才是速度变化量的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总课题 高三一轮复习----函数概念与基本初等函数 总课时8第7、8课时 课 题 推理与证明课型复习课教 学 目 标1、了解合情推理的含义,能利用归纳和类比等进行简单的推理;2、了解演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行一些简单推理;3、了解直接证明的两种基本方法——分析法和综合法,了解分析法和综合法的思考过程及特点;4、了解间接证明的一种基本方法——反证法,了解反证法的思考过程及特点。
教 学重 点合情推理与演绎推理、分析法与综合法、反证法。
教 学难 点演绎推理、反证法。
学 法指 导自主复习选修2-2教材,回顾以前所学,在充分自学和小组讨论的基础上完成导学案。
教 学准 备导学案导学 《步步高》一轮复习资料 自主学习高 考要 求1、合情推理与演绎推理 B2、分析法与综合法 A3、反证法A教 学 过 程师 生 互 动个案补充第7课时:一、基础知识梳理 1.推理从 得出另一个新命题的思维过程称为推理.推理一般分为 推理与 推理两类.推理⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧合情推理⎩⎪⎨⎪⎧⎩⎪⎨⎪⎧定义:由个别事实推演出 的结论.特点:是由 到整体、由 到一般的推理. ⎩⎪⎨⎪⎧定义:由两个(或两类)对象之间在某些方 面的相似或相同推演出它们在其他方面也相似或相同.演绎推理⎩⎪⎨⎪⎧模式:三段论⎩⎪⎨⎪⎧ ①大前提——已知的 ;②小前提——所研究的 ;③结论——根据一般原理,对作出的判断.特点:演绎推理是由 到 的推理.二、基础练习训练1.判断下面结论是否正确(请在括号中打“√”或“×”)(1)归纳推理得到的结论不一定正确,类比推理得到的结论一定正确. ( ) (2)由平面三角形的性质推测空间四面体的性质,这是一种合情推理. ( ) (3)在类比时,平面中的三角形与空间中的平行六面体作为类比对象较为合适.( )(4)“所有3的倍数都是9的倍数,某数m是3的倍数,则m一定是9的倍数”,这是三段论推理,但其结论是错误的. () (5)一个数列的前三项是1,2,3,那么这个数列的通项公式是a n=n(n∈N*). ()2.数列2,5,11,20,x,47,…中的x等于________.3.(2013·陕西)观察下列等式12=112-22=-312-22+32=612-22+32-42=-10……照此规律,第n个等式可为________.4.一切奇数都不能被2整除,2100+1是奇数,所以2100+1不能被2整除,其演绎推理的“三段论”的形式为大前提小前提结论三、典型例题分析题型一、归纳推理例1设f(x)=13x+3,先分别求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),然后归纳猜想一般性结论,并给出证明.变式:观察下列等式1=12+3+4=93+4+5+6+7=254+5+6+7+8+9+10=49…照此规律,第五个等式应为___________________.题型二、类比推理例2给出下列三个类比结论:①(ab)n=a n b n与(a+b)n类比,则有(a+b)n=a n+b n;②log a(xy)=log a x+log a y与sin(α+β)类比,则有sin(α+β)=sin αsin β;③(a+b)2=a2+2ab+b2与(a+b)2类比,则有(a+b)2=a2+2a·b+b2.其中结论正确的序号是________.变式:把一个直角三角形以两直角边为邻边补成一个矩形,则矩形的对角线长即为直角三角形外接圆直径,以此可求得外接圆半径r=a2+b22(其中a,b为直角三角形两直角边长).类比此方法可得三条侧棱长分别为a,b,c且两两垂直的三棱锥的外接球半径R=________. 小结:题型三、演绎推理例3指出对结论“已知2和3是无理数,证明2+3是无理数”的下述证明是否为“三段论”,证明有错误吗?变式:如图所示,D,E,F分别是BC,CA,AB上的点,∠BFD=∠A,且DE∥BA.求证:ED=AF(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来).小结:五、课堂总结:六、教(学)反思:七、课后作业1、《步练》P285 A组1、2、3、6;2、一轮复习作业纸4;第8课时:一、基础知识梳理1.直接证明综合法分析法定义从已知条件出发,以已知的定义、公理、定理为依据,逐步下推,直到推出要证明的结论为止.从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使结论成立的条件和已知事实吻合为止.思维过程由因导果执果索因证题步骤P(已知)⇒P1⇒P2⇒…⇒P n⇒Q(结论) Q(结论)⇐Q1⇐Q2⇐…⇐Q n⇐P(已知)文字语言因为…,所以…或由…,得…要证…,只需证…,即证…符号语言⇒⇐2.间接证明反证法定义要证明某一结论Q 是正确的,但不直接证明,而是先去假设Q 不成立(即Q 的反面非Q 是正确的),经过正确的推理,最后得出矛盾,因此说明假设非Q 是错误的,从而断定结论Q 是正确的,这种证明方法叫做反证法.证明步骤(1)反设——假设命题的结论不成立,即假定原结论的反面为真; (2)归谬——从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;(3)存真——由矛盾结果,断定反设不真,从而肯定原结论成立. 适用范围(1)否定性命题;(2)命题的结论中出现“至少”、“至多”、“唯一”等词语的; (3)当命题成立非常明显,而要直接证明所用的理论太少,且不容易说明,而其逆否命题又是非常容易证明的; (4)要讨论的情况很复杂,而反面情况很少.二、基础练习训练1.判断下面结论是否正确(请在括号中打“√”或“×”) (1)综合法是直接证明,分析法是间接证明. ( ) (2)分析法是从要证明的结论出发,逐步寻找使结论成立的充要条件. ( ) (3)用反证法证明结论“a >b ”时,应假设“a <b ”. ( ) (4)反证法是指将结论和条件同时否定,推出矛盾. ( ) (5)在解决问题时,常常用分析法寻找解题的思路与方法,再用综合法展现解决问题的过程. ( )2.若a ,b ,c 为实数,且a <b <0,则下列命题正确的是________.(填序号)①ac 2<bc 2 ②a 2>ab >b 2 ③1a <1b ④b a >ab3.若a >0,b >0,a +b =2,则下列不等式对一切满足条件的a ,b 恒成立的是________(写出所有正确命题的编号).①ab ≤1;②a +b ≤2;③a 2+b 2≥2;④a 3+b 3≥3;⑤1a +1b≥2.4.用反证法证明某命题时,对结论:“自然数a ,b ,c 中恰有一个偶数”正确的反设为 . 三、典型例题分析题型一、综合法例1 已知a ,b ,c 都是实数,求证:a 2+b 2+c 2≥ab +bc +ca .题型二、分析法例2 求证:3265->-小结:题型三、反证法例3 若a ,b ,c 均为实数,且a =x 2-2y +π2,b =y 2-2z +π3,c =z 2-2x +π6.求证:a ,b ,c 中至少有一个大于0.变式:已知a 、b 、c ∈(0,1),求证:(1-a )b ,(1-b )c ,(1-c )a 不能同时大于14.小结:四、当堂训练五、课堂总结:六、教(学)反思:七、课后作业1、《步练》P287 A 组1、2、3、5; 2、一轮复习作业纸4;一轮复习作业纸4:推理与证明1.(2010·珠海质检)给出下面类比推理命题(其中Q 为有理数集,R 为实数集,C 为复数集): ①“若a ,b ∈R ,则a -b =0⇒a =b ”类比推出“若a ,b ∈C ,则a -b =0⇒a =b ”;②“若a ,b ,c ,d ∈R ,则复数a +b i =c +d i ⇒a =c ,b =d ”类比推出“若a ,b ,c ,d ∈Q ,则a +b 2=c +d 2⇒a =c ,b =d ”;③“若a ,b ∈R ,则a -b >0⇒a >b ”类比推出“若a ,b ∈C ,则a -b >0⇒a >b ”.其中类比结论正确的序号为__________________2.(2010·陕西)观察下列等式:13+23=32,13+23+33=62,13+23+33+43=102,…,根据上述规律,第五个等式为________________________________.3.(2010·苏州统一测试)一切奇数都不能被2整除,2100+1是奇数,所以2100+1不能被2整除,其演绎推理的“三段论”的形式为________________________________________________________________________________________________________________________________________4、用综合法证明:设a ,b ,c >0,证明:a 2b +b 2c +c 2a≥a +b +c .5、用分析法证明:已知a >0,求证: a 2+1a 2-2≥a +1a-2.6、用反证法证明:若x ,y 都是正实数,且x +y >2,求证:1+x y <2与1+yx <2中至少有一个成立.。
