初一角线段易错题
部编数学七年级上册易错16角的计算(解析版)【突破易错·冲刺满分】含答案

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!【突破易错·冲刺满分】2021-2022学年七年级数学上册期末突破易错挑战满分(人教版)易错16角的计算【易错1例题】角的计算1-1.(2021·湖南宁乡·七年级期末)如图:点A,O,B在一条直线上,∠AOC=3∠COD,OE平分∠BOD.(1)若∠COD=10°,求∠BOE的度数;(2)若∠COE=75°,求∠COD的度数..【答案】(1)70°;(2)15°【分析】(1)先后求得∠AOC、∠AOD的度数,再利用角平分线的定义即可求得∠BOE的度数;(2)设∠COD的度数为x,则∠AOC=3x,∠EOD=∠COE-∠COD=75°-x,利用平角的定义列方程即可求得∠COD 的度数.【详解】解:(1)∵∠COD=10°,∴∠AOC=3∠COD=30°,∠AOD=∠AOC+∠COD=40°,∵点A,O,B在一条直线上,∴∠BOD=180°-∠AOD=140°,又OE平分∠BOD,∴∠BOE=12∠BOD=70°;(2)设∠COD的度数为x,则∠AOC=3x,∠EOD=∠COE-∠COD=75°-x,∴∠BOD=2∠EOD=150°-2x,∵点A,O,B在一条直线上,∴∠BOD+∠AOD=180°,即150°-2x+3x+x=180°,解得x=15°,即∠COD=15°.【点睛】本题考查了角平分线的定义余角和补角的知识,解题的关键是学会利用参数构建方程解决问题.1-2.(2021·湖南永定·七年级期末)如图1,直线AB经过点O,∠COD=90°,OE是∠BOC的平分线.(1)若∠AOC=130°,求∠DOE的度数;(2)若∠AOC=α,将图1中的∠COD绕顶点O逆时针旋转到图2的位置,其它条件不变,求∠DOE度数(用含α的式子表示).【答案】(1)65°;(2)180°﹣12α.【分析】(1)根据平角的定义得:∠BOC=180°-130°,由角平分线定义得:∠EOC= 12∠BOC=90°- 12×130°=25°,根据角的差可得结果;(2)根据平角的定义和角平分线的定义可得:∠DOE=∠COD+∠COE=180°- 12α.【详解】解:(1)∵∠AOC+∠BOC=180°,∠AOC=130°,∴∠BOC=180°﹣130°=50°,∵OE平分∠BOC,∴∠EOC=12∠BOC=25°,∵∠COD=90°,∴∠DOE=∠COD﹣∠COE=90°﹣25°=65°;(2)∵∠AOC+∠BOC=180°,∠AOC=α,∴∠BOC=180°﹣α,∵OE平分∠BOC,∴∠EOC=12∠BOC=90°﹣12α,∵∠COD=90°,∴∠DOE=∠COD+∠COE=90°+(90°﹣12α)=180°﹣12α.【点睛】本题主要考查了角平分线的定义,平角的定义及角的和与差,能根据图形确定所求角和已知各角的关系是解此题的关键.【专题训练】一、选择题1.(2021·黑龙江·肇源县超等蒙古族乡学校七年级期中)一个角的补角比这个角的余角大().A.70°B.80°C.90°D.100°【答案】C【分析】根据互补即两角的和为180°,互余的两角和为90°,设这个角为x,即可求出答案.【详解】解:设这个角为x,则这个角的补角为180°-x,这个角的补角为90°-x,根据题意得:180°-x-(90°-x)=90°,故选:C.【点睛】本题主要考查了余角和补角的概念与性质.互为余角的两角的和为90°,互为补角的两角之和为180°.2.(2021·辽宁西丰·七年级期末)如图,∠AOB=90°,∠BOC=15°,OC平分∠AOD,则∠BOD的度数是( )A .75°B .60°C .65°D .55°【答案】B 【分析】先求出∠AOC ,再根据角平分线的定义求出∠AOD ,然后根据∠BOD =∠AOD ﹣∠AOB 代入数据进行计算即可得解.【详解】解:∵∠AOB =90°,∠BOC =15°,∴∠AOC =∠AOB ﹣∠BOC =90°﹣15°=75°,∵OC 平分∠AOD ,∴∠AOD =2∠AOC =2×75°=150°,∴∠BOD =∠AOD ﹣∠AOB =150°﹣90°=60°,故选:B .【点睛】本题考查了角平分线的定义以及角的计算,熟记概念并准确识图是解题的关键.3.(2021·河南川汇·七年级期末)已知60AOB Ð=°,从顶点O 引一条射线OC ,若20AOC Ð=°,则BOC Ð=( )A .20°B .40°C .80°D .40°或80°【答案】D 【分析】分为两种情况:①当OC 在∠BOA 内部时,②当OC 在∠BOA 外部时,根据角之间的关系求出即可.【详解】解:分为两种情况:①当OC 在∠BOA 内部时,∠BOC =∠AOB -∠AOC =60°-20°=40°;②当OC 在∠BOA 外部时,∠BOC =∠AOB +∠AOC =60°+20°=80°.故选:D .【点睛】本题考查了角的有关计算的应用,主要考查了学生的计算能力,注意要进行分类讨论啊.4.(2021·全国·七年级课时练习)己知:2AOB AOM Ð=Ð;②12BOM AOB Ð=Ð;③12AOM BOM AOB Ð=Ð=Ð;④AOM BOM AOB Ð+Ð=Ð,其中能够得到射线OM 是AOB Ð的平分线的有( ).A .0个B .1个C .2个D .3个【答案】B 【分析】根据角平分线的定义逐个判断即可.【详解】解:①若OM 在∠AOB 的内部,2AOB AOM Ð=Ð,则OM 是AOB Ð的平分线,若OM 在∠AOB 的外部,则OM 不是AOB Ð的平分线,故①错误;②若OM 在∠AOB 的内部,12BOM AOB Ð=Ð,则OM 是AOB Ð的平分线,若OM 在∠AOB 的外部,则OM 不是AOB Ð的平分线,故②错误;③∵12AOM BOM AOB Ð=Ð=Ð,∴OM 在∠AOB 的内部,又∵AOM BOM Ð=Ð,∴OM 是AOB Ð的平分线,故③正确;④∵AOM BOM AOB Ð+Ð=Ð,∴OM 在∠AOB 的内部,但无法证明AOM BOM Ð=Ð,∴OM 不一定是AOB Ð的平分线,故④错误,故选:B .【点睛】本题考查了角的角平分线的定义,熟练掌握角平分线的定义是解决本题的关键.5.(2021·河北迁安·七年级期中)如图,∠AOB =α,OA 1、OB 1分别是∠AOM 和∠MOB 的平分线,OA 2、OB 2分别是∠A 1OM 和∠MOB 1的平分线,OA 3、OB 3分别是∠A 2OM 和∠MOB 2的平分线,…,OA n 、分别是∠A n -1OM 和∠MOB n -1的平分线,则∠A n OB n 的度数是( )A .anB .12n a -C .2na D .2a n 【答案】C 【分析】由∠AOB =α,OM 是∠AOB 中的一射线,可得∠AOM +∠MOB =α,由OA 1、OB 1分别是∠AOM 和∠MOB 的平分线,可得∠A 1OM =12AOM Ð,∠B 1OM =12BOM Ð,可得∠A 1OB 1=∠A 1OM +∠B 1OM =12AOM Ð+12BOM Ð=12a ,由OA 2、OB 2分别是∠A 1OM 和∠MOB 1的平分线,可求∠A 2OB 2=∠A 2OM +∠B 2OM =112A OM Ð+112B OM Ð=212a ,由OA 3、OB 3分别是∠A 2OM 和∠MOB 2的平分线,可求∠A 3OB 3=∠A 3OM +∠B 3OM =212A OM Ð+212B OMÐ=312a ,…,然后根据规律可求∠A n OB n =12n a .【详解】解:∵∠AOB =α,OM 是∠AOB 中的一射线,∴∠AOM +∠MOB =α,∵OA 1、OB 1分别是∠AOM 和∠MOB 的平分线,∴∠A 1OM =12AOM Ð,∠B 1OM =12BOMÐ∴∠A 1OB 1=∠A 1OM +∠B 1OM =12AOM Ð+12BOM Ð=()111222AOM BOM AOB a Ð+Ð=Ð=,∵OA 2、OB 2分别是∠A 1OM 和∠MOB 1的平分线,∴∠A 2OM =112A OM Ð,∠B 2OM =112B OM Ð,∴∠A 2OB 2=∠A 2OM +∠B 2OM =112A OM Ð+112B OM Ð=()11112111222A OM B OM AOB a Ð+Ð=Ð=,∵OA 3、OB 3分别是∠A 2OM 和∠MOB 2的平分线,∴∠A 3OM =212A OM Ð,∠B 3OM =212B OM Ð,∴∠A 3OB 3=∠A 3OM +∠B 3OM =212A OM Ð+212B OM Ð=()22223111222A OM B OM A OB a Ð+Ð=Ð=,…,∵OA n 、分别是∠A n -1OM 和∠MOB n -1的平分线,∴∠A n OM =112n A OM -Ð,∠B n OM =112n B OM -Ð,∴∠A n OB n =∠A n -1OM +∠B n -1OM =112n A OM -Ð+112n B OM -Ð=()1111111222n n n n n A OM B OM A OB a ----Ð+Ð=Ð=,故选择C .【点睛】本题考查角的和,与角平分线的定义,规律探索,利用角平分线求出∠A 1OB 1,∠A 2OB 2,∠A 3OB 3,找出规律是解题关键.二、填空题6.(2021·河北滦州·七年级期中)如图所示,90AOC Ð=°,点B ,O ,D 在同一直线上,若126Ð=°,则2Ð的度数为______.【答案】116°【分析】由图示可得,∠1与∠BOC 互余,结合已知可求∠BOC ,又因为∠2与∠COB 互补,即可求出∠2的度数.【详解】解:∵126Ð=°,∠AOC =90°,∴∠BOC=64°,∵∠2+∠BOC=180°,∴∠2=116°.故答案为:116°.【点睛】此题考查了余角和补角的知识,属于基础题,关键是掌握互余的两角之和为90°,互补的两角之和为180°.7.(2021·全国·七年级专题练习)如图所示,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:11,则∠AOB =_______.【答案】20°【分析】由∠AOB+∠BOC=∠BOC+∠COD知∠AOB=∠COD,设∠AOB=2α,则∠AOD=11α,故∠AOB+∠BOC=5α=90°,解得α即可.【详解】解:∵∠AOB+∠BOC=∠BOC+∠COD,∴∠AOB=∠COD,设∠AOB=2α,∵∠AOB:∠AOD=2:11,∴∠AOB+∠BOC=9α=90°,解得α=10°,∴∠AOB=20°.故答案为20°.【点睛】此题主要考查了角的计算以及余角和补角,正确表示出各角度数是解题关键.8.(2021·陕西神木·七年级期末)如图,已知∠BAE=∠CAF=110°,∠CAE=60°,AD是∠BAF的平分线,则∠BAD的度数为___°.【答案】80【分析】由∠BAE=110°,∠CAE=60°,可得∠BAC=110°﹣60°=50°,结合∠CAF=110°,可得∠BAF=110°+50°=160°,再由AD平分∠BAF即可得∠BAD=80°.【详解】∵∠BAE=110°,∠CAE=60°,∴∠BAC=110°﹣60°=50°,又∵∠CAF=110°,∴∠BAF=110°+50°=160°,又∵AD是∠BAF的角平分线,∴∠BAD=12∠BAF=12×160°=80°.故答案为:80.【点睛】本题主要考查了角平分线的定义和几何中角度的计算,解题的关键在于能够熟练掌握角平分线的定义.9.(2021·江西·南昌市心远中学七年级期末)如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若ABFÐ比EBFÐ大18°,则EBCÐ的度数是___________________度.【答案】24【分析】根据折叠角相等和正方形各内角为直角的性质即可求得∠EBF 的度数.【详解】解:∵∠FBE 是∠CBE 折叠形成,∴∠FBE =∠CBE ,∵∠ABF -∠EBF =18°,∠ABF +∠EBF +∠CBE =90°,∴∠EBF +18°+∠EBF +∠EBF +=90°,∴∠EBF =∠EBC = 24°,故答案为:24.【点睛】本题考查了折叠的性质,考查了正方形各内角为直角的性质,本题中求得∠FBE =∠CBE 是解题的关键.10.(2021·全国·七年级课时练习)如图,AOB Ð的内部有射线OC 、OD ,且AOC BOC Ð=Ð,12COD AOC Ð=Ð,则OC 是_______的平分线,OC 是_______的一条三等分线,OC 也是_______的一条四等分线,OD 是_______的平分线,OD 也是_______的一条四等分线.【答案】AOB ÐBOD Ð AOB Ð AOC Ð AOB Ð【分析】根据角平分线及三等分线和四等分线的定义逐个判断即可.解:∵AOC BOC Ð=Ð,∴OC 是AOB Ð的平分线,∵12COD AOC Ð=Ð,AOC BOC Ð=Ð,∴12Ð=ÐCOD BOC ,∴13COD BOD Ð=Ð,∴OC 是BOD Ð的一条三等分线,∵12COD AOC Ð=Ð,AOC BOC Ð=Ð,∴14AOD COD AOB Ð=Ð=Ð,∴OC 、OD 是AOB Ð的两条四等分线,∵12COD AOC Ð=Ð,∴OD 是AOC Ð的平分线,故答案为:AOB Ð;BOD Ð;AOB Ð;AOC Ð;AOB Ð.【点睛】本题考查了角的角平分线及三等分线和四等分线的定义,熟练掌握角平分线的定义是解决本题的关键.三、解答题11.(2021·湖南涟源·七年级月考)如图,直线AB 、CD 相交于O ,90EOC Ð=°,OF 是AOE Ð的角平分线,34COF Ð=°,求BOD Ð的度数.【答案】22°【分析】利用角的和差关系和角平分线定义可得∠AOF 的度数,然后计算出∠AOC 的度数,再根据对顶角相等可得∠BOD 的度数.解:∵∠EOC=90°,∠COF=34°,∴∠EOF=90°-34°=56°,又∵OF平分∠AOE,∴∠AOF=∠EOF=56°,∵∠COF=34°,∴∠AOC=56°-34°=22°,则∠BOD=∠AOC=22°.【点睛】本题考查的是角平分线的定义、余角和补角,对顶角,掌握它们的概念是解题的关键.12.(2021·甘肃瓜州·七年级期末)如图,已知O是直线AB上的一点,∠COD是直角,OE平分∠AOD.(1)如图1,若∠COE=20°,则∠DOB的度数为 °;(2)将图1中的∠COD放置图2的位置,其他条件不变,探究∠COE和∠DOB之间的数量关系,并说明理由.【答案】(1)40;(2)∠DOB=2∠COE,理由见解析【分析】(1)根据∠COD是直角,∠COE=20°可得∠EOD=70°,由OE平分∠AOD,可得∠AOD=140°,从而可得∠DOB =40°.(2)先根据∠COE与∠AOD之间的关系转化出∠AOD=180°﹣2∠COE,再根据∠DOB=180°﹣∠AOD这一关系代入化简即可得出∠DOB=2∠COE.【详解】解:(1)∵∠COD是直角,∠COE=20°,∴∠EOD=70°,又∵OE平分∠AOD,∴∠AOD=2∠EOD=140°,∴∠DOB=180°﹣∠AOD=40°.故答案为:40.(2)∠DOB=2∠COE.∵∠COD是直角,OE平分∠AOD,∴∠DOE=12∠AOD,∴∠COE=∠COD﹣∠DOE=90°﹣12∠AOD,∴∠AOD=180°﹣2∠COE,∴∠DOB=180°﹣∠AOD=180°﹣(180°﹣2∠COE)=2∠COE.【点睛】本题主要考查角度的计算和角平分线的定义,正确进行角度之间的转化是解题的关键.13.(2021·全国·七年级专题练习)如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.(1)求∠EOF的度数;(2)若∠AOC=x°,∠EOF=y°.则请用x的代数式来表示y;(3)如果∠AOC+∠EOF=156°,则∠EOF是多少度?【答案】(1)45°;(2)y=45°与x无关;(3)45°【分析】(1)根据角平分线的定义得:∠EOC=12∠AOC,∠COF=12∠BOC,而∠EOF=∠EOC-∠COF,据此解答;(2)利用(1)中的方法进行计算即可;(3)通过第(1)、(2)的计算,发现∠EOF=12∠AOB.【详解】解:(1)∵∠AOB 是直角,∠BOC =60°,∴∠AOC =∠AOB +∠BOC =90°+60°=150°,∵OE 平分∠AOC ,OF 平分∠BOC ,∴∠EOC =12∠AOC =12×150°=75°,∠COF =12∠BOC ==30°,∴∠EOF =∠EOC -∠COF =75°-30°=45°;(2)∵∠AOB 是直角,∠AOC =x °,∴∠BOC =∠AOC -∠AOB =x °-90°,∵OE 平分∠AOC ,OF 平分∠BOC ,∴∠EOC =12∠AOC = 12x °,∠COF =12∠BOC =12(x °-90°),∴∠EOF =∠EOC -∠COF =12x °-12(x °-90°)=45°;(3)根据(2)的规律发现,∠EOF 的度数只与∠AOB 有关,∠EOF =12∠AOB =12×90°=45°.【点睛】此题考查了角的计算与角平分线的定义.此题注意掌握数形结合思想与方程思想的应用.14.(2021·四川省成都市石室联合中学七年级开学考试)已知110AOB Ð=°,40COD Ð=°,OE 平分AOC Ð,OF 平分BOD Ð.(1)如图,当OB 、OC 重合时,求AOE BOF Ð-Ð的值;(2)若COD Ð从上图所示位置绕点O 以每秒3°的速度顺时针旋转t 秒(0t 10<<),在旋转过程中AOE BOF Ð-Ð的值是否会因t 的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.【答案】(1)35°;(2)是定值,35°【分析】(1)首先根据角平分线的定义求得∠AOE和∠BOF的度数,然后根据∠AOE-∠BOF求解;(2)首先由题意得∠BOC=3t°,再根据角平分线的定义得∠AOC=∠AOB+3t°,∠BOD=∠COD+3t°,然后由角平分线的定义得∠AOE=∠AOE=12∠AOC=12(110°+3t°),∠BOF=12∠BOD=12(40°+3t°),最后根据∠AOE-∠BOF求解可得.【详解】解:(1)∵OE平分∠AOC,OF平分∠BOD,∴∠AOE=12∠AOB=12×110°=55°,∠BOF=12∠COD=12×40°=20°,∴∠AOE-∠BOF=55°-20°=35°;(2)∠AOE-∠BOF的值是定值,如图2,由题意∠BOC=3t°,则∠AOC=∠AOB+3t°,∠BOD=∠COD+3t°,∵OE平分∠AOC,OF平分∠BOD,∴∠AOE=12∠AOC=12(110°+3t°),∠BOF=12∠BOD=12(40°+3t°),∴∠AOE-∠BOF=12(110°+3t°)-12(40°+3t°)=35°,∴∠AOE-∠BOF的值是定值.【点睛】本题考查了角度的计算以及角的平分线的性质,理解角度之间的和差关系是关键.15.(2021·广西南宁·七年级期末)如图,己知120AOBÐ=°,OC是AOBÐ内的一条射线,且:1:2AOC BOCÐÐ=.(1)求AOC Ð,BOC Ð的度数:(2)作射线OM 平分AOC Ð,在BOC Ð内作射线ON ,使得:1:3CON BON ÐÐ=,求MON Ð的度数;(3)过点O 作射线OD ,若23AOD BOD Ð=Ð,求COD Ð的度数.【答案】(1)40AOC =o ∠,80BOC Ð=o ;(2)40MON=Ðo ;(3)=32COD Ðo 或=176COD Ðo【分析】(1)由120AOB Ð=°,:1:2AOC BOC ÐÐ=即可求出AOC Ð,BOC Ð的度数;(2)由80BOC Ð=o ,:1:3CON BON ÐÐ=,求出CON Ð;由OM 平分AOC Ð,且40AOC =o ∠,求出COM Ð的度数;然后由MON=CON COM ÐÐ+Ð得到结果;(3)分类讨论,画出相关图形,当射线OD 在AOB Ð内部时,根据条件,计算出相关角度,由COD BOC BOD Ð=Ð-Ð,得到结果;当射线OD 在AOB Ð外部时,由+COD BOC BOD Ð=ÐÐ,得到结果.【详解】解:(1)∵120AOB Ð=°,:1:2AOC BOC ÐÐ=∴1120403AOC Ð=´=o o ,2120803BOC Ð=´=o o (2)∵80BOC Ð=o ,:1:3CON BON ÐÐ=∴180204CON Ð=´=o o又∵射线OM 平分AOC Ð,且40AOC =o∠∴140202COM Ð=´=o o∴202040MON=CON COM +=ÐÐ+Ð=o o o(3)分两种情况,讨论:①当射线OD 在AOB Ð内部时,作图如下:∵23AOD BODÐ=Ð∴ 32AOD BOD Ð=Ð 又∵AOD BOD AOB Ð+Ð=Ð,且120AOB Ð=o ∴3+=1202BOD BOD ÐÐo ∴2=120=485BOD дo o ,3=722AOD BOD Ð=Ðo 又∵COD BOC BODÐ=Ð-Ð∴804832COD Ð=-=o o o②当射线OD 在AOB Ð外部时,作图如下:∵++360AOD BOD AOB ÐÐÐ=o 且120AOB Ð=o∴+240AOD BOD ÐÐ=o又∵23AOD BODÐ=Ð∴3+=2402BOD BOD ÐÐo ∴2=240=965BOD дo o ,3=1442AOD BOD Ð=Ðo 又∵+COD BOC BODÐ=ÐÐ∴80+96=176COD Ð=o o o综上所述,=32COD Ðo 或=176COD Ðo【点睛】本题考查的是角度的计算,角平分线的性质等,利用分类讨论思想解题是关键.16.(2021·全国·七年级课时练习)如图,OM 是AOC Ð的平分线,ON 是BOC Ð的平分线.(1)如图1,当AOB Ð是直角,60BOC Ð=°时, NOC Ð=________,MOC Ð=________ ,MON Ð=________;(2)如图2,当AOB a Ð=,60BOC Ð=°时,猜想:MON Ð与a 的数量关系,并说明理由;(3)如图3,当AOB a Ð=,BOC b Ð= (b 为锐角)时,猜想:MON Ð与a 、b 有数量关系吗?如果有,请写出结论,并说明理由.【答案】(1)30°,75°,45°;(2)12MON Ð=a ,理由见解析;(3)有,12MON Ð=a ,理由见解析.【分析】(1)观察图形,结合角平分线的定义可得11603022NOC BOC ÐÐ==´°=°,09060150AOC AOB B C Ð=Ð+Ð=°+°=°,111507522MOC AOC ÐÐ===°´°即可求解;(2)观察图形,结合角平分线的定义可得60AOC AOB BOC ÐÐÐa =+=+°,11603022NOC BOC ÐÐ==´°=°,11303022MON MOC NOC ÐÐÐa a =-=+°-°=即可求解;(3)观察图形,结合角平分线的定义可得AOC AOB BOC a b Ð=Ð+Ð=+,1122NOC BOC b Ð=Ð=,111()222MON MOC NOC ÐÐÐa b b a =-=+-=即可求解;【详解】解:(1)∵ON 平分BOC Ð,∴11603022NOC BOC ÐÐ==´°=°, ∴09060150AOC AOB B C Ð=Ð+Ð=°+°=°,∵OM 是AOC Ð的平分线,∴111507522MOC AOC ÐÐ===°´°,∴753045MON MOC NOC ÐÐÐ=-=°-=°°;故答案为:30°,75°,45°;(2)12MON Ð=a .理由:60AOC AOB BOC ÐÐÐa =+=+°,OM 是AOC Ð的平分线,()1116030222MOC AOC ÐÐa a °==+=+°,因为ON 平分BOC Ð,所以11603022NOC BOC ÐÐ==´°=°,11303022MON MOC NOC ÐÐÐa a =-=+°-°=;(3)12MON Ð=a .理由:因为ON 平分BOC Ð,所以1122NOC BOC b Ð=Ð=,又因为AOC AOB BOC a b Ð=Ð+Ð=+,OM 是AOC Ð的平分线,所以11()22MOC AOC ÐÐa b ==+,111()222MON MOC NOC ÐÐÐa b b a =-=+-=.【点睛】本题主要考查了角平分线的定义及角的运算,解题的关键是掌握角平分线的定义并通过观察图形找到角与角之间的关系.17.(2021·黑龙江·哈尔滨市松雷中学校七年级月考)已知,O 是直线AB 上的一点,OC ⊥OE .(1)如图①,若∠COA =34°,求∠BOE 的度数.(2)如图②,当射线OC 在直线AB 下方时,OF 平分∠AOE ,∠BOE =130°,求∠COF 的度数.(3)在(2)的条件下,如图③,在∠BOE 内部作射线OM ,使∠COM +1710∠AOE =2∠BOM +∠FOM ,求∠BOM 的度数.【答案】(1)56°;(2)65°;(3)75°【分析】(1)根据平角的性质即可求解.(2)根据平角的性质先求出∠AOE ,再利用角平分线的性质求出∠EOF ,根据垂直的定义即可求解.(3)设∠BOM的度数为x,分别表示出∠COM,∠FOM,根据∠COM+1710∠AOE=2∠BOM+∠FOM列出方程,故可求解.【详解】(1)∵OC⊥OE,∠COA=34°,∴∠BOE=180°-90°-34°=56°;(2)∵∠BOE=130°,∴∠AOE=180°-∠BOE=50°∵OF平分∠AOE,∴∠EOF=12∠AOE=25°=∠AOF∵OC⊥OE.∴∠COF=90°-∠EOF=65°;(3)∵OC⊥OE,∴∠AOC=90°-∠AOE=40°设∠BOM的度数为x∴∠COM=∠AOC+∠AOM=40°+180°-x=220°-x,∠FOM=∠AOM-∠AOF=180°-x-25°=155°-x∵∠COM+1710∠AOE=2∠BOM+∠FOM,∴220°-x+1710×50°=2x+155°-x解得x=75°∴∠BOM的度数为75°.【点睛】此题主要考查角度的求解,解题的关键是熟知平角的性质、角平分线的性质及一元一次方程的应用.18.(2021·河北迁安·七年级期中)如图1,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.观察分析:(1)如图1,若∠MOC =28°,则∠BON 的度数为 ;(2)若将三角形MON 绕点O 旋转到如图2所示的位置,若∠BON =100°,求∠MOC 的度数.猜想探究:(3)若将三角形 MON 绕点O 旋转到如图3所示的位置,请你猜想∠BON 和∠MOC 之间的数量关系,并说明理由.【答案】(1)56°;(2)50°;(3)2BON MOC Ð=Ð,见解析【分析】(1)根据直角的定义求得NOC Ð的度数,根据角平分线的定义求得AOC CON Ð=Ð,进而根据平角的定义求得BON Ð;(2)根据平角的定义求得AON Ð,根据角平分线的定义求得AOC Ð,进而求得AOM ∠,根据MOC AOM AOC Ð=Ð+Ð即可求得∠MOC 的度数;(3))根据平角的定义求得AOC NOC Ð=Ð,根据图形可知90AOC NOC MOC °Ð=Ð=-Ð,进而根据1802BON NOC °Ð=-Ð即可得出2BON MOC Ð=Ð.【详解】解:(1)902862NOC MON MOC Ð=Ð-Ð=°-°=°Q 又Q OC 平分∠AON ,62AOC CON \Ð=Ð=°622834AOM AOC MOC \Ð=Ð-Ð=°-°=°180180349056BON AOM MON \Ð=°-Ð-Ð=°-°-°=°故答案为:56°(2)100BON °Ð=Q 80AON °\Ð=Q OC 平分AON Ð40AOC CON °\Ð=Ð=9010AOM AON °°Ð=-Ð=Q 50MOC AOM AOC °\Ð=Ð+Ð=(3)MOC Ð和BON Ð之间的数量关系2BON MOC Ð=ÐQ OC 平分AONÐAOC NOC\Ð=Ð90MON °Ð=Q 90AOC NOC MOC°\Ð=Ð=-Ð18021802(90)2BON NOC MOC MOC °°°\Ð=-Ð=--Ð=Ð即:2BON MOCÐ=Ð【点睛】本题考查了角平分线的定义,垂直的定义,平角的定义,掌握角度的计算是解题的关键.。
初一上册数学线段图形初步易错题

(1)CB ADA B C M N 数学易错题知识点一:对公式的运用。
例1、如图1,线段AD 上有两点B 、C,图中共有______条线段. 例2、下图中一共有______个角。
例3、99条直线最多有______个交点。
例4、两个火车站之间有6个站,则一共要准备______种车票例5、某次宴会一共有50人参加,每两人握一次手,则一共握______次手知识点二:两个定理运用 1、两点确定一条直线 2、两点之间线段最短例1、如图2,从家A 上学时要走近路到学校B ,最近的路线为 (填序号),理由是 ;例2、在墙上固定木条,至少需要 个钉子,理由 例3、AB 两地架设电线总是沿着直线架设,理由知识点三、线段的计算例1、如图,已知线段AB ,C 点分线段AB 为5:7两部分,D 点分线段AB 为5:11两部分,若CD=1,则AB 长度是多少?例2、如图,点C 在线段AB 上,AC = 8厘米,CB = 6厘米,点M 、N 分别是AC 、BC 的中点。
求线段MN 的长;例3、如图9,AD=12BD,E是BC的中点,BE=2cm,AC=10cm,求线段DE的长.例4、已知:如图(7),B 、C 是线段AD 上两点,且AB :BC :CD =2:4:3,M是AD 的中点,CD =6㎝,求线段MC 的长。
知识点四、角的计算,钟的认识C BDE F(1)(2)(3)图2 图9ADCBE1、钟的认识例1、晚上8点后,再过多少分钟时针与分针再次重合?例2、曼切斯特德比于9:38开始,此时时针与分针的夹角是多少度?例3、新闻联播每天于7:30结束,请问再过多少分钟时针与分针重合?例4、15、时钟表面11点28分时,时针与分针所夹角的度数是多少?2、角的换算:例1:25°20′24″=______度.42.79= 度 分 秒;例2、75°30′36″=______度. 31.56= 度 分 秒;例3、56°43′16″=______度.43.96= 度 分 秒;练习一、选择题:(每题3分,共18分)1、下列语句正确的是( )A 、平角就是一条直线B 、周角就是一条射线C 、小于平角的角是钝角D 、一周角等于四个直角 2、下列说法中,正确的有( )A 过两点有且只有一条直线 B.连结两点的线段叫做两点的距离 C.两点之间,直线最短 D .AB =BC ,则点B 是线段AC 的中点3、如图,点B 、C 是线段AD 上任意两点,M 是AB 的中点,N 是CD 的中点。
七年级角的计算易错题总结(含答案)

七年级角的计算易错题总结(含答案)一、填空题(本大题共3小题,共9.0分)1.如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”,如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ=______(用含α的式子表示).【答案】12α或13α或23α【解析】解:如图2,PQ平分∠MPN,即∠MPN=2∠MPQ=2∠NPQ,∵∠MPN=α,∴∠MPQ=12α;如图3,PQ是∠MPN的3等分线,即∠NPQ=2∠MPQ,∴∠MPQ=13α;如图4,PQ是∠MPN的3等分线,即∠MPQ=2∠NPQ,∴∠MPQ=23α;故答案为:12α或13α或23α.分3种情况,根据巧分线定义即可求解.本题考查了旋转的性质,巧分线定义,学生的阅读理解能力及知识的迁移能力.理解“巧分线”.的定义是解题的关键.2.如图是一副三角尺拼成的图案,其中∠ACB=∠EBD=90°,∠A=30°,∠ABC=60°,∠E=∠EDB=45°.若∠EBC=4∠ABD,则∠ABD的度数为______.【答案】30°【解析】解:∵∠EBC=4∠ABD,∴设∠ABD=x,则∠EBC=4x.∵∠DBE=90°,∠ABC=60°,∴∠DBC=60°−x,∴∠EBC=90°+60°−x=150°−x,∴150°−x=4x,∴x=30°,即∠ABD=30°.故答案为:30°.设∠ADB=x,则∠EBC=4x,根据题意列方程即可得到结论.本题主要考查了角的计算,数形结合是解答此题的关键.3.如图所示,AO⊥BO,CO⊥DO,∠AOC:∠BOC=1:4,则∠BOD=_________.【答案】150°【解析】【分析】本题主要考查了垂直的定义,周角的定义,熟记定义是解题的关键.由AO⊥BO,∠AOC:∠BOC=1:4,可求得∠AOC,再根据周角的定义求得结果.【解答】解:设∠AOC=x,∠BOC=4x,∴∠AOB=3x,∵AO⊥BO,∴3x=90°,∴x=30°,∴∠BOD=360°−90°−90°−30°=150°,故答案为:150°.二、计算题(本大题共1小题,共6.0分)4.将一副直角三角板按如图1摆放在直线AD上(直角三角板OBC和直角三角板MON,∠OBC=90°,∠BOC=45°,∠MON=90°,∠MNO=30°),保持三角板OBC不动,).将三角板MON绕点O以每秒8°的速度顺时针方向旋转t秒(0<t<454(1)如图2,∠NOD=______度(用含t的式子表示);(2)在旋转的过程中,是否存在t的值,使∠NOD=4∠COM?若存在,请求出t的值;若不存在,请说明理由.(3)直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒2°的速度顺时针旋转.①当t=______秒时,∠COM=15°;②请直接写出在旋转过程中,∠NOD与∠BOM的数量关系(关系式中不能含t).【答案】解:(1)∠NOD一开始为90°,然后每秒减少8°,因此∠NOD=90°−8t,故答案为(90−8t)(2)当MO在∠BOC内部时,即t<45时890°−8t=4(45°−8t)解得:t=154时当MO在∠BOC外部时,即t>45890°−8t=4(8t−45°)解得:t=274时(3)①当MO在∠BOC内部时,即t<4588t−2t=30°解得:t=5时当MO在∠BOC外部时,即t>4588t−2t=60°解得:t=10,故答案为5或10②∠NOD=90°−8t,∠BOM=6t∴3∠NOD+4∠BOM=3(90°−8t)+4×6t=270°即3∠NOD+4∠BOM=270°,故答案为:3∠NOD+4∠BOM=270°.【解析】(1)把旋转前∠NOD的大小减去旋转的度数就是旋转后的∠NOD的大小.(2)相对MO与CO的位置有两种情况,所以要分类讨论,然后根据∠NOD=4∠COM建立关于t的方程即可.(3)①其实是一个追赶问题,分MO没有追上CO与MO超过CO两种情况,然后分别列方程即可.②分别用t的代数式表示∠NOD和∠BOM,然后消去t即可得出它们的关系.本题一元一次方程和图象变换相结合的题目,考查了一元一次方程的应用,渗透了分类的思想方法.三、解答题(本大题共13小题,共104.0分)5.如图所示,OB,OC是∠AOD内的两条射线,OM和ON分别是∠AOB和∠COD内部的一条射线,且∠AOD=α,∠MON=β.(1)当∠AOM=∠BOM,∠DON=∠CON时,试用含α和β的代数式表示∠BOC.(2)①当∠AOM=2∠BOM,∠DON=2∠CON时,∠BOC等于多少(用含α和β的代数式表示)?②当∠AOM=3∠BOM,∠DON=3∠CON时,∠BOC等于多少(用含a和β的代数式表示)?(3)根据上面的结果,当∠AOM=n∠BOM,∠DON=n∠CON时,∠BOC=_________(n是正整数,用含α和β的代数式表示).【答案】解:(1)∵∠AOM=∠BOM=12∠AOB,∠CON=∠DON=12∠COD,∵∠BOC=∠MON−∠BOM−∠CON=∠MON−12∠AOB−12∠COD=∠MON−1 2(∠AOB+∠COD)=∠MON−12(∠AOD−∠BOC)=β−12(α−∠BOC)=β−12α+12∠BOC,则∠BOC=2β−α;(2)①当∠AOM=2∠BOM,∠DON=2∠CON时,∵∠BOM+∠CON=12(∠AOM+∠DON)=12(α−β),∴∠BOC=∠MON−(∠BOM+∠CON)=β−12(α−β)=32β−12α;②当∠AOM=3∠BOM,∠DON=3∠CON时,∵∠BOM+∠CON=13(∠AOM+∠DON)=13(α−β),∴∠BOC=∠MON−(∠BOM+∠CON)=β−13(α−β)=43β−13α;(3)n+1nβ−1nα【解析】(1)见答案;(2)见答案;(3)当∠AOM=n∠BOM,∠DON=n∠CON时,∵∠BOM+∠CON=1n (∠AOM+∠DON)=1n(α−β),∴∠BOC=∠MON−(∠BOM+∠CON)=β−1n (α−β)=n+1nβ−1nα;故答案为:n+1n β−1nα.【分析】(1)根据∠BOC=∠MON−∠BOM−∠CON,等量代换即可表示出∠BOC的大小;(2)①当∠AOM=2∠BOM,∠DON=2∠CON时,等量代换即可表示出∠BOC的大小;②当∠AOM=3∠BOM,∠DON=3∠CON时,等量代换即可表示出∠BOC的大小;(3)当∠AOM=n∠BOM,∠DON=n∠CON时,等量代换即可表示出∠BOC的大小;此题考查了角的计算,以及角平分线定义,利用了等量代换的思想,熟练掌握角平分线定义是解本题的关键.6.已知∠AOC和∠BOC是互为邻补角,∠BOC=50∘,将一个三角板的直角顶点放在点O处(注:∠DOE=90∘,∠DEO=30∘).(1)如图1,使三角板的短直角边OD与射线OB重合,则∠COE=______.(2)如图2,将三角板DOE绕点O逆时针方向旋转,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线.∠AOE时,求∠BOD的(3)如图3,将三角板DOE绕点O逆时针转动到使∠COD=14度数.(4)将图1中的三角板绕点O以每秒5∘的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,OE恰好与直线OC重合,求t的值.【答案】(1)40°,(2)∵OE平分∠AOC,∴∠COE=∠AOE=1∠COA,2∵∠EOD=90°,∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,∴∠COD=∠DOB,∴OD所在射线是∠BOC的平分线;(3)设∠COD=x°,则∠AOE=4x°,∵∠DOE=90°,∠BOC=50°,∴5x=40,∴x=8,即∠COD=8°∴∠BOD=58°.(4)如图,分两种情况:在一周之内,当OE与射线OC的反向延长线重合时,三角板绕点O旋转了140°,5t=140,t=28;当OE与射线OC重合时,三角板绕点O旋转了320°,5t=320,t=64.所以当t=28秒或64秒时,OE与直线OC重合.综上所述,t的值为28或64.【解析】【解析】∵∠BOE=∠COE+∠COB=90°,又∵∠BOC=50°,∴∠COE=40°,故答案为:40°;(2)见答案;(3)见答案.(4)见答案.(1)代入∠BOE=∠COE+∠COB求出即可;(2)求出∠AOE=∠COE,根据∠DOE=90°求出∠AOE+∠DOB=90°,∠COE+∠COD= 90°,推出∠COD=∠DOB,即可得出答案;(3)根据平角等于180°求出即可;(4)分两种情况:在一周之内,当OE与射线OC的反向延长线重合时,三角板绕点O 旋转了140°;当OE与射线OC重合时,三角板绕点O旋转了320°;依此列出方程求解即可.本题考查了角平分线定义和角的计算,能根据图形和已知求出各个角的度数是解此题的关键.7.(1)已知∠AOB=25°42′,则∠AOB的余角为____,∠AOB的补角为____;(2)已知∠AOB=α,∠BOC=β,OM平分∠AOB,ON平分∠BOC,用含α,β的代数式表示∠MON的大小;(3)如图,若以OA、OB中的一条为钟表上的时针,另一条为分针,且∠AOB=65°,时针在3点到4点之间,求此刻的时间.【答案】解:(1)64°18′;154°18′;(2)①如图1:∵∠AOB=α,∠BOC=β,∵OM平分∠AOB,ON平分∠BOC,∴∠AOM=∠BOM=12∠AOB=12α,∠CON=∠BON=12∠COB=12β,∴∠MON=∠BOM+∠CON=α+β2;②如图2,∠MON=∠BOM−∠BON=α−β2;③如图3,∠MON =∠BON −∠BOM =β−α2.∴∠MON 为α+β2或α−β2或β−α2.(3)设在下午3点至4点之间,从下午3点开始,经过x 分钟,时针与分针成65°角. ①当分针在时针上方时,由题意得:(3+x60)×30−6x =65, 解得:x =5011②当分针在时针下方时, 由题意得:6x −(3+x60)×30=65 解得:x =31011.∴此刻的时间为3点5011分或3点31011分. 【解析】 【分析】此题考查了余角和补角,角的计算以及钟面角,解题时注意:分针60分钟转一圈,每分钟转动的角度为:360°÷60=6°;时针12小时转一圈,每分钟转动的角度为:360°÷12÷60=0.5°.(1)根据余补角的定义解答;(2)分三种情况,分别画出图形,根据角平分线的定义解答即可;(3)分①当分针在时针上方时②当分针在时针下方时两种情况列出方程解答即可. 【解答】解:(1)∵∠AOB =25°42′,∴∠AOB 的余角=90°−25°42′=64°18′, ∠AOB 的补角=180°−25°42′=154°18′;故答案为:64°18′,154°18′;(2)见答案;(3)见答案.8.如图是一副三角尺拼成的图形,其中∠1比∠2的一半小30°,则∠1的余角的度数是多少?【答案】解:∴∠1+∠2=360°−90°−90°=180°,∴∠1=180°−∠2,∵∠1=12∠2−30°,∴∠2=140°,∴∠1=40°,∵90°−40°=50°,∴∠1的余角度数是50°.【解析】本题考查角的计算,余角的定义,属于基础题.根据图形即可推出∠1+∠2=360°−90°−90°=180°,然后由∠1=12∠2−30°,即可推出∠1的度数,再求其余角的度数即可.9.如图,OC,OB,OD是∠EOA内三条射线,OB平分∠DOA,OC平分∠EOA.(1)已知∠EOD=80°,∠AOB=20°,求∠BOC的度数.(2)设∠EOD=α,用含α的代数式表示∠BOC.(3)若∠EOD与∠BOC互余,求∠BOC的度数.【答案】解:(1)∵OB平分∠DOA,OC平分∠EOA.∴∠AOB=∠BOD=12∠AOD,∠EOC=∠AOC=12∠EOA,∵∠EOD=80°,∠AOB=20°,∴∠EOA=80°+20°×2=120°,∴∠EOC=∠AOC=12∠EOA=60°,∴∠BOC=∠AOC−∠AOB=60°−20°=40°.(2)∵∠BOC=∠AOC−∠AOB=∠DOE−∠COD−∠BOD=∠DOE−∠BOC,∴2∠BOC=∠DOE,∴∠BOC=12∠DOE=12α,(3)∵∠EOD与∠BOC互余,∴∠EOD+∠BOC=90°,∵∠BOC=12∠DOE,∴∠BOC=13×90°=30°.【解析】本题主要考查角平分线的意义,互余的意义,根据图形直观得出各个角的和或差是得出结论的前提,等量代换起到非常关键的作用.(1)根据角平分线和∠EOD=80°,∠AOB=20°,求出各个角,得出答案;(2)由特殊到一般,根据角平分线的意义,和各个角之间的和差关系,等量代换得出∠EOD 与∠BOC的数量关系,(3)利用(2)中的结论和∠EOD与∠BOC互余,求出∠BOC的度数.10.(1)已知∠1与∠2互为补角,且∠2的13比∠1小15∘,则∠1的余角为多少?(2)已知∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC,求∠MON的度数.【答案】解:(1)设∠1=x°,由题意可得,解得x=2254;(2)若OC在∠AOB内部,则∠MON=12∠AOB=45°,若OC在∠AOB外部,则∠MON=12(∠AOB+∠AOC)−12∠AOC=45°.【解析】本题考查了余角和补角,角平分线的定义以及角的计算,熟练掌握相关概念是解答本题的关键.(1)设∠1=x°,根据题意可列出方程,即可解答;(2)分两种情况:当若OC在∠AOB内部,当若OC在∠AOB外部进行分析.11.如图,0°<∠AOB<180°,射线OC,射线OD,射线OE,射线OF均在∠AOB内部,∠AOC=∠BOD=∠EOF,∠COE=∠DOF,∠COD=2∠EOF.(1)若∠COE=20°,求∠EOF的度数;(2)若∠EOF与∠COD互余,找出图中所有互补的角,并说明理由;(3)若∠EOF的其中一边与OA垂直,求∠AOB的度数.【答案】解:(1)∵∠COE=20°,∴∠COE=∠DOF=20°,∵∠COD=2∠EOF,即∠COE+∠DOF+∠EOF=2∠EOF,∴∠EOF=∠COE+∠DOF=20°+20°=40°;(2)设∠COE=∠DOF=x,∵∠COD=2∠EOF,∴∠COE+∠DOF+∠EOF=2∠EOF,∴∠EOF=∠COE+∠DOF=2x,∴∠AOC=∠BOD=∠EOF=2x.∵∠EOF与∠COD互余,∴∠EOF+∠COD=90°,即2x+4x=90°,∴x=15°,∴∠COE=∠DOF=15°,∠AOC=∠BOD=∠EOF=30°,∴∠COD=60°,∠AOB=120°,∴∠AOB+∠COD=120°+60°=180°,∠COB=90°,∠AOD=90°,∴∠COB+∠AOD=180°,∴互补的角为:∠AOB与∠COD,∠COB与∠AOD.(3)若OF与OA垂直,则∠AOF=∠AOC+∠COE+∠EOF=90°,设∠COE=∠DOF=x,∴2x+x+2x=90°,∴x=18°,∴∠AOB=8x=144°,若OE与OA垂直,则∠AOE=∠AOC+∠COE=90°,设∠COE=∠DOF=m,∴2m+m=90°,∴m=30°,∴∠AOB=8m=240°,∵0°<∠AOB<180°,∴这种情况应舍去,综上,∠AOB=144°.【解析】本题主要考查了角的计算,关键是正确地进行角的计算,正确列出方程.(1)根据角的关系进行计算便可;(2)根据互余角列出方程解答;(3)分两种情况讨论:OF与OA垂直和OE与OA垂直,进行解答.12.已知:∠AOD=156°,OB、OC、OM、ON是∠AOD内的射线.(1)如图1,若OM平分∠AOB,ON平分∠BOD.当OB绕点O在∠AOD内旋转时,则∠MON的大小为______;(2)如图2,若∠BOC=24°,OM平分∠AOC,ON平分∠BOD.当∠BOC绕点O在∠AOD内旋转时,求∠MON的大小;(3)在(2)的条件下,若∠AOB=30°,当∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍,求t的值【答案】解:(1)78°;(2)∵OM平分∠AOC,ON平分∠BOD,∴∠COM=12∠AOC,∠BON=12∠BOD,∴∠MON=∠BON+∠COM−∠BOC=12∠AOC+12∠BOD−24°=12(∠AOC+∠BOD)−24°,∴∠MON=12(∠AOD+∠BOC)−24°=12×180°−24°=66°;(3)∵∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒,OM平分∠AOC,ON平分∠BOD,∴∠AOC=(54+2t)°,∠AOM=(27+t)°,∠BOD=(126−2t)°,∠DON=(63−t)°,若∠AOM=2∠DON时,即27+t=2(63−t),∴t=33;若2∠AOM=∠DON,即2(27+t)=63−t,∴t=3;∴当t=3或t=33时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍.【解析】【分析】本题考查了角平分线的定义,一元一次方程的应用,分类讨论思想,利用一元一次方程解决问题是本题的关键.(1)由角平分线的定义可得∠BOM=12∠AOB,∠BON=12∠BOD,即可求∠MON的大小;(2)由角平分线的定义可得∠COM=12∠AOC,∠BON=12∠BOD,即可求∠MON的大小;(3)由题意可得∠AOC=(54+2t)°,∠AOM=(27+t)°,∠BOD=(126−2t)°,∠DON= (63−t)°,分∠AOM=2∠DON,∠DON=2∠AOM两种情况讨论,列出方程可求t的值.【解答】解:(1)∵OM平分∠AOB,ON平分∠BOD,∴∠BOM=12∠AOB,∠BON=12∠BOD,∵∠MON=∠BOM+∠BON=12∠AOD,∴∠MON=78°故答案为:78°(2)见答案;(3)见答案.13.已知直线AB与CD相交于点O,且∠AOD=90°,现将一个直角三角尺的直角顶点放在点O处,把该直角三角尺OEF绕着点O旋转,作射线OH平分∠AOE.(1)如图1所示,当∠DOE=20°时,∠FOH的度数是______.(2)若将直角三角尺OEF绕点O旋转至图2的位置,试判断∠FOH和∠BOE之间的数量关系,并说明理由.(3)若再作射线OG平分∠BOF,试求∠GOH的度数.【答案】解:(1)35°;(2)∠BOE=2∠FOH,理由如下:设∠AOH=x,因为OH平分∠AOE所以∠HOE=∠AOH=x所以∠FOH=90°−∠HOE=90°−x∠BOE=180°−∠AOE=180°−2x所以∠BOE=2∠FOH;(3)如图3,当OE落在∠BOD内时,OF落在∠AOD内因为OH平分∠AOE所以∠HOE=∠AOH=12∠AOE 因为OG平分∠BOF∠FOG=∠GOB=12∠BOF所以∠GOH=∠GOF−∠FOH=12∠BOF−(∠AOH−∠AOF)=12(180°−∠AOF)−12∠AOE+∠AOF=90°−12∠AOF−12(90°+∠AOF)+∠AOF=90°−12∠AOF−45°−12∠AOF+∠AOF=45°;所以∠GOH的度数为45°;如图4,当OE落在其他位置时因为OH平分∠AOE所以∠HOE=∠AOH=12∠AOE 因为OG平分∠BOF∠FOG=∠GOB=12∠BOF所以∠GOH=∠GOF+∠FOH=12∠BOF+∠AOH+∠AOF=12(180°−∠AOF)+12∠AOE+∠AOF=90°−12∠AOF+12(90°−∠AOF)+∠AOF=90°−12∠AOF+45°−12∠AOF+∠AOF=135°;所以∠GOH的度数为135°;综上所述:∠GOH的度数为45°或135°.【解析】解:(1)因为∠AOD=90°,∠DOE=20°所以∠AOE=∠AOD+∠DOE=110°因为OH平分∠AOE所以∠HOE=12∠AOE=55°所以∠FOH=90°−∠HOE=35°;故答案为35°;(2)∠BOE=2∠FOH,理由如下:设∠AOH=x,因为OH平分∠AOE所以∠HOE=∠AOH=x所以∠FOH=90°−∠HOE=90°−x∠BOE=180°−∠AOE=180°−2x 所以∠BOE=2∠FOH;(3)如图3,当OE落在∠BOD内时,OF落在∠AOD内因为OH平分∠AOE所以∠HOE=∠AOH=12∠AOE因为OG平分∠BOF∠FOG=∠GOB=12∠BOF所以∠GOH=∠GOF−∠FOH=12∠BOF−(∠AOH−∠AOF)=12(180°−∠AOF)−12∠AOE+∠AOF=90°−12∠AOF−12(90°+∠AOF)+∠AOF=90°−12∠AOF−45°−12∠AOF+∠AOF=45°;所以∠GOH的度数为45°;如图4,当OE落在其他位置时因为OH平分∠AOE所以∠HOE=∠AOH=12∠AOE 因为OG平分∠BOF∠FOG=∠GOB=12∠BOF所以∠GOH=∠GOF+∠FOH=12∠BOF+∠AOH+∠AOF=12(180°−∠AOF)+12∠AOE+∠AOF=90°−12∠AOF+12(90°−∠AOF)+∠AOF=90°−12∠AOF+45°−12∠AOF+∠AOF=135°;所以∠GOH的度数为135°;综上所述:∠GOH的度数为45°或135°.(1)根据∠AOD=90°,∠DOE=20°得∠AOE=∠AOD+∠DOE=110°,再根据OH平分∠AOE,即可求解;(2)可以设∠AOH=x,根据OH平分∠AOE,可得∠HOE=∠AOH=x,进而∠FOH= 90°−∠HOE=90°−x,∠BOE=180°−∠AOE=180°−2x,即可得结论;(3)分两种情况解答:当OE落在∠BOD内时,OF落在∠AOD内,当OE落在其他位置时,根据OH平分∠AOE,OG平分∠BOF即可求解.本题考查了余角和补角、角平分线定义,解决本题的关键是掌握角平分线定义,进行角的和差计算.14.以∠AOB的顶点O为端点引射线OC,使∠AOC=2∠BOC,若∠AOB=30°,请在图中作出射线OC,并求出∠AOC的度数.【答案】解:分两种情况:①如图1,若射线OC在∠AOB的内部,则∠AOC+∠BOC=30°,即2∠BOC+∠BOC=30°,所以∠BOC=10°,∠AOC=20°.②如图2,若射线OC在∠AOB外部,则由∠AOC=2∠BOC,可得OB就是∠AOC的平分线,所以∠AOC=2∠AOB=60°.综上,∠AOC的度数是20°或60°.【解析】本题考查了角的计算,属于基础题,关键是分两种情况进行讨论.分射线OC在∠AOB的内部和射线OC在∠AOB外部两种情况,进行讨论求解即可.15.(1)如图1所示,将两个正方形的一个顶点重合放置,若∠AOD=40°,则∠COB=_________(2)如图2所示,将三个正方形的一个顶点重合放置,求∠1的度数.(3)如图3所示,将三个正方形的一个顶点重合放置,若OF平分∠DOB,则OE平分∠AOC吗?为什么?【答案】解:(1)140°;(2)如图,由题意知,∠1+∠2=50°①,∠1+∠3=60°②,又∠1+∠2+∠3=90°③,①+②−③得∠1=20°;(3)OE平分∠AOC,理由如下:∵∠COD=∠AOB,∴∠COA=∠DOB(等角的余角相等).同理:∠EOA=∠FOB.∵OF平分∠DOB,∠DOB,∴∠DOF=∠FOB=12∴∠EOA=12∠DOB=12∠COA,∴OE平分∠AOC.【解析】【分析】本题考查了角的计算,余角和补角以及正方形的性质,根据所给出的图形,找到角与角的关系是本题的关键.(1)根据正方形各角等于90°,得出∠COD+∠AOB=180°,再根据∠AOD=40°,∠COB=∠COD+∠AOB−∠AOD,即可得出答案;(2)根据已知得出∠1+∠2,∠1+∠3的度数,再根据∠1+∠2+∠3=90°,最后用∠1+∠2+∠1+∠3−(∠1+∠2+∠3),即可求出∠1的度数;(3)根据∠COD=∠AOB和等角的余角相等得出∠COA=∠DOB,∠EOA=∠FOB,再根据角平分线的性质得出∠DOF=∠FOB=12∠DOB和∠EOA=12∠DOB=12∠COA,从而得出答案.【解答】解:(1)∵两个图形是正方形,∴∠COD=90°,∠AOB=90°,∴∠COD+∠AOB=180°,∵∠AOD=40°,∴∠COB=∠COD+∠AOB−∠AOD=140°.故答案为140°;(2)见答案;(3)见答案.16.如图,已知∠AOB=2∠BOC,又OD,OE分别为∠AOB和∠BOC的平分线,若∠DOE=66∘.求∠AOB的度数.【答案】解:∵OE,OD分别是∠BOC、∠AOB的平分线,∴∠BOC=2∠BOE,∠AOB=2∠DOB,∵∠DOE=66°,∴∠AOB+∠BOC=2∠DOB+2∠BOE=2∠DOE=132°,∵∠AOB=2∠BOC,×132°=88°.∴∠AOB=23【解析】本题考查的是角平分线的定义,角的计算有关知识,根据角平分线定义得出∠BOC=2∠BOE,∠AOB=2∠DOB,根据∠DOE=66°求出∠AOB+∠BOC=132°,根据∠AOB=2∠BOC求出即可.17.已知∠AOB是锐角,∠AOC=2∠BOD.(1)如图,射线OC,射线OD在∠AOB的内部(∠AOD>∠AOC),∠AOB与∠COD互余.①若∠AOB=60°,求∠BOD的度数.②若OD平分∠BOC,求∠BOD的度数.(2)若射线OD在∠AOB的内部,射线OC在∠AOB的外部,∠AOB与∠COD互补.方方同学说:∠BOD的度数是确定的;圆圆同学说:这个问题要分类讨论,一种情况下∠BOD的度数是确定的,另一种情况下∠BOD的度数不确定.你认为谁的说法正确?为什么?【答案】解(1)①∵∠AOB=60°,∠AOB与∠COD互余,∴∠COD=30°,∵∠AOC=2∠BOD,∴∠BOD=10°.②设∠BOD=x°,∵OD平分∠BOC,∠AOC=2∠BOD,∴∠BOD=∠COD=1∠BOC,∠AOC=2x°,2∵∠AOB与∠COD互余,∴4x+x=90,解得:x=18,∴∠BOD=18°.(2)设∠BOD=x,∠AOD=y.当射线OD在∠AOC内部时(如图1),由题意,得∠AOB+∠COD=180°,即x+y+2x−y=3x=180°,此时∠BOD=60°,确定.当射线OD在∠AOC外部时(如图2),由题意,得∠AOB+∠COD=180°,即x+y+y+2x=3x+2y=180°,此时∠BOD不确定;∴圆圆的说法正确.【解析】本题考查了角平分线的定义以及角的计算,还用到了方程的思想.注意(2)要根据射线OD的位置不同,分类讨论,分别求出∠BOD的度数.(1)①根据∠AOB=60°,∠AOB与∠COD互余,可得∠COD=30°,再根据∠AOC=2∠BOD,可得∠BOD的度数;②先设∠BOD=x°,则4x+x=90,求出x的值,进而可得出结论;(2)分射线OD在∠AOC的内部与在∠AOC的外部两种情况进行讨论.。
期末考试必复习直线、射线、线段、角概念选择题易错题
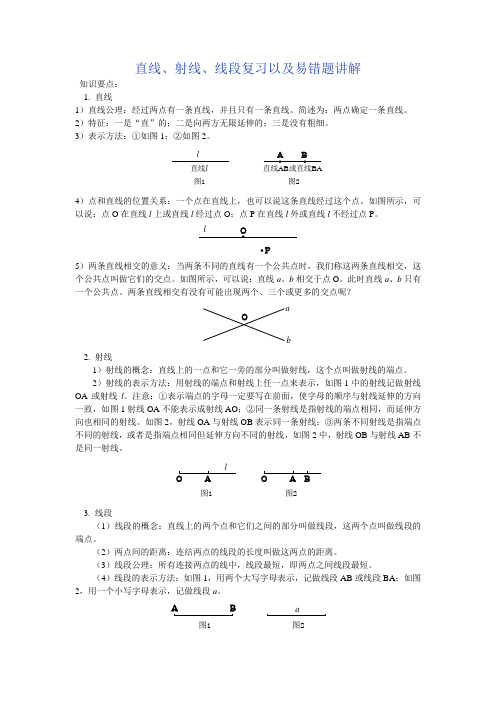
知识点:角平分线
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线,类似地,还有角的三等分线等。
知识点:余角、补角概念
如果两个角的和等于90°(直角),那么这两个角互为余角,其中一个角是另一个角的余角。即:若∠
(6)线段的中点及等分点的概念:如图1所示,点B把线段AC分成两条相等的线段,点B叫做线段AC的中点。有AB=BC=AC。如图2所示,点B和点C把线段AD分成三条相等的线段,点B、点C叫做线段AD的三等分点,有AB=BC=CD=AD。类似的还有线段的四等分点、五等分点等。
4.直线、射线、线段的区别
图形名称
C.线段AB的中点C到A、B两点的距离相等
D.A、B两点之间的距离是线段AB
9.下列说法中,正确的个数有().
(1)射线AB和射线BA是同一条射线
(2)延长射线MN到C
(3)延长线段MN到A使NA==2MN
(4)连结两点的线段叫做两点间的距离
A.1 B.2 C.3 D.4
10.下列说法中,错误的是().
A.3B.4C.5D.6
2.下列语句正确的是()
A.点a在直线l上B.直线ab过点p
C.延长直线AB到CD.延长线段AB到C
3.下列说法中:①两条直线相交只有一个交点;②两条直线不是一定有一个公共点;③直线AB与直线BA是两条不同直线;④两条不同直线不能有两个或更多个公共点,其中正确的是( )
A.①②B.①④C.①②④D.②③④
1+∠2=90°,则∠1与∠2互为余角。其中∠1是∠2的余角,∠2是∠1的余角;如果两个角和等于180°(平角),那么这两个角互为补角,其中一个角是另一个角的补角。即:若∠1+∠2=180°,则∠1与∠2互为补角。其中∠1是∠2的补角,∠2是∠1的补角。
七年级上数学第四章《图形认识初步》角的易错题集精讲

新人教版七年级上期数学(第四章几何图形认识初步)角的易错题集精讲一.选择题(共5小题)时2.在下列说法中,正确的是()①两条射线组成的图形叫做角;②角的大小与边的长短无关;3.如图中共有()个角.二.填空题(共10小题)6.长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为_________.7.已知线段AB=10cm,直线AB上有一点C,且BC=6cm,AC的长为_________.8.如图,已知线段AB=9厘米,C是直线AB上的一点,且BC=3厘米,则线段AC的长是_________厘米.9.已知线段AC和BC在同一直线上,若AC=20,BC=18,线段AC的中点为M,线段BC 的中点为N,则线段MN_________.10.点A、B、C在同一条直线上,线段AB=6cm,线段BC=4cm,则线段AC=_________.11.已知点B在直线AC上,AC=18cm,AB=8cm,则BC=_________.12.已知有共公顶点的三条射线OA,OB,OC,若∠AOB=120°,∠BOC=30°,则∠AOC= _________.13.已知平面上有公共顶点的三条射线OA,OB,OC,若∠AOB=100°,∠BOC=50°,则∠AOC=_________.14.已知∠AOB=30°,∠BOC=24°,∠AOD=15°,则锐角∠COD的度数_________.15.(1)如图,图中互补的角有_________对.(2)如果∠AOC=∠COD=∠BOD=60°,则图中互补的角有_________对.三.解答题(共15小题)16.(1999•杭州)已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.17.一个角的补角是123°24′16″,则这个角的余角是多少.18.如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.(1)指出图中∠AOD与∠BOE的补角;(2)试说明∠COD与∠COE具有怎样的数量关系.19.如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB 的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.20.一个角的余角比它的补角的还少20°,求这个角.21.已知一个角的补角等于这个角的余角的4倍,求这个角的度数.22.如图,将一副三角尺的直角顶点重合在一起.(1)若∠DOB与∠DOA的比是2:11,求∠BOC的度数.(2)若叠合所成的∠BOC=n°(0<n<90),则∠AOD的补角的度数与∠BOC的度数之比是多少?23.(1)已知∠BOC=120°,∠AOB=70°,求∠AOC的大小;(2)已知∠AOB=80°,过O作射线OC(不同于OA、OB),满足∠AOC=∠BOC,求∠AOC的大小.(注:本题中所说的角都是指小于平角的角)24.如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.(1)写出∠AOC与∠BOD的大小关系:_________,判断的依据是_________;(2)若∠COF=35°,求∠BOD的度数.25.把一副三角尺如图所示拼在一起,试确定图中∠A、∠B、∠AEB、∠ACD的度数,并用“<”将它们连起来.26.如图所示,设相邻两个角∠AOB,∠BOC的平分线分别为OE,OF,且∠EOF是直角,你能说明OA,OC为什么成一条直线吗?试试看吧!27.如图,∠AOB=110°,∠COD=70°,OA平分∠EOC,OB平分∠DOF,求∠EOF的大小.28.如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°,求∠AOB的度数.29.在飞机飞行时,飞行方向是用飞行路线与实际的南或北方向线之间的夹角大小来表示的,如图,用AN(南北线)与飞行线之间顺时针方向夹角作为飞行方向角,从A到B的飞行方向角为35°,从A到C的飞行方向角为60°,从A到D的飞行方向角为145°,试求AB与AC之间夹角为多少度?AD与AC之间夹角为多少度?并画出从A飞出且方向角为105°的飞行线.30.如图,OA的方向是北偏东15°,OB的方向是西偏北50度.(1)若∠AOC=∠AOB,则OC的方向是_________;(2)OD是OB的反向延长线,OD的方向是_________;(3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是_________;(4)在(1)、(2)、(3)的条件下,∠COE=_________.第4章《图形认识初步》角的易错题集精讲参考答案与试题解析一.选择题(共5小题)时个大格,其夹角为=82.5分时,时针与分针的夹角为(=90分时时针与分针的夹角为直角,正确;2.在下列说法中,正确的是()①两条射线组成的图形叫做角;②角的大小与边的长短无关;3.如图中共有()个角.二.填空题(共10小题)6.长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为8cm.7.已知线段AB=10cm,直线AB上有一点C,且BC=6cm,AC的长为4cm或16cm.8.如图,已知线段AB=9厘米,C是直线AB上的一点,且BC=3厘米,则线段AC的长是12或6厘米.9.已知线段AC和BC在同一直线上,若AC=20,BC=18,线段AC的中点为M,线段BC 的中点为N,则线段MN19或1.AC MN=AM+AN=AC+10.点A、B、C在同一条直线上,线段AB=6cm,线段BC=4cm,则线段AC=10cm或2cm.11.已知点B在直线AC上,AC=18cm,AB=8cm,则BC=10cm或26cm.12.已知有共公顶点的三条射线OA,OB,OC,若∠AOB=120°,∠BOC=30°,则∠AOC= 90°或150°.13.已知平面上有公共顶点的三条射线OA,OB,OC,若∠AOB=100°,∠BOC=50°,则∠AOC=150°或50°.14.已知∠AOB=30°,∠BOC=24°,∠AOD=15°,则锐角∠COD的度数69°、39°、21°、9°.15.(1)如图,图中互补的角有2对.(2)如果∠AOC=∠COD=∠BOD=60°,则图中互补的角有6对.三.解答题(共15小题)16.(1999•杭州)已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.17.一个角的补角是123°24′16″,则这个角的余角是多少.18.如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.(1)指出图中∠AOD与∠BOE的补角;(2)试说明∠COD与∠COE具有怎样的数量关系.COE=∠COD=COE=∠COE=∠BOC+AOC=COE=∠19.如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB 的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.由题意,得20.一个角的余角比它的补角的还少20°,求这个角.x=(21.已知一个角的补角等于这个角的余角的4倍,求这个角的度数.22.如图,将一副三角尺的直角顶点重合在一起.(1)若∠DOB与∠DOA的比是2:11,求∠BOC的度数.(2)若叠合所成的∠BOC=n°(0<n<90),则∠AOD的补角的度数与∠BOC的度数之比是多少?23.(1)已知∠BOC=120°,∠AOB=70°,求∠AOC的大小;(2)已知∠AOB=80°,过O作射线OC(不同于OA、OB),满足∠AOC=∠BOC,求∠AOC的大小.(注:本题中所说的角都是指小于平角的角)∠∠24.如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.(1)写出∠AOC与∠BOD的大小关系:相等,判断的依据是等角的补角相等;(2)若∠COF=35°,求∠BOD的度数.25.把一副三角尺如图所示拼在一起,试确定图中∠A、∠B、∠AEB、∠ACD的度数,并用“<”将它们连起来.26.如图所示,设相邻两个角∠AOB,∠BOC的平分线分别为OE,OF,且∠EOF是直角,你能说明OA,OC为什么成一条直线吗?试试看吧!27.如图,∠AOB=110°,∠COD=70°,OA平分∠EOC,OB平分∠DOF,求∠EOF的大小.28.如图,已知∠BOC=2∠AOC,OD平分∠AOB,且∠COD=20°,求∠AOB的度数.29.在飞机飞行时,飞行方向是用飞行路线与实际的南或北方向线之间的夹角大小来表示的,如图,用AN(南北线)与飞行线之间顺时针方向夹角作为飞行方向角,从A到B的飞行方向角为35°,从A到C的飞行方向角为60°,从A到D的飞行方向角为145°,试求AB与AC之间夹角为多少度?AD与AC之间夹角为多少度?并画出从A飞出且方向角为105°的飞行线.30.如图,OA的方向是北偏东15°,OB的方向是西偏北50度.(1)若∠AOC=∠AOB,则OC的方向是北偏东70°;(2)OD是OB的反向延长线,OD的方向是南偏东40°;(3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是南偏西50°;(4)在(1)、(2)、(3)的条件下,∠COE=160°.。
线段和角有关分类讨论中漏解产生易错(解析版) 2020-2021年七年级数学上册期末综合复习提优训练

2020-2021学年七年级数学上册期末综合复习专题提优训练(北师大版)易错04 线段和角有关分类讨论中漏解产生易错【线段中的分类讨论】一、填空题1.(2020·宜兴市树人中学七年级月考)已知点A 、B 、C 在一条直线上,AB =5cm ,BC =3cm ,则AC 的长为___________.【答案】2cm 或8cm .【分析】分类讨论,C 在线段AB 上,C 在线段AB 的延长线上,根据线段的和差,可得答案.【详解】解:若C 在线段AB 上,则532cm AC AB BC =-=-=;若C 在线段AB 的延长线上,则538cm AC AB BC =+=+=,故答案为:2cm 或8cm .【点睛】本题考查了线段的和差,分类讨论是解题关键.2.(2020·天津市滨海新区大港第二中学七年级期中)已知C 是线段AB 的中点,AB =10,若E 是直线AB 上的一点,且BE =3,则CE =_____【答案】2或8【分析】由已知C 是线段AB 中点,AB =10,求得BC '= 5,进一步分类探讨:E 在BC 内;E 在BC 的延长线上;由此画图得出答案即可.【详解】C 是线段AB 的中点, AB = 10,BC = AB = 5,如图,当E 在BC 内,CE = BC - BE = 5- 3=2;②如图,E 在BC 的延长线上,CE = BC + BE = 5+3=8 ;所以CE = 2或8;故本题答案为:2或8.【点睛】解决本题的关键突破口是分类讨论,本题考查了学生综合分析的能力,要求学生掌握线段中点的意义,线段的和与差. 3.(2020·成都市锦江区四川师大附属第一实验中学七年级期末)已知点D 为线段AB 的中点,且在直线AB 上有一点C ,且3AB BC ,若CD 的长为4cm ,则AB 的长为_________cm . 【答案】245或24. 【分析】。
专题06 线段的有关计算易错(解析版)-2020-2021学年七年级数学寒假温故知新汇编(人教版)

2020-2021学年七年级数学寒假温故知新汇编(人教版)专题06 线段的有关计算易错【典型例题】1.(2021·甘肃金昌市·)如图所示,点C 在线段AB 上,点M 、N 分别是AC 、BC 的中点.(1)若AC =8cm ,CB =6cm ,求线段MN 的长.(2)若C 为线段AB 上任意一点,满足AC+CB =a cm ,其他条件不变,你能猜想出MN 的长度吗?并说明理由.(3)若C 在线段AB 的延长线上,且满足AC ﹣CB =b cm ,M 、N 分别为AC 、BC 的中点,你能猜想出MN 的长度吗?请画出图形,写出你的结论,并说明理由.【答案】(1)MN =7cm ;(2)MN =2a m ,理由见解析;(3)画图形见解析,线段MN 的长是12bcm ,理由见解析.【分析】(1)根据线段的中点的性质,可得MC 、NC 的长,再根据线段的和差,可得答案;(2)根据线段的中点的性质,可得MC 、NC 的长,再根据线段的和差,可得答案;(3)根据线段中点得出CM =12AC ,CN =12BC ,求出MN =CM −CN =12AC −12BC ,代入即可得出答案. 【详解】(1)∵点M 、N 分别是AC 、BC 的中点,∴MC =12AC ,NC =12CB , 又∵AC =8cm ,BC =6cm ,∴MN =MC +NC =12(AC +BC )=7cm ;(2)由(1)知,MN =MC +NC =12(AC +BC ), ∵AC +CB =acm ,∴MN =2a m ; (3)如图:MN =12b , 理由是:∵点M 、N 分别是AC 、BC 的中点,AC −CB =bcm ,∴CM =12AC ,CN =12BC , ∴MN =CM −CN =12AC −12BC =12(AC −BC )=12bcm , 即线段MN 的长是12bcm . 【点睛】本题考查了线段中点定义和两点间的距离的应用,主要考查学生的计算能力,本题比较典型,是一道比较好且比较容易出错的题目.【专题训练】一、解答题1.(2021·安徽利辛县教育局七年级期末)如图,C ,D 是线段AB 上两点,已知AC :CD :DB =1:2:3,M 、N 分别为AC 、DB 的中点,且AB =8cm ,求线段MN 的长.【答案】线段MN 的长为163cm . 【分析】根据线段的比例,可得线段的长度,根据线段的和差,可得答案.【详解】AC :CD :DB =1:2:3,设AC :CD :DB =a :2a :3a ,AB =AC +CD +DB 2368a a a a =++==,43a =, ∴AC =43,CD =83,DB =4, ∵M 、N 分别为AC 、DB 的中点,AM =12AC =23,DN =12DB =2, ∴MN =AM +CD +DN =28162333++=(cm ). ∴线段MN 的长为163cm . 【点睛】本题考查了两点间的距离,掌握线段中点的概念、灵活运用数形结合思想是解题的关键.2.(2021·江阴市周庄中学七年级期末)如图,已知线段AB =10cm ,点C 是线段AB 的中点,点D 在AC 上且AD =35AC ,点E 是BD 的中点,求CD 和CE 的长.【答案】CD =2cm ,CE =1.5cm .【分析】根据线段中点的定义得到AC=BC12=AB=5cm,进而求得AD CD、长,根据线段中点的定义得到DE,进而求得CE.【详解】解:∵AB=10cm,点C是线段AB的中点,∴AC=BC12=AB=5cm,∴AD35=AC=3cm,∴CD=AC﹣AD=5﹣3=2cm,所以BD=AB﹣AD=7cm,∵E是BD的中点,∴DE=BE12=BD12=⨯7=3.5cm,∴CE=DE﹣CD=3.5﹣2=1.5cm.【点睛】本题考查了线段的和差,线段中点的定义,熟悉线段的加减运算是解题的关键.3.(2021·云南昆明市·七年级期末)如图,延长线段AB到C,使BC=3AB,点D是线段BC的中点,如果CD=9cm,那么线段AC的长度是多少?【答案】24cm【分析】已知CD的长度,CD是线段BC的一半,则BC长度可求出,根据3AB=BC,即可求出AB的长度,进而可求出AC的长度.【详解】解:∵点D是线段BC的中点,CD=9cm,∴BC=2CD=18cm,∵BC=3AB,∴AB=6cm,∴AC=AB+BC=6+18=24cm.【点睛】本题主要考查了线段中点的性质.解答此题的关键是结合图形根据题干中的信息得出各线段之间的关系.4.(2021·山东师范大学第二附属中学七年级期末)如图,线段AB=16cm,在AB上取一点C,M是AB的中点,N是AC中点,若MN=3cm,求线段AC的长.【答案】10cm【分析】根据线段中点的定义和线段的和差即可得到结论.【详解】解:∵AB=16cm,M是AB的中点,∴AM=AB 12=8cm,∵MN=3cm,∴AN=AM--MN=8-3=5cm,∵N是AC中点,∴AC=2AN=2×5=10.答:线段AC的长为10 cm.【点睛】本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.5.(2021·高台县城关初级中学七年级期末)如图,点B是线段AC上一点,且AB=24cm,BC=13 AB,(1)试求出线段AC的长;(2)如果点O是线段AC的中点,请求线段OB的长.【答案】(1)AC=32cm;(2)OB=8cm.【分析】(1)由B在线段AC上可知AC=AB+BC,把AB=24cm,BC=13AB=8cm代入即可求出结论;(2)根据O是线段AC的中点及AC的长可求出CO的长,由OB=CO−BC即可得出结果.【详解】解:(1),AB=24cm,BC=13 AB,,BC=8cm,,AC=AB+BC=24+8=32cm;(2)由(1)知:AC=32cm,,点O是线段AC的中点,,CO=12AC=12×32=16cm,,OB=CO−BC=16−8=8cm.【点睛】本题考查了与线段中点有关的计算问题,掌握线段的中点的性质、线段的和、差、倍的运算是解题的关键.6.(2021·内蒙古赤峰市·七年级期末)如图,已知点O在线段AB上,点C、D分别是线段AO、BO的中点,(1)若CO=3cm,DO=2cm,求线段AB的长度;(2)若点O在线段AB的延长线上,其他条件不变,AB=10cm,请画出图形,求出CD的长度.【答案】(1)10cm;(2)图见解析,5cm【分析】(1)根据点C、D分别是线段AO、BO的中点求出AO、BO,计算AB=AO+OB得到答案;(2)正确画出图形,根据线段中点的性质得到CO=12AO,DO=12BO,由此求出CD=12AB,代入数值计算.【详解】解:(1)∵C、D分别是AO、BO中点,CO=3cm,DO=2cm,∴AO=2OC=2×3=6cm,BO=2OD=2×2=4cm,∴AB=AO+OB=6+4=10cm;(2)解:如图,∵C、D分别是AO、BO中点,∴CO=12AO,DO=12BO,∴CD=CO-DO=12AO-12BO=12(AO-BO)=12AB=12×10=5cm..【点睛】此题考查线段中点的性质,与线段中点相关的计算,线段和差关系,正确理解图形中各线段的数量关系列式计算是解题的关键.7.(2021·四川绵阳市·东辰国际学校七年级期末)如图,点B是线段AC上一点,且AB=18cm,13BC AB=.(1)试求出线段AC的长;(2)如果点O是线段AC的中点,请求线段OB的长.【答案】(1)24cm;(2)6cm.【分析】(1)由点B在线段AC上可知AC=AB+BC,由AB=18cm,BC=13AB,,BC,代入计算后即可得到答案;(2)根据O是线段AC的中点及AC的长可求出OC的长,由OB=OC−BC即可得出答案.【详解】解:(1)∵AB=18cm,BC=13AB=6cm,∴AC=AB+BC=18+6=24(cm);(2)由(1)知:AC=24cm,∵点O是线段AC的中点,∴OC=12AC=12×24=12(cm).∴OB=OC−BC=12−6=6(cm).【点睛】本题主要考查线段的有关计算问题,掌握线段的中点的性质、线段的和、差、倍之间的运算是解题的关键.8.(2021·北京门头沟区·七年级期末)已知,如图,点C在线段AB上,6AC=,点D是线段AB的中点,点E是线段BC 的中点.求DE的长.请将下面的解题过程补充完整:解:∵点D 是线段AB 的中点(已知), ∴12DB =_________(理由:__________________).∵点E 是线段BC 的中点(已知),∴12BE =_________. ∵DE DB =-_________,∴()11112222DE AB BC AB BC =-=-=_________. ∵6AC =(已知), ∴DE =_________.【答案】AB ,中点定义,BC ,BE ,AC ,3.【分析】根据线段中点定义推出12DB =AB ,12BE =BC ,根据线段关系得到DE DB =-BE ,推出()11112222DE AB BC AB BC =-=-=AC ,即可求出答案. 【详解】∵点D 是线段AB 的中点(已知),∴12DB =AB (理由:中点定义).∵点E 是线段BC 的中点(已知),∴12BE =BC . ∵DE DB =-BE , ∴()11112222DE AB BC AB BC =-=-=AC . ∵6AC =(已知), ∴DE =3.故答案为:AB ,中点定义,BC ,BE ,AC ,3.【点睛】此题考查线段中点的定义,线段和差计算,掌握图形中各线段的位置关系是解题的关键.9.(2021·甘肃白银市·七年级期末)已知,点C 是线段AB 上的一点,点M 是线段AC 的中点,点N 是线段BC 的中点,(1)如果AB =10cm ,那么MN 等于多少?(2)如果AC :CB =3:2,NB =3.5 cm ,那么AB 等于多少?【答案】(1)MN =5cm ;(2)AB =17.5cm .【分析】(1)由已知点C 是线段AB 上的一点,点M 是线段AC 的中点,点N 是线段BC 的中点,得MN =CM +CN =12AC +12BC =12AB ; (2)由已知得AB =7÷25=17.5cm . 【详解】(1)MN =CM +CN =12AC +12BC =12AB =5cm ; (2)∵NB =3.5cm ,∴BC=7cm,∴AB=7÷25=17.5cm.【点睛】本题考查了比较线段的长短的知识,注意理解线段的中点的概念.利用中点性质转化线段之间的倍分关系是解题的关键.10.(2021·甘肃定西市·七年级期末)如图,点C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.(1)如果AB,10cm,AM,3cm,求CN的长;(2)如果MN,6cm,求AB的长.【答案】,1,CN,2(cm),,2,AB,12(cm),【分析】(1)根据点C为中点求出AC的长度,然后根据AB的长度求出BC的长度,最后根据点N为中点求出CN的长度;(2)根据中点的性质得出AC=2MC,BC=2NC,最后根据AB=AC+BC=2MC+2NC=2(MC+NC)=2MN得出答案.【详解】解:(1)∵M是线段AC的中点,∴CM=AM=3cm,AC=6cm.又AB=10cm,∴BC=4cm.∵N是线段BC的中点,∴CN=12BC=12×4=2(cm);(2)∵M是线段AC的中点,N是线段BC的中点,∴NC=12BC,CM=12AC,∴MN=NC+CM=12BC+12AC=12(BC+AC)=12AB,∴AB=2MN=2×6=12(cm).11.(2021·北京大兴区·七年级期末)如图,线段1145BD AB CD==,点E,F分别是线段AB,CD的中点,EF=14cm,求线段AC的长.请将下面的解题过程补充完整:解:因为1145BD AB CD==,所以设BD=x,则AB=4x,CD= x;所以AC= x.又因为点E,F分别是线段AB,CD的中点,所以AE=12AB=2x,FC= CD= x;又因为EF=14cm,可得方程=14解方程得;所以,AC= .【答案】5;8 ;12,52;5822x x x--;x=4;32cm.【分析】设BD=x,根据中点的定义和图中线段之间的关系,将AB、CD、AC、AE、FC、EF依次用含x的代数式表示出来,由EF=14cm可求出x,从而求出AC的长.【详解】解:因为1145BD AB CD==,所以设BD=x,则AB=4x,CD=5x;所以AC=AB-BD+DC=4x-x+5x=8x.又因为点E,F分别是线段AB,CD的中点,所以AE=12AB=2x,FC=1522CD x=,又因为EF=14cm,EF=AC-AE-FC,可得方程5822x x x--=14,解方程得4x=,所以,AC=8x=32(cm),即AC的长为32cm.【点睛】本题考查了线段和差运算,解题关键是依据线段的中点,利用线段的和差关系进行计算.12.(2021·山东师范大学第二附属中学七年级期末)已知有理数a,b,c在数轴上对应的点从左到右顺次为A,B,C,其中b 是最小的正整数,a在最大的负整数左侧1个单位长度,BC=2AB.(1)填空:a=,b=,c=(2)点D从点A开始,点E从点B开始,点F从点C开始,分别以每秒1个单位长度、1个单位长度、4个单位长度的速度在数轴上同时向左运动,点F追上点D时停止动,设运动时间为t秒.试问:①当三点开始运动以后,t为何值时,这三个点中恰好有一点为另外两点的中点?②F在追上E点前,是否存在常数k,使得DF k EF+⋅的值与它们的运动时间无关,为定值.若存在,请求出k和这个定值;若不存在,请说明理由.【答案】(1)-2,1,7;(2)①t =1或t =52;②k =-1 【分析】(1)根据有理数的性质,A 、B 、C 三点位置,数轴上两点的距公式及点的平移规律回答即可;(2)①分E 是DF 的中点和点F 是DE 的中点两种情况计论;②先用含t的代数式表示DF k EF +⋅,()9633DF k EF k k t +⋅=+-+,由3+3k =0求出k 问题即可求解【详解】解:(1)∵最小正数为1.最大的负整数为小-1,a 在最大的负整数左侧1个单位长度∴点A 表示的数a 为-1-1=-2,点B 表示的数b 为1,∴AB =1-(-2)=3∵223=6BC AB ==⨯,∴点C 表示的数为c =1+6=7,故答案为:-2,1,7;(2)①依题意,点F 的运动距离为4t ,点D 、E 运动的距离为t ,∴点D 、E 、F 分别表示的数为-2-t ,1-t , 7-4t ,当点F 追上点D 时,必将超过点B ,∴存在两种情况,即DE =EF 和DF =EF ,如图,当DE =EF ,即E 为DF 的中点时,()21=274t t t ----+,解得,t =1,如图,当EF =DF ,即F 为DE 中点时,()74=21t t t ---+-2,解得t =52,综上所述,当t=1秒和t=52时,满足题意. ②存在,理由:点D 、E 、F 分别表示的数为-2-t ,1-t ,7-4t ,如图,F 在追上E 点前, ()74-2=93DF t t t =----,()74-1=63EF t t t =---,()()93639633DF k EF t k t k k t +⋅=-+-=+-+,当DF k EF +⋅与t 无关时,需满足3+3k =0,即k =-1时,满足条件.【点睛】本题考查了数有理数的性质,数轴上点与数的对应关系及两点的距离,点的平移及线段的中点及分类讨论思想,正确理解点的运动与点的平移的关系是解本题的关键.13.(2021·北京大兴区·七年级期末)如图1,点C 把线段AB 分成两条线段AC 和BC ,如果AC =2BC 时,则称点C 是线段AB的内二倍分割点;如图2,如果BC=2AC时,则称点C是线段BA的内二倍分割点.例如:如图3,数轴上,点A、B、C、D分别表示数-1、2、1、0,则点C是线段AB的内二倍分割点;点D是线段BA内二倍分割点.(1)如图4,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为7.MN的内二倍分割点表示的数是;NM 的内二倍分割点表示的数是.(2)数轴上,点A所表示的数为-30,点B所表示的数为20.点P从点B出发,以2个单位每秒的速度沿数轴向左运动,设运动时间为t(t>0)秒.,线段BP的长为;(用含t的式子表示),求当t为何值时,P、A、B三个点中恰有一个点为其余两点的内二倍分割点.【答案】(1)4 ;1;(2),线段BP的长为2t;,当t为253或503或752或75秒时,P、A、B中恰有一个点为其余两点的内二倍分割点.【分析】(1)根据内二倍分割点的定义,找到MN的三等分点表示的数即可;(2),根据速度与路程的关系,可得BP=2t, ,分P为其余两点的内二倍分割点和A为其余两点的内二倍分割点两种情况,按照内二倍分割点的定义,列方程求解即可.【详解】解:(1)MN的内二倍分割点就是MN的三等分点且距N近,MN=9,则MN的内二倍分割点在N的左侧,距N点3个单位,所以,表示的数为4 ;同理,则NM的内二倍分割点在N的左侧,距N点6个单位,所以,表示的数为1;(2), 则线段BP 的长为 2t ., 当P 在线段AB 上时,有以下两种情况:如果P 是AB 的内二倍分割点时,则AP =2BP ,所以50-2t = 2×2t ,解得t =253; 如果P 是BA 的内二倍分割点时,则BP =2AP ,所以2t =2(50-2t ),解得t =503; 当P 在点A 左侧时,有以下两种情况:如果A 是BP 的内二倍分割点时,则BA =2P A ,所以50=2(2t -50)解得t =752; 如果A 是PB 的内二倍分割点时,则P A =2BA ,所以2t -50=2×50,解得t =75;综上所述:当t 为253或503或752或75秒时,P 、A 、B 中恰有一个点为其余两点的内二倍分割点. 【点睛】本题考查了新定义内二倍分割点、速度与路程的关系和分类讨论的思想;准确理解定义,恰当的用速度与时间表示线段长,分类讨论,建立方程是解题的关键.14.(2021·辽宁大连市·七年级期末)已知,点D 是射线AB 上的点,线段4AB a =,(01)BD nAB n =<<,点C 是线段AD 的中点.(1)如图1,若点D 在线段AB 上,当1a =,12n =时,求线段CD 的长; (2)如图2,若点D 在线段AB 的延长线上,当12n =时,求线段CD 的长;(用含a 的式子表示) (3)若点D 在射线AB 上,请直接写出线段CD 的长______________.(用含a 和n 的式子表示) 【答案】(1)1;(2)3a ;(3)22a na -或22a na +.【分析】(1)根据题意求得AB 与BD 的长,利用线段间数量关系求得AD 的长,然后根据线段的中点定义求解CD 的长; (2)解析思路同第(1)问;(3)利用第(1)(2)问的解题思路,分点D 在线段AB 和线段AB 的延长线上两种情况讨论解答.【详解】解:(1)当1a =,12n =时, 44AB a ∴==,122BD nAB AB ===. 422AD AB BD ∴=-=-=.点C 是线段AD 的中点,112CD AD ∴==.(2)当12n =时, 4AB a ∴=,122BD nAB AB a ===. 426AD AB BD a a a ∴=+=+=.点C 是线段AD 的中点,132CD AD a ∴==. (3)①当点D 在线段AB 上时4AB a ∴=,4BD nAB na ==.44AD AB BD a na ∴=-=-.点C 是线段AD 的中点,11(44)2222CD AD a na a na ∴==-=-. ②当点D 在线段AB 的延长线上时4AB a ∴=,4BD nAB na ==.44AD AB BD a na ∴=+=+.点C 是线段AD 的中点,11(44)2222CD AD a na a na ∴==+=+. 综上,线段CD 的长为:22a na -或22a na +.【点睛】本题考查线段中点的定义及线段间的数量关系计算,利用数形结合思想分类讨论解题是关键.15.(2021·河北唐山市·七年级期末)[知识背景]:数轴上,点A ,B 表示的数为a ,b ,则A ,B 两点的距离AB a b ,A ,B 的中点P 表示的数为2a b +, [知识运用]:若线段AB 上有一点P ,当PA PB =时,则称点P 为线段AB 的中点.已知数轴上A ,B 两点对应数分别为a 和b ,()2240a b ++-=,P 为数轴上一动点,对应数为x .(1)a =______,b =______;(2)若点P 为线段AB 的中点,则P 点对应的数x 为______.若B 为线段AP 的中点时则P 点对应的数x 为______ (3)若点A 、点B 同时向左运动,点A 的速度为1个单位长度/秒,点B 的速度为3个单位长度/秒,则经过多长时间点B 追上点A ?(列一元一次方程解应用题);此时点B 表示的数是______ (4)若点A 、点B 同时向左运动,它们的速度都为1个单位长度/秒,与此同时点P 从-16处以2个单位长度/秒的速度向右运动,经过多长时间后,点A 、点B 、点P 三点中其中一点是另外两点的中点?__________________(直接写出答案.) 【答案】(1)﹣2、4;(2)1、10;(3)经过3秒点B 追上点A .此时点B 表示的数是-5;(4)83s 、173s 、263s 【分析】(1)利用非负数的性质解即可;(2)利用线段中点定义,和数轴求两点距离的方法列出方程,解方程即可;(3)利用点A 的行程+AB 间距离=B 行程,列出方程t +6=3t 求出t ,点B 表示的数用4减B 点行程即可;(4)设运动的时间为tS ,先用“t ”表示A 、B 、P 表示的数分三种情况考虑,①点A 为点P 与点B 的中点,P A =AB ,列方程4-t -(-2-t )=-2-t -(-16+2t ),②点P 为点A 与点B 的中点,即AP =PB ,列方程-16+2t -(-2-t )=4-t -(-16+2t )③点B 为点A 与点P 中点,即AB =BP 列方程-16+2t -(4-t )=4-t -(-2-t )解方程即可. 【详解】解:(1)∵()2240a b ++-=,()22040a b +≥-≥,, ∴20a +=,40b -=,∴2a =-,4b =,故答案为:﹣2;4;(2)∵点P 为线段AB 的中点,P 点对应的数为x ,∴4-x =x -(-2), ∴x =1,∵B 为线段AP 的中点时则P 点对应的数x ,∴x -4=4-(-2),∴x =10,故答案为:1、10;(3)解:设经过t 秒点B 追上点A .t +6=3t ,(316)t =-,3t =,B 表示的数为:4-3×3=-5,∴经过3秒点B 追上点A .此时点B 表示的数是-5,答案为:经过3秒点B 追上点A ;-5;(4)设运动的时间为tS,点P表示-16+2t,点A表示-2-t,点B表示4-t,①点A为点P与点B的中点,P A=AB,4-t-(-2-t)=-2-t-(-16+2t),3t=8,t=83 s,②点P为点A与点B的中点,即AP=PB,-16+2t-(-2-t)=4-t-(-16+2t),6t=34,t=173s,③点B为点A与点P中点,即AB=BP,-16+2t-(4-t)=4-t-(-2-t),3t=26,t=263s,故答案为:83s、173s、263s.【点睛】本题考查非负数的性质,数轴上动点,中点定义,两点间距离,一元一次方程及其解法,掌握非负数的性质,中点定义,两点间距离,一元一次方程及其解法,关键是利用分类思想解题可以达到思维清晰,思考问题周密,不遗漏,不重复.。
线段和角的有关计算问题易错点剖析

线段、角错解示例一、对直线的定义理解不透彻例1 下面说法是否正确:延长直线AB到C点.错解:正确.错解分析:因为直线是向两方无限延长的,所以,延长直线AB到C点的说法是错误的.二、对线段中点的定义理解不透彻例2判断:如果AB=AC,则点A就是线段BC的中点.错解:对错解分析:上述回答只考虑了A,B,C 三点共线的情形,而当A,B,C 三点不共线时,虽有AB=AC,但点A不在线段BC上,故不是线段BC的中点.三、忽略了距离定义中“长度”的含义例3判断:连结两点的线段叫做这两点的距离.错解:正确.错解分析:距离指的是长度,而线段是几何图形,他们是两个不同的概念.因此,上述说法是错误的.正确的说法应是:连结两点的线段的长度叫两点间的距离.四、考虑问题不全面例4经过三点A,B,C有几条直线?错解:只有一条直线.错解分析:题目中未指明这三点A,B,C的位置关系,于是,A可能在直线BC上,也可能不在直线BC上,而上述回答只考虑了前一种情形,是不全面的.正解:(1)当点A在直线BC上时,过三点A,B,C只有1条直线;(2)当点A在不在直线BC上时,过三点A,B,C有3条直线.五、对射线的定义理解不全面例5试回答:射线AB和射线BA是否是同一条射线.错解:是同一条射线.错解分析:由射线的定义可知,表示射线的头一个字母为射线的端点,而在射线AB中,端点是A,在射线BA中,其端点是B.因此,射线AB与射线BA 不是同一条射线.六、混淆平角和直线的定义例6有的同学说:平角是一条直线,这种说法对吗?错解:对错解分析:平角是角,而直线是线,这是两个不同的概念,不能把二者混为一谈,应叙述为“平角的两边构成一条直线”.七、例7 3条直线两两相交,可以得到几条射线,几条线段?错解:得到12条射线,3条线段.错解分析:此题忽略了3条直线交于一点的特殊情况,正确答案应为:6条射线、0条线段或12条射线, 3条线段.八、被题目误导,考虑问题不全面例8如果两个角互补,那么这两个角( )(A)可能是两个锐角 (B)可能是钝角(C)一定是一个锐角和一个钝角 (D)以上说法都不对错解:选C.错解分析:应选D .上面的解法中,忽视了两个角都是直角的情况九、例9 如图,∠AOB =∠BOF =∠COD =90°,OC ,OE 分别为∠AOB ,∠AOD 的平分线,试指出∠EOC 的所有的余角.错解:∠EOC 的余角是∠DOE . 错解分析: 对互为余角的概念模糊,误认为互余的两个角一定是邻角,漏掉了∠AOE .正解:∠EOC 的余角是∠DOE 和∠AOE .十、例10 若∠AOB =170°,∠AOC =70°,∠BOD =60°,求∠COD 的度数. 错解:如图所示,∠COD =360°-∠AOB -∠AOC -∠BOD =360°-170°- 70°-60°=60°.错解分析: 题目中未给图形,应对图形的各种情况都要考虑,正确答案应为4个:即∠COD 的度数为40°,160°,180°或60°,另外3种图形请自己画出,并写出求解过程.十一、概念模糊例 11 判断正误:一条直线是一个平角,一条射线是一个周角.( ) 错解:(√)错解分析:平角的图形与直线相似,周角的图形与射线相似.根据图形相似,就错误地认为概念也一致.其实平角、周角是角,角是有顶点、两条边的,而直O AB CD E F B A DO线、射线则不是.正解:(×)点拨:平角、周角都是特殊角,虽然它们与一般角形象不同,但是它们仍然是角.它们都具有一个顶点和两条边,只不过平角的两边成一条直线,周角的两边重合成一条射线罢了,而直线无顶点,射线是从一点(端点)开始向任意一方向无限延伸的.十二、角的表示错误例12 下列图形中,能用∠AOB、∠O、∠1 三种方法表示同一个角的是()(A) (B) (C) (D)错解:选 A.错解分析:本题没有弄清角的表示方法.选项A中以O为顶点的角不是一个,故不能用∠O表示一个角.正解:选 C点拨:当某顶点处不只存在一个角时,不能用顶点处的一个大写字母表示其中的角,应用三个大写字母表示,其中表示顶点的字母要写在中间.只有以某点为顶点的角唯一时,才能用一个大写字母表示.十三、数错角的个数例 13 指出图中一共有几个角.错解:一共有6个角,它们分别是∠AOB,∠AOC,∠BOC,∠COA,∠COB,∠BOA.错解分析:本题错在没有弄清楚角的概念及表示方法,误认为∠AOB 与∠BOA,∠COA 与∠AOC 是不同的角,其实它们是一个角的两种不同表示方法. 数角的个数时必须做到不重不漏,要按一定的顺序去数.每一条射线都与另一条射线可组成一个角,可按顺时针方向数,也可按逆时针方向数.正解:有 3 个,它们分别是∠AOB,∠AOC,∠BOC.点拨:计算角的个数时,先确定角的一条始边,再确定终边,始边、终边相同的视为同一个角.把以这条边为始边的角数完,再数另外的角;从一个点出发引 n 条射线,可以确定2)1(nn个角.十四、角度的计算出错例 14 计算下列各题:(1)61°26′÷3;(2)25.36°-17°22′.错解:(1)61°26′÷3=20°12′;(2)25.36°-17°22′=8.14°.错解分析:(1)错用了角度的进制,误以为1°=10′;(2)错在没有统一形式就开始相减.正解:(1)61°26′÷3=(60°+84′+120″)÷3=20°28′40″;(2)25.36°-17°22′=25°+0.36 ×60′-17°22′=25°21′+0.6×60″-17°22′=25°21′36″-17°22′=7°59′36″.点拨:在进行角度的和、差运算时,应先统一单位,都化成度或分、秒表示(如90°=89°59′60″),然后进行计算.在进行乘法运算时,往往先把分、秒分别乘以倍数,将结果满60″进1′,满 60′进1°.对于除法运算则是从度开始除,依次进行下去,若除不尽往往四舍五入.。
