7[1].5.6二次函数图象的几何变换.题库学生版

合集下载

二次函数的图像与性质专项练习

二次函数的图像与性质专项练习【知识要点】1．二次函数：形如的函数叫做二次函数.2．二次函数的图像性质：（1）二次函数的图像是；（2）二次函数),,,0(2为常数c b a a c bx ax y ≠++=通过配方可得c b a a ab ac a b x a y ,,,0(44)2(22≠-++=为常数），其顶点坐标为。

（3）当0>a 时，抛物线开口，并向上无限延伸；在对称轴左侧)2(a b x -<即时，y 随x 的增大而减小；在对称轴右侧)2(abx ->即时，y 随x 的增大而增大；当abx 2-=时，函数有 .当0<a 时，抛物线开口，并向下无限延伸；在对称轴左侧)2(abx -<即时，y 随着x 的增大而增大；在对称轴右侧)2(abx ->即时，y 随着x 的增大而减小；当,2时a bx -=函数有。

3．二次函数的图像平移：（1）二次函数k h x a y h x a y ax y +-=-==222)(,)(,的图像都是抛物线，并且形状相同，只是位置不同（a 的取值决定抛物线的形状）.将2ax y =的图像向右（h>0）、向左（h<0）平移h 个单位，就得到函数2)(h x a y -=的图像；再将此抛物线向上(k>0)、向下(k<0)平移k 个单位得到函数k h x a y +-=2)(的图像.上述平移的规律是：“h 值正、负、右、左移；k 值正、负、上、下移.” 4.抛物线与坐标轴的交点：（1）抛物线).,0(2c y c bx ax y 轴交于点与++=（2）若方)0,)(0,(,,0212212x x x c bx ax y x x c bx ax 轴点交则抛物线有两根++==++ 核心考点突破考点㈠二次函数的图像性质例1定义[,,a b c ]为函数2y ax bx c =++的特征数, 下面给出特征数为 [2m ，1 – m , –1– m ] 的函数的一些结论：① 当m = – 3时，函数图象的顶点坐标是(31，38)； ② 当m > 0时，函数图象截x 轴所得的线段长度大于23；③ 当m < 0时，函数在x >41时，y 随x 的增大而减小； ④ 当m ≠ 0时，函数图象经过同一个点.其中正确的结论有 A. ①②③④ B. ①②④ C. ①③④ D. ②④ 变式训练1.已知二次函数2y ax bx c =++的图像如图所示，则下列结论正确的是（）A.0a >B. 0c <C.240b ac -<D.0a b c ++>第（1）题第（3）题 2．已知二次函数2y ax bx c =++(0a ≠)的图象如图所示，有下列结论：（）①240b ac ->；②0abc >；③80a c +>；④930a b c ++<．3. 已知二次函数)0(2≠++=a c bx ax y 的图象如图所示，有下列5个结论：① 0>abc ；② c a b +<；③ 024>++c b a ；④ b c 32<；⑤ )(b am m b a +>+，（1≠m 的实数）其中正确的结论有（）A. 2个B. 3个C. 4个D. 5个考点㈡二次函数图像平移例2. 抛物线c bx x y ++=2图像向右平移2个单位再向下平移3个单位，所得图像的解析式为322--=x x y ，则b 、c 的值为（） A . b=2， c=2 B. b=2，c=0 C . b= -2，c=-1 D. b= -3， c=2 变式训练1．把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，则平移后抛物线的表达式（）2.若把函数y=x 的图象用E （x ，x ）记，函数y=2x+1的图象用E （x ，2x+1）记，……则E （x ，122+-x x ）可以由E （x ，2x ）怎样平移得到？3．如图，点A ，B 的坐标分别为（1, 4）和（4, 4）,抛物线n m x a y +-=2)(的顶点在线段AB 上运动，与x 轴交于C 、D 两点（C 在D 的左侧），点C 的横坐标最小值为3-，则点D 的横坐标最大值为( )第（2）题A ．－3B ．1C ．5D ．8OB OA ⊥，且2OB OA =，点A 的坐标是(12)-，．P ，使得ABP ABO S S =△△． 1x 轴的交点如图所示，根据图中信息可得到m 的值第2题图2．已知二次函数()()221y x a a =-+-（a 为常数），当a 取不同的值时，其图象构成一个“抛物线系”．下图分别是当1a =-，0a =，1a =，2a =时二次函数的图象.它们的顶点在一条直线上，这条直线的解析式是y = . 3.如图，已知二次函数c bx x y ++-=221的图象经过A （2，0）、B （0，－6）两点。

中考数学专项复习《二次函数图像的几何变换》练习题及答案

中考数学专项复习《二次函数图像的几何变换》练习题及答案一、单选题1．若二次函数y=mx2-（m2-3m）x+1-m的图象关于y轴对称，则m的值为（）A．0B．3C．1D．0或32．抛物线y＝（x+2）2+1可由抛物线y＝x2平移得到，下列平移正确的是（）A．先向右平移2个单位，再向上平移1个单位B．先向右平移2个单位，再向下平移1个单位C．先向左平移2个单位，再向上平移1个单位D．先向左平移2个单位，再向下平移1个单位3．将抛物线y＝﹣2（x+1）2﹣3先向右平移4个单位长度，再向上平移5个单位长度，得到的抛物线的函数表达式是（）A．y＝﹣2（x﹣5）2+8B．y＝﹣2（x﹣3）2+8C．y＝﹣2（x﹣5）2+2D．y＝﹣2（x﹣3）2+24．抛物线y=（x+2）2﹣3可以由抛物线y=x2平移得到，则下列平移过程正确的是（）A．先向左平移2个单位，再向上平移3个单位B．先向左平移2个单位，再向下平移3个单位C．先向右平移2个单位，再向下平移3个单位D．先向右平移2个单位，再向上平移3个单位5．如图，一条抛物线与x轴相交于A、B两点（点A在点B的左侧），其顶点P在线段MN上移动．若点M、N的坐标分别为（﹣1，﹣2）、（1，﹣2）点B的横坐标的最大值为3，则点A的横坐标的最小值为（）A．-3B．-1C．1D．36．在平面直角坐标系中将二次函数y=x2的图象向上平移2个单位，所得图象的解析式为（）A．y=x2﹣2B．y=x2+2C．y=（x﹣2）2D．y=（x+2）27．函数y=2x2+4x+1①；y=2x2－4x+1②的图象的位置关系是()A．②在①的上方B．②在①的下方C．②在①的左方D．②在①的右方8．将抛物线y=x2向左平移一个单位，再向上平移2个单位，得到的抛物线解析式为（）A．y=(x−1)2+2B．y=(x+1)2−2C．y=(x+1)2+2D．y=(x+2)2+1 9．在平面直角坐标系中如果抛物线y＝2x2+1不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是()A．y＝2(x－2)2+ 3B．y＝2(x－2)2－1C．y＝2(x + 2)2－1D．y＝2(x + 2)2 + 310．把抛物线y=（x﹣1）2+2向左平移1个单位，再向下平移2个单位，所得抛物线是（）A．y=x2B．y=（x﹣2）2C．y=（x﹣2）2+4D．y=x2+411．把抛物线y=x2+1向左平移3个单位，再向下平移2个单位，得到的抛物线表达式为（）A．y=（x﹣3）2+2 B．y=（x﹣3）2﹣1C．y=（x+3）2﹣1 D．y=（x﹣3）2﹣212．函数y＝ax2+bx+c的图象如图所示，那么关于x的方程ax2+bx+c－3＝0 的根情况是（）A．有两个相等的实数根B．有一个实数根C．有两个不相等的实数根D．没有实数根二、填空题13．已知将二次函数y=x2+bx+c的图象向右平移2个单位再向下平移3个单位，所得图象的解析式为y=x2﹣4x﹣5，则b=，c=．14．抛物线y=x2﹣6x+5向上平移2个单位长度，再向右平移1个单位长度后，得到的抛物线解析式是．15．把抛物线y=12x2−1先向右平移1个单位，再向下平移2个单位，得到的抛物线的解析式为.16．将二次函数y＝﹣（x﹣1）2的图象沿x轴向左平移2个单位，得到的函数表达式为．17．一抛物线和另一抛物线y＝﹣2x2的形状和开口方向完全相同，且顶点坐标是（﹣2，1），则该抛物线的解析式为.18．在平面直角坐标系中将抛物线y=x2﹣x﹣12向上（下）或左（右）平移m个单位，使平移后的抛物线恰巧经过原点，则|m|的最小值为．三、综合题19．在同一个直角坐标系中作出y＝12x2，y＝12x2－1的图象．（1）分别指出它们的开口方向、对称轴以及顶点坐标；（2）抛物线y＝12x2－1与抛物线y＝12x2有什么关系？20．如图，二次函数y=(x−1)(x−a)（a为常数）的图象的对称轴为直线x=2.（1）求a的值.（2）向下平移该二次函数的图象，使其经过原点，求平移后图象所对应的二次函数的表达式. 21．已知二次函数y=x2﹣2mx+m2+3（m是常数）．（1）求证：不论m为何值，该函数的图象与x轴没有公共点；（2）把该函数的图象沿y轴向下平移多少个单位长度后，得到的函数的图象与x轴只有一个公共点？22．如图①，抛物线y=−x2+bx+c与x轴交于两点A，B(4，0)（点A位于点B的左侧），与y轴交于点C(0，4)，拋物线的对称轴l与x轴交于点N，长为2的线段PQ（点P位于点Q的上方）在x轴上方的抛物线对称轴上运动．（1）求抛物线的关系式；（2）在线段PQ运动过程中当PC+PA的值最小时，求此时点P的坐标；（3）如图②过点P作PM⊥y轴于点M，当△CPM和△QBN相似时，求点Q的坐标．23．已知抛物线y＝x2＋bx＋c经过点（﹣2，1），它的对称轴为直线x＝﹣1（1）求抛物线的表达式和顶点坐标.（2）如图，已知点A（P，t）（P＞0）在（1）中的抛物线上，将该抛物线向右平移若干个单位后得到抛物线l，点A在抛物线l上的对应点为点B（t，t），若抛物线l恰好经过点C（2，0），求P，t 的值.24．如图，抛物线y=x2﹣3x+k与x轴交于A、B两点，与y轴交于点C（0，﹣4）．（1）k=；（2）点A的坐标为，B的坐标为；（3）设抛物线y=x2﹣3x+k的顶点为M，求四边形ABMC的面积．参考答案1．【答案】B2．【答案】C3．【答案】D4．【答案】B5．【答案】A6．【答案】B7．【答案】D8．【答案】C9．【答案】C10．【答案】A11．【答案】C12．【答案】A13．【答案】0；-614．【答案】y=（x﹣4）2﹣315．【答案】y=12(x−1)2−316．【答案】y＝﹣(x+1)2 17．【答案】y＝﹣2（x+2）2+1 18．【答案】319．【答案】（1）解：如图所示：抛物线y＝12x2开口向上，对称轴为y轴，顶点坐标(0，0)；抛物线y＝12x2－1开口向上，对称轴为y轴，顶点坐标(0，－1)（2）解：抛物线y＝12x2－1可由抛物线y＝12x2向下平移1个单位长度得到20．【答案】（1）解：y=(x−1)(x−a)=x2−(1+a)x+a. ∵图象的对称轴为直线x=2∴a+12=2∴a =3 .（2）解：∵a =3∴二次函数的表达式为 y =x 2−4x +3 ∴抛物线向下平移3个单位后经过原点∴平移后图象所对应的二次函数的表达式为 y =x 2−4x .21．【答案】（1）证明：∵△=（﹣2m ）2﹣4×1×（m 2+3）=4m 2﹣4m 2﹣12=﹣12＜0∴方程x 2﹣2mx+m 2+3=0没有实数解即不论m 为何值，该函数的图象与x 轴没有公共点（2）解：y=x 2﹣2mx+m 2+3=（x ﹣m ）2+3把函数y=（x ﹣m ）2+3的图象沿y 轴向下平移3个单位长度后，得到函数y=（x ﹣m ）2的图象，它的顶点坐标是（m ，0）因此，这个函数的图象与x 轴只有一个公共点所以，把函数y=x 2﹣2mx+m 2+3的图象沿y 轴向下平移3个单位长度后，得到的函数的图象与x 轴只有一个公共点22．【答案】（1）解：∵y =−x 2+bx +c 过B(4，0)，C(0，4)∴0=−16+4b +c ∴b =3 c =4∴抛物线的关系式为y =−x 2+3x +4；（2）解：∵A 点关于对称轴l 的对称点是B ，连接CB 交对称轴l 于点P ，连接PB 由对称性可知 PA =PB ∴PC +PA =PC +PB ≥CB当C 、P 、B 三点在一条直线上时，PC +PA 有最小值 ∵B(4，0) C(0，4)设直线BC 的解析式为y =kx +b ∴{4k +b =0b =4 解得{k =−1b =4 ∴y =−x +4∵由在y =−x 2+3x +4得抛物线对称轴为直线x =−3−2=32 ∴y =−32+4=52∴P(32，52)；（3）解：如图：由在y =−x 2+3x +4得抛物线对称轴为直线x =−3−2=32 设Q(32，t)(t >0)，则P(32，t +2) M(0，t +2) N(32，0)∵B(4，0) C(0，4)；∴BN =52QN =t PM =32 CM =|t −2|∵∠CMP =∠QNB =90°∴△CPM 和△QBN 相似，只需CM QN =PM BN 或CM BN =PMQN ①当CM QN =PM BN 时，|t−2|t =3252 解得t =54或t =5 ∴Q(32，54)或(32，5)；②当CM BN =PM QN 时，|t−2|52=32t 解得t =2+√192或t =2−√192（舍去） ∴Q(32，2+√192)综上所述，Q 的坐标是(32，54)或(32，5)或(32，2+√192)．23．【答案】（1）解：y ＝x 2＋bx ＋c 经过点（﹣2，1）对称轴为直线x ＝﹣1，即 −b2a=−1 ∴b =2∴y =x 2+2x +c将点（﹣2，1）代入得： 1=4−4+c 解得： c =1 ∴y =x 2+2x +1∵y =x 2+2x +1=(x +1)2∴y ≥0 恒成立，当 x =−1 时取得最小值， y =0 ∴顶点坐标为： (−1，0) ；（2）解：∵y 向右平移若干单位与l 重合，且l 过点（2，0） ∴平移距离为 2−(−1)=3 ，且A （P ，t ）平移到B （t ，t ）∴t =p +3 ，即 p =t −3∴A （ t −3 ，t ）代入 y =(x +1)2 得： t =(t −3+1)2 ，即 t 2−5t +4=0 解得： t 1=1 t 2=4∴p =t −3=1−3=−2 或 p =t −3=4−3=1 ∵P ＞0∴p =−2 (舍去) ∴p =1，t =4 .24．【答案】（1）k=﹣4（2）（﹣1，0）；（4，0）（3）解：∵y=x 2﹣3x ﹣4= (x −32)2−254∴M(32，−254)设抛物线的对称轴与x 轴交于N ，如图所示：则四边形ABMC 的面积=S △ACN +S △NCM +S △NMB = 12×AN ×OC +12×NM ×ON +12×NB ×NM = 12×52×4+12×254×32+12×52×254 = 352∴四边形ABMC 的面积是 352．。

中考数学总复习《二次函数图像的几何变换》专项测试卷-附参考答案

中考数学总复习《二次函数图像的几何变换》专项测试卷-附参考答案一、单选题(共12题；共24分)1．已知抛物线y=3（x+1）2+4是由抛物线y=3x2（）得到的．A．先向右平移1个单位，再向上平移4个单位B．先向右平移1个单位，再向下平移4个单位C．先向左平移1个单位，再向上平移4个单位D．先向左平移1个单位，再向下平移4个单位2．把抛物线y=-x2+4x-3先向左平移3个单位，再向下平移2个单位，则变换后的抛物线解析式是（）A．y＝－(x＋3)2－2B．y＝－(x＋1)2－1C．y＝－x2＋x－5D．前三个答案都不正确3．抛物线y=-2x2-4x-5经过平移得到y=-2x2，平移方法是（）A．向左平移1个单位，再向下平移3个单位B．向左平移1个单位，再向上平移3个单位C．向右平移1个单位，再向下平移3个单位D．向右平移1个单位，再向上平移3个单位4．要由抛物线y=−2x2平移得到y=−2x2−4x−2，则平移的方法是（）A．向左平移1个单位B．向上平移1个单位C．向下平移1个单位D．向右平移1个单位5．在平面直角坐标系中，二次函数y=−x2+2x+3的图象交x轴于点A、B（点A在点B的左侧）．若把点B向上平移m（m>0）个单位长度得点B1，若点B1向左平移n (n>0)个单位长度，将与该二次函数图象上的点B2重合；若点B1向左平移(n+2)个单位长度，将与该二次函数图象上的点B3重合．则n的值为（）A．1B．2C．3D．46．在同一平面直角坐标系内，将函数y=2x2+4x+1的图象沿x轴方向向右平移2个单位长度后再沿y轴向下平移1个单位长度，得到图象的顶点坐标是（）A．（﹣1，1）B．（1，﹣2）C．（2，﹣2）D．（1，﹣1）7．将y=2x2的函数图象向左平移2个单位长度后，得到的函数解析式是（）A．y=2x2+2B．y=2（x+2）2C．y=（x－2）2D．y=2x2－28．将抛物线y=x2平移得到抛物线y=（x+2）2，则这个平移过程正确的是（）A．向左平移2个单位B．向右平移2个单位C．向上平移2个单位D．向下平移2个单位9．将二次函数y=x2的图象向左平移1个单位，则平移后图象的函数表达式为（）A．y=x2−1B．y=x2+1C．y=(x−1)2D．y=(x+1)2 10．已知：二次函数y=x2−4x−a，下列说法中错误的个数是（）①若图象与轴有交点，则a≤4．②若该抛物线的顶点在直线y=2x上，则a的值为−8．③当a=−3时，则不等式x2−4x+a>0的解集是1<x<3．④若将图象向上平移1个单位，再向左平移3个单位后过点(1,−2)，则a=−1．⑤若抛物线与x轴有两个交点，横坐标分别为x1、x2，则当x取x1+x2时的函数值与x取0时的函数值相等．A．1B．2C．3D．411．对于抛物线y= 23（x+4）2﹣5，下列说法正确的是（）A．开口向下B．对称轴是直线x=4C．顶点坐标（4，﹣5 ）D．向右平移4个单位，再向上平移5个单位得到y= x212．抛物线y＝3x2向右平移一个单位得到的抛物线是（）A．y＝3x2+1B．y＝3x2﹣1C．y＝3（x+1）2D．y＝3（x﹣1）2二、填空题(共6题；共7分)13．已知抛物线p：y=ax2+bx+c的顶点为C，与x轴相交于A、B两点（点A在点B的左侧），点C 关于x轴的对称点为C′，我们称以A为顶点且过点C′，对称轴与y轴平行的抛物线为抛物线p的“关联”抛物线，直线AC′为抛物线p的“关联”直线．若一条抛物线的“关联”抛物线和“关联”直线分别是y=x2+2x+1和y=2x+2，则这条抛物线的解析式为．14．将二次函数y=−x2−4x+1的图象先向右平移a个单位再向下平移2a个单位．（1）若平移后的二次函数图象经过点(1，−1)，则a＝．（2）平移后的二次函数图象与y轴交点的纵坐标最大值为．15．如图，在平面直角坐标系中，正方形ABCD的顶点A、B的坐标分别为(0，2)、(1，0)，顶点C在函数y＝13x2＋bx－1的图象上，将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′，点D的对应点D′落在抛物线上，则点D与其对应点D′之间的距离为．16．把二次函数y=（x﹣1）2+2的图象绕原点旋转180°后得到的图象的解析式为．17．如图，抛物线L1：y=ax2+bx+c(a≠0)与x轴只有一个公共点A(1，0)，与y轴交于点B(0，2)，虚线为其对称轴，若将抛物线向下平移两个单位长度得抛物线L2，则图中两个阴影部分的面积和为．18．将二次函数y=2x2-4x+3的图象先向左平移3个单位长度，再向下平移1个单位长度得到函数的图象的表达式是。

中考数学总复习《二次函数图像的几何变换》练习题及答案

中考数学总复习《二次函数图像的几何变换》练习题及答案班级:___________姓名：___________考号：_____________一、单选题1．抛物线y=x2向下平移一个单位得到抛物线（）A．y=(x+1)2B．y=(x−1)2C．y=x2+1D．y=x2−12．抛物线y＝x2＋4x＋5是由抛物线y＝x2＋1经过某种平移得到，则这个平移可以表述为() A．向上平移2个单位B．向左平移2个单位C．向下平移4个单位D．向右平移2个单位3．如果一种变换是将抛物线向右平移2个单位或向上平移1个单位，我们把这种变换称为抛物线的简单变换．已知抛物线经过两次简单变换后的一条抛物线是y=x2+1，则原抛物线的解析式不可能的是（）A．y=x2﹣1 B．y=x2+6x+5 C．y=x2+4x+4 D．y=x2+8x+174．将抛物线y＝x2﹣2向左平移3个单位长度，再向上平移3个单位长度后，所得抛物线的解析式为（）A．y＝（x+3）2+3B．y＝（x﹣3）2+1C．y＝（x+2）2+1D．y＝（x+3）2+15．对于实数c、d，我们可用min{ c，d }表示c、d两数中较小的数，如min{3，-1}=-1.若关于x的函数y = min{2x2，a(x-t)2}的图象关于直线x=3对称，则a、t的值可能是A．3，6B．2，-6C．2，6D．-2，66．将抛物线y=x2﹣2x+2先向右平移3个单位长度，再向上平移2个单位长度，则经过这两次平移后所得抛物线的顶点坐标是（）A．（﹣2，3）B．（﹣1，4）C．（3，4）D．（4，3）7．抛物线y=x2+bx+c的图象先向右平移2个单位，再向下平移3个单位，所得图象的函数解析式为y=（x﹣1）2﹣4，则b、c的值为（）A．b=2，c=﹣6B．b=2，c=0C．b=﹣6，c=8D．b=﹣6，c=28．已知抛物线y=-x2+1，下列结论：①抛物线开口向上；②抛物线与x轴交于点（-1，0）和点（1，0）；③抛物线的对称轴是y轴；④抛物线的顶点坐标是（0，1）；⑤抛物线y=-x2+1是由抛物线y=−x2向上平移1个单位得到的.其中正确的个数有A．5个B．4个C．3个D．2个9．在平面直角坐标系中，抛物线y=－12x2+2x－1关于点（－1，2）对称的图象解析式为() A．y= 12x2－2x+1B．y= 12x2+4x+11C．y=－12x2－2x-1D．y= 12x2+4x+1910．抛物线y=x2+bx+c的图象向右平移2个单位，再向下平移3个单位，所得图象的解析式为y=x2-2x-3，则b、c的值为()A．b=2，c=2B．b=2，c=0C．b=-2，c=-1D．b=-3，c=211．函数y=(x+3)2的图象可以由函数y=x2的图象()得到A．向左平移3个单位B．向右平移3个单位C．向上平移3个单位D．向下平移3个单位12．将抛物线y=x2−6x+5向上平移两个单位长度，再向右平移一个单位长度后，得到的抛物线解析式是（）A．y=(x−4)2−6B．y=(x−1)2−3C．y=(x−2)2−2D．y=(x−4)2−2二、填空题13．将抛物线y=x2﹣4x+9向平移个单位，向平移个单位，得到抛物线y=x2﹣6x+5．14．在平面直角坐标系中，已知A(−1,m)和B(5,m)是抛物线y=x2+bx+1上的两点，将抛物线y=x2+bx+1的图象向上平移n（n是正整数）个单位，使平移后的图象与x轴没有交点，则n 的最小值为．15．在平面直角坐标系中，若将抛物线y＝−（x＋3）2＋1先向左平移2个单位长度，再向下平移3个单位长度，则经过这两次平移后所得抛物线的顶点坐标是16．如图，抛物线y=−2x2+8x−6与x轴交于点A，B，把抛物线在x轴及其上方的部分记作C1，将C1向右平移得C2，C2与x轴交于点B，D，若直线y=x+m与C1，C2共有3个不同的交点，则m的取值范围是.17．将抛物线y= 13x2先向左平移1个单位，再向上平移2个单位，得到y=．18．如图，一条抛物线y=﹣x（x﹣2）（0≤x≤2）的一部分，记为C1，它与x轴交于O，A1两点，将C1绕点A1旋转180°得到C2，交x轴于点A2；将C2绕点A2旋转180°得到C3，交x轴于A3；如此进行下去，直至得到C6，若点P（2017，y）在抛物线C n上，则y=．三、综合题19．如图，在平面直角坐标系xOy中，将二次函数y=x2﹣1的图象M沿x轴翻折，把所得到的图象向右平移2个单位长度后再向上平移8个单位长度，得到二次函数图象N．（1）求N的函数表达式；（2）设点P（m，n）是以点C（1，4）为圆心、1为半径的圆上一动点，二次函数的图象M与x 轴相交于两点A、B，求PA2+PB2的最大值；（3）若一个点的横坐标与纵坐标均为整数，则该点称为整点．求M与N所围成封闭图形内（包括边界）整点的个数．20．在同一个直角坐标系中作出y＝12x2，y＝12x2－1的图象．（1）分别指出它们的开口方向、对称轴以及顶点坐标；（2）抛物线y＝12x2－1与抛物线y＝12x2有什么关系？21．已知二次函数y＝(x﹣m)2﹣(x﹣m)．（1）判断该二次函数图象与x轴交点个数，并说明理由；（2）若该二次函数的顶点坐标为( 72，n)，求m、n的值；（3）若把函数图象向上平移k个单位，使得对于任意的x都有y大于0，求证：k＞1 4．22．如图是小明站在点O处长抛篮球的路线示意图，球在点A处离手，且OA=1m.第一次在点D处落地，然后弹起在点E处落地，篮球在距O点6m的点B处正上方达到最高点，最高点C距地面的高度BC =4m ，点E 到篮球框正下方的距离EF =2m ，篮球框的垂直高度为3m .据试验，两次划出的抛物线形状相同，但第二次的最大高度为第一次的12，以小明站立处点O 为原点，建立如图所示的平面直角坐标系.（1）求抛物线ACD 的函数解析式；（2）求篮球第二次的落地点E 到点O 的距离.（结果保留整数）（3）若小明想一次投中篮球框，他应该向前走多少米？（结果精确到0.1m ）（参考数据：√3≈1.73，√6≈2.45）23．如图，抛物线 y =12x 2+2x +c 经过点 A(0，3) ，将该抛物线平移后，点 A(0，3) 到达点 B(4，1) 的位置.（1）求平移后抛物线的解析式，并在同一平面直角坐标系中画出平移后的抛物线；（2）过点B 画平行于y 轴的直线交原抛物线于点C ，求线段 BC 的长；（3）若平行于y 轴的直线 l ：x =m 与两条抛物线的交点是 P ，Q ，当线段 PQ 的长度超过6时，求m 的取值范围.24．已知抛物线y=ax 2+bx+c 与x 轴交于点A(1，0)，B(3，0)，且过点C(0，-3).（1）求抛物线的解析式和顶点坐标；（2）请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=-x 上，并写出平移后抛物线的解析式.参考答案1．【答案】D 2．【答案】B 3．【答案】B 4．【答案】D 5．【答案】C 6．【答案】D 7．【答案】B 8．【答案】B 9．【答案】B 10．【答案】B 11．【答案】A 12．【答案】D13．【答案】右；1；下；9 14．【答案】4 15．【答案】(-5,-2) 16．【答案】−3<m <−15817．【答案】13 （x+1）2+2 18．【答案】219．【答案】（1）解：二次函数y=x 2﹣1的图象M 沿x 轴翻折得到函数的解析式为y=﹣x 2+1，此时顶点坐标（0，1）将此图象向右平移2个单位长度后再向上平移8个单位长度得到二次函数图象N 的顶点为（2，9）故N 的函数表达式y=﹣（x ﹣2）2+9=﹣x 2+4x+5 （2）解：∵A （﹣1，0），B （1，0）∴PA 2+PB 2=（m+1）2+n 2+（m ﹣1）2+n 2=2（m 2+n 2）+2=2•PO 2+2∴当PO 最大时PA 2+PB 2最大．如图，延长OC 与⊙O 交于点P ，此时OP 最大∴OP的最大值=OC+PO= √17+1∴PA2+PB2最大值=2（√17+1）2+2=38+4 √17（3）解：M与N所围成封闭图形如图所示由图象可知，M与N所围成封闭图形内（包括边界）整点的个数为25个20．【答案】（1）解：如图所示：抛物线y＝12x2开口向上，对称轴为y轴，顶点坐标(0，0)；抛物线y＝12x2－1开口向上，对称轴为y轴，顶点坐标(0，－1)（2）解：抛物线y＝12x2－1可由抛物线y＝12x2向下平移1个单位长度得到21．【答案】（1）解：该二次函数图象与x轴有2个交点．理由如下：y＝(x﹣m)2﹣(x﹣m)＝x2﹣(2m+1)x+m2+m ∵⊙＝(2m+1)2﹣4(m2+m)＝1＞0∴该二次函数图象与x轴有2个交点（2）解：∵该二次函数的顶点坐标为( 72，n)∴﹣−(2m+1)2＝72∴m＝3，n＝﹣1 4（3）解：证明：y＝x2﹣(2m+1)x+m2+m＝(x﹣2m+12)2﹣14抛物线y＝(x﹣2m+12)2﹣14的顶点坐标为(2m+12，﹣14)把抛物线y＝(x﹣2m+12)2﹣14向上平移k个单位后顶点坐标为(2m+12,−14+k)∵把函数图象向上平移k个单位，使得对于任意的x都有y大于0∴平移后的抛物线在x轴上方∴﹣14+k＞0∴k＞1 422．【答案】（1）解：由题意知设抛物线ACD的函数解析式为y=a(x−k)2+ℎ(a≠0)；将A(0，1)、C(6，4)代入表达式得，1=a(0−6)2+4解得a=−112；∴y=−112(x−6)2+4；令y=0得∴抛物线ACD的函数解析式为y=−112(x−6)2+4(0≤x≤4√3+6)；（2）解：由题意，将y=−112(x−6)2+4向下平移两个单位得令y=0得，0=−112(x−6)2+2，解得：x1=6+2√6，x2=6−2√6∴4√3+6−(6−2√6)=4√3+2√6∴4√3+2√6+6+2√6=4√3+4√6+6∴E(4√3+4√6+6，0)∴OE=4√3+4√6+6≈23(m)（3）解：令y=3得解得：x1=6+2√3，x2=6−2√3OF=OE+EF=4√3+4√6+8(m)4√3+4√6+8−(6+2√3)=4√6+2√3+2≈15.3(m)4√3+4√6+8−(6−2√3)=4√6+6√3+2≈22.2(m)∴小明想一次投中篮球框，他应该向前走15.3m或22.2m.23．【答案】（1）解：∵抛物线y＝12x2+2x+c经过点A（0，3）∴c＝3∴y＝12x2+2x+3＝12（x+2）2+1由题意可知，抛物线向右平移4个单位，向下平移2个单位∴平移后抛物线的解析式为y＝12（x+2﹣4）2+1﹣2，即y＝12（x﹣2）2﹣1如图（2）解：把x＝4代入y＝12x2+2x+3得，y＝12×16+2×4+3＝19∴C（4，19）∴BC＝19﹣1＝18；（3）解：当12m2+2m+3−(12m2−2m+1)=6时，m=1；当12m2−2m+1−(12m2+2m+3)=6时，m=-2；由图象可知，当m＞1或m＜﹣2时，线段PQ的长度超过6.24．【答案】（1）解：∵抛物线与x轴交于点A（1，0），B（3，0）可设抛物线解析式为y=a（x-1）（x-3）把C（0，-3）代入得：3a=-3解得：a=-1故抛物线解析式为y=-（x-1）（x-3）即y=-x2+4x-3∵y=-x2+4x-3=-（x-2）2+1∴顶点坐标（2，1）（2）解：先向左平移2个单位，再向下平移1个单位，得到的抛物线的解析式为y=-x2，平移后抛物线的顶点为（0，0）落在直线y=-x上．。

初三数学二次函数图像性质及几何变换

初三数学二次函数图像性质及几何变换一．选择题（共50小题）1．抛物线y＝﹣3（x﹣2）2+4的开口方向和顶点坐标分别是（）A．向上，（2，4）B．向上，（﹣2，4）C．向下，（2，4）D．向下，（﹣2，4）2．关于y＝2（x﹣3）2+2的图象，下列叙述正确的是（）A．顶点坐标为（﹣3，2）B．对称轴为直线y＝3C．当x≥3时，y随x增大而增大D．当x≥3时，y随x增大而减小3．关于抛物线y＝﹣x2﹣2x的叙述，正确的是（）A．开口向下，对称轴是直线x＝﹣1B．开口向下，对称轴是直线x＝1C．开口向上，对称轴是直线x＝﹣1D．开口向上，对称轴是直线x＝14．关于二次函数y＝x2+2x﹣8，下列说法正确的是（）A．图象的对称轴在y轴的右侧B．图象与y轴的交点坐标为（0，8）C．当x＞﹣1时，y随x的增大而减小D．y的最小值为﹣95．关于二次函数y＝（x+1）2﹣3，下列说法错误的是（）A．图象的开口方向向上B．函数的最小值为﹣3C．图象的顶点坐标为（1，﹣3）D．当x＜﹣1时，y随x的增大而减小6．关于抛物线y＝﹣x2+2x﹣3的判断，下列说法正确的是（）A．抛物线的开口方向向上B．抛物线的对称轴是直线x＝﹣1C．当x＜1时，y随x的增大而减小D．抛物线与y轴的交点坐标为（0，﹣3）7．对二次函数y＝x2+2x+3的性质描述正确的是（）A．函数图象开口朝下B．当x＜0时，y随x的增大而减小C．该函数图象的对称轴在y轴左侧D．该函数图象与y轴的交点位于y轴负半轴8．关于二次函数y＝（x+2）2﹣4，下列说法正确的是（）A．函数图象的开口向下B．函数图象的顶点坐标是（2，﹣4）C．该函数的最大值是﹣4D．当x≥﹣2时，y随x的增大而增大9．已知点（﹣4，y1）、（﹣1，y2）、（2，y3）都在函数y＝﹣x2+5的图象上，则y1、y2、y3的大小关系为（）A．y1＞y2＞y3B．y3＞y2＞y1C．y2＞y3＞y1D．y3＞y1＞y210．已知点A（4，y1），B（1，y2），C（﹣2，y3）都在二次函数y＝（x﹣2）2﹣1的图象上，则y1，y2，y3从小到大排列（）A．y1＜y3＜y2B．y2＜y1＜y3C．y1＜y2＜y3D．y3＜y1＜y211．若二次函数y＝x2﹣4x+k的图象经过点（﹣1，y1），（3，y2），则y1与y2的大小关系为（）A．y1＝y2B．y1＞y2C．y1＜y2D．不能确定12．已知二次函数y＝a（x﹣1）2+4的图象开口向上，若点A（﹣2，y1），B（﹣1，y2），C（5，y3）都在该函数图象上，则y1，y2，y3三者之间的大小关系是（）A．y1＜y2＜y3B．y1＜y3＜y2C．y2＜y1＜y3D．y3＜y1＜y213．已知（﹣1，y1），（﹣2，y2），（﹣4，y3）是抛物线y＝﹣2x2﹣8x+m上的点，则（）A．y1＜y2＜y3B．y3＜y2＜y1C．y2＞y1＞y3D．y2＞y3＞y114．已知抛物线y＝﹣x2+2x+c，若点（0，y1）（1，y2）（3，y3）都在该抛物线上，则y1、y2、y3的大小关系是（）A．y3＞y1＞y2B．y3＜y2＜y1C．y3＞y2＞y1D．y3＜y1＜y215．已知抛物线y＝ax2﹣2ax+3（a＞0），A（﹣1，y1），B（2，y2），C（4，y3）是抛物线上三点，则y1，y2，y3由小到大的排列是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y1＜y2D．y2＜y3＜y116．若A（﹣4，y1），B（﹣3，y2），C（1，y3）为二次函数y＝ax2+4ax﹣5（a＞0）的图象上的三点，则y1，y2，y3的大小关系是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y1＜y2D．y1＜y3＜y217．点（﹣1，y1），（2，y2），（4，y3）都在抛物线y＝﹣x2+2x+c上，则y1，y2，y3的大小关系为（）A．y1＜y2＜y3B．y3＜y2＜y1C．y2＜y1＜y3D．y3＜y1＜y218．点（3，y1），（﹣2，y2），（0，y3）在抛物线y＝mx2﹣4mx+n（m＜0）上，则y1，y2，y3的大小关系是（）A．y2＜y3＜y1B．y1＜y3＜y2C．y1＜y2＜y3D．y3＜y1＜y219．把抛物线y＝x2+1向右平移3个单位，再向下平移2个单位，得到抛物线（）A．y＝（x+3）2﹣1B．y＝（x+3）2+3C．y＝（x﹣3）2﹣1D．y＝（x﹣3）2+320．在平面直角坐标系中，将抛物线y＝x2+3先沿x轴向左平移3个单位长度，再沿y轴向下平移4个单位长度，则平移后得到的抛物线是（）A．y＝（x﹣3）2﹣4B．y＝（x﹣3）2﹣1C．y＝（x+3）2﹣4D．y＝（x+3）2﹣121．在平面直角坐标系中，将二次函数y＝（x﹣2）2+1的图象向左平移2个单位长度，再向下平移2个单位长度，所得图象对应的函数表达式为（）A．y＝（x+2）2﹣1B．y＝（x+2）2+3C．y＝x2﹣1D．y＝x2+322．要将抛物线y＝x2平移后得到抛物线y＝x2+4x+5，下列平移方法正确的是（）A．向左平移2个单位，再向上平移1个单位B．向左平移2个单位，再向下平移1个单位C．向右平移2个单位，再向上平移1个单位D．向右平移2个单位，再向下平移1个单位23．把抛物线y＝ax2+bx+c的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式为y＝x2﹣2x+3，则b+c 的值为（）A．12B．9C．﹣14D．1024．抛物线y＝3x2﹣6x﹣3的图象向左平移2个单位，再向上平移2个单位，所得图象的解析式为y＝3x2+bx+c，则b，c的值为（）A．b＝6，c＝﹣1B．b＝﹣18，c＝23C．b＝6，c＝﹣5D．b＝﹣18，c＝2925．二次函数y＝x2+2x+3图象上的两点A（x1，y1）与B（x2，y2）关于对称轴对称，则（）A．x1+x2＝﹣2；y1＝y2B．x1+x2＝﹣1；y1＝﹣y2C．x1＝x2；y1＝y2D．x1＝﹣x2；y1＝﹣y226．将抛物线y＝x2﹣2x+1向上平移2个单位长度，再向左平移3个单位长度，得到抛物线y＝x2+bx+c，则b，c的值为（）A．b＝﹣8，c＝18B．b＝8，c＝14C．b＝﹣4，c＝6D．b＝4，c＝627．如果将抛物线y＝ax2+bx+c向右平移2个单位，再向上平移3个单位，得到新的抛物线y＝x2﹣2x+1，那么（）A．b＝6，c＝12B．b＝﹣6，c＝6C．b＝2，c＝﹣2D．b＝2，c＝428．先将抛物线y＝（x﹣1）2+2关于x轴作轴对称变换，所得的新抛物线的解析式为（）A．y＝﹣（x﹣1）2+2B．y＝﹣（x+1）2+2C．y＝﹣（x﹣1）2﹣2D．y＝﹣（x+1）2﹣229．在平面直角坐标系中，先将抛物线y＝x2+2x﹣8关于y轴作轴对称变换，再将所得的抛物线关于x轴作轴对称变换，那么经过两次变换后所得的新抛物线的解析式为（）A．y＝﹣x2﹣2x﹣8B．y＝﹣x2﹣2x+8C．y＝﹣x2+2x﹣8D．y＝﹣x2+2x+830．在平面直角坐标系中，先将抛物线y＝x2+x﹣2关于x轴作轴对称变换，再将所得的抛物线关于y轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为（）A．y＝﹣x2﹣x+2B．y＝﹣x2+x﹣2C．y＝﹣x2+x+2D．y＝x2+x+231．将抛物线y＝（x﹣1）2+2沿y轴折叠后得到的新抛物线的解析式为（）A．y＝（x+1）2﹣2B．y＝（x﹣1）2﹣2C．y＝﹣（x﹣1）2﹣2D．y＝（x+1）2+232．二次函数y＝﹣x2+6x+a的最大值是10，那么a的值等于（）A．﹣1B．1C．3D．433．已知二次函数y＝ax2+bx+c（a＜0）的图象如图，当﹣5≤x≤0时，下列说法正确的是（）A．有最小值﹣5、最大值0B．有最小值﹣3、最大值6C．有最小值0、最大值6D．有最小值2、最大值634．当0≤x≤3，函数y＝﹣x2+4x+5的最大值与最小值分别是（）A．9，5B．8，5C．9，8D．8，435．已知0≤x≤1，那么函数y＝﹣2x2+8x﹣6的最大值是（）A．﹣6B．0C．2D．436．已知二次函数的图象（0≤x≤4）如图，关于该函数在所给自变量的取值范围内，下列说法正确的是（）A．有最大值2，有最小值﹣2.5B．有最大值2，有最小值1.5C．有最大值1.5，有最小值﹣2.5D．有最大值2，无最小值37．当a﹣1≤x≤a时，二次函数y＝x2﹣4x+3的最小值为8，则a的值为（）A．﹣1 或5B．0或6C．﹣1或6D．0或538．当a≤x≤a+2时，二次函数y＝x2﹣4x+4的最小值为1，则a的值为（）A．﹣1B．3C．﹣1或3D．0或339．已知二次函数y＝x2+2x+3，当0≤x≤3时，下列说法正确的是（）A．有最小值2，最大值18B．有最小值3，最大值18C．有最小值0，最大值3D．有最小值2，最大值1240．二次函数y＝﹣x2﹣2x+c在﹣3≤x≤2的范围内有最大值为﹣5，则c的值是（）A．﹣2B．3C．﹣3D．﹣641．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，其对称轴是直线x＝﹣1．下列结论中：①ac＜0；②b2＞4ac；③2a+b＝0；④a+b+c＞0．正确的有（）A．1个B．2个C．3个D．4个42．如图是二次函数y＝ax2+bx+c图象的一部分，其对称轴为x＝﹣1，且过点（﹣3，0）．则下列说法：①abc＜0；②2a﹣b＝0；③a+b+c＝0；④若（﹣6，y1），是抛物线上的两点，则y1＞y2．其中正确的有（）个．A．1B．2C．3D．443．如图，抛物线y＝ax2+bx+c的对称轴是直线x＝1，则以下五个结论①abc＞0，②2a+b＝0，③b2＞4ac，④4a+2b+c ＞0，⑤3a+c＜0中，正确的有（）A．1个B．2个C．3个D．4个44．二次函数y＝ax2+bx+c（a≠0）图象如图，下列结论：①abc＞0；②2a+b＝0；③4a+2b+c＞0；④a﹣b+c＞0；⑤b2﹣4ac＞0．其中正确的是（）A．②③④⑤B．①②④C．②③⑤D．①②③④⑤45．二次函数y＝ax2+bx+c图象的对称轴为直线x＝1，其图象如图所示，现有下列结论：①abc＞0；②b﹣2a＜0；③4a+2b+c＜0；④a+b≥m（am+b）．其中正确的结论有（）个．A．1个B．2个C．3个D．4个46．二次函数y＝ax2+bx+c的图象如图所示，以下结论正确的个数为（）①abc＜0；②c+2a＜0；③9a﹣3b+c＝0；④am2﹣a+bm+b＞0（m为任意实数）A．1个B．2个C．3个D．4个47．二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝1．下列结论：①abc＞0；②3a+c＞0；③（a+c）2﹣b2＜0；④a+b≤m（am+b）（m为实数）．其中结论正确的为（）A．①④B．②③④C．①②④D．①②③④48．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x＝1，下列结论：①abc＜0；②方程ax2+bx+c＝0（a≠0）必有一个根大于2且小于3；③11a+2c＞0；④对于任意实数m，都有m（am+b）≥a+b，其中正确结论的个数是（）A．1个B．2个C．3个D．4个49．二次函数y＝ax2+bx+c（a≠0）图象如图．下列结论：①abc＞0；②a﹣b+c＜0；③若m为任意实数，则有a+b≥am2+bm；④若，且x1≠x2，则x1+x2＝2；其中正确的有（）A．1个B．2个C．3个D．4个50．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列4个结论：①abc＞0；②2a﹣b＝0；③若A（﹣1，y1），B（2，y2），C（4，y3）是抛物线上三点，则y3＜y2＜y1；④3a+c＞0；⑤am2+bm＜a+b（m≠1）；⑥关于x的方程|ax2+bx+c|＝1有四个根，且这四个根的和为4，其中正确的结论有（）A．1个B．2个C．3个D．4个( 50题) ( 59题)二．填空题（共10小题）51．若抛物线y＝x2+6x﹣m与x轴有公共点，则m的取值范围为．52．若二次函数y＝x2﹣6x+k与x轴有两个交点，则k的取值范围是．53．若关于x的函数y＝x2﹣2x+k+1的图象与x轴只有1个交点，则k的值是．54．二次函数y＝（k﹣1）x2﹣2x+1的图象与x轴有交点，则k的取值范围是．55．二次函数y＝x2﹣6x+5的图象与x轴交点坐标是．56．已知二次函数y＝x2+4x+c的图象与x轴的一个交点坐标是（2，0），则它与x轴的另一个交点坐标是．57．已知抛物线y＝ax2﹣2ax+c与x轴的一个交点坐标为（3，0），与x轴的另一个交点坐标为．58．抛物线y＝ax2+bx+c与x轴的两个交点坐标分别为（﹣3，0）和（1，0），则抛物线的对称轴为直线．59．如图，抛物线y＝ax2+bx+c的对称轴是直线x＝1，关于x的方程ax2+bx+c＝0的一个根为x＝4，则另一个根为．60．抛物线y＝﹣4（x+3）2与x轴的交点坐标是，与y轴的交点坐标是．。

二次函数的图像与性质经典练习题(11套)附带详细答案

练习一1．二次函数的图像开口向＿＿＿＿，对称轴是＿＿＿＿，顶点坐标是＿＿＿＿，图像有最＿＿＿点，x ＿＿＿时，y 随x 的增大而增大，x ＿＿＿时，y 随x 的增大而减小。

2．关于，，的图像，下列说法中不正确的是（） A ．顶点相同 B ．对称轴相同 C ．图像形状相同 D ．最低点相同 3．两条抛物线与在同一坐标系内，下列说法中不正确的是（） A ．顶点相同 B ．对称轴相同 C ．开口方向相反 D ．都有最小值 4．在抛物线上，当y ＜0时，x 的取值范围应为（） A ．x ＞0 B ．x ＜0 C ．x ≠0 D ．x ≥0 5．对于抛物线与下列命题中错误的是（） A ．两条抛物线关于轴对称 B ．两条抛物线关于原点对称 C ．两条抛物线各自关于轴对称 D ．两条抛物线没有公共点6．抛物线y=－b ＋3的对称轴是＿＿＿，顶点是＿＿＿。

7．抛物线y=－－4的开口向＿＿＿，顶点坐标＿＿＿，对称轴＿＿＿，x ＿＿＿时，y 随x 的增大而增大，x ＿＿＿时，y 随x 的增大而减小。

8．抛物线的顶点坐标是（）A ．（1，3）B ．（1，3）C ．（1，3）D ．（1，3）9．已知抛物线的顶点为（1，2），且通过（1，10），则这条抛物线的表达式为（） A ．y=3－2 B ．y=3＋22y ax =213y x =2y x =23y x =2y x =2y x =-2y x =-2y x =2y x =-x y 2x 21(2)2x +22(1)3y x =+-------2(1)x -2(1)x +C ．y=3－2D ．y=－3－210．二次函数的图像向左平移2个单位，向下平移3个单位，所得新函数表达式为（）A ．y=a ＋3B ．y=a －3C ．y=a ＋3D ．y=a －3 11．抛物线的顶点坐标是（）A ．（2，0）B ．（2，-2）C ．（2，-8）D ．（-2，-8）12．对抛物线y=－3与y=－＋4的说法不正确的是（） A ．抛物线的形状相同 B ．抛物线的顶点相同 C ．抛物线对称轴相同 D ．抛物线的开口方向相反13．函数y=a ＋c 与y=ax ＋c(a ≠0)在同一坐标系内的图像是图中的（）14．化为y=为a 的形式是＿＿＿＿，图像的开口向＿＿＿＿，顶点是＿＿＿＿，对称轴是＿＿＿＿。

2024中考数学一轮复习专题精练专题13 二次函数(学生版)

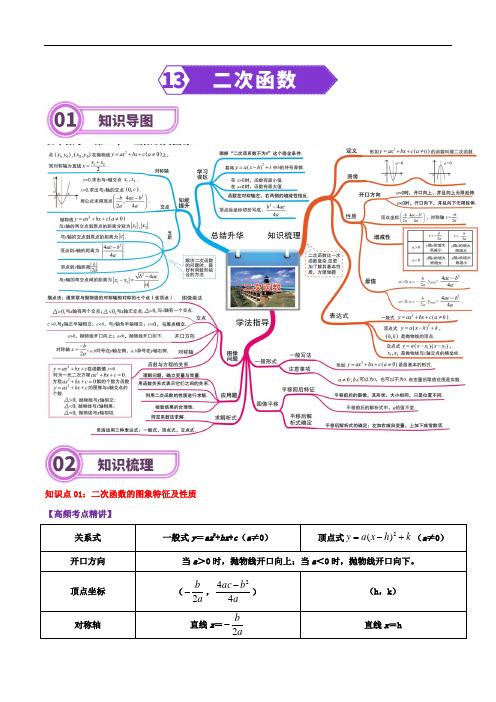
知识点01：二次函数的图象特征及性质【高频考点精讲】关系式一般式y ＝ax 2+bx +c （a ≠0）顶点式k h x a y +-=2)(（a ≠0）开口方向当a ＞0时，抛物线开口向上；当a ＜0时，抛物线开口向下。

顶点坐标（ab2-，a b ac 442-）（h ，k ）对称轴直线x ＝ab2-直线x ＝h增减性a＞0x＜ab2-时，y随x增大而减小；x＞ab2-时，y随x增大而增大。

x＜h时，y随x增大而减小；x＞h时，y随x增大而增大。

a＜0x＜ab2-时，y随x增大而增大；x＞ab2-时，y随x增大而增大。

x＜h时，y随x增大而增大；x＞h时，y随x增大而减小。

最值a＞0当x＝ab2-时，abacy442-=最小值。

当x＝h时，ky=最小值。

a＜0当x＝ab2-时，abacy442-=最大值。

当x＝h时，ky=最大值。

知识点02：二次函数图象与系数的关系【高频考点精讲】1．a决定抛物线的开口方向及大小（1）a＞0，抛物线开口向上；a＜0，抛物线开口向下。

（2）|a|越大，抛物线的开口越小；|a|越小，抛物线的开口越大。

2．a、b共同决定抛物线对称轴的位置（1）当b＝0时，对称轴x＝ab2-＝0，对称轴为y轴。

（2）当a、b同号时，对称轴x＝ab2-＜0，对称轴在y轴左侧。

（3）当a、b异号时，对称轴x＝ab2-＞0，对称轴在y轴右侧。

3．c 决定抛物线与y 轴的交点位置（1）当c ＝0时，抛物线过原点。

（2）当c ＞0时，抛物线与y 轴交于正半轴。

（3）当c ＜0时，抛物线与y 轴交于负半轴。

4．ac b 42-决定抛物线与x 轴的交点位置（1）当ac b 42-＝0时，抛物线与x 轴有唯一交点。

（2）当ac b 42-＞0时，抛物线与x 轴有两个交点。

（3）当ac b 42-＜0时，抛物线与x 轴没有交点。

5．特殊值（1）当x=1时，y=a+b+c ；当x=﹣1时，y=a-b+c ；当x=2时，y=4a+2b+c ；当x=﹣2时，y=4a-2b+c 。

中考数学复习----《二次函数之函数变换》知识点总结与专项练习题(含答案解析)

中考数学复习----《二次函数之函数变换》知识点总结与专项练习题（含答案解析）知识点总结1.二次函数的平移：①若函数进行左右平移，则在函数的自变量上进行加减。

左加右减。

②若函数进行上下平移，则在函数解析式整体后面进行加减。

上加下减。

2.一次函数的对称变换：①若二次函数关于x轴对称，则自变量不变，函数值变为相反数。

②若二次函数关于y轴对称，则函数值不变，自变量变成相反数。

③若二次函数关于原点对称，则自变量与函数值均变成相反数。

练习题1、（2022•通辽）在平面直角坐标系中，将二次函数y＝（x﹣1）2+1的图像向左平移1个单位长度，再向下平移2个单位长度，所得函数的解析式为（）A．y＝（x﹣2）2﹣1 B．y＝（x﹣2）2+3 C．y＝x2+1 D．y＝x2﹣1【分析】根据图像的平移规律，可得答案．【解答】解：将二次函数y＝（x﹣1）2+1的图像向左平移1个单位长度，再向下平移2个单位长度，得到的抛物线的解析式是y＝（x﹣1+1）2+1﹣2，即y＝x2﹣1．故选：D．2、（2022•玉林）小嘉说：将二次函数y＝x2的图像平移或翻折后经过点（2，0）有4种方法：①向右平移2个单位长度②向右平移1个单位长度，再向下平移1个单位长度③向下平移4个单位长度④沿x 轴翻折，再向上平移4个单位长度你认为小嘉说的方法中正确的个数有（）A ．1个B ．2个C ．3个D ．4个【分析】分别求出平移或翻折后的解析式，将点（2，0）代入可求解．【解答】解：①向右平移2个单位长度，则平移后的解析式为y ＝（x ﹣2）2，当x ＝2时，y ＝0，所以平移后的抛物线过点（2，0），故①符合题意；②向右平移1个单位长度，再向下平移1个单位长度，则平移后的解析式为y ＝（x ﹣1）2﹣1，当x ＝2时，y ＝0，所以平移后的抛物线过点（2，0），故②符合题意；③向下平移4个单位长度，则平移后的解析式为y ＝x 2﹣4，当x ＝2时，y ＝0，所以平移后的抛物线过点（2，0），故③符合题意；④沿x 轴翻折，再向上平移4个单位长度，则平移后的解析式为y ＝﹣x 2+4，当x ＝2时，y ＝0，所以平移后的抛物线过点（2，0），故④符合题意；故选：D ．3、（2022•泸州）抛物线y ＝﹣21x 2+x +1经平移后，不可能得到的抛物线是（） A ．y ＝﹣21x 2+x B ．y ＝﹣21x 2﹣4 C ．y ＝﹣21x 2+2021x ﹣2022 D ．y ＝﹣x 2+x +1【分析】根据抛物线的平移规律，可得答案．【解答】解：∵将抛物线y ＝﹣x 2+x +1经过平移后开口方向不变，开口大小也不变， ∴抛物线y ＝﹣x 2+x +1经过平移后不可能得到的抛物线是y ＝﹣x 2+x +1．故选：D ．4、（2022•湖州）将抛物线y ＝x 2向上平移3个单位，所得抛物线的解析式是（）A．y＝x2+3 B．y＝x2﹣3 C．y＝（x+3）2D．y＝（x﹣3）2【分析】根据二次函数变化规律：左加右减，上加下减，进而得出变化后解析式．【解答】解：∵抛物线y＝x2向上平移3个单位，∴平移后的解析式为：y＝x2+3．故选：A．5、（2022•牡丹江）抛物线y＝x2﹣2x+3向右平移2个单位长度，再向上平移3个单位长度，得到抛物线的顶点坐标是．【分析】利用平移规律可求得平移后的抛物线的解析式，可求得其顶点坐标．【解答】解：∵抛物线y＝x2﹣2x+3＝（x﹣1）2+2，∴抛物线y＝x2﹣2x+3向右平移2个单位长度，再向上平移3个单位长度，得到抛物线y＝（x﹣1﹣2）2+2+3，即y＝（x﹣3）2+5，∴平移后的抛物线的顶点坐标为（3，5）．故答案为：（3，5）．6、（2022•黑龙江）把二次函数y＝2x2的图像向左平移1个单位长度，再向下平移2个单位长度，平移后抛物线的解析式为．【分析】直接根据“上加下减，左加右减”的原则进行解答．【解答】解：由“左加右减”的原则可知，将二次函数y＝2x2的图像向左平移1个单位长度所得抛物线的解析式为：y＝2（x+1）2；由“上加下减”的原则可知，将抛物线y ＝2（x+1）2向下平移2个单位长度所得抛物线的解析式为：y＝2（x+1）2﹣2，故答案为：y＝2（x+1）2﹣2．7、（2022•黔东南州）在平面直角坐标系中，将抛物线y＝x2+2x﹣1先绕原点旋转180°，再向下平移5个单位，所得到的抛物线的顶点坐标是．【分析】先求出绕原点旋转180°的抛物线解析式，再求出向下平移5个单位长度的解析式，配成顶点式即可得答案．【解答】解：将抛物线y＝x2+2x﹣1绕原点旋转180°后所得抛物线为：﹣y＝（﹣x）2+2（﹣x）﹣1，即y＝﹣x2+2x+1，再将抛物线y＝﹣x2+2x+1向下平移5个单位得y＝﹣x2+2x+1﹣5＝﹣x2+2x﹣4＝﹣（x﹣1）2﹣3，∴所得到的抛物线的顶点坐标是（1，﹣3），故答案为：（1，﹣3）．8、（2022•荆州）规定：两个函数y1，y2的图像关于y轴对称，则称这两个函数互为“Y 函数”．例如：函数y1＝2x+2与y2＝﹣2x+2的图像关于y轴对称，则这两个函数互为“Y 函数”．若函数y＝kx2+2（k﹣1）x+k﹣3（k为常数）的“Y函数”图像与x轴只有一个交点，则其“Y函数”的解析式为．【分析】根据关于y轴对称的图形的对称点的坐标特点，分情况讨论求解．【解答】解：∵函数y＝kx2+2（k﹣1）x+k﹣3（k为常数）的“Y函数”图像与x轴只有一个交点，∴函数y＝kx2+2（k﹣1）x+k﹣3（k为常数）的图像与x轴也只有一个交点，当k＝0时，函数解析式为y＝﹣2x﹣3，它的“Y函数”解析式为y＝2x﹣3，它们的图像与x轴只有一个交点，当k≠0时，此函数是二次函数，∵它们的图像与x轴都只有一个交点，∴它们的顶点分别在x轴上，∴＝0，解得：k＝﹣1，∴原函数的解析式为y＝﹣x2﹣4x﹣4＝﹣（x+2）2，∴它的“Y函数”解析式为y＝﹣（x﹣2）2＝﹣x2+4x﹣4，综上，“Y函数”的解析式为y＝2x﹣3或y＝﹣x2+4x﹣4，故答案为：y＝2x﹣3或y＝﹣x2+4x﹣4．。

中考数学每日一练：二次函数图象的几何变换练习题及答案_2020年综合题版

1.答案：
2.答案：
3.答案： 4.答案：
5.答案：
部分）．
考点：二次函数图象的几何变换;待定系数法求二次函数解析式;
答案
~~第5题~~
(2019大连.中考真卷) 把函数
称是关于点的相关函数.
（1）填空：的值为（用含
（2）若
，当
的图象绕点的图象的对称轴与轴交点坐标为的代数式表示）时，函数的最大值为，最小值为
旋转
.
，且
，得到新函数的图象，我们，求的解析式；
考点：二次函数图象的几何变换;待定系数法求二次函数解析式;二次函数与一次函数的综合应用;
答案
~~第2题~~
(2020长兴.中考模拟) 已知抛物线y=x2+bx+1经过点（3，-2），
（1）求b的值；
（2）求将抛物线向左平移3个单位后的抛物线解析式.
考点：二次函数图象的几何变换;待定系数法求二次函数解析式;
考点：二次函数图象的几何变换;
答案
~~第4题~~ (2019揭阳.中考模拟) 如图①，已知抛物线
经过点A（0，3），B（3，0），C（4，3）．
（1）求抛物线的函数表达式；
（2）求抛物线的顶点坐标和对称轴；
（3）把抛物线向上平移，使得顶点落在x轴上，直接写出两条抛物线、对称轴和y轴围成的图形的面积S（图②中阴影
答案
~~第3题~~ (2020西安.中考模拟) 已知：抛物线y=ax2+bx+1经过A（1，0）、B（-1，3）两点。
（1）求a，b的值：
（2）以线段AB为边作正方形ABB'A'，能否将己知抛物线平移，使其经过A'、B'两点？若能，求出平移后经过A'、B'

人教版九年级上册数学《二次函数图象与几何变换》专项练习(含答案)

二次函数图象与几何变换一、选择题（本大题共6小题）1.如果二次函数的图象与已知二次函数22y x x =-的图象关于y 轴对称，那么这个二次函数的解析式是（）A ．22y x x =-+B ．22y x x =+C ．22y x x =--D ．212y x x=- 2.把二次函数()2132y x =-+的图象经过翻折、平移得到二次函数()2132y x =-的图象，下列对此过程描述正确的是（） A ．先沿y 轴翻折，再向下平移6个单位 B ．先沿y 轴翻折，再向左平移6个单位 C ．先沿x 轴翻折，再向左平移6个单位 D ．先沿x 轴翻折，再向右平移6个单位3.将二次函数2y x =的图象平移后，可得到二次函数()21y x =+的图象，平移的方法是（） A ．向上平移1个单位 B ．向下平移1个单位 C ．向左平移1个单位 D ．向右平移1个单位4.把二次函数2y x =的图象沿x 轴向右平移1个单位，再沿y 轴向上平移3个单位，那么平移后所得图象的函数解析式是（） A ．()213y x =-- B ．()213y x =+- C ．()213y x =-+ D ．()213y x =++5.二次函数()2231y mx m m x m =--+-的图象关于y 轴对称，则m 的值（）．A ．0B ．3C ．1D ．0或36.平面直角坐标系中，若平移二次函数()()200920104y x x =--+的图象，使其与x 轴交于两点，且此两点的距离为1个单位，则平移方式为（） A ．向上平移4个单位 B ．向下平移4个单位 C ．向左平移4个单位 D ．向右平移4个单位二、填空题（本大题共9小题）7.将抛物线22453y x x =-+向下平移2个单位，此时抛物线的解析式为8.将抛物线22453y x x =-+向左平移4个单位，此时抛物线的解析式为 9.将二次函数22810y x x =-+的图象沿x 轴向左平移3个单位，沿y 轴向上平移410.将抛物线22y x x =-向上平移3个单位,再向右平移4个单位等到的抛物线是 .11.把抛物线2y ax bx c =++的图象先向右平移3个单位，再向下平移2个单位，所得的图象的解析式是235y x x =-+，则a b c ++=________________． 12.将二次函数()21y x =-的图象进行适当的平移或轴对称变换后所得图象的函数表达式为()212y x =---，请写出一种符合条件的变换13.函数2y x =与2y x =-的图象关于______________对称，也可以认为2y x =是函数2y x =-的图象绕__________旋转 °得到的。

二次函数、学生版

【变式 1】二次函数 y=-x2 +bx+c 的图象如图所示：若点 A（x1 ，y1 ），B（x2 ，y2 ）在此函数图象上，x1 ＜x2 ＜1，y1 与 y2 的大小关系是（）
Hale Waihona Puke A． y1≤y2B． y1＜ y2
C． y1≥y2
D． y1＞ y2
【例2】已知二次函数 y x 3 x
2
2 1 D.4 个
其中结论正确的有（ A.1 个 B.2 个
） C.3 个
【例 2】二次函数 y=ax2 +bx+c （a≠0）的图象如图如图所示，若 M=a+b-c， N=4a-2b+c， P=2a-b．则 M，N，P 中，值小于 0 的数有（）
A．3 个
B．2 个
C． 1 个
D． 0 个）
二次函数
【题型 1】根据实际问题列二次函数关系式【例 1】（2010•丽水）如图，四边形 ABCD 中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设 CD 的长为 x，四边形 ABCD 的面积为 y，则 y 与 x 之间的函数关系式是（）
【变式】（2009•泰安）如图所示，矩形 ABCD 中，AB=8，BC=6，P 是线段 BC 上一点（P 不与 B 重合），M 是 DB 上一点，且 BP=DM，设 BP=x，△MBP 的面积为 y，则 y 与 x 之间的函数关系式为
2
【变式 1】函数 y=x2 +mx-4，当 x＜2 时，y 随 x 的增大而减小，则 m 的取值范围是
【变式 2】（2014•南宁）如图，已知二次函数 y=-x2 +2x，当-1＜x＜a 时，y 随 x 的增大而增大，则实数 a 的取值范围是（）

中考数学《二次函数图形的几何变换》专项练习题(附答案)

中考数学《二次函数图形的几何变换》专项练习题(附答案)一、单选题1．在平面直角坐标系中，二次函数y=(x+1)(x−3)的图象向右平移2个单位后的函数为（）A．y=(x−1)(x−5)B．y=(x+2)(x−2)C．y=(x+3)(x−1)D．y=(x+1)(x+5)2．把抛物线y=-x2向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（）A．y=-（x-1）2-3B．y=-（x+1）2-3C．y=-（x-1）2+3D．y=-（x+1）2+33．在平面直角坐标系中，抛物线y＝（x+5）（x﹣3）经变换后得到抛物线y＝（x+3）（x﹣5），则这个变换可以是（）A．向左平移2个单位B．向右平移2个单位C．向左平移8个单位D．向右平移8个单位4．要得到函数y=−x2+3的图像，可以将函数y=−x2的图像（）A．向左平移3个单位B．向右平移3个单位C．向上平移3个单位D．向下平移3个单位5．将抛物线y＝2（x﹣1）2﹣3向右移动2个单位，再向下移动3个单位，得到的抛物线的解析式为（）A．y＝2（x+1）2B．y＝2（x+1）2﹣6C．y＝2（x﹣3）2D．y＝2（x﹣3）2﹣66．抛物线y=−2x2向左平移2个单位，再向下平移3个单位，得到的抛物线解析式为（）A．y=−2(x−2)2−3B．y=−2(x+2)2−3C．y=2(x−2)2−3D．y=2(x+2)2−37．已知抛物线y=ax2−2ax+a2+1(a≠0).当x≥3时，y随x的增大而增大；当−2≤x≤0时，y的最大值为10.那么与抛物线y=ax2−2ax+a2+1关于y轴对称的抛物线在−2≤x≤3内的函数最大值为（）A．10B．17C．5D．28．将抛物线y=4x2向右平移1个单位，再向上平移3个单位，得到的抛物线是（）A．y=4（x+1）2+3B．y=4（x﹣1）2+3C．y=4（x+1）2﹣3D．y=4（x﹣1）2﹣39．将抛物线y=ax2﹣1平移后与抛物线y=a（x﹣1）2重合，抛物线y=ax2﹣1上的点A（2，3）同时平移到A′，那么点A′的坐标为（）A．（3，4）B．（1，2）C．（3，2）D．（1，4）10．将抛物线y=x2向右平移1个单位长度，再向上平移2个单位长度所得的抛物线解析式为（）A．y=（x﹣1）2+2B．y=（x+1）2+2C．y=（x﹣1）2﹣2D．y=（x+1）2﹣211．将抛物线y=x2+2x先向左平移2个长度单位，再向上平移3个长度单位，所得到的抛物线是（）A．y=(x+1)2+3B．y=(x+3)2+2C．y=(x−1)2−4D．y=(x−3)2+112．将抛物线y＝﹣3x2﹣1向左平移2个单位长度，再向下平移2个单位长度，所得到的抛物线为（）A．y＝﹣3（x+2）2+1B．y＝﹣3（x﹣2）2﹣3C．y＝﹣3（x+2）2﹣3D．y＝﹣3（x﹣2）2+1二、填空题13．把抛物线y=−3x2向上平移2个单位，所得抛物线是．14．如图，抛物线C1：y=12x2经过平移得到抛物线C2：y=12x2+2x，抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是．15．将二次函数y＝2x2的图象沿y轴向上平移2个单位长度所得图象的解析式为. 16．把抛物线y=5x2向左平移3个单位长度，再向下平移7个单位长度，得到的抛物线解析式为．17．抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是. 18．在平面直角坐标系中，将解析式为y=2x2的图象沿着x轴方向向左平移4个单位，再沿着y轴方向向下平移3个单位，此时图象的解析式为．三、综合题19．如图，经过点A（0，﹣4）的抛物线y= 12x2+bx+c与x轴相交于B（﹣2，0），C两点，O为坐标原点．（1）求抛物线的解析式；（2）将抛物线y= 12x2+bx+c向上平移72个单位长度，再向左平移m（m＞0）个单位长度得到新抛物线，若新抛物线的顶点P在△ABC内，求m的取值范围；（3）设点M在y轴上，△OMB+△OAB=△ACB，求AM的长．20．如图，顶点M在y轴上的抛物线y=ax2+c与直线y=x+1相交于A，B两点，且点A在x轴上，点B的横坐标为2，连接AM，BM（1）求抛物线对应的函数表达式；（2）判断⊿ABM的形状，并说明理由；（3）若将（1）中的抛物线沿y轴上下平移，则如何平移才能使平移后的抛物线过点(−2，−3)？21．定义新运算：对于任意实数m，n都有m☆n＝m2﹣mn+n，等式右边是常用的加法、减法、乘法及乘方运算．例如：−3☆2＝(−3)2−(−3)×2+2＝17．根据以上知识解决问题：（1）若x☆3＝1，求x的值；（2）求抛物线y＝(2−x)☆(−1)的顶点坐标；（3）将（2）中的抛物线绕着原点旋转180°，写出得到的新的抛物线解析式．22．课题学习：我们知道二次函数的图象是抛物线，它也可以这样定义：如果一个动点M（x，y）到定点A（0，m）（m＞0）的距离与它到定直线y=﹣m的距离相等，那么动点M形成的图形就是抛物线y=ax2（a＞0）的图象，如图所示．（1）探究：当x≠0时，a与m有何数量关系？（2）应用：已知动点M（x，y）到定点A（0，4）的距离与到定直线y=﹣4的距离相等，请写出动点M形成的抛物线的解析式．（3）拓展：根据抛物线的平移变换，抛物线y= 14（x﹣1）2+2的图象可以看作到定点A（，）的距离与它到定直线y=的距离相等的动点M（x，y）所形成的图形．（4）若点D的坐标是（1，8），在（2）中求得的抛物线上是否存在点P，使得PA+PD最短？若存在，求出点P的坐标，若不存在，请说明理由．23．在平面直角坐标系xOy中（如图）．已知抛物线y=﹣12x2+bx+c经过点A（﹣1，0）和点B（0，52），顶点为C，点D在其对称轴上且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．（1）求这条抛物线的表达式；（2）求线段CD的长；（3）将抛物线平移，使其顶点C移到原点O的位置，这时点P落在点E的位置，如果点M在y 轴上，且以O、D、E、M为顶点的四边形面积为8，求点M的坐标．24．如图①，已知抛物线y=ax2+bx+c经过点A（0，3），B（3，0），C（4，3）．（1）求抛物线的函数表达式；（2）求抛物线的顶点坐标和对称轴；（3）把抛物线向上平移，使得顶点落在x轴上，直接写出两条抛物线、对称轴和y轴围成的图形的面积S（图②中阴影部分）．参考答案1．【答案】A 2．【答案】D 3．【答案】B 4．【答案】C 5．【答案】D 6．【答案】B 7．【答案】B 8．【答案】B 9．【答案】A 10．【答案】A 11．【答案】B 12．【答案】C13．【答案】y =−3x 2+2 14．【答案】4 15．【答案】y ＝2x 2+216．【答案】y =5(x +3)2−7 17．【答案】y=﹣2x 2﹣4x ﹣3 18．【答案】y=2（x+4）2﹣319．【答案】（1）解：将A （0，﹣4）、B （﹣2，0）代入抛物线y= 12x 2+bx+c 中，得：{0+c =−412×4−2b +c =0 解得： {b =−1c =−4故抛物线的解析式：y= 12x 2﹣x ﹣4（2）解：由题意，新抛物线的解析式可表示为：y= 12 （x+m ）2﹣（x+m ）﹣4+ 72 ，即：y= 12x 2+（m ﹣1）x+ 12 m 2﹣m ﹣ 12 ；它的顶点坐标P ：（1﹣m ，﹣1）；由（1）的抛物线解析式可得：C （4，0）；设直线AC 的解析式为y=kx+b （k≠0），把x=4，y=0代入 ∴4k+b=0，b=﹣4 ∴y=x ﹣4．同理直线AB ：y=﹣2x ﹣4；当点P在直线AB上时，﹣2（1﹣m）﹣4=﹣1，解得：m= 5 2；当点P在直线AC上时，（1﹣m）﹣4=﹣1，解得：m=﹣2；∴当点P在△ABC内时，﹣2＜m＜5 2；又∵m＞0∴符合条件的m的取值范围：0＜m＜5 2（3）解：由A（0，﹣4）、C（4，0）得：OA=OC=4，且△OAC是等腰直角三角形；如图，在OA上取ON=OB=2，则△ONB=△ACB=45°；∴△ONB=△NBA+△OAB=△ACB=△OMB+△OAB，即△OMB=△NBA；如图，在△ABN、△AM1B中△BAN=△M1AB，△ABN=△AM1B∴△ABN△△AM1B，得：AB2=AN•AM1；易得：AB2=（﹣2）2+42=20，AN=OA﹣ON=4﹣2=2；∴AM1=20÷2=10；而△BM1A=△BM2A=△ABN∴OM1=OM2=6，AM2=OM2﹣OA=6﹣4=2．综上，AM的长为10或2．20．【答案】（1）解：当y=0时，有x+1=0，则x=-1．∴A（-1，0）当x=2时，y=2+1=3∴B（2，3）将A，B两点代入y=ax2+c中得{0=a+c3=4a+c，解得{a=1 c=−1∴抛物线的解析式为y=x2−1．（2）解：三角形ABM为直角三角形，理由如下：在抛物线中，当x=0时，y=-1∴M（0，-1）又∵A（-1，0），B（2，3）∴AB=3√2，AM=√2BM=2√5又∵AM2+AB2=20=BM2∴三角形ABM为直角三角形．（3）解：设抛物线y=x2−1沿y轴平移后的解析式为y=x2−1+m 将点（-2，-3）代入上式，得m=-6则向下平移6个单位过点（-2，-3）．21．【答案】（1）解：根据题意，得x2−3x+3＝1移项、合并同类项，得x2−3x+2＝0整理，得(x−1)(x−2)=0解得：x1=1，x2=2；（2）解：根据题意知整理得：y=x2−5x+5=(x−52)2−54所以，顶点坐标（52，−54）（3）解：根据题意知，新的抛物线解析式为y=−(−x−52)2+54=−(x+52)2+54．22．【答案】（1）解：由定义可知，MA=MB∴x2+（y﹣m）2=（y+m）2∵y=ax2∴x2= y a∴ya=4my∴a=1 4m（2）解：由（1）可知，a= 1 16∴抛物线的解析式为y= 116x2．（3）1；3；1（4）解：如图所示，过点D作直线y=﹣4的垂线垂足为M，与抛物线的交点就是的点P，此时PA+PD=PD+PM最短（垂线段最短）此时点P坐标（1，1 16）．23．【答案】（1）解：把A（﹣1，0）和点B（0，52）代入y=﹣12x2+bx+c得（2）解：∵y=﹣12（x﹣2）2+ 92，∴C（2，92），抛物线的对称轴为直线x=2，如图，设CD=t，则D（2，92﹣t），∵线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处∴△PDC=90°，DP=DC=t∴P（2+t，92﹣t），把P（2+t，92﹣t）代入y=﹣12x2+2x+ 52得﹣12（2+t）2+2（2+t）+52= 92﹣t，整理得t2﹣2t=0，解得t1=0（舍去），t2=2，∴线段CD的长为2（3）解：P点坐标为（4，92），D点坐标为（2，52），∵抛物线平移，使其顶点C（2，92）移到原点O的位置，∴抛物线向左平移2个单位，向下平移92个单位，而P点（4，92）向左平移2个单位，向下平移92个单位得到点E，∴E点坐标为（2，﹣2）设M（0，m）当m＞0时，12•（m+52+2）•2=8，解得m= 72，此时M点坐标为（0，72）；当m＜0时，12•（﹣m+52+2）•2=8，解得m=﹣72，此时M点坐标为（0，﹣72）；综上所述，M点的坐标为（0，72）或（0，﹣72）24．【答案】（1）解：∵抛物线y=ax2+bx+c经过点A（0，3），B（3，0），C（4，3）∴{c=39a+3b+c=016a+4b+c=3，解得{a=1b=−4c=3。

中考数学《二次函数图像的几何变换》专项练习题及答案

中考数学《二次函数图像的几何变换》专项练习题及答案一、单选题1．在平面直角坐标系中，将抛物线y=x2﹣4先向右平移两个单位，再向上平移两个单位，得到的抛物线的解析式是（）A．y=（x+2）2+2B．y=（x﹣2）2﹣2C．y=（x﹣2）2+2D．y=（x+2）2﹣22．将抛物线影响y=-x2向左平移2个单位后，得到的抛物线的解析式是（）A．y=-（x+2）2B．y=-x2+2C．y=-（x-2）2D．y=-x2-23．若将抛物线y=5x2先向右平移2个单位，再向下平移3个单位，可得到新的抛物线是（）A．y=5(x+2)2+3B．y=5(x−2)2+3C．y=5(x+2)2−3D．y=5(x−2)2−34．在平面直角坐标系内，将抛物线y=(x+2)2−3经过两次平移后，得到的新抛物线为y=(x−1)2−4.下列对这一平移过程描述正确的是（）A．先向右平移3个单位长度，再向下平移1个单位长度B．先向左平移3个单位长度，再向下平移1个单位长度C．先向右平移3个单位长度，再向上平移1个单位长度D．先向左平移3个单位长度，再向下平移1个单位长度5．下列平移中，不能使二次函数y=2x2+4x−6经过原点的是（）A．向左平移1个单位B．向右平移3个单位C．向上平移6个单位D．向上平移8个单位6．二次函数y＝x2－1的图象可由下列哪个函数图象向右平移2个单位，向下平移2个单位得到（）A．y=(x−2)2+1B．y=(x+2)2+1C．y=(x−2)2−3D．y=(x+2)2+37．如图，在直角坐标系中，O为坐标原点，点A（4，0），以OA为对角线作正方形ABOC，若将抛物线y= 12x2沿射线OC平移得到新抛物线y= 12（x-m）2+k（m＞0）．则当新抛物线与正方形的边AB有公共点时，m的值一定是（）A．2，6，8B．0<m≤6C．0<m≤8 D．0<m≤2 或6 ≤ m≤88．将抛物线y＝3x2的图象先向右平移2个单位，再向上平移5个单位后，得到的抛物线解析式是（）A．y＝3（x﹣2）2﹣5B．y＝3（x﹣2）2+5C．y＝3（x+2）2﹣5D．y＝3（x+2）2+59．在平面直角坐标系中，对于二次函数y=(x−2)2+1，下列说法中错误的是（）A．y的最小值为1B．图象顶点坐标为（2，1），对称轴为直线x=2C．当x<2时，y的值随x值的增大而增大，当x≥2时，y的值随x值的增大而减小D．它的图象可以由y=x2的图象向右平移2个单位长度，再向上平移1个单位长度得到10．抛物线y＝12x2向左平移1个单位，再向上平移2个单位后，所得抛物线的表达式是（）A．y＝12（x+1）2﹣2B．y＝12（x﹣1）2+2C．y＝12（x﹣1）2﹣2D．y＝12（x+1）2+211．将二次函数y=x2的图象如何平移可得到y=x2+4x+3的图象（）A．向右平移2个单位，向上平移一个单位B．向右平移2个单位，向下平移一个单位C．向左平移2个单位，向下平移一个单位D．向左平移2个单位，向上平移一个单位12．把抛物线y=(x+2)2向下平移2个单位长度，再向右平移1个单位长度，所得抛物线是（）A．y=(x+2)2+2B．y=(x+1)2−2C．y=x2+2D．y=x2−2二、填空题13．将抛物线y=﹣x2先向下平移2个单位，再向右平移3个单位后所得抛物线的解析式为．14．抛物线y=-x2-2x+3可由抛物线y=ax2平移得到，则a的值是。

中考数学总复习《二次函数图像的几何变换》练习题附有答案

中考数学总复习《二次函数图像的几何变换》练习题附有答案一、单选题(共12题；共24分)1．把抛物线y=-x2向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为（）A．B．C．D．2．如果要得到y=x2－6x＋7的图象，需将y=x2的图象（）.A．由向左平移3个单位，再向上平移2个单位B．由向右平移3个单位，再向下平移2个单位C．由向右平移3个单位，再向上平移2个单位D．由向左平移3个单位，再向下平移2个单位3．将抛物线C1：y＝（x－3）2＋2向左平移3个单位长度，得到抛物线C2，抛物线C2与抛物线C3关于x轴对称，则抛物线C3的解析式为（）．A．y＝x2－2B．y＝－x2＋2C．y＝x2＋2D．y＝－x2－24．已知抛物线y=x2+ax+b对称轴是直线x=1，与x轴两个交点间的距离为2，将此抛物线先向左平移2个单位，再向下平移3个单位，则所得新抛物线与x轴两个交点间的距离为（）A．2B．3C．4D．55．关于x的方程（x﹣3）（x﹣5）=m（m＞0）有两个实数根α，β（α＜β），则下列不符合题意的是（）A．3＜α＜β＜5B．3＜α＜5＜βC．α＜2＜β＜5D．α＜3且β＞56．把抛物线y=2x2向右平移1个单位，所得抛物线的函数解析式为（）A．y=2x2+1B．y=2(x+1)2C．y=2x2−1D．y=2(x−1)27．如图，抛物线y=ax2+bx+c关于原点对称的抛物线是（）A．y=﹣ax2﹣bx+c B．y=ax2﹣bx﹣cC．y=﹣ax2+bx﹣c D．y=﹣ax2﹣bx﹣c8．将抛物线y=4x2向右平移1个单位，再向上平移3个单位，得到的抛物线是（）A．y=4（x+1）2+3B．y=4（x﹣1）2+3C．y=4（x+1）2﹣3D．y=4（x﹣1）2﹣39．将抛物线y=2x2向右平移1个单位，再向下平移3个单位得到的抛物线表达式是（）A．y=2(x+1)2+3B．y=2(x−1)2−3C．y=2(x−1)2+3D．y=2(x+1)2−310．如图，抛物线y=﹣2x2+8x﹣6与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C1，将C1向右平移得C2，C2与x轴交于点B，D．若直线y=x+m与C1、C2共有3个不同的交点，则m的取值范围是（）A．﹣2＜m＜18B．﹣3＜m＜﹣74C．﹣3＜m＜﹣2D．﹣3＜m＜﹣15811．将抛物线y=(x−1)2+2向右平移1个单位，再向上平移5个单位后所得抛物线的解析式为（）A．y=(x−2)2+7B．y=(x−1)2+3C．y=x2+7D．y=x2+312．在平面直角坐标系中，如果抛物线y=2x2不动，而把x轴、y轴分别向上、向右平移3个单位，那么在新坐标系下抛物线的解析式是（）A．y=2(x+3)2-3B．y=2(x-3)2+3C．y=2(x-3)2-3D．y=2(x+3)2+3二、填空题(共6题；共6分)13．一抛物线和另一抛物线y＝﹣2x2的形状和开口方向完全相同，且顶点坐标是（﹣2，1），则该抛物线的解析式为.14．把二次函数y=（x﹣2）2+1的图象绕原点旋转180°后得到的图象的解析式为．15．如图，在平面直角坐标系中，抛物线y=x2经过平移得到抛物线y=x2﹣2x，其对称轴与两抛物线所围成的阴影部分的面积是．16．把抛物线y=ax2+bx+c的图象先向右平移3个单位长度，再向下平移2个单位长度，所得图象的解析式是y=2（x﹣3）2+1，则a+b+c=．17．如图，抛物线y=x2+bx+ 92与y轴相交于点A，与过点A平行于x轴的直线相交于点B（点B在第一象限）．抛物线的顶点C在直线OB上，对称轴与x轴相交于点D．平移抛物线，使其经过点A、D，则平移后的抛物线的解析式为．18．将二次函数y=−x2+mx+n（m，n为常数）的图象，先向左平移1个单位长度，再向上平移2个单位长度后，得到的图象顶点为(0，4)，则m+n的值为.三、综合题(共6题；共111分)19．已知二次函数图象的对称轴为y轴，且经过点（1，5）和（﹣12，114）.（1）求此二次函数的解析式；（2）若将该二次函数先向下平移4个单位，再沿x轴翻折后与x轴交于A，B两点，设顶点为P，求△AOP的面积.20．在平面直角坐标系内，二次函数y=x2+bx+c的图象经过点A(3，0)和B(2，−3)．（1）求这个二次函数的表达式；（2）求出二次函数的顶点坐标；（3）将该二次函数的图象向右平移几个单位，可使平移后所得的图象经过坐标原点．21．已知二次函数y＝2x2＋4x－6．（1）将其化成y＝a(x－h)2＋k的形式；（2）写出开口方向，对称轴方程，顶点坐标；（3）求图象与两坐标轴的交点坐标；（4）画出函数图象；（5）说明其图象与抛物线y＝x2的关系；（6）当x取何值时y随x增大而减小；（7）当x取何值时y＞0，y＝0，y＜0；（8）当x取何值时函数y有最值?其最值是多少?（9）当y取何值时－4＜x＜0；（10）求函数图象与两坐标轴交点所围成的三角形面积．22．已知二次函数y＝ax2+bx+c中自变量x和函数值y的部分对应值如表：x…-10123…y…105212…（2）在所给的直角坐标系中画出此函数的图象；（3）作该二次函数y＝ax2+bx+c的图象关于x轴对称的新图象，则新图象的函数关系式为.23．把y= −12x2的图象向上平移2个单位.（1）求新图象的解析式、顶点坐标和对称轴；（2）画出平移后的函数图象；（3）求平移后的函数的最大值或最小值，并求对应的x的值.24．已知抛物线y=ax2+bx−1经过A(1，2)，B(−3，2)两点．（1）求该抛物线的函数关系式；（2）若将该抛物线向上平移3个单位长度，求出平移后的函数关系式并直接写出开口方向及顶点坐标．参考答案1．【答案】D 2．【答案】B 3．【答案】D 4．【答案】C 5．【答案】D 6．【答案】D 7．【答案】C 8．【答案】B 9．【答案】B 10．【答案】D 11．【答案】A 12．【答案】A13．【答案】y ＝﹣2（x+2）2+1 14．【答案】y=﹣（x+2）2﹣1 15．【答案】1 16．【答案】517．【答案】y=x 2﹣ 92 x+ 9218．【答案】319．【答案】（1）解：设函数的解析式为y ＝ax 2+c将（1，5）和（﹣ 12 ， 114 ）分别代入函数解析式，得 {a +c =514a +c =114 . 解得 {a =3c =2故此二次函数的解析式y ＝3x 2+2；（2）解：二次函数先向下平移4个单位得到：y ＝3x 2﹣2；然后沿x 轴翻折后解析式为：y ＝﹣3x 2+2.此时P （0，2），A （ √62 ，0），B （﹣ √62 ，0）所以S △AOP ＝ 12 × √62 ×2＝ √62.20．【答案】（1）解：把点A(3，0)和B(2，−3)的坐标代入y =x 2+bx +c 得：{9+3b +c =04+2b +c =−3解得： {b =−2c =−3∴二次函数表达式为y=x2−2x−3；（2）解：∵y=x2−2x−3=x2−2x+1−4=(x−1)2−4∴二次函数图象的顶点坐标是(1，−4)；（3）解：当y=0时x2−2x−3=0解得：x1=−1，x2=3∴抛物线y=x2−2x−3与x轴的交点坐标为C(−1，0)，A(3，0)，如下图所示∴将二次函数图象向右平移一个单位，可以使图象经过原点．【分析】21．【答案】（1）解：通过配方法可以将y＝2x2＋4x－6配方成y＝2(x＋1)2－8.（2）解：由图像可以看出开口向上，由顶点式得对称轴为直线x＝－1，顶点坐标为(－1，－8)；（2）根据二次函数的性质可解答。

二次函数图象和几何变换试题

3．如图抛物线y=ax2-5ax+4a与x轴相交于点）求a的值和该抛物线顶点P的坐标．4．（1）请在坐标系中画出二次函数）在同一个坐标系中画出5．如图1，在平面直角坐标系中，点（2）平移抛物线l1，使平移后的抛物线过A、B两点，记抛物线为l2，如图2，求抛物线l2的函数解析式及顶点C的坐标；（3）设P为y轴上一点，且S△ABC=S△ABP，求点P的坐标；（4）请在图2上用尺规作图的方式探究抛物线l2上是否存在点Q，使△QAB为等腰三角形．若存在，请判断点Q共有几个可能的位置（保留作图痕迹）；若不存在，请说明理由．6．已知二次函数y=x2-2x-1．（1）求此二次函数的图象与x轴的交点坐标；（2）二次函数y=x2的图象如图所示，将y=x2的图象经过怎样的平移，就可以得到二次函数y=x2-2x-1的图象．7．已知点A（-2，-c）向右平移8个单位得到点A′，A与A′两点均在抛物线y=ax2+bx+c上，且这条抛物线与y轴的交点的纵坐标为-6，求这条抛物线的顶点坐标．8．如图，抛物线y1=-x2+2向右平移1个单位得到抛物线y2，回答下列问题：（1）抛物线y2的顶点坐标；（2）阴影部分的面积S= ；（3）若再将抛物线y2绕原点O旋转180°得到抛物线y3，求抛物线y3的解析式．9．下表给出了代数式x2+bx+c与x的一些对应值：（1）请在表内的空格中填入适当的数；（2）设y=x2+bx+c，则当x取何值时，y＞0；（3）请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象？10．已知抛物线C1的解析式是y=2x2-4x+5，抛物线C2与抛物线C1关于x轴对称，求抛物线C2的解析式．11．如图已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称，并与y轴交于点M，与x轴交于点A 和B．求出y=mx2+nx+p的解析式，试猜想出一般形式y=ax2+bx+c关于y轴对称的二次函数解析式（不。

二次函数平移、旋转、轴对称变换汇总

二次函数专题训练（平移、旋转、轴对称变换）一、二次函数图象的平移、旋转（只研究中心对称）、轴对称变换1、抛物线的平移变换：一般都是在顶点式的情况下进行的。

抛物线的上下平移：___________________y=a（x-h）2+k y=a（x-h）2+k ± m抛物线的左右平移：___________________y=a（x-h）2+k y=a（x-h ± m）2+k练习：（ 1）函数图象沿 y 轴向下平移 2 个单位，再沿 x 轴向右平移 3个单位，得到函数______________ 的图象。

（2）抛物线y x2 2x 5向左平移3个单位，再向下平移 6 个单位，所得抛物线的解析式是。

2、抛物线的旋转变换（只研究中心对称）：一般都是在顶点式的情况下进行的。

1）将抛物线绕其顶点旋转180 （即两条抛物线关于其顶点成中心对称）22y a x h k 关于顶点对称后，得到的解析式是 y a x h k 。

（2）将抛物线绕原点旋转180 （即两条抛物线关于原点成中心对称）22y a x h k 关于原点对称后，得到的解析式是 y a x h k 。

练（1）抛物线y 2x2 4x 6 绕其顶点旋转180 后，所得抛物线的解析式是（2）将抛物线y＝x2＋1绕原点O旋转180°，则旋转后抛物线的解析式为（）22 2 2A．y＝－x2B．y＝－x2＋1 C．y＝x2－1 D．y＝－x2－13、抛物线的轴对称变换：关于 x 轴对称y ax2 bx c关于 x轴对称后，得到的解析式是 y ax2 bx c ；22y a x h k 关于 x 轴对称后，得到的解析式是 y a x h k ；关于y 轴对称22 y ax2 bx c关于y 轴对称后，得到的解析式是 y ax2 bx c；22y a x h k 关于y 轴对称后，得到的解析式是y a x h k ；练习：已知抛物线C1：y （x 2）2 3 （1）抛物线C2与抛物线C1关于y 轴对称，则抛物线C2的解析式为2）抛物线C3与抛物线C1关于x 轴对称，则抛物线 C 3的解析式为总结：根据平移、旋转、轴对称的性质，显然无论作何种变换，抛物线的形状一定不会发生变化，因此 a 永远不变。

二次函数图象的几何变换

一、二次函数图象的平移变换（1）具体步骤：先利用配方法把二次函数化成2()y a x h k =-+的形式，确定其顶点(,)h k ，然后做出二次函数2y ax =的图像，将抛物线2y ax =平移，使其顶点平移到(,)h k .具体平移方法如图所示：（2）平移规律：在原有函数的基础上“左加右减”.二、二次函数图象的对称变换二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4. 关于顶点对称2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式．知识点拨二次函数图象的几何变换一、二次函数图象的平移变换【例1】函数23(2)1y x =+-的图象可由函数23y x =的图象平移得到，那么平移的步骤是：（）A. 右移两个单位，下移一个单位B. 右移两个单位，上移一个单位C. 左移两个单位，下移一个单位D. 左移两个单位，上移一个单位【例2】函数22(1)1y x =---的图象可由函数22(2)3y x =-++的图象平移得到，那么平移的步骤是（）A. 右移三个单位，下移四个单位B. 右移三个单位，上移四个单位C. 左移三个单位，下移四个单位D. 左移四个单位，上移四个单位【例3】二次函数2241y x x =-++的图象如何移动就得到22y x =-的图象（）A. 向左移动1个单位，向上移动3个单位.B. 向右移动1个单位，向上移动3个单位.C. 向左移动1个单位，向下移动3个单位.D. 向右移动1个单位，向下移动3个单位.【例4】将函数2y x x =+的图象向右平移()0a a >个单位，得到函数232y x x =-+的图象，则a 的值为（）A ．1B ．2C ．3D ．4【例5】把抛物线2y ax bx c =++的图象先向右平移3个单位，再向下平移2个单位，所得的图象的解析式是235y x x =-+，则a b c ++=________________．【例6】对于每个非零自然数n ，抛物线()()221111n y x x n n n n +=-+++与x 轴交于n n A B 、两点，以n n A B 表示这两点间的距离，则112220092009A B A B A B +++…的值是（）A ． 20092008B ．20082009C ．20102009D ．20092010【例7】把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为A ．()213y x =--- B ．()213y x =-+- C ．()213y x =--+D ．()213y x =-++【例8】将抛物线22y x =向下平移1个单位，得到的抛物线是（）A ．()221y x =+B ．()221y x =-C ．221y x =+D ．221y x =-【例9】将抛物线23y x =向上平移2个单位，得到抛物线的解析式是（）A. 232y x =-B. 23y x =C. 23(2)y x =+D. 232y x =+【例10】一抛物线向右平移3个单位，再向下平移2个单位后得抛物线224y x x =-+，则平移前抛物线的解析式为________________．【例11】已知二次函数5632+-=x x y ，求满足下列条件的二次函数的解析式：（1）图象关于x 轴对称；（2）图象关于y 轴对称；（3）图象关于经过其顶点且平行于x 轴的直线对称例题精讲【例12】如图，ABCD 中，4AB =，点D 的坐标是(0，8)，以点C 为顶点的抛物线2y ax bx c =++经过x 轴上的点A ，B ．⑴ 求点A ，B ，C 的坐标．⑵ 若抛物线向上平移后恰好经过点D ，求平移后抛物线的解析式．【例13】抛物线254y ax x a =-+与x 轴相交于点A B 、，且过点()54C ，． ⑴ 求a 的值和该抛物线顶点P 的坐标．⑵ 请你设计一种平移的方法，使平移后抛物线的顶点落要第二象限，并写出平移后抛物线的解析式．二、二次函数图象的对称变换【例14】函数2y x =与2y x =-的图象关于______________对称，也可以认为2y x =是函数2y x =-的图象绕__________旋转得到．【例15】已知二次函数221y x x =--，求：⑴关于x 轴对称的二次函数解析式；⑵关于y 轴对称的二次函数解析式；⑶关于原点对称的二次函数解析式．【例16】在平面直角坐标系中，先将抛物线22y x x =+-关于x 轴作轴对称变换，再将所得的抛物线关于y轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为 A ．22y x x =--+ B ．22y x x =-+- C ．22y x x =-++ D ．22y x x =++【例17】已知二次函数2441y ax ax a =++-的图象是1c ．⑴ 求1c 关于()10R ，成中心对称的图象2c 的函数解析式； ⑵ 设曲线12c c 、与y 轴的交点分别为A B ，，当18AB =时，求a 的值．【例18】已知抛物线265y x x =-+，求⑴ 关于y 轴对称的抛物线的表达式；⑵ 关于x 轴对称的抛物线的表达式； ⑶ 关于原点对称的抛物线的表达式．【例19】设曲线C 为函数()20y ax bx c a =++≠的图象，C 关于y 轴对称的曲线为1C ，1C关于x 轴对称的曲线为2C ，则曲线2C 的函数解析式为________________．【例20】对于任意两个二次函数：()2211112222120y a x b x c y a x b x c a a =++=++≠，，当12a a =时，我们称这两个二次函数的图象为全等抛物线，现有ABM ∆，()()1010A B -，，，，记过三点的二次函数抛物线为“C”（“□□□”中填写相应三个点的字母）．⑴ 若已知()01M ，，ABM ABN ∆∆≌（图1），请通过计算判断ABM C 与ABN C 是否为全等抛物线；⑵ 在图2中，以A B M 、、三点为顶点，画出平行四边形．① 若已知()0M n ，，求抛物线ABM C 的解析式，并直接写出所有过平行四边形中三个顶点且能与ABM C 全等的抛物线解析式．② 若已知()M m n ，，当m n 、满足什么条件时，存在抛物线ABM C ？根据以上的探究结果，判断是否存在过平行四边形中三个顶点且能与ABM C 全等的抛物线．若存在，请写出所有满足条件的抛物线“C”；若不存在，请说明理由．【例21】已知：抛物线2:(2)5f y x =--+．试写出把抛物线f 向左平行移动2个单位后，所得的新抛物线1f 的解析式；以及f 关于x 轴对称的曲线2f 的解析式．画出1f 和2f 的略图，并求：⑴ x 的值什么范围，抛物线1f 和2f 都是下降的；⑵ x 的值在什么范围，曲线1f 和2f 围成一个封闭图形；⑶ 求在1f 和2f 围成封闭图形上，平行于y 轴的线段的长度的最大值．。

二次函数图象与几何变换

二次函数图象与几何变换1．将抛物线y=x2﹣2x+3平移得到抛物线y=x2，则这个平移过程正确的是（）A．先向左平移1个单位，再向下平移2个单位B．先向左平移2个单位，再向下平移1个单位C．先向右平移1个单位，再向上平移2个单位D．先向右平移2个单位，再向上平移1个单位【变式1】．将函数y=x2+x+b的图象向右平移a（a＞0）个单位，再向上平移2个单位，得到函数y=x2﹣3x+4的图象，则a、b的值分别为（）A．a=1、b=4 B．a=2、b=2 C．a=2、b=0 D．a=3、b=2【变式2】如果抛物线A：y=x2﹣1通过左右平移得到抛物线B，再通过上下平移抛物线B得到抛物线C：y=x2﹣2x+2，那么抛物线B的表达式为（）A．y=x2+2 B．y=x2﹣2x﹣1 C．y=x2﹣2x D．y=x2﹣2x+1【变式3】．若抛物线y=x2﹣2x+3不动，将平面直角坐标系xOy先沿水平方向向右平移一个单位，再沿铅直方向向上平移三个单位，则原抛物线图象的解析式应变为（）A．y=（x﹣2）2+3 B．y=（x﹣2）2+5 C．y=x2﹣1 D．y=x2+4【变式4】．将抛物线y=x2﹣4x+3向上平移至顶点落在x轴上，如图所示，则两条抛物线、对称轴和y轴围成的图形的面积S（图中阴影部分）是（）A．1 B．2 C．3 D．42．与抛物线y=x2﹣2x﹣4关于x轴对称的图象表示为（）A．y=﹣x2+2x+4 B．y=﹣x2+2x﹣4 C．y=x2﹣2x+6 D．y=x2﹣2x﹣4【变式】．二次函数y=x2﹣4x﹣5的图象关于直线x=﹣1对称的图象的表达式是（）A．y=x2﹣16x+55 B．y=x2+8x+7 C．y=﹣x2+8x+7 D．y=x2﹣8x+73．如图，抛物线y=ax2+bx+c关于原点对称的抛物线是（）A．y=﹣ax2﹣bx+c B．y=ax2﹣bx﹣c C．y=﹣ax2+bx﹣c D．y=﹣ax2﹣bx﹣c【变式1】．将二次函数y=x2﹣2x﹣1的图象绕坐标原点O旋转180°，则旋转后的图象对应的解析式为（）A．y=x2+2x+3 B．y=﹣x2﹣2x+1 C．y=x2﹣2x﹣1 D．y=﹣x2+2x﹣3【变式2】顶点为M的抛物线y=x2+2x+3与y轴交于点A，在顶点不变的情况下，把抛物线绕顶点M旋转180°得到一条新的抛物线，且新抛物线与y轴交于点B，则△AMB的面积为（）A．6 B．3 C．2 D．1【变式3】在平面直角坐标系中，把一条抛物线先向上平移3个单位长度，然后绕原点旋转180°得到抛物线y=x2+5x+6，则原抛物线的解析式是（）A．y=﹣（x﹣）2﹣B．y=﹣（x+）2﹣C．y=﹣（x﹣）2﹣D．y=﹣（x+）2+4．已知P（﹣3，m）和Q（1，m）是抛物线y=x2+bx﹣3上的两点．（1）求b的值；（2）将抛物线y=x2+bx﹣3的图象向上平移k（是正整数）个单位，使平移后的图象与x轴无交点，求k的最小值；（3）将抛物线y=x2+bx﹣3的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合新图象回答：当直线y=x+n与这个新图象有两个公共点时，求n的取值范围．【变式】．如图，四边形ABCO为矩形，点A在x轴上，点C在y轴上，且点B的坐标为（﹣1，2），将此矩形绕点O 顺时针旋转90°得矩形DEFO，抛物线y=﹣x2+bx+c过B，E两点．（1）求此抛物线的函数关系式．（2）将矩形ABCO向左平移，并且使此矩形的中心在此抛物线上，求平移距离．（3）将矩形DEFO向上平移距离d，并且使此抛物线的顶点在此矩形的边上，则d的值是．5．在平面直角坐标系xOy中，抛物线C：y=x2+（3﹣m）x经过点A（﹣1，0）．（1）求抛物线C的表达式；（2）将抛物线C沿直线y=1翻折，得到的新抛物线记为C1，求抛物线C1的顶点坐标；（3）将抛物线C沿直线y=n翻折，得到的图象记为C2，设C与C2围成的封闭图形为M，在图形M上内接一个面积为4的正方形（四个顶点均在M上），且这个正方形的边分别与坐标轴平行．求n的值．6．如果抛物线C1的顶点在抛物线C2上，同时，抛物线C2的顶点在抛物线C1上，那么，我们称抛物线C1与C2关联．（1）已知两条抛物线①：y=x2+2x﹣1，②：y=﹣x2+2x+1，判断这两条抛物线是否关联，并说明理由；（2）抛物线C1：y=（x+1）2﹣2，动点P的坐标为（t，2），将抛物线C1绕点P（t，2）旋转180°得到抛物线C2，若抛物线C2与C1关联，求抛物线C2的解析式．【课后练习】一．选择题（共4小题）1．（西城区期末）将抛物线y=﹣3x2平移，得到抛物线y=﹣3 （x﹣1）2﹣2，下列平移方式中，正确的是（）A．先向左平移1个单位，再向上平移2个单位B．先向左平移1个单位，再向下平移2个单位C．先向右平移1个单位，再向上平移2个单位D．先向右平移1个单位，再向下平移2个单位2．（东城区期末）在平面直角坐标系中，将抛物线y=x2﹣2x﹣1先向上平移3个单位长度，再向左平移2个单位长度，所得的抛物线的解析式是（）A．y=（x+1）2+1 B．y=（x﹣3）2+1 C．y=（x﹣3）2﹣5 D．y=（x+1）2+23．（通州区期末）把二次函数的图象经过翻折、平移得到二次函数的图象，下列对此过程描述正确的是（）A．先沿y轴翻折，再向下平移6个单位B．先沿y轴翻折，再向左平移6个单位C．先沿x轴翻折，再向左平移6个单位D．先沿x轴翻折，再向右平移6个单位4．（顺义区一模）在平面直角坐标系x′O′y′中，如果抛物线y′=2x′2不动，而把x轴、y轴分别向下、向左平移2个单位，则在新坐标系下抛物线的表达式为（）A．y=2（x+2）2﹣2 B．y=2（x+2）2+2 C．y=2（x﹣2）2﹣2 D．y=2（x﹣2）2+2二．填空题（共4小题）5．（石景山区期末）如图，抛物线C1：y=x2经过平移得到抛物线C2：y=x2+2x，抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是．6．（昌平区期末）如图，我们把抛物线y=﹣x（x﹣3）（0≤x≤3）记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x 轴于另一点A2；将C2绕点A2旋转180°得C3，交x 轴于另一点A3；…；如此进行下去，直至得C2016．①C1的对称轴方程是；②若点P（6047，m）在抛物线C2016上，则m=．7．（海淀区期末）已知点P（﹣1，m）在二次函数y=x2﹣1的图象上，则m的值为；平移此二次函数的图象，使点P与坐标原点重合，则平移后的函数图象所对应的解析式为．8．（通州区期末）如图：在平面直角坐标系中，A（﹣2，0），B（0，1），有一组抛物线L n，它们的顶点C n（X n，Y n）在直线AB上，并且经过点（X n+1，0），当n=1，2，3，4，5…时，X n=2，3，5，8，13…，根据上述规律，写出抛物线L1的表达式为，抛物线L6的顶点坐标为，抛物线L6D的解析式为．三．解答题（共4小题）9．（门头沟区期末）在平面直角坐标系xOy中，二次函数图象所在的位置如图所示：（1）请根据图象信息求该二次函数的表达式；（2）将该图象（x＞0）的部分，沿y轴翻折得到新的图象，请直接写出翻折后的二次函数表达式；（3）在（2）的条件下与原有二次函数图象构成了新的图象，记为图象G，现有一次函数y=x+b的图象与图象G有4个交点，请画出图象G的示意图并求出b的取值范围．10．（门头沟区期末）在平面直角坐标系xOy中，抛物线经过点A（0，2）和B（1，）．（1）求该抛物线的表达式；（2）已知点C与点A关于此抛物线的对称轴对称，点D在抛物线上，且点D的横坐标为4，求点C与点D的坐标；（3）在（2）的条件下，将抛物线在点A，D之间的部分（含点A，D）记为图象G，如果图象G向下平移t（t＞0）个单位后与直线BC只有一个公共点，求t的取值范围．11．（东城区二模）二次函数C1：y=x2+bx+c的图象过点A（﹣1，2），B（4，7）．（1）求二次函数C1的解析式；（2）若二次函数C2与C1的图象关于x轴对称，试判断二次函数C2的顶点是否在直线AB上；（3）若将C1的图象位于A，B两点间的部分（含A，B两点）记为G，则当二次函数y=﹣x2+2x+1+m与G有且只有一个交点时，直接写出m满足的条件．12．（海淀区一模）在平面直角坐标系xOy中，抛物线y=﹣x+2与y轴交于点A，顶点为点B，点C与点A关于抛物线的对称轴对称．（1）求直线BC的解析式；（2）点D在抛物线上，且点D的横坐标为4．将抛物线在点A，D之间的部分（包含点A，D）记为图象G，若图象G 向下平移t（t＞0）个单位后与直线BC只有一个公共点，求t的取值范围．。