第7章习题答案
第7章_微型计算机存储器习题参考答案

第7章_微型计算机存储器习题参考答案计算机存储器7.1 ⼀个微机系统中通常有哪⼏级存储器?它们各起什么作⽤?性能上有什么特点?答:⼀个微机系统中通常有3级存储器结构:⾼速缓冲存储器、内存储器和辅助存储器。
⾼速缓冲存储器简称快存,是⼀种⾼速、⼩容量存储器,临时存放指令和数据,以提⾼处理速度。
内存存取速度快,CPU可直接对它进⾏访问,⽤来存放计算机运⾏期间的⼤量程序和数据。
辅存存储容量⼤,价格低,CPU不能直接进⾏访问,通常⽤来存放系统程序、⼤型⽂件及数据库等。
7.2 半导体存储器分为哪两⼤类?随机存取存储器由哪⼏个部分组成?答:根据存取⽅式的不同,半导体存储器可分为随机存取存储器RAM和只读存储器ROM 两类。
其中随机存取存储器主要由地址译码电路、存储体、三态数据缓冲器和控制逻辑组成。
7.3 什么是SRAM,DRAM,ROM,PROM,EPROM和EEPROM?答:SRAM:静态随机存取存储器;DRAM:动态随机存取存储器;ROM:掩膜只读存储器;PROM:可编程的只读存储器;EPROM:可擦除可编程只读存储器;EEPROM:⽤电可擦除可编程只读存储器。
7.4 常⽤的存储器⽚选控制⽅法有哪⼏种?它们各有什么优缺点?答:常⽤的存储器⽚选控制译码⽅法有线选法、全译码法和部分译码法。
线选法:当存储器容量不⼤、所使⽤的存储芯⽚数量不多、⽽CPU寻址空间远远⼤于存储器容量时,可⽤⾼位地址线直接作为存储芯⽚的⽚选信号,每⼀根地址线选通⼀块芯⽚,这种⽅法称为线选法。
直观简单,但存在地址空间重叠问题。
全译码法:除了将低位地址总线直接与各芯⽚的地址线相连接之外,其余⾼位地址总线全部经译码后作为各芯⽚的⽚选信号。
采⽤全译码法时,存储器的地址是连续的且唯⼀确定,即⽆地址间断和地址重叠现象。
部分译码法:将⾼位地址线中的⼀部分进⾏译码,产⽣⽚选信号。
该⽅法常⽤于不需要全部地址空间的寻址、采⽤线选法地址线⼜不够⽤的情况。
采⽤部分译码法存在地址空间重叠的问题。
离散习题(附答案) (7)

习题7.11.设Z是整数集合,Z上的二元运算*定义为:a*b=ab+2(a+b+1)。
证明代数系统<Z,*>是半群。
证明:由于任意两个整数经加、减、乘运算后,其结果仍然是整数。
所以运算*对于是封闭的。
现证*是可结合运算。
由于(a*b)*c=(ab+2(a+b+1))*c=(ab+2(a+b+1))c+2(ab+2(a+b+1)+c+1)=abc+2ac+2bc+2c+2ab+4a+4b+2c+6=abc+2(ab+bc+ca)+4(a+b+c)+6a*(b*c)=a*(bc+2(b+c+1))=a(bc+2(b+c+1))+2(a+bc+2(b+c+1)+1)=abc+2ab+2ac+2a+2a+2bc+4b+4c+6=abc+2(ab+bc+ca)+4(a+b+c)+6所以(a*b)*c=a*(b*c)。
由此证得*是可结合运算,<Z,*>是半群。
在证明*是可结合运算时,还可先把*的定义改写如下:a*b=ab+2(a+b+1)=ab+2a+2b+2=a(b+2)+2(b+2)−2=(a+2)(b+2)−2从而有(a*b)*c=((a +2)(b+2)−2)*c=(((a +2)(b+2)−2)+2)(c+2)−2=(a +2)(b+2)(c +2)−2a*(b*c)=a*((b +2)(c+2)−2)=(a +2)(((b +2)(c+2)−2)+2)−2=(a +2)(b+2)(c +2)−2于是(a*b)*c=a*(b*c)。
显然,上述证明方法,不仅简明清晰,而且可以对运算过程和运算结果有较好的把握和预测,避免了盲目性。
2.写出独异点<A,*>的所有子独异点,其中A=⎨1,2,3,4,5⎬,a*b=max(a,b)。
解:对于A中任意元素a,都有1*a=a*1=max(a,1)=a所以1是独异点<A,*>的幺元。
由于<A,*>的子独异点必须与<A,*>有相同的幺元,因此,<A,*>的所有子独异点分别为<⎨1⎬,*>,<⎨1,2⎬,*>,<⎨1,3⎬,*>,<⎨1,4⎬,*>,<⎨1,5⎬,*>,<⎨1,2,3⎬,*>,<⎨1,2,4⎬,*>,<⎨1,2,5⎬,*>,<⎨1,3,4⎬,*>,<⎨1,3,5⎬,*>,<⎨1,4,5⎬,*>,<⎨1,2,3,4⎬,*>,<⎨1,2,3,5⎬,*>,<⎨1,2,4,5⎬,*>,<⎨1,3,4,5⎬,*>,<A,*>。
第七章 习题答案
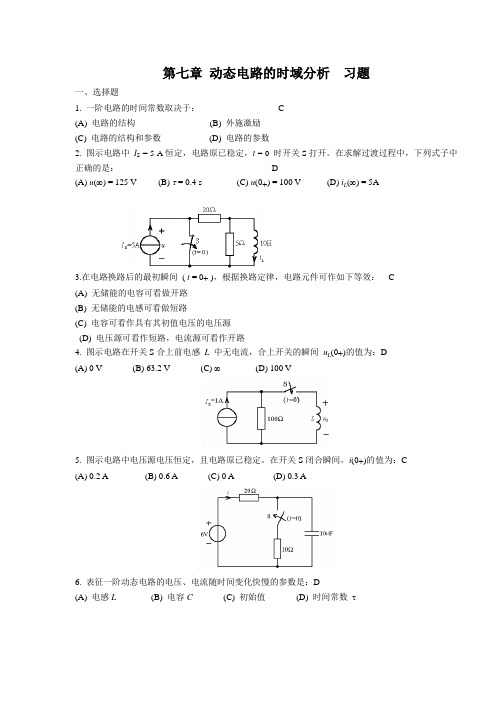
第七章动态电路的时域分析习题一、选择题1. 一阶电路的时间常数取决于: C(A) 电路的结构(B) 外施激励(C) 电路的结构和参数(D) 电路的参数2. 图示电路中I S = 5 A恒定,电路原已稳定,t = 0时开关S打开。
在求解过渡过程中,下列式子中正确的是: D(A) u(∞) = 125 V (B) τ = 0.4 s (C) u(0+) = 100 V (D) i(∞) = 5AL3.在电路换路后的最初瞬间( t = 0+ ),根据换路定律,电路元件可作如下等效: C(A) 无储能的电容可看做开路(B) 无储能的电感可看做短路(C) 电容可看作具有其初值电压的电压源(D) 电压源可看作短路,电流源可看作开路(0+)的值为:D4. 图示电路在开关S合上前电感L中无电流,合上开关的瞬间uL(A) 0 V (B) 63.2 V (C) ∞(D) 100 V5. 图示电路中电压源电压恒定,且电路原已稳定。
在开关S闭合瞬间,i(0+)的值为:C(A) 0.2 A (B) 0.6 A (C) 0 A (D) 0.3 A6. 表征一阶动态电路的电压、电流随时间变化快慢的参数是:D(A) 电感L(B) 电容C(C) 初始值(D) 时间常数τ7. 图示正弦脉冲信号的数学表达式为:B (A) sin ω t ⋅ ε (t ) + sin ω ( t - T ) ⋅ ε ( t - T ) (B) sin ω t ⋅ ε (t ) - sin ω t ⋅ ε ( t - T ) (C) sin ω t ⋅ ε (t ) - sin ω ( t - T ) ⋅ ε ( t - T ) (D) sin ω t ⋅ ε (t ) + sin ω t ⋅ ε ( t - T )8. 图示电路中,原已达稳态, t = 0开关 S 打开,电路的时间常数为:D (A)s 41 (B) s 61(C) s 4 (D)s 69. 示电路中,t = 0 时开关打开,则 u (0+)为:C(A) 0V (B) 3.75V (C) – 6V (D) 6V10.图示电路中,开关打开已久,在 t = 0 时开关闭合,i (0+) 为:D(A) 0A (B) 0.8A(C) 2A (D)1A11.R 、C 串联电路,已知全响应()()10C 83V,0t u t e t -=-≥,其零状态响应为:(A )(A) 1088V te-- (B) 1083V t e -- (C) 103V t e -- (D) 105V t e -12. .一阶电路的全响应()()10C 106V,0tu t et -=-≥若初始状态不变而输入增加一倍,则全响应u C (t)为 ( D ) (A) 20-12e -10t ; (B) 20-6e -10t ; (C) 10-12e -10t ; (D) 20-16 e -10t 。
微观经济学第七章 习题答案

MR,试求:图7—1(1)A点所对应的MR值;(2)B点所对应的MR值。
解答:(1)根据需求的价格点弹性的几何意义,可得A点的需求的价格弹性为e d =eq \f(15-5,5)=2或者e d =eq \f(2,3-2)=2再根据公式MR=P eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,e d ))),则A点的MR值为MR=2×eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,2)))=1(2)与(1)类似,根据需求的价格点弹性的几何意义,可得B点的需求的价格弹性为e d =eq \f(15-10,10)=eq \f(1,2)或者e d =eq \f(1,3-1)=eq \f(1,2)再根据公式MR=P eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,e d ))),则B点的MR值为MR=1×eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,1/2)))=-12. 图7—2(即教材第205页的图7—19)是某垄断厂商的长期成本曲线、需求曲线和收益曲线。
试在图中标出:(1)长期均衡点及相应的均衡价格和均衡产量;(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线;(3)长期均衡时的利润量。
图7—2图7—3(1)长期均衡点为E点,因为在E点有MR=LMC。
由E点出发,均衡价格为P0,均衡数量为Q0。
(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线如图7—3所示。
在Q0的产量上,SAC曲线和LAC曲线相切;SMC曲线和LMC曲线相交,且同时与MR曲线相交。
(3)长期均衡时的利润量由图7—3中阴影部分的面积表示,即π=[AR(Q0)-SAC(Q0)]·Q 0。
3. 已知某垄断厂商的短期总成本函数为STC=0.1Q3-6Q2+140Q+3 000,反需求函数为P=150-3.25Q。
第七章课后习题参考答案

2. 试简单说明下列协议的作用:IP、ARP、RARP和ICMP。
答:IP协议:实现网络互连。
使参与互连的性能各异的网络从用户看起来好像是一个统一的网络。
ARP协议:完成IP地址到MAC地址的映射。
RARP:使只知道自己硬件地址的主机能够知道其IP地址。
ICMP:允许主机或路由器报告差错情况和提供有关异常情况的报告。
5. 试说明IP 地址与硬件地址的区别。
为什么要使用这两种不同的地址?答:IP地址在IP数据报的首部,而硬件地址则放在MAC帧的首部。
在网络层以上使用的是IP地址,而链路层及以下使用的是硬件地址。
在IP层抽象的互连网上,我们看到的只是IP数据报,路由器根据目的站的IP地址进行选路。
在具体的物理网络的链路层,我们看到的只是 MAC 帧,IP 数据报被封装在 MAC 帧里面。
MAC帧在不同的网络上传送时,其MAC帧的首部是不同的。
这种变化,在上面的IP层上是看不到的。
每个路由器都有IP 地址和硬件地址。
使用IP地址与硬件地址,尽管连接在一起的网络的硬件地址体系各不相同,但IP层抽象的互连网却屏蔽了下层这些很复杂的细节,并使我们能够使用统一的、抽象的IP地址进行通信。
6.(1)子网掩码为255.255.255.0代表什么意思?(2)一网络的子网掩码为255.255.255.248,问该网络能够连接多少台主机?(1)一A类网络和一B类网络的子网号subnet-id分别为16bit的8bit,问这两个网络的子网掩码有何不同?(2)一个B类地址的子网掩码是255.255.240.0。
试问在其中每一个子网上的主机数最多是多少?(3)一个A类地址的子网掩码为255.255.0.255。
它是否为一个有效的子网掩码?(4)某个IP地址的十六进制表示是C22F1481,试将其转换为点分十进制的形式.这个地址是哪一类IP 地址?(5)C类网络使用子网掩码有无实际意义?为什么?答:(1)C类地址对应的子网掩码值。
第七章习题答案

第七章1.计算氢原子核外电子从第三能级跃迁到第二能级时产生的谱线H α的波长与频率。
解: ν = R H ⎪⎭⎫ ⎝⎛-222111n n= 3.289 ⨯ 1015⎪⎪⎭⎫⎝⎛-223121s -1= 4.57⨯1014s -1νλc= =11418s 1057.4s m 10998.2--⨯⋅⨯= 656⨯10-9m= 656nm2.计算基态氢原子的电离能为多少? 解: I = ∆E = h ν= 6.626⨯10-34 J ⋅s ⨯3.289⨯1015s -1(1/12 -1/∞)=2.179⨯10-18J3.下列各组量子数哪些是不合理的?为什么?n l m(1) 2 1 0(2) 2 2 -1(3) 2 3 +2解:(1)合理;(2) l 取值不合理,应小于n ;(3) l 、m 取值不合理,l 应小于n ,m 取值为0, ±1, ±2,⋯ ± l ;4.用合理的量子数表示:(1)3d 能级; (2)4s 1电子解:(1)3d 能级: n =3,l =2;(2)4s 1电子:n =4,l =0,m = 0;5.分别写出下列元素基态原子的电子分布式,并分别指出各元素在周期表中的位置。
9F 10Ne 25Mn 29Cu 24Cr 55Cs 71Lu解:9F 1s 22s 22p 5 第二周期VIIA 族 10Ne [He]2s 22p 6 第二周期VIIIA 族25Mn [Ar]3d 54s 2 第四周期VIIB 族 29Cu [Ar]3d 104s 1 第四周期I B 族24Cr [Ar]3d 54s 1 第四周期VI B 族 55Cs [Xe]6s 1 第六周期I A 族71Lu [Xe]4f 145d 16s 2 第六周期IIIB 族6.以(1)为例,完成下列(2)~(4)题。
(1)Na (Z = 11) [Ne]3s 1 ; (3 ) (Z =24) [ ? ] 3d 54s 1;(2) 1s 22s 22p 63s 23p 3 ; (4 ) Kr (Z = ) [ ? ] 3d 104s 24p 6;解:(1) Na (Z = 11) [Ne]3s 1 ; (3 ) Cr (Z =24) [Ar ] 3d 54s 1;(2) P(Z=15) 1s 22s 22p 63s 23p 3 ; (4 ) Kr (Z = 36 ) [Ar] 3d 104s 24p 6;7.写出下列离子的最外层电子分布式:S 2-K + Pb 2+ Ag + Mn 2+ Co 2+ 解:8.试完成下表。
南昌大学大学化学第七章习题答案
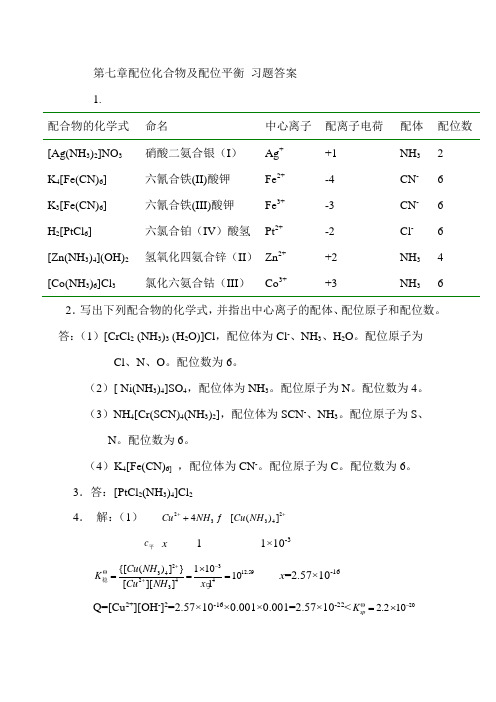
第七章配位化合物及配位平衡 习题答案 1.配合物的化学式 命名 中心离子 配离子电荷 配体 配位数 [Ag(NH 3)2]NO 3 硝酸二氨合银(I ) Ag + +1 NH 3 2 K 4[Fe(CN)6] 六氰合铁(II)酸钾 Fe 2+ -4 CN - 6 K 3[Fe(CN)6] 六氰合铁(III)酸钾Fe 3+-3 CN - 6 H 2[PtCl 6] 六氯合铂(IV )酸氢 Pt 2+ -2 Cl - 6 [Zn(NH 3)4](OH)2 氢氧化四氨合锌(II ) Zn 2+ +2 NH 3 4 [Co(NH 3)6]Cl 3氯化六氨合钴(III )Co 3++3NH 362.写出下列配合物的化学式,并指出中心离子的配体、配位原子和配位数。
答:(1)[CrCl 2 (NH 3)3 (H 2O)]Cl ,配位体为Cl -、NH 3、H 2O 。
配位原子为Cl 、N 、O 。
配位数为6。
(2)[ Ni(NH 3)4]SO 4,配位体为NH 3。
配位原子为N 。
配位数为4。
(3)NH 4[Cr(SCN)4(NH 3)2],配位体为SCN -、NH 3。
配位原子为S 、N 。
配位数为6。
(4)K 4[Fe(CN)6] ,配位体为CN -。
配位原子为C 。
配位数为6。
3.答:[PtCl 2(NH 3)4]Cl 24. 解:(1) 223344[()]Cu NH Cu NH +++ c 平 x 1 1×10-32312.59342443{[()]}11010[][]1Cu NH K Cu NH x +-Θ+⨯=== 稳x =2.57×10-16 Q=[Cu 2+][OH -]2=2.57×10-16×0.001×0.001=2.57×10-22<202.210sp K Θ-=⨯无沉淀。
(2) Q=[Cu 2+][S 2-]=2.57×10-16×0.001=2.57×10-19>366.310sp K Θ-=⨯,有沉淀。
第七章 练习题参考答案

V1 V3 V6
7. 对下图所示的有向图
(1) 画出它的邻接表 (2) 根据邻接表写出其拓扑排序序列
解:(1)邻接表为
0
2
5∧
2
3
4∧
2 3∧
4∧
1
2
3
6∧
1
4∧
(2)由邻接表可得拓朴排序序列:
1 5 2 3 64
8.已知n个顶点的有向图用邻接矩阵表示,编 写函数,计算每对顶点之间的最短路径。
4 18 ∧
2
1 12
32
5 22 ∧
3
1 16
22
44∧
4
1 18
34
5 10 ∧
5
2 22
4 10 ∧
解:(1) V1
12 V2
16 2
18
4 V3 22
V4
10 V5
(2)深度优先遍历的结点序列:v1,v2,v3,v4,v5
广度优先搜索的结点序列:v1,v2,v3,v4,v5
(3)最小生成树
CD CA CAB
CD CA CAB
CD CA CABΒιβλιοθήκη CD3DB
DB
DB DBC
DBCA DB DBC
DBCA DB DBC
10.对于如图所示的AOE网,求出各活动可能 的最早开始时间和允许的最晚开始时间, 哪些是关键活动?
a1=4
v2
v1
a3=2
a2=3
v3
a5=6 v4
a4=4
解:
顶点 Ve Vl V1 0 0 V2 4 4 V3 6 6 v4 10 10
if(length[i][k]+length[k][j]<length[i][j]) { length[i][j]=length[i][k]+length[k][j];
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第7章习题答案1.设总体ξ有分布律其中30<<θ为待估参数,求θ的矩估计。
).2(81ˆ2ˆ-8.28)31(*2*02*)1(ξθθξθθθθξ-=+=+-=-++-=,则令解:E 的矩估计。
为待估参数,求其中其他有分布密度设总体θθθθθξ0,00),(2)(2.2>⎪⎩⎪⎨⎧<<-=x x x f .3ˆ,3ˆ.3)(2)(02ξθθξθθθξθ===-==⎰⎰∞∞-则令解:dx x x dx x xf E 的矩估计。
为待估参数,求上服从均匀分布,其中在设总体b a b a b a b a ,0,0]3,[.3>>+-ξ.~321ˆ,21ˆ21)2(~)2()()(,)1(2221)(222223S b a S a dx x f x E E D a dx ba xdx x xf E ba ba +-==≈-=-=≈=+==⎰⎰⎰∞∞-∞∞-+-ξξξξξξξ)得,),(由(;解:作出矩估计。
及寿命方差泡的平均使用寿命试用矩估计法对这批灯,,,,,,,,)的抽取样本:有一批灯泡寿命(小时21496153613821478149013511614156213951458.4σμ6198.56.ˆ]476.211496)476.211395()476.211458[(101~1476.2ˆ1496153613821478149013511614156213951458101222222=≈-+⋯⋯+-+-==≈+++++++++=σσμμξ解得,)(;解得,)(解:S的最大似然估计。
求,,,,,,,,小时)如下:台,测得寿命的数据(,现随机抽取其中密度函数为服从指数分布,其分布寿命已知某电子设备的使用θθθξθ12001300113010401250120011201080110010501000,0,0,1)(5./>⎪⎩⎪⎨⎧≤>=-x x e x f x.1147ˆ,0),(ln ./ln 101ln ),(ln ,1)(),(101101/10101(小时)解得令两边取对数得解:似然函数为最大似然估计===--=∑==∏∑==-=x d x L d x x L ex f x L i i i i i x i i i i θθθθθθθθθ计。
的矩估计与最大似然估求总体参数为未知,其中~的一个样本,是取自总体,设p p p p B n ,10),,1(,,6.21<<⋯⋯ξξξξξ.ˆ,0),(ln .)1(),(ˆ,11)(ξξξξξξξξξ===-==≈=∑∏==-npdpp L d p p p L p p E ni ii ni n i i i 最大似然函数矩估计得令,似然函数为得解:由数据如下:秒内通过汽车辆数,得在某道口观察每157.根据以上数据求每15秒钟内通过该道口的汽车辆数ξ的ξE 和ξD 的无偏估计。
.83.0]1*)8.04(11*)8.03(28*)8.02(68*)8.01(92*)8.00[(1991.8.0200161)1*411*328*268*192*0(2001222222=-+-+-+-+-===++++=S D E 的无偏估计的无偏估计解:ξξξ的无偏估计。
是的无偏估计不是)(的无偏估计;是)(求证:为未知,其中的一个样本,是取自总体设2212212121)3(;21,10),,1(~,2,,,.8p p p p p p B n n ξξξξξξξξξ<<≥⋯⋯的无偏估计。
是即独立,所以因为的无偏估计。
不是,所以)(的无偏估计。
是,即)证明:(22122121212212212122221,,)3(2)1()(1p p E E E E E p p E p p p p p E D E E ξξξξξξξξξξξξξξξξξ===≠=+-=+==一个最好?个估计量的方差,问哪的无偏估计,并求出每都是);();()(证下面三个估计量:中抽取的一个样本,验是从总体服从正态分布设总体μξξμξξμξξμξξξμξ213212211212121ˆ34341ˆ23132ˆ1,),1,(9.+=+=+=N 最小,也即最好。
)独立,则(解:由214141)2121(ˆ)3(.167169161)4341(ˆ)2(.959194)3132(ˆ1,21213212122121121=+=+==+=+==+=+=ξξξξμξξξξμξξξξμξξD D D D D D D D D D D D 未知时。
)当(;已知测量精度)根据以往长期经验,(的置信区间:的,求总体温度真值假定重复测量所得温度)次,得(单位:,重复测量用某仪器间接测量温度σσμσμξ211195%),(~1275,1260,1245,1265,1250:5.0120=N C .1273.8151244.185(*),5,937.11,78.2)4(t 0.05,0.95,-112591275126012451265125051,*1,1)(,1)/()1(,1),1(~,/)2(1268.6251249.375(*),5,11,96.1u 0.05,0.95,-112591275126012451265125051,*1,1)(,1)/(,1),1,0(~,/),,()1(/22/2/2/2/2/2//22/2/2/2/2/2/2),的置信区间为(求得代入查表得,)(将)()的置信区间为(的置信概率为即即使得可求出对于给定的置信概率则有取统计量);,的置信区间为(求得代入查表得,)(将)()的置信概率为即即使得可求出对于给定的置信概率则有取统计量~已知解:μααξξμξαμαξμξαμξαμξμσααξσξμσξαμασξμσξασμξασμξσμξαααααααααααααα======++++=+<<---=+<<--=<-----=======++++=+<<---=+<<--=<---=n S nS t nS t n S t nS t P t nS P n t n t t nS t n nu nu nu n u P u n P u N U nU n N少个游客?问至少需要随机调查多元,的绝对误差小于的置信概率确信这估计小于进行估计,为了能以不的平均消费额游客元,今要对该地每一个且~游客的消费额假定到某地旅游的一个5095%500),,(11.2μσσμξ=N 人。
即随机调查人数不少于将已知数据代入求得因而只需又知即为确保,解:已知385,16.384,/50%,951/||%,95/50/||%,95)50|(|.96.1u 0.05,0.95,-15002/2/025.0/2≥≥=-=⎪⎪⎭⎫⎝⎛<-≥⎪⎪⎭⎫ ⎝⎛<-≥<-=====n u n u n P n n P P u ααασασμξσσμξμξαασ0.01.0.0532.0531.0331.8730.0031.6429.6632.566)1.1,05.32(~12.2==ααξ,同的显著性水平:厘米?检查使用两个不度是否就是试问这批零件的平均长,,,,,)为:单位:件,测得它们的长度(,现从中抽查已知某种零件的长度cm N 。
时,接受因而时,当时,拒绝因而时,作出判断。
当观察值得将以上数据代入计算,,求观察值。
已知使查正态分布表求)(水平求临界值。
给定显著性找统计量。
确定统计量)提出假设,解:(01005.02/01025.02/102/2/0000.01,58.2||,58.20.01;0.05,96.1||,96.10.05)5.(056.2.127.31)03.3187.3100.3064.3166.2956.32(61,61.132.05)4(.1)|(|,,10)3()1,0(~/)2.(32.05:1H u u u H u u u u U n u U P u N nU H =<====>===-==+++++====-=<<<-===ααααξσμααασμξμμαααα)?(显著性水平是否成立,试检验个样品,计算得中抽取从正态总体0.015:5.32100)1,(13.0===αμξμH N 。
时,拒绝因而时,)作出判断。
当(得观察值将以上数据代入计算,,求观察值。
已知使查正态分布表求)(水平求临界值。
给定显著性找统计量。
确定统计量)提出假设,解:(01005.02/102/2/0000.01,58.2||,58.20.0152.3.32.5,10015)4(.1)|(|,,10)3()1,0(~/)2.(5:1H u u u u U n u U P u N nU H =>========-=<<<-===ααξσμααασμξμμααα范围内?)灌装精度是否在标准(灌装量是否符合标准?下,问在显著性水平,,,,,,,,)为位:灌装样品的灌装量(单支,现测量机的正常灌装量装营养液,设自动灌装某公司用自动灌装机灌2(1)0.0599.5.100.5102.199.798.3101.2100.598.799.39)2.1,100(~14.2=αξg N围内。
,即灌装精度在标准范因而接受时,作出判断。
当得观察值将以上数据代入,,求观察值。
已知使查正态分布表求)(水平求临界值。
给定显著性找统计量。
确定统计量提出假设,)(,即灌装量符合标准。
因而接受时,)作出判断。
当(得观察值将以上数据代入计算,,求观察值。
已知使查正态分布表求)(水平求临界值。
给定显著性找统计量。
确定统计量提出假设,)解:(0022/2122/122/22/22/122/1212022/222/122/122/22912022220001025.02/102/2/000),()(,19)9()(,7.2)9()(0.05).(17.8,91.2100).(1))()(()(),(,10)()(~)(1).(1.2:)(2,96.1||,96.10.05.05.0.98.99,91.2100)(.1)|(|,,10)()1,0(~/).(100:)(1H n n n n v n iv n n P n n iii n ii H i H u u u v u U n iv u U P u iii N nU ii H i i iαααααααααααααχχχχχχχαχχσμαχχχχχααχμξσχσσαξσμααασμξμμ<<=========-=<<<<-===<===-=====-=<<<-===-----=∑。
