(新)江苏版2018年高考数学一轮复习专题2.6函数性质综合运用测
2018年高考数学一轮复习(讲+练+测): 专题2.2 函数定义域、值域(讲)

专题2.2 函数定义域、值域【考纲解读】【直击考点】题组一 常识题1.下列函数中,其定义域和值域分别与函数y =10lg x的定义域和值域相同的是________.A .y =xB .y =lg xC .y =2xD .y =1x【答案】D 【解析】y =10lg x=x ,定义域与值域均为(0,+∞),只有选项D 满足题意.2.已知函数y =f (x +1)的定义域是[-2,3],则y =f (2x -1)的定义域为________.【答案】 ⎣⎢⎡⎦⎥⎤0,52 【解析】 由x ∈[-2,3],得x +1∈[-1,4],由2x -1∈[-1,4],得x ∈⎣⎢⎡⎦⎥⎤0,52 3.[教材改编] 函数f (x )=8-xx +3的定义域是________. 【答案】(-∞,-3)∪(-3,8]【解析】要使函数有意义,则需8-x ≥0且x +3≠0,即x ≤8且x ≠-3,所以其定义域是(-∞,-3)∪(-3,8]. 题组二 常错题4.函数y =f (cos x )的定义域为⎣⎢⎡⎦⎥⎤2k π-π6,2k π+2π3(k ∈Z ),则函数y =f (x )的定义域为________.【答案】 ⎣⎢⎡⎦⎥⎤-12,1【解析】 由于函数y =f (cos x )的定义域是⎣⎢⎡⎦⎥⎤2k π-π6,2k π+2π3(k ∈Z ),所以u =cos x 的值域是⎣⎢⎡⎦⎥⎤-12,1,所以函数y =f (x )的定义域是⎣⎢⎡⎦⎥⎤-12,1.5.已知函数f (x )=⎩⎪⎨⎪⎧3x,x ∈[0,1],92-32x ,x ∈(1,3],当t ∈[0,1]时,f [f (t )]∈[0,1],则实数t 的取值范围是______________. 【答案】⎣⎢⎡⎦⎥⎤log 373,1【解析】 因为t ∈[0,1],所以f (t )=3t ∈[1,3],所以f [f (t )]=f (3t)=92-32·3t ∈[0,1],即73≤3t≤3,所以log 373≤t ≤1.6.若函数f (x )=x -4mx 2+4mx +3的定义域为R ,则实数m 的取值范围是________.【答案】⎣⎢⎡⎭⎪⎫0,34. 【解析】函数的定义域为R ,即mx 2+4mx +3≠0恒成立.①当m =0时,符合题意;②当m ≠0时,Δ=(4m )2-4×m ×3<0,即m (4m -3)<0,解得0<m <34.综上所述,实数m 的取值范围是⎣⎢⎡⎭⎪⎫0,34.题组三 常考题7.若一系列函数的解析式相同、值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y =x 2,值域为{1,4}的“同族函数”共有________个. 【答案】98. 函数f (x )=lg(x 2+x -6)的定义域是________. 【答案】{x |x <-3或x >2}【解析】 要使函数有意义,则需x 2+x -6>0,解得x <-3或x >2.9.设函数f (x )在区间[0,1]上有意义,若存在x ∈R 使函数f (x -a )+f (x +a )有意义,则a 的取值范围为________. 【答案】 [-2,-1].【知识清单】1 函数的定义域1.已知函数解析式,求定义域,其主要依据是使函数的解析式有意义,主要形式有:(1)分式函数,分母不为0;(2)偶次根式函数,被开方数非负数; (3)一次函数、二次函数的这定义域为R ; (4)0x 中的底数不等于0; (5)指数函数x y a =的定义域为R ;(6)对数函数log a y x =的定义域为{}|0x x >; (7)sin ,cos y x y x ==的定义域均为R ;(8)tan y x =的定义域均为|,2x x k k z ππ⎧⎫≠+∈⎨⎬⎩⎭; 2.求抽象函数的定义域:(1)由()y f x =的定义域为D ,求[()]y f g x =的定义域,须解()f x D ∈; (2)由[()]y f g x =的定义域D ,求()y f x =的定义域,只须解()g x 在D 上的值域就是函数()y f x = 的定义域;(3)由[()]y f g x =的定义域D ,求[()]y f h x =的定义域.3.实际问题中的函数的定义域,除了使解析式本身有意义,还要使实际问题有意义. 2 函数的值域 函数值域的求法:(1)利用函数的单调性:若y=f(x)是 [a,b]上的单调增(减)函数,则f(a),f(b)分别是f(x)在区间[a,b]上取得最小(大)值,最大(小)值.(2)利用配方法:形如2(0)y ax bx c a =++≠型,用此种方法,注意自变量x 的范围. (3)利用三角函数的有界性,如sin [1,1],x ∈-cos [1,1]x ∈-.(4)利用“分离常数”法:形如y=ax b cx d ++ 或2ax bx ey cx d++=+ (a,c 至少有一个不为零)的函数,求其值域可用此法.(5)利用换元法:形如y ax b =+,可用此法求其值域. (6)利用基本不等式:(7)导数法:利用导数与函数的连续性求图复杂函数的极值和最值,然后求出值域【考点深度剖析】定义域是函数的灵魂,高考中考查的定义域多以填空形式出现,难度不大;有时也在解答题的某一小问当中进行考查;值域是定义域与对应法则的必然产物,值域的考查往往与最值联系在一起,难度中等.【重点难点突破】考点1 函数的定义域 【1-1】函数y(+)的定义域为_________.【答案】(-∞,-1)∪(-1,0).【1-2】函数22-25+1+)cos (=x x log y 的定义域为_________.【答案】33x x ππ⎧⎫-≤≤⎨⎬⎩⎭【解析】由已知条件,自变量x 需满足22log cos 10250x x +≥⎧⎨-≥⎩得1cos 22,23355x k x k k Z x ππππ⎧≥⇒-+≤≤+∈⎪⎨⎪-≤≤⎩ 所以33x ππ-≤≤故而所求函数定义域为33x x ππ⎧⎫-≤≤⎨⎬⎩⎭.【1-3】设()x x x f -+=22lg,则⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛x f x f 22的定义域为________.【答案】()()2,11,2 --【解析】由202x x +>-得,()f x 的定义域为{}|22x x -<<.故22,222 2.xx⎧-<<⎪⎪⎨⎪-<<⎪⎩,解得()()4,11,4x ∈--.故⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛x f x f 22的定义域为()()2,11,2 -- 【1-4】若函数f (x )= 2x 2+2ax -a -1的定义域为R ,则a 的取值范围为________. 【答案】[-1,0]【思想方法】(1)已知具体函数的解析式,则构造使解析式有意义的不等式(组)求解. (2)对实际问题:由实际意义及使解析式有意义构成的不等式(组)求解. (3)对抽象函数:①若已知函数f (x )的定义域为[a ,b ],则函数f (g (x ))的定义域由不等式a ≤g (x )≤b 求出;②若已知函数f (g (x ))的定义域为[a ,b ],则f (x )的定义域为g (x )在x ∈[a ,b ]时的值域.【温馨提醒】对于含有字母参数的函数定义域,应注意对参数取值的讨论;对于实际问题的定义域一定要使实际问题有意义;而分段函数的定义域是各段区间的并集、各个段上的定义域交集为空集,即各个段的端点处不能重复. 考点2 函数的值域【2-1】求函数y =x +4x(x <0)的值域.【答案】(-∞,-4].【解析】∵x <0,∴x +4x=-⎝ ⎛⎭⎪⎫-x -4x ≤-4,当且仅当x =-2时等号成立. ∴y ∈(-∞,-4]. ∴函数的值域为(-∞,-4].【2-2】 求函数y =x 2+2x (x ∈[0,3])的值域. 【答案】[0,15].【解析】(配方法)y =x 2+2x =(x +1)2-1,∵y =(x +1)2-1在[0,3]上为增函数, ∴0≤y ≤15,即函数y =x 2+2x (x ∈[0,3])的值域为[0,15]. 【2-3】 求函数y =1-x21+x 2的值域.【答案】(-1,1].【2-4】 求函数f (x )=x -1-2x .的值域.【答案】1(,]2-∞.【解析】法一:(换元法)令1-2x =t ,则t ≥0且x =1-t22,于是y =1-t 22-t =-12(t +1)2+1,由于t ≥0,所以y ≤12,故函数的值域是1(,]2-∞.法二:(单调性法)容易判断f (x )为增函数,而其定义域应满足1-2x ≥0,即x ≤12,所以11()22y f ≤=即函数的值域是1(,]2-∞.【2-5】 求函数y =x 2-xx 2-x +1的值域.【答案】1[,1)3-【思想方法】求函数值域常用的方法(1)配方法,多适用于二次型或可转化为二次型的函数. (2)换元法. (3)基本不等式法. (4)单调性法. (5)分离常数法.【温馨提醒】求函数值域的方法多样化,需结合函数解析式的特点选用恰当的方法【易错试题常警惕】分段函数的参数求值问题,一定要注意自变量的限制条件. 如:已知实数0a ≠,函数()2,12,1x a x f x x a x +<⎧=⎨--≥⎩,若()()11f a f a -=+,则a 的值为_______.【分析】当0a >时,11a -<,11a +>,由()()11f a f a -=+得2212a a a a -+=---,解得32a =-,不合题意;当0a <时,11a ->,11a +<,由()()11f a f a -=+得 1222a a a a -+-=++,解得34a =-.所以a 的值为34-.【易错点】没有对a 进行讨论,以为11a -<,11a +>直接代入求解而致误;求解过程中忘记检验所求结果是否符合要求而致误. 【练一练】函数f (x )=⎩⎪⎨⎪⎧log 2 x ,x >0,4x ,x ≤0,则f (f (-1))的值为________.【答案】-2【解析】∵f (-1)=4-1=14,∴f (f (-1))=f ⎝ ⎛⎭⎪⎫14=log 2 14=-2.。
(新)江苏版2018年高考数学一轮复习专题2.6函数性质综合运用练

专题2.6 函数性质综合运用1. 【2017山东改编,理10】已知当[]0,1x ∈时,函数()21y mx =-的图象与y x m =+的图象有且只有一个交点,则正实数m 的取值范围是 【答案】(][)0,13,+∞2. 【2017天津改编,理6】已知奇函数()f x 在R 上是增函数, ()()g x xf x =.若2(log 5.1)a g =-,0.8(2)b g =,(3)c g =,则a ,b ,c 的大小关系为 【答案】b a c <<【解析】因为()f x 是奇函数且在R 上是增函数,所以在0x >时,()0f x >, 从而()()g x xf x =是R 上的偶函数,且在[0,)+∞上是增函数,22(log 5.1)(log 5.1)a g g =-=,0.822<,又4 5.18<<,则22log 5.13<<,所以即0.8202log 5.13<<<,0.82(2)(log 5.1)(3)g g g <<,所以b a c <<.3. 【2017课标3,理15】设函数10()20x x x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是_________. 【答案】1,4⎛⎫-+∞ ⎪⎝⎭4. 【2017北京,理13】能够说明“设a,b,c是任意实数.若a>b>c,则a+b>c”是假命题的一组整数a,b,c的值依次为______________________________.【答案】-1,-2,-3(答案不唯一)5. 【2017山东,理15】若函数()x e f x ( 2.71828e =是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质.下列函数中所有具有M 性质的函数的序号为 .①()2x f x -=②()3x f x -=③()3f x x =④()22f x x =+【答案】①④6. 【2017北京,理14】三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点A i 的横、纵坐标分别为第i 名工人上午的工作时间和加工的零件数,点B i 的横、纵坐标分别为第i 名工人下午的工作时间和加工的零件数,i =1,2,3.①记Q 1为第i 名工人在这一天中加工的零件总数,则Q 1,Q 2,Q 3中最大的是_________. ②记p i 为第i 名工人在这一天中平均每小时加工的零件数,则p 1,p 2,p 3中最大的是_________.【答案】1Q ;2.p【解析】7. 【2017浙江,17】已知αR ,函数a a xx x f +-+=|4|)(在区间[1,4]上的最大值是5,则的取值范围是___________. 【答案】9(,]2-∞ 【解析】8【2017江苏,11】已知函数31()2e ex x f x x x =-+-, 其中e 是自然对数的底数. 若2(1)(2)0f a f a -+≤,则实数的取值范围是 ▲ . 【答案】1[1,]2-9. 【2017江苏,14】设()f x 是定义在R 且周期为1的函数,在区间[0,1)上,2,,(),,x x D f x x x D ⎧∈⎪=⎨∉⎪⎩其中集合1,*n D x x n n -⎧⎫==∈⎨⎬⎩⎭N ,则方程()lg 0f x x -=的解的个数是 ▲ .【答案】810.已知函数f (x )=⎩⎪⎨⎪⎧lg x , 0<x ≤10,⎪⎪⎪⎪⎪⎪-12x +6, x >10,若a ,b ,c 互不相等,且f (a )=f (b )=f (c ),则a +b +c 的取值范围是________.【答案】(25,34)【解析】令-12x +6=0,得x =12.因为a ,b ,c 互不相等,令a<b<c ,作出f(x)的图像,如图所示.令f(a)=f(b)=f(c)=t ,则根据图像可得1<a<10,b +c =2×12=24,故a +b +c∈(25,34).11.偶函数f (x )满足f (x -1)=f (x +1),且在x ∈[0,1]时,f (x )=x ,则关于x 的方程f (x )=⎝ ⎛⎭⎪⎫110x在x ∈[0,4]上解的个数是________. 【答案】4【解析】由f(x -1)=f(x +1)可知T =2.∵x∈[0,1]时,f(x)=x ,又∵f(x)是偶函数,∴可得图像如图.∴f (x )=⎝ ⎛⎭⎪⎫110x在x ∈[0,4]上解的个数是4个.12.已知函数f (x )=2x(x ∈R ),且f (x )=g (x )+h (x ),其中g (x )为奇函数,h (x )为偶函数.若不等式2ag (x )+h (2x )≥0对任意x ∈[1,2]恒成立,则实数a 的取值范围是________.【答案】⎣⎢⎡⎭⎪⎫-1712,+∞13.如图,矩形ABCD 的三个顶点A ,B ,C 分别在函数y =log22x ,y =x 12,y =⎝ ⎛⎭⎪⎫22x 的图像上,且矩形的边分别平行于两坐标轴.若点A 的纵坐标为2,则点D 的坐标为________.【答案】⎝ ⎛⎭⎪⎫12,14.14.已知函数f (x )=a log 2x -b log 3x +2,若f ⎝ ⎛⎭⎪⎫12 014=4,则f (2 014)的值为________.【答案】0【解析】令g (x )=f (x )-2=a log 2x -b log 3x ,可得g (x )满足g ⎝ ⎛⎭⎪⎫1x =-g (x ).所以由g ⎝⎛⎭⎪⎫12 014=f ⎝⎛⎭⎪⎫12 014-2=2,得g (2 014)=-2,所以f (2 014)=0.。
(新)江苏专用2018版高考数学大一轮复习第三章导数及其应用3_2导数的应用第3课时导数与函数的综合问题教师

第3课时 导数与函数的综合问题题型一 导数与不等式有关的问题 命题点1 解不等式例1 设f (x )是定义在R 上的奇函数,f (2)=0,当x >0时,有xf ′x -f xx 2<0恒成立,则不等式x 2f (x )>0的解集是________________. 答案 (-∞,-2)∪(0,2) 解析 ∵当x >0时,⎣⎢⎡⎦⎥⎤f x x ′<0,∴φ(x )=f xx为减函数, 又φ(2)=0,∴当且仅当0<x <2时,φ(x )>0, 此时x 2f (x )>0.又f (x )为奇函数,∴h (x )=x 2f (x )也为奇函数. 故x 2f (x )>0的解集为(-∞,-2)∪(0,2). 命题点2 证明不等式例2 (2016·全国丙卷)设函数f (x )=ln x -x +1. (1)讨论f (x )的单调性;(2)证明:当x ∈(1,+∞)时,1<x -1ln x<x ;(3)设c >1,证明:当x ∈(0,1)时,1+(c -1)x >c x.(1)解 由题设,f (x )的定义域为(0,+∞),f ′(x )=1x-1,令f ′(x )=0,解得x =1.当0<x <1时,f ′(x )>0,f (x )单调递增;当x >1时,f ′(x )<0,f (x )单调递减. (2)证明 由(1)知,f (x )在x =1处取得最大值,最大值为f (1)=0. 所以当x ≠1时,ln x <x -1.故当x ∈(1,+∞)时,ln x <x -1,ln 1x <1x-1,即1<x -1ln x<x .(3)证明 由题设c >1,设g (x )=1+(c -1)x -c x,则g ′(x )=c -1-c xln c ,令g ′(x )=0,解得x 0=lnc -1ln c ln c.当x <x 0时,g ′(x )>0,g (x )单调递增; 当x >x 0时,g ′(x )<0,g (x )单调递减.由(2)知1<c -1ln c<c ,故0<x 0<1.又g (0)=g (1)=0,故当0<x <1时,g (x )>0. 所以当x ∈(0,1)时,1+(c -1)x >c x. 命题点3 不等式恒成立或有解问题 例3 已知函数f (x )=1+ln xx.(1)若函数f (x )在区间(a ,a +12)上存在极值,求正实数a 的取值范围;(2)如果当x ≥1时,不等式f (x )≥kx +1恒成立,求实数k 的取值范围.解 (1)函数的定义域为(0,+∞),f ′(x )=1-1-ln x x 2=-ln xx2, 令f ′(x )=0,得x =1;当x ∈(0,1)时,f ′(x )>0,f (x )单调递增; 当x ∈(1,+∞)时,f ′(x )<0,f (x )单调递减. 所以x =1为极大值点,所以0<a <1<a +12,故12<a <1,即实数a 的取值范围为(12,1). (2)当x ≥1时,k ≤x +11+ln xx恒成立,令g (x )=x +11+ln xx,则g ′(x )=1+ln x +1+1xx -x +11+ln xx 2=x -ln xx 2. 再令h (x )=x -ln x ,则h ′(x )=1-1x≥0, 所以h (x )≥h (1)=1,所以g ′(x )>0, 所以g (x )为单调增函数,所以g (x )≥g (1)=2, 故k ≤2.所以实数k 的取值范围是(-∞,2]. 引申探究本题(2)中,若改为存在x 0∈[1,e],使不等式f (x )≥kx +1成立,求实数k 的取值范围.解 当x ∈[1,e]时,k ≤x +11+ln xx有解,令g (x )=x +11+ln xx,由例3(2)解题知,g (x )为单调增函数,∴g (x )max =g (e)=2+2e,∴k ≤2+2e ,即实数k 的取值范围是(-∞,2+2e ].思维升华 (1)利用导数解不等式的思路已知一个含f ′(x )的不等式,可得到和f (x )有关的函数的单调性,然后可利用函数单调性解不等式.(2)利用导数证明不等式的方法证明f (x )<g (x ),x ∈(a ,b ),可以构造函数F (x )=f (x )-g (x ),如果F ′(x )<0,则F (x )在(a ,b )上是减函数,同时若F (a )≤0,由减函数的定义可知,x ∈(a ,b )时,有F (x )<0,即证明了f (x )<g (x ).(3)利用导数解决不等式的恒成立问题的策略①首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围.②也可分离变量,构造函数,直接把问题转化为函数的最值问题.(2015·福建)已知函数f (x )=ln x -x -122.(1)求函数f (x )的单调递增区间; (2)证明:当x >1时,f (x )<x -1;(3)确定实数k 的所有可能取值,使得存在x 0>1,当x ∈(1,x 0)时,恒有f (x )>k (x -1).(1)解 f ′(x )=1x -x +1=-x 2+x +1x,x ∈(0,+∞).由f ′(x )>0,得⎩⎪⎨⎪⎧x >0,-x 2+x +1>0.解得0<x <1+52.故f (x )的单调递增区间是⎝⎛⎭⎪⎫0,1+52.(2)证明 令F (x )=f (x )-(x -1),x ∈(0,+∞). 则有F ′(x )=1-x2x.当x ∈(1,+∞)时,F ′(x )<0, 所以F (x )在(1,+∞)上单调递减, 故当x >1时,F (x )<F (1)=0, 即当x >1时,f (x )<x -1.(3)解 由(2)知,当k =1时,不存在x 0>1满足题意. 当k >1时,对于x >1,有f (x )<x -1<k (x -1), 则f (x )<k (x -1), 从而不存在x 0>1满足题意.当k <1时,令G (x )=f (x )-k (x -1),x ∈(0,+∞), 则有G ′(x )=1x -x +1-k =-x 2+1-k x +1x.由G ′(x )=0,得-x 2+(1-k )x +1=0. 解得x 1=1-k -1-k 2+42<0,x 2=1-k +1-k 2+42>1.当x ∈(1,x 2)时,G ′(x )>0, 故G (x )在(1,x 2)内单调递增.从而当x ∈(1,x 2)时,G (x )>G (1)=0, 即f (x )>k (x -1).综上,k 的取值范围是(-∞,1). 题型二 利用导数研究函数零点问题例4 (2016·扬州模拟)设函数f (x )=x e x-a sin x cos x (a ∈R ,其中e 是自然对数的底数). (1)当a =0时,求f (x )的极值;(2)若对于任意的x ∈[0,π2],f (x )≥0恒成立,求a 的取值范围;(3)是否存在实数a ,使得函数f (x )在区间(0,π2)上有两个零点?若存在,求出a 的取值范围;若不存在,请说明理由.解 (1) 当a =0时,f (x )=x e x,f ′(x )=e x(x +1), 令f ′(x )=0,得x =-1. 列表如下:↘↗所以函数f (x )的极小值为f (-1)=-1e,无极大值.(2)①当a ≤0时,由于对于任意x ∈[0,π2],有sin x cos x ≥0,所以f (x )≥0恒成立,即当a ≤0时,符合题意;②当0<a ≤1时,因为f ′(x )=e x(x +1)-a cos 2x ≥e 0(0+1)-a cos 0=1-a ≥0, 所以函数f (x )在[0,π2]上为增函数.所以f (x )≥f (0)=0,即当0<a ≤1时,符合题意; ③当a >1时,f ′(0)=1-a <0, f ′(π4)=4e(π4+1)>0,设f ′(α)=0,其中α是f ′(x )=0中最接近x =0的零点. 所以f (x )在(0,α)上为减函数,此时f (x )<f (0)=0, 即当a >1时,不符合题意.综上所述,a 的取值范围是(-∞,1].(3)不存在实数a ,使得函数f (x )在区间(0,π2)上有两个零点.由(2)知,当a ≤1时,f (x )在(0,π2)上是增函数,且f (0)=0,故函数f (x )在区间(0,π2)上无零点.当a >1时,f ′(x )=e x(x +1)-a cos 2x . 令g (x )=e x(x +1)-a cos 2x , 则g ′(x )=e x (x +2)+2a sin 2x ,当x ∈(0,π2)时,恒有g ′(x )>0,所以g (x )在(0,π2)上是增函数.由g (0)=1-a <0,g (π2)=2e π(π2+1)+a >0, 故g (x )在(0,π2)上存在唯一的零点x 0,即方程f ′(x )=0在(0,π2)上存在唯一解x 0.且当x ∈(0,x 0)时,f ′(x )<0; 当x ∈(x 0,π2)时,f ′(x )>0,即函数f (x )在(0,x 0)上单调递减, 在(x 0,π2)上单调递增.当x ∈(0,x 0)时,f (x )<f (0)=0,即f (x )在(0,x 0)上无零点; 当x ∈(x 0,π2)时,由于f (x 0)<f (0)=0,f (π2)=π22e π>0,所以f (x )在(x 0,π2)上有唯一零点.所以,当a >1时,f (x )在(0,π2)上有一个零点.综上所述,不存在实数a ,使得函数f (x )在区间(0,π2)上有两个零点.思维升华 利用导数研究方程的根(函数的零点)的策略研究方程的根或曲线的交点个数问题,可构造函数,转化为研究函数的零点个数问题.可利用导数研究函数的极值、最值、单调性、变化趋势等,从而画出函数的大致图象,然后根据图象判断函数的零点个数.(2016·南通模拟)已知函数f (x )=a +xln x (a ∈R ).(1)求f (x )的单调区间;(2)试求f (x )的零点个数,并证明你的结论.解 (1)由f (x )=a +x ln x 知函数f (x )的定义域为(0,+∞),f ′(x )=12x (2+ln x ).令f ′(x )=0,得x =1e2.当x 变化时,f ′(x ),f (x )的变化情况如下表:所以,函数f (x )的单调减区间为(0,1e 2),单调增区间为(1e 2,+∞).(2)由(1)知[f (x )]min =f (1e 2)=a -2e.①若a >2e ,因为f (x )≥[f (x )]min =f (1e 2)=a -2e >0,所以此时函数f (x )的零点个数为0. ②若a =2e ,则[f (x )]min =f (1e 2)=a -2e=0,而函数f (x )在(0,1e 2)上是单调减函数,在(1e2,+∞)上是单调增函数,即当0<x <1e 2时,f (x )>f (1e 2)=0;当x >1e 2时,f (x )>f (1e2)=0.于是,此时f (x )有唯一零点1e 2,即零点个数为1.③若a <2e ,则[f (x )]min =f (1e 2)=a -2e <0.当a ≤0时,因为当x ∈(0,1e 2]时,f (x )=a +x ln x <a ≤0,所以函数f (x )在区间(0,1e2]上无零点;因为函数f (x )在[1e 2,+∞)上是单调增函数,且f (1e 2)=a -2e <0,而e-2a∈(1e2,+∞),f (e -2a )=a (1-2e -a)≥0, 所以函数f (x )在(1e 2,e -2a)上恰有一个零点.于是函数f (x )在[1e 2,+∞)上恰有一个零点.从而当a ≤0时,函数f (x )的零点个数为1; 当0<a <2e时,因为函数f (x )在[1e 2,+∞)上是单调增函数,且f (1)=a >0,f (1e 2)=a -2e<0,所以函数f (x )在(1e 2,1)上恰有一个零点,于是函数f (x )在(1e2,+∞)上也恰有一个零点.因为函数f (x )在(0,1e 2)上是单调减函数,且f (1e 2)=a -2e <0,而441e e a a-=∈(0,1e2),且f (4ea-)=24eaa a ->a -4a ·22a 2=0(利用结论:“当x >0时,e x >x 2”进行放缩),此时,函数f (x )在(0,1e2)上恰有一个零点,故当0<a <2e 时,函数f (x )的零点个数为2.综上,当a >2e 时,函数f (x )的零点个数为0;当a =2e 或a ≤0时,函数f (x )的零点个数为1;当0<a <2e 时,函数f (x )的零点个数为2.题型三 利用导数研究生活中的优化问题例5 某商场销售某种商品的经验表明,该商品每日的销售量y (单位:千克)与销售价格x (单位:元/千克)满足关系式y =ax -3+10(x -6)2,其中3<x <6,a 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克. (1)求a 的值;(2)若该商品的成本为3元/千克,试确定销售价格x 的值,使商场每日销售该商品所获得的利润最大.解 (1)因为当x =5时,y =11,所以a2+10=11,a =2.(2)由(1)可知,该商品每日的销售量为y =2x -3+10(x -6)2. 所以商场每日销售该商品所获得的利润为f (x )=(x -3)[2x -3+10(x -6)2]=2+10(x -3)(x -6)2,3<x <6.从而,f ′(x )=10[(x -6)2+2(x -3)(x -6)] =30(x -4)(x -6).于是,当x 变化时,f ′(x ),f (x )的变化情况如下表:由上表可得,当x =4时,函数f (x )取得极大值,也是最大值. 所以,当x =4时,函数f (x )取得最大值且最大值等于42.答 当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大. 思维升华 利用导数解决生活中的优化问题的四个步骤(1)分析实际问题中各个量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系式y =f (x ).(2)求函数的导数f ′(x ),解方程f ′(x )=0.(3)比较函数在区间端点和使f ′(x )=0的点的函数值的大小,最大(小)者为最大(小)值;若函数在开区间内只有一个极值点,那么该极值点就是最值点. (4)回归实际问题作答.(2016·苏北四市调研)经市场调查,某商品每吨的价格为x (1<x <14)百元时,该商品的月供给量为y 1吨,y 1=ax +72a 2-a (a >0);月需求量为y 2万吨,y 2=-1224x 2-1112x +1,当该商品的需求量大于供给量时,销售量等于供给量;当该商品的需求量不大于供给量时,销售量等于需求量,该商品的月销售额等于月销售量与价格的乘积.(1)若a =17,问商品的价格为多少时,该商品的月销售额最大?(2)记需求量与供给量相等时的价格为均衡价格,若该商品的均衡价格不低于每吨6百元,求实数a 的取值范围.解 (1) 若a =17,由y 2>y 1,得-1224x 2-1112x +1>17x +72(17)2-17,解得-40<x <6 . 因为1<x <14,所以1<x <6. 设该商品的月销售额为g (x ),则g (x )=⎩⎪⎨⎪⎧y 1·x ,1<x <6,y 2·x ,6≤x <14.当1<x <6时,g (x )=17(x -12)x <g (6)=337.当6≤x <14时,g (x )=(-1224x 2-1112x +1)x ,则g ′(x )=-1224(3x 2+4x -224)=-1224(x -8)(3x +28),由g ′(x )>0,得x <8,所以g (x )在[6,8)上是增函数,在(8,14)上是减函数, 故当x =8时,g (x )有最大值g (8)=367.(2)设f (x )=y 1-y 2=1224x 2+(1112+a )x +72a 2-1-a ,因为a >0,所以f (x )在区间(1,14)上是增函数,若该商品的均衡价格不低于6百元,则函数f (x )在区间[6,14)上有零点,所以⎩⎪⎨⎪⎧f6≤0,f 14>0,即⎩⎪⎨⎪⎧7a 2+10a -117≤0,72a 2+13a >0,解得0<a ≤17.答 (1)若a =17,商品的每吨价格定为8百元时,月销售额最大;(2)若该商品的均衡价格不低于每吨6百元,实数a 的取值范围是(0,17].一审条件挖隐含典例 (16分)设f (x )=a x+x ln x ,g (x )=x 3-x 2-3.(1)如果存在x 1,x 2∈[0,2]使得g (x 1)-g (x 2)≥M 成立,求满足上述条件的最大整数M ; (2)如果对于任意的s ,t ∈[12,2],都有f (s )≥g (t )成立,求实数a 的取值范围.(1)存在x 1,x 2∈[0,2]使得g (x 1)-g (x 2)≥M ↓(正确理解“存在”的含义) [g (x 1)-g (x 2)]max ≥M↓挖掘[g (x 1)-g (x 2)]max 的隐含实质g (x )max -g (x )min ≥M↓求得M 的最大整数值(2)对任意s ,t ∈[12,2]都有f (s )≥g (t )↓(理解“任意”的含义)f (x )min ≥g (x )max↓求得g (x )max =1ax+x ln x ≥1恒成立 ↓分离参数aa ≥x -x 2ln x 恒成立↓求h (x )=x -x 2ln x 的最大值a ≥h (x )max =h (1)=1↓a ≥1规范解答解 (1)存在x 1,x 2∈[0,2]使得g (x 1)-g (x 2)≥M 成立,等价于[g (x 1)-g (x 2)]max ≥M . [2分]由g (x )=x 3-x 2-3,得g ′(x )=3x 2-2x =3x (x -23).令g ′(x )>0,得x <0或x >23,又x ∈[0,2],所以g (x )在区间[0,23]上单调递减,在区间[23,2]上单调递增,所以g (x )min=g (23)=-8527,g (x )max =g (2)=1.故[g (x 1)-g (x 2)]max =g (x )max -g (x )min =11227≥M ,则满足条件的最大整数M =4.[7分](2)对于任意的s ,t ∈[12,2],都有f (s )≥g (t )成立,等价于在区间[12,2]上,函数f (x )min ≥g (x )max .[9分]由(1)可知在区间[12,2]上,g (x )的最大值为g (2)=1.在区间[12,2]上,f (x )=a x+x ln x ≥1恒成立等价于a ≥x -x 2ln x 恒成立.设h (x )=x -x 2ln x ,h ′(x )=1-2x ln x -x ,可知h ′(x )在区间[12,2]上是减函数,又h ′(1)=0,所以当1<x <2时,h ′(x )<0;当12<x <1时,h ′(x )>0.[14分]即函数h (x )=x -x 2ln x 在区间(12,1)上单调递增,在区间(1,2)上单调递减,所以h (x )max=h (1)=1,所以a ≥1,即实数a 的取值范围是[1,+∞).[16分]1.函数f (x )=(x -1)2(x -2)2的极大值是________. 答案116解析 ∵f (x )=(x -1)2(x -2)2, ∴f ′(x )=2(x -1)(2x -3)(x -2).令f ′(x )=0,得可能的极值点x 1=1,x 2=32,x 3=2.当x 变化时,f ′(x ),f (x )的变化情况如下表:↘↘∴f (32)=116是函数的极大值.2.已知曲线y =x 2+a ln x (a >0)上任意一点处的切线的斜率为k ,若k 的最小值为4,则此时切点的坐标为________. 答案 (1,1)解析 函数y =x 2+a ln x (a >0)的定义域为{x |x >0},y ′=2x +ax≥22a =4,则a =2,当且仅当x =1时,“=”成立,将x =1代入曲线方程得y =1,故所求的切点坐标是(1,1). 3.如果不等式ln kx x ≤1e 对任意的正实数x 恒成立,则实数k 的取值范围为____________.答案 (0,1]解析 由题意知k >0,令f (x )=ln kxx(x >0),则f (x )=ln kx x =ln k +ln xx,因此f ′(x )=1-ln kx x 2,令f ′(x )=0,解得x =e k ,且函数f (x )在x =e k处取得极大值,也是最大值,由题意有k e ≤1e,所以0<k ≤1.4.若商品的年利润y (万元)与年产量x (百万件)的函数关系式:y =-x 3+27x +123(x >0),则获得最大利润时的年产量为________百万件. 答案 3解析 y ′=-3x 2+27=-3(x +3)(x -3), 当0<x <3时,y ′>0; 当x >3时,y ′<0.故当x =3时,该商品的年利润最大.5.(2017·南京质检)直线x =t 分别与函数f (x )=e x+1的图象及g (x )=2x -1的图象相交于点A 和点B ,则AB 的最小值为________. 答案 4-2ln 2解析 由题意得,AB =|e x+1-(2x -1)| =|e x -2x +2|,令h (x )=e x-2x +2,则h ′(x )=e x-2,所以h (x )在(-∞,ln 2)上单调递减, 在(ln 2,+∞)上单调递增, 所以h (x )min =h (ln 2)=4-2ln 2>0, 即AB 的最小值是4-2ln 2.6.已知函数f (x )=⎩⎪⎨⎪⎧-x 2+2xx ≤0,ln x +1x >0,若|f (x )|≥ax ,则a 的取值范围是____________. 答案 [-2,0] 解析 |f (x )|≥ax ⇔⎩⎪⎨⎪⎧--x 2+2x ≥ax x ≤0,1ln x +1≥ax x >0, 2成立.①由(1)得x (x -2)≥ax 在区间(-∞,0]上恒成立. 当x =0时,a ∈R ;当x <0时,有x -2≤a 恒成立, 所以a ≥-2.故a ≥-2.②由(2)得ln(x +1)-ax ≥0在区间(0,+∞)上恒成立,设h (x )=ln(x +1)-ax (x >0), 则h ′(x )=1x +1-a (x >0),可知h ′(x )为减函数. 当a ≤0时,h ′(x )>0,故h (x )为增函数, 所以h (x )>h (0)=0恒成立; 当a ≥1时,因为1x +1∈(0,1), 所以h ′(x )=1x +1-a <0,故h (x )为减函数, 所以h (x )<h (0)=0恒成立,显然不符合题意;当0<a <1时,对于给定的一个确定值a ,总可以至少找到一个x 0>0,满足h (x 0)=ln(x 0+1)-ax 0<0成立.如a =12时,取x 0=4,则h (x 0)=ln 5-2<0成立,可知0<a <1时,不符合题意.故a ≤0.由①②可知a 的取值范围是[-2,0].7.若函数f (x )=ax 2+4x -3在[0,2]上有最大值f (2),则a 的取值范围是________.答案 [-1,+∞)解析 f ′(x )=2ax +4,由f (x )在[0,2]上有最大值f (2),则要求f (x )在[0,2]上单调递增,则2ax +4≥0在[0,2]上恒成立.当a ≥0时,2ax +4≥0恒成立;当a <0时,要求4a +4≥0恒成立,即a ≥-1.∴a 的取值范围是[-1,+∞).8.(2016·苏州模拟)定义在R 上的函数f (x )满足:f (x )+f ′(x )>1,f (0)=4,则不等式e x f (x )>e x+3(其中e 为自然对数的底数)的解集为________________. 答案 (0,+∞)解析 设g (x )=e x f (x )-e x(x ∈R ), 则g ′(x )=e x f (x )+e x f ′(x )-e x=e x[f (x )+f ′(x )-1],∵f (x )+f ′(x )>1,∴f (x )+f ′(x )-1>0, ∴g ′(x )>0,∴y =g (x )在定义域上单调递增, ∵e x f (x )>e x+3,∴g (x )>3, 又∵g (0)=e 0f (0)-e 0=4-1=3, ∴g (x )>g (0),∴x >0.9.已知函数f (x )=ax 3-3x 2+1,若f (x )存在唯一的零点x 0且x 0>0,则a 的取值范围是________. 答案 (-∞,-2)解析 当a =0时,f (x )=-3x 2+1有两个零点,不合题意,故a ≠0,f ′(x )=3ax 2-6x =3x (ax -2),令f ′(x )=0,得x 1=0,x 2=2a.若a >0,由三次函数图象知f (x )有负数零点,不合题意,故a <0. 由三次函数图象及f (0)=1>0知,f (2a)>0, 即a ×(2a )3-3×(2a)2+1>0,化简得a 2-4>0,又a <0,所以a <-2.10.已知函数f (x )=ax 3-3x +1对x ∈(0,1]总有f (x )≥0成立,则实数a 的取值范围是________. 答案 [4,+∞)解析 当x ∈(0,1]时不等式ax 3-3x +1≥0可化为a ≥3x -1x 3,设g (x )=3x -1x3,x ∈(0,1],g ′(x )=3x 3-3x -1·3x2x 6=-6x -12x4. g ′(x )与g (x )随x 的变化情况如下表:x (0,12)12 (12,1) g ′(x ) + 0 - g (x )↗极大值4↘因此g (x )的最大值为4, 则实数a 的取值范围是[4,+∞).11.(2016·盐城模拟)已知f (x )=(1-x )e x-1. (1)求函数f (x )的最大值; (2)设g (x )=f xx,x >-1且x ≠0,证明:g (x )<1. (1)解 f ′(x )=-x e x.当x ∈(-∞,0)时,f ′(x )>0,f (x )单调递增; 当x ∈(0,+∞)时,f ′(x )<0,f (x )单调递减. 所以f (x )的最大值为f (0)=0.(2)证明 由(1)知,当x >0时,f (x )<0,g (x )<0<1. 当-1<x <0时,g (x )<1等价于f (x )>x . 设h (x )=f (x )-x ,则h ′(x )=-x e x-1. 当x ∈(-1,0)时,0<-x <1,0<e x<1, 则0<-x e x<1,从而当x ∈(-1,0)时,h ′(x )<0,h (x )在(-1,0)上单调递减.当-1<x <0时,h (x )>h (0)=0,即g (x )<1. 综上,当x >-1且x ≠0时总有g (x )<1.。
(江苏专用)2018年高考数学一轮复习 第二章 函数 2.2 函数的基本性质课件

3
.
22
思路分析 利用函数的奇偶性将原不等式转化为f(2|a-1|)>f( 2),结合函数f(x)在(0,+∞)上单调递 减即可求得a的取值范围.
C组 教师专用题组
1.(2013四川理改编,10,5分)设函数f(x)= ex x a (a∈R,e为自然对数的底数).若曲线y=sin x上存
a,b,c的大小关系为
.(用“<”连接)
答案 b<a<c
解析 本题考查函数的奇偶性、单调性的应用,对数值大小的比较.
奇函数f(x)在R上是增函数,当x>0时, f(x)>f(0)=0,当x1>x2>0时, f(x1)>f(x2)>0,∴x1 f(x1)>x2 f(x2),∴g(x) 在(0,+∞)上单调递增,且g(x)=xf(x)是偶函数,∴a=g(-log25.1)=g(log25.1).2<log25.1<3,1<20.8<2,由g(x)在 (0,+∞)上单调递增,得g(20.8)<g(log25.1)<g(3),∴b<a<c.
3.(2017江苏泰州中学第一学期第一次质量检测,10)已知函数f(x)=
x x
ln x 5,0 9 m, x
x 1
x
1
1,
的值域为R,
则实数m的取值范围为
.
答案 m≤1
解析 当0<x≤1时,f(x)=x+ln x+5∈(-∞,6],当x>1时,f(x)=x+ 9 +m=x+1+ 9 +m-1≥2
在点(x0,y0)使得f(f(y0))=y0,则a的取值范围是
(江苏专用)2018年高考数学一轮复习 第二章 函数 2.6 函数模型及其应用课件

|x-01|+
2
|1-y|
= 1 -1 (y-x),又y-x1> ,∴|f(x)-f(y1)|<1 -1 1× = .
22
2
22 2 4
综上所述,对所有x,y∈[0,1],都有|f(x)-f(y)|< 1 .因此,k≥1 ,即k的最小值为1 .
4
4
4
3.(2013课标全国Ⅰ理,21,12分)设函数f(x)=x2+ax+b,g(x)=ex(cx+d).若曲线y=f(x)和曲线y=g(x)都过 点P(0,2),且在点P处有相同的切线y=4x+2. (1)求a,b,c,d的值; (2)若x≥-2时, f(x)≤kg(x),求k的取值范围.
t3
,B
3t 2
,.0
0,
3
000 t2
故f(t)=
32=t 2
3
,t0t20∈0 [52 ,2032].
t2
4 106 t4
②设g(t)=t2+ 41,则06 g'(t)=2t- .1令6g1'(0t6)=0,解得t=10 .
t4
t5
2
当t∈(5,10 2)时,g'(t)<0,g(t)是减函数;
解得n> 24 ,
5
又∵n∈N*, ∴n≥5, ∴该公司全年投入的研发资金开始超过200万元的年份是2019年.
5.(2015四川,13,5分)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=ekx+b(e
=2.718…为自然对数的底数,k,b为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜
(江苏版)2018年高考数学一轮复习(讲+练+测): 专题2.11 函数与方程(测)-数学备课大师【全免费】

专题2.11 函数与方程班级__________ 姓名_____________ 学号___________ 得分__________(满分100分,测试时间50分钟)一、填空题:请把答案直接填写在答题卡相应的位置........上(共10题,每小题6分,共计60分). 1. 【2016-2017学年度江苏苏州市高三期中调研考试】已知函数()221,0,0x x f x x x x ->⎧=⎨+≤⎩,若函数()()g x f x m =-有三个零点,则实数m 的取值范围是__________. 【答案】1,04⎛⎤- ⎥⎝⎦【解析】2. 【江苏省苏州市2017届高三暑假自主学习测试】已知函数311,,()11,,x f x x x x ⎧>⎪=⎨-≤≤⎪⎩若关于x的方程()(1)f x k x =+有两个不同的实数根,则实数k 的取值范围是 ▲ . 【答案】1(0,)2【解析】3. 【泰州中学2016-2017年度第一学期第一次质量检测文科】定义在R 上的奇函数()f x ,当0x ≥时,2,[0,1),()11|3|,[1,),xx f x x x x -⎧∈⎪=+⎨⎪--∈+∞⎩则函数1()()F x f x π=-的所有零点之和为 . 【答案】112π-【解析】试题分析:由图知,共五个零点,从左到右交点横坐标依次为12345,,x x x x x ,,,满足1234516,,612x x x x x π+=-=+=-,因此所有零点之和为112π-4. 【江苏省南通中学2017届高三上学期期中考试】已知函数2+1, 1,()(), 1,a x x f x x a x ⎧-⎪=⎨->⎪⎩≤ 函数()2()g x f x =-,若函数()()y f x g x =- 恰有4个零点,则实数a 的取值范围是 ▲ .【答案】23a <≤ 【解析】试题分析:()()0()1f x g x f x -=⇒=,所以要有4个零点,需满足21,1+11,23(1)1,1,a a a a a ⎧>-≤⎪⇒<≤⎨->>⎪⎩5. 【泰州中学2017届高三上学期期中考试】已知函数()()23,0(01)log 11,0a x a x f x a a x x ⎧+<⎪=>≠⎨++≥⎪⎩且在R 上单调递减,且关于x 的方程()2f x x =-恰好有两个不相等的实数解,则a 的取值范围是_________.【答案】123,334⎡⎤⎧⎫⎨⎬⎢⎥⎣⎦⎩⎭【解析】26. 【泰州中学2017届高三上学期期中考试】定义在R 上的函数()f x 满足()()516f x f x ++=,当()1,4x ∈-时,x x x f 2)(2-=,则函数()f x 在[]0,2016上的零点个数是__________. 【答案】605 【解析】7. 【无锡市普通高中2017届高三上学期期中基础性检测】若函数2,0ln ,0x a x y x a x x ⎧-≤=⎨-+>⎩,在区间()2,2-上有两个零点,则实数a 的取值范围为__________. 【答案】[)0,2ln2+ 【解析】试题分析:由题设可知函数a x y -=2与函数x a x y ln +-=在给定的区间]0,2(-和区间)2,0(内分别有一个根,结合图象可得⎪⎩⎪⎨⎧>+->-≤-02ln 2040a a a ,即⎪⎩⎪⎨⎧+<<≥2ln 240a a a ,所以2ln 20+<≤a ,故应填答案[)0,2ln 2+.8.已知函数f (x )=4x +m ·2x +1仅有一个零点,则m 的取值范围为 . 【答案】m =-29. [x ]表示不超过x 的最大整数,例如[2.9]=2,[-4.1]=-5,已知f (x )=x -[x ](x ∈R ),g (x )=log 4(x -1),则函数h (x )=f (x )-g (x )的零点个数是 .【答案】2【解析】作出函数f (x )与g (x )的图像如图所示,发现有两个不同的交点,故选B.10. 已知函数f (x )=⎩⎪⎨⎪⎧x 3,x ≤a ,x 2,x >a ,若存在实数b ,使函数g (x )=f (x )-b 有两个零点,则a 的取值范围是________.【答案】(-∞,0)∪(1,+∞)【解析】函数g (x )有两个零点,即方程f (x )-b =0有两个不等实根,则函数y =f (x )和y =b 的图象有两个公共点.①若a <0,则当x ≤a 时,f (x )=x 3,函数单调递增;当x >a 时,f (x )=x 2,函数先单调递减后单调递增,f (x )的图象如图(1)实线部分所示,其与直线y =b 可能有两个公共点. ②若0≤a ≤1,则a 3≤a 2,函数f (x )在R 上单调递增,f (x )的图象如图(2)实线部分所示,其与直线y =b 至多有一个公共点.③若a >1,则a 3>a 2,函数f (x )在R 上不单调,f (x )的图象如图(3)实线部分所示,其与直线y =b 可能有两个公共点.综上,a <0或a >1.二、解答题:解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指.定区域内....。
(江苏版)2018年高考数学一轮复习(讲、练、测):_专题4.5_函数y=Asin(ωx+φ)的图象及其应用(练)(有解析)

专题4.5 函数y =Asin (ωx +φ)的图象及其应用【基础巩固】一、填空题1.(2016·全国Ⅱ卷改编)若将函数y =2sin 2x 的图象向左平移π12个单位长度,则平移后图象的对称轴为________. 【答案】x =k π2+π6(k ∈Z )2.(2017·衡水中学金卷)若函数y =sin(ωx -φ)(ω>0,|φ|<π2)在区间⎣⎢⎡⎦⎥⎤-π2,π上的图象如图所示,则ω,φ的值分别是________.【答案】2,π3【解析】由题图可知,T =2⎣⎢⎡⎦⎥⎤π6-⎝ ⎛⎭⎪⎫-π3=π,所以ω=2πT =2,又sin ⎝ ⎛⎭⎪⎫2×π6-φ=0,所以π3-φ=k π(k∈Z ),即φ=π3-k π(k ∈Z ),而|φ|<π2,所以φ=π3.3.(2017·苏北四市调研)如图,已知A ,B 分别是函数f (x )=3sin ωx (ω>0)在y 轴右侧图象上的第一个最高点和第一个最低点,且∠AOB =π2,则该函数的周期是________.【答案】4【解析】设函数的周期为T ,由图象可得A ⎝ ⎛⎭⎪⎫T 4,3,B ⎝ ⎛⎭⎪⎫3T 4,-3,则OA →·OB →=3T 216-3=0,解得T =4.4.(2017·南京师大附中、淮阴中学、海门中学、天一中学四校联考)将函数y =sin(2x +φ)(0<φ<π)的图象沿x 轴向左平移π8个单位后,得到函数y =f (x )的图象,若函数f (x )的图象过原点,则φ=________.【答案】3π4【解析】将函数y =sin(2x +φ)(0<φ<π)的图象沿x 轴向左平移π8个单位后,得到函数f (x )=sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π8+φ=sin ⎝ ⎛⎭⎪⎫2x +π4+φ的图象,若函数f (x )的图象过原点,则f (0)=sin ⎝ ⎛⎭⎪⎫π4+φ=0,π4+φ=k π,k ∈Z ,φ=k π-π4,k ∈Z ,又0<φ<π,则φ=3π4.5.(2017·南京调研)如图,它是函数f (x )=A sin(ωx +φ)(A >0,ω>0,φ∈[0,2π))图象的一部分,则f (0)的值为________.【答案】3226.(2017·龙岩模拟)某城市一年中12个月的平均气温与月份的关系可近似地用函数y =a +A cos ⎣⎢⎡⎦⎥⎤π6x -(x =1,2,3,…,12)来表示,已知6月份的月平均气温最高为28 ℃,12月份的月平均气温最低为18 ℃,则10月份的平均气温为________℃. 【答案】20.5【解析】因为当x =6时,y =a +A =28; 当x =12时,y =a -A =18,所以a =23,A =5, 所以y =f (x )=23+5cos ⎣⎢⎡⎦⎥⎤π6x -, 所以当x =10时,f (10)=23+5cos ⎝ ⎛⎭⎪⎫π6×4 =23-5×12=20.5.7.已知函数f (x )=sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,-π2≤φ≤π2的图象上的两个相邻的最高点和最低点的距离为22,且过点⎝ ⎛⎭⎪⎫2,-12,则函数f (x )的解析式为________.【答案】f (x )=sin ⎝⎛⎭⎪⎫πx 2+π68.函数f (x )=3sin π2x -log 12x 的零点的个数是________.【答案】5【解析】函数y =3sin π2x 的周期T =2ππ2=4,由log 12x =3,可得x =18.由log 12x =-3,可得x =8.在同一平面直角坐标系中,作出函数y =3sin π2x 和y =log 12x 的图象(如图所示),易知有5个交点,故函数f (x )有5个零点.二、解答题9.已知函数f (x )=sin ωx +cos ⎝⎛⎭⎪⎫ωx +π6,其中x ∈R ,ω>0.(1)当ω=1时,求f ⎝ ⎛⎭⎪⎫π3的值;(2)当f (x )的最小正周期为π时,求f (x )在⎣⎢⎡⎦⎥⎤0,π4上取得最大值时x 的值.10.(2017·苏、锡、常、镇四市调研)已知函数f (x )=3sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,-π2≤φ<π2的图象关于直线x =π3对称,且图象上相邻最高点的距离为π.(1)求f ⎝ ⎛⎭⎪⎫π4的值; (2)将函数y =f (x )的图象向右平移π12个单位后,得到y =g (x )的图象,求g (x )的单调递减区间.解 (1)因为f (x )的图象上相邻最高点的距离为π,所以f (x )的最小正周期T =π,从而ω=2πT=2.又f (x )的图象关于直线x =π3对称,所以2×π3+φ=k π+π2(k ∈Z ),因为-π2≤φ<π2,所以k =0, 所以φ=π2-2π3=-π6,所以f (x )=3sin ⎝ ⎛⎭⎪⎫2x -π6,则f ⎝ ⎛⎭⎪⎫π4=3sin ⎝ ⎛⎭⎪⎫2×π4-π6=3sin π3=32.(2)将f (x )的图象向右平移π12个单位后,得到f ⎝⎛⎭⎪⎫x -π12的图象,所以g (x )=f ⎝ ⎛⎭⎪⎫x -π12=3sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x -π12-π6=3sin ⎝⎛⎭⎪⎫2x -π3. 当2k π+π2≤2x -π3≤2k π+3π2(k ∈Z ),即k π+5π12≤x ≤k π+11π12(k ∈Z )时,g (x )单调递减.因此g (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π+5π12,k π+11π12(k ∈Z ).【能力提升】11.(2017·南京模拟)设函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6,给出下列结论:①f (x )的图象关于直线x =π3对称;②f (x )的图象关于点⎝⎛⎭⎪⎫π6,0对称;③f (x )的最小正周期为π,且在⎣⎢⎡⎦⎥⎤0,π12上为增函数;④把f (x )的图象向右平移π12个单位,得到一个偶函数的图象.其中正确的是________(填序号). 【答案】③12.(2017·泰州一模)已知函数f (x )=2sin ωx 在区间⎣⎢⎡⎦⎥⎤-π3,π4上的最小值为-2,则ω的取值范围是________.【答案】(-∞,-2]∪⎣⎢⎡⎭⎪⎫32,+∞ 【解析】当ω>0时,-π3ω≤ωx ≤π4ω,由题意知-π3ω≤-π2,即ω≥32;当ω<0时,π4ω≤ωx ≤-π3ω,由题意知π4ω≤-π2,∴ω≤-2.综上可知,ω的取值范围是(-∞,-2]∪⎣⎢⎡⎭⎪⎫32,+∞.13.(2015·湖南卷)已知ω>0,在函数y =2sin ωx 与y =2cos ωx 的图象的交点中,距离最短的两个交点的距离为23,则ω=________. 【答案】π214.(2017·扬州中学质检)如图,函数y =2cos(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,0≤φ≤π2的部分图象与y 轴交于点(0,3),最小正周期是π.(1)求ω,φ的值;(2)已知点A ⎝ ⎛⎭⎪⎫π2,0,点P 是该函数图象上一点,点Q (x 0,y 0)是PA 的中点,当y 0=32,x 0∈⎣⎢⎡⎦⎥⎤π2,π时,求x 0的值.解 (1)将点(0,3)代入y =2cos(ωx +φ), 得cos φ=32, ∵0≤φ≤π2,∴φ=π6.∵最小正周期T =π,且ω>0,∴ω=2πT=2.(2)由(1)知y =2cos ⎝⎛⎭⎪⎫2x +π6.∵A ⎝ ⎛⎭⎪⎫π2,0,Q (x 0,y 0)是PA 中点,y 0=32, ∴P ⎝ ⎛⎭⎪⎫2x 0-π2,3.。
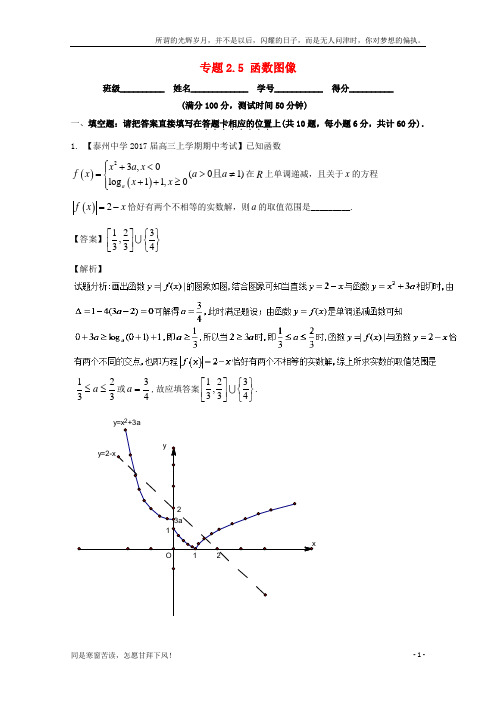
(新)江苏版2018年高考数学一轮复习专题2.5函数图像测
专题2.5 函数图像班级__________ 姓名_____________ 学号___________ 得分__________(满分100分,测试时间50分钟)一、填空题:请把答案直接填写在答题卡相应的位置........上(共10题,每小题6分,共计60分).1. 【泰州中学2017届高三上学期期中考试】已知函数()()23,0(01)log11,0ax a xf x a ax x⎧+<⎪=>≠⎨++≥⎪⎩且在R上单调递减,且关于x的方程()2f x x=-恰好有两个不相等的实数解,则a的取值范围是_________.【答案】123,334⎡⎤⎧⎫⎨⎬⎢⎥⎣⎦⎩⎭【解析】3231≤≤a或43=a,故应填答案123,334⎡⎤⎧⎫⎨⎬⎢⎥⎣⎦⎩⎭.3a2121y=2-x2Oyx2. 【泰州中学2017届高三上学期期中考试】定义在R上的函数()f x满足()()516f x f x++=,当()1,4x∈-时,xxxf2)(2-=,则函数()f x在[]0,2016上的零点个数是__________.【答案】605【解析】3. 【无锡市普通高中2017届高三上学期期中基础性检测】若函数2,0ln,0x a xyx a x x⎧-≤=⎨-+>⎩,在区间()2,2-上有两个零点,则实数a的取值范围为__________.【答案】[)0,2ln2+【解析】试题分析:由题设可知函数axy-=2与函数xaxy ln+-=在给定的区间]0,2(-和区间)2,0(内分别有一个根,结合图象可得⎪⎩⎪⎨⎧>+->-≤-2ln24aaa,即⎪⎩⎪⎨⎧+<<≥2ln24aaa,所以2ln20+<≤a,故应填答案[)0,2ln2+.4. 【泰州中学2016-2017年度第一学期第一次质量检测】设函数22,0,(),0,x x xf xx x⎧+<⎪=⎨-≥⎪⎩若(())2f f a≤,则实数a的取值范围是.【答案】2a≤【解析】试题分析:结合图像知(())2()22f f a f a a≤⇒≥-⇒≤5. 【泰州中学2016-2017年度第一学期第一次质量检测文科】定义在R上的奇函数()f x,当0x≥时,2,[0,1),()11|3|,[1,),xxf x xx x-⎧∈⎪=+⎨⎪--∈+∞⎩则函数1()()F x f xπ=-的所有零点之和为.【答案】112π-【解析】6.若函数y=f(x+3)的图象经过点P(1,4),则函数y=f(x)的图象必经过点________.【答案】(4,4)【解析】函数y=f(x)的图象是由y=f(x+3)的图象向右平移3个单位长度而得到的.故y=f(x)的图象经过点(4,4).7.一个体积为V的棱锥被平行于底面的平面所截,设截面上部的小棱锥的体积为y,截面下部的几何体的体积为x,则y与x的函数关系可以表示为________(填入正确图象的序号).【答案】③【解析】∵x+y=V,∴y=-x+V,∴由y =-x +V 的图象可知应为③.8.已知函数f (x )满足f (x +1)=-f (x ),且f (x )是偶函数,当x ∈[0,1]时,f (x )=x 2.若在区间[-1,3]内,函数g (x )=f (x )-kx -k 有4个零点,则实数k 的取值范围为________.【答案】⎝ ⎛⎦⎥⎤0,14.9.已知定义在区间[0,1]上的函数y =f (x )的图象如图所示.对满足0<x 1<x 2<1的任意x 1,x 2,给出下列结论:①f (x 1)-f (x 2)>x 1-x 2; ②f (x 1)-f (x 2)<x 1-x 2; ③x 2f (x 1)>x 1f (x 2); ④f x 1+f x 22<f (x 1+x 22).其中正确结论的序号是________. 【答案】③④ 【解析】10.函数y=11-x的图象与函数y=2sin πx(-2≤x≤4)的图象所有交点的横坐标之和等于________.【答案】8【解析】如上图,两个函数图象都关于点(1,0)成中心对称,两个图象在[-2,4]上共8个公共点,每两个对应交点横坐标之和为2,故所有交点的横坐标之和为8.二、解答题:解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指.定区域内....。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题 2.6 函数性质综合运用
班级__________ 姓名_____________ 学号___________ 得分__________
(满分100分,测试时间50分钟)
一、填空题:请把答案直接填写在答题卡相应的位置
........上(共10
题,每小题6分,共计60分). 1. 【苏北三市(连云港、徐州、宿迁)2017届高三年级第三次调研考试】如图,已知正方形
的边长为2,
平行于轴,顶点
,和
分别在函数
,
和
的图象上,则实数的值为__________.
【答案】
2. 【2016-2017学年度苏锡常镇四市高三教学情况调研(二)】已知函数
()24,0,
3
,0,x x x f x x x
⎧-≥⎪
=⎨<⎪⎩若函数()()3g x f x x b =-+有三个零点,则实数b 的取值范围
为 .
【答案】
3. 【南京市、盐城市2017届高三年级第一次模拟】在平面直角坐标系xOy 中,已知点P 为函数2ln y x =的图象与圆2
2
2
:(3)M x y r -+=的公共点,且它们在点P 处有公切线,若二次函数()y f x =的图象经过点,,O P M ,则()y f x =的最大值为 ▲ . 【答案】
98
【解析】设00(,)P x y ,则由2y x '=得00
000
0022111(3)32PM y k y x x x x x ⋅=-⇒⋅=-⇒=---,而二次函数1(3)2y x x =-
-正好过,,O P M 三点,所以19
()(3)28
f x x x =--≤
4.
【镇江市2017届高三年级第一次模拟】已知函数1221+=+x x y 与函数x
x y 1
+=的图象共有
k (*∈N k )个公共点:),(111y x A , ),(222y x A ,… ,),(k k k y x A ,则
=+∑=k
i i i
y x
1
)( .
【答案】2
【解析】函数1
221
+=+x x y 与函数x x y 1+=的图象都关于)1,0(对称,共有2个公共点:所以
220)(1
=+=+∑=k
i i
i
y x
5. 【2017年第三次全国大联考江苏卷】已知()1980,()ln
()x
f x ax
g x a a
=-=∈R ,若在*x ∈N 上恒有()()0f x g x ≥,则实数a 的取值范围是_____________.
【答案】[44,45]
6.已知幂函数f(x)=x 2+m 是定义在区间[-1,m]上的奇函数,则f(m+1)=__________. 【答案】8.
【解析】因为幂函数在[-1,m]上是奇函数, 所以m=1,所以f(x)=x 2+m =x 3, 所以f(m+1)=f(1+1)=f(2)=23=8. 7.已知函数f(x)=x 2+,g(x)=-m.若∀x 1∈ [1,2],∃x 2∈[-1,1]使f(x 1)≥g(x 2),则实数m
的取值范围是__________. 【答案】
【解析】要使∀x 1∈[1,2],∃x 2∈[-1,1],
8. f(x)是定义在R上的偶函数,当x<0时,有f(x)+xf′(x)<0,且f(-4)=0,则不等式xf(x)>0的解集为________.
【答案】(-∞,-4)∪(0,4)
【解析】因为[xf(x)]′=f(x)+xf′(x),根据已知条件可知,x<0时,
[xf(x)]′<0,所以F(x)=xf(x)在(-∞,0)上递减,又因为f(x)是R上的偶函数,所以F(x)是R 上的奇函数,则F(x)在(0,+∞)上递减,因为f(-4)=0,f(x)为R上的偶函数,所以f(4)=0,则F(-4)=F(4)=0,
综合图象可知xf(x)>0的解集应为(-∞,-4)∪(0,4).
9已知符号函数sgn(x)=则函数f(x)=sgn(lnx)-lnx的零点个数为________.
【答案】3
【解析】依题意得f(x)=sgn(lnx)-lnx=令f(x)=0,得x=e,1,,所以函数有3个零点.
10.已知f(x)为R上的可导函数,且∀x∈R,均有f(x)>f′(x),则f(2014)与e2014f(0)大小关系为________.
【答案】f(2014)<e2014f(0)
【解析】构造函数g(x)=,
则g′(x)==.
因为∀x∈R,均有f(x)>f′(x),并且e x>0,
所以g′(x)<0,故函数g(x)=在R上单调递减,
所以g(2014)<g(0),
即<f(0),
也就是f(2014)<e2014f(0)
二、解答题:解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的
指定区域内
.....。
(共4题,每小题10分,共计40分).
11.设函数f(x)=log3(9x)·log3(3x),≤x≤9.
(1)若m=log3x,求m的取值范围.
(2)求f(x)的最值,并给出最值时对应的x的值.
【答案】(1) [-2,2]. (2) x=时取最小值-,x=9时取最大值12.
12.已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x-+.
(1)求函数f(x)的最小值.
(2)对于∀x1,x2∈[0,2],f(x1)>g(x2)恒成立,求实数a的取值范围.
【答案】(1) f(x)min= (2) (-∞,-5)∪(1,+∞).
【解析】(1)函数f(x)的对称轴是x=a,
当a≤1时,f(x)min=f(2)=a2+4a-3,
当a>1时,f(x)min=f(0)=1+a2,
所以f(x)min=
(2)令=t(t∈[0,]),则x=2-t2,
所以g (x)=h(t)=-t2+t+,
因为对称轴t=∈,所以g(x)max=h(t)max=2,
由题意,要使对于∀x1,x2∈[0,2],f(x1)>g(x2)恒成立,只要f(x)min>g(x)max即可,
所以当a≤1时,f(x)min=a2+4a-3>2,
解得:a<-5,
当a>1时,f(x)min=1+a2>2,解得:a>1,
综上所述,a∈(-∞,-5)∪(1,+∞).
13.设a∈[-2,0],已知函数f(x)=
(1)证明f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增.
(2)设曲线y=f(x)在点P i(x i,f(x i))(i=1,2,3)处的切线相互平行,且x1x2x3≠0,证明x1+x2+x3>-.
【答案】(1)详见解析, (2) 详见解析.
由3-(a+5)=g(x 2)<a,解得-<x 1<0,所以x 1+x 2+x 3>-+,设
t=,则a=,因为a∈,所以t∈,故
x 1+x 2+x 3>-t+=(t-1)2
-≥-,即x 1+x 2+x 3>-.
14. 【2016高考上海理数】已知a R ∈,函数21
()log ()f x a x
=+. (1)当5a =时,解不等式()0f x >;
(2)若关于x 的方程2()log [(4)25]0f x a x a --+-=的解集中恰好有一个元素,求a 的取值范围;
(3)设0a >,若对任意1
[,1]2
t ∈,函数()f x 在区间[,1]t t +上的最大值与最小值的差不超过1,求a 的取值范围. 【答案】(1)()1,0,4x ⎛⎫∈-∞-
+∞ ⎪⎝⎭
.
(2)(]{}1,23,4.(3)2,3⎡
⎫
+∞⎪⎢⎣⎭
.
(3)当120x x <<时,
1211
a a x x +>+,221211log log a a x x ⎛⎫⎛⎫+>+ ⎪ ⎪⎝⎭⎝⎭
,。
